Predictive QSAR Models for the Toxicity of Disinfection Byproducts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Toxicity Data
2.2. Molecular Structure Descriptors
2.3. Data Splits and Model Development
2.4. Model Validation
2.5. Applicability Domain
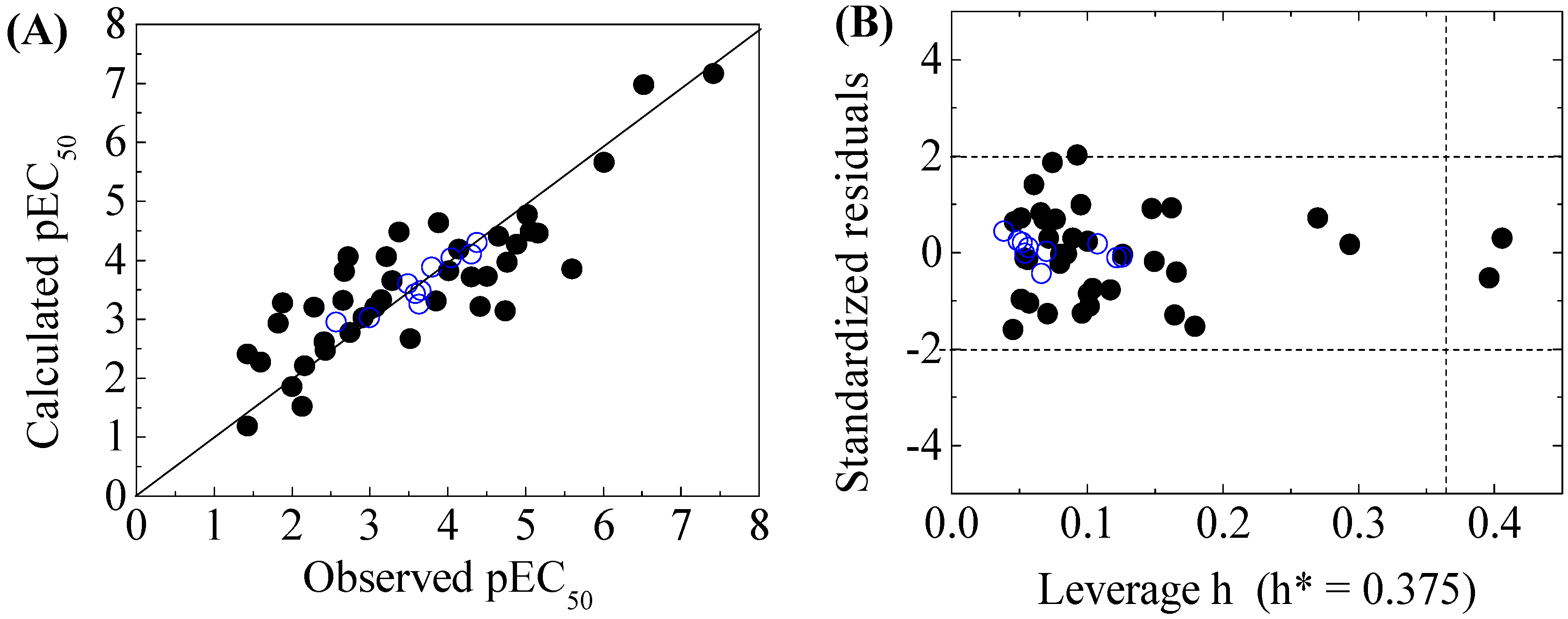
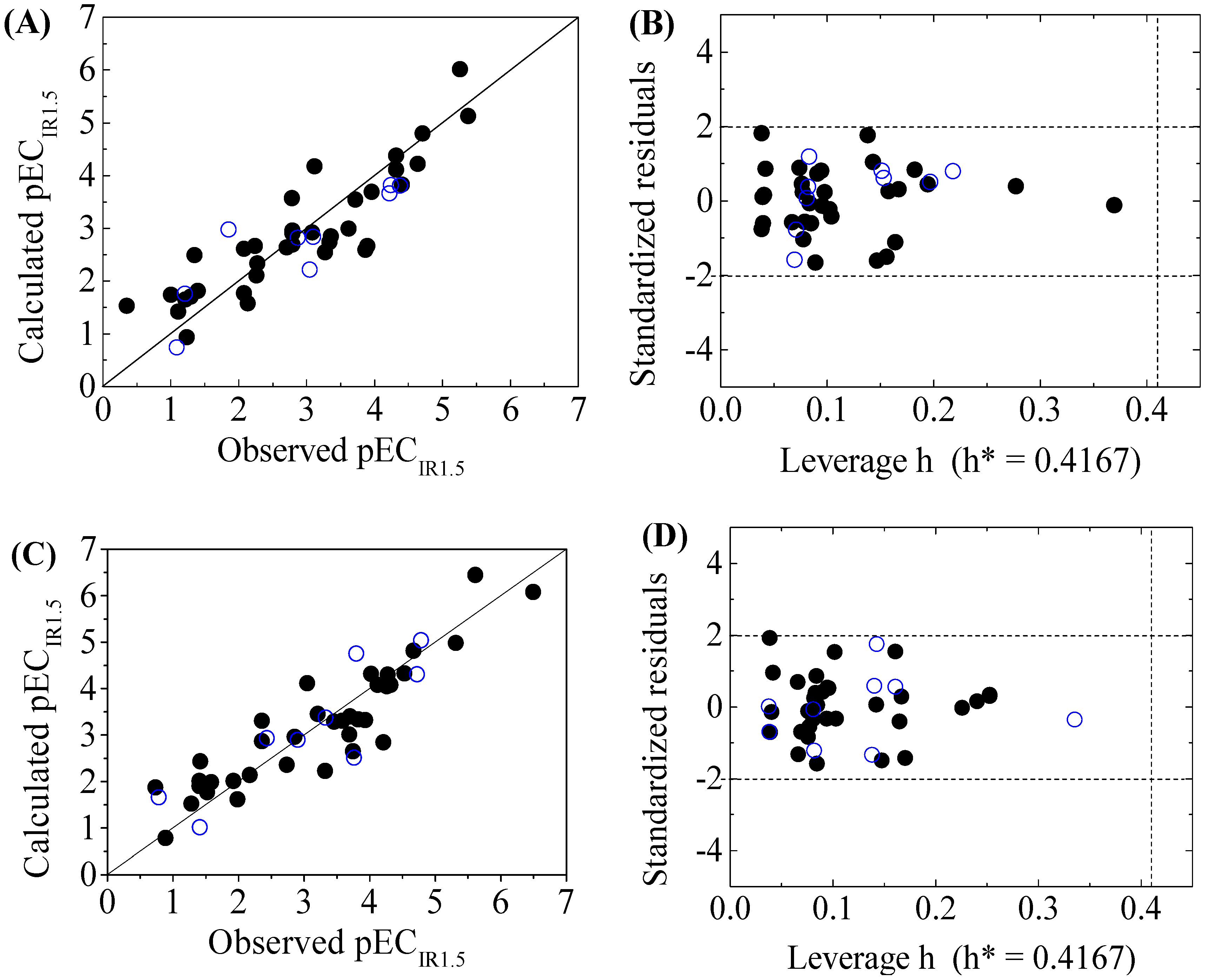
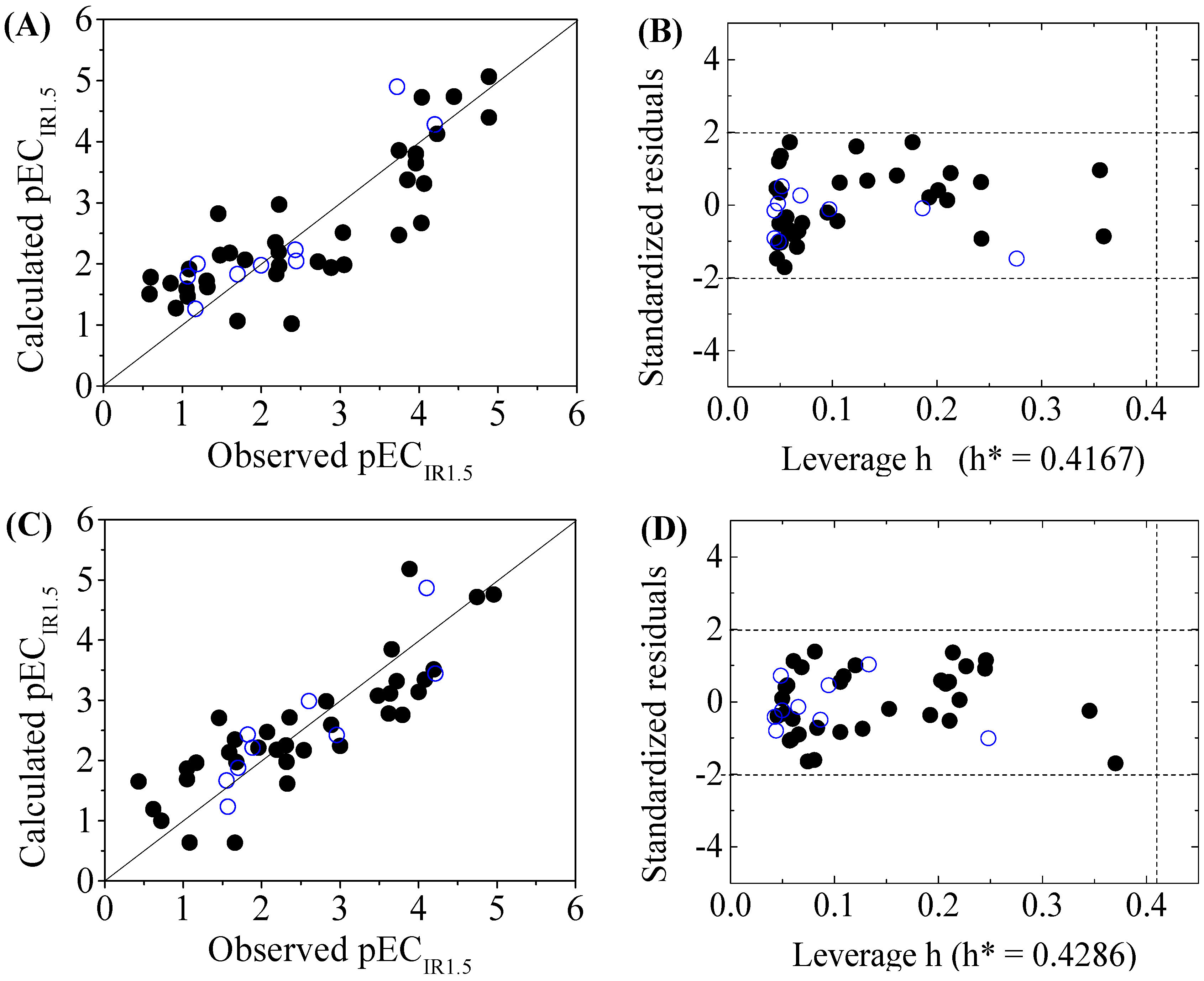
3. Results and Discussion
3.1. Selected Descriptors
3.2. Models Development and Validation
3.3. Domain of Applicability
3.4. Explanation of Descriptors
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rook, J.J. Formation of haloforms during chlorination of natural waters. Water Treat. Exam. 1974, 23, 234–243. [Google Scholar]
- Chen, B.; Zhang, T.; Bond, T.; Gan, Y. Development of quantitative structure activity relationship (QSAR) model for disinfection byproduct (DBP) research: A review of methods and resources. J. Hazard. Mater. 2015, 299, 260–279. [Google Scholar] [PubMed]
- Grellier, J.; Rushton, L.; Briggs, D.J.; Nieuwenhuijsen, M.J. Assessing the human health impacts of exposure to disinfection by-products—A critical review of concepts and methods. Environ. Int. 2015, 78, 61–81. [Google Scholar] [PubMed]
- Stalter, D.; O’Malley, E.; von Gunten, U.; Escher, B.I. Fingerprinting the reactive toxicity pathways of 50 drinking water disinfection by-products. Water Res. 2016, 91, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Hunter, E.S.; Rogers, E.; Blanton, M.; Richard, A.; Chernoff, N. Bromochloro-haloacetic acids: Effects on mouse embryos in vitro and QSAR considerations. Reprod. Toxicol. 2006, 21, 260–266. [Google Scholar] [PubMed]
- Perez-Garrido, A.; Gonzalez, M.P.; Escudero, A.G. Halogenated derivatives QSAR model using spectral moments to predict haloacetic acids (HAA) mutagenicity. Bioorg. Med. Chem. 2008, 16, 5720–5732. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.Z.; Wang, F. Quantitative structure activity relationship (QSAR) of chlorine effects on E-LUMO of disinfection by-product: Chlorinated alkanes. Chemosphere 2010, 78, 914–921. [Google Scholar] [CrossRef] [PubMed]
- Stalter, D.; Dutt, M.; Escher, B.I. Headspace-Free setup of in vitro bioassays for the evaluation of volatile disinfection by-products. Chem. Res. Toxicol. 2013, 26, 1605–1614. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.J.; Fan, R.L.; Zhang, L.F.; Yue, J.Q.; Webster, R.D.; Lim, T.T. Photodegradation of iodinated trihalomethanes in aqueous solution by UV 254 irradiation. Water Res. 2014, 49, 275–285. [Google Scholar] [PubMed]
- Yang, M.T.; Zhang, X.R. Comparative developmental toxicity of new aromatic halogenated DBPs in a chlorinated saline sewage effluent to the marine polychaete Platynereis dumerilii. Environ. Sci. Technol. 2013, 47, 10868–10876. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.M.; Fang, H.; Tong, W.; Wu, J.; Perkins, R.; Blair, R.M.; Branham, W.S.; Dial, S.L.; Moland, C.L.; Sheehan, D.M. QSAR models using a large diverse set of estrogens. J. Chem. Inf. Comput. Sci. 2001, 41, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Schüürmann, G.; Ebert, R.U.; Chen, J.W.; Wang, B.; Kuhne, R. External validation and prediction employing the predictive squared correlation coefficient - test set activity mean vs training set activity mean. J. Chem. Inf. Model. 2008, 48, 2140–2145. [Google Scholar] [CrossRef] [PubMed]
- Consonni, V.; Ballabio, D.; Todeschini, R. Evaluation of model predictive ability by external validation techniques. J. Chemom. 2010, 24, 194–201. [Google Scholar] [CrossRef]
- Chirico, N.; Gramatica, P. Real external predictivity of QSAR models. Part 2. New intercomparable thresholds for different validation criteria and the need for scatter plot inspection. J. Chem. Inf. Model. 2012, 52, 2044–2058. [Google Scholar] [CrossRef] [PubMed]
- Chirico, N.; Gramatica, P. Real external predictivity of QSAR models: How to evaluate it? comparison of different validation criteria and proposal of using the concordance correlation coefficient. J. Chem. Inf. Model. 2011, 51, 2320–2335. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Mitra, I.; Kar, S.; Ojha, P.K.; Das, R.N.; Kabir, H. Comparative studies on some metrics for external validation of QSPR models. J. Chem. Inf. Model. 2012, 52, 396–408. [Google Scholar] [CrossRef] [PubMed]
- Ojha, P.K.; Mitra, I.; Das, R.N.; Roy, K. Further exploring R2M metrics for validation of QSPR models. Chemom. Intell. Lab. Syst. 2011, 107, 194–205. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Mode.l 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Qin, L.T.; Liu, S.S.; Chen, F.; Wu, Q.S. Development of validated quantitative structure–retention relationship models for retention indices of plant essential oils. J. Sep. Sci. 2013, 36, 1553–1560. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.T.; Liu, S.S.; Chen, F.; Xiao, Q.F.; Wu, Q.S. Chemometric model for predicting retention indices of constituents of essential oils. Chemosphere 2013, 90, 300–305. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Benfenati, E.; Leszczynska, D.; Leszczynski, J. QSAR model as a random event: A case of rat toxicity. Bioorg. Med. Chem. 2015, 23, 1223–1230. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P.; Chirico, N.; Papa, E.; Cassani, S.; Kovarich, S. QSARINS: A new software for the development, analysis, and validation of QSAR MLR models. J. Comput. Chem. 2013, 34, 2121–2132. [Google Scholar] [CrossRef]
- Gramatica, P.; Cassani, S.; Chirico, N. QSARINS-chem: Insubria datasets and new QSAR/QSPR models for environmental pollutants in QSARINS. J. Comput. Chem. 2014, 35, 1036–1044. [Google Scholar] [CrossRef] [PubMed]
- Kiralj, R.; Ferreira, M.M.C. Is your QSAR/QSPR descriptor real or trash? J. Chemom. 2010, 24, 681–693. [Google Scholar] [CrossRef]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Organisation for Economic Co-operation and Development. Guidance Document on the Validation of (quanTitative) Structure-Activity Relationship [(Q)SAR] Models; ENV/JM/MONO: Paris, France, 2007; pp. 1–154. [Google Scholar]
Sample Availability: Not available. |
| Bioassay | Test Species (Strain/Cell Line) a | Endpoint | Detected Signal |
|---|---|---|---|
| Microtox | Aliivibrio fischeri | Cytotoxicity | Bioluminescence as indicator for cell viability |
| E. coli ± GSH | Escherichia coli MJF335 (GSH−) and MJF276 (GSH+) | Interaction with proteins/peptides | OD at 600 nm as indicator for cell density and descriptor of cell growth |
| E. coli ± DNA | Escherichia coli MV4108 (DNA−) and MV1161 (DNA+) | Interaction with DNA | OD at 600 nm as indicator for cell density and descriptor of cell growth |
| No. | Name | X-Microtox | GSH+ | GSH− | DNA+ | DNA− | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Observed pEC50 | Calculated pEC50 | Observed pECIR1.5 | Calculated pECIR1.5 | Observed pECIR1.5 | Calculated pECIR1.5 | Observed pECIR1.5 | Calculated pECIR1.5 | Observed pECIR1.5 | Calculated pECIR1.5 | ||
| Halomethanes | |||||||||||
| 1 | 1,1-dichloroethene | 3.1549 | 3.3214 | 1.3516 | 2.4847 | 1.4145 | 2.4357 | 1.0706 * | 1.7985 * | 0.4318 | 1.6512 |
| 2 | dichloromethane | 2.2840 | 3.1963 | 1.0888 * | 0.7391 * | 0.8861 | 0.7818 | 0.8539 | 1.6828 | 0.7212 | 0.9997 |
| 3 | bromochloromethane | 5.0706 | 4.4813 | 1.2182 | 1.6474 | 0.7328 | 1.8741 | 0.6021 | 1.7808 | - | - |
| 4 | chloroform | 2.4318 | 2.4675 | 1.2366 | 0.9330 | 1.4089 * | 1.0149 * | 1.1675 * | 1.2621 * | 1.0809 | 0.6385 |
| 5 | bromodichloromethane | 5.0269 | 4.7723 | 1.2111 * | 1.7614 * | 1.4034 | 1.9032 | 1.3188 | 1.6196 | 1.5686 * | 1.2324 * |
| 6 | bromoform | 3.6383 * | 3.2549 * | 1.0066 | 1.7407 | 1.5850 | 1.9863 | 1.0862 | 1.9166 | 1.1675 | 1.9629 |
| 7 | dibromochloromethane | 3.0000 * | 3.0193 * | 2.0809 | 1.7617 | 1.9208 | 2.0116 | 1.6990 * | 1.8321 * | 1.5528 * | 1.6647 * |
| 8 | dichloroiodomethane | 3.4949 * | 3.5960 * | 2.7959 | 2.9585 | 3.2076 | 3.4508 | 2.1938 | 1.8353 | 2.3279 | 1.6163 |
| 9 | bromochloroiodomethane | 1.6021 | 2.2717 | 2.7959 | 2.8967 | 3.3279 * | 3.3766 * | 2.2291 | 2.9723 | 2.3188 | 1.9777 |
| 10 | dibromoiodomethane | 4.0506 * | 4.0353 * | 2.8697 * | 2.8209 * | 3.4559 | 3.2854 | 2.0000 * | 1.9755 * | 1.9586 | 2.2126 |
| 11 | chlorodiiodomethane | 4.6576 | 4.4046 | 3.0809 | 2.9161 | 3.6990 | 3.3999 | 2.4437 * | 2.0457 * | 2.3098 | 2.2495 |
| 12 | bromodiiodomethane | 5.6021 | 3.8512 | 3.0969 * | 2.8369 * | 3.5850 | 3.3046 | 3.0506 | 1.9836 | 2.9586 * | 2.4210 * |
| 13 | triiodomethane | 2.4202 | 2.6149 | 3.3615 | 2.8486 | 3.9337 | 3.3188 | 2.8861 | 1.9398 | 2.8861 | 2.5894 |
| Halonitromethanes | |||||||||||
| 14 | trichloronitromethane | 4.3098 | 3.7132 | 4.6383 | 4.2152 | 5.3143 | 4.9812 | 4.2007 * | 4.2819 * | 4.0809 | 3.3428 |
| 15 | tribromonitromethane | 2.7447 | 2.7705 | 5.3820 | 5.1283 | 6.4949 | 6.0793 | 4.8861 | 5.0640 | 4.7447 | 4.7139 |
| Haloacetonitriles | |||||||||||
| 16 | dichloroacetonitrile | 4.5086 | 3.7184 | 3.2757 | 2.5481 | 3.7632 * | 2.5119 * | 3.0362 | 2.5123 | 2.8239 | 2.9808 |
| 17 | trichloroacetonitrile | 4.8861 | 4.2672 | 3.8979 | 2.6617 | 3.7447 | 2.6486 | 3.7447 | 3.8560 | 3.4815 | 3.0753 |
| 18 | bromochloroacetonitrile | 4.0132 | 3.8159 | 4.3188 | 4.1067 | 4.2757 | 4.2982 | 3.8539 | 3.3736 | 3.7212 | 3.3159 |
| 19 | dibromoacetonitrile | 4.7696 | 3.9655 | 4.7100 | 4.7981 | 4.7825 * | 5.0416 * | 4.2291 | 4.1282 | 4.1938 | 3.5113 |
| Haloketones | |||||||||||
| 20 | 1,1-dichloropropanone | 2.7212 | 4.0555 | 3.0506 * | 2.2187 * | 3.3188 | 2.2263 | 2.4318 * | 2.2303 * | 2.3565 | 2.7129 |
| 21 | 1,1,1-trichloropropanone | 3.6576 * | 3.4857 * | 2.2803 | 2.3311 | 2.7364 | 2.3615 | 2.3872 | 1.0225 | 3.0000 | 2.2423 |
| Haloacetic acids | |||||||||||
| 22 | chloroacetic acid | 6.0088 | 5.6592 | 2.1367 | 1.5737 | 1.9851 | 1.6179 | 1.6990 | 1.0652 | 1.6576 | 2.3448 |
| 23 | bromoacetic acid | 1.8861 | 3.2782 | 3.8697 | 2.5921 | 4.2111 | 2.8428 | 4.0655 | 3.3127 | 4.0000 | 3.1346 |
| 24 | iodoacetic acid | 2.6778 | 3.8068 | 4.3768 * | 3.8079 * | 4.7212 * | 4.305 * | 3.7447 | 2.4730 | 3.6576 | 3.8483 |
| 25 | dichloroacetic acid | 3.2147 | 4.0622 | 1.2967 | 1.6975 | 1.5229 | 1.7669 | 0.9208 | 1.2745 | 0.6198 | 1.1912 |
| 26 | bromochloroacetic acid | 5.1612 | 4.4508 | 2.0783 | 2.6122 | 2.3565 | 2.8669 | 1.1938 * | 1.9983 * | 1.6990 * | 1.8777 * |
| 27 | dibromoacetic acid | 4.1487 | 4.1865 | 2.2403 | 2.6637 | 2.4318 * | 2.9289 * | 1.6021 | 2.1776 | 1.8861 * | 2.2108 * |
| 28 | chloroiodoacetic acid | 1.8239 | 2.9267 | 4.4034 | 3.8242 | 4.5302 | 4.3246 | 4.0362 | 4.7239 | 4.1024 * | 4.8634 * |
| 29 | bromoiodoacetic acid | 3.7959 * | 3.8762 * | 4.2403 * | 3.8168 * | 4.0200 | 4.3157 | 3.7212 * | 4.8968 * | 3.8861 | 5.1786 |
| 30 | trichloroacetic acid | 3.2924 | 3.6489 | 1.4034 | 1.8108 | 1.4034 | 2.0112 | 1.0555 | 1.5905 | 1.0506 | 1.6881 |
| 31 | bromodichloroacetic acid | 1.4318 | 2.4029 | 2.7100 | 2.6367 | 2.9031 * | 2.8964 * | 1.7959 | 2.0658 | 1.6576 | 0.6340 |
| 32 | dibromochloroacetic acid | 3.5229 | 2.6718 | 2.7959 | 2.6882 | 2.8539 | 2.9584 | 1.4815 | 2.1417 | 1.4559 | 2.7074 |
| 33 | tribromoacetic acid | 4.4202 | 3.2073 | 3.3372 | 2.7322 | 3.6882 | 3.0113 | 2.1805 | 2.3490 | 2.6021 * | 2.9859 * |
| Haloacetaldehyde | |||||||||||
| 34 | chloral hydrate | 2.1675 | 2.2067 | 2.2636 | 2.1046 | 2.1707 | 2.1359 | 1.3098 | 1.7185 | 1.6778 | 1.9750 |
| Haloacetamides | |||||||||||
| 35 | dichloracetamide | 6.5229 | 6.9769 | 1.1135 | 1.4161 | 1.2798 | 1.5222 | 0.5850 | 1.5056 | 1.0506 | 1.6881 |
| 36 | bromochloroacetamide | 2.5686 * | 2.9516 * | 1.8539 * | 2.9712 * | 2.3565 | 3.3043 | 1.4559 | 2.8215 | 1.8239 * | 2.4295 * |
| 37 | dibromoacetamide | 3.0706 | 3.2043 | 4.2218 * | 3.6626 * | 4.2596 | 4.0477 | 3.9586 | 3.6467 | 3.6198 | 2.7807 |
| 38 | chloroiodoacetamide | 2.6576 | 3.3142 | 3.7212 | 3.5437 | 4.1192 | 4.0810 | 2.7212 | 2.0333 | 2.5376 | 2.1670 |
| 39 | bromoiodoacetamide | 3.3768 | 4.4729 | 3.1163 | 4.1762 | 3.7959 * | 4.7536 * | 2.2291 | 1.9651 | 2.0706 | 2.4718 |
| 40 | diiodoacetamide | 1.4318 | 1.1768 | 2.7825 | 3.5724 | 3.0482 | 4.1155 | 2.2218 | 2.1941 | 2.1938 | 2.1785 |
| 41 | trichloroacetamide | 2.0000 | 1.8559 | 0.3565 | 1.5288 | 0.7825 * | 1.6577 * | 1.0706 | 1.4651 | 1.5850 | 2.1329 |
| 42 | bromodichloroacetamide | 4.3098 * | 4.099 * | 3.6198 | 2.9951 | 3.8239 | 3.3331 | 4.0315 | 2.6693 | 3.7959 | 2.7569 |
| 43 | dibromochloroacetamide | 4.3768 * | 4.2953 * | 3.9566 | 3.6865 | 4.3188 | 4.0764 | 3.9586 | 3.8000 | 3.6383 | 3.1107 |
| 44 | tribromoacetamide | 2.1308 | 1.5148 | 4.3233 | 4.3703 | 4.6676 | 4.8106 | 4.4437 | 4.7359 | 4.2147 * | 3.4421 * |
| Nitrosamines | |||||||||||
| 45 | n-nitrosodimethylamine | 2.9208 | 3.0246 | - | - | - | - | - | - | - | - |
| 46 | n-nitrosodiethylamine | 7.4202 | 7.1686 | - | - | - | - | - | - | - | - |
| 47 | n-nitrosopiperidine | 3.8861 | 4.6292 | - | - | - | - | - | - | - | - |
| 48 | n-nitrosomorpholine | 3.8539 | 3.3096 | - | - | - | - | - | - | - | - |
| 49 | nitrosodi-n-butylamine | 3.5850 * | 3.4285 * | - | - | - | - | - | - | - | - |
| Furanone | |||||||||||
| 50 | 3-chloro-4-(dichloromethyl)-5- | 4.7447 | 3.1323 | 5.2596 | 6.0139 | 5.6108 | 6.4454 | 4.8861 | 4.3949 | 4.9586 | 4.7578 |
| Endpoint | Equation a | Modeling b | Internal Validation c | External Validation d | Golbraikh & Tropsha e |
|---|---|---|---|---|---|
| X-Microtox | pEC50 = −11.8502 + 0.1230 SpDiam_B(m) + 4.9744 AVS_B(v) + 0.8805 Eig05_AEA(dm) − 3.3986 SddsN | ntr = 40, R2 = 0.7152, = 0.6826, RMSEtr = 0.7682, F = 21.9717 | = 0.6374, RMSEcv = 0.8668, = 0.6216, = 0.1034, = −0.2452 | ntest = 10, RMSEext = 0.2040, = 0.8660, = 0.8508, = 0.8496, = 0.9799, CCC = 0.9115 = 0.7185, = 0.1439 | k = 1.0136, k’ = 0.9837, = 0.8018, = 0.8584 |
| GSH+ | pECIR1.5 = −2.4744 + 0.1022C% + 0.3184SpDiam_B(m) + 0.0725 P_VSA_LogP_8+ 0.2132 T(N..Br) | ntr = 36, R2 = 0.7837, = 0.7558, RMSEtr = 0.5927, F = 28.0843 | = 0.6956, RMSEcv = 0.7032, = 0.6644, = 0.1121, = −0.2323 | ntest = 9, RMSEext = 0.6010, = 0.7715, = 0.7502, = 0.7502, = 0.7776, CCC = 0.8500, = 0.6558, = 0.1915 | k = 1.0596, k’ = 0.9119, = 0.6964, = 0.7709 |
| GSH- | pECIR1.5 = −2.4133 + 0.0894 C% + 0.3829SpDiam_B(m) + 0.0835 P_VSA_LogP_8 + 0.2270 T(N..Br) | ntr = 36, R2 = 0.8166, = 0.7929, RMSEtr = 0.5936, F = 34.5096 | = 0.7332, RMSEcv = 0.7160, = 0.6634, = 0.1140, = −0.2349 | ntest = 9, RMSEext = 0.6578, = 0.7593, = 0.7436, = 0.7430, = 0.7748, CCC = 0.8703, = 0.6688, = 0.0426 | k = 0.9659, k’ = 0.9969, = 0.7376, = 0.7510 |
| DNA+ | pECIR1.5 = 1.8732 + 0.0493 P_VSA_LogP_7 − 0.2258 Mor04s + 0.2798 T(N..Br) − 0.8971 T(N..I) | ntr = 36, R2 = 0.7019, = 0.6635, RMSEtr = 0.7113, F = 18.2520 | = 0.6287, RMSEcv = 0.7940, = 0.6338, = 0.1139, = −0.2471 | ntest = 9, RMSEext = 0.5570, = 0.8232, = 0.7482, = 0.7228, = 0.8173, CCC = 0.8781, = 0.7541, = 0.0264 | k = 0.8805, k ’= 1.0974, = 0.8132, = 0.8186 |
| DNA- | pECIR1.5 = 0.9105 + 0.3091Sv + 0.0493 P_VSA_LogP_7 + 0.2008 Mor03s − 1.0911 T(N..I) | ntr = 36, R2 = 0.7164, = 0.6786, RMSEtr = 0.6540, F = 18.9496 | = 0.6221, RMSEcv = 0.7550, = 0.5291, = 0.1200, = −0.2504 | ntest = 9, RMSEext = 0.4991, = 0.7774, = 0.7505, = 0.7500, = 0.8348, CCC = 0.8787, = 0.6920, = 0.0076 | k = 0.9538, k’ = 1.0145, = 0.7643, = 0.7664 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Zhang, X.; Chen, Y.; Mo, L.; Zeng, H.; Liang, Y. Predictive QSAR Models for the Toxicity of Disinfection Byproducts. Molecules 2017, 22, 1671. https://doi.org/10.3390/molecules22101671
Qin L, Zhang X, Chen Y, Mo L, Zeng H, Liang Y. Predictive QSAR Models for the Toxicity of Disinfection Byproducts. Molecules. 2017; 22(10):1671. https://doi.org/10.3390/molecules22101671
Chicago/Turabian StyleQin, Litang, Xin Zhang, Yuhan Chen, Lingyun Mo, Honghu Zeng, and Yanpeng Liang. 2017. "Predictive QSAR Models for the Toxicity of Disinfection Byproducts" Molecules 22, no. 10: 1671. https://doi.org/10.3390/molecules22101671
APA StyleQin, L., Zhang, X., Chen, Y., Mo, L., Zeng, H., & Liang, Y. (2017). Predictive QSAR Models for the Toxicity of Disinfection Byproducts. Molecules, 22(10), 1671. https://doi.org/10.3390/molecules22101671






