Halogen Bonds Formed between Substituted Imidazoliums and N Bases of Varying N-Hybridization
Abstract
:1. Introduction
2. Systems and Methods
3. Results
3.1. Geometries and Energetics
3.2. Underlying Electronic Structure Patterns
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Grabowski, S.J. Hydrogen Bonding—New Insights; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Cybulski, S.; Scheiner, S. Hydrogen bonding and proton transfers involving triply bonded atoms. Acetylene and hydrocyanic acid. J. Am. Chem. Soc. 1987, 109, 4199–4206. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond; Oxford University Press: Oxford, UK, 2009; p. 313. [Google Scholar]
- Cuma, M.; Scheiner, S.; Kar, T. Effect of adjoining aromatic ring upon excited state proton transfer. O-hydroxybenzaldehyde. J. Mol. Struct. (Theochem) 1999, 467, 37–49. [Google Scholar] [CrossRef]
- Schuster, P. Hydrogen Bonds; Springer: Berlin, Germany, 1984; Volume 120, p. 117. [Google Scholar]
- Scheiner, S.; Wang, L. Hydrogen bonding and proton transfers of the amide group. J. Am. Chem. Soc. 1993, 115, 1958–1963. [Google Scholar] [CrossRef]
- Cybulski, S.M.; Scheiner, S. Hydrogen bonding and proton transfers involving the carboxylate group. J. Am. Chem. Soc. 1989, 111, 23–31. [Google Scholar] [CrossRef]
- Bartashevich, E.V.; Tsirelson, V.G. Interplay between non-covalent interactions in complexes and crystals with halogen bonds. Russ. Chem. Rev. 2014, 83, 1181–1203. [Google Scholar] [CrossRef]
- Tawfik, M.; Donald, K.J. Halogen bonding: Unifying perspectives on organic and inorganic cases. J. Phys. Chem. A 2014, 118, 10090–10100. [Google Scholar] [CrossRef] [PubMed]
- Shahi, A.; Arunan, E. Hydrogen bonding, halogen bonding and lithium bonding: An atoms in molecules and natural bond orbital perspective towards conservation of total bond order, inter- and intra-molecular bonding. Phys. Chem. Chem. Phys. 2014, 16, 22935–22952. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Nepal, B.; Scheiner, S. NX...Y halogen bonds. Comparison with NH...Y h-bonds and CX...Y halogen bonds. Phys. Chem. Chem. Phys. 2016, 18, 18015–18023. [Google Scholar] [CrossRef] [PubMed]
- Priimagi, A.; Cavallo, G.; Metrangolo, P.; Resnati, G. The halogen bond in the design of functional supramolecular materials: Recent advances. Acc. Chem. Res. 2013, 46, 2686–2695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riley, K.E.; Hobza, P. The relative roles of electrostatics and dispersion in the stabilization of halogen bonds. Phys. Chem. Chem. Phys. 2013, 15, 17742–17751. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Detailed comparison of the pnicogen bond with chalcogen, halogen and hydrogen bonds. Int. J. Quantum Chem. 2013, 113, 1609–1620. [Google Scholar] [CrossRef]
- Jungbauer, S.H.; Schindler, S.; Herdtweck, E.; Keller, S.; Huber, S.M. Multiple multidentate halogen bonding in solution, in the solid state, and in the (calculated) gas phase. Chem. Eur. J. 2015, 21, 13625–13636. [Google Scholar] [CrossRef] [PubMed]
- Caminati, W.; Evangelisti, L.; Feng, G.; Giuliano, B.M.; Gou, Q.; Melandri, S.; Grabow, J.-U. On the Cl...C halogen bond: A rotational study of CF3Cl-CO. Phys. Chem. Chem. Phys. 2016, 18, 17851–17855. [Google Scholar] [CrossRef] [PubMed]
- Anable, J.P.; Hird, D.E.; Stephens, S.L.; Zaleski, D.P.; Walker, N.R.; Legon, A.C. Characterisation of the weak halogen bond in N2...ICF3 by pure rotational spectroscopy. Chem. Phys. Lett. 2015, 625, 179–185. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Ciborowski, S.; Bowen, K. Stabilizing otherwise unstable anions with halogen bonding. Angew. Chem. Int. Ed. 2017, 56, 9897–9900. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Zheng, R.; Zhen, Y.; Yu, Z.; Dong, H.; Fu, H.; Shi, Q.; Hu, W. Rational design of charge-transfer interactions in halogen-bonded co-crystals toward versatile solid-state optoelectronics. J. Am. Chem. Soc. 2015, 137, 11038–11046. [Google Scholar] [CrossRef] [PubMed]
- Jungbauer, S.H.; Bulfield, D.; Kniep, F.; Lehmann, C.W.; Herdtweck, E.; Huber, S.M. Toward molecular recognition: Three-point halogen bonding in the solid state and in solution. J. Am. Chem. Soc. 2014, 136, 16740–16743. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen bonds in crystal engineering: Like hydrogen bonds yet different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef] [PubMed]
- Aakeröy, C.B.; Baldrighi, M.; Desper, J.; Metrangolo, P.; Resnati, G. Supramolecular hierarchy among halogen-bond donors. Chem. Eur. J. 2013, 19, 16240–16247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedin, M.; Karim, A.; Reitti, M.; Carlsson, A.-C.C.; Topic, F.; Cetina, M.; Pan, F.; Havel, V.; Al-Ameri, F.; Sindelar, V.; et al. Counterion influence on the n-i-n halogen bond. Chem. Sci. 2015, 6, 3746–3756. [Google Scholar] [CrossRef]
- Wang, R.; Dols, T.S.; Lehmann, C.W.; Englert, U. The halogen bond made visible: Experimental charge density of a very short intermolecular Cl...Cl donor–acceptor contact. Chem. Commun. 2012, 48, 6830–6832. [Google Scholar] [CrossRef] [PubMed]
- Erdelyi, M. Halogen bonding in solution. Chem. Soc. Rev. 2012, 41, 3547–3557. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Zhang, J.; Lei, L.; Kong, W. Self-assembly of iodine in superfluid helium droplets: Halogen bonds and nanocrystals. Angew. Chem. Int. Ed. 2017, 56, 3541–3545. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Li, J.; Yuan, Y.; Dong, M.; Zha, B.; Miao, X.; Hu, Y.; Deng, W. Halogen bonding versus hydrogen bonding induced 2D self-assembled nanostructures at the liquid-solid interface revealed by stm. Phys. Chem. Chem. Phys. 2017, 19, 3143–3150. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.K.; Pandey, S.K.; Misra, N. (CH3Br...Nh3)@C60: The effect of nanoconfinement on halogen bonding. Chem. Phys. Lett. 2016, 662, 240–243. [Google Scholar] [CrossRef]
- Zheng, Q.-N.; Liu, X.-H.; Chen, T.; Yan, H.-J.; Cook, T.; Wang, D.; Stang, P.J.; Wan, L.-J. Formation of halogen bond-based 2D supramolecular assemblies by electric manipulation. J. Am. Chem. Soc. 2015, 137, 6128–6131. [Google Scholar] [CrossRef] [PubMed]
- Ochoa-Resendiz, D.; Batista-Romero, F.A.; Hernández-Lamoneda, R. Communication: Evidence of halogen bonds in clathrate cages. J. Chem. Phys. 2016, 145, 161104. [Google Scholar] [CrossRef] [PubMed]
- Swords, W.B.; Simon, S.J.C.; Parlane, F.G.L.; Dean, R.K.; Kellett, C.W.; Hu, K.; Meyer, G.J.; Berlinguette, C.P. Evidence for interfacial halogen bonding. Angew. Chem. Int. Ed. 2016, 55, 5956–5960. [Google Scholar] [CrossRef] [PubMed]
- Dumele, O.; Trapp, N.; Diederich, F. Halogen bonding molecular capsules. Angew. Chem. Int. Ed. 2015, 54, 12339–12344. [Google Scholar] [CrossRef] [PubMed]
- Danelius, E.; Andersson, H.; Jarvoll, P.; Lood, K.; Gräfenstein, J.; Erdélyi, M. Halogen bonding: A powerful tool for modulation of peptide conformation. Biochemistry 2017, 56, 3265–3272. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Yan, X.; He, W.; Li, X.; Li, Z.; Mo, Y.; Liu, M.; Jiang, Y.-B. C–I···π halogen bonding driven supramolecular helix of bilateral N-amidothioureas bearing β-turns. J. Am. Chem. Soc. 2017, 139, 6605–6610. [Google Scholar] [CrossRef] [PubMed]
- Lange, A.; Günther, M.; Büttner, F.M.; Zimmermann, M.O.; Heidrich, J.; Hennig, S.; Zahn, S.; Schall, C.; Sievers-Engler, A.; Ansideri, F.; et al. Targeting the gatekeeper met146 of c-jun N-terminal kinase 3 induces a bivalent halogen/chalcogen bond. J. Am. Chem. Soc. 2015, 137, 14640–14652. [Google Scholar] [CrossRef] [PubMed]
- Fanfrlík, J.; Ruiz, F.X.; Kadlčíková, A.; Řezáč, J.; Cousido-Siah, A.; Mitschler, A.; Haldar, S.; Lepšík, M.; Kolář, M.H.; Majer, P.; et al. The effect of halogen-to-hydrogen bond substitution on human aldose reductase inhibition. ACS Chem. Biol. 2015, 10, 1637–1642. [Google Scholar] [CrossRef] [PubMed]
- Bulfield, D.; Huber, S.M. Halogen bonding in organic synthesis and organocatalysis. Chem. Eur. J. 2016, 22, 14434–14450. [Google Scholar] [CrossRef] [PubMed]
- Kee, C.W.; Wong, M.W. In silico design of halogen-bonding-based organocatalyst for diels–alder reaction, claisen rearrangement, and cope-type hydroamination. J. Org. Chem. 2016, 81, 7459–7470. [Google Scholar] [CrossRef] [PubMed]
- Jungbauer, S.H.; Huber, S.M. Cationic multidentate halogen-bond donors in halide abstraction organocatalysis: Catalyst optimization by preorganization. J. Am. Chem. Soc. 2015, 137, 12110–12120. [Google Scholar] [CrossRef] [PubMed]
- Massena, C.J.; Wageling, N.B.; Decato, D.A.; Martin Rodriguez, E.; Rose, A.M.; Berryman, O.B. A halogen-bond-induced triple helicate encapsulates iodide. Angew. Chem. Int. Ed. 2016, 55, 12398–12402. [Google Scholar] [CrossRef] [PubMed]
- Simon, S.J.C.; Parlane, F.G.L.; Swords, W.B.; Kellett, C.W.; Du, C.; Lam, B.; Dean, R.K.; Hu, K.; Meyer, G.J.; Berlinguette, C.P. Halogen bonding promotes higher dye-sensitized solar cell photovoltages. J. Am. Chem. Soc. 2016, 138, 10406–10409. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Vazquez, M.; Umemura, C.; Miller, C.; Tran, K.-A. Exploring the (very flat) potential energy landscape of R−Br...π interactions with accurate ccsd(t) and sapt techniques. Chem. Eur. J. 2016, 22, 17690–17695. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Ford, C.L., Jr.; Demouchet, K. Comparison of hydrogen bonds, halogen bonds, Ch..Π interactions, and CX..Π interactions using high-level ab initio methods. Chem. Phys. Lett. 2015, 621, 165–170. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Uchimaru, T.; Wakisaka, A.; Ono, T. Magnitude and directionality of halogen bond of benzene with C6F5X, C6H5X, and CF3X (X = I, BR, CL, and F). J. Phys. Chem. A 2016, 120, 7020–7029. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Horatscheck, A.; Martos, V.; Bartetzko, M.; Uhrig, U.; Lentz, D.; Schmieder, P.; Nazaré, M. Direct experimental evidence for halogen–aryl π interactions in solution from molecular torsion balances. Angew. Chem. Int. Ed. 2017, 56, 6454–6458. [Google Scholar] [CrossRef] [PubMed]
- Forni, A.; Pieraccini, S.; Franchini, D.; Sironi, M. Assessment of dft functionals for qtaim topological analysis of halogen bonds with benzene. J. Phys. Chem. A 2016, 120, 9071–9080. [Google Scholar] [CrossRef] [PubMed]
- Lv, H.; Zhuo, H.-Y.; Li, Q.-Z.; Yang, X.; Li, W.-Z.; Cheng, J.-B. Halogen bonds with n-heterocyclic carbenes as halogen acceptors: A partially covalent character. Mol. Phys. 2014, 112, 3024–3032. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Alkorta, I.; Elguero, J. Complexes between dihydrogen and amine, phosphine, and arsine derivatives. Hydrogen bond versus pnictogen interaction. J. Phys. Chem. A 2013, 117, 3243–3251. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Kirina, Y.V.; Kukushkin, V.Y. Halogen bonding between metal centers and halocarbons. Chem. Commun. 2016, 52, 5565–5568. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, V.; Cremer, D. Transition from metal-ligand bonding to halogen bonding involving a metal as halogen acceptor a study of Cu, Ag, Au, Pt, and Hg complexes. Chem. Phys. Lett. 2017, 681, 56–63. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, N.; Tang, Y. Halogen bonding in the complexes of ch3i and ccl4 with oxygen-containing halogen-bond acceptors. J. Phys. Chem. A 2017, 121, 5045–5055. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J.; Sokalski, W.A. Are various σ-hole bonds steered by the same mechanisms? ChemPhysChem 2017, 18, 1569–1577. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, U.; Scheiner, S. Sensitivity of pnicogen, chalcogen, halogen and h-bonds to angular distortions. Chem. Phys. Lett. 2012, 532, 31–35. [Google Scholar] [CrossRef]
- Stone, A.J. Are halogen bonded structures electrostatically driven? J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Sensitivity of noncovalent bonds to intermolecular separation: Hydrogen, halogen, chalcogen, and pnicogen bonds. CrystEngComm 2013, 15, 3119–3124. [Google Scholar] [CrossRef]
- Nepal, B.; Scheiner, S. Long-range behavior of noncovalent bonds. Neutral and charged h-bonds, pnicogen, chalcogen, and halogen bonds. Chem. Phys. 2015, 456, 34–40. [Google Scholar] [CrossRef]
- Molina, P.; Zapata, F.; Caballero, A. Anion recognition strategies based on combined noncovalent interactions. Chem. Rev. 2017, 117, 9907–9972. [Google Scholar] [CrossRef] [PubMed]
- Sabater, P.; Zapata, F.; Caballero, A.; de la Visitación, N.; Alkorta, I.; Elguero, J.; Molina, P. Comparative study of charge-assisted hydrogen- and halogen-bonding capabilities in solution of two-armed imidazolium receptors toward oxoanions. J. Org. Chem. 2016, 81, 7448–7458. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.; Beer, P.D. Halogen bonding anion recognition. Chem. Commun. 2016, 52, 8645–8658. [Google Scholar] [CrossRef] [PubMed]
- Toure, M.; Charles, L.; Chendo, C.; Viel, S.; Chuzel, O.; Parrain, J.-L. Straightforward and controlled shape access to efficient macrocyclic imidazolylboronium anion receptors. Chem. Eur. J. 2016, 22, 8937–8942. [Google Scholar] [CrossRef] [PubMed]
- Langton, M.J.; Serpell, C.J.; Beer, P.D. Anion recognition in water: Recent advances from a supramolecular and macromolecular perspective. Angew. Chem. Int. Ed. 2016, 55, 1974–1987. [Google Scholar] [CrossRef] [PubMed]
- Nepal, B.; Scheiner, S. Building a better halide receptor: Optimum choice of spacer, binding unit, and halosubstitution. ChemPhysChem 2016, 17, 836–844. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Assembly of effective halide receptors from components. Comparing hydrogen, halogen, and tetrel bonds. J. Phys. Chem. A 2017, 121, 3606–3615. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, H.; Han, S. The chemical nature of the +C–HX– (X = Cl or Br) interaction in imidazolium halide ionic liquids. J. Chem. Phys. 2006, 124, 044504. [Google Scholar] [CrossRef] [PubMed]
- An, X.; Yang, X.; Xiao, B.; Cheng, J.; Li, Q. Comparison of hydrogen and halogen bonds between dimethyl sulfoxide and hypohalous acid: Competition and cooperativity. Mol. Phys. 2017, 115, 1614–1623. [Google Scholar] [CrossRef]
- Geboes, Y.; De Proft, F.; Herrebout, W.A. Effect of fluorination on the competition of halogen bonding and hydrogen bonding: Complexes of fluoroiodomethane with dimethyl ether and trimethylamine. J. Phys. Chem. A 2017, 121, 4180–4188. [Google Scholar] [CrossRef] [PubMed]
- Domagała, M.; Lutyńska, A.; Palusiak, M. Halogen bond versus hydrogen bond: The many-body interactions approach. Int. J. Quantum Chem. 2017, 117. [Google Scholar] [CrossRef]
- Del Bene, J.E.; Alkorta, I.; Elguero, J. Anionic complexes of F− and Cl− with substituted methanes: Hydrogen, halogen, and tetrel bonds. Chem. Phys. Lett. 2016, 655–656, 115–119. [Google Scholar] [CrossRef]
- Sutradhar, D.; Chandra, A.K.; Zeegers-Huyskens, T. Theoretical study of the interaction of fluorinated dimethyl ethers and the ClF and HF molecules. Comparison between halogen and hydrogen bonds. Int. J. Quantum Chem. 2016, 116, 670–680. [Google Scholar] [CrossRef]
- Hogan, S.W.L.; van Mourik, T. Competition between hydrogen and halogen bonding in halogenated 1-methyluracil: Water systems. J. Comput. Chem. 2016, 37, 763–770. [Google Scholar] [CrossRef] [PubMed]
- Robertson, C.C.; Wright, J.S.; Carrington, E.J.; Perutz, R.N.; Hunter, C.A.; Brammer, L. Hydrogen bonding vs. Halogen bonding: The solvent decides. Chem. Sci. 2017, 8, 5392–5398. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2009.
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis set exchange: A community database for computational sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zeng, Y.; Li, X.; Meng, L.; Zhang, X. The mutual influence between π-hole pnicogen bonds and σ-hole halogen bonds in complexes of po2cl and XCN/C6H6 (X = F, Cl, Br). Struct. Chem. 2016, 27, 1427–1437. [Google Scholar] [CrossRef]
- Spada, L.; Gou, Q.; Geboes, Y.; Herrebout, W.A.; Melandri, S.; Caminati, W. Rotational study of dimethyl ether–chlorotrifluoroethylene: Lone pair···π interaction links the two subunits. J. Phys. Chem. A 2016, 120, 4939–4943. [Google Scholar] [CrossRef] [PubMed]
- Nziko, V.d.P.N.; Scheiner, S. Comparison of p-hole tetrel bonding with s-hole halogen bonds in complexes of XCN (X = F, Cl, Br, I) and NH3. Phys. Chem. Chem. Phys. 2016, 18, 3581–3590. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Li, Q. Non-additivity of f substituent in enhancing the halogen bond in C6H5I...NCH. Comput. Theor. Chem. 2015, 1070, 21–26. [Google Scholar] [CrossRef]
- Li, W.; Zeng, Y.; Li, X.; Sun, Z.; Meng, L. The competition of y...O and x...N halogen bonds to enhance the group v σ-hole interaction in the ncy...O=ph3...Ncx and o=ph3...Ncx...Ncy (x, y=f, cl, and br) complexes. J. Comput. Chem. 2015, 36, 1349–1358. [Google Scholar] [CrossRef] [PubMed]
- Geboes, Y.; Proft, F.D.; Herrebout, W.A. Expanding lone pair···π interactions to nonaromatic systems and nitrogen bases: Complexes of C2F3X (X = F, CL, BR, I) and tma-d9. J. Phys. Chem. A 2015, 119, 5597–5606. [Google Scholar] [CrossRef] [PubMed]
- Lang, T.; Li, X.; Meng, L.; Zheng, S.; Zeng, Y. The cooperativity between the σ-hole and π-hole interactions in the clo···xono2/xono···nh3 (x = cl, br, i) complexes. Struct. Chem. 2015, 26, 213–221. [Google Scholar] [CrossRef]
- Scheiner, S. Highly selective halide receptors based on chalcogen, pnicogen, and tetrel bonds. Chem. Eur. J. 2016, 22, 18850–18858. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Intramolecular pnicogen interactions in phosphorus and arsenic analogues of proton sponges. Phys. Chem. Chem. Phys. 2014, 16, 15900–15909. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yao, L.; Lin, X. Theoretical study of (fh2x)n·y (x = p and as, n = 1–4, y = F−, Cl−, Br−, i−, No3− and So42−): The possibility of anion recognition based on pnicogen bonding. Comput. Theor. Chem. 2014, 1036, 44–50. [Google Scholar] [CrossRef]
- Scheiner, S. Systematic elucidation of factors that influence the strength of tetrel bonds. J. Phys. Chem. A 2017, 121, 5561–5568. [Google Scholar] [CrossRef] [PubMed]
- Hauchecorne, D.; Herrebout, W.A. Experimental characterization of c–x···y–c (x = br, i; y = f, cl) halogen–halogen bonds. J. Phys. Chem. A 2013, 117, 11548–11557. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Cheng, J.; Li, Q.; Li, W. Competition of hydrogen, halogen, and pnicogen bonds in the complexes of harf with xh2p (x = f, cl, and br). Spectrochim. Acta A 2013, 101, 172–177. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Levine, I.N. Physical Chemistry, 3rd ed.; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Zhurko, G.A. Chemcraft. Available online: www.chemcraftprog.com (accessed on 29 September 2017).
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Nbo 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules, a Quantum Theory; Clarendon Press: Oxford, UK, 1990; Volume 22, p. 438. [Google Scholar]
- Keith, T.A. Aimall, TK Version 17.01.25; Gristmill Software: Overland Park, KS, USA, 2013.
- Szalewicz, K.; Jeziorski, B. Symmetry-adapted perturbation theory of intermolecular interactions. In Molecular Interactions. From van der Waals to Strongly Bound Complexes; Scheiner, S., Ed.; Wiley: New York, NY, USA, 1997; pp. 3–43. [Google Scholar]
- Moszynski, R.; Wormer, P.E.S.; Jeziorski, B.; van der Avoird, A. Symmetry-adapted perturbation theory of nonadditive three-body interactions in van der waals molecules. I. General theory. J. Chem. Phys. 1995, 103, 8058–8074. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Schütz, M.; Celani, P.; Knizia, G.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. Molpro, version 2015.1; TTI GmbH: Stuttgart, Germany, 2006. Available online: http://www.molpro.net(accessed on 29 September 2017).
- Li, W.; Zeng, Y.; Li, X.; Sun, Z.; Meng, L. Insight into the pseudo p-hole interactions in the m3h6...(ncf)n (m = c, si, ge, sn, pb; n = 1, 2, 3) complexes. Phys. Chem. Chem. Phys. 2016, 18, 24672–24680. [Google Scholar] [CrossRef] [PubMed]
- Esrafili, M.D.; Mohammadian-Sabet, F.; Vessally, E. An ab initio study on the nature of σ-hole interactions in pnicogen-bonded complexes with carbene as an electron donor. Mol. Phys. 2016, 114, 2115–2122. [Google Scholar] [CrossRef]
- Duarte, D.J.R.; Sosa, G.L.; Peruchena, N.M.; Alkorta, I. Halogen bonding. The role of the polarizability of the electron-pair donor. Phys. Chem. Chem. Phys. 2016, 18, 7300–7309. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Elguero, J.; Del Bene, J.E. Exploring the px3:Nch and px3:Nh3 potential surfaces, with X = F, Cl, and Br. Chem. Phys. Lett. 2015, 641, 84–89. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Strength of the pnicogen bond in complexes involving group va elements N, P, and As. J. Phys. Chem. A 2015, 119, 1642–1656. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Comparison of halide receptors based on H, Halogen, Chalcogen, Pnicogen, and tetrel bonds. Faraday Discuss. Chem. Soc. 2017. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |
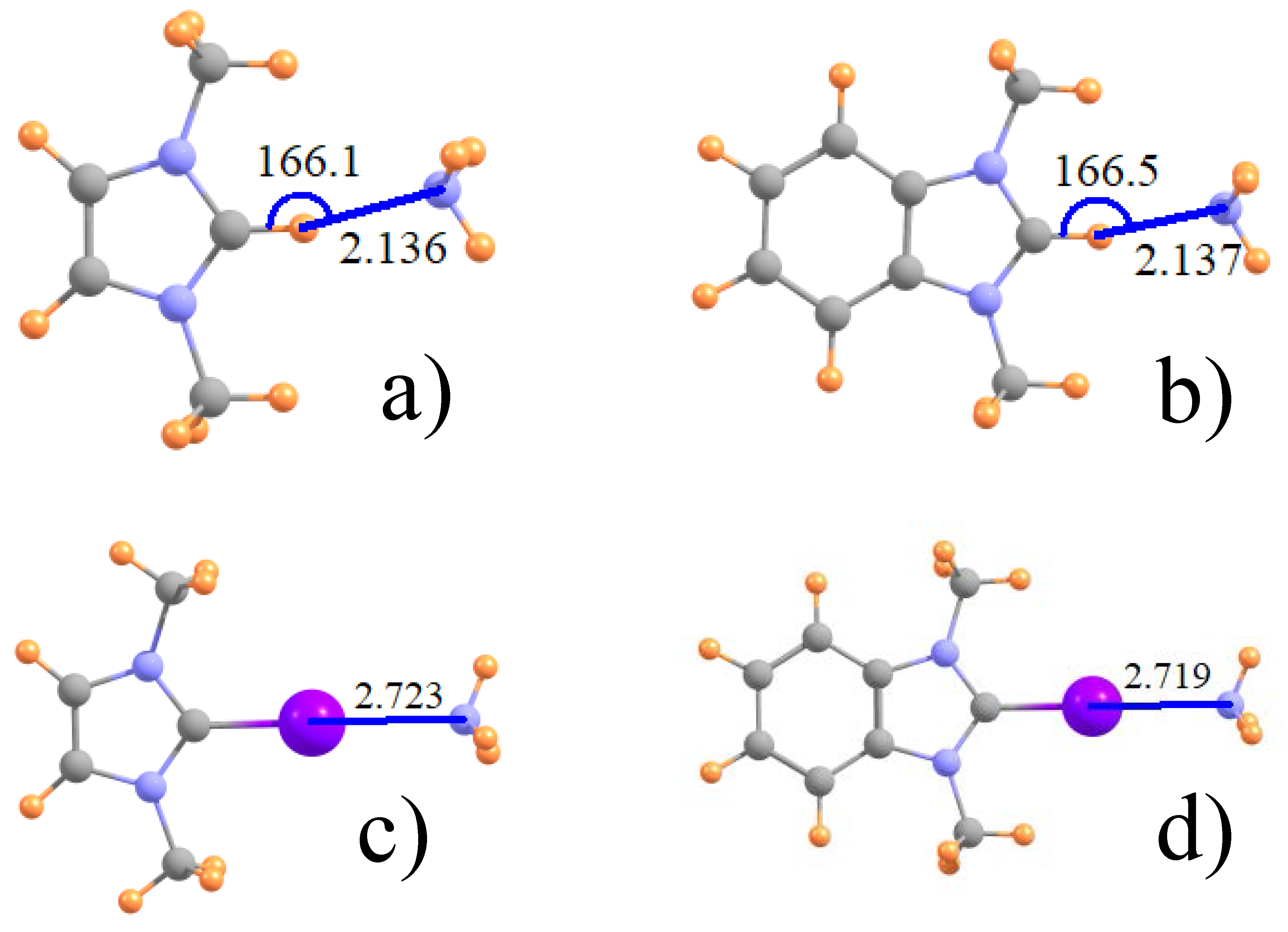


| Acid | Base | H | Cl | Br | I |
|---|---|---|---|---|---|
| ImZ+ | NH3 | 2.136 | 2.826 | 2.803 | 2.723 |
| PhImZ+ | NH3 | 2.137 | 2.829 | 2.806 | 2.719 |
| ImZ+ | NMe3 | 1.964 | 2.712 | 2.583 | 2.549 |
| ImZ+ | MeN=CHMe | 2.081 | 2.773 | 2.708 | 2.603 |
| PhImZ+ | MeN=CHMe | 2.087 | 2.774 | 2.712 | 2.595 |
| ImZ+ | N≡CMe | 2.178 | 2.820 | 2.833 | 2.806 |
| Acid | Base | H | Cl | Br | I |
|---|---|---|---|---|---|
| ImZ+ | NH3 | −11.07 | −8.42 | −10.71 | −15.13 |
| PhImZ+ | NH3 | −10.87 | −8.32 | −10.56 | −15.00 |
| ImZ+ | NMe3 | −13.36 | −9.13 | −12.81 | −19.60 |
| ImZ+ | MeN=CHMe | −13.36 | −9.57 | −12.34 | −17.97 |
| PhImZ+ | MeN=CHMe | −13.11 | −9.48 | −12.21 | −17.89 |
| ImZ+ | N≡CMe | −14.27 | −10.15 | −11.66 | −14.69 |
| Acid | Base | H | Cl | Br | I |
|---|---|---|---|---|---|
| ImZ+ | NH3 | −4.10 | −2.69 | −4.58 | −8.71 |
| PhImZ+ | NH3 | −4.52 | −2.94 | −4.91 | −9.33 |
| ImZ+ | NMe3 | −4.94 | −3.85 | −6.28 | −12.05 |
| ImZ+ | MeN=CHMe | −5.01 | −3.21 | −5.07 | −9.38 |
| PhImZ+ | MeN=CHMe | −5.54 | −3.42 | −5.45 | −10.13 |
| ImZ+ | N≡CMe | −3.51 | −2.26 | −3.28 | −5.35 |
| Acid | Base | H | Cl | Br | I |
|---|---|---|---|---|---|
| ImZ+ | NH3 | 4.83 | 5.34 | 4.21 | 1.10 |
| PhImZ+ | NH3 | 4.84 | 4.68 | 4.31 | 0.62 |
| ImZ+ | NMe3 | 6.08 | 5.59 | 4.69 | 0.09 |
| ImZ+ | MeN=CHMe | 5.59 | 6.30 | 5.55 | 2.34 |
| PhImZ+ | MeN=CHMe | 6.24 | 8.58 | 4.87 | 1.87 |
| ImZ+ | N≡CMe | 5.30 | 5.16 | 4.38 | 4.63 |
| Base | H | Cl | Br | I |
|---|---|---|---|---|
| NH3 | 0.0225 | 0.0180 | 0.0221 | 0.0314 |
| NMe3 | 0.0325 | 0.0243 | 0.0383 | 0.0487 |
| MeN=CHMe | 0.0242 | 0.0199 | 0.0271 | 0.0407 |
| N≡CMe | 0.0173 | 0.0156 | 0.0179 | 0.0229 |
| Lewis Acid | Vs,max | Lewis Base | Vs,min |
|---|---|---|---|
| ImH | 124.31 | NH3 | −38.02 |
| ImCl | 97.14 | NMe3 | −32.12 |
| ImBr | 100.35 | MeN=CHMe | −32.25 |
| ImI | 110.91 | N≡CMe | −38.09 |
| Base | H | Cl | Br | I |
|---|---|---|---|---|
| NH3 | 15.76 | 4.93 | 9.61 | 20.31 |
| NMe3 | 15.10 | 5.97 | 16.74 | 32.73 |
| MeN=CHMe | 12.64 | 4.69 | 11.04 | 26.78 |
| N≡CMe | 7.97 | 2.76 | 5.35 | 11.03 |
| Base | H | Cl | Br | I |
|---|---|---|---|---|
| NH3 | 0.015 | 0.006 | 0.016 | 0.048 |
| NMe3 | 0.025 | 0.013 | 0.042 | 0.088 |
| MeN=CHMe | 0.014 | 0.008 | 0.024 | 0.068 |
| N≡CMe | 0.004 | 0.000 | 0.005 | 0.022 |
| Base | H | Cl | Br | I |
|---|---|---|---|---|
| NH3 | −180.2 | −3.9 | −5.5 | −2.7 |
| NMe3 | −375.9 | −11.8 | −16.9 | −7.9 |
| MeN=CHMe | −169.4 | −7.7 | −6.7 | −7.8 |
| N≡CMe | −28.8 | +0.8 | −0.8 | −2.2 |
| Component | H | Cl | Br | I |
|---|---|---|---|---|
| ES | −14.70 | −12.53 | −16.98 | −28.33 |
| EXCH | 12.52 | 19.68 | 36.27 | 65.83 |
| IND | −5.25 | −10.92 | −24.02 | −60.36 |
| DISP | −3.48 | −3.33 | −4.27 | −6.35 |
| total | −10.92 | −7.11 | −9.00 | −29.21 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheiner, S. Halogen Bonds Formed between Substituted Imidazoliums and N Bases of Varying N-Hybridization. Molecules 2017, 22, 1634. https://doi.org/10.3390/molecules22101634
Scheiner S. Halogen Bonds Formed between Substituted Imidazoliums and N Bases of Varying N-Hybridization. Molecules. 2017; 22(10):1634. https://doi.org/10.3390/molecules22101634
Chicago/Turabian StyleScheiner, Steve. 2017. "Halogen Bonds Formed between Substituted Imidazoliums and N Bases of Varying N-Hybridization" Molecules 22, no. 10: 1634. https://doi.org/10.3390/molecules22101634





