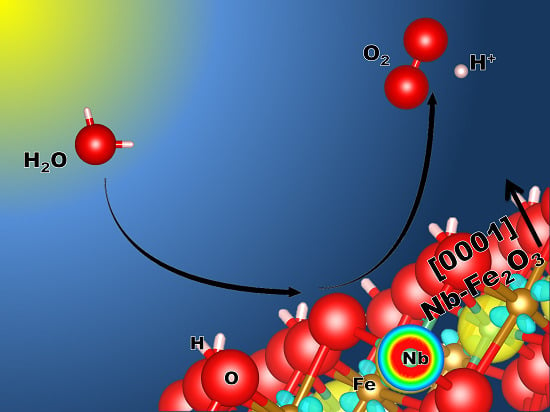
Hazardous Doping for Photo-Electrochemical Conversion: The Case of Nb-Doped Fe2O3 from First Principles
Abstract
:1. Introduction
2. Computational Details
- (1)
- (2)
- (3)
- (4)
- (5)
3. Results and Discussion
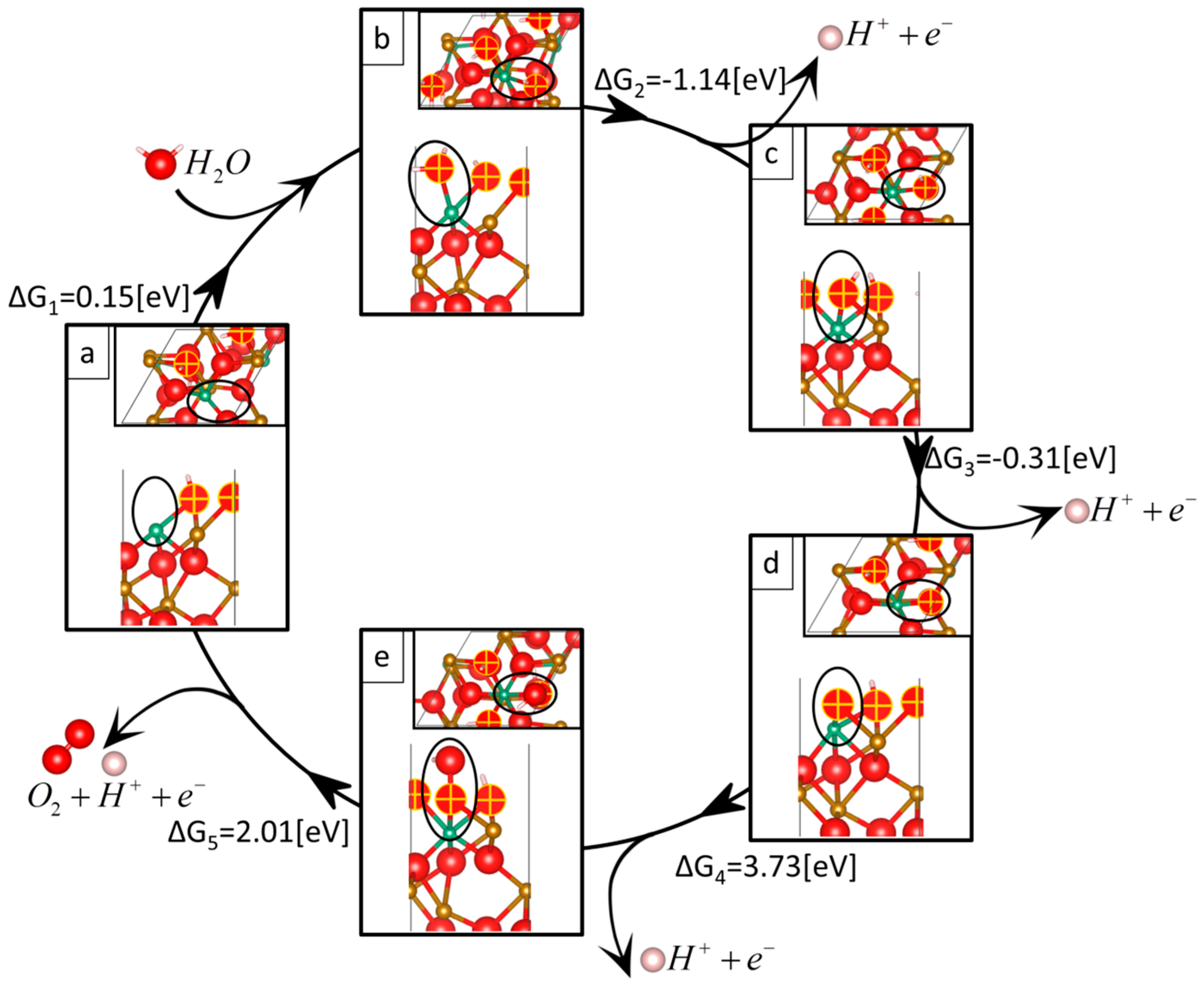
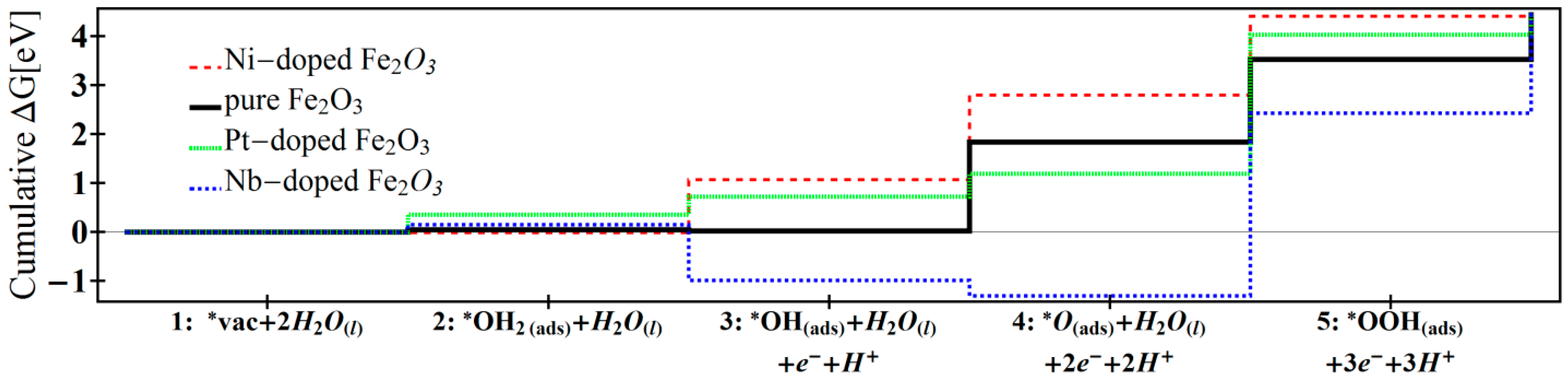
| Reaction 1 | Reaction 2 | Reaction 3 | Reaction 4 | Reaction 5 | Overpotential | |
|---|---|---|---|---|---|---|
| Ni-doped [12] | −0.01 | 1.08 | 1.73 | 1.61 | 0.03 | 0.62 |
| Pure [12] | 0.05 | −0.03 | 1.82 | 1.68 | 0.91 | 0.71 |
| Pt-doped [13] | 0.35 | 0.36 | 0.47 | 2.83 | 0.40 | 1.72 |
| Nb-doped | 0.15 | −1.14 | −0.31 | 3.73 | 2.01 | 2.62 |
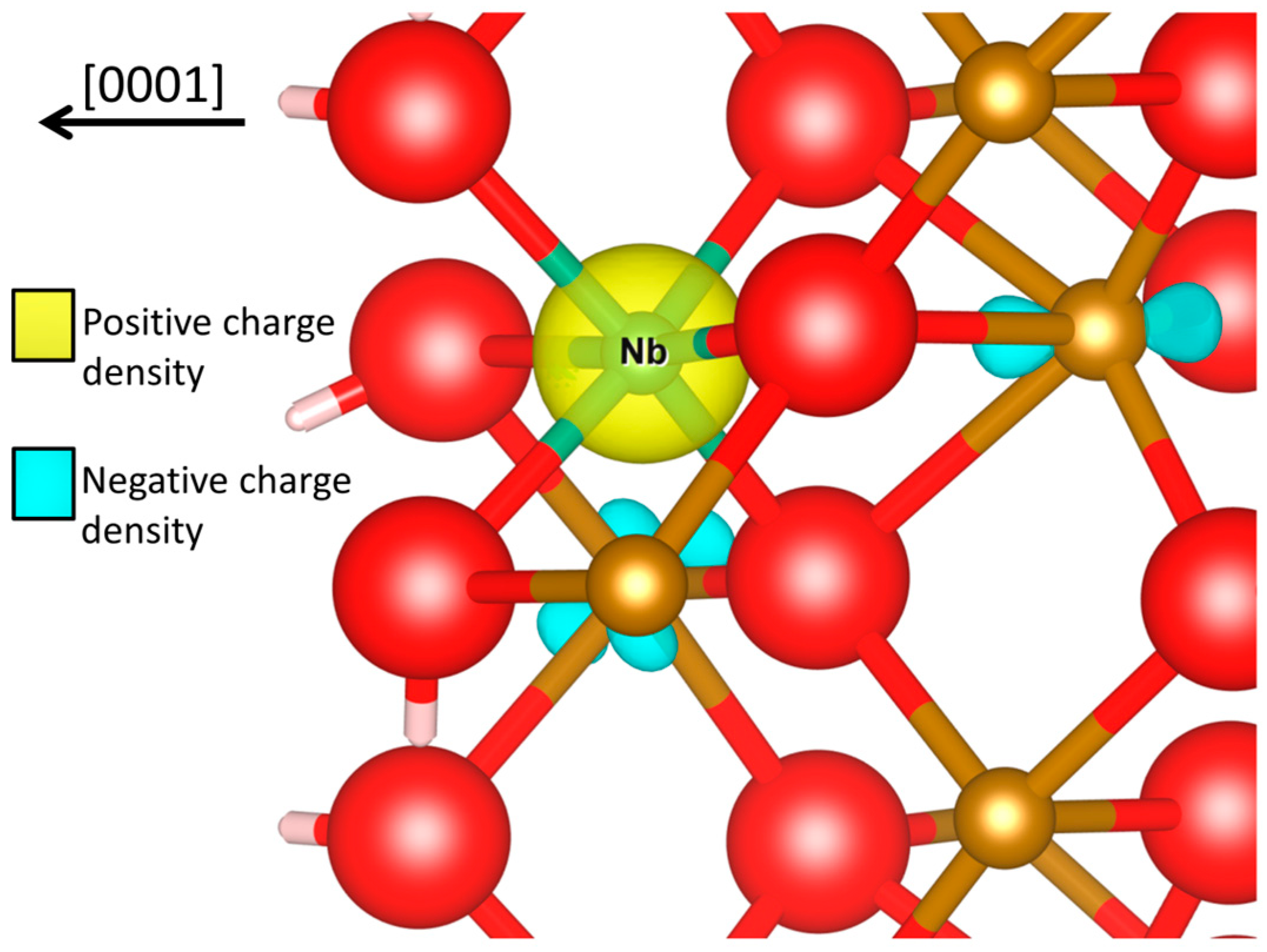
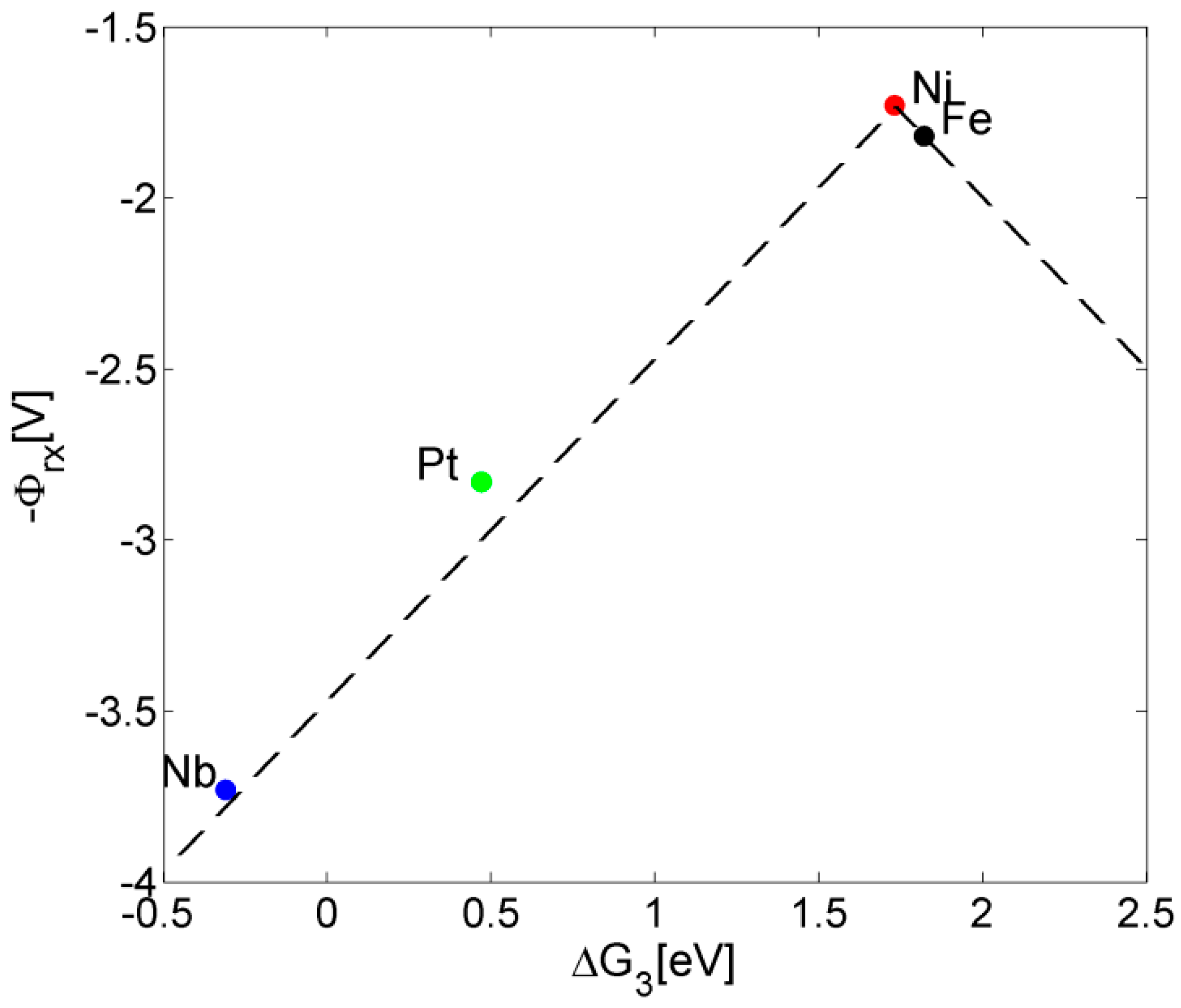
4. Conclusions
Supplementary Material
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kemppainen, E.; Halme, J.; Lund, P. Physical Modeling of Photoelectrochemical Hydrogen Production Devices. J. Phys. Chem. C 2015, 119, 21747–21766. [Google Scholar] [CrossRef]
- Zandi, O.; Hamann, T.W. The potential versus current state of water splitting with hematite. PCCP 2015, 17, 22485–22503. [Google Scholar] [CrossRef] [PubMed]
- Monllor-Satoca, D.; Bartsch, M.; Fabrega, C.; Genc, A.; Hilaire, S.; Andreu, T.; Arbiol, J.; Niederberger, M.; Morante, J.R. What Do you Do, Titanium? Insight into the Role of Titanium Oxide as Water Oxidation Promoter in Hematite-based Photoanodes. Energy Environ. Sci. 2015. [Google Scholar] [CrossRef]
- Wang, D.; Chen, H.; Chang, G.; Lin, X.; Zhang, Y.; Aldalbahi, A.; Peng, C.; Wang, J.; Fan, C. Uniform Doping of Titanium in Hematite Nanorods for Efficient Photoelectrochemical Water Splitting. ACS Appl. Mater. Interfaces 2015, 7, 14072–14078. [Google Scholar] [CrossRef] [PubMed]
- Abel, A.J.; Garcia-Torregrosa, I.; Patel, A.M.; Opasanont, B.; Baxter, J.B. SILAR-deposited Hematite Films for Photoelectrochemical Water Splitting: Effects of Sn, Ti, Thickness, and Nanostructuring. J. Phys. Chem. C 2015, 119, 4454–4465. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, G.; Ding, C.; Chen, Z.; Zhang, F.; Shi, J.; Li, C. Synergetic Effect of Conjugated Ni(OH)2/IrO2 Cocatalyst on Titanium-Doped Hematite Photoanode for Solar Water Splitting. J. Phys. Chem. C 2015, 119, 19607–19612. [Google Scholar] [CrossRef]
- Yang, T.-Y.; Kang, H.-Y.; Sim, U.; Lee, Y.-J.; Lee, J.-H.; Koo, B.; Nam, K.T.; Joo, Y.-C. A new hematite photoanode doping strategy for solar water splitting: Oxygen vacancy generation. PCCP 2013, 15, 2117–2124. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Han, S. Thermodynamics of native point defects in [small alpha]-Fe2O3: An ab initio study. PCCP 2013, 15, 18906–18914. [Google Scholar] [CrossRef] [PubMed]
- Kronawitter, C.X.; Zegkinoglou, I.; Shen, S.H.; Liao, P.; Cho, I.S.; Zandi, O.; Liu, Y.S.; Lashgari, K.; Westin, G.; Guo, J.H.; et al. Titanium incorporation into hematite photoelectrodes: Theoretical considerations and experimental observations. Energy Environ. Sci. 2014, 7, 3100–3121. [Google Scholar] [CrossRef]
- Chatman, S.; Pearce, C.I.; Rosso, K.M. Charge Transport at Ti-Doped Hematite (001)/Aqueous Interfaces. Chem. Mater. 2015, 27, 1665–1673. [Google Scholar] [CrossRef]
- Liao, P.; Toroker, M.C.; Carter, E.A. Electron Transport in Pure and Doped Hematite. Nano Lett. 2011, 11, 1775–1781. [Google Scholar] [CrossRef] [PubMed]
- Liao, P.; Keith, J.A.; Carter, E.A. Water oxidation on pure and doped hematite (0001) surfaces: Prediction of Co and Ni as effective dopants for electrocatalysis. J. Am. Chem. Soc. 2012, 134, 13296–13309. [Google Scholar] [CrossRef] [PubMed]
- Neufeld, O.; Toroker, M.C. Platinum-Doped α-Fe2O3 for Enhanced Water Splitting Efficiency: A DFT+U Study. J. Phys. Chem. C 2015, 119, 5836–5847. [Google Scholar] [CrossRef]
- Toroker, M.C. Theoretical Insights into the Mechanism of Water Oxidation on Nonstoichiometric and Titanium-Doped Fe2O3(0001). J. Phys. Chem. C 2014, 118, 23162–23167. [Google Scholar] [CrossRef]
- Aroutiounian, V.M.; Arakelyan, V.M.; Shahnazaryan, G.E.; Stepanyan, G.M.; Khachaturyan, E.A.; Wang, H.; Turner, J.A. Photoelectrochemistry of semiconductor electrodes made of solid solutions in the system Fe2O3–Nb2O5. Sol. Energy 2006, 80, 1098–1111. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Dudarev, S.; Botton, G.; Savrasov, S.; Humphreys, C.; Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Zhou, F.; Cococcioni, M.; Marianetti, C.A.; Morgan, D.; Ceder, G. First-principles prediction of redox potentials in transition-metal compounds with LDA+U. Phys. Rev. B 2004, 70, 235121. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Lichtenstein, A. First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA+U method. J. Phys. Condens. Matter 1997, 9, 767–808. [Google Scholar] [CrossRef]
- Rollmann, G.; Rohrbach, A.; Entel, P.; Hafner, J. First-principles calculation of the structure and magnetic phases of hematite. Phys. Rev. B 2004, 69, 1124–1133. [Google Scholar] [CrossRef]
- Mosey, N.J.; Liao, P.; Carter, E.A. Rotationally invariant ab initio evaluation of Coulomb and exchange parameters for DFT+U calculations. J. Chem. Phys. 2008, 129, 014103. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Lehmann, G.; Taut, M. On the numerical calculation of the density of states and related properties. Phys. Status Solidi b 1972, 54, 469–477. [Google Scholar] [CrossRef]
- Lad, R.J.; Henrich, V.E. Structure of α-Fe2O3 single crystal surfaces following Ar+ ion bombardment and annealing in O2. Surf. Sci. 1988, 193, 81–93. [Google Scholar] [CrossRef]
- Nguyen, M.-T.; Seriani, N.; Piccinin, S.; Gebauer, R. Photo-driven oxidation of water on α-Fe2O3 surfaces: An ab initio study. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sec. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Sanchez, C.; Hendewerk, M.; Sieber, K.D.; Somorjai, G.A. Synthesis, bulk, and surface characterization of niobium-doped Fe2O3 single crystals. J. Solid State Chem. 1986, 61, 47–55. [Google Scholar] [CrossRef]
- Turnock, A.C. Fe-Nb Oxides: Phase Relations at 1180 °C. J. Am. Ceram. Soc. 1966, 49, 177–180. [Google Scholar] [CrossRef]
- Rossmeisl, J.; Qu, Z.-W.; Zhu, H.; Kroes, G.-J.; Nørskov, J.K. Electrolysis of water on oxide surfaces. J. Electroanal. Chem. 2007, 607, 83–89. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Valdes, A.; Qu, Z.-W.; Kroes, G.-J.; Rossmeisl, J.; Nørskov, J.K. Oxidation and photo-oxidation of water on TiO2 surface. J. Phys. Chem. C 2008, 112, 9872–9879. [Google Scholar] [CrossRef]
- Man, I.C.; Su, H.Y.; Calle-Vallejo, F.; Hansen, H.A.; Martínez, J.I.; Inoglu, N.G.; Kitchin, J.; Jaramillo, T.F.; Nørskov, J.K.; Rossmeisl, J. Universality in oxygen evolution electrocatalysis on oxide surfaces. ChemCatChem 2011, 3, 1159–1165. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jonsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Sanchez, C.; Sieber, K.D.; Somorjai, G.A. The photoelectrochemistry of niobium doped α-Fe2O3. J. Electroanal. Chem. Interfacial Electrochem. 1988, 252, 269–290. [Google Scholar] [CrossRef]
- Aroutiounian, V.M.; Arakelyan, V.M.; Shahnazaryan, G.E.; Stepanyan, G.M.; Khachaturyan, E.A.; Turner, J.A. Investigations of the structure of the iron oxide semiconductor-electrolyte interface. C. R. Chim. 2006, 9, 325–331. [Google Scholar] [CrossRef]
- Sample Availability: Not apply.
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yatom, N.; Toroker, M.C. Hazardous Doping for Photo-Electrochemical Conversion: The Case of Nb-Doped Fe2O3 from First Principles. Molecules 2015, 20, 19900-19906. https://doi.org/10.3390/molecules201119668
Yatom N, Toroker MC. Hazardous Doping for Photo-Electrochemical Conversion: The Case of Nb-Doped Fe2O3 from First Principles. Molecules. 2015; 20(11):19900-19906. https://doi.org/10.3390/molecules201119668
Chicago/Turabian StyleYatom, Natav, and Maytal Caspary Toroker. 2015. "Hazardous Doping for Photo-Electrochemical Conversion: The Case of Nb-Doped Fe2O3 from First Principles" Molecules 20, no. 11: 19900-19906. https://doi.org/10.3390/molecules201119668
APA StyleYatom, N., & Toroker, M. C. (2015). Hazardous Doping for Photo-Electrochemical Conversion: The Case of Nb-Doped Fe2O3 from First Principles. Molecules, 20(11), 19900-19906. https://doi.org/10.3390/molecules201119668