Measuring Dynamic and Kinetic Information in the Previously Inaccessible Supra-tc Window of Nanoseconds to Microseconds by Solution NMR Spectroscopy
Abstract
:1. Introduction
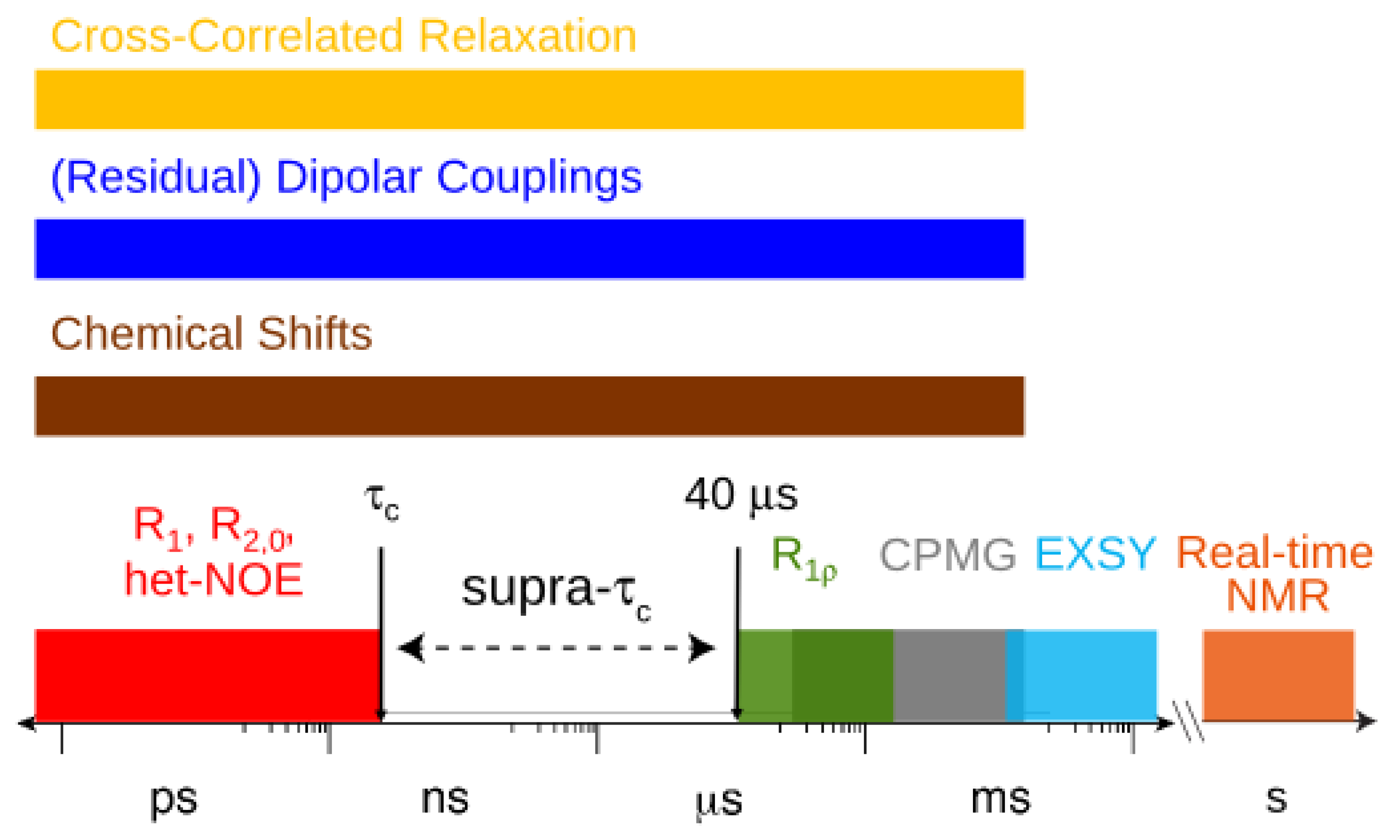
2. Dynamic Content of the Supra-τc Range
2.1. Introduction to Residual Dipolar Couplings
2.2. Alignment Tensor Determination
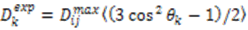

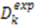 depends on
depends on 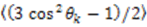 , which is ensemble averaged over the time-scale covered by the RDC measurement (denoted by the angular brackets). The time-averaged or ensemble averaged information covers up to the millisecond time-scale or roughly 1/D, spanning the supra-τc scale [30].
, which is ensemble averaged over the time-scale covered by the RDC measurement (denoted by the angular brackets). The time-averaged or ensemble averaged information covers up to the millisecond time-scale or roughly 1/D, spanning the supra-τc scale [30].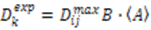

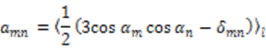
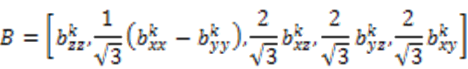
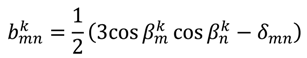
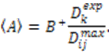
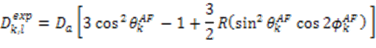
 , the rhombicity is
, the rhombicity is 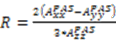 ,
, 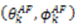 are the polar angles defining the inter-nuclear vector in the AF, and
are the polar angles defining the inter-nuclear vector in the AF, and 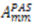 are the eigenvalues resulting from the diagonalization of 〈A(2)〉. From the eigenvectors (
are the eigenvalues resulting from the diagonalization of 〈A(2)〉. From the eigenvectors ( 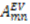 ), the Euler angles describing the rotation of 〈A〉 and B into the PAS are defined:
), the Euler angles describing the rotation of 〈A〉 and B into the PAS are defined:
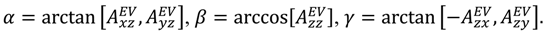
 is included in 〈A〉. The rows of B are defined by Equation (6) and the columns of A are given by Equation (4). As with the SVD approach to a single alignment media, the calculation of 〈A〉 for all alignment media at once requires a nonsingular B matrix:
is included in 〈A〉. The rows of B are defined by Equation (6) and the columns of A are given by Equation (4). As with the SVD approach to a single alignment media, the calculation of 〈A〉 for all alignment media at once requires a nonsingular B matrix:
2.3. Model Free Analysis and Direct Interpretation of Dipolar Couplings
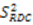 , which possesses dynamic information on the picosecond to millisecond time-scale, which includes the supra-τc range (Figure 1). Within the framework of ensemble averaging, Equations (11) and (12) become:
, which possesses dynamic information on the picosecond to millisecond time-scale, which includes the supra-τc range (Figure 1). Within the framework of ensemble averaging, Equations (11) and (12) become:
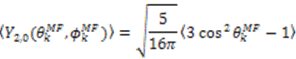
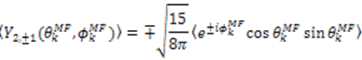
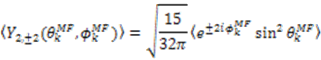
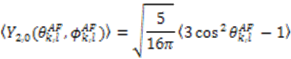
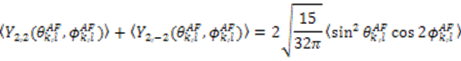
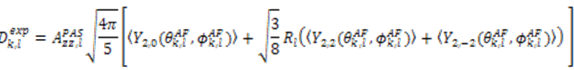
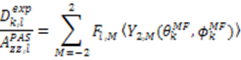
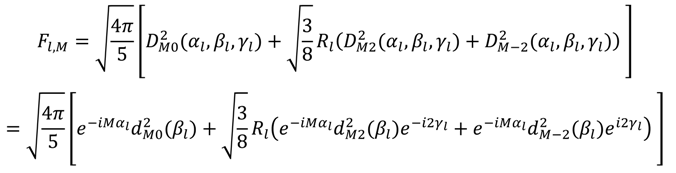
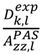 which results in the condition number being lower than in the unnormalized case. In other words, this normalization helps to even out the contributions of each RDC set to the calculation of 〈Y〉refined. Each row of 〈Y〉refined is used to determine
which results in the condition number being lower than in the unnormalized case. In other words, this normalization helps to even out the contributions of each RDC set to the calculation of 〈Y〉refined. Each row of 〈Y〉refined is used to determine 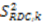 :
:
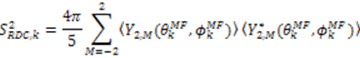
 , can be obtained. Maximizing
, can be obtained. Maximizing 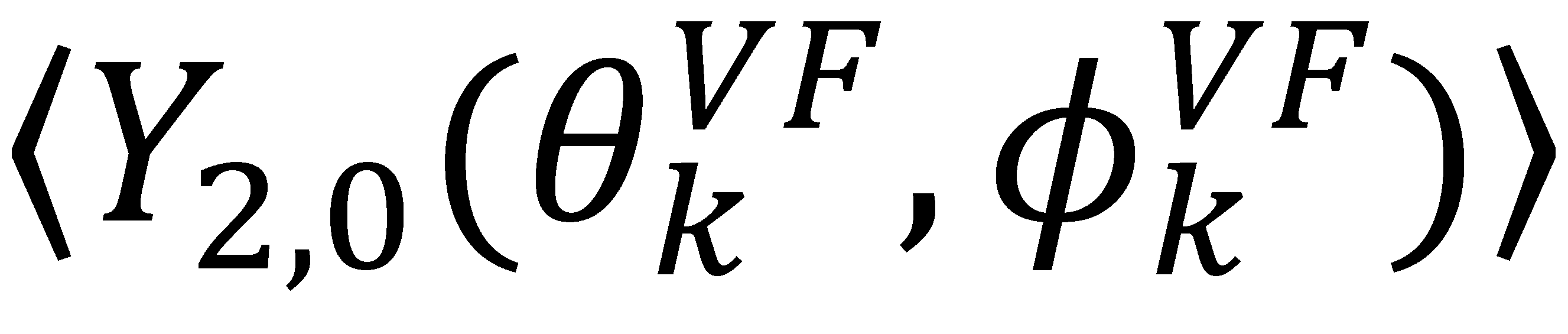 places the z-axis of the vector’s axis system, termed the vector frame (VF), in the center of the inter-nuclear vector’s orientational distribution:
places the z-axis of the vector’s axis system, termed the vector frame (VF), in the center of the inter-nuclear vector’s orientational distribution:

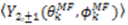 vanish in the VF and
vanish in the VF and 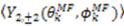 possesses information on the amplitude of anisotropy, ηk, and the orientation of anisotropic motions,
possesses information on the amplitude of anisotropy, ηk, and the orientation of anisotropic motions,  :
:

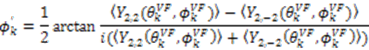
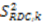 is the same in any frame, thus:
is the same in any frame, thus:
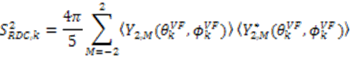
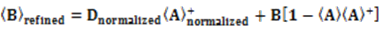
 .
. [34]:
[34]:
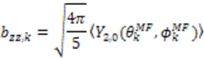
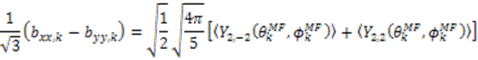
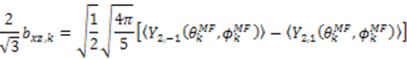
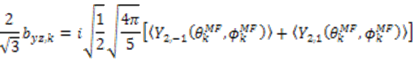
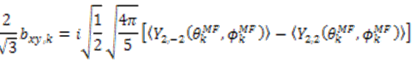
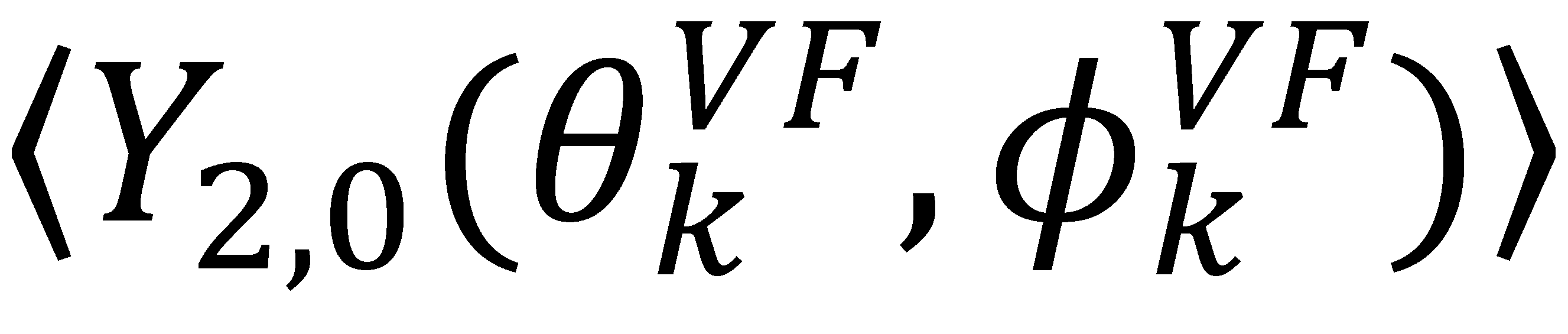 and defining each inter-nuclear vector in a unique principal axis system [103]. The resulting eigenvalues (
and defining each inter-nuclear vector in a unique principal axis system [103]. The resulting eigenvalues ( 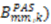 contain the dynamic information for each vector
contain the dynamic information for each vector 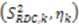 , while the eigenvectors,
, while the eigenvectors, 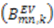 , encompass the bond orientations
, encompass the bond orientations 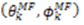 and the direction of the anisotropic local motion
and the direction of the anisotropic local motion 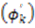 . The following equations detail how the dynamic parameters are calculated from
. The following equations detail how the dynamic parameters are calculated from  . The Saupe order parameters are defined as:
. The Saupe order parameters are defined as:
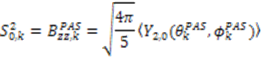
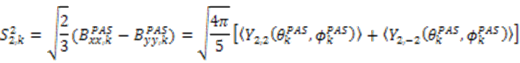
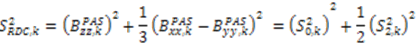
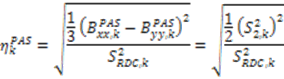
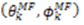 and
and 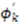 are extracted from the transpose of the resulting
are extracted from the transpose of the resulting  matrix:
matrix:
 or D a,l is not known, which will lead to
or D a,l is not known, which will lead to  values being only relative in nature to the true absolute value [27,72]. The other alignment tensor parameters {R, α, β, γ}l are unaffected by the reduction in the magnitude of D a,l. The correct scaling parameter, termed Soverall, is crucial for distinguishing sub- and supra-τc motion. All three iterative schemes have addressed this issue in different manners. In the iterative DIDC, order parameters are scaled relative to the largest
values being only relative in nature to the true absolute value [27,72]. The other alignment tensor parameters {R, α, β, γ}l are unaffected by the reduction in the magnitude of D a,l. The correct scaling parameter, termed Soverall, is crucial for distinguishing sub- and supra-τc motion. All three iterative schemes have addressed this issue in different manners. In the iterative DIDC, order parameters are scaled relative to the largest 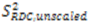 leaving one order parameter equal to one [68,104]. Sub- and supra-tc motion happening for each vector equally will not be detected by this approach, which will underestimate the motion. With the MFA/SCRM procedure,
leaving one order parameter equal to one [68,104]. Sub- and supra-tc motion happening for each vector equally will not be detected by this approach, which will underestimate the motion. With the MFA/SCRM procedure, 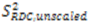 is scaled relative to the Lipari-Szabo order parameters (
is scaled relative to the Lipari-Szabo order parameters ( 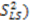 calculated for each residue [27,102], as long as
calculated for each residue [27,102], as long as 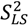 are available for the inter-nuclear vectors being analyzed. This approach as been successfully applied to ubiquitin, however, supra-tc motion affecting all nuclei equally will not be picked up by this method. Finally, ORIUM uses the inter-nuclear vector’s motional variance, which is directly related to the resulting eigenvalues calculated from diagonalization of
are available for the inter-nuclear vectors being analyzed. This approach as been successfully applied to ubiquitin, however, supra-tc motion affecting all nuclei equally will not be picked up by this method. Finally, ORIUM uses the inter-nuclear vector’s motional variance, which is directly related to the resulting eigenvalues calculated from diagonalization of  into a local axis system. By definition, variance cannot be negative, and therefore, a uniform scaling parameter, Soverall, is necessary to insure that the variance for each inter-nuclear vector about each of the three principal axes is positive. The advantage of this method is that Soverall is derived based on variances of a single type of RDC without needing
into a local axis system. By definition, variance cannot be negative, and therefore, a uniform scaling parameter, Soverall, is necessary to insure that the variance for each inter-nuclear vector about each of the three principal axes is positive. The advantage of this method is that Soverall is derived based on variances of a single type of RDC without needing  as a constraint, and hence does not possess any time-scale bias. Yet, it should be noted that Soverall determined by this procedure could underestimate motion if there is a uniform sub- or supra-tc motion affecting all inter-nuclear vectors equally.
as a constraint, and hence does not possess any time-scale bias. Yet, it should be noted that Soverall determined by this procedure could underestimate motion if there is a uniform sub- or supra-tc motion affecting all inter-nuclear vectors equally.2.4. Gaussian Axial Fluctuation Model
 .
.
 . This procedure was most effective when using the full 3D-GAF model. For ubiquitin, a comparison of
. This procedure was most effective when using the full 3D-GAF model. For ubiquitin, a comparison of 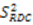 derived from the SCRM [102] approach of constraining with
derived from the SCRM [102] approach of constraining with 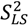 with the SF-GAF method
with the SF-GAF method 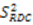 displayed remarkable agreement.
displayed remarkable agreement.2.5. Supra-τc Dynamics Determined from RDCs is linked to Molecular Recognition
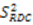 and
and 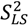 :
:
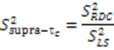
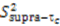 are involved with binding to interaction partners. When considering the interacting partners SH3 and ubiquitin, they both appear to possess a significant amount of supra-τc motion at their respective binding interfaces [102,113].
are involved with binding to interaction partners. When considering the interacting partners SH3 and ubiquitin, they both appear to possess a significant amount of supra-τc motion at their respective binding interfaces [102,113].3. Kinetics from the Supra-τc Range
3.1. Sub-τc Relaxation is Limited to the Overall Tumbling Time
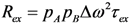 in which pA is the population of the major state (pB = 1 – pA) [159,162]. The next section explores how RD experiments work to disentangle these parameters that modify transverse relaxation.
in which pA is the population of the major state (pB = 1 – pA) [159,162]. The next section explores how RD experiments work to disentangle these parameters that modify transverse relaxation.3.2. Relaxation Dispersion Experiments
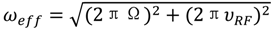 (rad s−1). The incomplete refocusing of state B (vector diagram on the left) leads to a dephasing of the magnetization, which translates to a larger relaxation rate. Upon sufficient refocusing of both magnetization vectors (vector diagram on the right) the relaxation rate decreases to R2,0. The cones directly reflect the size of the nutation generated from the applied spin-lock field. In the fast regime, the dependence of R2,eff with an increasing νRF gives a Lorentzian profile [Equation (44)]. If no conformational exchange exists, then R2,eff remains constant for all applied νRF values.
(rad s−1). The incomplete refocusing of state B (vector diagram on the left) leads to a dephasing of the magnetization, which translates to a larger relaxation rate. Upon sufficient refocusing of both magnetization vectors (vector diagram on the right) the relaxation rate decreases to R2,0. The cones directly reflect the size of the nutation generated from the applied spin-lock field. In the fast regime, the dependence of R2,eff with an increasing νRF gives a Lorentzian profile [Equation (44)]. If no conformational exchange exists, then R2,eff remains constant for all applied νRF values.
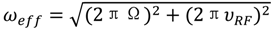 (rad s−1). The incomplete refocusing of state B (vector diagram on the left) leads to a dephasing of the magnetization, which translates to a larger relaxation rate. Upon sufficient refocusing of both magnetization vectors (vector diagram on the right) the relaxation rate decreases to R2,0. The cones directly reflect the size of the nutation generated from the applied spin-lock field. In the fast regime, the dependence of R2,eff with an increasing νRF gives a Lorentzian profile [Equation (44)]. If no conformational exchange exists, then R2,eff remains constant for all applied νRF values.
(rad s−1). The incomplete refocusing of state B (vector diagram on the left) leads to a dephasing of the magnetization, which translates to a larger relaxation rate. Upon sufficient refocusing of both magnetization vectors (vector diagram on the right) the relaxation rate decreases to R2,0. The cones directly reflect the size of the nutation generated from the applied spin-lock field. In the fast regime, the dependence of R2,eff with an increasing νRF gives a Lorentzian profile [Equation (44)]. If no conformational exchange exists, then R2,eff remains constant for all applied νRF values.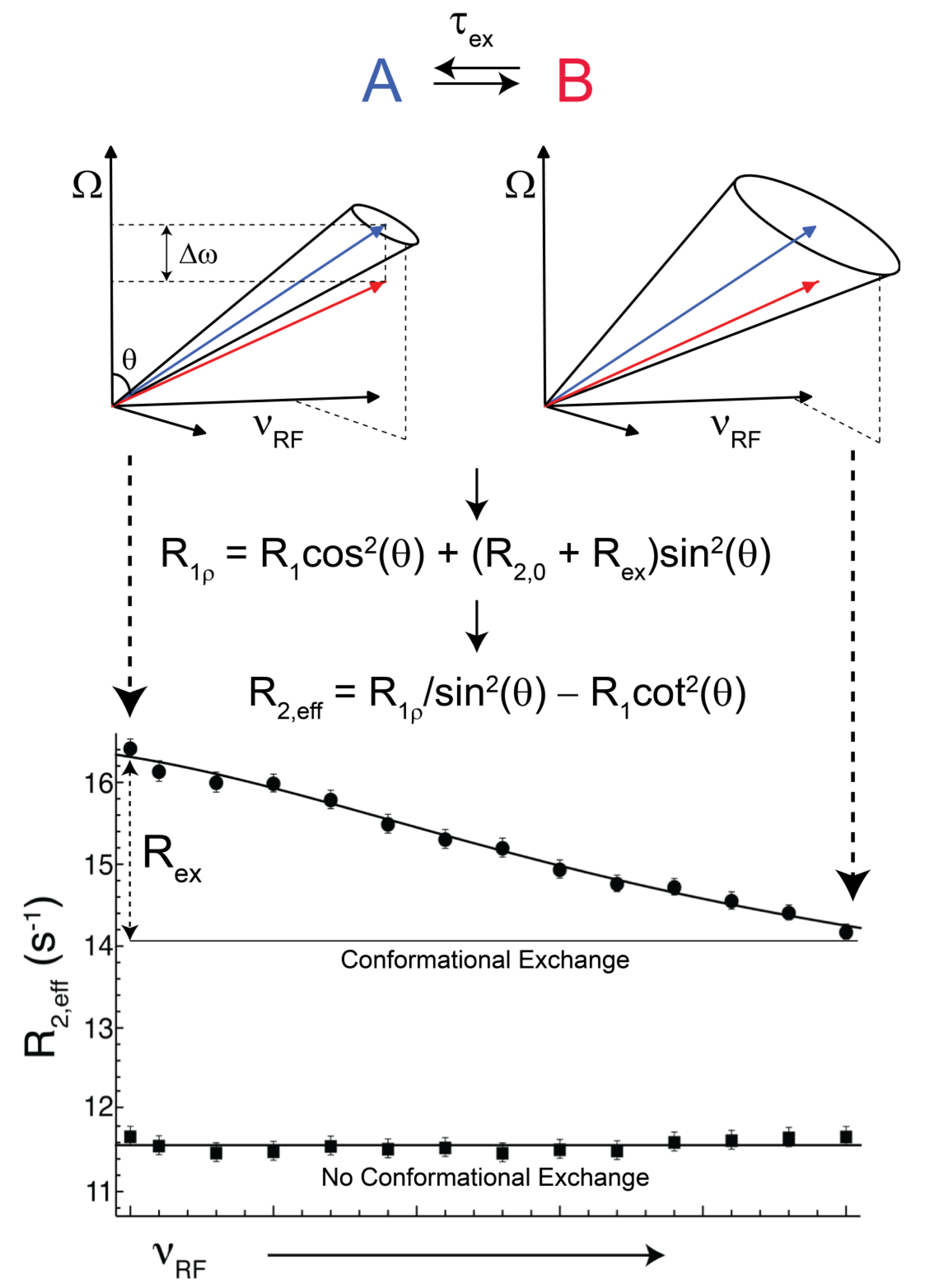
3.3. Off/On-Resonance R1ρ
 (rad·s−1)). If an interconversion event exists, then assuming a two-state process, the populated coherences will be differentially spin-locked (Figure 2). At this point, the alternatively populated coherence is not sufficiently refocused and dephasing leads to an elevated effective relaxation rate (R2,eff) (Figure 2). As ωeff is sufficiently increased to encompass the exchanging magnetization vectors, the relaxation rate decreases to R2,0 or to the point at which the exchange contribution to R2,eff is quenched (Figure 2).
(rad·s−1)). If an interconversion event exists, then assuming a two-state process, the populated coherences will be differentially spin-locked (Figure 2). At this point, the alternatively populated coherence is not sufficiently refocused and dephasing leads to an elevated effective relaxation rate (R2,eff) (Figure 2). As ωeff is sufficiently increased to encompass the exchanging magnetization vectors, the relaxation rate decreases to R2,0 or to the point at which the exchange contribution to R2,eff is quenched (Figure 2).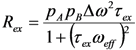
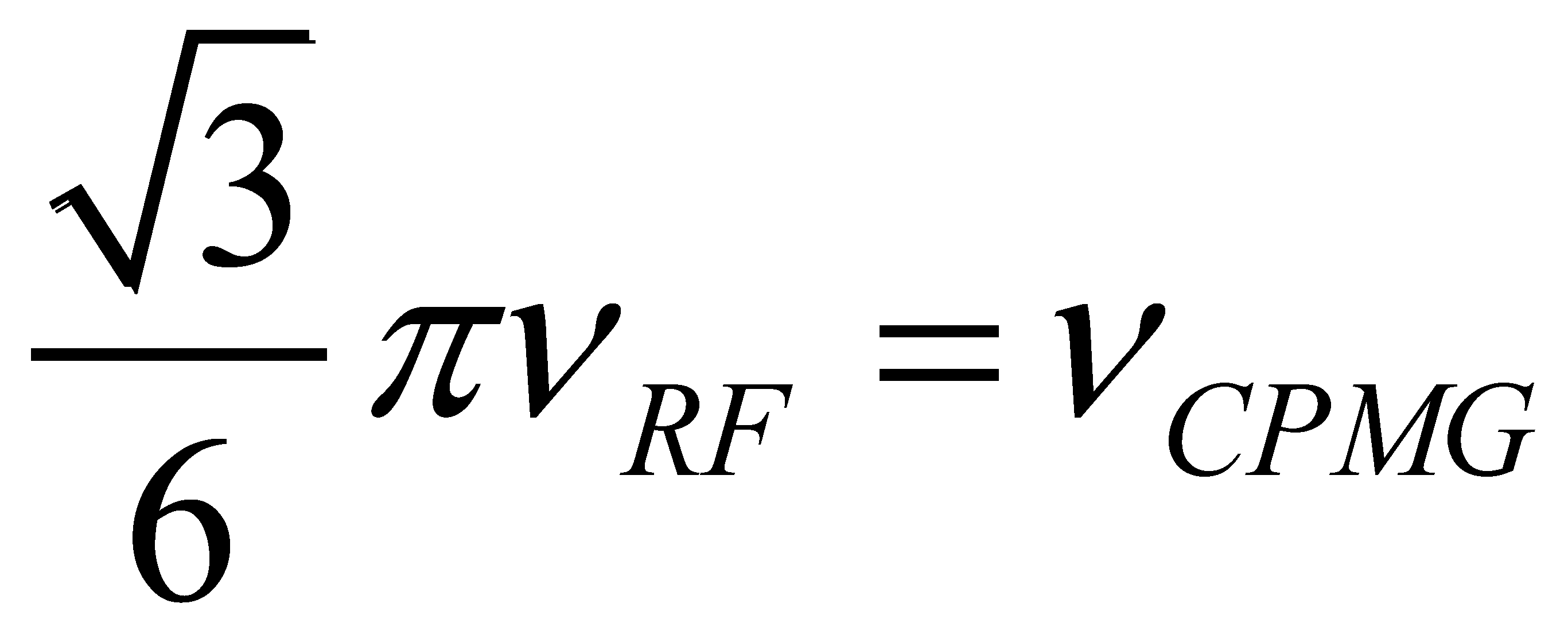 ) [180].
) [180].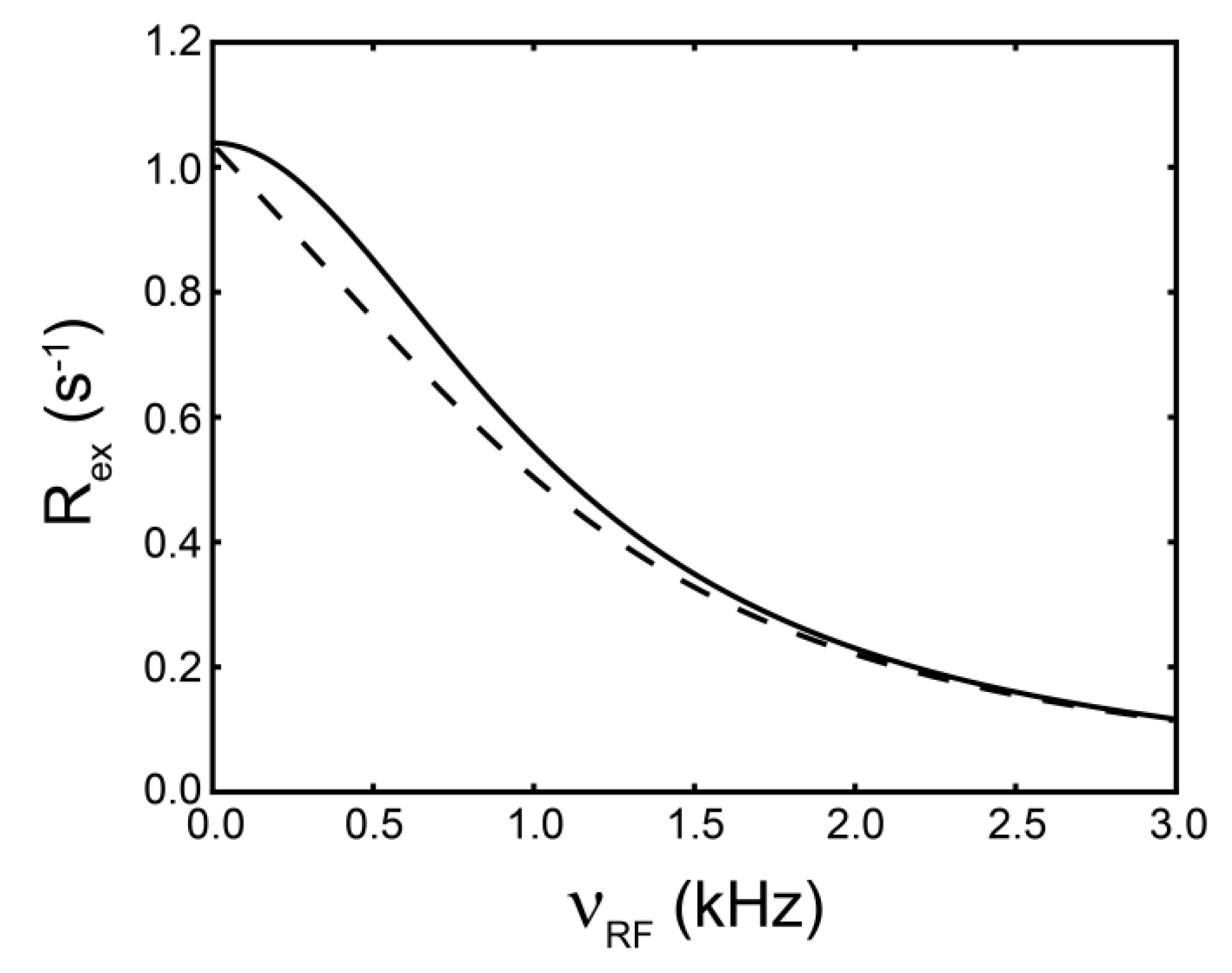
3.4. Off-Resonance R1ρ in Super-Cooled Conditions
3.5. Exceeding the Limit with Cryogenically Cooled Probeheads
3.6. Experimental Aspects for Kinetic Measurements in the Supra-τc Range
4. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
References
- Palmer III, A.G. NMR characterization of the dynamics of biomacromolecules. Chem. Rev. 2004, 104, 3623–3640. [Google Scholar] [CrossRef]
- Meier, B.H.; Ernst, R.R. Elucidation of Chemical-Exchange Networks by 2-Dimensional NMR-Spectroscopy — Heptamethylbenzenonium Ion. J. Am. Chem. Soc. 1979, 101, 6441–6442. [Google Scholar] [CrossRef]
- Wagner, G.; Bodenhausen, G.; Müller, N.; Rance, M.; Sørensen, O.W.; Ernst, R.R.; Wüthrich, K. Exchange of two-spin order in nuclear magnetic resonance: Separation of exchange and cross-relaxation processes. J. Am. Chem. Soc. 1985, 107, 6440–6446. [Google Scholar] [CrossRef]
- Chapman, B.E.; Stewart, I.M.; Bulliman, B.T.; Mendz, G.L.; Kuchel, P.W. 31P Magnetization Transfer in the Phosphoglyceromutase-Enolase Coupled Enzyme-System. Eur. Biophys. J. 1988, 16, 187–191. [Google Scholar]
- Kuchel, P.W.; Bulliman, B.T.; Chapman, B.E. Mutarotase equilibrium exchange kinetics studied by 13C-NMR. Biophys. Chem. 1988, 32, 89–95. [Google Scholar] [CrossRef]
- Mendz, G.L.; Robinson, G.; Kuchel, P.W. Direct quantitative-analysis of enzyme-catalyzed reactions by two-dimensional nuclear-magnetic-resonance spectroscopy–Adenylate kinase and phosphoglyceromutase. J. Am. Chem. Soc. 1986, 108, 169–173. [Google Scholar] [CrossRef]
- Farrow, N.A.; Zhang, O.W.; Forman-Kay, J.D.; Kay, L.E. A Heteronuclear correlation experiment for simultaneous determination of 15N longitudinal decay and chemical-exchange rates of systems in slow equilibrium. J. Biomol. NMR 1994, 4, 727–734. [Google Scholar] [CrossRef]
- Wider, G.; Neri, D.; Wüthrich, W. Studies of slow conformational equilibria in macromolecules by exchange of heteronuclear longitudinal 2-spin-order in a 2D difference correlation experiment. J. Biomol. NMR 1991, 1, 93–98. [Google Scholar] [CrossRef]
- Haupt, C.; Patzschke, R.; Weininger, U.; Gröger, S.; Kovermann, M.; Balbach, J. Transient enzyme-substrate recognition monitored by real-time NMR. J. Am. Chem. Soc. 2011, 133, 11154–11162. [Google Scholar]
- Zeeb, M.; Balbach, J. Protein folding studied by real-time NMR spectroscopy. Methods 2004, 34, 65–74. [Google Scholar] [CrossRef]
- Schanda, P.; Brutscher, B. Very fast two-dimensional NMR spectroscopy for real-time investigation of dynamic events in proteins on the time scale of seconds. J. Am. Chem. Soc. 2005, 127, 8014–8015. [Google Scholar] [CrossRef]
- Frydman, L.; Scherf, T.; Lupulescu, A. The acquisition of multidimensional NMR spectra within a single scan. Proc. Nat. Acad. Sci. USA 2002, 99, 15858–15862. [Google Scholar] [CrossRef]
- Rennella, E.; Cutuil, T.; Schanda, P.; Ayala, I.; Forge, V.; Brutscher, B. Real-time NMR characterization of structure and dynamics in a transiently populated protein folding intermediate. J. Am. Chem. Soc. 2012, 134, 8066–8069. [Google Scholar] [CrossRef]
- Bowen, S.; Hilty, C. Time-resolved dynamic nuclear polarization enhanced NMR spectroscopy. Angew. Chem. Int. Edit. 2008, 47, 5235–5237. [Google Scholar] [CrossRef]
- Harris, T.; Giraudeau, P.; Frydman, L. Kinetics from indirectly detected hyperpolarized NMR spectroscopy by using spatially selective coherence transfers. Chem. Eur. J. 2011, 17, 697–703. [Google Scholar] [CrossRef]
- Berjanskii, M.V.; Wishart, D.S. A simple method to predict protein flexibility using secondary chemical shifts. J. Am. Chem. Soc. 2005, 127, 14970–14971. [Google Scholar] [CrossRef]
- Li, D.W.; Brüschweiler, R. Certification of molecular dynamics trajectories with NMR chemical shifts. J. Phys. Chem. Lett. 2010, 1, 246–248. [Google Scholar] [CrossRef]
- Robustelli, P.; Stafford, K.A.; Palmer, A.G. Interpreting protein structural dynamics from NMR chemical shifts. J. Am. Chem. Soc. 2012, 134, 6365–6374. [Google Scholar] [CrossRef]
- Xue, Y.; Ward, J.M.; Yuwen, T.R.; Podkorytov, I.S.; Skrynnikov, N.R. Microsecond time-scale conformational exchange in proteins: Using long molecular dynamics trajectory to simulate NMR relaxation dispersion data. J. Am. Chem. Soc. 2012, 134, 2555–2562. [Google Scholar] [CrossRef]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.B.; Wriggers, W. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef]
- Reif, B.; Hennig, M.; Griesinger, C. Direct measurement of angles between bond vectors in high-resolution NMR. Science 1997, 276, 1230–1233. [Google Scholar] [CrossRef]
- Vögeli, B. Comprehensive description of NMR cross-correlated relaxation under anisotropic molecular tumbling and correlated local dynamics on all time scales. J. Chem. Phys. 2010, 133, 014501:1–014501:13. [Google Scholar]
- Vugmeyster, L.; Pelupessy, P.; Vugmeister, B.E.; Abergel, D.; Bodenhausen, G. Cross-correlated relaxation in NMR of macromolecules in the presence of fast and slow internal dynamics. C.R. Phys. 2004, 5, 377–386. [Google Scholar] [CrossRef]
- Pelupessy, P.; Ravindranathan, S.; Bodenhausen, G. Correlated motions of successive amide N-H bonds in proteins. J. Biomol. NMR 2003, 25, 265–280. [Google Scholar] [CrossRef]
- Vögeli, B.; Yao, L.S. Correlated dynamics between protein hn and hc bonds observed by NMR cross relaxation. J. Am. Chem. Soc. 2009, 131, 3668–3678. [Google Scholar] [CrossRef]
- Ban, D.; Gossert, A.D.; Giller, K.; Becker, S.; Griesinger, C.; Lee, D. Exceeding the limit of dynamics studies on biomolecules using high spin-lock field strengths with a cryogenically cooled probehead. J. Magn. Reson. 2012, 221, 1–4. [Google Scholar] [CrossRef]
- Lakomek, N.A.; Carlomagno, T.; Becker, S.; Griesinger, C.; Meiler, J. A thorough dynamic interpretation of residual dipolar couplings in ubiquitin. J. Biomol. NMR 2006, 34, 101–115. [Google Scholar] [CrossRef]
- Lange, O.F.; Lakomek, N.A.; Farés, C.; Schröder, G.F.; Walter, K.F.; Becker, S.; Meiler, J.; Grubmüller, H.; Griesinger, C.; de Groot, B.L. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science 2008, 320, 1471–1475. [Google Scholar] [CrossRef]
- Tjandra, N.; Bax, A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science 1997, 278, 1111–1114. [Google Scholar] [CrossRef]
- Tolman, J.R.; Flanagan, J.M.; Kennedy, M.A.; Prestegard, J.H. NMR evidence for slow collective motions in cyanometmyoglobin. Nat. Struct. Mol. Biol. 1997, 4, 292–297. [Google Scholar] [CrossRef]
- Saupe, A.; Englert, G. High-resolution nuclear magnetic resonance spectra of orientated molecules. Phys. Rev. Lett. 1963, 11, 462–464. [Google Scholar] [CrossRef]
- Saupe, A. Kernresonanzen in kristallinen flüssigkeiten und in kristallinflussigen lösungen. I. Z. Naturforsch. A 1964, A 19, 161–171. [Google Scholar]
- Saupe, A. Recent results in field of liquid crystals. Angew. Chem. Int. Edit. 1968, 7, 97–118. [Google Scholar] [CrossRef]
- Snyder, L.C. Analysis of nuclear magnetic resonance spectra of molecules in liquid-crystal solvents. J. Chem. Phys. 1965, 43, 4041–4050. [Google Scholar] [CrossRef]
- Gayathri, C.; Bothner-By, A.A.; van Zijl, P.C.M.; Maclean, C. Dipolar magnetic-field effects in NMR-spectra of liquids. Chem. Phys. Lett. 1982, 87, 192–196. [Google Scholar] [CrossRef]
- Lohman, J.A.B.; Maclean, C. Alignment Effects on High-Resolution NMR-spectra, Induced by the magnetic-field. Chem. Phys. 1978, 35, 269–274. [Google Scholar] [CrossRef]
- van Zijl, P.C.M.; Ruessink, B.H.; Bulthuis, J.; Maclean, C. NMR of partially aligned liquids–Magnetic-susceptibility anisotropies and dielectric-properties. Acc. Chem. Res. 1984, 17, 172–180. [Google Scholar] [CrossRef]
- Celebre, G.; Longeri, M.; Emsley, J.W. The Nature of the internal rotational barrier in benzyl-chloride - an interpretation of the dipolar coupling-constants obtained from the analysis of the proton NMR-spectra of samples dissolved in liquid-crystal solvents. Mol. Phys. 1988, 64, 715–723. [Google Scholar] [CrossRef]
- Celebre, G.; Longeri, M.; Emsley, J.W. An investigation by NMR-spectroscopy of the dependence on internal motion of the orientational ordering of ethoxybenzene and 4-fluoroethoxybenzene when dissolved in a nematic solvent. Liq. Cryst. 1989, 6, 689–700. [Google Scholar] [CrossRef]
- Counsell, C.J.R.; Emsley, J.W.; Luckhurst, G.R.; Sachdev, H.S. Orientational order in the 4-n-alkyloxy-4'-cyanobiphenyls–a comparison between experiment and theory. Mol. Phys. 1988, 63, 33–47. [Google Scholar] [CrossRef]
- Emsley, J.W.; Foord, E.K.; Gandy, P.J.F.; Turner, D.L.; Zimmermann, H. Assignment of the quadrupolar splittings in fully deuteriated alkyl chains of liquid-crystalline compounds–the case of 4-n-hexyloxy-4'-cyanobiphenyl. Liq. Cryst. 1994, 17, 303–309. [Google Scholar] [CrossRef]
- Emsley, J.W.; Heaton, N.J.; Kimmings, M.K.; Longeri, M. The conformation and orientational order of 1-ethoxy-4-chlorobenzene dissolved in a nematic liquid-crystal. Mol. Phys. 1987, 61, 433–442. [Google Scholar] [CrossRef]
- Emsley, J.W.; Luckhurst, G.R. The effect of internal motion on the orientational order parameters for liquid-crystalline systems. Mol. Phys. 1980, 41, 19–29. [Google Scholar] [CrossRef]
- Emsley, J.W.; Luckhurst, G.R.; Stockley, C.P. The deuterium and proton-(Deuterium) NMR-spectra of the partially deuteriated nematic liquid-crystal 4-n-pentyl-4'-cyanobiphenyl. Mol. Phys. 1981, 44, 565–580. [Google Scholar] [CrossRef]
- Rosen, M.E.; Rucker, S.P.; Schmidt, C.; Pines, A. 2-Dimensional proton NMR-studies of the conformations and orientations of n-alkanes in a liquid-crystal solvent. J. Phys. Chem. 1993, 97, 3858–3866. [Google Scholar] [CrossRef]
- Sinton, S.W.; Zax, D.B.; Murdoch, J.B.; Pines, A. Multiple-quantum NMR-study of molecular-structure and ordering in a liquid-crystal. Mol. Phys. 1984, 53, 333–362. [Google Scholar] [CrossRef]
- Tolman, J.R.; Flanagan, J.M.; Kennedy, M.A.; Prestegard, J.H. Nuclear magnetic dipole interactions in field-oriented proteins–information for structure determination in solution. Proc. Nat. Acad. Sci. USA 1995, 92, 9279–9283. [Google Scholar] [CrossRef]
- Kung, H.C.; Wang, K.Y.; Goljer, I.; Bolton, P.H. Magnetic alignment of duplex and quadruplex DNAs. J. Magn. Reson. Ser. B 1995, 109, 323–325. [Google Scholar] [CrossRef]
- Tjandra, N.; Grzesiek, S.; Bax, A. Magnetic field dependence of nitrogen-proton J splittings in N-15-enriched human ubiquitin resulting from relaxation interference and residual dipolar coupling. J. Am. Chem. Soc. 1996, 118, 6264–6272. [Google Scholar] [CrossRef]
- Clore, G.M.; Starich, M.R.; Gronenborn, A.M. Measurement of residual dipolar couplings of macromolecules aligned in the nematic phase of a colloidal suspension of rod-shaped viruses. J. Am. Chem. Soc. 1998, 120, 10571–10572. [Google Scholar] [CrossRef]
- Hansen, M.R.; Mueller, L.; Pardi, A. Tunable alignment of macromolecules by filamentous phage yields dipolar coupling interactions. Nat. Struct. Mol. Biol. 1998, 5, 1065–1074. [Google Scholar] [CrossRef]
- Hansen, M.R.; Rance, M.; Pardi, A. Observation of long-range H-1-H-1 distances in solution by dipolar coupling interactions. J. Am. Chem. Soc. 1998, 120, 11210–11211. [Google Scholar] [CrossRef]
- Barrientos, L.G.; Dolan, C.; Gronenborn, A.M. Characterization of surfactant liquid crystal phases suitable for molecular alignment and measurement of dipolar couplings. J. Biomol. NMR 2000, 16, 329–337. [Google Scholar] [CrossRef]
- Prosser, R.S.; Losonczi, J.A.; Shiyanovskaya, I.V. Use of a novel aqueous liquid crystalline medium for high-resolution NMR of macromolecules in solution. J. Am. Chem. Soc. 1998, 120, 11010–11011. [Google Scholar] [CrossRef]
- Rückert, M.; Otting, G. Alignment of biological macromolecules in novel nonionic liquid crystalline media for NMR experiments. J. Am. Chem. Soc. 2000, 122, 7793–7797. [Google Scholar] [CrossRef]
- Chou, J.J.; Gaemers, S.; Howder, B.; Louis, J.M.; Bax, A. A simple apparatus for generating stretched polyacrylamide gels, yielding uniform alignment of proteins and detergent micelles. J. Biomol. NMR 2001, 21, 377–382. [Google Scholar] [CrossRef]
- Sass, H.J.; Musco, G.; Stahl, S.J.; Wingfield, P.T.; Grzesiek, S. Solution NMR of proteins within polyacrylamide gels: Diffusional properties and residual alignment by mechanical stress or embedding of oriented purple membranes. J. Biomol. NMR 2000, 18, 303–309. [Google Scholar]
- Tycko, R.; Blanco, F.J.; Ishii, Y. Alignment of biopolymers in strained gels: A new way to create detectable dipole-dipole couplings in high-resolution biomolecular NMR. J. Am. Chem. Soc. 2000, 122, 9340–9341. [Google Scholar] [CrossRef]
- Koenig, B.W.; Hu, J.S.; Ottiger, M.; Bose, S.; Hendler, R.W.; Bax, A. NMR measurement of dipolar couplings in proteins aligned by transient binding to purple membrane fragments. J. Am. Chem. Soc. 1999, 121, 1385–1386. [Google Scholar] [CrossRef]
- Sass, J.; Cordier, F.; Hoffmann, A.; Cousin, A.; Omichinski, J.G.; Lowen, H.; Grzesiek, S. Purple membrane induced alignment of biological macromolecules in the magnetic field. J. Am. Chem. Soc. 1999, 121, 2047–2055. [Google Scholar] [CrossRef]
- Bax, A.; Kontaxis, G.; Tjandra, N. Dipolar couplings in macromolecular structure determination. Methods Enzymol. 2001, 339, 127–174. [Google Scholar] [CrossRef]
- Chen, K.; Tjandra, N. The use of residual dipolar coupling in studying proteins by NMR. Top. Curr. Chem. 2012, 326, 47–67. [Google Scholar] [CrossRef]
- Tolman, J.R.; Ruan, K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem. Rev. 2006, 106, 1720–1736. [Google Scholar] [CrossRef]
- Bax, A.; Vuister, G.W.; Grzesiek, S.; Delaglio, F.; Wang, A.C.; Tschudin, R.; Zhu, G. Measurement of Homonuclear and Heteronuclear J-Couplings from Quantitative J-Correlation. Methods Enzymol. 1994, 239, 79–105. [Google Scholar] [CrossRef]
- Prestegard, J.H.; Al-Hashimi, H.M.; Tolman, J.R. NMR structures of biomolecules using field oriented media and residual dipolar couplings. Quart. Rev. Biophys. 2000, 33, 371–424. [Google Scholar] [CrossRef]
- Prestegard, J.H.; Mayer, K.L.; Valafar, H.; Benison, G.C. Determination of protein backbone structures from residual dipolar couplings. Methods Enzymol. 2005, 394, 175–209. [Google Scholar] [CrossRef]
- Losonczi, J.A.; Andrec, M.; Fischer, M.W.F.; Prestegard, J.H. Order matrix analysis of residual dipolar couplings using singular value decomposition. J. Magn. Reson. 1999, 138, 334–342. [Google Scholar] [CrossRef]
- Tolman, J.R. A novel approach to the retrieval of structural and dynamic information from residual dipolar couplings using several oriented media in biomolecular NMR spectroscopy. J. Am. Chem. Soc. 2002, 124, 12020–12030. [Google Scholar] [CrossRef]
- Zweckstetter, M. NMR: Prediction of molecular alignment from structure using the PALES software. Nat. Protoc. 2008, 3, 679–690. [Google Scholar] [CrossRef]
- Zweckstetter, M.; Bax, A. Prediction of sterically induced alignment in a dilute liquid crystalline phase: Aid to protein structure determination by NMR. J. Am. Chem. Soc. 2000, 122, 3791–3792. [Google Scholar] [CrossRef]
- Valafar, H.; Prestegard, J.H. REDCAT: A residual dipolar coupling analysis tool. J. Magn. Reson. 2004, 167, 228–241. [Google Scholar] [CrossRef]
- Meiler, J.; Prompers, J.J.; Peti, W.; Griesinger, C.; Brüschweiler, R. Model-free approach to the dynamic interpretation of residual dipolar couplings in globular proteins. J. Am. Chem. Soc. 2001, 123, 6098–6107. [Google Scholar] [CrossRef]
- Louhivuori, M.; Otten, R.; Lindorff-Larsen, K.; Annila, A. Conformational fluctuations affect protein alignment in dilute liquid crystal media. J. Am. Chem. Soc. 2006, 128, 4371–4376. [Google Scholar] [CrossRef]
- Salvatella, X.; Richter, B.; Vendruscolo, M. Influence of the fluctuations of the alignment tensor on the analysis of the structure and dynamics of proteins using residual dipolar couplings. J. Biomol. NMR 2008, 40, 71–81. [Google Scholar] [CrossRef]
- Bernadó, P.; Blanchard, L.; Timmins, P.; Marion, D.; Ruigrok, R.W.H.; Blackledge, M. A structural model for unfolded proteins from residual dipolar couplings and small-angle x-ray scattering. Proc. Nat. Acad. Sci. USA 2005, 102, 17002–17007. [Google Scholar] [CrossRef]
- Bertoncini, C.W.; Jung, Y.S.; Fernández, C.O.; Hoyer, W.; Griesinger, C.; Jovin, T.M.; Zweckstetter, M. Release of long-range tertiary interactions potentiates aggregation of natively unstructured alpha-synuclein. Proc. Nat. Acad. Sci. USA 2005, 102, 1430–1435. [Google Scholar] [CrossRef]
- Rodriguez-Castañeda, F.; Haberz, P.; Leonov, A.; Griesinger, C. Paramagnetic tagging of diamagnetic proteins for solution NMR. Magn. Reson. Chem. 2006, 44, S10–S16. [Google Scholar] [CrossRef]
- Bertini, I.; Del Bianco, C.; Gelis, I.; Katsaros, N.; Luchinat, C.; Parigi, G.; Peana, M.; Provenzani, A.; Zoroddu, M.A. Experimentally exploring the conformational space sampled by domain reorientation in calmodulin. Proc. Nat. Acad. Sci. USA 2004, 101, 6841–6846. [Google Scholar] [CrossRef]
- Zhang, Q.; Throolin, R.; Pitt, S.W.; Serganov, A.; Al-Hashimi, H.M. Probing motions between equivalent RNA domains using magnetic field induced residual dipolar couplings: Accounting for correlations between motions and alignment. J. Am. Chem. Soc. 2003, 125, 10530–10531. [Google Scholar]
- Louhivuori, M.; Pääkkönen, K.; Fredriksson, K.; Permi, P.; Lounila, J.; Annila, A. On the origin of residual dipolar couplings from denatured proteins. J. Am. Chem. Soc. 2003, 125, 15647–15650. [Google Scholar] [CrossRef]
- Shortle, D.; Ackerman, M.S. Persistence of native-like topology in a denatured protein in 8 M urea. Science 2001, 293, 487–489. [Google Scholar] [CrossRef]
- Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.R.; Jensen, M.R.; Segard, S.; Bernadó, P.; Charavay, C.; Blackledge, M. Flexible-meccano: a tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef]
- Jensen, M.R.; Houben, K.; Lescop, E.; Blanchard, L.; Ruigrok, R.W.H.; Blackledge, M. Quantitative conformational analysis of partially folded proteins from residual dipolar couplings: Application to the molecular recognition element of Sendai virus nucleoprotein. J. Am. Chem. Soc. 2008, 130, 8055–8061. [Google Scholar] [CrossRef]
- Nodet, G.; Salmon, L.; Ozenne, V.; Meier, S.; Jensen, M.R.; Blackledge, M. Quantitative description of backbone conformational sampling of unfolded proteins at amino acid resolution from NMR residual dipolar couplings. J. Am. Chem. Soc. 2009, 131, 17908–17918. [Google Scholar] [CrossRef]
- Skrynnikov, N.R.; Goto, N.K.; Yang, D.W.; Choy, W.Y.; Tolman, J.R.; Mueller, G.A.; Kay, L.E. Orienting domains in proteins using dipolar couplings measured by liquid-state NMR: Differences in solution and crystal forms of maltodextrin binding protein loaded with beta-cyclodextrin. J. Mol. Biol. 2000, 295, 1265–1273. [Google Scholar] [CrossRef]
- Koehler, J.; Meiler, J. Expanding the utility of NMR restraints with paramagnetic compounds: Background and practical aspects. Prog. Nucl. Magn. Reson. Spectros. 2011, 59, 360–389. [Google Scholar] [CrossRef]
- Xu, X.F.; Keizers, P.H.J.; Reinle, W.; Hannemann, F.; Bernhardt, R.; Ubbink, M. Intermolecular dynamics studied by paramagnetic tagging. J. Biomol. NMR 2009, 43, 247–254. [Google Scholar] [CrossRef]
- Xu, X.F.; Reinle, W.G.; Hannemann, F.; Konarev, P.V.; Svergun, D.I.; Bernhardt, R.; Ubbink, M. Dynamics in a pure encounter complex of two proteins studied by solution scattering and paramagnetic NMR spectroscopy. J. Am. Chem. Soc. 2008, 130, 6395–6403. [Google Scholar] [CrossRef]
- Barbieri, R.; Bertini, I.; Lee, Y.M.; Luchinat, C.; Velders, A.H. Structure-independent cross-validation between residual dipolar couplings originating from internal and external orienting media. J. Biomol. NMR 2002, 22, 365–368. [Google Scholar] [CrossRef]
- Bertini, I.; Gupta, Y.K.; Luchinat, C.; Parigi, G.; Peana, M.; Sgheri, L.; Yuan, J. Paramagnetism-based NMR restraints provide maximum allowed probabilities for the different conformations of partially independent protein domains. J. Am. Chem. Soc. 2007, 129, 12786–12794. [Google Scholar]
- Pintacuda, G.; Keniry, M.A.; Huber, T.; Park, A.Y.; Dixon, N.E.; Otting, G. Fast structure-based assignment of 15N HSQC spectra of selectively 15N-labeled paramagnetic proteins. J. Am. Chem. Soc. 2004, 126, 2963–2970. [Google Scholar]
- Otting, G. Protein NMR using paramagnetic ions. Annu. Rev. Biophys. 2010, 39, 387–405. [Google Scholar] [CrossRef]
- Gaponenko, V.; Altieri, A.S.; Li, J.; Byrd, R.A. Breaking symmetry in the structure determination of (large) symmetric protein dimers. J. Biomol. NMR 2002, 24, 143–148. [Google Scholar] [CrossRef]
- Gaponenko, V.; Sarma, S.P.; Altieri, A.S.; Horita, D.A.; Li, J.; Byrd, R.A. Improving the accuracy of NMR structures of large proteins using pseudocontact shifts as long-range restraints. J. Biomol. NMR 2004, 28, 205–212. [Google Scholar] [CrossRef]
- Wöhnert, J.; Franz, K.J.; Nitz, M.; Imperiali, B.; Schwalbe, H. Protein alignment by a coexpressed lanthanide-binding tag for the measurement of residual dipolar couplings. J. Am. Chem. Soc. 2003, 125, 13338–13339. [Google Scholar] [CrossRef]
- Barthelmes, K.; Reynolds, A.M.; Peisach, E.; Jonker, H.R.A.; DeNunzio, N.J.; Allen, K.N.; Imperiali, B.; Schwalbe, H. Engineering Encodable Lanthanide-Binding Tags into Loop Regions of Proteins. J. Am. Chem. Soc. 2011, 133, 808–819. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, X.Y.; Watt, E.D.; Al-Hashimi, H.M. Resolving the motional modes that code for RNA adaptation. Science 2006, 311, 653–656. [Google Scholar] [CrossRef]
- Zhang, Q.; Stelzer, A.C.; Fisher, C.K.; Al-Hashimi, H.M. Visualizing spatially correlated dynamics that directs RNA conformational transitions. Nature 2007, 450, 1263–1267. [Google Scholar] [CrossRef]
- Hus, J.C.; Brüschweiler, R. Principal component method for assessing structural heterogeneity across multiple alignment media. J. Biomol. NMR 2002, 24, 123–132. [Google Scholar] [CrossRef]
- Hus, J.C.; Peti, W.; Griesinger, C.; Brüschweiler, R. Self-consistency analysis of dipolar couplings in multiple alignments of ubiquitin. J. Am. Chem. Soc. 2003, 125, 5596–5597. [Google Scholar]
- Peti, W.; Meiler, J.; Brüschweiler, R.; Griesinger, C. Model-free analysis of protein backbone motion from residual dipolar couplings. J. Am. Chem. Soc. 2002, 124, 5822–5833. [Google Scholar] [CrossRef]
- Lakomek, N.A.; Walter, K.F.; Farés, C.; Lange, O.F.; de Groot, B.L.; Grubmüller, H.; Brüschweiler, R.; Munk, A.; Becker, S.; Meiler, J.; et al. Self-consistent residual dipolar coupling based model-free analysis for the robust determination of nanosecond to microsecond protein dynamics. J. Biomol. NMR 2008, 41, 139–155. [Google Scholar] [CrossRef]
- Meirovitch, E.; Lee, D.; Walter, K.F.; Griesinger, C. Standard tensorial analysis of local ordering in proteins from residual dipolar couplings. J. Phys. Chem. B 2012, 116, 6106–6117. [Google Scholar] [CrossRef]
- Yao, L.; Vögeli, B.; Torchia, D.A.; Bax, A. Simultaneous NMR study of protein structure and dynamics using conservative mutagenesis. J. Phys. Chem. B 2008, 112, 6045–6056. [Google Scholar]
- Sabo, T.M.; Smith, C.A.; Ban, D.; Mazur, A.; Lee, D.; Griesinger, C. ORIUM: Optimized RDC-based iterative and unified model-free analysis. J. Biomol. NMR 2013, in press. [Google Scholar]
- Bremi, T.; Brüschweiler, R. Locally anisotropic internal polypeptide backbone dynamics by NMR relaxation. J. Am. Chem. Soc. 1997, 119, 6672–6673. [Google Scholar] [CrossRef]
- Brüschweiler, R.; Wright, P.E. NMR order parameters of biomolecules–A new analytical representation and application to the gaussian axial fluctuation model. J. Am. Chem. Soc. 1994, 116, 8426–8427. [Google Scholar] [CrossRef]
- Lienin, S.F.; Bremi, T.; Brutscher, B.; Brüschweiler, R.; Ernst, R.R. Anisotropic intramolecular backbone dynamics of ubiquitin characterized by NMR relaxation and MD computer simulation. J. Am. Chem. Soc. 1998, 120, 9870–9879. [Google Scholar] [CrossRef]
- Bernadó, P.; Blackledge, M. Local dynamic amplitudes on the protein backbone from dipolar couplings: Toward the elucidation of slower motions in biomolecules. J. Am. Chem. Soc. 2004, 126, 7760–7761. [Google Scholar] [CrossRef]
- Bernadó, P.; Blackledge, M. Anisotropic small amplitude peptide plane dynamics in proteins from residual dipolar couplings. J. Am. Chem. Soc. 2004, 126, 4907–4920. [Google Scholar] [CrossRef]
- Bouvignies, G.; Bernadó, P.; Meier, S.; Cho, K.; Grzesiek, S.; Brüschweiler, R.; Blackledge, M. Identification of slow correlated motions in proteins using residual dipolar and hydrogen-bond scalar couplings. Proc. Nat. Acad. Sci. USA 2005, 102, 13885–13890. [Google Scholar] [CrossRef]
- Salmon, L.; Bouvignies, G.; Markwick, P.; Lakomek, N.; Showalter, S.; Li, D.W.; Walter, K.; Griesinger, C.; Brüschweiler, R.; Blackledge, M. Protein conformational flexibility from structure-free analysis of nmr dipolar couplings: Quantitative and absolute determination of backbone motion in ubiquitin. Angew. Chem. Int. Edit. 2009, 48, 4154–4157. [Google Scholar] [CrossRef]
- Salmon, L.; Pierce, L.; Grimm, A.; Roldan, J.L.O.; Mollica, L.; Jensen, M.R.; van Nuland, N.; Markwick, P.R.L.; McCammon, J.A.; Blackledge, M. Multi-timescale conformational dynamics of the sh3 domain of cd2-associated protein using NMR spectroscopy and accelerated molecular dynamics. Angew. Chem. Int. Edit. 2012, 51, 6103–6106. [Google Scholar] [CrossRef]
- Farés, C.; Lakomek, N.A.; Walter, K.F.A.; Frank, B.T.C.; Meiler, J.; Becker, S.; Griesinger, C. Accessing ns-μs side chain dynamics in ubiquitin with methyl RDCs. J. Biomol. NMR 2009, 45, 23–44. [Google Scholar] [CrossRef]
- Ban, D.; Funk, M.; Gulich, R.; Egger, D.; Sabo, T.M.; Walter, K.F.; Fenwick, R.B.; Giller, K.; Pichierri, F.; de Groot, B.L.; et al. Kinetics of conformational sampling in ubiquitin. Angew. Chem. Int. Ed. Engl. 2011, 50, 11437–11440. [Google Scholar] [CrossRef]
- Fenwick, R.B.; Esteban-Martín, S.; Richter, B.; Lee, D.; Walter, K.F.; Milovanovic, D.; Becker, S.; Lakomek, N.A.; Griesinger, C.; Salvatella, X. Weak long-range correlated motions in a surface patch of ubiquitin involved in molecular recognition. J. Am. Chem. Soc. 2011, 133, 10336–10339. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef]
- Markwick, P.R.L.; Bouvignies, G.; Blackledge, M. Exploring multiple timescale motions in protein GB3 using accelerated molecular dynamics and NMR spectroscopy. J. Am. Chem. Soc. 2007, 129, 4724–4730. [Google Scholar] [CrossRef]
- Markwick, P.R.L.; Bouvignies, G.; Salmon, L.; McCammon, J.A.; Nilges, M.; Blackledge, M. Toward a unified representation of protein structural dynamics in solution. J. Am. Chem. Soc. 2009, 131, 16968–16975. [Google Scholar]
- Fuglestad, B.; Gasper, P.M.; Tonelli, M.; McCammon, J.A.; Markwick, P.R.L.; Komives, E.A. The Dynamic Structure of Thrombin in Solution. Biophys. J. 2012, 103, 79–88. [Google Scholar] [CrossRef]
- Gasper, P.M.; Fuglestad, B.; Komives, E.A.; Markwick, P.R.L.; McCammon, J.A. Allosteric networks in thrombin distinguish procoagulant vs. anticoagulant activities. Proc. Nat. Acad. Sci. USA 2012, 109, 21216–21222. [Google Scholar]
- Cervantes, C.F.; Markwick, P.R.L.; Sue, S.C.; McCammon, J.A.; Dyson, H.J.; Komives, E.A. Functional dynamics of the folded ankyrin repeats of iκbα revealed by nuclear magnetic resonance. Biochemistry 2009, 48, 8023–8031. [Google Scholar] [CrossRef]
- Farrow, N.A.; Muhandiram, R.; Singer, A.U.; Pascal, S.M.; Kay, C.M.; Gish, G.; Shoelson, S.E.; Pawson, T.; Forman-Kay, J.D.; Kay, L.E. Backbone dynamics of a free and phosphopeptide-complexed Src homology 2 domain studied by 15N NMR relaxation. Biochemistry 1994, 33, 5984–6003. [Google Scholar] [CrossRef]
- Kay, L.E.; Torchia, D.A.; Bax, A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: Application to staphylococcal nuclease. Biochemistry 1989, 28, 8972–8979. [Google Scholar] [CrossRef]
- Cordier, F.; Brutscher, B.; Marion, D. Measurement of 13Cα-13CO cross-relaxation rates in 15N- /13C -labelled proteins. J. Biomol. NMR 1996, 7, 163–168. [Google Scholar]
- Daragan, V.A.; Mayo, K.H. Motional model analyses of protein and peptide dynamics using 13C and 15N-NMR relaxation. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 63–105. [Google Scholar] [CrossRef]
- Muhandiram, D.R.; Yamazaki, T.; Sykes, B.D.; Kay, L.E. Measurement of 2H T1 and T1ρ relaxation times in uniformly 13C-labeled and fractionally 2H-labeled proteins in solution. J. Am. Chem. Soc. 1995, 117, 11536–11544. [Google Scholar] [CrossRef]
- Palmer III, A.G.; Rance, M.; Wright, P.E. Intramolecular motions of a zinc finger DNA-binding domain from XFIN characterized by proton-detected natural abundance 13C heteronuclear NMR spectroscopy. J. Am. Chem. Soc. 1991, 113, 4371–4380. [Google Scholar] [CrossRef]
- Yamazaki, T.; Muhandiram, R.; Kay, L.E. NMR experiments for the measurement of carbon relaxation properties in highly enriched, uniformly 13C, 15N-labeled proteins: Application to 13Cα carbons. J. Am. Chem. Soc. 1994, 116, 8266–7278. [Google Scholar] [CrossRef]
- Zeng, L.; Fischer, M.W.F.; Zuiderweg, E.R.P. Study of protein dynamics in solution by measurement of 13Cα-13CO NOE and 13CO longitudinal relaxation. J. Biomol. NMR 1996, 7, 157–162. [Google Scholar]
- Cavanagh, J.; Fairbrother, W.J.; Palmer III, A.G.; Rance, M.; Skelton, N.J. Principles and Practice: Protein NMR Spectroscopy, 2nd ed.; Elsevier: London, United Kingdom, 2007. [Google Scholar]
- Korzhnev, D.M.; Billeter, M.; Arseniev, A.S.; Orekhov, V.Y. NMR studies of Brownian tumbling and internal motions in proteins. Prog. Nucl. Magn. Reson. Spectros. 2001, 38, 197–266. [Google Scholar] [CrossRef]
- Lüginbuhl, P.; Wüthrich, K. Semi-classical nuclear spin relaxation theory revisted for use with biological macromolecules. Prog. Nucl. Magn. Reson. Spectros. 2002, 40, 199–247. [Google Scholar] [CrossRef]
- Palmer III, A.G. NMR probes of molecular dynamics: Overview and comparison with other techniques. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 129–155. [Google Scholar] [CrossRef]
- Ishima, R. Recent developments in 15N NMR relaxation studies that probe protein backbone dynamics. Top. Curr. Chem. 2012, 326, 99–122. [Google Scholar]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxtion in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982, 104, 4546–4559. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-Free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982, 104, 4559–4570. [Google Scholar] [CrossRef]
- Yang, D.; Kay, L.E. Contributions to conformational entropy arising from bond vector fluctuations measured from NMR-derived order parameters: application to protein folding. J. Mol. Biol. 1996, 263, 369–382. [Google Scholar]
- Akke, M.; Brüschweiler, R.; Palmer, A.G., 3rd. NMR order parameters and free energy: an analytical approach and its application to cooperative Ca2+ binding by calbindin D9k. J. Am. Chem. Soc. 1993, 115, 9832–9833. [Google Scholar] [CrossRef]
- Lee, A.L.; Kinnear, S.A.; Wand, A.J. Redistribution and loss of side chain entropy upon formation of a calmodulin-peptide complex. Nat. Struct. Biol. 2000, 7, 72–77. [Google Scholar] [CrossRef]
- Sabo, T.M.; Bakhtiari, D.; Walter, K.F.A.; McFeeters, R.L.; Giller, K.; Becker, S.; Griesinger, C.; Lee, D. Thermal coefficients of the methyl groups within ubiquitin. Protein Sci. 2012, 21, 562–570. [Google Scholar] [CrossRef]
- Clore, G.M.; Szabo, A.; Bax, A.; Kay, L.E.; Driscoll, P.C.; Gronenborn, A.M. Deviations from the simple two-paramter model-free approach to the interpretation of nitrogen-15 nuclear magnetic relaxation of proteins. J. Am. Chem. Soc. 1990, 112, 4989–4991. [Google Scholar] [CrossRef]
- Tjandra, N.; Feller, S.E.; Pastor, R.W.; Bax, A. Rotational diffusion anisotropy of human ubiquitin from 15N NMR relaxation. J. Am. Chem. Soc. 1995, 117, 12562–12566. [Google Scholar] [CrossRef]
- Baber, J.L.; Szabo, A.; Tjandra, N. Analysis of slow interdomain motion of macromolecules using NMR relaxation data. J. Am. Chem. Soc. 2001, 123, 3953–3959. [Google Scholar] [CrossRef]
- Brüschweiler, R.; Liao, X.; Wright, P.E. Long-range motional restrictions in a multidomain zinc-finger protein from anisotropic tumbling. Science 1995, 268, 886–889. [Google Scholar]
- Jackson, S.E. How do small single-domain proteins fold? Fold. Des. 1998, 3, R81–R91. [Google Scholar] [CrossRef]
- Korzhnev, D.M.; Salvatella, X.; Vendruscolo, M.; Di Nardo, A.A.; Davidson, A.R.; Dobson, C.M.; Kay, L.E. Low-populated folding intermediates of Fyn SH3 characterized by relaxation dispersion NMR. Nature 2004, 430, 586–590. [Google Scholar] [CrossRef]
- Kubelka, J.; Hofrichter, J.; Eaton, W.A. The protein folding ‘speed limit’. Curr. Opin. Struct. Biol. 2004, 14, 76–88. [Google Scholar] [CrossRef]
- Neira, J.L. NMR as a tool to identify and characterize protein folding intermediates. Arch. Biochem. Biophys. 2013, 531, 90–99. [Google Scholar] [CrossRef]
- Bhabha, G.; Lee, J.; Ekiert, D.C.; Gam, J.; Wilson, I.A.; Dyson, H.J.; Benkovic, S.J.; Wright, P.E. A dynamic knockout reveals that conformational fluctuations influence the chemical step of enzyme catalysis. Science 2011, 332, 234–238. [Google Scholar] [CrossRef]
- Boehr, D.D.; McElheny, D.; Dyson, H.J.; Wright, P.E. The dynamic energy landscape of dihydrofolate reductase catalysis. Science 2006, 313, 1638–1642. [Google Scholar]
- Eisenmesser, E.Z.; Millet, O.; Labeikovsky, W.; Korzhnev, D.M.; Wolf-Watz, M.; Bosco, D.A.; Skalicky, J.J.; Kay, L.E.; Kern, D. Intrinsic dynamics of an enzyme underlies catalysis. Nature 2005, 438, 117–121. [Google Scholar] [CrossRef]
- Boehr, D.D.; Dyson, H.J.; Wright, P.E. An NMR perspective on enzyme catalysis. Chem. Rev. 2006, 106, 3055–3079. [Google Scholar] [CrossRef]
- Wang, L.; Pang, Y.; Holder, T.; Brender, J.R.; Kurochkin, A.V.; Zuiderweg, E.R.P. Functional dynamics in the active site of the ribonuclease binase. Proc. Nat. Acad. Sci. USA 2001, 98, 7684–7689. [Google Scholar]
- Janin, J. The kinetics of protein-protein recognition. Protein. Struct. Funct. Genet. 1997, 28, 153–161. [Google Scholar] [CrossRef]
- McCammon, J.A. Theory of biomolecular recognition. Curr. Opin. Struct. Biol. 1998, 8, 245–249. [Google Scholar] [CrossRef]
- Sugase, K.; Dyson, H.J.; Wright, P.E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 2007, 447, 1021–1025. [Google Scholar] [CrossRef]
- Neudecker, P.; Lundström, P.; Kay, L.E. Relaxation dispersion NMR spectroscopy as a tool for detailed studies of protein folding. Biophys. J. 2009, 96, 2045–2054. [Google Scholar] [CrossRef]
- Palmer III, A.G.; Kroenke, C.D.; Loria, J.P. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 2001, 339, 204–238. [Google Scholar] [CrossRef]
- Palmer III, A.G.; Massi, F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem. Rev. 2006, 106, 1700–1719. [Google Scholar] [CrossRef]
- Luz, Z.; Meiboom, S. Nuclear magnetic resonance study of the protolysis of trimethylammonium ion in aqueous solution-order of the reaction with respect to solvent. J. Chem. Phys. 1963, 39, 366–370. [Google Scholar] [CrossRef]
- Wennerström, H. Nuclear magnetic relaxation induced by chemical exchange. Mol. Phys. 1972, 24, 69–80. [Google Scholar] [CrossRef]
- Millet, O.; Loria, J.P.; Kroenke, C.D.; Pons, M.; Palmer, A.G., 3rd. The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. J. Am. Chem. Soc. 2000, 122, 2867–2877. [Google Scholar] [CrossRef]
- Deverell, C.; Morgan, R.E.; Strange, J.H. Studies of chemical exchange by nuclear magnetic relaxation in the rotating frame. Mol. Phys. 1970, 18, 553–559. [Google Scholar] [CrossRef]
- Carr, H.Y.; Purcell, E.M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 54, 630–638. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, S. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
- Korzhnev, D.M.; Religa, T.L.; Banachewicz, W.; Fersht, A.R.; Kay, L.E. A transient and low-populated protein-folding intermediate at atomic resolution. Science 2010, 329, 1312–1316. [Google Scholar] [CrossRef]
- Mangia, S.; Traaseth, N.J.; Veglia, G.; Garwood, M.; Michaeli, S. Probing slow protein dynamics by adiabatic R1ρ and R2ρ NMR experiments. J. Am. Chem. Soc. 2010, 132, 9979–9981. [Google Scholar] [CrossRef]
- Traaseth, N.J.; Chao, F.; Masterson, L.R.; Mangia, S.; Garwood, M.; Michaeli, S.; Seelig, B.; Veglia, G. Heteronuclear adiabatic relaxation dispersion (HARD) for quantitative analysis of conformational dynamics in proteins. J. Magn. Reson. 2012, 219, 75–82. [Google Scholar] [CrossRef]
- Davis, D.G.; Perlman, M.E.; London, R.E. Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1ρ and T2 (CPMG) methods. J. Magn. Reson. 1994, 104, 266–275. [Google Scholar] [CrossRef]
- Loria, J.P.; Rance, M.; Palmer III, A.G. A relaxation-compensated carr-purcell-meiboom-gill sequence for characterizing chemical exchange by nmr spectroscopy. J. Am. Chem. Soc. 1999, 121, 2331–2332. [Google Scholar] [CrossRef]
- Mulder, F.A.A.; Skrynnikov, N.R.; Hon, B.; Dahlquist, F.W.; Kay, L.E. Measurement of slow (micro- to millisecond) time scale dynamics in protein side chains by 15N relaxation dispersion NMR spectroscopy: Application to Asn and Gln residues in a cavity mutant of T4 lysozyme. J. Am. Chem. Soc. 2001, 123, 967–975. [Google Scholar]
- Skrynnikov, N.R.; Mulder, F.A.; Hon, B.; Dahlquist, F.W.; Kay, L.E. Probing slow time scale dynamics at methyl-containing side chains in proteins by relaxation dispersion NMR measurements: application to methionine residues in a cavity mutant of T4 lysozyme. J. Am. Chem. Soc. 2001, 123, 4556–4566. [Google Scholar] [CrossRef]
- Tollinger, M.; Skrynnikov, N.R.; Mulder, F.A.; Forman-Kay, J.D.; Kay, L.E. Slow dynamics in folded and unfolded states of an SH3 domain. J. Am. Chem. Soc. 2001, 123, 11341–11352. [Google Scholar]
- Akke, M.; Liu, J.; Cavanagh, J.; Erickson, H.P.; Palmer III, A.G. Pervasive conformational fluctuations on microsecond time scales in a fibronectin type III domain. Nat. Struct. Biol. 1998, 5, 55–59. [Google Scholar] [CrossRef]
- Akke, M.; Palmer III, A.G. Monitoring macromolecular motions on microsecond to Milliesecond time scales by R1ρ-R1 constant relaxation time NMR spectrosocpy. J. Am. Chem. Soc. 1996, 118, 911–912. [Google Scholar] [CrossRef]
- Vugmeyster, L.; Kroenke, C.D.; Picart, F.; Palmer III, A.G.; Raleigh, P. 15N R1r measurements allow the determination of ultrafast protein folding rates. J. Am. Chem. Soc. 2000, 122, 5387–5388. [Google Scholar] [CrossRef]
- Dethoff, E.A.; Petzold, K.; Chugh, J.; Casiano-Negroni, A.; Al-Hashimi, H.M. Visualizing transient low-populated structures of RNA. Nature 2012, 491, 724–728. [Google Scholar]
- Nikolova, E.N.; Kim, E.; Wise, A.A.; O'Brien, P.J.; Andricioaei, I.; Al-Hashimi, H.M. Transient hoogsteen base pairs in canonical duplex DNA. Nature 2011, 470, 498–502. [Google Scholar] [CrossRef]
- Ishima, R.; Torchia, D.A. Estimating the time scale of chemical exchange of proteins from measurements of transverse relaxation rates in solution. J. Biomol. NMR 1999, 14, 369–372. [Google Scholar] [CrossRef]
- Carver, J.P.; Richards, R.E. A general two-site solution for the chemical exchange produced dependence of T2 upon the Carr-Purcell pulse separation. J. Magn. Reson. 1972, 6, 89–105. [Google Scholar]
- Korzhnev, D.M.; Orekhov, V.Y.; Dahlquist, F.W.; Kay, L.E. Off-resonance R1ρ relaxation outside of the fast exchange limit: An experimental study of a cavity mutant of T4 lysozyme. J. Biomol. NMR 2003, 26, 39–48. [Google Scholar] [CrossRef]
- Korzhnev, D.M.; Orekhov, V.Y.; Kay, L.E. Off-resonance R1ρ NMR studies of exchange dynamics in proteins with low spin-lock fields: an application to a Fyn SH3 domain. J. Am. Chem. Soc. 2005, 127, 713–721. [Google Scholar] [CrossRef]
- Trott, O.; Palmer, A.G., 3rd. R1ρ relaxation outside of the fast-exchange limit. J. Magn. Reson. 2002, 154, 157–160. [Google Scholar] [CrossRef]
- Massi, F.; Grey, M.J.; Palmer, A.G., 3rd. Microsecond timescale backbone conformational dynamics in ubiquitin studied with NMR R1ρ relaxation experiments. Protein Sci. 2005, 14, 735–742. [Google Scholar] [CrossRef]
- Salvi, N.; Ulzega, S.; Ferrage, F.; Bodenhausen, G. Timescales of slow motions in ubiquitin explored by heteronuclear double resonance. J. Am. Chem. Soc. 2012, 134, 2481–2484. [Google Scholar] [CrossRef]
- Wolf, M.; Gulich, R.; Lunkenheimer, P.; Loidl, A. Relaxation dynamics of a protein solution investigated by dielectric spectroscopy. Biochim. Biophys. Acta 2012, 1824, 723–730. [Google Scholar] [CrossRef]
- Ban, D.; Mazur, A.; Carneiro, M.G.; Sabo, T.M.; Giller, K.; Koharudin, L.M.I.; Becker, S.; Gronenborn, A.M.; Griesinger, C.; Lee, D. Enhanced accuracy of kinetic information from CT-CMPG experiments by transverse rotating-frame spectroscopy. J. Biomol. NMR 2013, 57, 73–82. [Google Scholar] [CrossRef]
- Ishima, R.; Wingfield, P.T.; Stahl, S.J.; Kaufman, J.D.; Torchia, D.A. Using amide 1H and 15N transverse relaxation to detect millisecond time-scale motions in perdeuterated proteins: application to HIV-1 protease. J. Am. Chem. Soc. 1998, 120, 10534–10542. [Google Scholar] [CrossRef]
- Ishima, R.; Torchia, D.A. Extending the range of amide proton relaxation dispersion experiments in proteins using a constant-time relaxation-compensated CPMG approach. J. Biomol. NMR 2003, 25, 243–248. [Google Scholar] [CrossRef]
- Eichmüller, C.; Skrynnikov, N.R. A new amide proton R1ρ experiment permits accurate characterization of microsecond time-scale conformational exchange. J. Biomol. NMR 2005, 32, 281–293. [Google Scholar] [CrossRef]
- Desvaux, H.; Berthault, P. Study of dynamic processes in liquids using off-resonance rf irradiation. Prog. Nucl. Magn. Reson. Spectros. 1999, 35, 295–340. [Google Scholar] [CrossRef]
- Mills, J.L.; Szyperski, T. Protein dynamics in supercooled water: the search for slow motional modes. J. Biomol. NMR 2002, 23, 63–67. [Google Scholar] [CrossRef]
- Skalicky, J.J.; Sukumaran, D.K.; Mills, J.L.; Szyperski, T. Toward structural biology in supercooled water. J. Am. Chem. Soc. 2000, 122, 3230–3231. [Google Scholar] [CrossRef]
- Igumenova, T.I.; Palmer, A.G., III. Off-Resonance TROSY-selected R1ρ experiment with improved sensitivity for medium- and high-molecular wegith proteins. J. Am. Chem. Soc. 2006, 128, 8110–8111. [Google Scholar] [CrossRef]
- Kempf, J.G.; Jung, J.; Sampson, N.S.; Loria, J.P. Off-resonance TROSY (R1ρ-R1) for quantitation of fast exchange processes in large proteins. J. Am. Chem. Soc. 2003, 125, 12064–12065. [Google Scholar] [CrossRef]
- Pervushin, K.; Riek, R.; Wider, G.; Wüthrich, K. Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc. Nat. Acad. Sci. USA 1997, 94, 12366–12371. [Google Scholar] [CrossRef]
- Nietlispach, D. Suppression of anti-TROSY lines in a sensitivity enhanced gradient selection TROSY scheme. J. Biomol. NMR 2005, 31, 161–166. [Google Scholar] [CrossRef]
- Wang, A.C.; Bax, A. Minimizing the effects of radio-frequency heating in multidimensional NMR experiments. J. Biomol. NMR 1993, 3, 715–720. [Google Scholar]
- Jones, J.A.; Hodgkinson, P.; Barker, A.L.; Hore, P.J. Optimal sampling strategies for the measurement of spin-spin relaxation times. J. Magn. Reson. 1996, 113, 25–34. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multi-Model Inference; Springer: New York, NY, USA, 2002. [Google Scholar]
- Al-Hashimi, H.M.; Gosser, Y.; Gorin, A.; Hu, W.D.; Majumdar, A.; Patel, D.J. Concerted motions in HIV-1 TAR RNA may allow access to bound state conformations: RNA dynamics from NMR residual dipolar couplings. J. Mol. Biol. 2002, 315, 95–102. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ban, D.; Sabo, T.M.; Griesinger, C.; Lee, D. Measuring Dynamic and Kinetic Information in the Previously Inaccessible Supra-tc Window of Nanoseconds to Microseconds by Solution NMR Spectroscopy. Molecules 2013, 18, 11904-11937. https://doi.org/10.3390/molecules181011904
Ban D, Sabo TM, Griesinger C, Lee D. Measuring Dynamic and Kinetic Information in the Previously Inaccessible Supra-tc Window of Nanoseconds to Microseconds by Solution NMR Spectroscopy. Molecules. 2013; 18(10):11904-11937. https://doi.org/10.3390/molecules181011904
Chicago/Turabian StyleBan, David, T. Michael Sabo, Christian Griesinger, and Donghan Lee. 2013. "Measuring Dynamic and Kinetic Information in the Previously Inaccessible Supra-tc Window of Nanoseconds to Microseconds by Solution NMR Spectroscopy" Molecules 18, no. 10: 11904-11937. https://doi.org/10.3390/molecules181011904
APA StyleBan, D., Sabo, T. M., Griesinger, C., & Lee, D. (2013). Measuring Dynamic and Kinetic Information in the Previously Inaccessible Supra-tc Window of Nanoseconds to Microseconds by Solution NMR Spectroscopy. Molecules, 18(10), 11904-11937. https://doi.org/10.3390/molecules181011904



