Research on the Thermal Characteristics of an 18650 Lithium-Ion Battery Based on an Electrochemical–Thermal Flow Coupling Model
Abstract
:1. Introduction
2. Establishment of a Lithium-Ion Battery Model
2.1. Basic Electrochemical Model
2.1.1. Conservation of Charge
2.1.2. Conservation of Matter
2.1.3. Electrochemical Reaction Kinetics
2.2. Basic Thermal Model
2.3. An Electrochemical–Thermal Flow Coupling Model
3. Model Parameters and Experimental Verification
3.1. Lithium-Ion Battery Model Parameters
3.2. Experimental Verification of Model Validity
4. Simulation Results and Analysis
4.1. Results and Analysis of Battery Heat Generation Behavior
4.1.1. Effect of Charge–Discharge Rate on Heat Generation of Battery
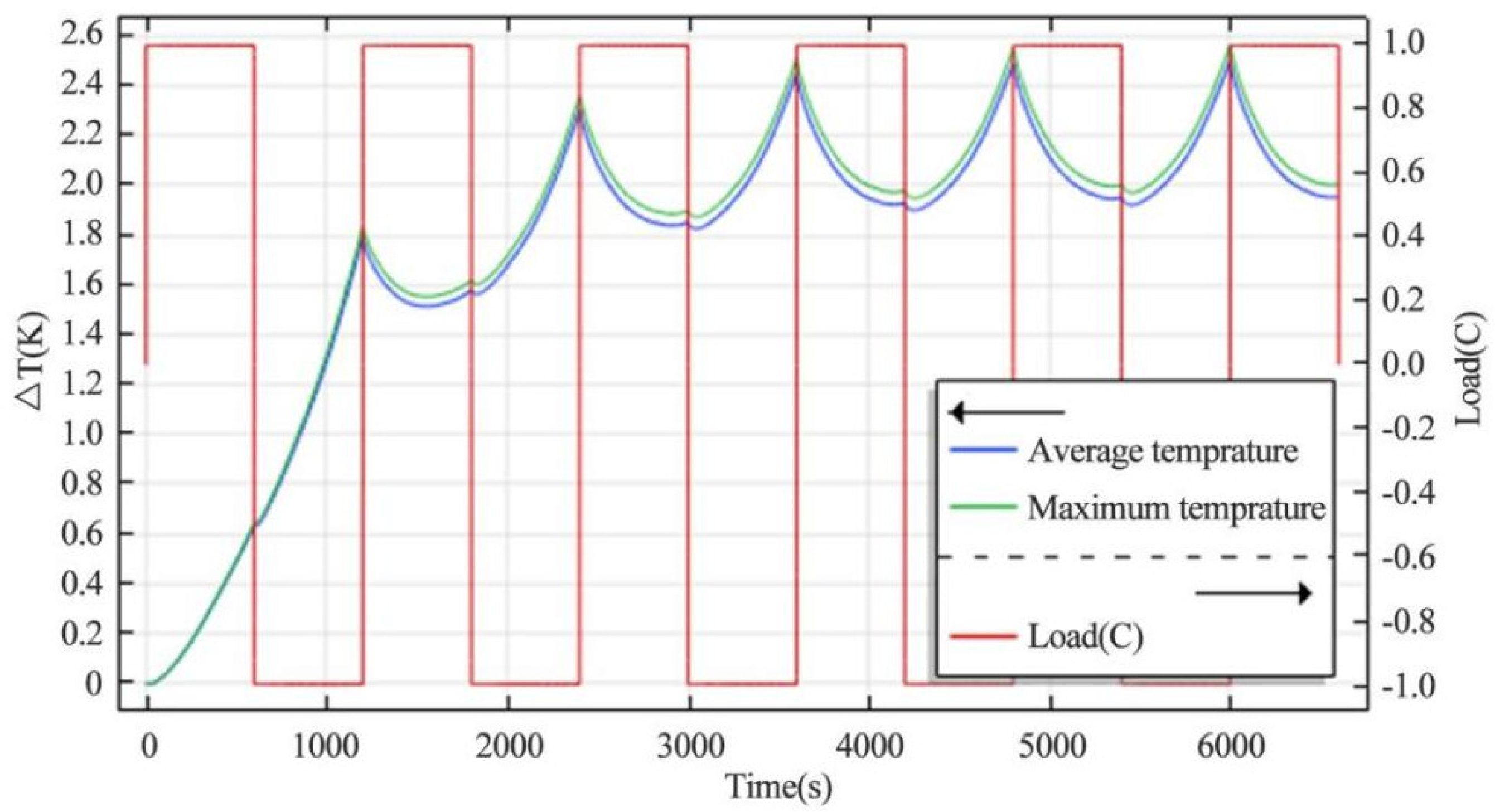
4.1.2. Heating Rate of Continuous Charge–Discharge Cycles
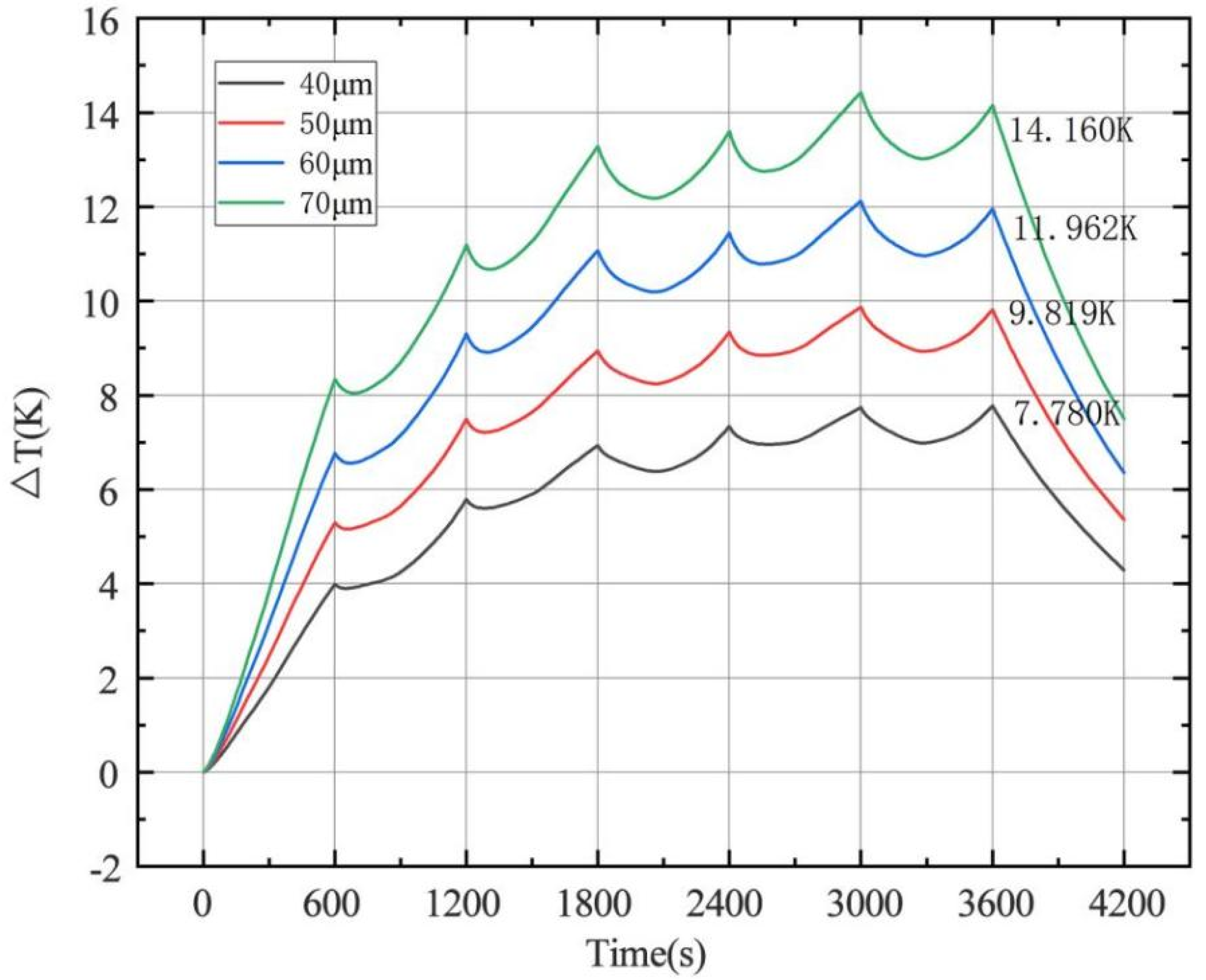
4.1.3. Effect of Electrode Thickness on Temperature
4.2. Results and Analysis of Battery Heat Dissipation Behavior
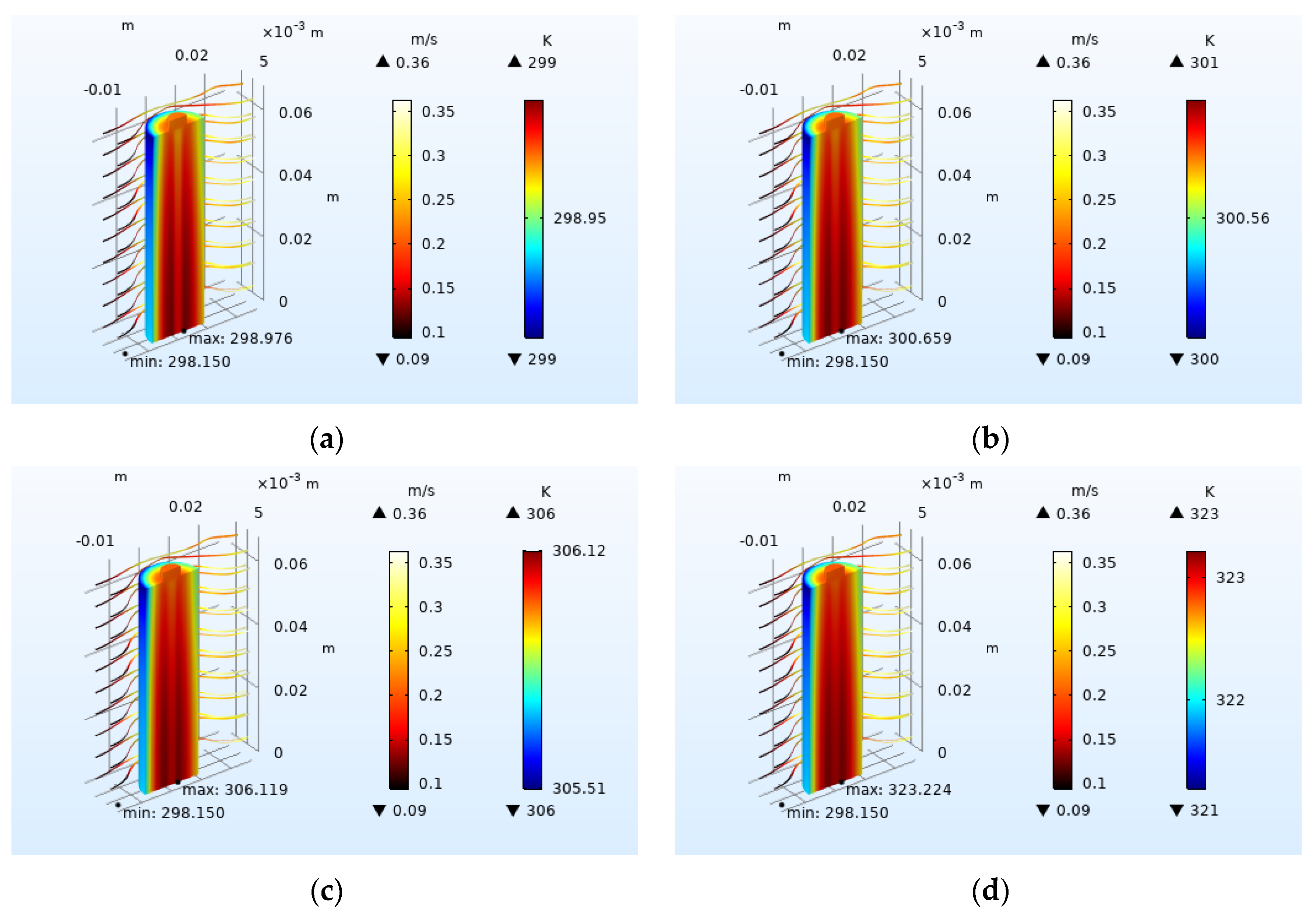
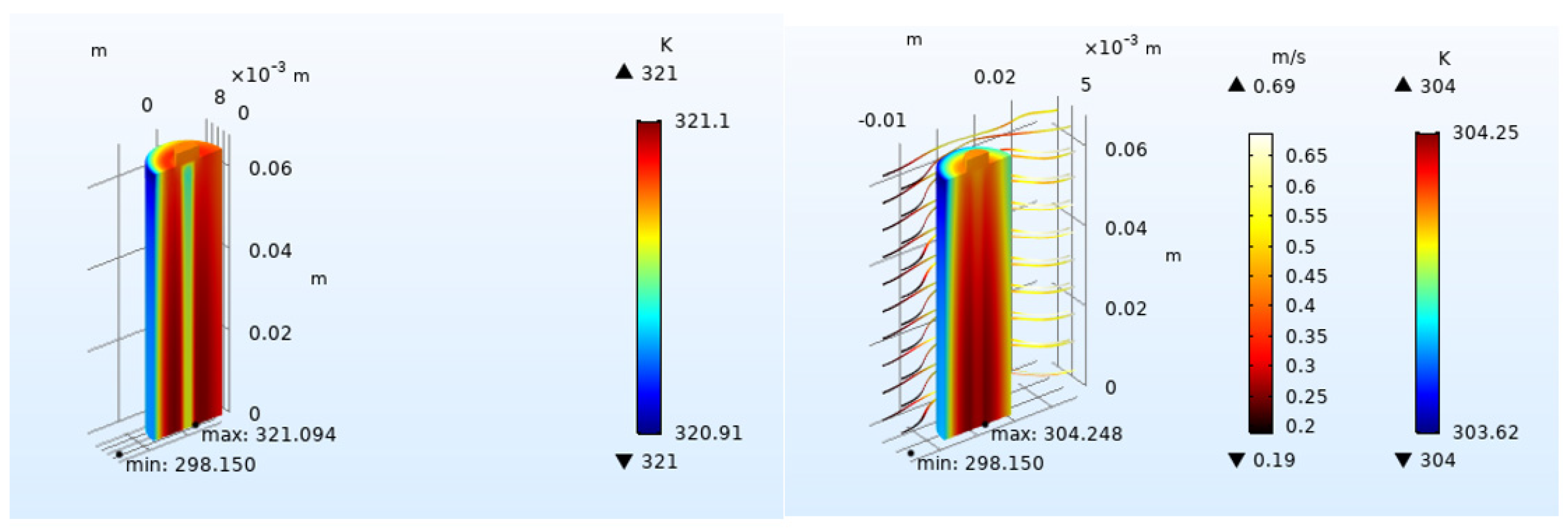
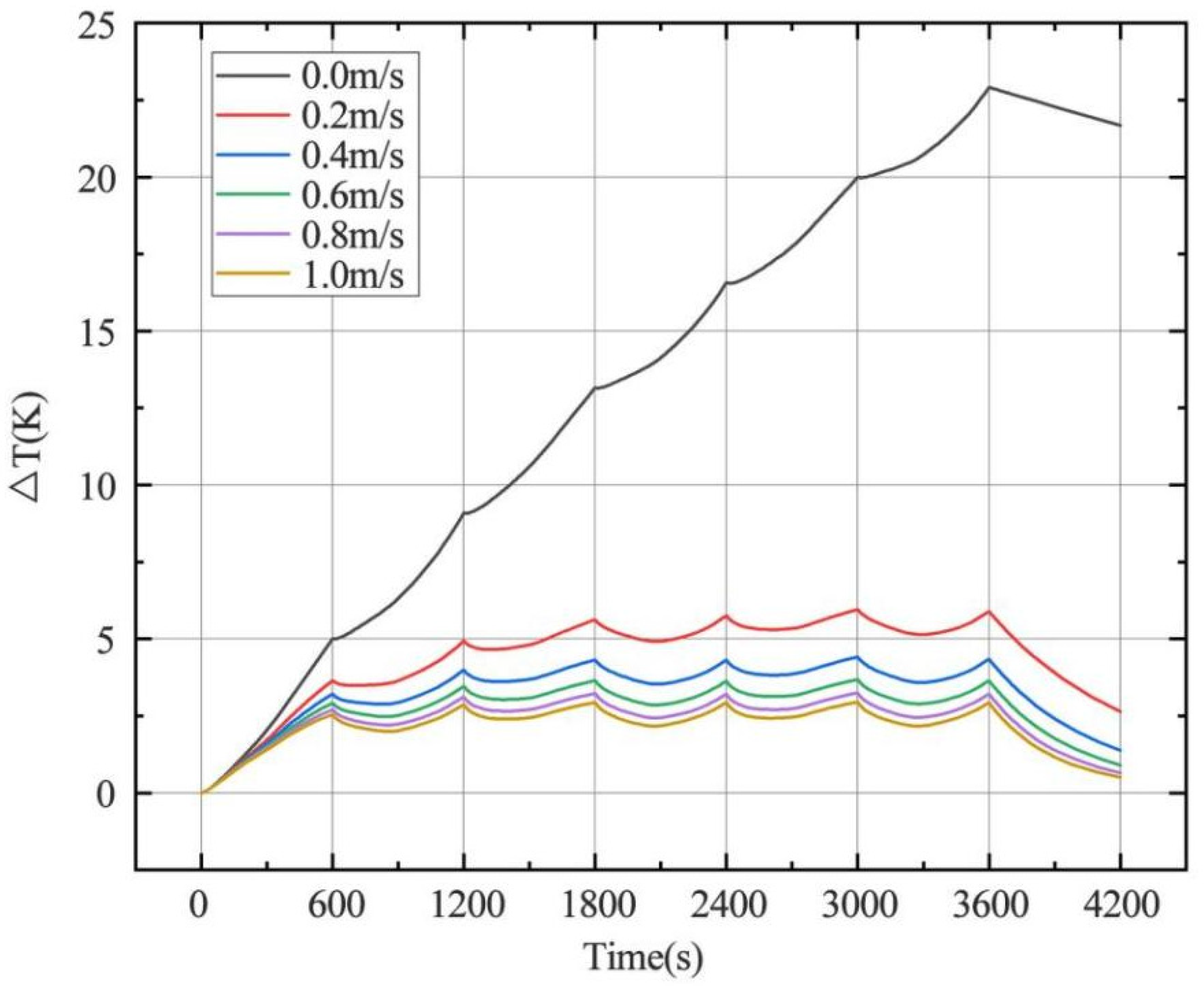
4.2.1. Effect of Inlet Airflow Velocity on Battery Heat Dissipation
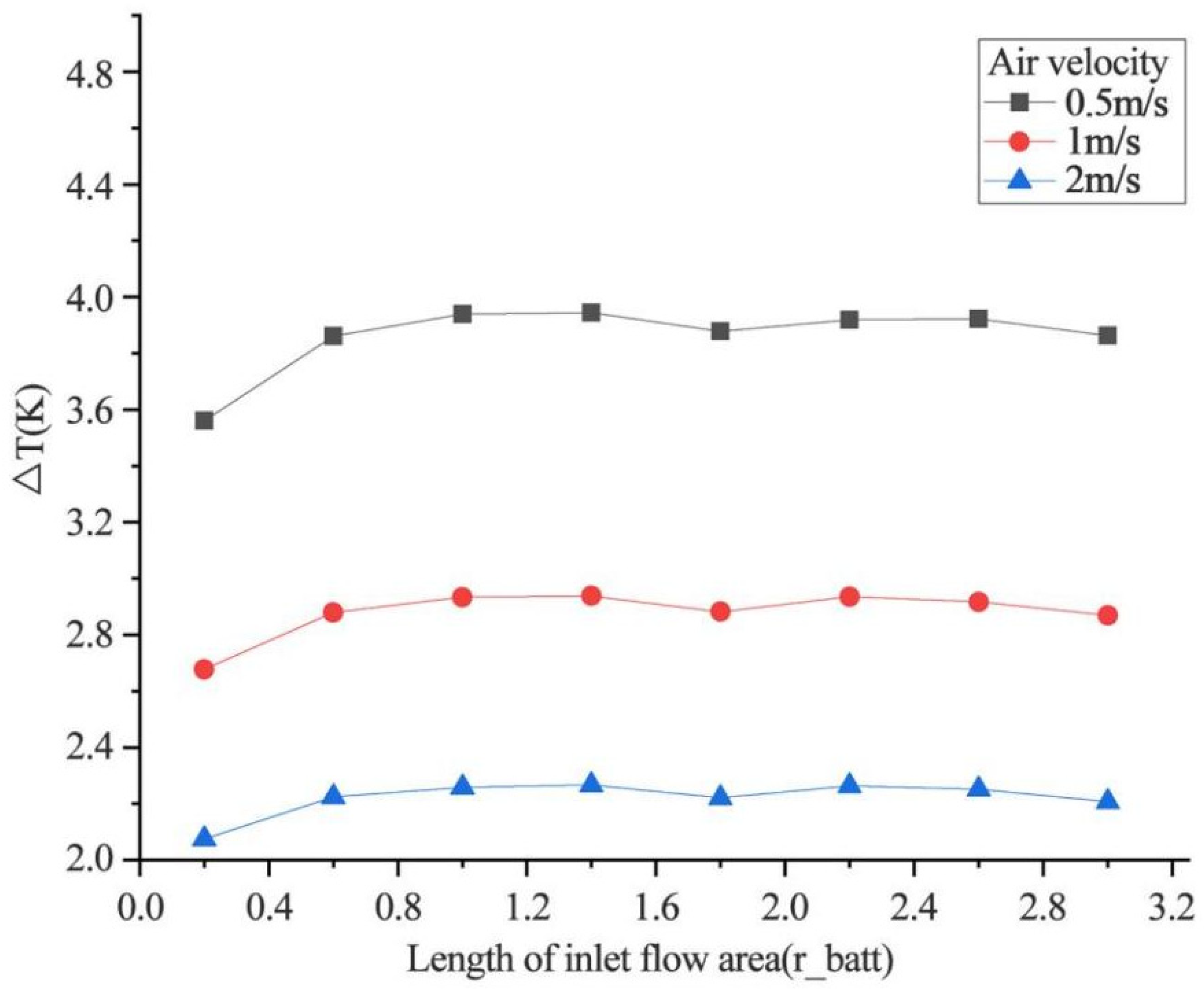
4.2.2. Effect of Inlet Flow Area Size on Heat Dissipation
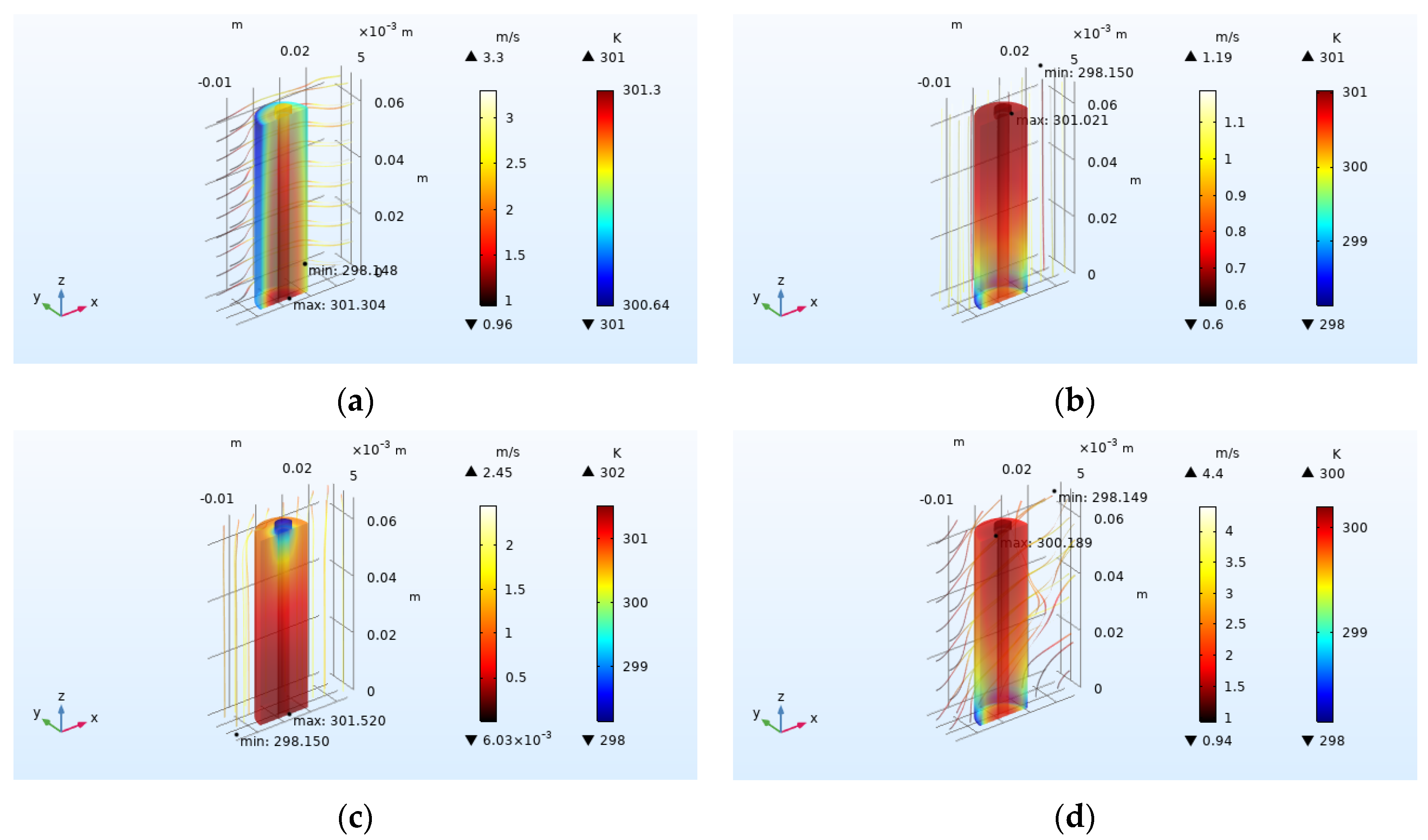
4.2.3. Effect of Airflow Field Direction on Heat Dissipation
5. Conclusions
- (1)
- By establishing a three-dimensional electrochemical–thermal current coupling model of the lithium-ion battery, it is convenient and accurate to study the thermal characteristics of the lithium-ion battery, which is more conducive to observing the temperature distribution inside the battery under different working conditions and can obtain results that are difficult to measure by traditional experiments.
- (2)
- The change of charge and discharge rate has a non-linear effect on the temperature of the battery, and the high-rate charge–discharge has a greater effect on the battery temperature. In the condition of short-time continuous charge–discharge cycles, the temperature rise rate is the highest in the first charge–discharge process. After several cycles, the battery temperature is stable. The thickness of battery electrode is directly proportional to the battery capacity and temperature rise.
- (3)
- Increasing the airflow field is of great help to the heat dissipation of the battery. Increasing the inlet airflow velocity can increase the cooling effect of the battery. The greater the inlet velocity, the better the heat dissipation effect. The closer the inlet flow area is to the battery, the better the heat dissipation effect, but the effect on the battery temperature after exceeding one time of the battery radius is not obvious. In the condition of the single airflow field, the cooling effect is best when air enters the positive electrode from the negative electrode of the battery along the axis. In the future, the temperature distribution in the case of battery groups will be studied, and the airflow field will be added to optimize the heat dissipation of battery packs based on the results obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| List of Symbols | |
| reaction surface area | |
| electrode area | |
| C | ) |
| D | |
| F | |
| convective heat transfer coefficient of the battery | |
| I | |
| L | |
| Q | |
| ohmic heat | |
| reaction heat | |
| active polarization heat | |
| heat dissipation rate | |
| T | temperature (°C) |
| t | |
| Greek Letters | |
| density | |
| Subscripts/Superscripts | |
| current collector | |
| electrolyte | |
| filler | |
| effective | |
| solid | |
| negative | |
| positive | |
| surf | surface |
References
- Omariba, Z.B.; Zhang, L.; Kang, H.; Sun, D. Parameter identification and state estimation of lithium-ion batteries for electric vehicles with vibration and temperature dynamics. World Electr. Veh. J. 2020, 11, 50. [Google Scholar] [CrossRef]
- Hossain, L.; Hannan, M.A.; Aini, H.; Hoque, M.M.; Ker, P.J.; Saad, M.; Afida, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar]
- Yan, Y.; Wang, Q.; Jiang, B.; Li, B. A critical review of thermal management models and solutions of lithium-ion batteries for the development of pure electric vehicles. Renew. Sust. Energ. Rev. 2016, 64, 106–128. [Google Scholar]
- Maleki, H.; Hallaj, S.A.; Selman, J.R.; Dinwiddie, R.B.; Wang, H. Thermal properties of lithium-ion battery and components. J. Electrochem. Soc. 2015, 146, 947–954. [Google Scholar] [CrossRef]
- Zhang, X. Thermal analysis of a cylindrical lithium-ion battery. Electrochim. Acta 2011, 56, 1246–1255. [Google Scholar] [CrossRef]
- Duan, X.; Jiang, W.; Zou, Y.; Zeng, S. A coupled electrochemical-thermal-mechanical model for spiral-wound Li-ion batteries. J. Mater. Sci. 2018, 53, 10987–11001. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. A pseudo three-dimensional electrochemical–thermal model of a prismatic LiFePO4 battery during discharge process. Energy 2015, 80, 303–317. [Google Scholar] [CrossRef]
- Dai, H.; Zhu, L.; Zhu, J.; Wei, X.; Sun, Z. Adaptive Kalman filtering based internal temperature estimation with an equivalent electrical network thermal model for hard-cased batteries. J. Power Sources 2015, 293, 351–365. [Google Scholar] [CrossRef]
- Wu, X.; Wang, W.; Sun, Y.; Wen, T.; Du, J. Study on the Capacity Fading Effect of Low-Rate Charging on Lithium-Ion Batteries in Low-Temperature Environment. World Electr. Veh. J. 2020, 11, 55. [Google Scholar] [CrossRef]
- Cheng, X.; Nan, S.; Yang, L.; Wang, S. Engineering-Oriented Modeling for Thermal Behaviors of 18650 Li-ion Batteries. Energy Procedia 2017, 105, 4757–4762. [Google Scholar] [CrossRef]
- Jaguemont, J.; Omar, N.; Martel, F.; Peter, V.; Mierlo, J.V. Streamline three-dimensional thermal model of a lithium titanate pouch cell battery in extreme temperature conditions with module simulation. J. Power Sources 2017, 367, 24–33. [Google Scholar] [CrossRef]
- Du, S.L.; Lai, Y.Q.; Jia, M.; Cheng, Y.; Liu, Y.X. Electrothermal characteristics simulation of cylindrical automotive lithium-ion battery. Chin. J. Nonferr. Metals 2014, 24, 1823–1830. [Google Scholar]
- Chen, J. Analysis of Thermal Performance of 18650 Li-Ion Battery Based on an Electrochemical-Thermal Coupling Model. Hans J. Chem. Eng. Technol. 2018, 8, 97–107. [Google Scholar] [CrossRef]
- Edouard, C.; Petit, M.; Forgez, C.; Bernard, J.; Revel, R. Parameter sensitivity analysis of a simplified electrochemical and thermal model for Li-ion batteries aging. J. Power Sources 2016, 325, 482–494. [Google Scholar] [CrossRef]
- Tran, N.T.; Farrell, T.; Vilathgamuwa, M.; Choi, S.S.; Li, Y. A computationally efficient coupled electrochemical-thermal model for large format cylindrical lithium ion batteries. J. Electrochem. Soc. 2019, 166, A3059–A3071. [Google Scholar] [CrossRef]
- Capron, O.; Samba, A.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Thermal behaviour investigation of a large and high power lithium iron phosphate cylindrical cell. Energies 2015, 8, 10017–10042. [Google Scholar] [CrossRef] [Green Version]
- Chiew, J.; Chin, C.S.; Toh, W.D.; Gao, Z.; Jia, J.; Zhang, C.Z. A pseudo three-dimensional electrochemical-thermal model of a cylindrical LiFePO4/graphite battery. Appl. Therm. Eng. 2019, 147, 450–463. [Google Scholar] [CrossRef] [Green Version]
- Ghaznavi, M.; Chen, P. Sensitivity analysis of a mathematical model of lithium e sulfur cells part I: Applied discharge current and cathode conductivity. J. Power Sources 2013, 257, 4–11. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, A1–A10. [Google Scholar] [CrossRef] [Green Version]
- Doyle, M.; Gozdz, A.S.; Schmutz, C.N. Comparison of Modeling Predictions with Experimental Data From Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Hunt, M.J.; Brosa Planella, F.; Theil, F.; Widanage, W.D. Derivation of an effective thermal electrochemical model for porous electrode batteries using asymptotic homogenisation. J. Eng. Math. 2020, 122, 31–57. [Google Scholar] [CrossRef]
- Nie, P.; Zhang, S.; Ran, A.; Yang, C.; Chen, S.; Li, Z. Full-cycle electrochemical-thermal coupling analysis for commercial lithium-ion batteries. Appl. Therm. Eng. 2020, 184, 116258. [Google Scholar] [CrossRef]
- Hosseinzadeh, E.; Marco, J.; Jennings, P. Electrochemical-Thermal Modelling and Optimisation of Lithium-Ion Battery Design Parameters Using Analysis of Variance. Energies 2017, 10, 1278. [Google Scholar] [CrossRef] [Green Version]
- Rao, L.; Newman, J. Heat-generation rate and general energy balance for insertion battery systems. J. Electrochem. Soc. 1997, 144, 2697–2704. [Google Scholar] [CrossRef]
- Gu, B.; Wang, C. Thermal-Electrochemical Modeling of Battery System. J. Electrochem. 2000, 147, 2910–2922. [Google Scholar] [CrossRef]
- Kim, U.S.; Shin, C.B.; Kim, C.S. Effect of electrode configuration on the thermal behavior of a lithium-polymer battery. J. Power Sources 2009, 180, 909–916. [Google Scholar] [CrossRef]
- Ianniciello, L.; Biwolé, P.H.; Achard, P. Electric vehicles batteries thermal management systems employing phase change materials. J. Power Sources 2018, 378, 383–403. [Google Scholar] [CrossRef]
- Miranda, D.; Costa, C.M.; Almeida, A.M.; Lanceros-Méndez, S. Computer simulation of the influence of thermal conditions on the performance of conventional and unconventional lithium-ion battery geometries. Energy 2018, 149, 262–278. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Ai, L.; Jia, M.; Du, S.; Yin, B.; Zhang, H. 3D simulation on the internal distributed properties of lithium-ion battery with planar tabbed configuration. J. Power Sources 2015, 293, 993–1005. [Google Scholar] [CrossRef]
- Ecker, M.; Käbitz, S.; Laresgoiti, I.; Sauer, D.U. Parameterization of a physico-chemical model of a lithium-ion battery: II. Model validation. J. Electrochem. Soc. 2015, 162, A1836–A1848. [Google Scholar] [CrossRef]
- Naoki, N.; Feixiang, W.; Jung, T.; Gleb, Y. Li-ion battery materials: Present and future. Mater. Today 2015, 6, 18. [Google Scholar]
- Brown, S.; Mellgren, N.; Vynnycky, M.; Lindbergh, G. Impedance as a Tool for Investigating Aging in Lithium-Ion Porous Electrodes. II. Positive Electrode Examination. J. Electrochem. Soc. 2008, 155, A320. [Google Scholar] [CrossRef]
- Nyman, A.; Behm, M.; Lindbergh, G. Electrochemical characterisation and modelling of the mass transport phenomena in LiPF6-EC-EMC. Electrochim. Acta 2008, 53, 6356. [Google Scholar] [CrossRef]
- Gerver, R.E.; Meyers, J.P. Three-Dimensional Modeling of Electrochemical Performance and Heat Generation of Lithium-Ion Batteries in Tabbed Planar Configurations. J. Electrochem. Soc. 2011, 158, A835. [Google Scholar] [CrossRef]
- Wang, S.; Li, K.; Tian, Y.; Wang, J.; Wu, Y.; Ji, S. An experimental and numerical examination on the thermal inertia of a cylindrical lithium-ion power battery. Appl. Therm. Eng. 2019, 154, 676–685. [Google Scholar] [CrossRef] [Green Version]
- Cheng, F.; Roger, L.; Jia, M. Simulation study on heat dissipation structure of power lithium battery module. Chin. J. Nonferr. Metals 2015, 6, 1067–1616. [Google Scholar]
- Smith, K.; Wang, C.Y. Solid-state diffusion limitations on pulse operation of a lithium ion cell for hybrid electric vehicles. J. Power Sources 2006, 161, 628–639. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. Two-dimensional electrochemical-thermal coupled modeling of cylindrical LiFePO4 batteries. J. Power Sources 2014, 256, 233–243. [Google Scholar] [CrossRef]
- Gerd, L.; Ulf, K.; Stefan, G.; Frank, S.; Carsten, A. The Impact of Environmental Factors on the Thermal Characteristic of a Lithium-ion Battery. Batteries 2020, 6, 3. [Google Scholar]
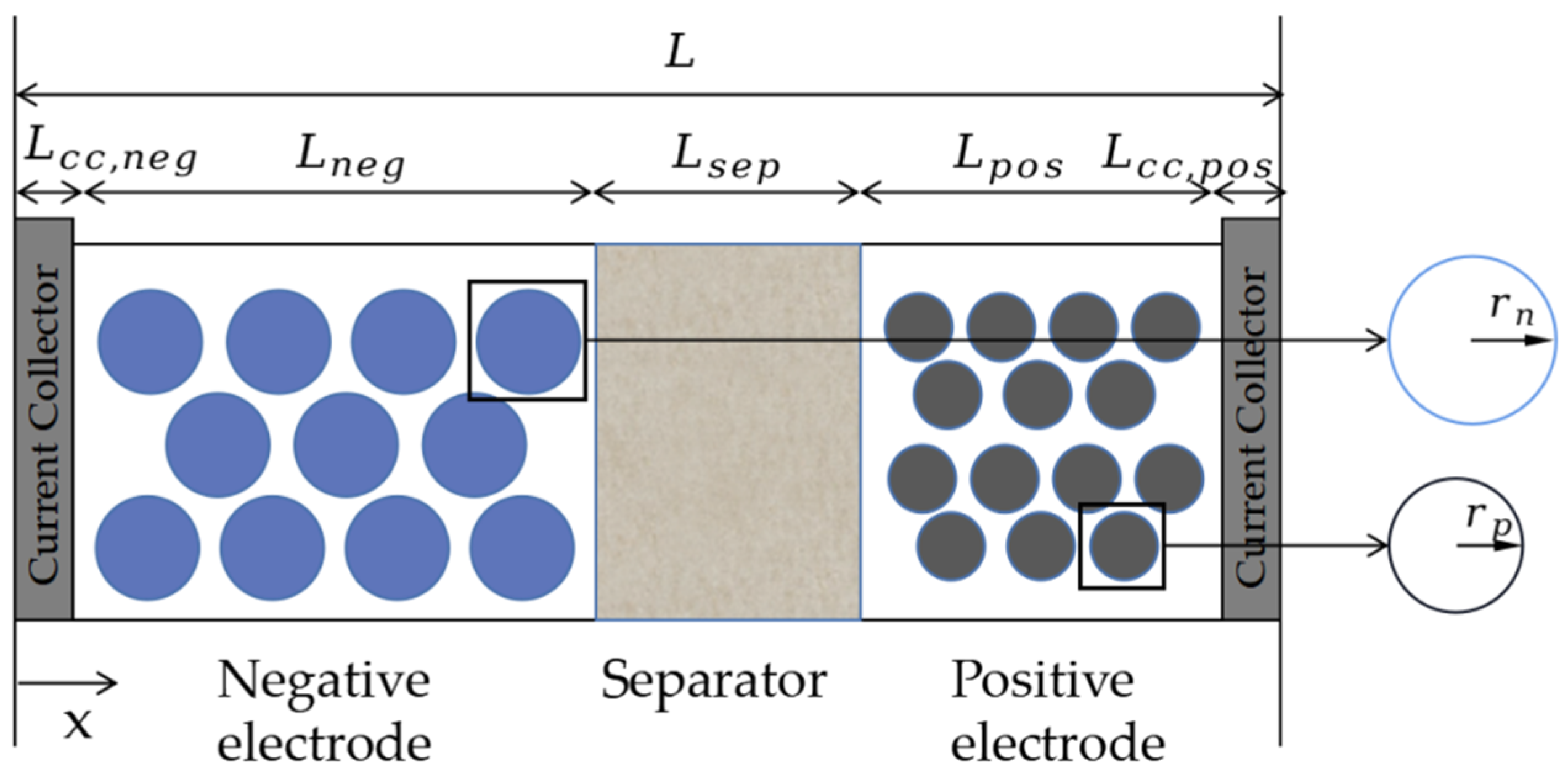

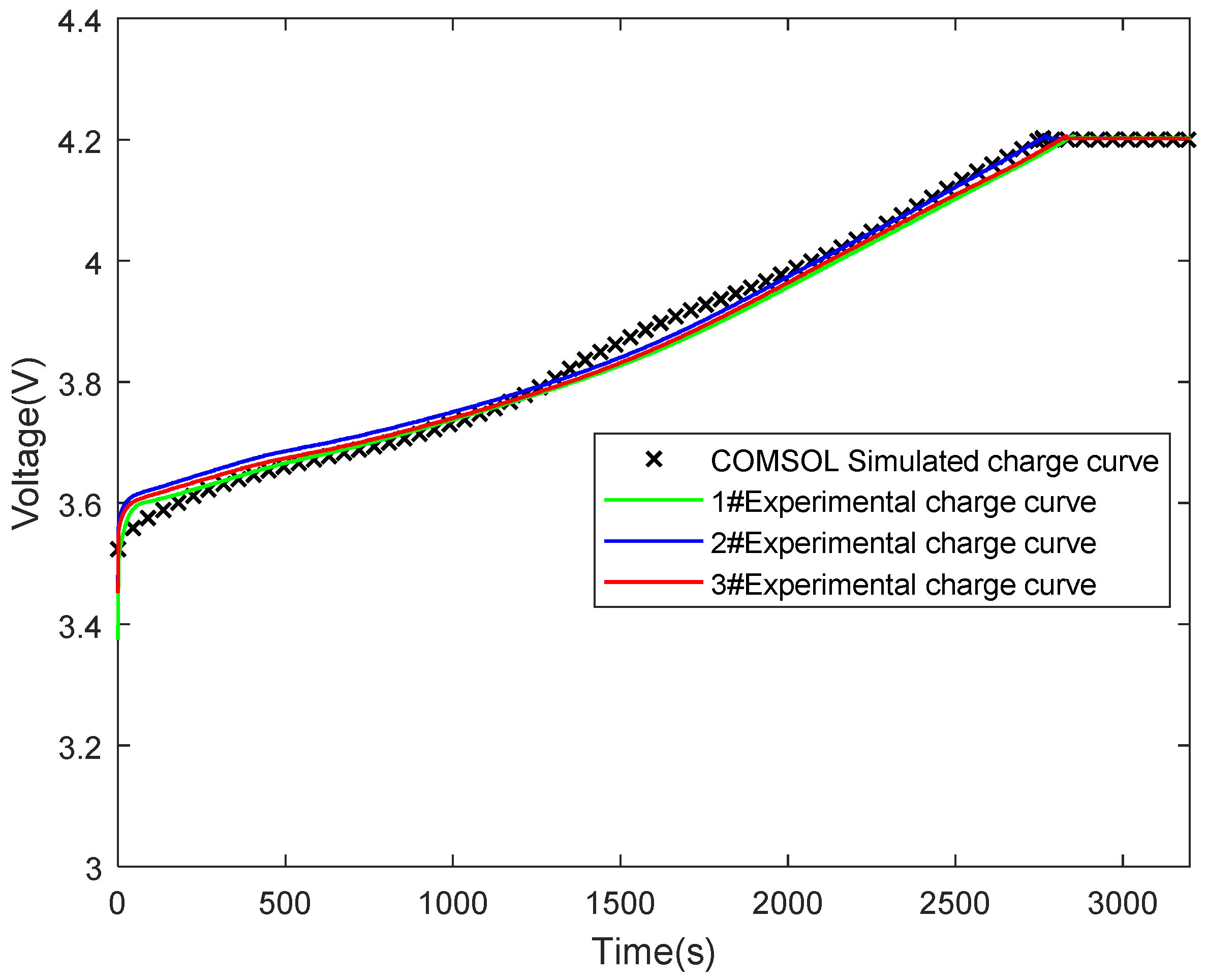

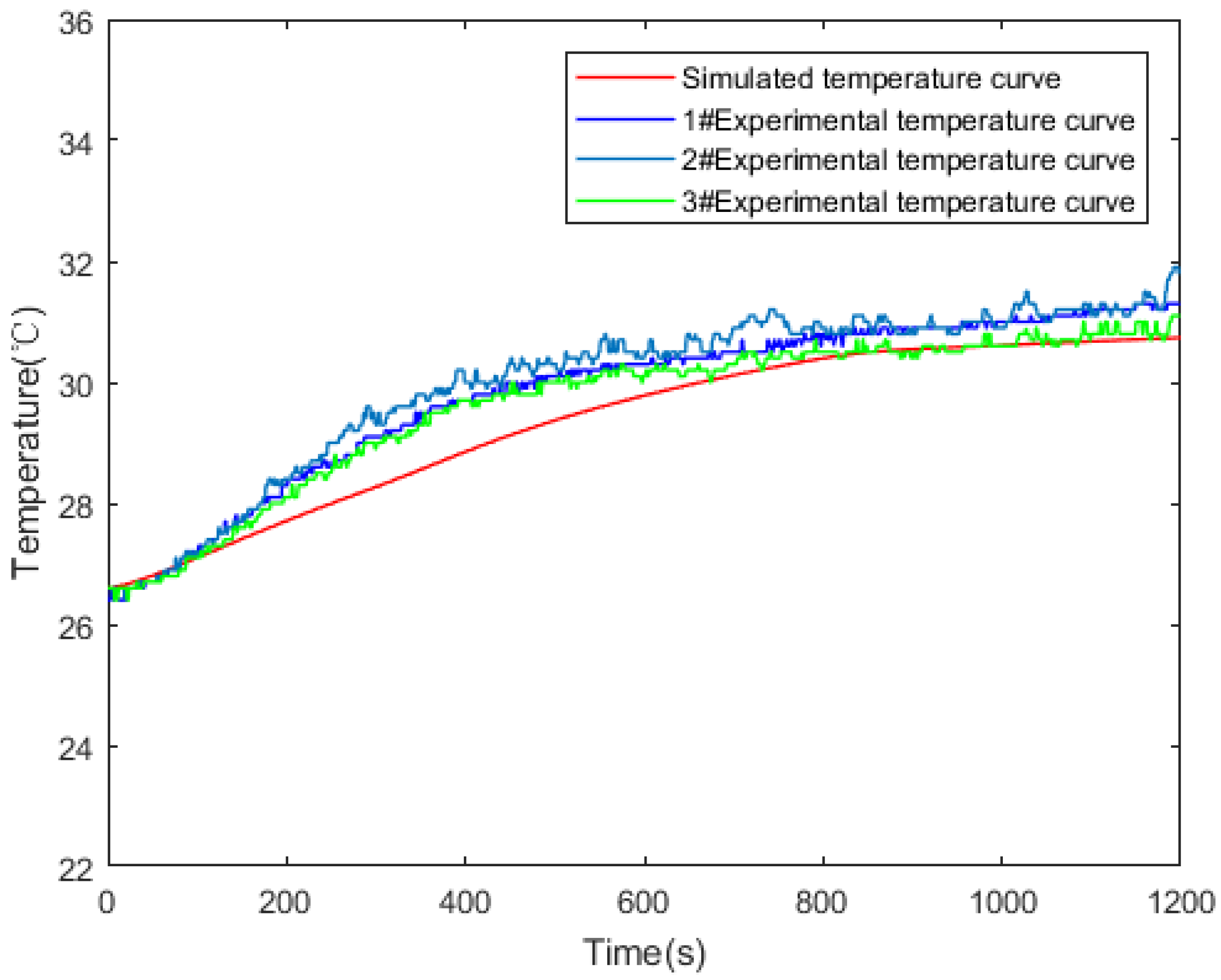
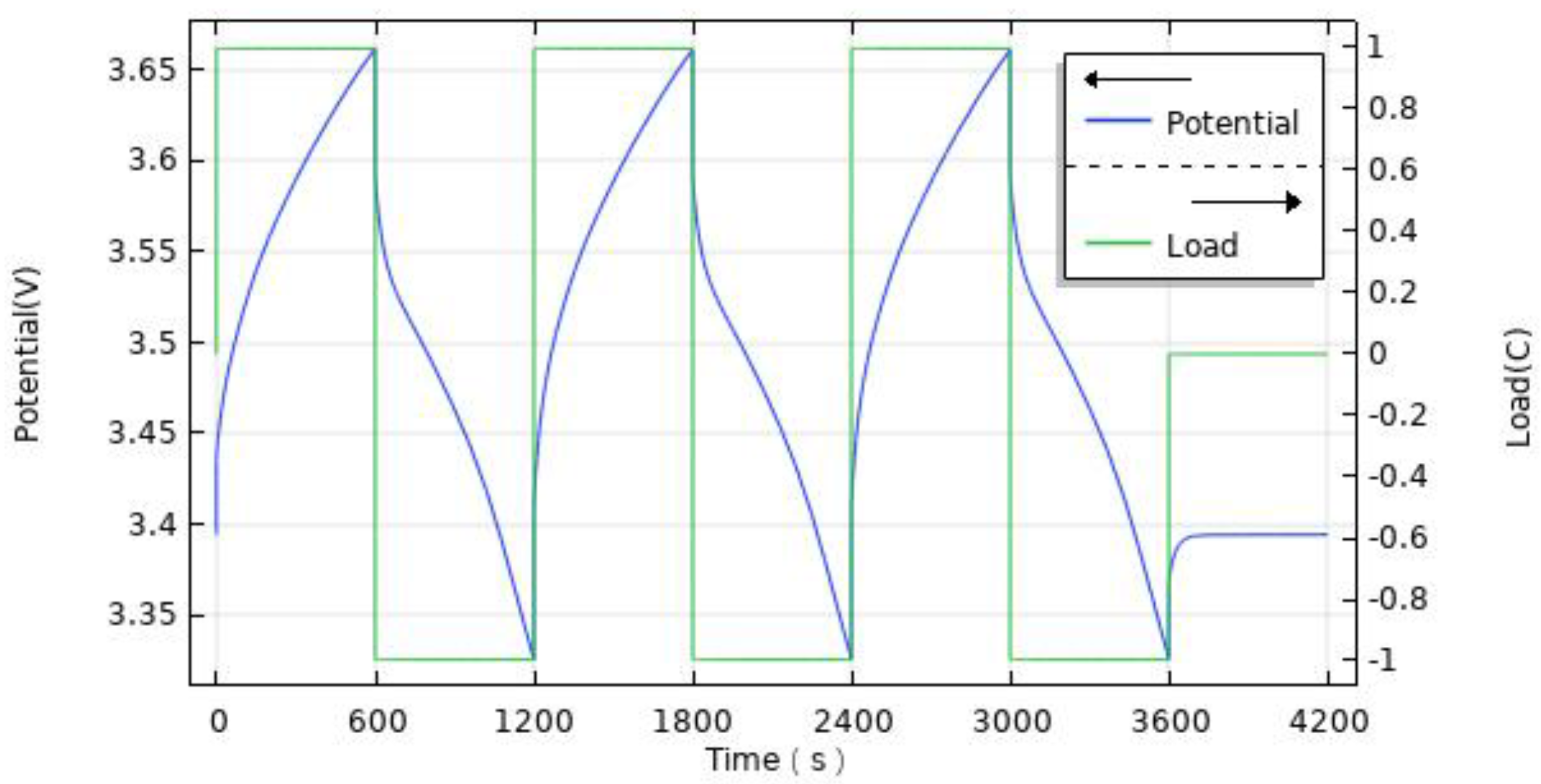



| Technical Parameter | Parameter Value |
|---|---|
| Capacity (Ah) | 2.9 |
| Operating nominal voltage (V) | 3.7 |
| Charging cutoff voltage (V) | 4.2 |
| Discharge cutoff voltage (V) | 2.5 |
| Positive electrode material | |
| Negative electrode material | |
| Electrolyte | |
| Diameter (mm) | |
| Height (mm) |
| Parameter | Positive Electrode [31,32] | Separator [33] | Negative Electrode [34,35] |
|---|---|---|---|
| ) | 0.25 | 2.5 | |
| Volume fraction of active substances | 0.42 | 0.384 | |
| Electrolyte volume fraction [23] | 0.41 | 0.37 | 0.444 |
| ) [23] | 1200 | ||
| ) | 48,000 | 31,507 | |
| ) | 700 | 1978.2 | 1437.4 |
| ) | 5 | 0.334 | 1.04 |
| s) [36] | |||
| ) | 40 | 30 | 55 |
| Average Temperature Rise (K) | Maximum Temperature Rise (K) | |||
|---|---|---|---|---|
| 40 | 55.00 | 16.210 | 7.780 | 7.969 |
| 45 | 61.88 | 18.236 | 8.801 | 9.015 |
| 50 | 68.75 | 20.262 | 9.819 | 10.058 |
| 55 | 75.63 | 22.288 | 10.880 | 11.147 |
| 60 | 82.50 | 24.314 | 11.962 | 12.257 |
| 65 | 89.38 | 26.345 | 13.063 | 13.388 |
| 70 | 96.25 | 28.367 | 14.160 | 14.514 |
| Airflow Field Direction | Average Temperature Rise (K) | Maximum Temperature Rise (K) | Average Temperature Drop (K) | Heat Dissipation Efficiency |
|---|---|---|---|---|
| No flow field | 22.913 | 22.950 | 0 | 0 |
| Radial X | 2.934 | 3.154 | 19.979 | 0.872 |
| Axial Z | 2.425 | 2.873 | 20.488 | 0.894 |
| Axial −Z | 2.948 | 3.370 | 19.965 | 0.871 |
| Axis-diameter coupling | 1.701 | 2.051 | 21.212 | 0.926 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zhang, L. Research on the Thermal Characteristics of an 18650 Lithium-Ion Battery Based on an Electrochemical–Thermal Flow Coupling Model. World Electr. Veh. J. 2021, 12, 250. https://doi.org/10.3390/wevj12040250
Liu G, Zhang L. Research on the Thermal Characteristics of an 18650 Lithium-Ion Battery Based on an Electrochemical–Thermal Flow Coupling Model. World Electric Vehicle Journal. 2021; 12(4):250. https://doi.org/10.3390/wevj12040250
Chicago/Turabian StyleLiu, Guanchen, and Lijun Zhang. 2021. "Research on the Thermal Characteristics of an 18650 Lithium-Ion Battery Based on an Electrochemical–Thermal Flow Coupling Model" World Electric Vehicle Journal 12, no. 4: 250. https://doi.org/10.3390/wevj12040250
APA StyleLiu, G., & Zhang, L. (2021). Research on the Thermal Characteristics of an 18650 Lithium-Ion Battery Based on an Electrochemical–Thermal Flow Coupling Model. World Electric Vehicle Journal, 12(4), 250. https://doi.org/10.3390/wevj12040250







