The Evolutionary Game Analysis and Optimization Algorithm of Electric Vehicle Cell Innovation Diffusion Based on a Patent Pool Strategy
Abstract
:1. Introduction
2. Literature Background
- (1)
- What are the innovation diffusion structures under the patent pool scenario?
- (2)
- What are the factors that influenced the adoption of patent pools, which are the most important factors, and how do these factors influence each other?
- (3)
- What is the best strategy to maximize the return of the players?
3. Proposed Model
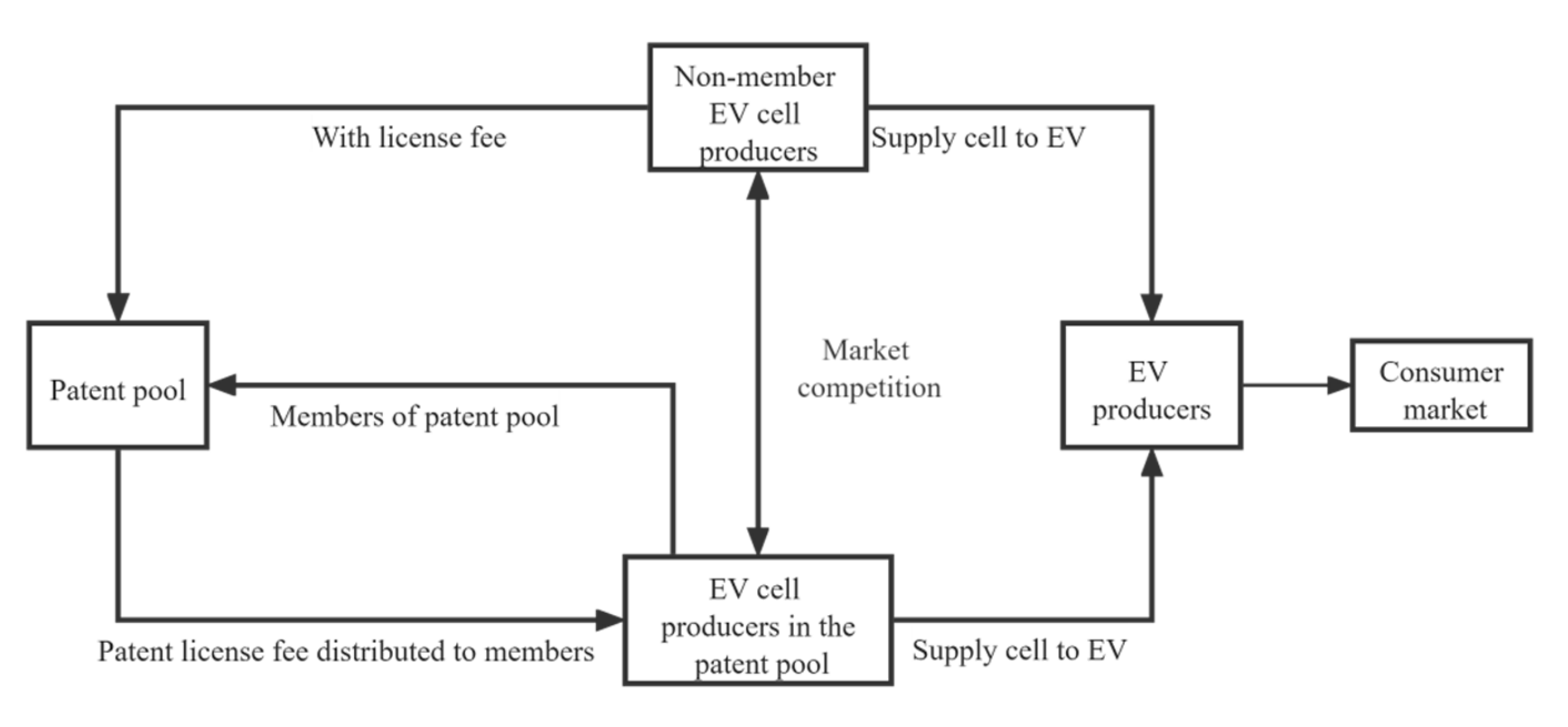
3.1. The Innovation Diffusion Channel of the EV Cell Patent Pool
3.2. Assumptions
- (1)
- Market potential assumptions: We assumed that the overall potential market size after its long-term evolution and the actual current market size follow a logistic growth model (i.e., short term to long term).
- (2)
- Technology advantage assumptions: We assumed that the EV cell technology in the patent pool has a competitive advantage over other options, i.e., the EV cell has higher safety and performance, such as shorter charging time and longer battery range. The advantage ratio of the potential market share of the EV cell patent pool is in the range of [0.5, 1].
- (3)
- Patent pool licensing assumptions: We assumed that patent holders in the patent pool can use the patents in the patent pool free of charge, while non-members need to pay a patent licensing fee to the patent pool at a package cost. The licensing fee is distributed to the members of the patent pool based on their contributions to the patent pool.
- (4)
- Player assumptions: We assumed that there are EV cell patent holders in the patent pool (number n), that there are non-member licensees outside the patent pool (number s), and that each member or non-member owns one EV cell producer.
- (5)
- Adoption decision-making assumptions: We assumed that producers’ adoption decision making is based on calculations and comparisons of the benefits and costs. If the benefit is greater than the cost to adopt the patent pool, then the adopter will choose to adopt; otherwise, they will not.
3.3. Payoff for Players
3.4. Replicator Dynamic Equation
4. Simulation
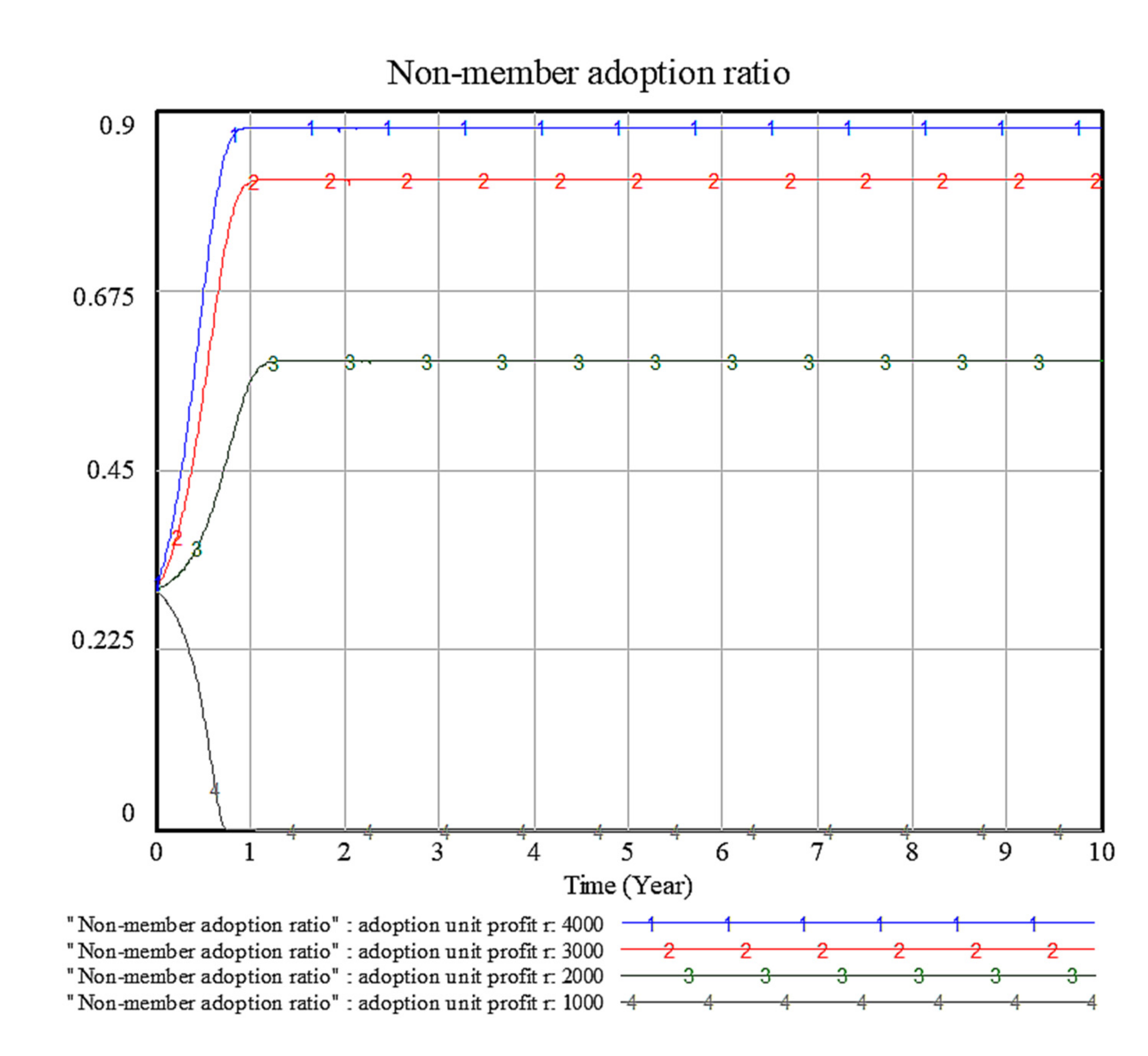
4.1. Sensitivity Analysis of Factor r: Unit Profit of Non-Member EV Cell Producers That Adopts the Patent Pool
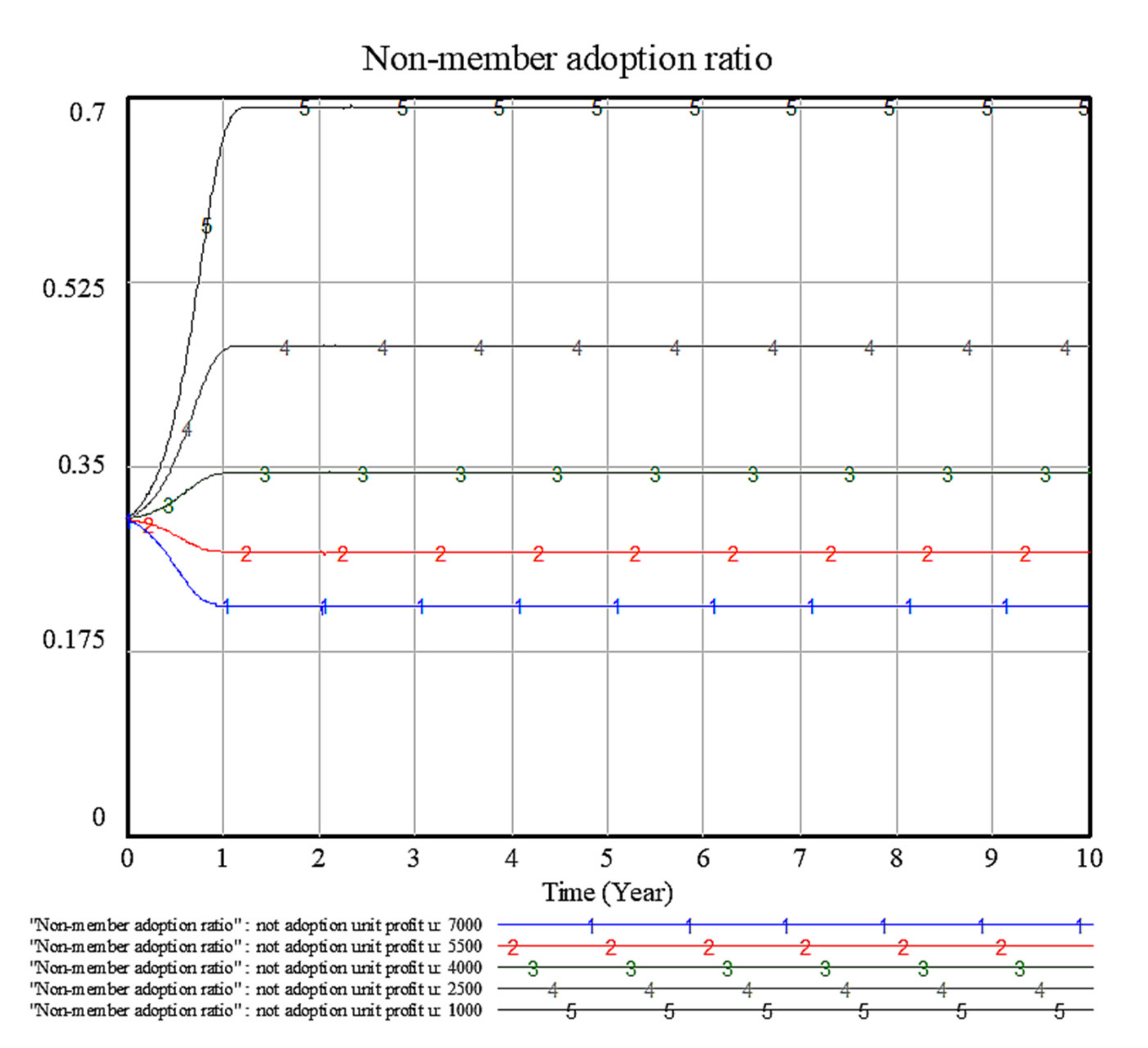
4.2. Sensitivity Analysis of Factor u: Unit Profit of Non-member EV Cell Producers That Adopted the Non-Patent Pool Technology
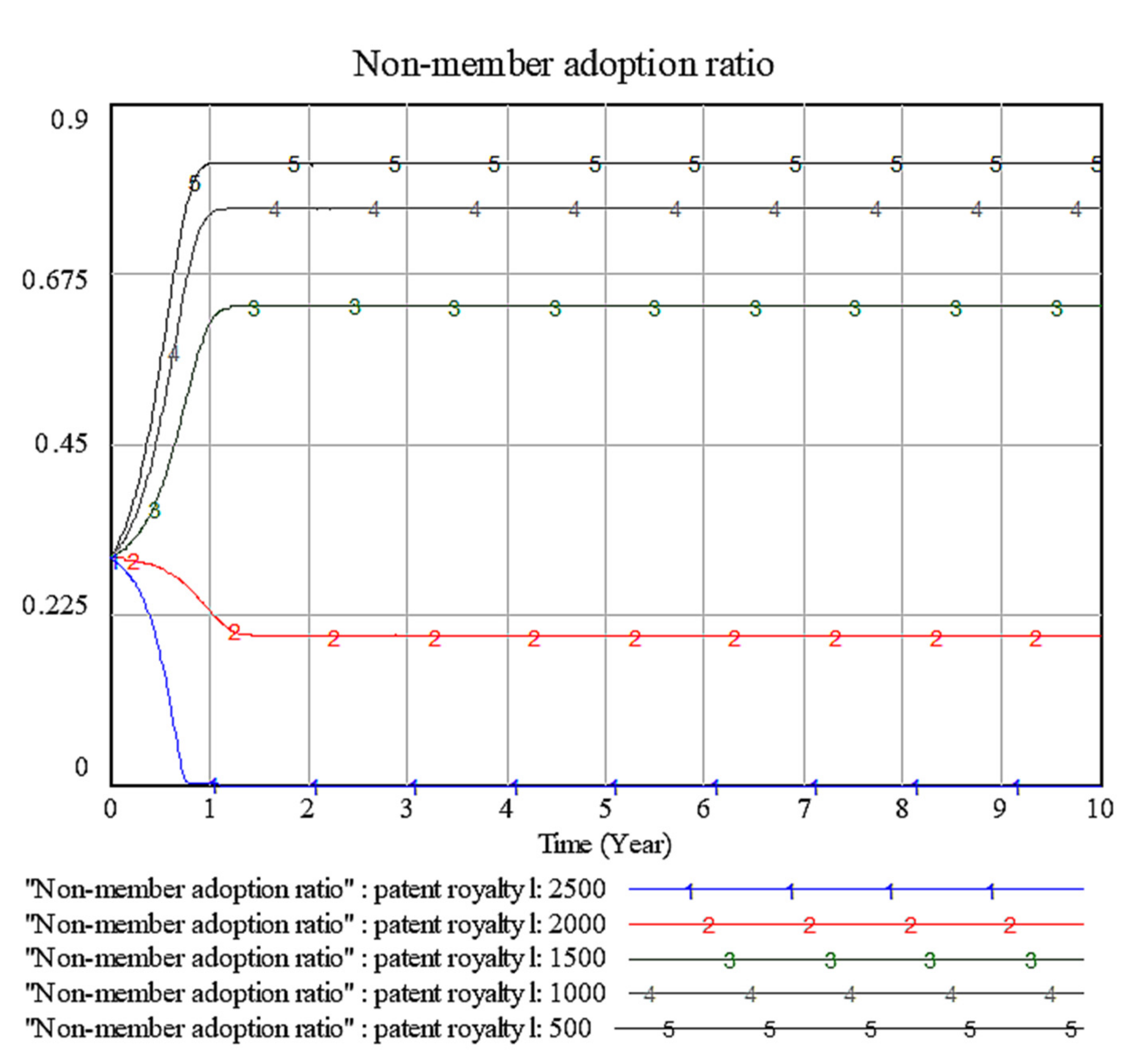
4.3. Sensitivity Analysis of Factor l: The Patent Royalty of Each Unit EV Cell of Each EV Cell Producer That Pays for the Patent Pool
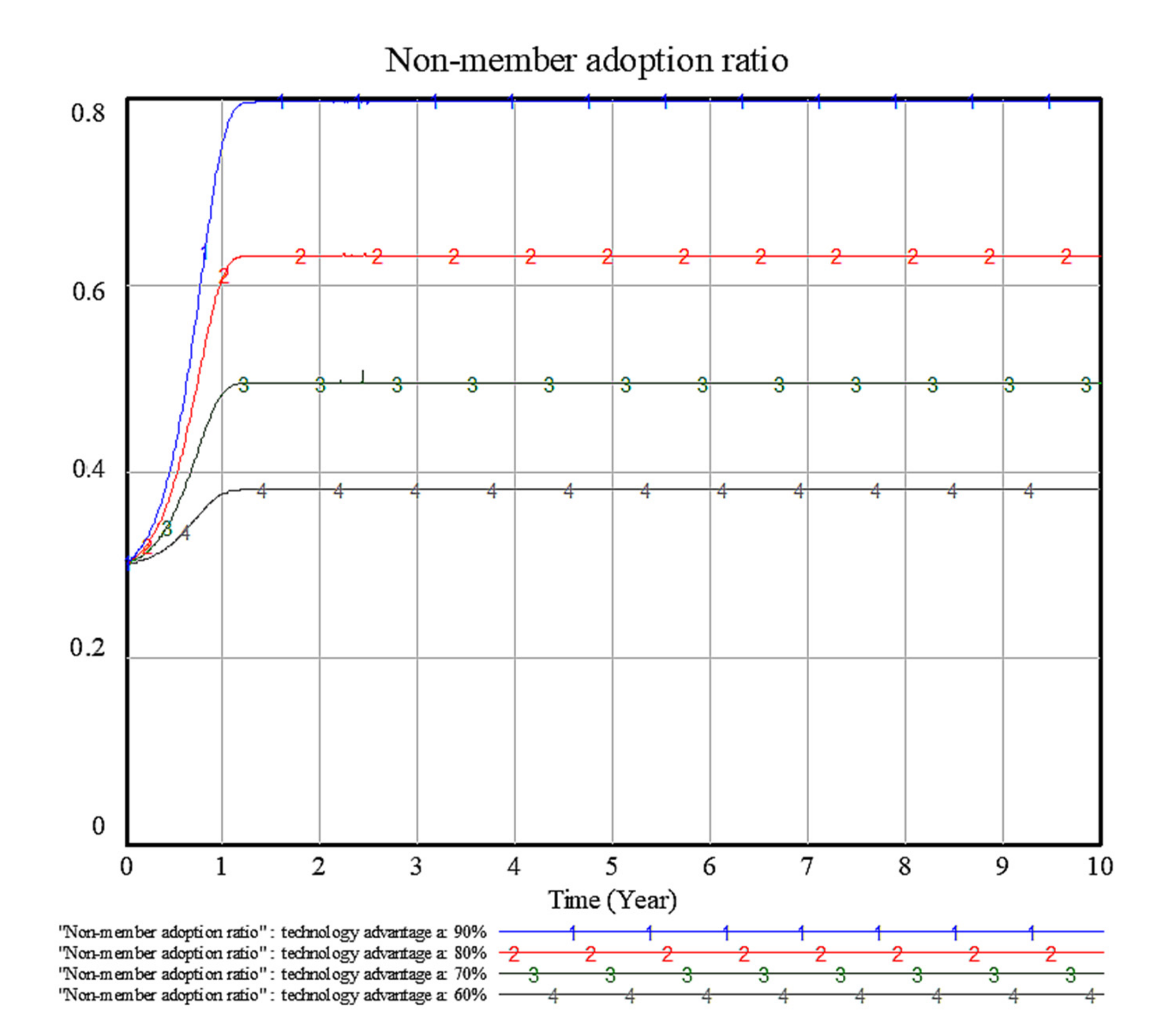
4.4. Sensitivity Analysis of Factor a: Patented Patent Pool Technology Advantage Coefficient
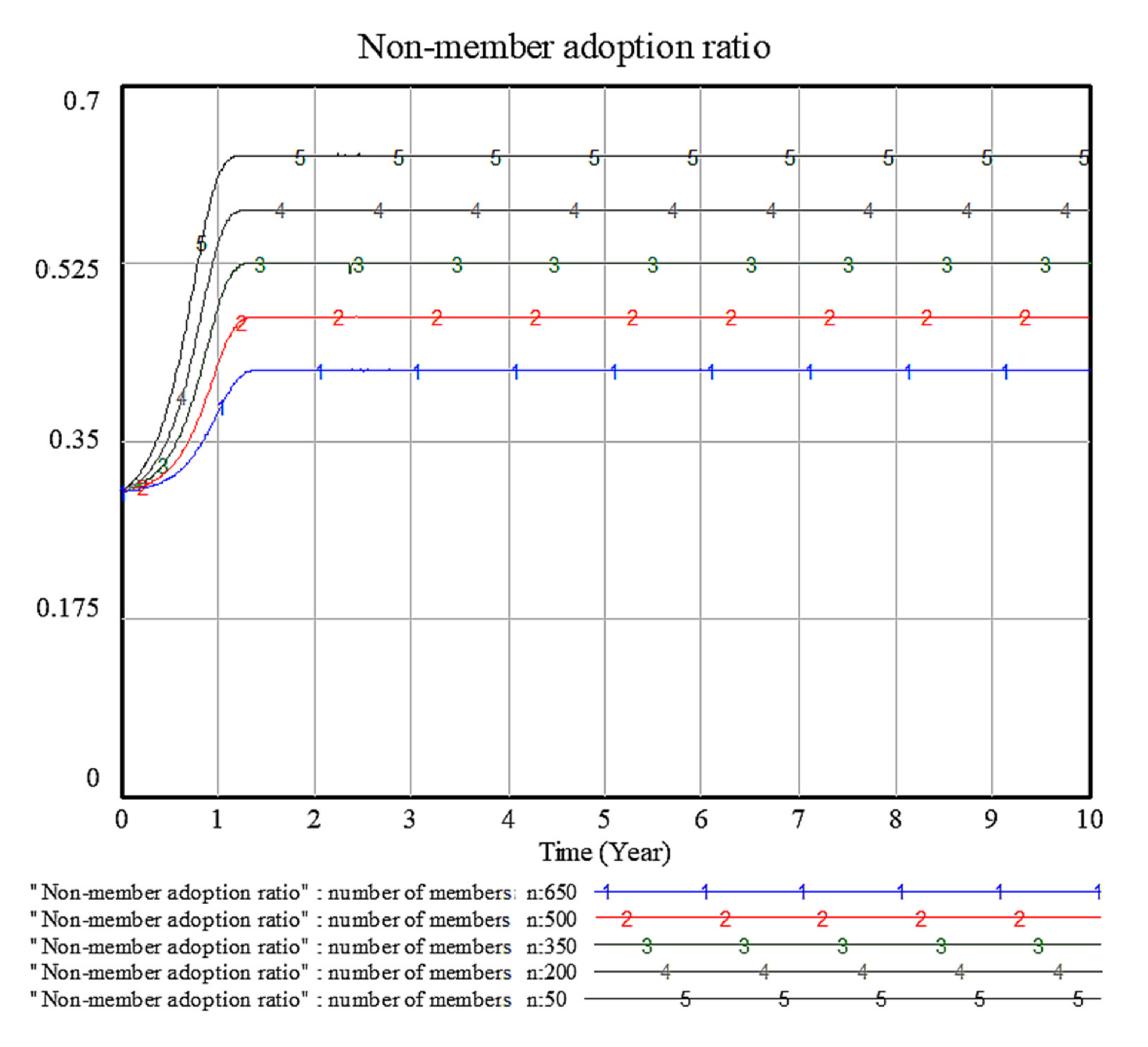
4.5. Sensitivity Analysis of Factor n: Total Number of Patent Pool Members
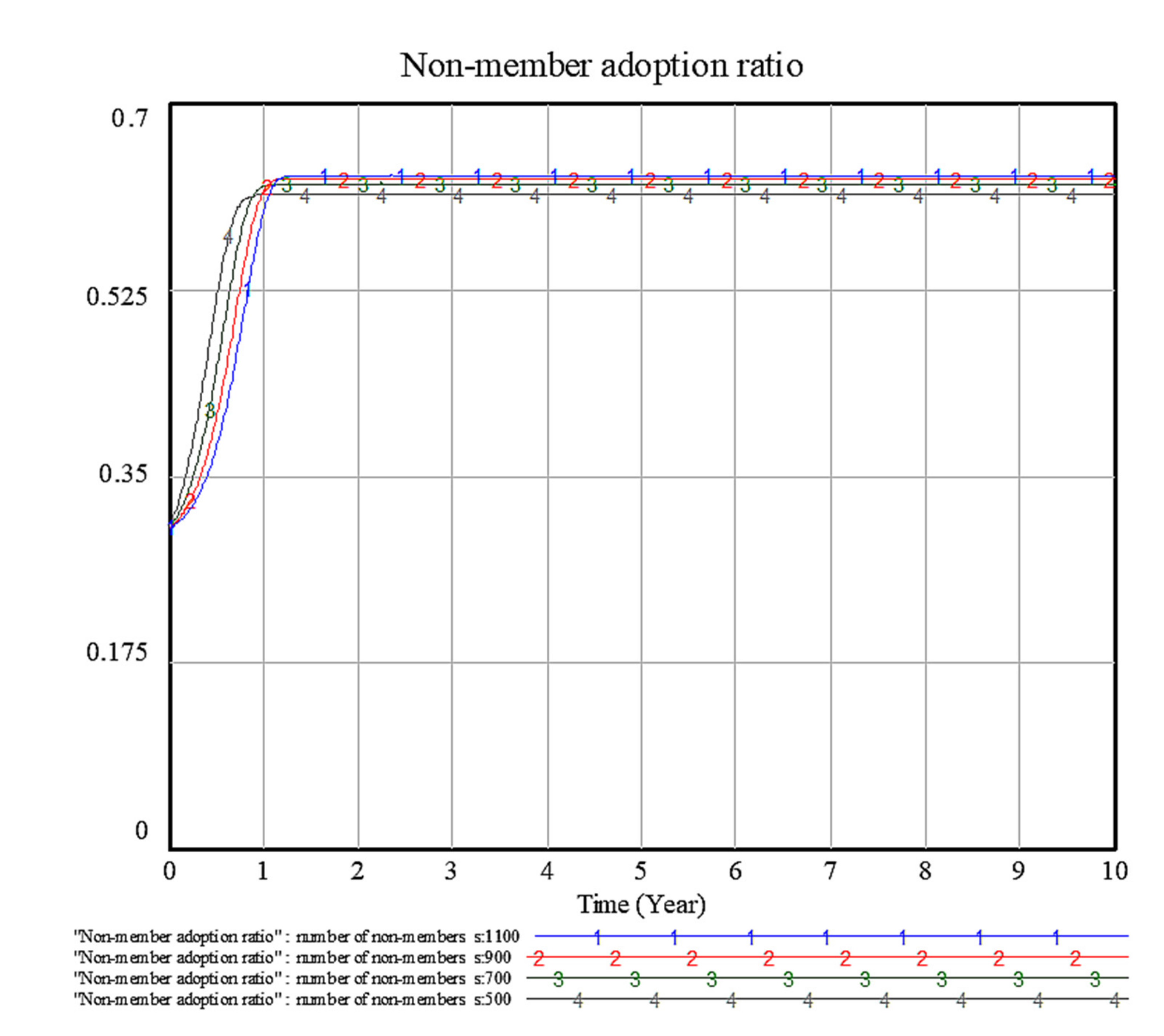
4.6. Sensitivity Analysis of Factors: Total Amount of Non-Member EV Cell Producers
5. Optimization Algorithm
- Step 1.
- Initialize the parameters;
- Step 2.
- For a (0, 1);
- Step 3.
- For n (n_low, n_upper);
- Step 4.
- For l (l_low, l_upper);
- Step 5.
- If calculate x* (x_low, 1);
- Step 6.
- If deviation of x* < 0;
- Step 7.
- Calculate the weight object function;
- Step 8.
- Compare and record the max_obj;
- Step 9.
- Update l under assigned step;
- Step 10.
- Update n under assigned step;
- Step 11.
- Update a under assigned step;
- Step 12.
- Return max_obj.
6. Discussion and Conclusions
- First, this study contributed to investigating the innovation diffusion of electric vehicle cells via considering patent pool strategies by establishing an innovation diffusion channel model, which included members of the patent pool and non-members outside the patent pool, which were interlinked with relationships, such as the patent licensing relationship, patent pool mutual licensing relationship, and market competition relationship. The model can be a reference to clarify the roles of and complex relationships between players in the electric vehicle cell supply chain, which is different from other industries or supply structures in the literature. Additionally, the model that was developed in this study extended the innovation diffusion theory by integrating all the key players and their relationships into one model, which can also be helpful for other related research areas.
- Second, the pay-off matrix and ESS of the players was analyzed based on several factors, including market competition factors and patent licensing factors, such as the technology advantage coefficient, number of patent pool members, number of non-member EV cell producers outside the patent pool, patent license fee, and unit profit for adopters when adopting different EV cell technologies. The evolutionary game model and its analysis extended the innovation diffusion study regarding electric vehicle cells and can also help decision makers in the industry to identify which factors need to be considered.
- Third, based on the simulation of the evolutionary game, we distinguished the important and unimportant factors that impact the adoption ratio and the diffusion ratio, which can aid decision makers in the electric vehicle industry with finding and changing key factors. We found that the patent licensing fees, the advantage of the patent pool technology, and the unit profit of the non-patent pool technology were the most significant factors. Decision makers should focus on improving the competitive advantage of the patent pool technology and deliver more profit to its licensees with reasonable patent and production costs.
- Fourth, we found that the return to the patent pool members had a non-linear relationship with several factors, and these factors influenced each other. For example, the stabilized diffusion ratio depended on other factors, and the advantage ratio could have both positive and negative effects on the members. Since competition and patent licensing relationships exist in the supply chain, it is difficult to find the maximum return for the patent pool members.
- Lastly, for certain decision and policy makers, besides the financial return, there are other social and environmental returns to be considered. For example, a patent pool cell can have more energy-friendly benefits. Therefore, the weighted object function was introduced to have a more comprehensive object based on patent license returns, market returns, and diffusion depth. Furthermore, an optimization algorithm was introduced to find the maximum weighted object function, and the weight of the diffusion ratio can reflect other social or environmental benefits or returns.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chuffart-Finsterwald, S. Patent Markets: An Opportunity for Technology Diffusion and FRAND Licensing? Marq. Intellect. Prop. L. Rev. 2014, 18, 335. [Google Scholar]
- Sun, H.; Geng, Y.; Hu, L.; Shi, L.; Xu, T. Measuring China’s new energy vehicle patents: A social network analysis approach. Energy 2018, 153, 685–693. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Z. Promoting Electric Vehicle Cell Innovation Diffusion Considering Patent Licensing Strategy: A Combination of Evolutionary Game and Optimization Algorithm Approach. World Electr. Veh. J. 2021, 12, 95. [Google Scholar] [CrossRef]
- Liu, J.; Sun, R.; Liu, F. Outsourcing strategy with patent licensing in an electronic product supply chain. IEEE Access 2021, 8, 98359–98368. [Google Scholar] [CrossRef]
- Bagchi, A.; Mukherjee, A. Technology licensing in a differentiated oligopoly. Int. Rev. Econ. Financ. 2014, 29, 455–465. [Google Scholar] [CrossRef] [Green Version]
- Hill, C.W. Strategies for Exploiting Technological Innovations: When and When Not to License. Organ. Sci. 1992, 3, 428–441. [Google Scholar] [CrossRef]
- Wang, X.H. Fee versus royalty licensing in a Cournot duopoly model. Econ. Lett. 1998, 60, 55–62. [Google Scholar] [CrossRef]
- Wu, C.H. Price competition and technology licensing in a dynamic duopoly. Eur. J. Oper. Res. 2018, 267, 570–584. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Zaccour, G.; Tang, W. Strategic technology licensing in a supply chain. Eur. J. Oper. Res. 2018, 267, 162–175. [Google Scholar] [CrossRef]
- Narasipuram, R.P.; Mopidevi, S. A technological overview & design considerations for developing electric vehicle charging stations. J. Energy Storage 2021, 43, 103225. [Google Scholar] [CrossRef]
- Yuan, W. Analysis of the Threshold of the Firms’ Number in the Formation of Patent Pool. Oper. Res. Manag. Sci. 2021, 3, 199–203. [Google Scholar]
- Fang, Y.; Wei, W.; Mei, S.; Chen, L.; Zhang, X.; Huang, S. Promoting electric vehicle charging infrastructure considering policy incentives and user preferences: An evolutionary game model in a small-world network. J. Clean. Prod. 2020, 258, 120753. [Google Scholar] [CrossRef]
- Huan, H. Quantitative Identification of Fragmentation of Patent Resources—An Empirical Study on China’s New Energy Vehicle Power Battery Patents. J. Intell. 2021, 7, 16–22. [Google Scholar]
- Chu, Y.; Zhu, T. Research on Forecast of Electric Vehicle’s Ownership in China Based on Bass Model and GM(1,1) Model. Math. Pract. Theory 2021, 11, 21–32. [Google Scholar]
- Zhang, G.; Chen, H.; Li, H. Research on Forecast of Electric Vehicle’s Ownership Based on the Comparison of Bass Model and Lotka-Volterra Model. J. Wuhan Univ. Technol. 2017, 8, 91–98. [Google Scholar]
- Li, J.; Jiao, J.; Tang, Y. An evolutionary analysis on the effect of government policies on electric vehicle diffusion in complex network. Energy Policy 2019, 129, 1–12. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, B. Exploring the development of electric vehicles under policy incentives: A scenario-based system dynamics model. Energy Policy 2018, 120, 8–23. [Google Scholar] [CrossRef]
- Vilchez, J.J.G.; Thiel, C. The Effect of Reducing Electric Car Purchase Incentives in the European Union. World Electr. Veh. J. 2019, 10, 64. [Google Scholar] [CrossRef] [Green Version]
- Rogers, E.M. The Diffusion of Innovations; Free Press: Glencoe, IL, USA, 1962. [Google Scholar]
- Forrester, J.W. Principles of Systems; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Eberlein, R.L.; Peterson, D.W. Understanding models with Vensim™. Eur. J. Oper. Res. 1992, 59, 216–219. [Google Scholar] [CrossRef]

| Game Players | Potential Non-Member Licensee 2 | ||
|---|---|---|---|
| Adopted Patent Pool (x) | Not Adopted Patent Pool (1−x) | ||
| Potential Non Member Licensee 1 | Adopted Patent Pool (x) | B1, B1 | B1, B2 |
| Not Adopted Patent Pool (1−x) | B2, B1 | B2, B2 | |
| Equilibrium Point x | Derivative | Stability |
| 0 | Uncertain | |
| Uncertain |
| Symbol | Note | Initial Value | Unit |
|---|---|---|---|
| m0 | Total market potential amount of EV cell—initial | 300 | Unit |
| mp | Total market potential amount of EV cell—long term | 15,000,000 | Unit |
| a | Patent pool EV cell technology advantage coefficient | 80 | % |
| s | Total number of non-member EV cell producers | 1000 | Unit |
| n | Total number of patent pool members | 50 | Unit |
| x | Share of non-member EV cell producers that adopted the patent pool technology | 30 | % |
| l | The patent royalty an EV cell producer that pays the patent pool produces from each unit | 1500 | USD |
| q | Profit for a patent holder in the patent pool that sells one EV cell unit | 2100 | USD |
| r | Unit profit for a non-member EV cell producer that adopts the patent pool | 2100 | USD |
| u | Unit profit for non-member EV cell producer that does not adopt the patent pool | 1300 | USD |
| Object Function | Advantage Coefficient | Patent Royalty | Patent Pool Member | Diffusion Ratio |
|---|---|---|---|---|
| USD 61,138,462 | 60.00% | 600 | 150 | 52.39% |
| USD 76,233,333 | 60.00% | 600 | 100 | 56.06% |
| USD 33,950,000 | 70.00% | 600 | 400 | 51.25% |
| USD 36,514,286 | 70.00% | 600 | 350 | 53.96% |
| USD 39,600,000 | 70.00% | 600 | 300 | 56.67% |
| USD 43,440,000 | 70.00% | 600 | 250 | 59.38% |
| USD 48,471,429 | 70.00% | 600 | 200 | 62.08% |
| USD 75,761,538 | 70.00% | 1100 | 150 | 53.49% |
| USD 55,661,538 | 70.00% | 600 | 150 | 64.79% |
| USD 95,825,000 | 70.00% | 1100 | 100 | 57.06% |
| USD 67,800,000 | 70.00% | 600 | 100 | 67.50% |
| USD 33,630,000 | 80.00% | 1100 | 500 | 50.94% |
| USD 28,420,000 | 80.00% | 600 | 500 | 64.38% |
| USD 35,785,965 | 80.00% | 1100 | 450 | 53.40% |
| USD 30,126,316 | 80.00% | 600 | 450 | 66.16% |
| USD 38,283,333 | 80.00% | 1100 | 400 | 55.85% |
| USD 32,077,778 | 80.00% | 600 | 400 | 67.95% |
| USD 41,228,571 | 80.00% | 1100 | 350 | 58.30% |
| USD 34,342,857 | 80.00% | 600 | 350 | 69.73% |
| USD 44,787,500 | 80.00% | 1100 | 300 | 60.75% |
| USD 37,025,000 | 80.00% | 600 | 300 | 71.51% |
| USD 49,240,000 | 80.00% | 1100 | 250 | 63.21% |
| USD 40,293,333 | 80.00% | 600 | 250 | 73.29% |
| USD 55,114,286 | 80.00% | 1100 | 200 | 65.66% |
| USD 44,457,143 | 80.00% | 600 | 200 | 75.07% |
| USD 63,584,615 | 80.00% | 1100 | 150 | 68.11% |
| USD 50,184,615 | 80.00% | 600 | 150 | 76.85% |
| USD 104,100,000 | 80.00% | 1600 | 100 | 52.73% |
| USD 78,050,000 | 80.00% | 1100 | 100 | 70.57% |
| USD 59,366,667 | 80.00% | 600 | 100 | 78.63% |
| USD 34,380,000 | 90.00% | 1600 | 500 | 55.17% |
| USD 29,565,000 | 90.00% | 1100 | 500 | 74.76% |
| USD 26,960,000 | 90.00% | 600 | 500 | 82.43% |
| USD 36,470,175 | 90.00% | 1600 | 450 | 57.41% |
| USD 31,314,035 | 90.00% | 1100 | 450 | 76.02% |
| USD 28,484,211 | 90.00% | 600 | 450 | 83.31% |
| USD 38,866,667 | 90.00% | 1600 | 400 | 59.66% |
| USD 33,308,333 | 90.00% | 1100 | 400 | 77.28% |
| USD 30,205,556 | 90.00% | 600 | 400 | 84.19% |
| USD 41,657,143 | 90.00% | 1600 | 350 | 61.90% |
| USD 35,614,286 | 90.00% | 1100 | 350 | 78.54% |
| USD 32,171,429 | 90.00% | 600 | 350 | 85.07% |
| USD 44,975,000 | 90.00% | 1600 | 300 | 64.14% |
| USD 38,331,250 | 90.00% | 1100 | 300 | 79.81% |
| USD 34,450,000 | 90.00% | 600 | 300 | 85.95% |
| USD 49,040,000 | 90.00% | 1600 | 250 | 66.38% |
| USD 41,620,000 | 90.00% | 1100 | 250 | 81.07% |
| USD 37,146,667 | 90.00% | 600 | 250 | 86.82% |
| USD 54,257,143 | 90.00% | 1600 | 200 | 68.62% |
| USD 45,771,429 | 90.00% | 1100 | 200 | 82.33% |
| USD 40,442,857 | 90.00% | 600 | 200 | 87.70% |
| USD 61,507,692 | 90.00% | 1600 | 150 | 70.86% |
| USD 51,407,692 | 90.00% | 1100 | 150 | 83.59% |
| USD 44,707,692 | 90.00% | 600 | 150 | 88.58% |
| USD 73,300,000 | 90.00% | 1600 | 100 | 73.10% |
| USD 60,275,000 | 90.00% | 1100 | 100 | 84.85% |
| USD 50,933,333 | 90.00% | 600 | 100 | 89.46% |
| Weighted Object Function | Advantage Coefficient | Patent Royalty | Patent Pool Member | Diffusion Ratio |
|---|---|---|---|---|
| 0.830 | 60.00% | 600 | 150 | 52.39% |
| 0.942 | 60.00% | 600 | 100 | 56.06% |
| 0.682 | 70.00% | 600 | 400 | 51.25% |
| 0.722 | 70.00% | 600 | 350 | 53.96% |
| 0.765 | 70.00% | 600 | 300 | 56.67% |
| 0.811 | 70.00% | 600 | 250 | 59.38% |
| 0.863 | 70.00% | 600 | 200 | 62.08% |
| 0.914 | 70.00% | 1100 | 150 | 53.49% |
| 0.926 | 70.00% | 600 | 150 | 64.79% |
| 1.050 | 70.00% | 1100 | 100 | 57.06% |
| 1.014 | 70.00% | 600 | 100 | 67.50% |
| 0.678 | 80.00% | 1100 | 500 | 50.94% |
| 0.786 | 80.00% | 600 | 500 | 64.38% |
| 0.713 | 80.00% | 1100 | 450 | 53.40% |
| 0.812 | 80.00% | 600 | 450 | 66.16% |
| 0.750 | 80.00% | 1100 | 400 | 55.85% |
| 0.840 | 80.00% | 600 | 400 | 67.95% |
| 0.789 | 80.00% | 1100 | 350 | 58.30% |
| 0.869 | 80.00% | 600 | 350 | 69.73% |
| 0.831 | 80.00% | 1100 | 300 | 60.75% |
| 0.900 | 80.00% | 600 | 300 | 71.51% |
| 0.878 | 80.00% | 1100 | 250 | 63.21% |
| 0.934 | 80.00% | 600 | 250 | 73.29% |
| 0.932 | 80.00% | 1100 | 200 | 65.66% |
| 0.973 | 80.00% | 600 | 200 | 75.07% |
| 0.999 | 80.00% | 1100 | 150 | 68.11% |
| 1.019 | 80.00% | 600 | 150 | 76.85% |
| 1.048 | 80.00% | 160 | 100 | 52.73% |
| 1.096 | 80.00% | 1100 | 100 | 70.57% |
| 1.083 | 80.00% | 600 | 100 | 78.63% |
| 0.724 | 90.00% | 160 | 500 | 55.17% |
| 0.895 | 90.00% | 1100 | 500 | 74.76% |
| 0.959 | 90.00% | 600 | 500 | 82.43% |
| 0.756 | 90.00% | 160 | 450 | 57.41% |
| 0.917 | 90.00% | 1100 | 450 | 76.02% |
| 0.976 | 90.00% | 600 | 450 | 83.31% |
| 0.791 | 90.00% | 160 | 400 | 59.66% |
| 0.939 | 90.00% | 1100 | 400 | 77.28% |
| 0.993 | 90.00% | 600 | 400 | 84.19% |
| 0.827 | 90.00% | 160 | 350 | 61.90% |
| 0.964 | 90.00% | 1100 | 350 | 78.54% |
| 1.012 | 90.00% | 600 | 350 | 85.07% |
| 0.866 | 90.00% | 160 | 300 | 64.14% |
| 0.990 | 90.00% | 1100 | 300 | 79.81% |
| 1.032 | 90.00% | 600 | 300 | 85.95% |
| 0.909 | 90.00% | 160 | 250 | 66.38% |
| 1.019 | 90.00% | 1100 | 250 | 81.07% |
| 1.054 | 90.00% | 600 | 250 | 86.82% |
| 0.957 | 90.00% | 160 | 200 | 68.62% |
| 1.052 | 90.00% | 1100 | 200 | 82.33% |
| 1.079 | 90.00% | 600 | 200 | 87.70% |
| 1.016 | 90.00% | 160 | 150 | 70.86% |
| 1.093 | 90.00% | 1100 | 150 | 83.59% |
| 1.109 | 90.00% | 600 | 150 | 88.58% |
| 1.098 | 90.00% | 160 | 100 | 73.10% |
| 1.150 | 90.00% | 1100 | 100 | 84.85% |
| 1.149 | 90.00% | 600 | 100 | 89.46% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Yuan, M.; Zhang, Z. The Evolutionary Game Analysis and Optimization Algorithm of Electric Vehicle Cell Innovation Diffusion Based on a Patent Pool Strategy. World Electr. Veh. J. 2021, 12, 251. https://doi.org/10.3390/wevj12040251
Sun W, Yuan M, Zhang Z. The Evolutionary Game Analysis and Optimization Algorithm of Electric Vehicle Cell Innovation Diffusion Based on a Patent Pool Strategy. World Electric Vehicle Journal. 2021; 12(4):251. https://doi.org/10.3390/wevj12040251
Chicago/Turabian StyleSun, Weiwei, Min Yuan, and Zheng Zhang. 2021. "The Evolutionary Game Analysis and Optimization Algorithm of Electric Vehicle Cell Innovation Diffusion Based on a Patent Pool Strategy" World Electric Vehicle Journal 12, no. 4: 251. https://doi.org/10.3390/wevj12040251
APA StyleSun, W., Yuan, M., & Zhang, Z. (2021). The Evolutionary Game Analysis and Optimization Algorithm of Electric Vehicle Cell Innovation Diffusion Based on a Patent Pool Strategy. World Electric Vehicle Journal, 12(4), 251. https://doi.org/10.3390/wevj12040251






