FLRW Cosmological Models with Dynamic Cosmological Term in Modified Gravity
Abstract
:1. Introduction
2. Basic Equations
3. Solution to Field Equations
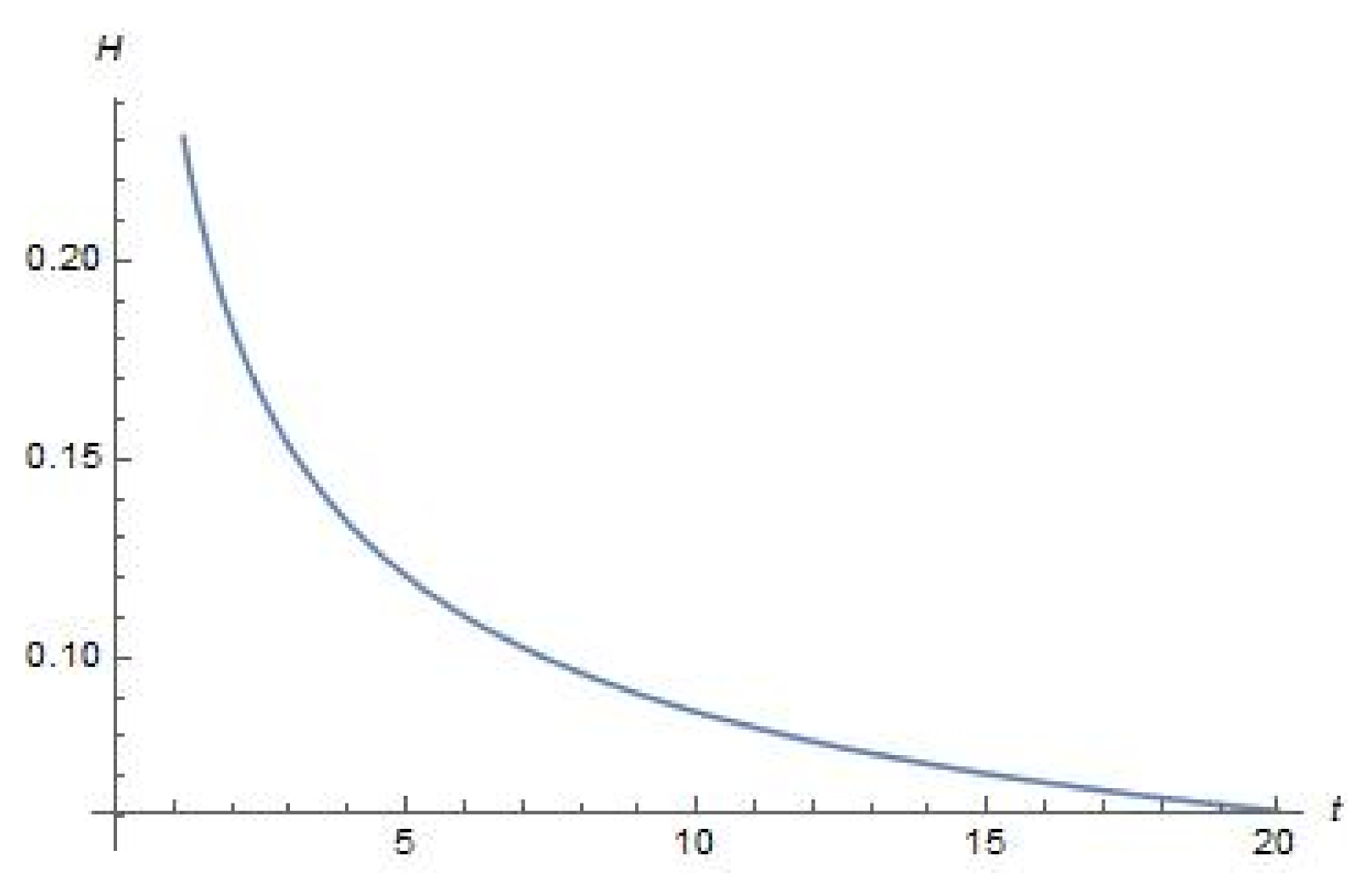
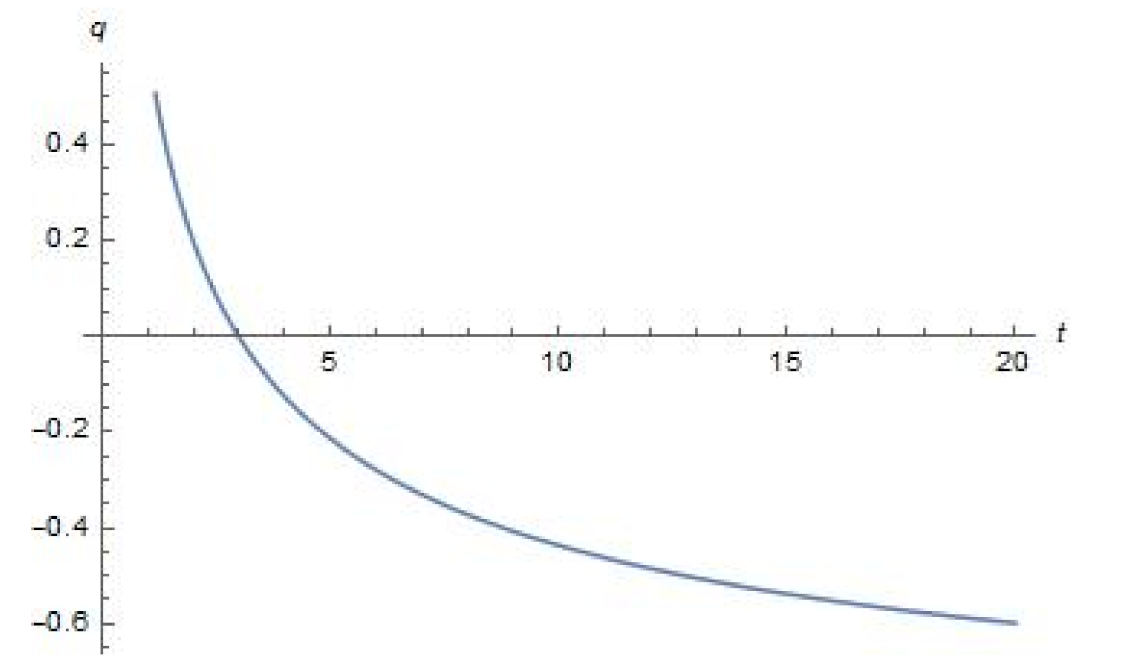
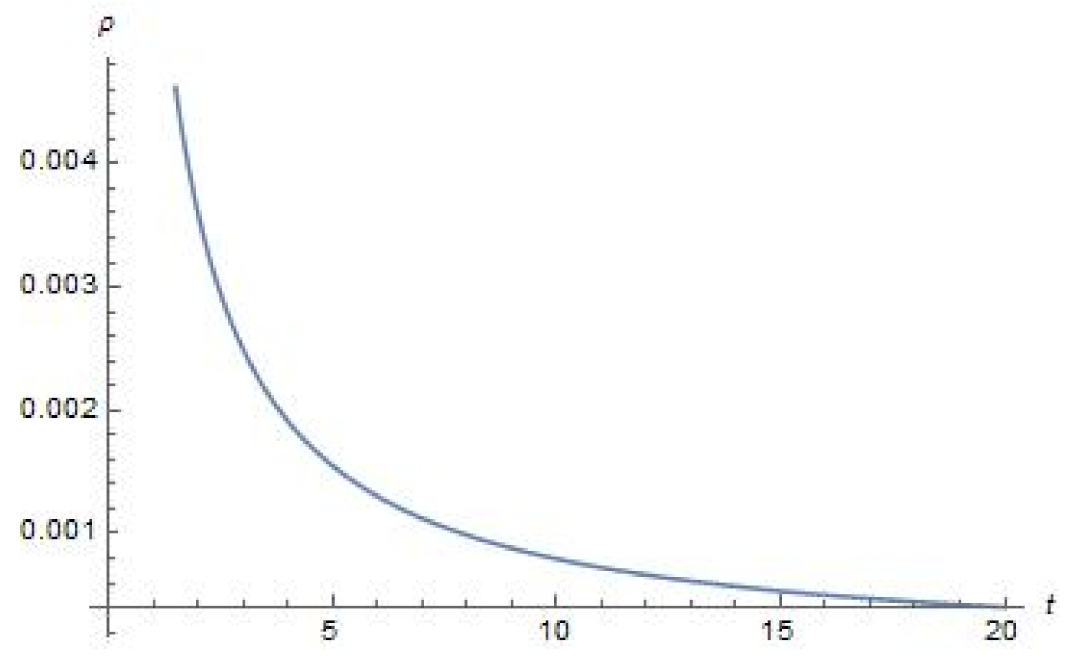
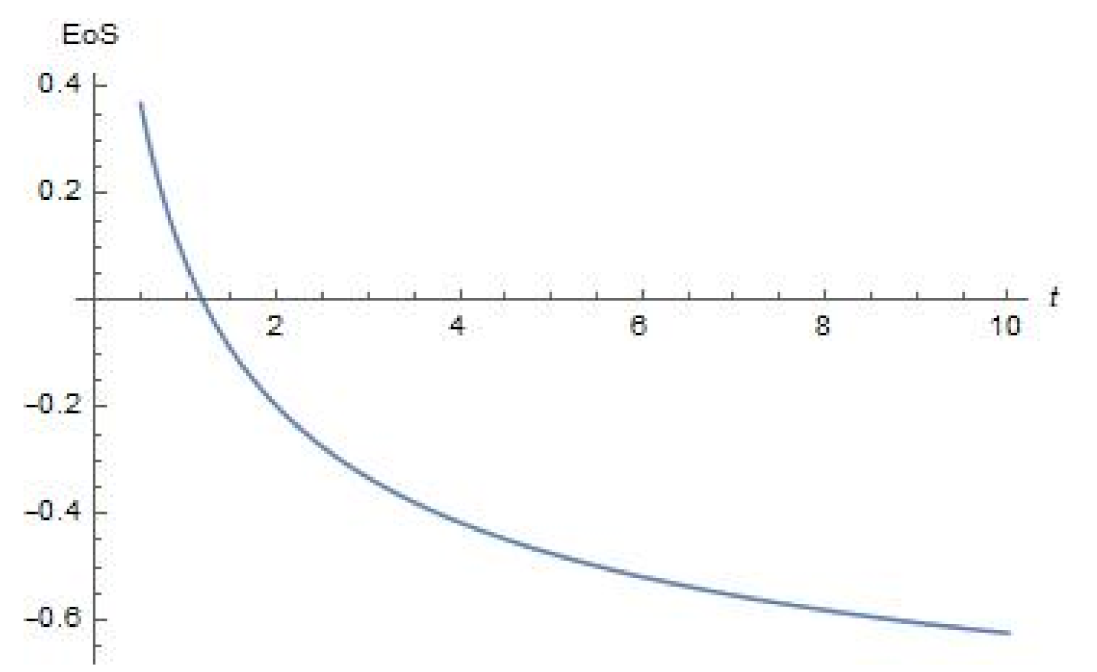
4. Plots of Parameters
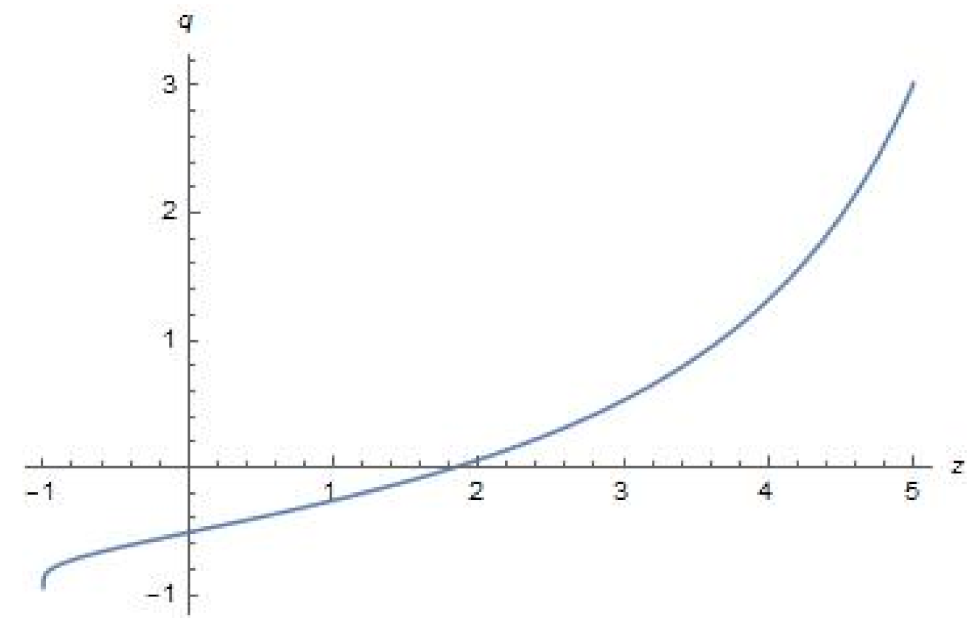
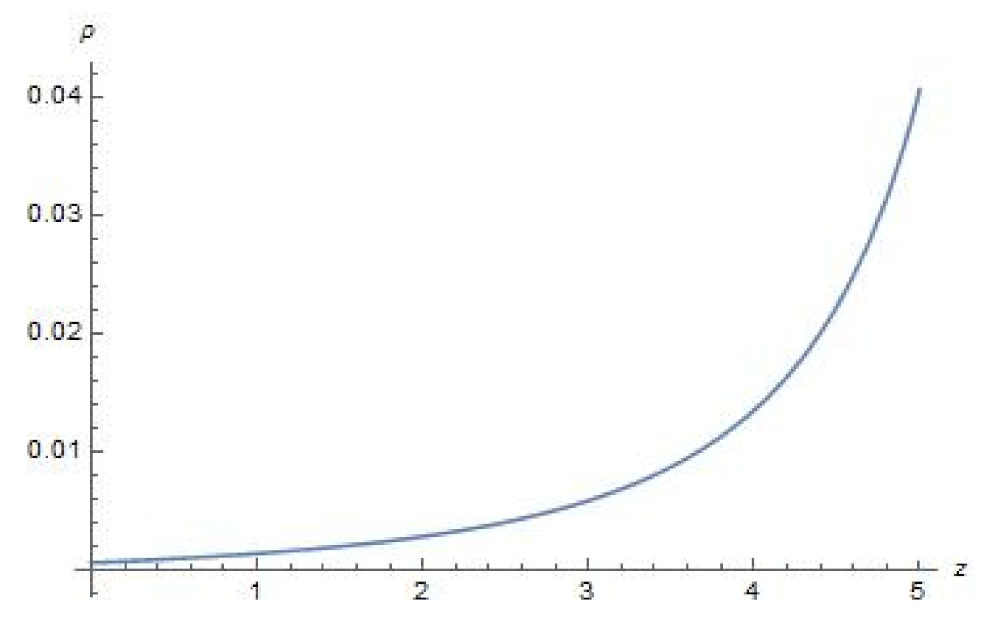
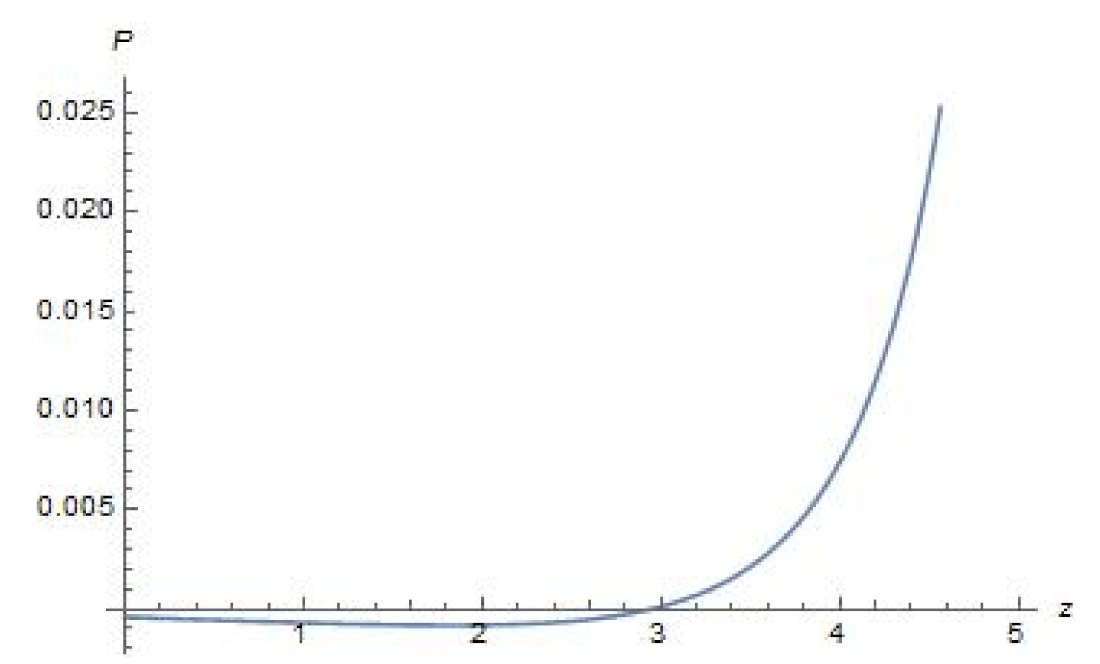
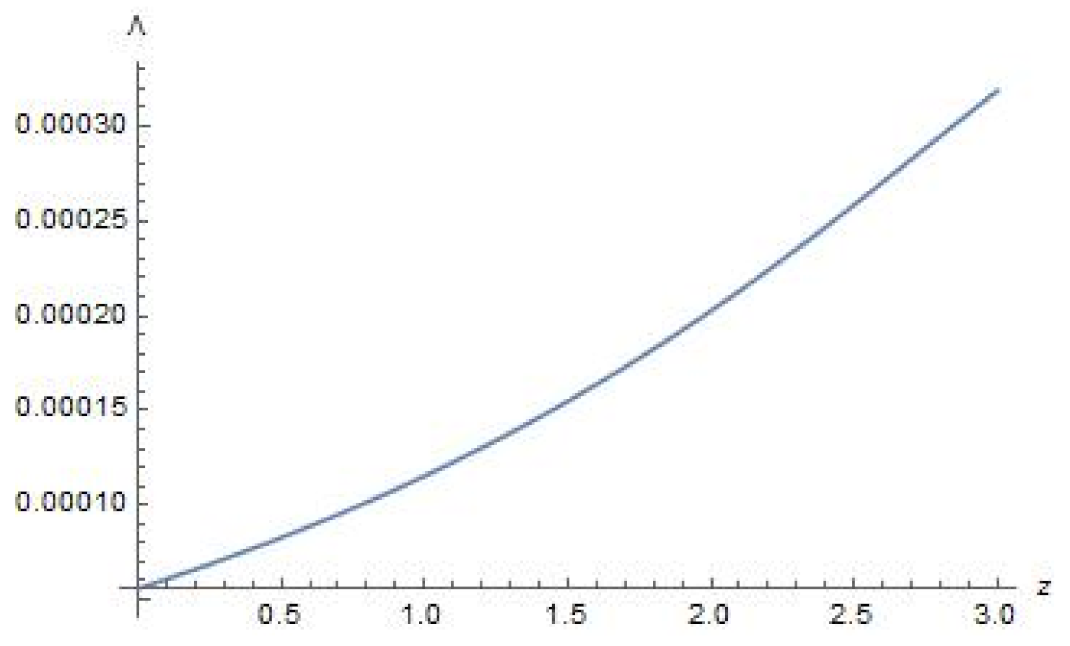
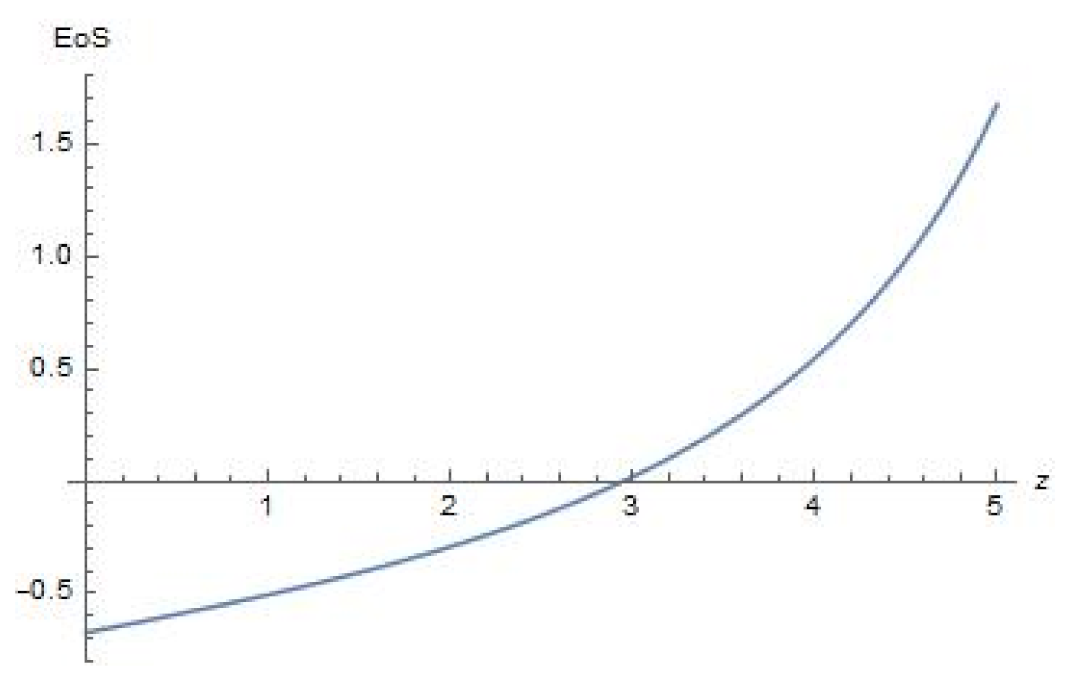
5. Parameters and Their Evolution in Terms of Redshift
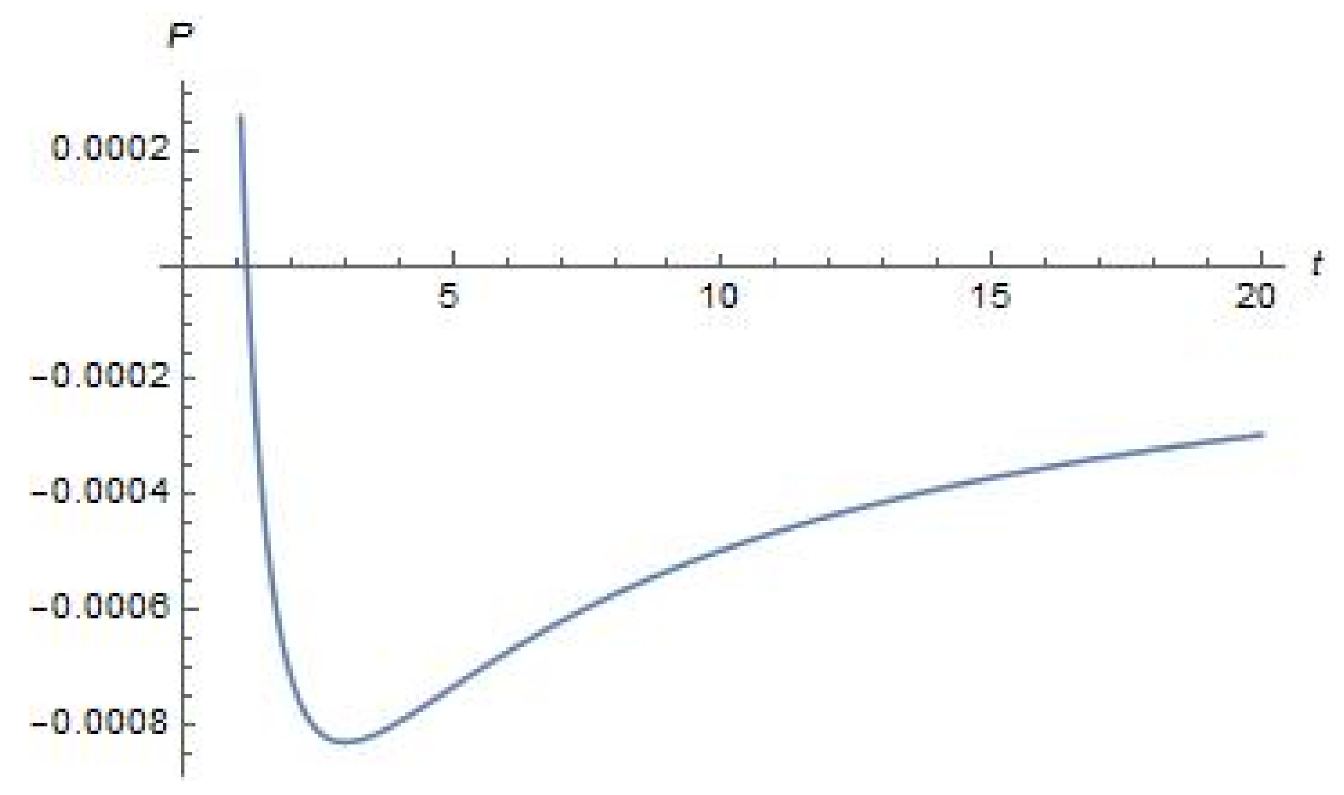
6. Energy Conditions
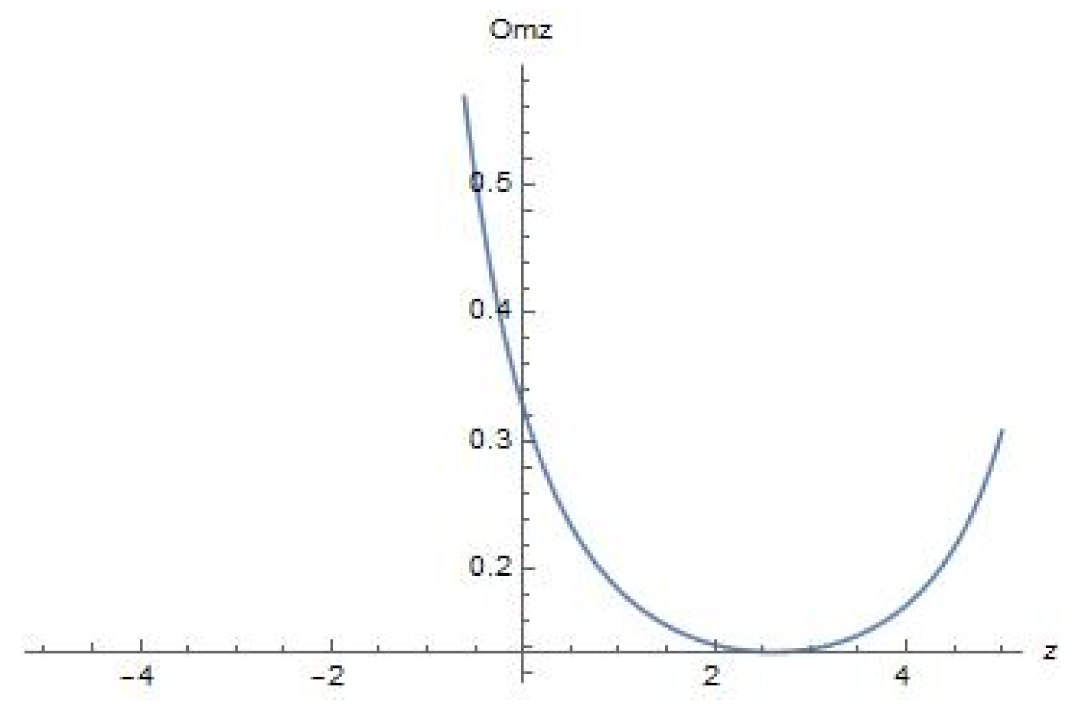
7. Om Diagnostic Analysis
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.G.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Percival, W.J.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; Collins, C.; Couch, W.; Dalton, G.; et al. The 2dF Galaxy Redshift Survey: The power spectrum and the matter content of the universe. Mon. Not. R. Astron. Soc. 2001, 327, 1297–1306. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. J. Cosmol. Astropart. Phys. 2010, 1002, 008. [Google Scholar]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nicho, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Sahni, V. The case for a positive cosmological Lambda-TERM. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef] [Green Version]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Jimenez, J.B.; Bentivegna, E.; Camera, S.; Clesse, S.; Davis, J.H.; et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Phys. Dark Univ. 2016, 12, 56–99. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Babourova, A.; Frolov, B. The Solution of the Cosmological Constant Problem: The Cosmological Constant Exponential Decrease in the Super-Early Universe. Universe 2020, 6, 230. [Google Scholar] [CrossRef]
- Geng, C.; Lee, C.; Yin, L. Constraints on a running vacuum model. Eur. Phys. J. C 2020, 80, 69. [Google Scholar] [CrossRef]
- Sola, J. Cosmological constant vis-a-vis dynamical vacuum: Bold challenging the Lambda CDM. Int. J. Mod. Phys. A 2016, 31, 16300350. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological Imprint of an Energy Component with General Equation of State. Phys. Rev. Lett. 1998, 80, 1582. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Sami, M.; Dadhich, N. Cosmological dynamics of phantom field. Phys. Rev. D 2003, 68, 023522. [Google Scholar] [CrossRef] [Green Version]
- Sami, M.; Toporensky, A. Phantom field and the fate of the Universe. Mod. Phys. Lett. A 2004, 19, 1509. [Google Scholar] [CrossRef] [Green Version]
- Parker, L.; Raval, A. Nonperturbative effects of vacuum energy on the recent expansion of the universe. Phys. Rev. D 1999, 60, 063512. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Quantum deSitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Nojiri, S.; Odintsov, S.D.; Yurov, A.V. Phantom cosmology without Big Rip singularity. Phys. Lett. B 2012, 709, 396. [Google Scholar] [CrossRef] [Green Version]
- Boyle, L.A.; Caldwell, R.R.; Kamionkowski, M. Spintessence! New models for dark matter and dark energy. Phys. Lett. B 2002, 545, 17. [Google Scholar] [CrossRef] [Green Version]
- Armendariz-Picon, T.; Mukhanov, V.F. k-Inflation. Phys. Lett. B 1999, 458, 209. [Google Scholar] [CrossRef] [Green Version]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef] [Green Version]
- Feng, B.; Wang, X.; Zhang, X. Dark Energy Constraints from the Cosmic Age and Supernova. Phys. Lett. B 2005, 607, 35. [Google Scholar] [CrossRef]
- Sen, A. Tachyon Matter. J. High Energy Phys. 2002, 0207, 065. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef] [Green Version]
- Khoury, J.; Weltman, A. Chameleon Fields: Awaiting Surprises for Tests of Gravity in Space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef] [Green Version]
- Chaplygin, S. On gas jets. Sci. Mem. Moscow Univ. Math. Phys. 1904, 21, 1–121. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef] [Green Version]
- Sami, M.; Myrzakulov, R. Late time cosmic acceleration: ABCD of dark energy and modified theories of gravity. Int. J. Mod. Phys. D 2016, 25, 1630031. [Google Scholar] [CrossRef] [Green Version]
- Sami, M. Dark energy and possible alternatives. arXiv 2009, arXiv:0901.0756v1. [Google Scholar]
- Yoo, J.; Watanabe, Y. Theoretical models of dark energy. Int. J. Mod. Phys. D 2012, 21, 1230002. [Google Scholar] [CrossRef] [Green Version]
- Durrer, R.; Maartens, R. Dark Energy and Dark Gravity. Gen. Relativ. Grav. 2008, 40, 301–328. [Google Scholar] [CrossRef] [Green Version]
- Brax, P. What makes the Universe accelerate? A review on what dark energy could be and how to test it. Rep. Prog. Phys. 2018, 81, 016902. [Google Scholar] [CrossRef]
- Silvestri, A.; Trodden, M. Approaches to understanding cosmic acceleration. Rep. Prog. Phys. 2009, 72, 096901. [Google Scholar] [CrossRef] [Green Version]
- Tawfik, A.N.; El-Dahab, E.I. Review on Dark Energy Models. Grav. Cosm. 2019, 25, 103–115. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nokiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef] [Green Version]
- Harko, T. Thermodynamic interpretation of the generalized gravity models with geometry-matter coupling. Phys. Rev. D 2014, 90, 044067. [Google Scholar] [CrossRef] [Green Version]
- Alvarenga, F.G.; de la Cruz-Dombriz, A.; Houndjo, M.J.S.; Rodrigues, E.; Saez-Gaomez, D. Dynamics of scalar perturbations in f(R,T) gravity. Phys. Rev. D 2013, 87, 103526. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Zubair, M. Energy conditions in f(R,T,RμνTμν) gravity. J. High Energy Phys. 2013, 12, 079. [Google Scholar] [CrossRef]
- Kiani, F.; Nozari, K. Energy conditions in F(T,Θ) gravity and compatibility with a stable deSitter solution. Phys. Lett. B 2014, 728, 554–561. [Google Scholar] [CrossRef] [Green Version]
- Alvarenga, F.G.; Houndjo, M.J.S.; Monwanou, A.V.; Chabi Orou, J.B.C. Testing some f(R,T) gravity models from energy conditions. J. Mod. Phys. 2013, 4, 130–139. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Zubair, M. Thermodynamics in f(R,T) Theory of Gravity. J. Cosmol. Astropart. Phys. 2012, 3, 28. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Momeni, D.; Ratbay, M. Violation of First Law of Thermodynamics in f(R,T) Gravity. Chin. Phys. Lett. 2012, 29, 109801. [Google Scholar] [CrossRef] [Green Version]
- Zubair, M.; Waheed, S.; Ahmad, Y. Static spherically symmetric wormholes in f(R,T) gravity. Eur. Phys. J. C 2016, 76, 444–457. [Google Scholar] [CrossRef] [Green Version]
- Moraes, P.H.R.S.; Sahoo, P.K. Modeling wormholes in f(R,T) gravity. Phys. Rev. D 2017, 96, 44038. [Google Scholar] [CrossRef] [Green Version]
- Moraes, P.H.R.S.; Correa, R.A.C.; Lobato, R.V. Analytical general solutions for static wormholes in f(R,T) gravity. J. Cosmol. Astropart. Phys. 2017, 7, 29. [Google Scholar] [CrossRef] [Green Version]
- Yousaf, Z.; Bamba, K.; Bhatti, M.Z.H. Causes of irregular energy density in f(R,T) gravity. Phys. Rev. D 2016, 93, 124048. [Google Scholar] [CrossRef] [Green Version]
- Moraes, P.H.R.S. Cosmological solutions from induced matter model applied to 5D f(R,T) gravity and the shrinking of the extra coordinate. Eur. Phys. J. C 2015, 75, 168–176. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.K.; Sahoo, P.; Bishi, B.K. Anisotropic cosmological models in f(R,T) gravity with variable deceleration parameter. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750097. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.K.; Sahoo, P.; Bishi, B.K.; Aygun, S. Magnetized strange quark model with Big Rip singularity in f(R,T) gravity. Mod. Phys. Lett. A 2017, 32, 1750105. [Google Scholar] [CrossRef] [Green Version]
- Perez, A.; Sudarsky, D. Dark energy as the weight of violating energy conservation. Phys. Rev. Lett. 2019, 118, 021102. [Google Scholar]
- Tiwari, R.K.; Beesham, A. Anisotropic model with decaying cosmological term. Astrophys. Space Sci. 2018, 363, 234. [Google Scholar] [CrossRef]
- Beesham, A.; Tiwari, R.K.; Shukla, B.K. Reconstruction of models with variable cosmological parameter in f(R,T) theory. In Proceedings of the 1st Electronic Conference on Universe, Basel, Switzerland, 22–28 February 2021; MDPI: Basel, Switzerland, 2021. [Google Scholar]
- Pasqua, A.; Chattopadhyay, S.; Khomenko, I. A reconstruction of modified holographic Ricci dark energy in f(R,T) gravity. Can. J. Phys. 2013, 91, 632–638. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Cosmographic analysis with Chebyshev. polynomials. Mon. Not. R. Astron. Soc. 2018, 476, 3924–3938. [Google Scholar] [CrossRef] [Green Version]
- Gruber, C.; Luongo, O. Energy conditions in f(Q,T) gravity. Phys. Rev. D 2014, 89, 103506. [Google Scholar] [CrossRef] [Green Version]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Dark degeneracy and interacting cosmic components. Phys. Rev. D 2014, 90, 043531. [Google Scholar] [CrossRef] [Green Version]
- de la Cruz-Dombriz, A.; Dunsby, P.K.S.A.; Luongo, O.; Reverberi, L. Model-independent limits and constraints on extended theories of gravity from cosmic reconstruction techniques. J. Cosmol. Astropart. Phys. 2016, 12, 042. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Liu, D.; Zou, X.; Wei, H. New generalizations of cosmography inspired by the Pade approximant. Eur. Phys. J. C 2016, 76, 281. [Google Scholar] [CrossRef] [Green Version]
- Akarsu, O.; Dereli, T. Cosmological models with linearly varying deceleration parameter. Int. J. Theor. Phys. 2012, 51, 612–621. [Google Scholar] [CrossRef] [Green Version]
- Garg, P.; Zia, R.; Pradhan, A. Transit cosmological models in FRW universe under the two-fluid scenario. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950007. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. Behaviour of the cosmological model with variable deceleration parameter. Eur. Phys. J. Plus 2016, 131, 447–456. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. Cosmological models with viscous fluid and variable deceleration parameter. Eur. Phys. J. Plus 2017, 132, 20. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. Scenario of a two-fluid FRW cosmological model with dark energy. Eur. Phys. J. Plus 2017, 132, 126. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. Scenario of two-fluid dark energy models in Bianchi type-III Universe. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850155. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. Cosmological model with variable deceleration parameter in f(R,T) modified gravity. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850189. [Google Scholar] [CrossRef]
- Jusus, J.F. Gaussian process estimation of transition redshift. J. Cosmol. Astropart. Phys. 2020, 4, 53. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef] [Green Version]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Momeni, D.; Myrzakulov, R. Wormholes in a viable f(T) gravity. Eur. Phys. J. C 2013, 73, 2347. [Google Scholar] [CrossRef]
- de Fromont, P.; de Rham, C.; Heisenberg, L.; Matas, A. Superluminality in the bi-and multi-Galileon. J. High Energy Phys. 2013, 7, 67. [Google Scholar] [CrossRef] [Green Version]
- Zunckel, C.; Clarkson, C. Consistency Tests for the Cosmological Constant. Phys. Rev. Lett. 2008, 101, 181301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giostri, R.; dos Santos, M.V.; Waga, I.; Reis, R.R.R.; Calvao, M.O.; Lago, B.L. From cosmic deceleration to acceleration: New constraints from SN Ia and BAO/CMBJ. J. Cosmol. Astropart. Phys. 2012, 3, 27. [Google Scholar] [CrossRef] [Green Version]
- Garnavich, P.; Jha, S.; Challis, P.; Clocchiatti, A.; Diercks, A.; Filippenko, A.V.; Gilliland, R.L.; Hogan, C.J.; Kirshner, R.P.; Leibundgut, B.; et al. Supernova Limits on the Cosmic Equation of State. Astrophys. J. 1998, 509, 74–79. [Google Scholar] [CrossRef] [Green Version]
- Nurbaki, A.N.; Capozziello, S.; Deliduman, C. Spherical and cylindrical solutions in f(T) gravity by Noether symmetry approach. Eur. Phys. J. C 2020, 80, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Geom. Meth. Mod. Phys. 2019, 28, 1930016. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.K.; Singh, R.; Shukla, B.K. A Cosmological Model with Variable Deceleration Parameter. Afr. Rev. Phys. 2015, 10, 48. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, R.K.; Beesham, A.; Shukla, B.K. FLRW Cosmological Models with Dynamic Cosmological Term in Modified Gravity. Universe 2021, 7, 319. https://doi.org/10.3390/universe7090319
Tiwari RK, Beesham A, Shukla BK. FLRW Cosmological Models with Dynamic Cosmological Term in Modified Gravity. Universe. 2021; 7(9):319. https://doi.org/10.3390/universe7090319
Chicago/Turabian StyleTiwari, Rishi Kumar, Aroonkumar Beesham, and Bhupendra Kumar Shukla. 2021. "FLRW Cosmological Models with Dynamic Cosmological Term in Modified Gravity" Universe 7, no. 9: 319. https://doi.org/10.3390/universe7090319
APA StyleTiwari, R. K., Beesham, A., & Shukla, B. K. (2021). FLRW Cosmological Models with Dynamic Cosmological Term in Modified Gravity. Universe, 7(9), 319. https://doi.org/10.3390/universe7090319





