Abrupt Change Detection Method Based on Features of Lorenz Trajectories
Abstract
:1. Introduction
2. Dynamic Definition and Detection Method of Abrupt Changes
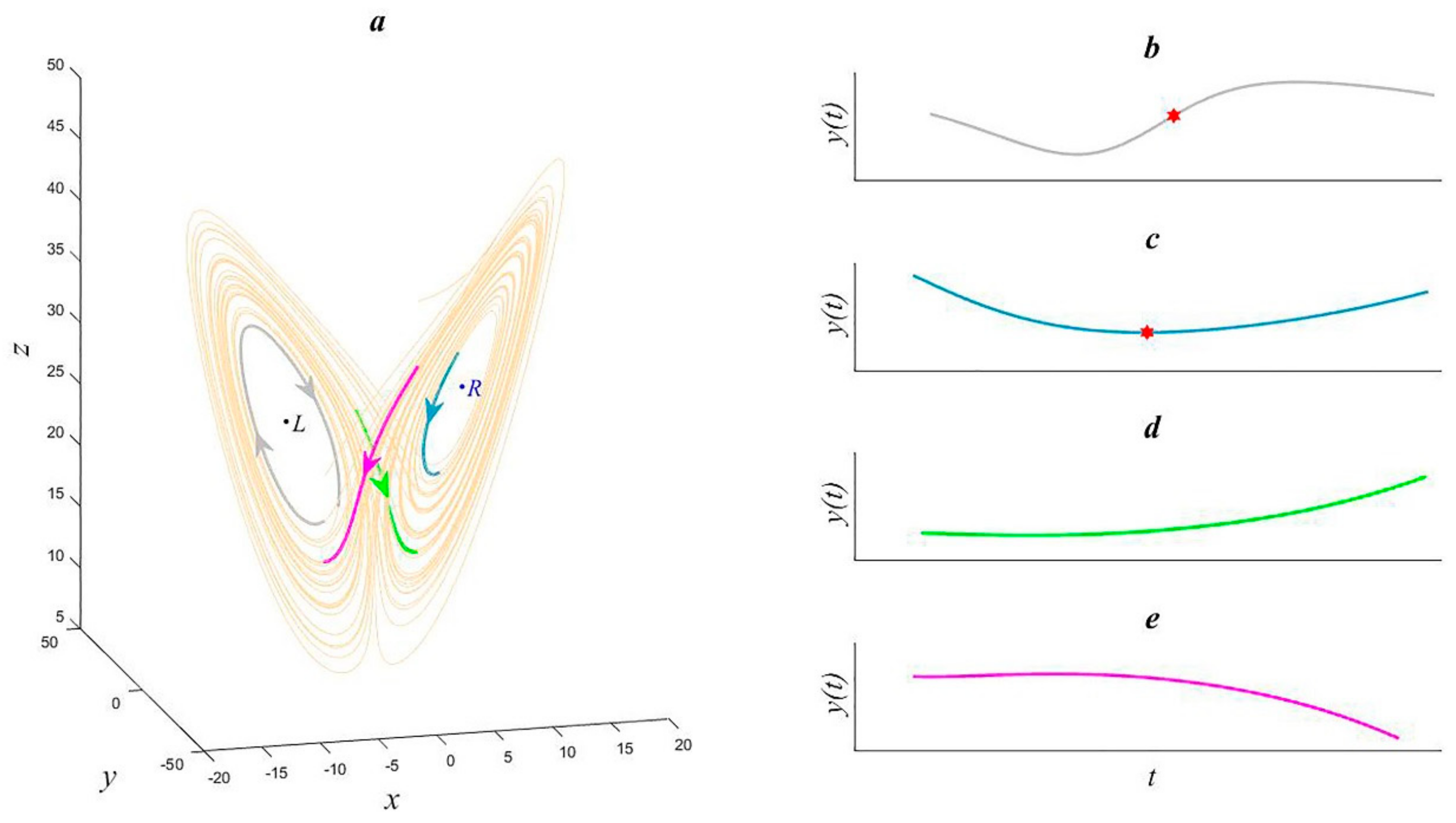
2.1. Abrupt Changes Based on Bifurcation Features
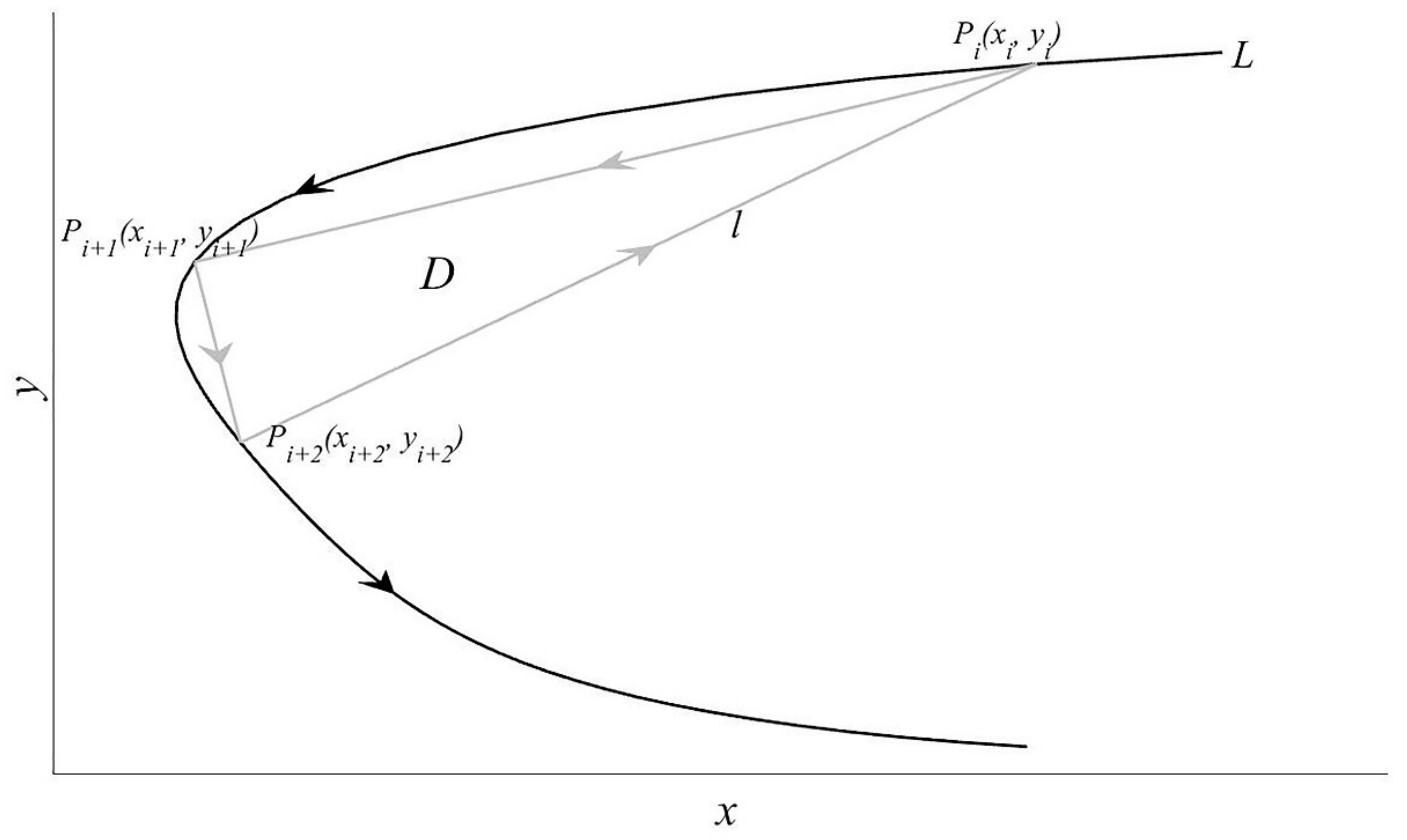
2.2. Bifurcation-Type Abrupt Change Detection Method
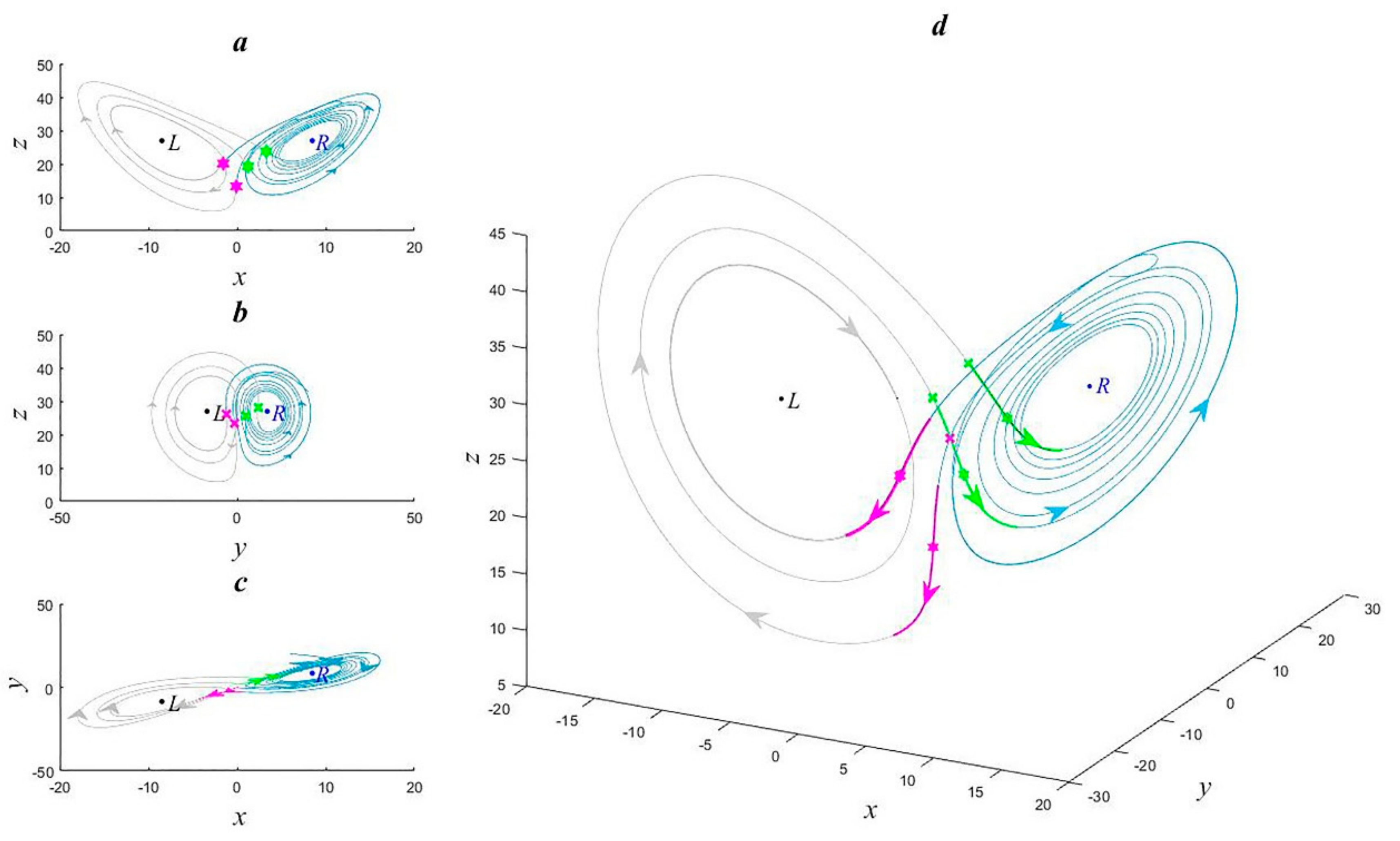
2.3. Bifurcation-Type Abrupt Change Detection Test
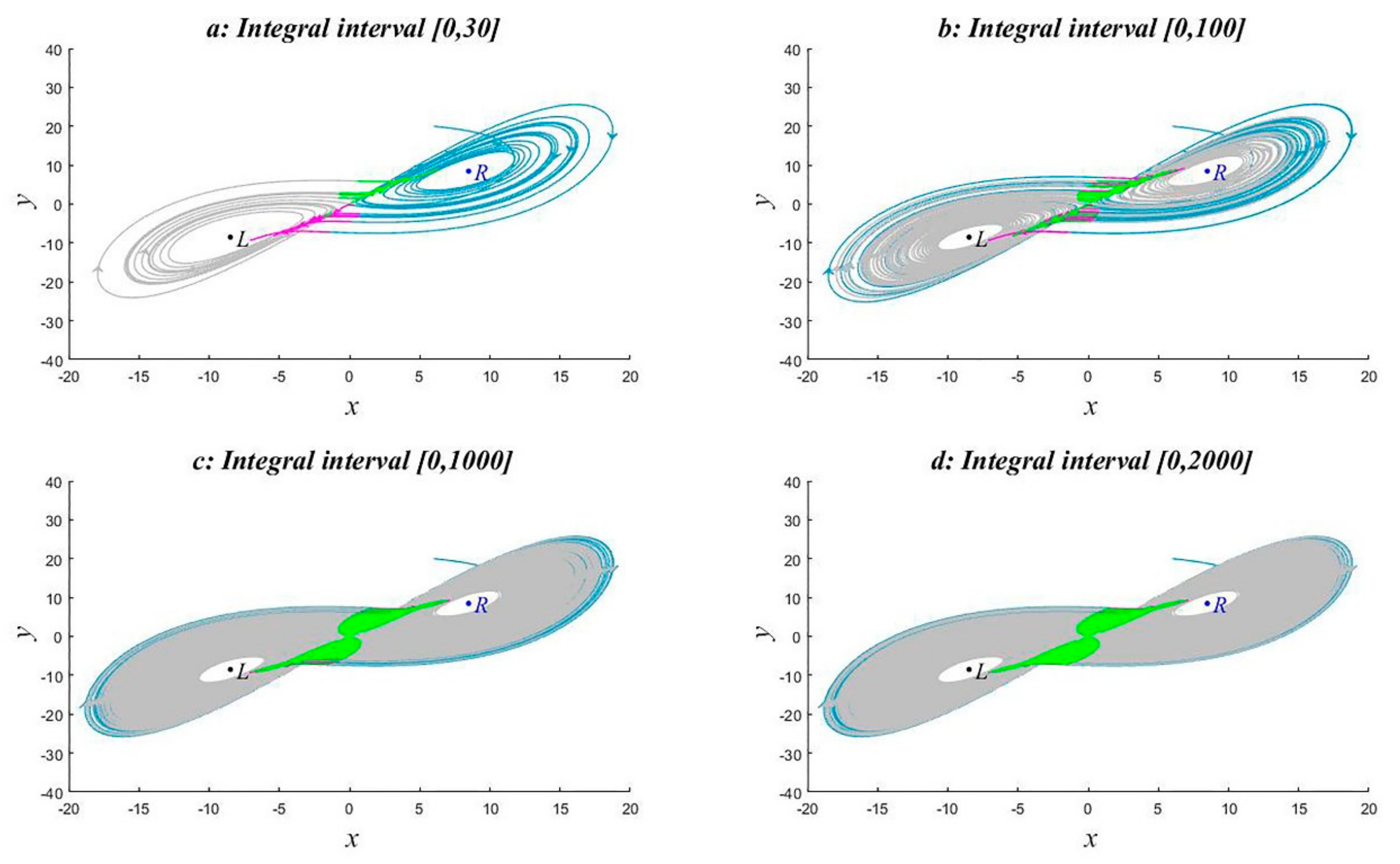
2.3.1. Single-Index Time Series Abrupt Change Detection
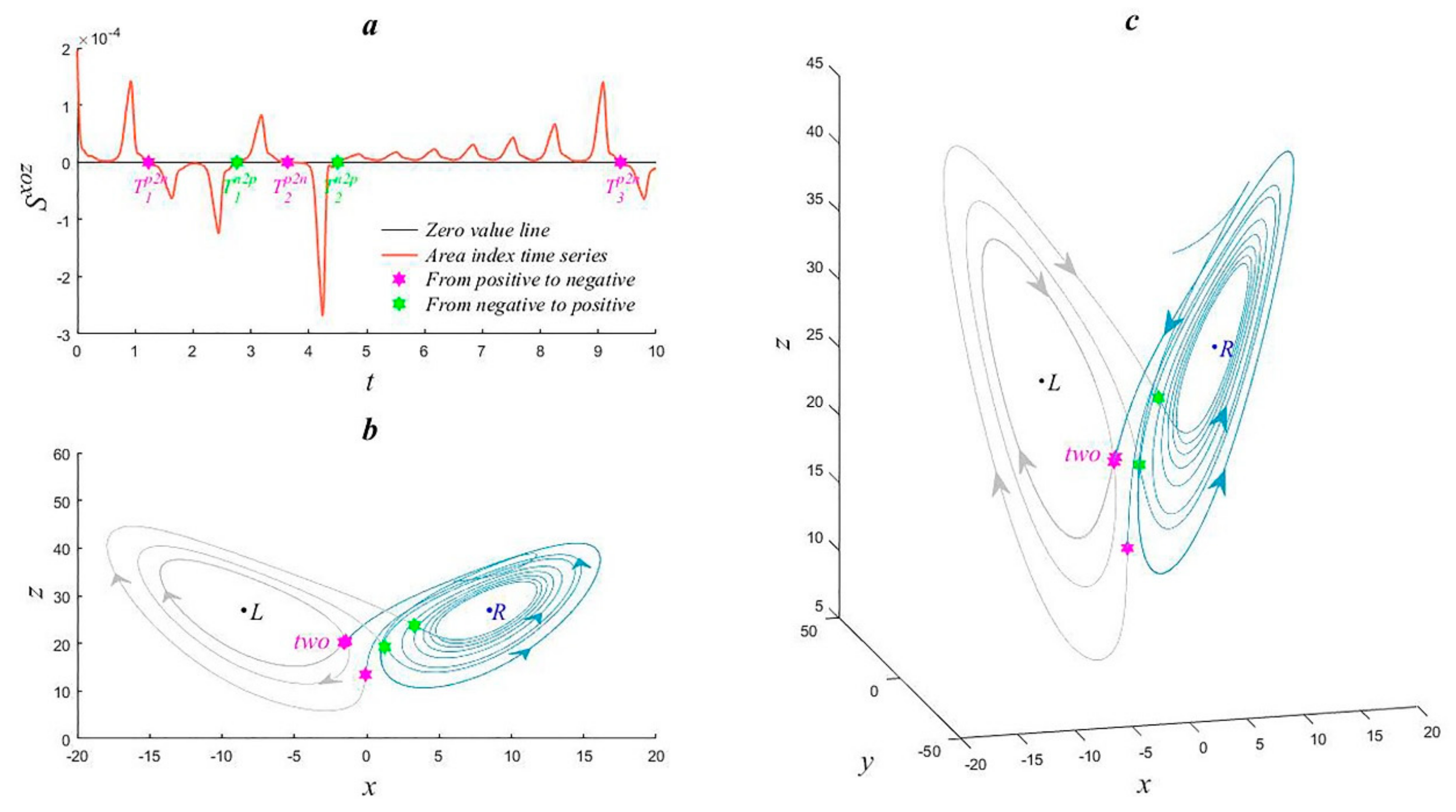
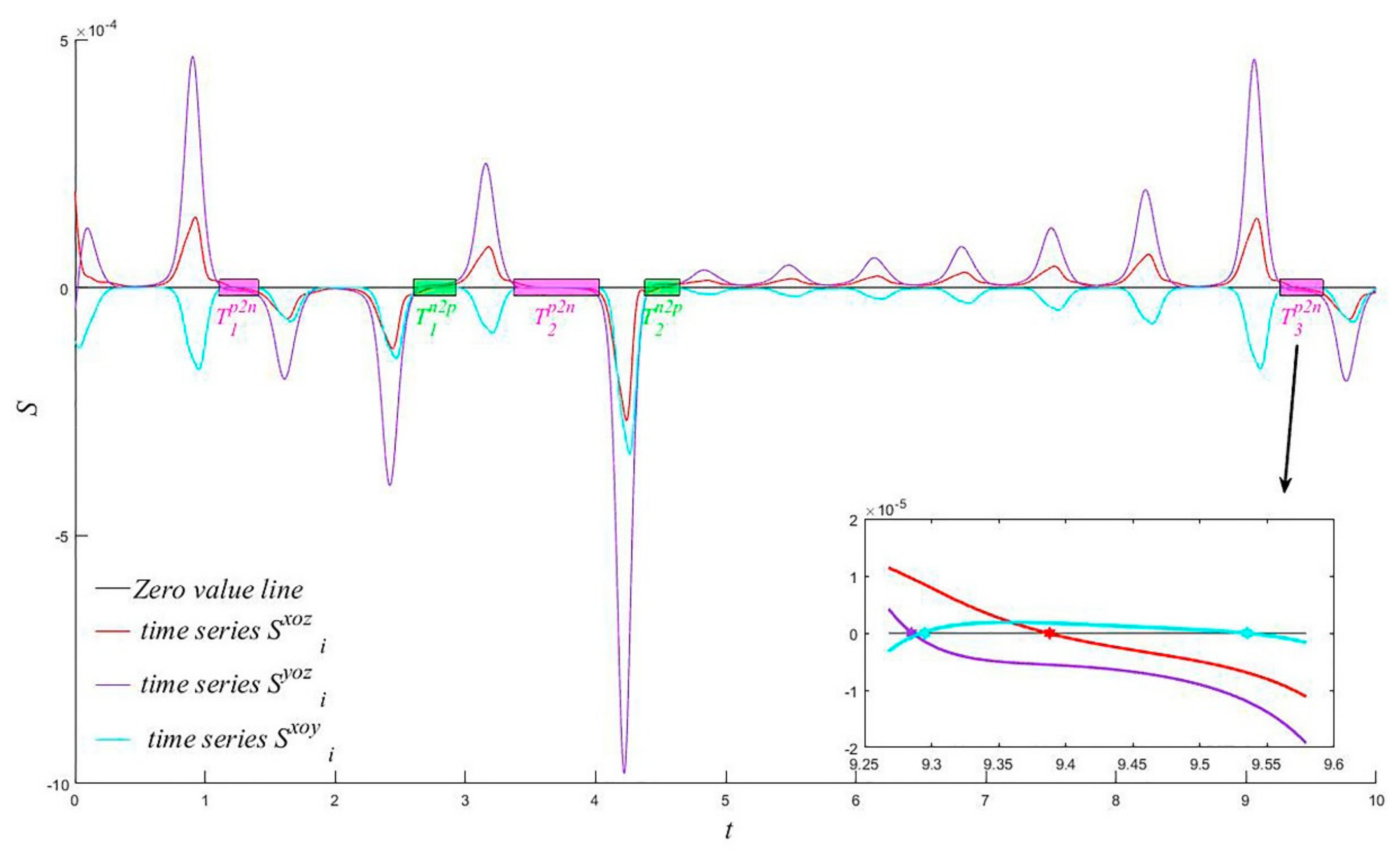
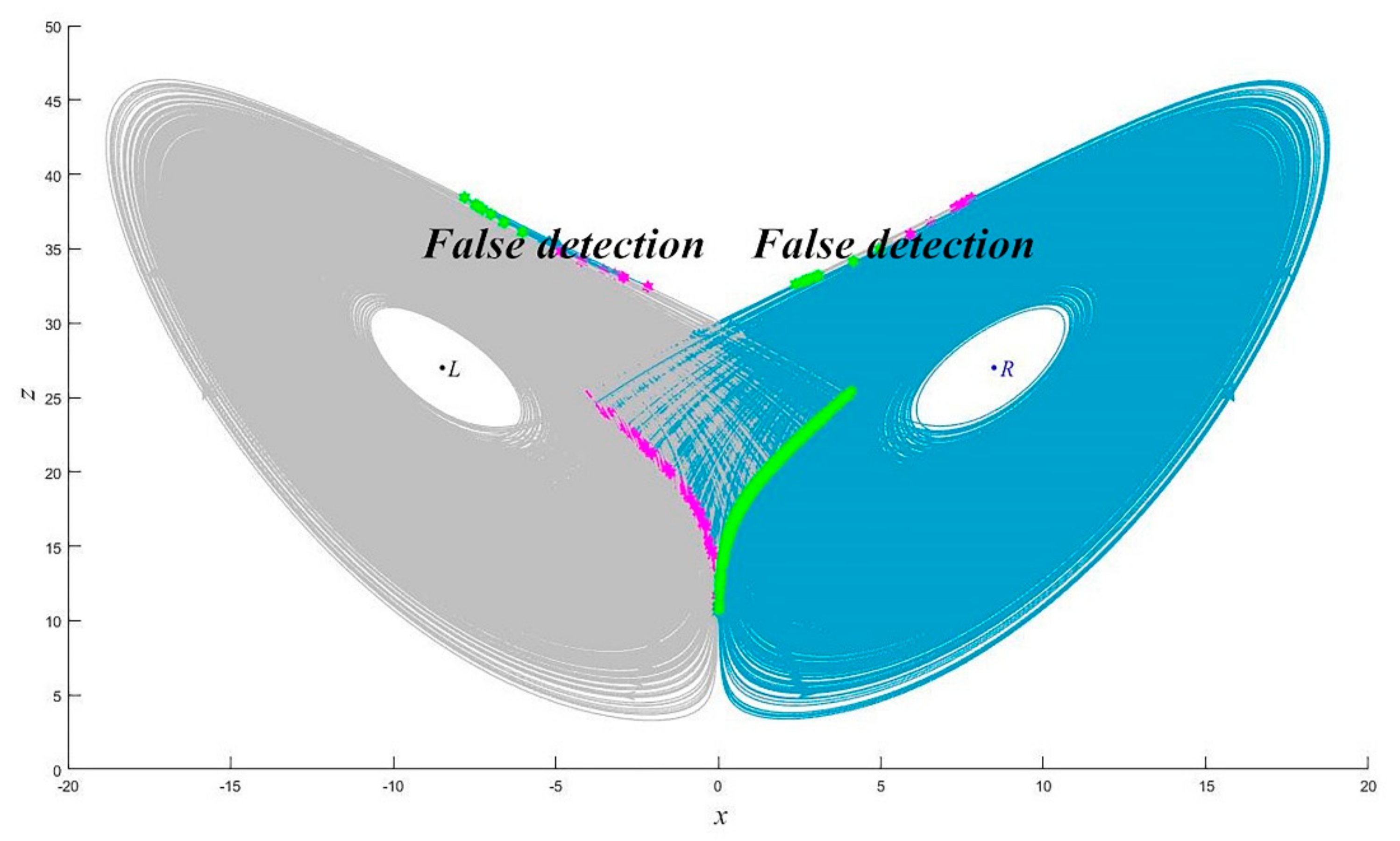
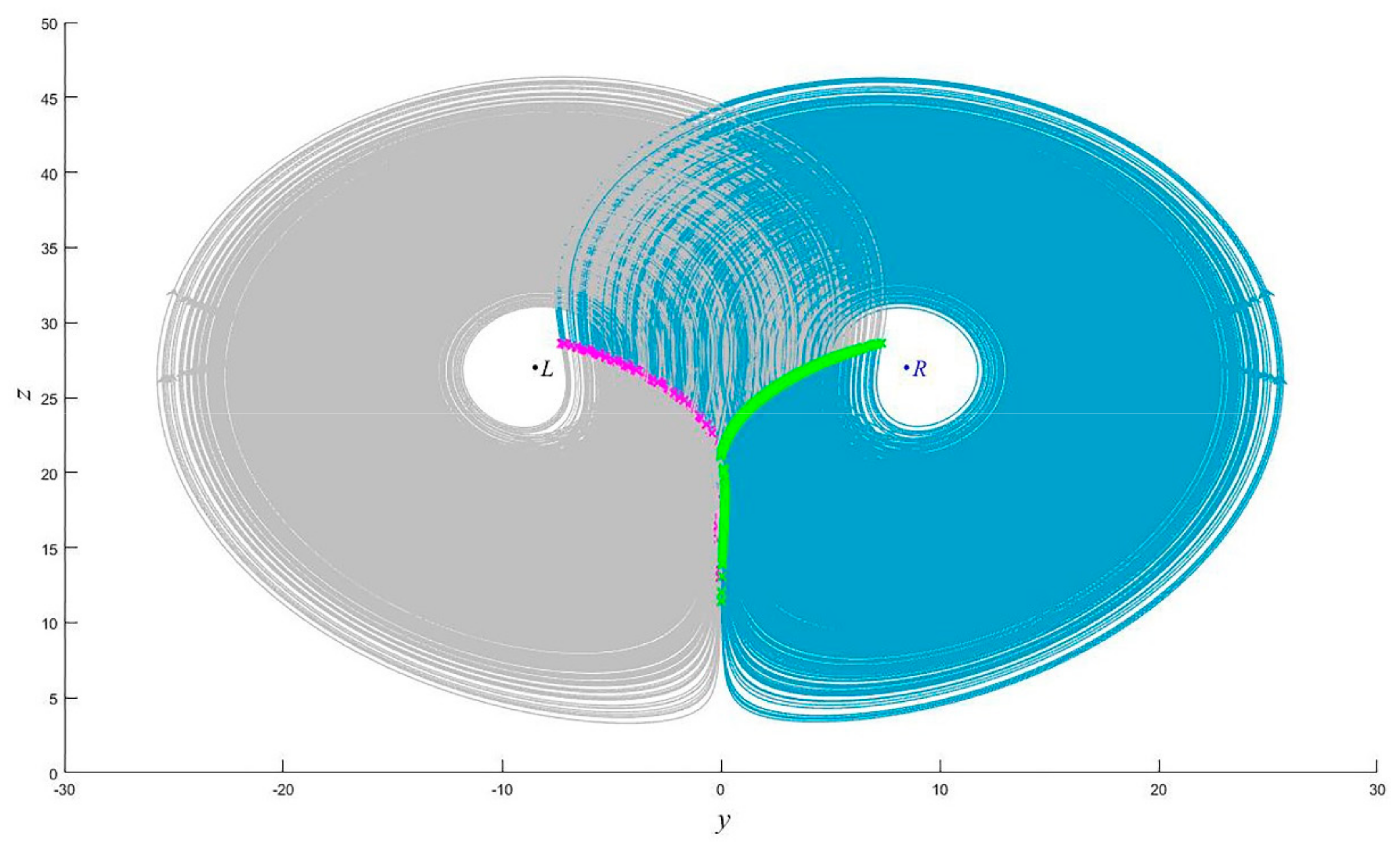
2.3.2. Multi-Index Time Series Abrupt Change Detection
2.3.3. Abrupt Change Detection Effect
3. Conclusions and Implications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Wu, Z.; Wang, X.; Zhang, D.; Xiao, M. The Characteristics of Summer Precipitation in China since 1981 and its Relationship with SST and Pre-circulation. Plateau Meteorol. 2020, 39, 58–67. [Google Scholar]
- Yu, R.; Zhai, P. Ocean and cryosphere change related extreme events, abrupt change and its impact and risk. Clim. Chang. Res. 2020, 16, 194–202. [Google Scholar]
- Wang, G.; Lu, L.; Sun, J. Stability of Surrounding rock and Thrust Calculation of Shield Passing through Geological mediums. Chin. J. Rock Mech. Eng. 2015, 34, 2362–2372. [Google Scholar]
- Zeng, H.; Li, D.; Huang, H. Distribution Pattern of Ploidy Variation of Actinidia chinensis and A deliciosa. J. Wuhan Bot. Res. 2009, 27, 312–317. [Google Scholar]
- Zhao, X.; Zhou, B.; Li, Y. Application of T-DNA Insertion Mutagenesis in Functional Genomics of Plant. Lett. Biotechnol. 2009, 20, 880–884. [Google Scholar]
- Li, Z.; Zou, Y.; Jiang, Y.; Hu, Y.; Qin, Y.; Li, M.; Zhan, Y.; Wang, D.; Wang, N. Bioinformatics Analysis of Cap Protein Sequences of Porcine Circovirus Type. Lett. Biotechnol. 2020, 24, 13–20. [Google Scholar]
- Jin, C.; Zhao, Y. Progress in the study of KRAS mutation in lung adenocarcinoma. J. Int. Oncol. 2020, 47, 180–184. [Google Scholar]
- Gao, Z. Human capital, industrial structure mutation and economic catching up. China Mark. 2007, 40, 28–29. [Google Scholar]
- Liu, J. Social, Cultural and Psychological Factors of Network Language Variation. Xijiang Moon. 2013. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=ee3b00947b1b20c4b9861fc83f709e7d&site=xueshu_se (accessed on 17 June 2021).
- Thom, R. Stabilité structurelle et morphogenèse. Poetics 1974, 3, 7–19. [Google Scholar] [CrossRef]
- Zeeman, E.C. Catastrophe Theory: A reply to Thom (Dynamical Systems-Warwick 1974); Springer: Berlin/Heidelberg, Germany, 1975; pp. 373–383. [Google Scholar]
- Daniell, P.J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations by J Hadamard; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- Lorenz, E.N. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Wang, Q. The definition and detection of the Abrupt Climatic Change. Chin. J. Atmos. Sci. 1992, 16, 15–21. [Google Scholar]
- Fu, C. Studies on the Observed Abrupt Climatic Change. Sci. Atmos. Sin. 1994, 18, 373–384. [Google Scholar]
- Zhu, K. East Asian monsoon and rainfall in China. Acta Geogr. Sinica. 1934, 1, 23–30. [Google Scholar]
- Tu, C.; Huang, T. Advance and retreat of summer monsoon in China. Acta Meteorol. Sin. 1944, 28, 234–247. [Google Scholar]
- Tao, S.; Chen, L. Structure of atmospheric circulation over Asian continent in summer. Chin. Sci. Bull. 1957, 7, 24–25. [Google Scholar]
- Ding, Y.; Zhang, L. Intercomparison of the time for climate abrupt change between the Tibetan Plateau and other regions in China. Chin. J. Atmos. Sci. 2008, 32, 794–805. [Google Scholar]
- Krishnamurti, T.N.; Ramanathan, Y. Sensitivity of the Monsoon Onset to Differential Heating. J. Atmos. Sci. 1979, 39, 1290–1306. [Google Scholar] [CrossRef] [Green Version]
- Shinoda, M.; Mikami, T.; Iwasaki, K.; Kitajima, H.; Eguchi, T.; Matsumoto, J.; Masuda, K. Global Simultaneity of the Abrupt Seasonal Changes in Precipitation during May and June of 1979. J Meteorol. Soc. Jpn. 1986, 64, 531–546. [Google Scholar] [CrossRef] [Green Version]
- Feng, G.; Gong, Z.; Dong, W.; Li, J. Abrupt climate change detection based on heuristic segmentation algorithm. Acta Phys. Sin. 2005, 54, 5494–5499. [Google Scholar]
- Hou, W.; Feng, G.; Dong, W.; Li, J. A technique for distinguishing dynamical species in the temperature time series of north China. Acta Phys. Sin. 2006, 53, 2663–2668. [Google Scholar]
- Gong, Z.; Feng, G.; Dong, W.; Li, J. The research of dynamic structure abrupt change of nonlinear time series. Acta Phys. Sin. 2006, 53, 3180–3187. [Google Scholar]
- Feng, G.; Gong, Z.; Zhi, R. Latest advances of climate change detecting technologies. Acta Meteorol. Sin. 2008, 66, 892–905. [Google Scholar]
- Zhi, R.; Gong, Z.; Wang, D.; Feng, G. Analysis of the spatio-temporal characteristics of precipitation of China based on the power-law exponent. Acta Phys. Sin. 2006, 53, 6185–6191. [Google Scholar]
- Huang, J.P.; Yi, Y.H.; Wang, S.W.; Chou, J.F. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Q. J. R. Meteorol. Soc. 1993, 119, 547–565. [Google Scholar]
- He, W.P.; Liu, Q.Q.; Gu, B.; Zhao, S.S. A novel method for detecting abrupt dynamic change based on the changing hurst exponent of spatial images. Clim. Dyn. 2016, 47, 2561–2571. [Google Scholar] [CrossRef]
- Halifa-Marín, A.; Lorente-Plazas, R.; Pravia-Sarabia, E.; Montávez, J.P.; Jiménez-Guerrero, P. Atlantic and mediterranean influence promoting an abrupt change in winter precipitation over the southern iberian peninsula. Atmos. Res. 2021, 253, 105485. [Google Scholar] [CrossRef]
- Guo, F.; Yan, M.; Zhang, K.; Lei, H.; Guo, L. The climate change in qingdao during 1899–2015 and its response to global warming. J. Geosci. Environ. Prot. 2018, 6, 58–70. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.R.; Lateh, H. Spatio-temporal analysis of warming in bangladesh using recent observed temperature data and GIS. Clim. Dyn. 2016, 46, 2943–2960. [Google Scholar] [CrossRef]
- Fang, S.; Yue, Q.; Han, G.; Li, Q.; Zhou, G. Changing trends and abrupt features of extreme temperature in mainland china from 1960 to 2010. Atmosphere 2016, 7, 22. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Da, C.; Shen, B.; Song, J.; Xaiwu, C.; Feng, G. Abrupt Change Detection Method Based on Features of Lorenz Trajectories. Atmosphere 2021, 12, 781. https://doi.org/10.3390/atmos12060781
Da C, Shen B, Song J, Xaiwu C, Feng G. Abrupt Change Detection Method Based on Features of Lorenz Trajectories. Atmosphere. 2021; 12(6):781. https://doi.org/10.3390/atmos12060781
Chicago/Turabian StyleDa, Chaojiu, Binglu Shen, Jian Song, Cairang Xaiwu, and Guolin Feng. 2021. "Abrupt Change Detection Method Based on Features of Lorenz Trajectories" Atmosphere 12, no. 6: 781. https://doi.org/10.3390/atmos12060781





