Assessment of GPM IMERG Satellite Precipitation Estimation under Complex Climatic and Topographic Conditions
Abstract
1. Introduction
2. Materials and Methods
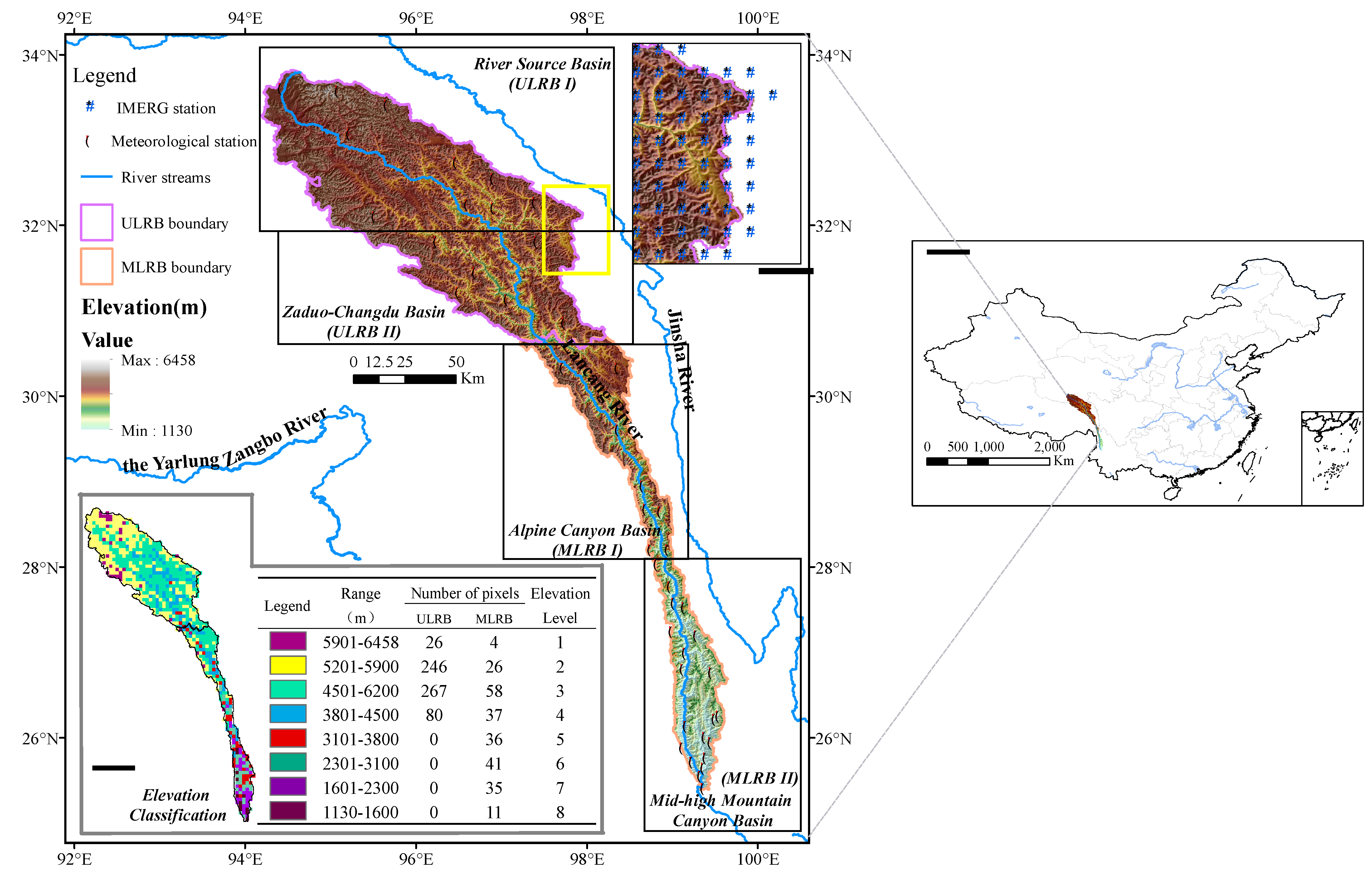
2.1. Study Region
2.2. Data
2.2.1. Rain Gauge Data
2.2.2. Satellite Data
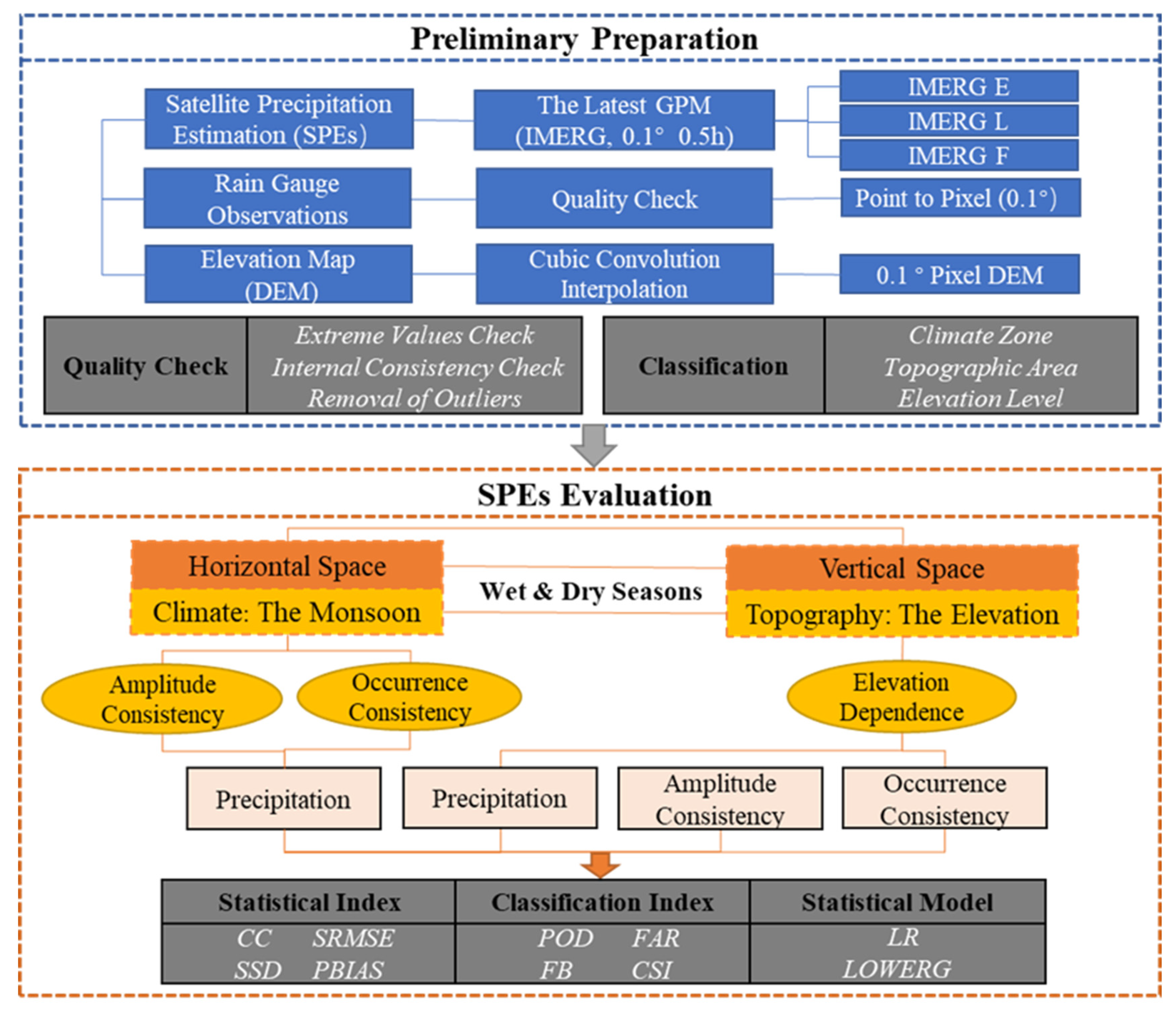
2.3. Methodology
2.3.1. Performance Representation
Amplitude Consistency
2.3.2. Linear Regression (LR) and Local Weighted Regression (LOWERG)
2.3.3. Regional and Elevation Level Division
2.3.4. Analytical Procedure
3. Results
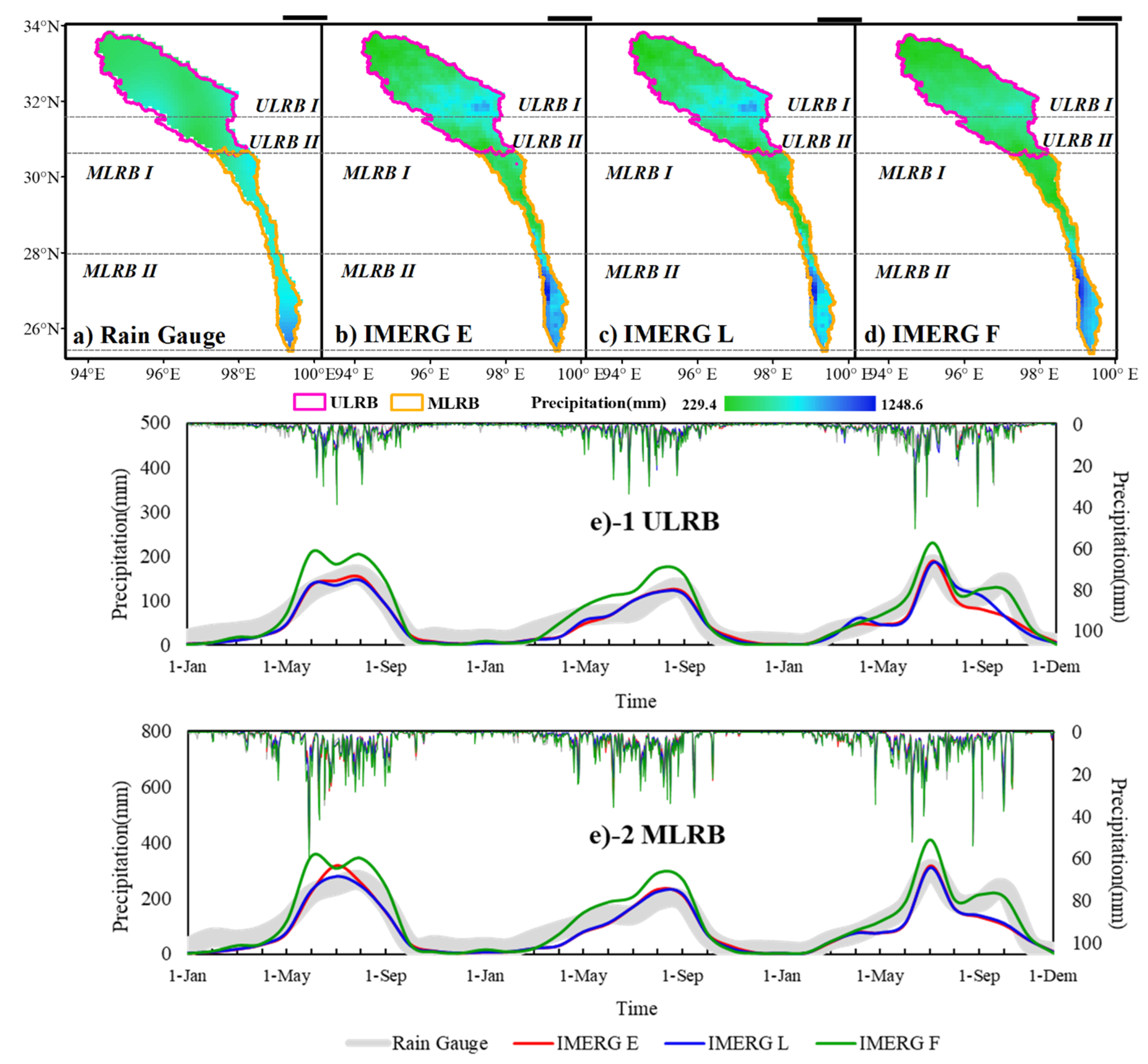
3.1. Multi–Year Average Precipitation and Precipitation in Dry/Wet Seasons in UMLRB
3.2. Influence of Monsoons on IMERG Horizontal Spatial Performance in UMLRB
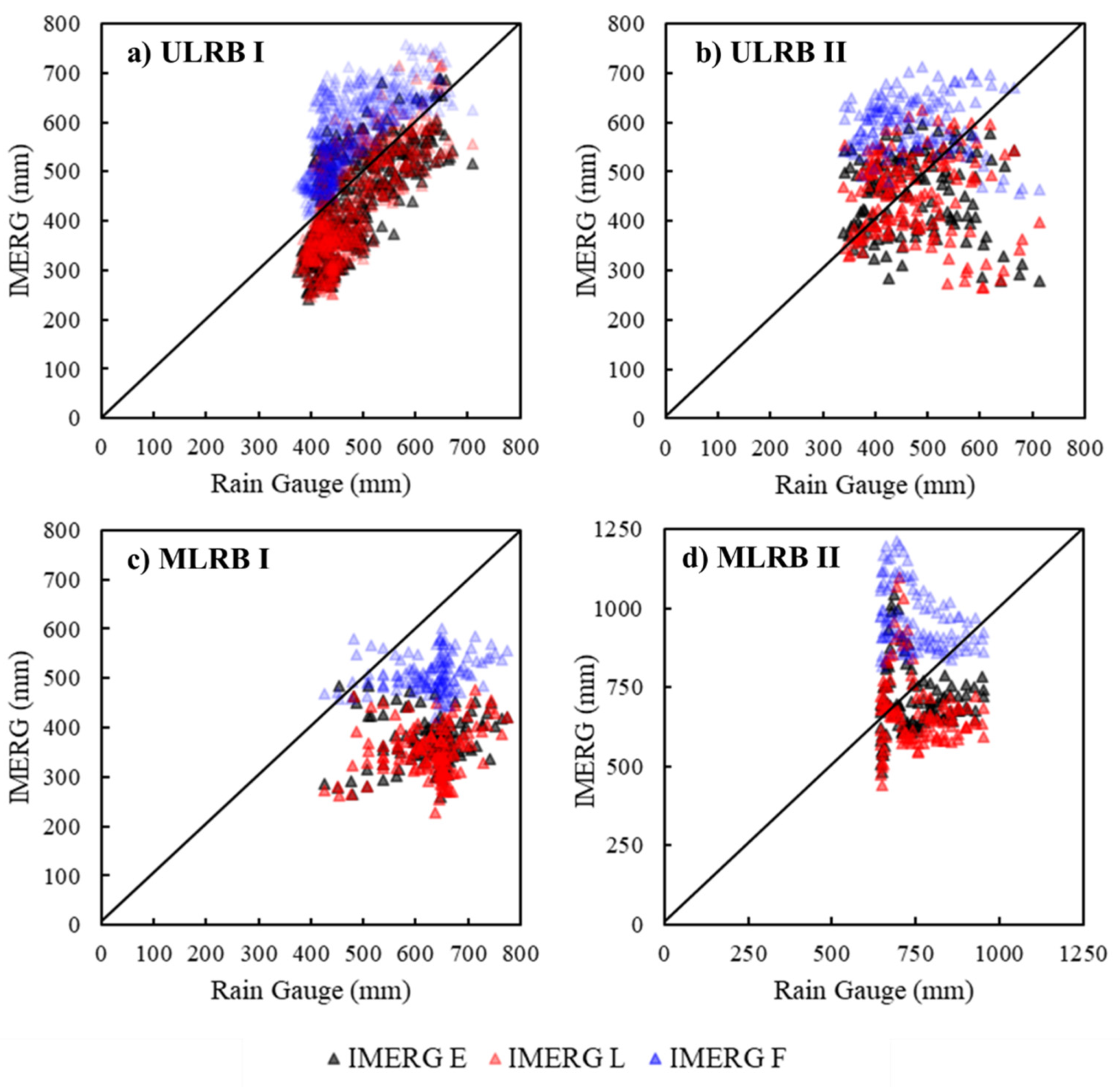
3.2.1. Amplitude Consistency of Precipitation in Dry/Wet Seasons
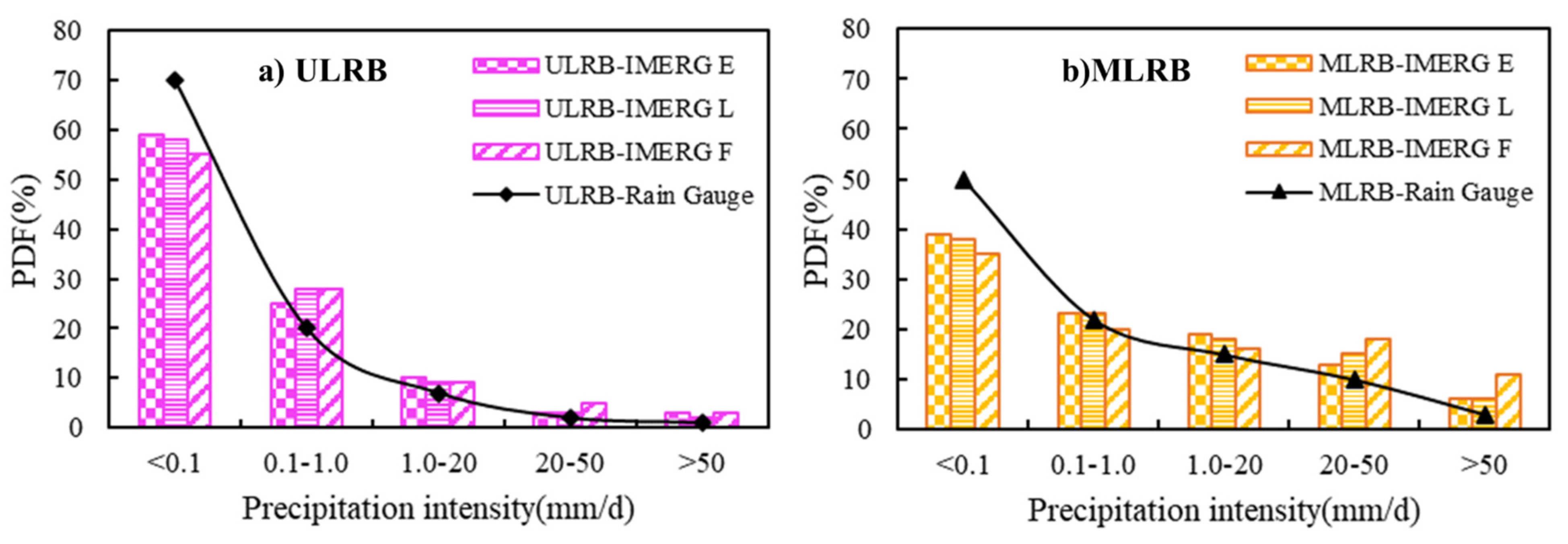
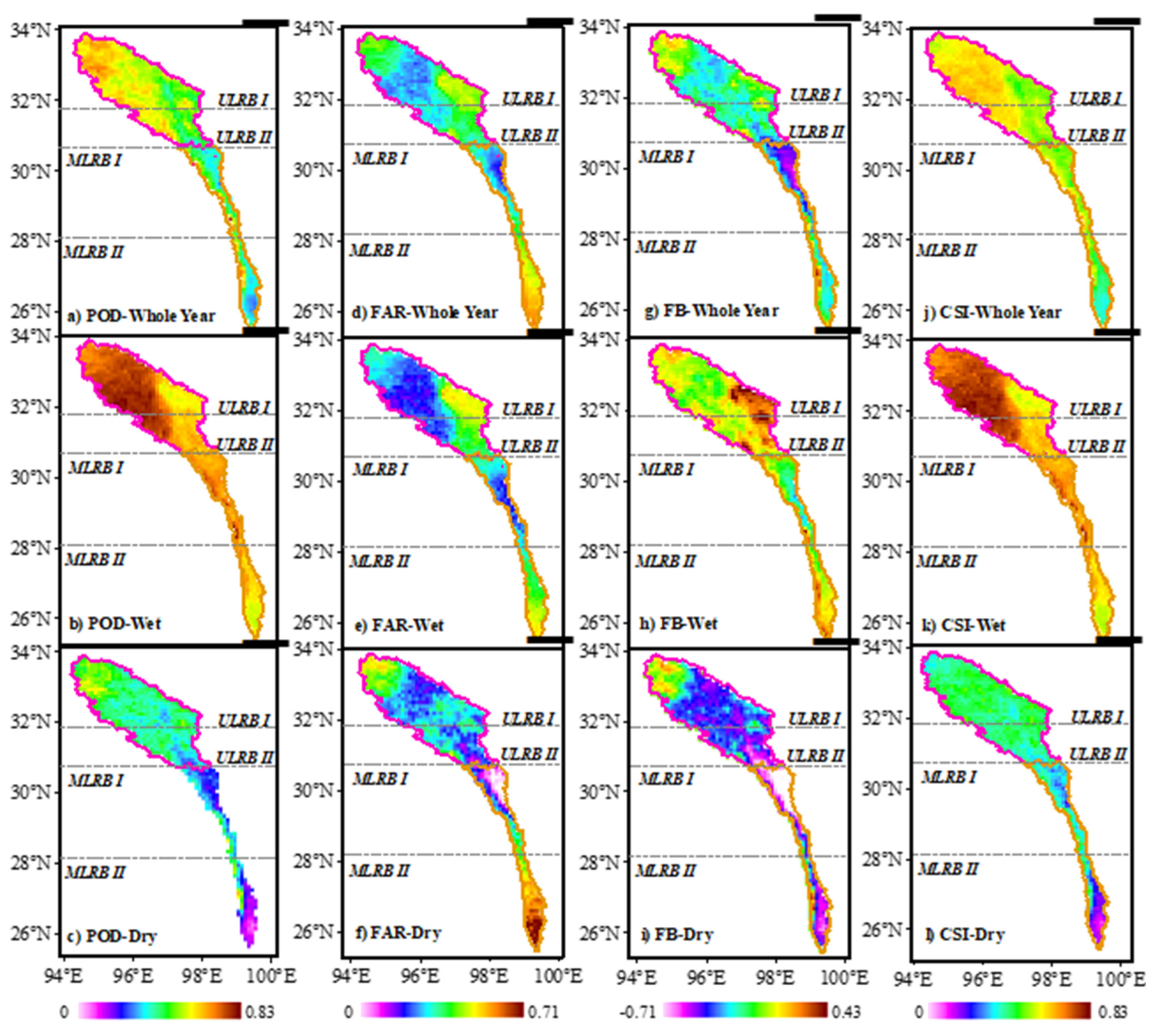
3.2.2. Occurrence Consistency of Precipitation in Dry/Wet Seasons
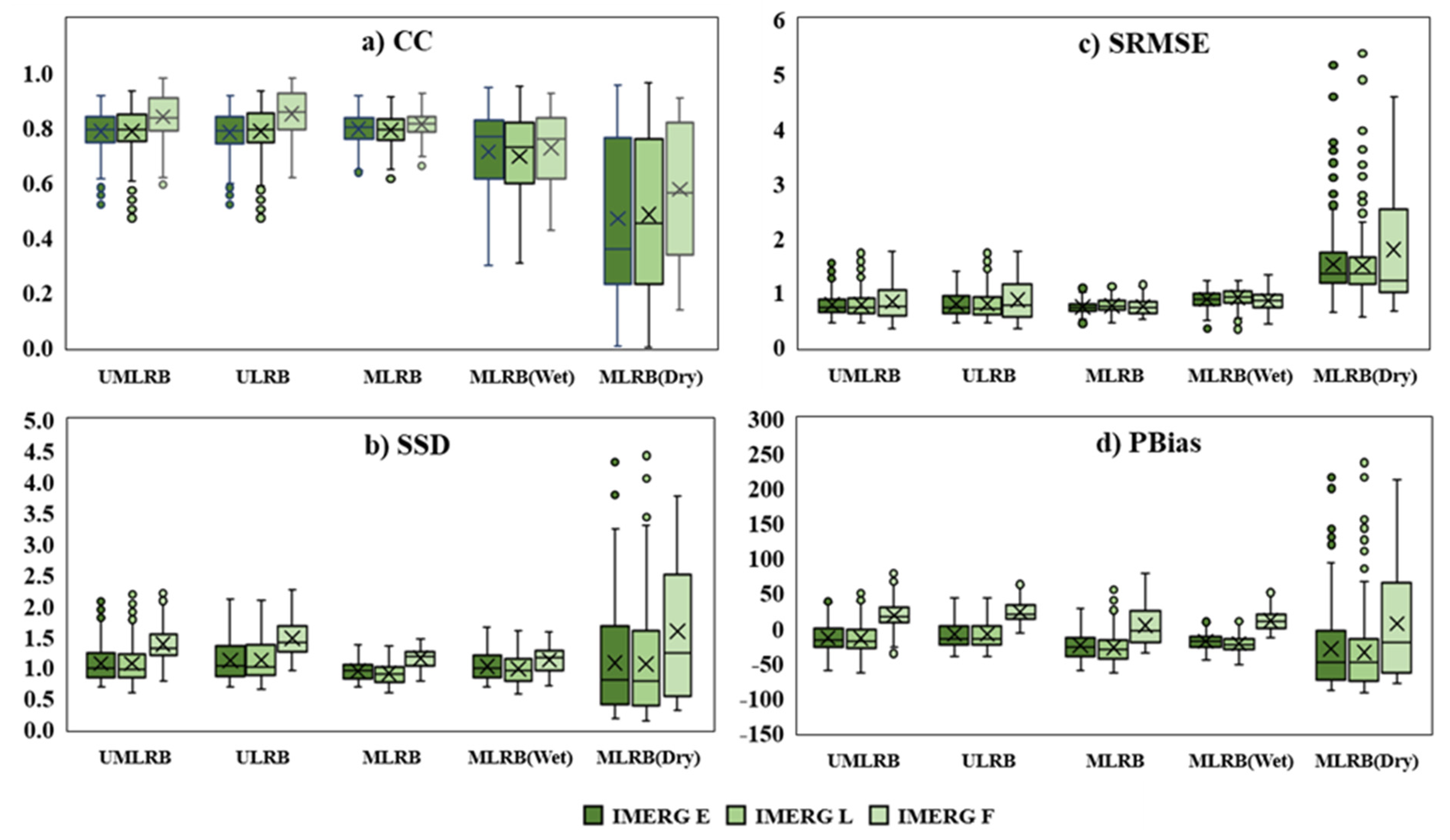
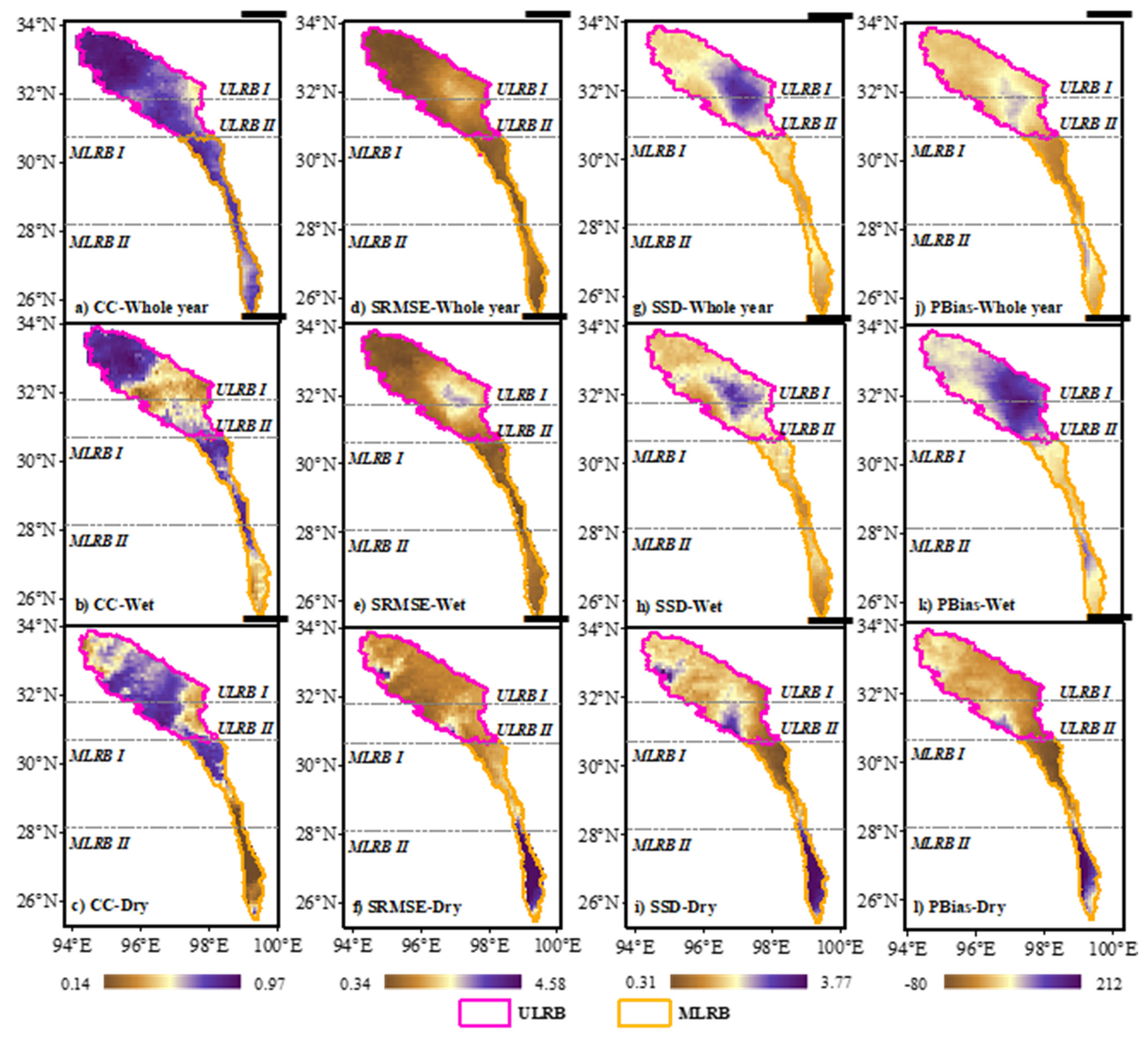
3.3. Influence of Topography on the Vertical Spatial Performance of IMERG in UMLRB
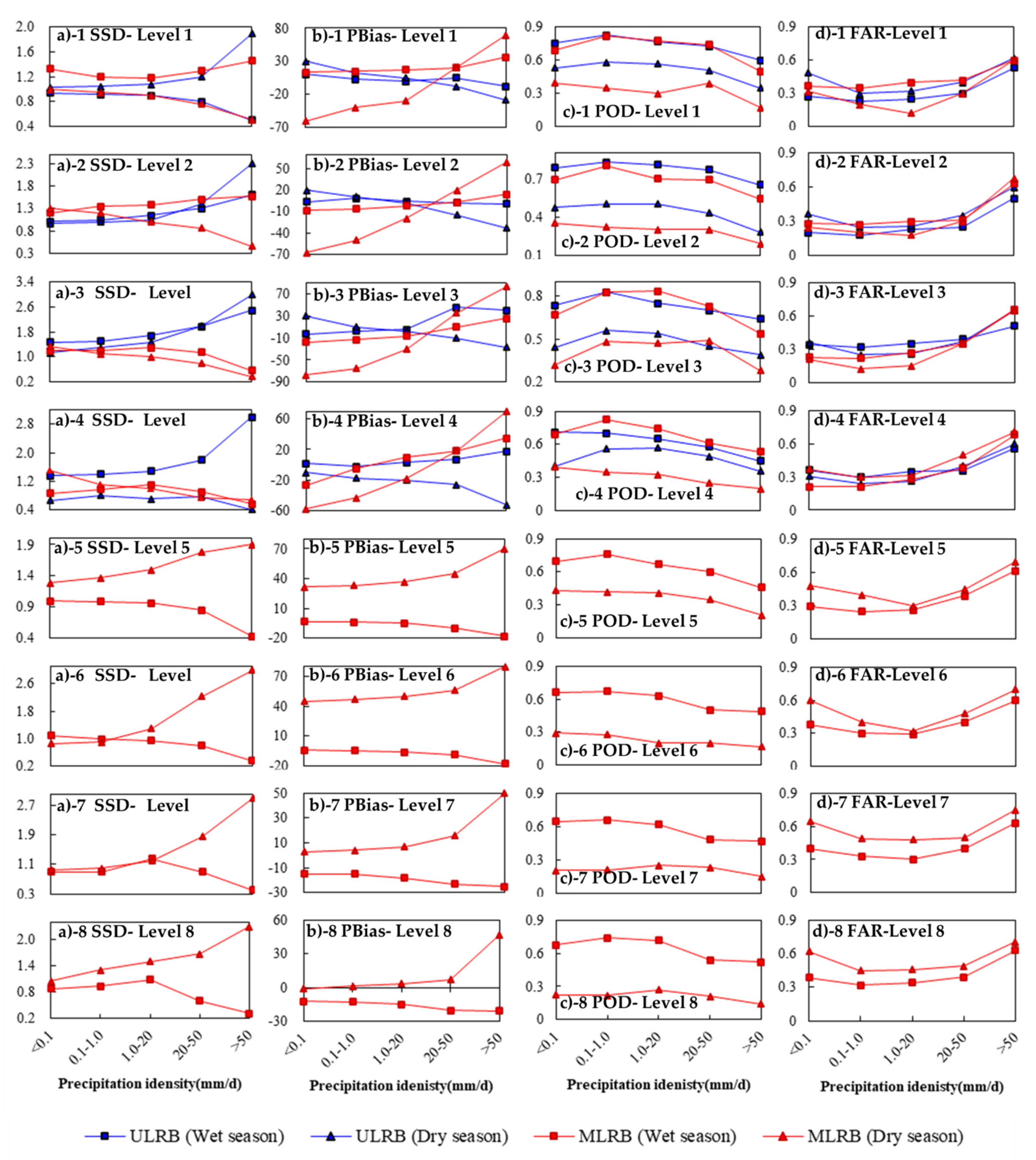
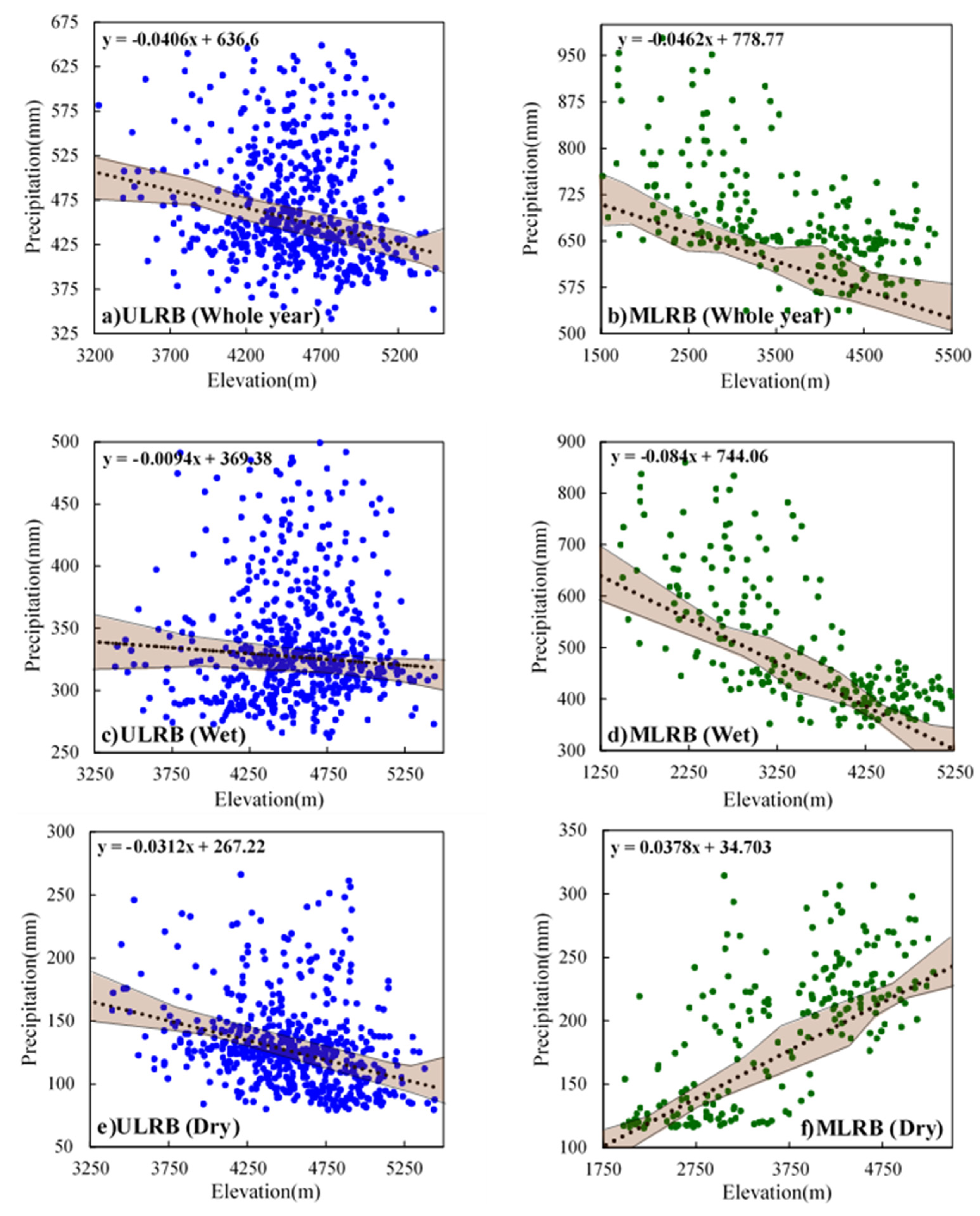
3.3.1. Elevation Dependence of Precipitation in Dry/Wet Seasons
3.3.2. Elevation Dependence of Amplitude in Dry/Wet Seasons
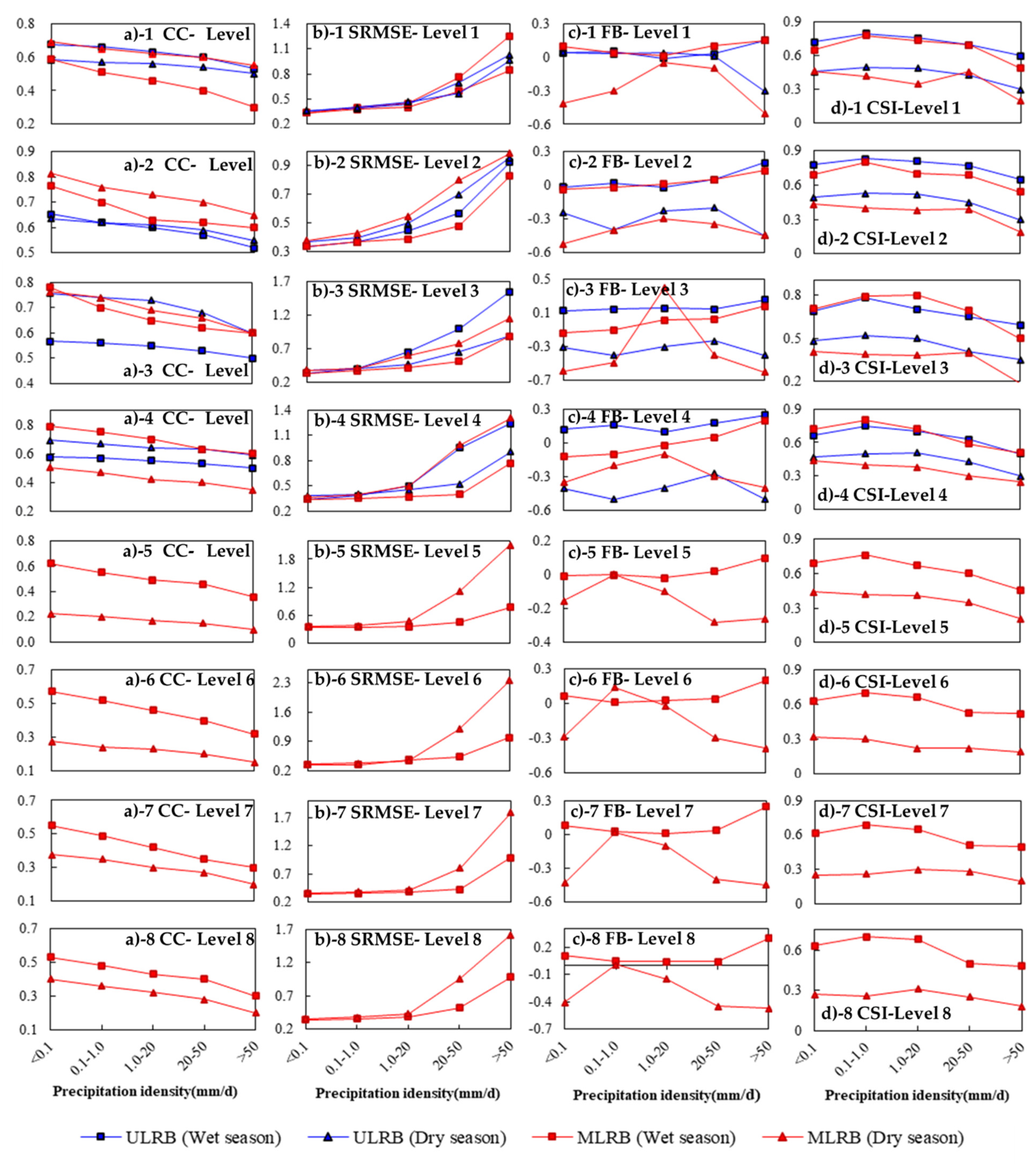
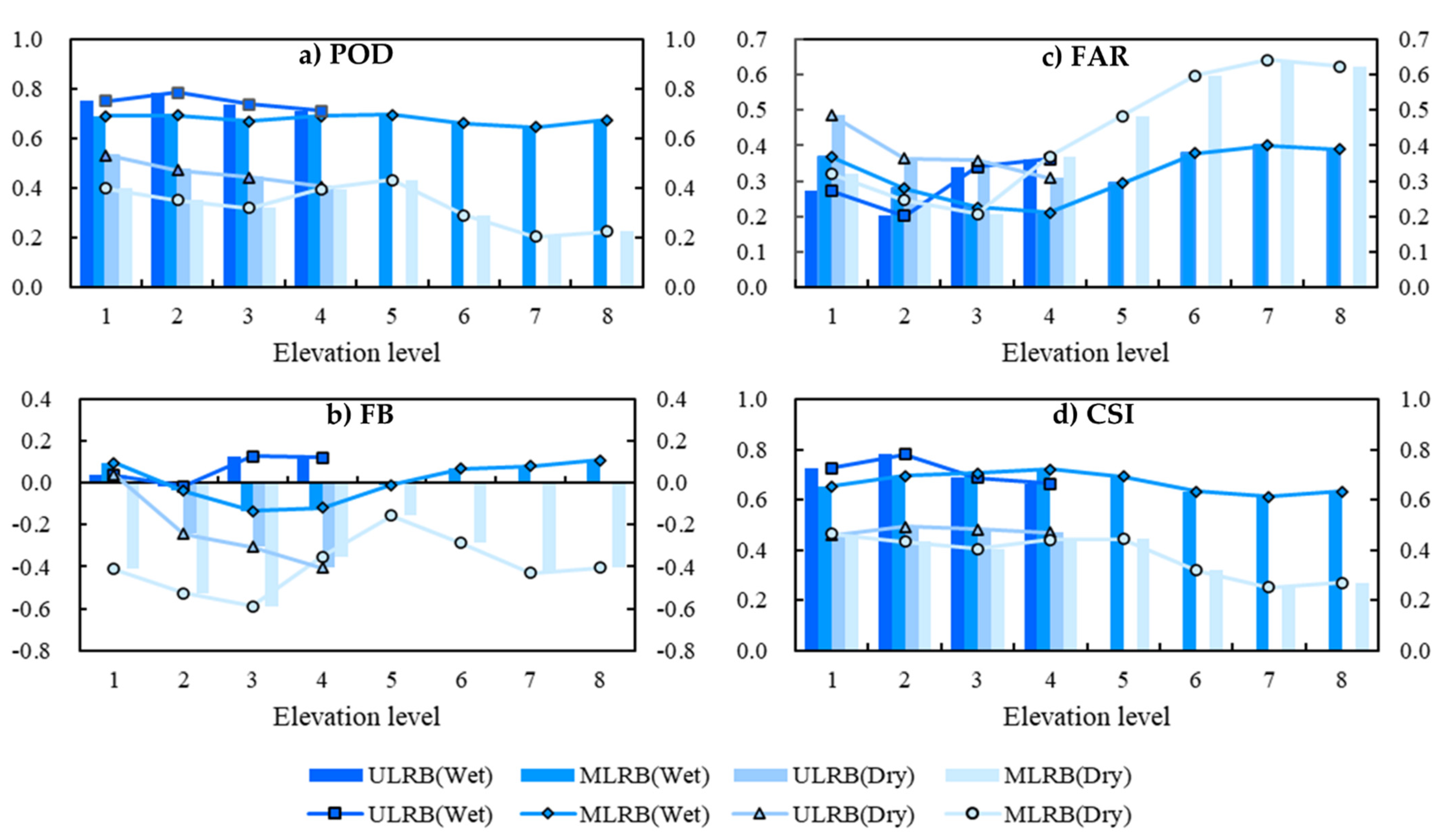
3.3.3. Elevation Dependence of Occurrence in Dry/Wet Seasons
4. Discussion
4.1. Factors Affecting the Amplitude Consistency of Precipitation of IMERG in Dry and Wet Season
4.2. Factors Affecting the Occurrence Consistency of Precipitation of IMERG in Dry and Wet Season
4.3. Factors Affecting the Elevation Dependence of IMERG in Dry and Wet Season
4.4. Effect of Altitude on Precipitation in UMLRB
4.5. Limitations
5. Conclusions
- The factors affecting the amplitude consistency of precipitation of IMERG in both seasons can be summarized as two points: monsoon and solid precipitation (e.g., snow). The climate difference brought spatial heterogeneity to the precipitation in dry and wet seasons. The Alpine Climate Region (ULRB) was little affected by the monsoon while the Climate Transition Zone (MLRB) was greatly affected by the monsoon. IMERG performed well in dry seasons than in wet seasons in ULRB, while the MLRB was opposite. The ability for IMERG to detect precipitation accurately of wet seasons in ULRB was limited due to the abnormal wind field and radiation, which led to the difference of precipitation amplitude between IMERG and rain gauge. Although IMERG’s ability to retrieve solid precipitation areas was improved, it tended to underestimate precipitation during the dry season in ULRB II and MLRB I due to the presence of snow. IMERG E and IMERG L tended to underestimate precipitation while IMERG F often overestimated precipitation.
- Aerosol was regarded as the most important influencing factor of occurrence consistency of precipitation in UMLRB. The increase in aerosol concentration changed the size of the cloud droplets, the thermal structure of atmosphere and radiative budget, so that the precipitation was affected to some extent. UMLRB was representative of typical clean atmospheric conditions with low aerosol concentration but aerosol concentration (dust and anthropogenic pollutants) was still increasing, which led to overestimation of precipitation events in the wet season in some areas such as ULRB I.
- Topography and wind–induced errors were the main factors affecting elevation dependence of IMERG in both seasons in UMLRB. The complex topography brought the foehn effect to the leeward slope of MLRB, which reduced the reflection sensitivity of sensors of IMERG and enhanced the elevation dependence in wet seasons in MLRB. At the same time, rain gauge tended to underestimate precipitation of high–elevation areas due to wind–induced errors.
- The LOWERG model accurately simulated the nonlinear relationship between precipitation and elevation in both seasons, compensating for IMERG’s lack of sufficient precipitation detection ability in complex terrain, especially in high–elevation areas.
- Under the same precipitation intensity, the amplitude consistency and the occurrence consistency of both seasons increased with elevation, which worsened with increasing precipitation intensity regardless of elevation. In the case of extreme precipitation (>50 mm/d), the IMERG amplitude consistency in both seasons decreased sharply. IMERG had the highest probability of correctly detecting precipitation events such as light (0.1–1.0 mm/d) and moderate (1.0–20 mm/d) rain.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Udo, S.; Ziese, M.; Meyer–Christoffer, A.; Finger, P.; Rustemeier, E.; Becker, A. The New Portfolio of Global Precipitation Data Products of the Global Precipitation Climatology Centre Suitable to Assess and Quantify the Global Water Cycle and Resources. Proc. Int. Assoc. Hydrol. Sci. 2016, 374, 29–34. [Google Scholar]
- Daly, C.; Slater, M.E.; Roberti, J.A.; Laseter, S.H.; Swift, L.W., Jr. High–Resolution Precipitation Mapping in a Mountainous Watershed: Ground Truth for Evaluating Uncertainty in a National Precipitation Dataset. Int. J. Climatol. 2017, 37, 124–137. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Wanders, N.; Pan, M.; Wood, E.F. Correction of Real–Time Satellite Precipitation with Multi–Sensor Satellite Observations of Land Surface Variables. Remote Sens. Environ. 2015, 160, 206–221. [Google Scholar] [CrossRef]
- Chung–Chen, J.; Kot, S.C.; Tepper, M. Comparing Noaa–12 and Radiosonde Atmospheric Sounding Profiles for Mesoscale Weather Model Initialization. In Proceedings of the COSPAR Colloquia Series, Tainan, Taiwan, 14–17 December 1997; Volume 8, pp. 103–109. [Google Scholar]
- Shi, H.; Li, T.; Wei, J. Evaluation of the Gridded Cru Ts Precipitation Dataset with the Point Raingauge Records over the Three–River Headwaters Region. J. Hydrol. 2017, 548, 322–332. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, B.; Shi, C.; Cui, W.; Zhao, C.; Liu, Y.; Ren, L.; Zhang, L.; Zhu, Y.; Chen, T.; et al. Evaluation of Hydrological Utility of Imerg Final Run V05 and Tmpa 3b42v7 Satellite Precipitation Products in the Yellow River Source Region, China. J. Hydrol. 2018, 567, 696–711. [Google Scholar] [CrossRef]
- Chappell, A.; Renzullo, L.J.; Raupach, T.H.; Haylock, M. Evaluating Geostatistical Methods of Blending Satellite and Gauge Data to Estimate near Real–Time Daily Rainfall for Australia. J. Hydrol. 2013, 493, 105–114. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Hong, Y. Multi–Scale Evaluation of High–Resolution Multi–Sensor Blended Global Precipitation Products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, Z.; Shen, Y.; Zhang, S.; Shi, R. Evaluation of Satellite Rainfall Estimates over the Chinese Mainland. Remote Sens. 2014, 6, 11649–11672. [Google Scholar] [CrossRef]
- Hou, A.; Ramesh, Y.; Kakar, K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Palomino–Ángel, S.; Anaya–Acevedo, J.A.; Botero, B.A. Evaluation of 3b42v7 and Imerg Daily–Precipitation Products for a Very High–Precipitation Region in Northwestern South America. Atmos. Res. 2019, 217, 37–48. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of Gpm–Imerg and Other Precipitation Products against Gauge Data under Different Topographic and Climatic Conditions in Iran: Preliminary Results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Skofronick–Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (Gpm) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Ahmad, I.; Ijaz, M.W.; Farid, H.U.; Yagoub, Y.E.; Zaman, M.; Adnan, M. Performance Evaluation of Latest Integrated Multi–Satellite Retrievals for Global Precipitation Measurement (Imerg) over the Northern Highlands of Pakistan. Atmos. Res. 2018, 205, 134–146. [Google Scholar] [CrossRef]
- Chen, F.; Li, X. Evaluation of Imerg and Trmm 3b43 Monthly Precipitation Products over Mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Kirstetter, P.-E.; Hong, Y.E.; Gourley, J.J.; Huffman, G.J.; Petersen, W.A.; Xue, X.; Schwaller, M.R. To What Extent Is the Day 1 Gpm Imerg Satellite Precipitation Estimate Improved as Compared to Trmm Tmpa–Rt? J. Geophys. Res. Atmos. 2018, 123, 1694–1707. [Google Scholar] [CrossRef]
- Tan, M.; Duan, Z. Assessment of Gpm and Trmm Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Tan, M.L.; Li, X.; Wang, G.; He, R. Nine–Year Systematic Evaluation of the Gpm and Trmm Precipitation Products in the Shuaishui River Basin in East–Central China. Remote Sens. 2020, 12, 1042. [Google Scholar] [CrossRef]
- Wang, X.; Ding, Y.; Zhao, C.; Wang, J. Similarities and Improvements of Gpm Imerg Upon Trmm 3b42 Precipitation Product under Complex Topographic and Climatic Conditions over Hexi Region, Northeastern Tibetan Plateau. Atmos. Res. 2019, 218, 347–363. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ahmad, I.; Ding, Y.; Shangguan, D.; Ijaz, M.Z.W.; Sarwar, K.; Han, H.; Yang, M. Assessment of Imerg–V06 Precipitation Product over Different Hydro–Climatic Regimes in the Tianshan Mountains, North–Western China. Remote Sens. 2019, 11, 2314. [Google Scholar] [CrossRef]
- Golian, S.; Moazami, S.; Kirstetter, P.; Hong, Y. Evaluating the Performance of Merged Multi–Satellite Precipitation Products over a Complex Terrain. Water Resour. Manag. 2015, 29, 4885–4901. [Google Scholar] [CrossRef]
- Liu, j.; Xia, J.; She, D.; Li, L.; Wang, Q.; Zou, L. Evaluation of Six Satellite–Based Precipitation Products and Their Ability for Capturing Characteristics of Extreme Precipitation Events over a Climate Transition Area in China. Remote Sens. 2019, 11, 1477. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J.; Wang, J.; Qiao, X.; Zhang, J. Evaluation of Gpm Imerg V05b and Trmm 3b42v7 Precipitation Products over High Mountainous Tributaries in Lhasa with Dense Rain Gauges. Remote Sens. 2019, 11, 2080. [Google Scholar] [CrossRef]
- Yu, C.; Hu, D.; Liu, M.; Wang, S.; Di, Y. Spatio–Temporal Accuracy Evaluation of Three High–Resolution Satellite Precipitation Products in China Area. Atmos. Res. 2020, 241, 104952. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, X.; Meng, S.; Wu, D.; Chen, Y.; Jiang, F.; Zhu, B. Magnitude Agreement, Occurrence Consistency, and Elevation Dependency of Satellite–Based Precipitation Products over the Tibetan Plateau. Remote Sens. 2020, 12, 1750. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Shao, H.; Chen, S.; Liu, T.; Chen, C.; Ding, Q.; Du, H. Evaluation and Intercomparison of High–Resolution Satellite Precipitation Estimates—Gpm, Trmm, and Cmorph in the Tianshan Mountain Area. Remote Sens. 2018, 10, 1543. [Google Scholar] [CrossRef]
- Yang, M.; Liu, G.; Chen, T.; Chen, Y.; Xia, C. Evaluation of Gpm Imerg Precipitation Products with the Point Rain Gauge Records over Sichuan, China. Atmos. Res. 2020, 246, 105101. [Google Scholar] [CrossRef]
- Sharma, S.; Chen, Y.; Zhou, X.; Yang, K.; Li, X.; Niu, X.; Hu, X.; Khadka, N. Evaluation of Gpm–Era Satellite Precipitation Products on the Southern Slopes of the Central Himalayas against Rain Gauge Data. Remote Sens. 2020, 12, 1836. [Google Scholar] [CrossRef]
- de Sousa Afonso, J.M.; Vila, D.A.; Gan, M.A.; Quispe, D.P.; de Jesus da Costa Barreto, N.; Chinchay, J.H.H.; Palharini, R.S.A. Precipitation Diurnal Cycle Assessment of Satellite–Based Estimates over Brazil. Remote Sens. 2020, 12, 2339. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.; Gao, S.; Hong, Z.; Tang, G.; Wen, Y.; Gourley, J.J.; Hong, Y. Cross–Examination of Similarity, Difference and Deficiency of Gauge, Radar and Satellite Precipitation Measuring Uncertainties for Extreme Events Using Conventional Metrics and Multiplicative Triple Collocation. Remote Sens. 2020, 12, 1258. [Google Scholar] [CrossRef]
- Ma, M.; Wang, H.; Jia, P.; Tang, G.; Wang, D.; Ma, Z.; Yan, H. Application of the Gpm–Imerg Products in Flash Flood Warning: A Case Study in Yunnan, China. Remote Sens. 2020, 12, 1954. [Google Scholar] [CrossRef]
- Xiao, S.; Xia, J.; Zou, L. Evaluation of Multi–Satellite Precipitation Products and Their Ability in Capturing the Characteristics of Extreme Climate Events over the Yangtze River Basin, China. Water 2020, 12, 1179. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of Trmm– and Gpm–Era Multiple–Satellite Precipitation Products for Flood Simulations at Sub–Daily Scales in a Sparsely Gauged Watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef]
- Navarro, A.; García–Ortega, E.; Merino, A.; Sánchez, J.L. Extreme Events of Precipitation over Complex Terrain Derived from Satellite Data for Climate Applications: An Evaluation of the Southern Slopes of the Pyrenees. Remote Sens. 2020, 12, 2171. [Google Scholar] [CrossRef]
- Alsumaiti, T.S.; Hussein, K.; Ghebreyesus, D.T.; Sharif, H.O. Performance of the Cmorph and Gpm Imerg Products over the United Arab Emirates. Remote Sens. 2020, 12, 1426. [Google Scholar] [CrossRef]
- He, Z.; Yang, L.; Tian, F.; Ni, G.; Hou, A.; Lu, H. Intercomparisons of Rainfall Estimates from Trmm and Gpm Multisatellite Products over the Upper Mekong River Basin. J. Hydrometeorol. 2017, 18, 413–430. [Google Scholar] [CrossRef]
- Yu, L.; Ma, L.; Li, H.; Zhang, Y.; Kong, F.; Yang, Y. Assessment of High–Resolution Satellite Rainfall Products over a Gradually Elevating Mountainous Terrain Based on a High–Density Rain Gauge Network. Int. J. Remote Sens. 2020, 41, 5620–5644. [Google Scholar] [CrossRef]
- Rojas, Y.; Minder, J.R. Assessment of Gpm Imerg Satellite Precipitation Estimation and Its Dependence on Microphysical Rain Regimes over the Mountains of South–Central Chile. Atmos. Res. 2021, 253, 105454. [Google Scholar] [CrossRef]
- Nepal, B.; Shrestha, D. Assessment of Gpm–Era Satellite Products’(Imerg and Gsmap) Ability to Detect Precipitation Extremes over Mountainous Country Nepal. Atmosphere 2021, 12, 254. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. Cmorph: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Gebremicael, T.G.; Mohamed, Y.A.; van der Zaag, P.; Gebremedhin, A.; Gebremeskel, G.; Yazew, E.; Kifle, M. Evaluation of Multiple Satellite Rainfall Products over the Rugged Topography of the Tekeze–Atbara Basin in Ethiopia. Int. J. Remote Sens. 2019, 40, 4326–4345. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early Assessment of Integrated Multi–Satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Kim, J.-H.; Ou, M.-L.; Park, J.-D.; Morris, K.R.; Schwaller, M.R.; Wolff, D.B. Global Precipitation Measurement (Gpm) Ground Validation (Gv) Prototype in the Korean Peninsula. J. Atmos. Ocean. Technol. 2014, 31, 1902–1921. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Z.; Wu, X.; Chen, X.; Lai, C.; Zeng, Z. Accuracy Evaluation of Gpm Multi–Satellite Precipitation Products in the Hydrological Application over Alpine and Gorge Regions with Sparse Rain Gauge Network. Hydrol. Res. 2019, 50, 1710–1729. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Lai, C.; Zhong, R.; Chen, X.; Yu, H. Hydrologic Assessment of the Tmpa 3b42–V7 Product in a Typical Alpine and Gorge Region: The Lancang River Basin, China. Hydrol. Res. 2018, 49, 2002–2015. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H.; Zhao, T.; Jiang, L.; Shi, J. Evaluation and Comparison of Daily Rainfall from Latest Gpm and Trmm Products over the Mekong River Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2540–2549. [Google Scholar] [CrossRef]
- He, D. Analysis of Hydrological Characteristics in Lancang–Mekong River. Yunnan Geogr. Environ. Res. 1995, 7, 59–73. (In Chinese) [Google Scholar]
- Gao, H.; Xiao, Z.; Zhao, L. A Study on the Abrupt Change of Summer Rainfall over Lancang River Basin and the Associated Atmospheric Circulation in the Early 21st Century. Clim. Environ. Res. 2019, 24, 513–524. (In Chinese) [Google Scholar]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K. Multiscale Comparative Evaluation of the Gpm Imerg V5 and Trmm 3b42 V7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Xu, W.; Li, Q.; Wang, X.; Yang, S. Homogenization of Chinese Daily Surface Air Temperatures and Analysis of Trends in the Extreme Temperature Indices. J. Geophys. Res. Atmos. 2013, 118, 9708–9720. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L. Imerg and Tmpa Version–7 Legacy Products over Mainland China at Multiple Spatiotemporal Scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Legates, D.R.; Willmott, C.J. Mean Seasonal and Spatial Variability in Gauge–Corrected, Global Precipitation. Int. J. Climatol. 1990, 10, 111–127. [Google Scholar] [CrossRef]
- Lin, Y.; Duan, W.; Liu, Y. Analysis of Torrential Rain Characteristics in the Upper Reaches of Lancang River. Sci. Technol. Inf. 2015, 32, 104–109. (In Chinese) [Google Scholar]
- Liu, C.; Gao, Y.; Yi, J.; Yang, S. An Modis–Based Analysis of Spatio–Temporal Variations of Aerosol Optical Depth in Southwest of China. J. Southwest Univ. 2014, 36, 182–189. [Google Scholar]
- Zhou, Y.; Han, Y.; Wu, Y.; Wang, T. Optical Properties and Spatial Variation of Tropical Cyclone Cloud Systems from Trmm and Modis in the East Asia Region: 2010–2014. J. Geophys. Res. Atmos. 2018, 123, 9542–9558. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Woodley, W.L.; Khain, A.; Cotton, W.R.; Carrió, G.; Ginis, I.; Golden, J.H. Aerosol Effects on Microstructure and Intensity of Tropical Cyclones. Bull. Am. Meteorol. Soc. 2012, 93, 987–1001. [Google Scholar] [CrossRef]
- Wang, Y.; Lee, K.-H.; Lin, Y. Distinct Effects of Anthropogenic Aerosols on Tropical Cyclones. Nat. Clim. Chang. 2014, 4, 368–373. [Google Scholar] [CrossRef]
- Dong, X.; Li, R.; Wang, Y.; Fu, Y. Potential Impacts of Sahara Dust Aerosol on Rainfall Vertical Structure over the Atlantic Ocean as Identified from Eof Analysis. J. Geophys. Res. Atmos. 2018, 123, 8850–8868. [Google Scholar] [CrossRef]
- Guo, J.; Liu, H.; Li, Z.; Rosenfeld, D. Aerosol–Induced Changes in the Vertical Structure of Precipitation: A Perspective of Trmm Precipitation Radar. Atmos. Chem. Phys. 2018, 18, 13329–13343. [Google Scholar] [CrossRef]
- Wang, Y.; Wan, Q.; Meng, W. Long–Term Impacts of Aerosols on Precipitation and Lightning over the Pearl River Delta Megacity Area in China. Atmos. Chem. Phys. 2011, 11, 12421–12436. [Google Scholar] [CrossRef]
- Squires, P. The Spatial Variation of Liquid Water and Droplet Concentration in Cumuli. Tellus 1958, 10, 372–380. [Google Scholar] [CrossRef]
- Twomey, S. The Influence of Pollution on the Shortwave Albedo of Clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Fan, J.; Rosenfeld, D.; Zhang, Y. Substantial Convection and Precipitation Enhancements by Ultrafine Aerosol Particles. Sci. Technol. Inf. 2018, 359, 411–418. [Google Scholar] [CrossRef]
- Xu, C.; Ma, Y.M.; You, C. The Regional Distribution Characteristics of Aerosol Optical Depth over the Tibetan Plateau. Atmos. Chem. Phys. 2015, 15, 12065–12078. [Google Scholar] [CrossRef]
- Liaoa, T.; Guib, K.; Liab, Y. Seasonal Distribution and Vertical Structure of Different Types of Aerosols in Southwest China Observed from Caliop. Atmos. Environ. 2021, 246, 118145. [Google Scholar] [CrossRef]
- Xu, X.; Wu, H.; Yang, X. Distribution and Transport Characteristics of Dust Aerosol over Tibetan Plateau and Taklimakan Desert in China Using Merra–2 and Calipso Data. Atmos. Environ. 2020, 237, 117670. [Google Scholar] [CrossRef]
- Huang, J.; Fu, Q.; Su, J. Taklimakan Dust Aerosol Radiative Heating Derived from Calipso Observations Using the Fu–Liou Radiation Model with Ceres Constraints. Atmos. Chem. Phys. 2009, 9, 4011–4021. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover–Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of Satellite Rainfall Products over East Africa’s Complex Topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Li, Q. Flora Analysis and Phytocommunity Studies on the Deciduous Monsoon Forest at Lower Reaches of Luozha River in Yunxian. Master’s Thesis, Chinese Academy of Sciences, Beijing, China, June 2007. [Google Scholar]
- Tahir, A.A.; Adamowski, J.; Chevallier, P. Comparative Assessment of Spatiotemporal Snow Cover Changes and Hydrological Behavior of the Gilgit, Astore and Hunza River Basins (Hindukush–Karakoram–Himalaya Region, Pakistan). Meteorol. Atmos. Phys. 2016, 128, 793–811. [Google Scholar] [CrossRef]
- Azmat, M.; Liaqat, U.; Qamar, M. Impacts of Changing Climate and Snow Cover on the Flow Regime of Jhelum River, Western Himalayas. Reg. Environ. Chang. 2017, 17, 813–825. [Google Scholar] [CrossRef]
- Porcù, F.; Milani, L.; Petracca, M. On the Uncertainties in Validating Satellite Instantaneous Rainfall Estimates with Raingauge Operational Network. Atmos. Res. 2014, 144, 73–81. [Google Scholar] [CrossRef]
- Dahri, Z.H.; Ludwig, F.; Moors, E. An Appraisal of Precipitation Distribution in the High–Altitude Catchments of the Indus Basin. Sci. Total Environ. 2016, 548, 289–306. [Google Scholar] [CrossRef] [PubMed]

| Temporal Extent | Resolutions | Coverage | Description | |
|---|---|---|---|---|
| IMERG E | January 2015–Demcember 2017 | 0.1°/30 min | 60° N–60° S | PMW+IR. Forward propagation. Near real–time (4 h) |
| IMERG L | January 2015–December 2017 | 0.1°/30 min | 60° N–60° S | PMW+IR. Backward and forward propagation. Near real–time (12 h) |
| IMERG F | January 2015–December 2017 | 0.1°/30 min | 60° N–60° S | PMW+IR. monthly GPCC gauge analysis. Post real–time (3.5 months) |
| Metrics | Index Type | Index Name | Equation | Unit | Perfect Score |
|---|---|---|---|---|---|
| Amplitude consistency | Statistical index | Correlation coefficient (CC) | NA | 1 | |
| Root mean square error (RMSE) | mm | 0 | |||
| The standard deviation (SD) | mm | 1 | |||
| Percentage of bias (PBias) | NA | 0 | |||
| Occurrence consistency | Classification index | The detection probability (POD) | NA | 1 | |
| The false alarm ratio (FAR) | NA | 0 | |||
| The frequency deviation (FB) | NA | 0 | |||
| The critical success index (CSI) | NA | 1 |
| IMERG | |||
| ≥0.1 mm | <0.1 mm | ||
| Rain Gauge | rain gauge observations ≥ 0.1 mm | A | C |
| rain gauge observations < 0.1 mm | B | D | |
| Rainfall Intensity | No Rain | Light Rain | Moderate Rain | Heavy Rain | Extreme Rainfall |
|---|---|---|---|---|---|
| Range (mm/d) | (0–0.1) | (0.1–1) | (1–20) | (20–50) | (>50) |
| Zone Name | Latitude | Elevation | Climate Zone | Topographic Area | |
|---|---|---|---|---|---|
| ULRB | River Source Basin (ULRB I) | 31 to 32.9 (°N) | 3801 to 6458 (m) | Alpine Climate Region (no clear distinction between dry and wet seasons) | Plateau Area (high elevation) |
| Zaduo–Changdu Basin (ULRB II) | |||||
| MLRB | Alpine Canyon Basin (MLRB I) | 25.4 to 31 (°N) | 1130 to 6458 (m) | Climate Transition Zone (dry and wet seasons are distinct) | Alpine Canyon Area (great difference in elevation) |
| Mid–high Mountain Canyon Basin (MLRB II) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Ye, J.; Fang, G.; Huang, X.; Yan, M. Assessment of GPM IMERG Satellite Precipitation Estimation under Complex Climatic and Topographic Conditions. Atmosphere 2021, 12, 780. https://doi.org/10.3390/atmos12060780
Lu C, Ye J, Fang G, Huang X, Yan M. Assessment of GPM IMERG Satellite Precipitation Estimation under Complex Climatic and Topographic Conditions. Atmosphere. 2021; 12(6):780. https://doi.org/10.3390/atmos12060780
Chicago/Turabian StyleLu, Chengxuan, Jian Ye, Guohua Fang, Xianfeng Huang, and Min Yan. 2021. "Assessment of GPM IMERG Satellite Precipitation Estimation under Complex Climatic and Topographic Conditions" Atmosphere 12, no. 6: 780. https://doi.org/10.3390/atmos12060780
APA StyleLu, C., Ye, J., Fang, G., Huang, X., & Yan, M. (2021). Assessment of GPM IMERG Satellite Precipitation Estimation under Complex Climatic and Topographic Conditions. Atmosphere, 12(6), 780. https://doi.org/10.3390/atmos12060780





