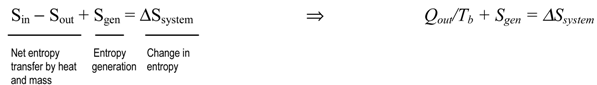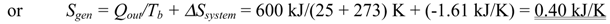Energy, Entropy and Exergy Concepts and Their Roles in Thermal Engineering

Abstract

Energy, entropy and exergy concepts come from thermodynamics and are applicable to all fields of science and engineering. Therefore, this article intends to provide background for better understanding of these concepts and their differences among various classes of life support systems with a diverse coverage. It also covers the basic principles, general definitions and practical applications and implications. Some illustrative examples are presented to highlight the importance of the aspects of energy, entropy and exergy and their roles in thermal engineering.

Introduction

Thermodynamics is broadly viewed as the science of energy, and thermal engineering is concerned with making the best use of available energy resources. The name thermodynamics stems from the Greek words therme (heat) and dynamics (force), which is most descriptive of the early efforts to convert heat into power. Today the same name is broadly interpreted to include all aspects of energy and energy transformations, including power production, refrigeration, and relationships among the properties of matter.

The science of thermodynamics is built primarily on two fundamental natural laws, known as the first and the second laws. The first law of thermodynamics is simply an expression of the conservation of energy principle. It asserts that energy is a thermodynamic property, and that during an interaction, energy can change from one form to another but the total amount of energy remains constant. The second law of thermodynamics asserts that energy has quality as well as quantity, and actual processes occur in the direction of decreasing quality of energy. The high-temperature thermal energy is degraded as it is transferred to a lower temperature body. The attempts to quantify the quality or “work potential” of energy in the light of the second law of thermodynamics has resulted in the definition of the properties entropy and exergy.

The first and second laws of thermodynamics emerged simultaneously in the 1850s, primarily out of the works of William Rankine, Rudolph Clausius, and William Thomson (later Lord Kelvin). Although the principles of thermodynamics have been in existence since the creation of the universe, thermodynamics did not emerge as a science until the construction of the first successful atmospheric steam engines in England by Thomas Savery in 1697 and Thomas Newcomen in 1712. These engines were very slow and inefficient, but they opened the way for the development of a new science.

The scope of this article is partly illustrated in Fig. 1, where the domains of energy, entropy and exergy are shown. This paper focuses on the portion of the field of thermodynamics that intersects with the energy, entropy and exergy fields, and particularly emphasizes the intersection of all three domains. Note that entropy and exergy are also used in other fields (such as statistics and information theory), and therefore they are not subsets of energy. Also, some forms of energy (such as shaft work) are entropy-free, and thus entropy subtends only part of the energy field. Likewise, exergy subtends only part of the energy field as well since some systems (such as air at atmospheric conditions) possess energy but no exergy. Most thermodynamic systems (such as steam in a power plant) possess energy, entropy, and exergy, and thus appear at the intersection of these three fields.

Figure 1. Interactions between the domains of energy, entropy and exergy.

Figure 1. Interactions between the domains of energy, entropy and exergy.

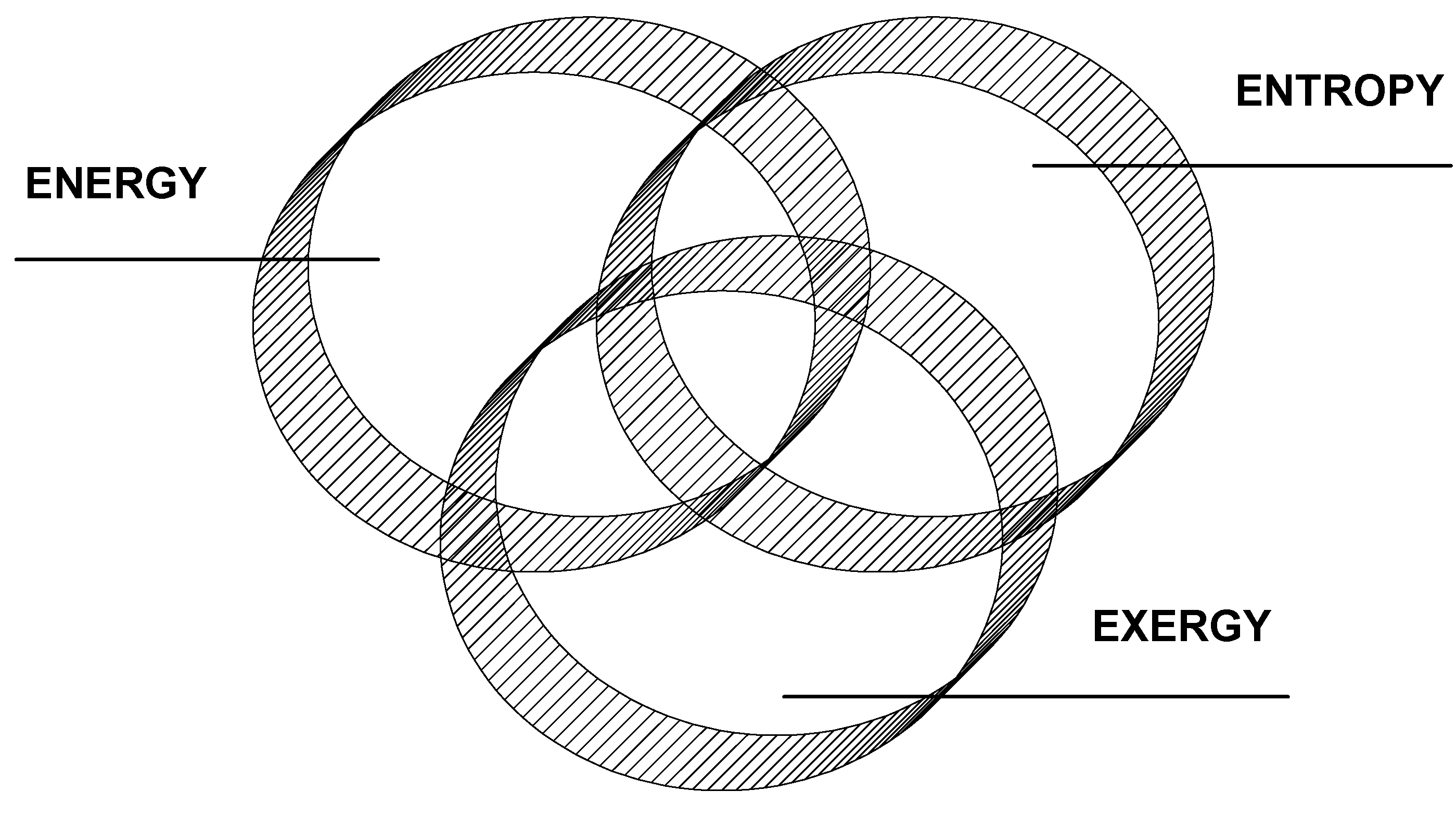
2. Energy

2.1 Introduction

Thermodynamics plays a key role in the analysis of systems and devices in which energy transfer and energy transformation take place. Thermodynamics' implications are far-reaching, and its applications span the whole range of the human enterprise. All along our technological history, the development of sciences has enhanced our ability to harness energy and use it for society's needs. The industrial revolution is a result of the discovery of how to exploit energy and how to convert heat into work. Nature allows the conversion of work completely into heat, but heat is taxed when converted into work. For this reason, the return on our investment of heat transfer is compared with the output work transfer and attempts are made to maximize this return.

Most of our daily activities involve energy transfer and energy change. The human body is a familiar example of a biological system in which the chemical energy of the food or body fat is transformed into other forms of energy such as heat transfer and work transfer. Our encounter with the environment also reveals a wide area of engineering applications. These include power plants to generate electricity, engines to run automobiles and aircraft, refrigeration and air conditioning systems, and so on.

In the hydroelectric power system the potential energy of the water is converted into mechanical energy through the use of a hydraulic turbine. The mechanical energy is then converted into electric energy by an electric generator coupled to the shaft of the turbine. In a steam power generating plant, chemical or nuclear energy is converted into thermal energy in a boiler or a reactor. The energy is imparted to water, which vaporizes into steam. The energy of the steam is used to drive a steam turbine, and the resulting mechanical energy is used to operate a generator to produce electric power. The steam leaving the turbine is then condensed, and the condensate is pumped back to the boiler to complete the cycle. Breeder reactors use uranium-235 as a fuel source and can produce some more fuel in the process. A solar power plant uses solar concentrators (parabolic or flat mirrors) to heat a working fluid in a receiver located on a tower. The heated fluid then expands in a turbogenerator in a similar manner as in a conventional power plant. In a spark-ignition internal combustion engine, the chemical energy of the fuel is converted into mechanical work. An air-fuel mixture is compressed and combustion is initiated by a spark device. The expansion of the combustion gases pushes against the piston, which results in the rotation of the crankshaft. Gas turbine engines, commonly used for aircraft propulsion, convert the chemical energy of the fuel into thermal energy that is used to run a gas turbine. The turbine is directly coupled to a compressor that supplies the air required for combustion. The exhaust gases, upon expanding in a nozzle, create the necessary thrust. For power generation, the turbine is coupled to an electric generator and drives both the compressor and the generator. In a liquid-fuel rocket, a fuel and an oxidizer are combined, and the combustion gases expand in a nozzle creating a propulsive force (thrust) to propel the rocket. A typical nuclear rocket propulsion engine offers a higher specific impulse when compared to chemical rockets. The fuel cell converts chemical energy into electric energy directly making use of an ion-exchange membrane. When a fuel such as hydrogen is ionized, it flows from the anode through the membrane toward the cathode. The released electrons at the anode flow through an external load. In a magnetohydrodynamic generator, electricity is produced by moving a high-temperature plasma through a magnetic field. The refrigeration system utilizes work supplied by the electric motor to transfer heat from a refrigerated space. Low-temperature boiling fluids such as ammonia and refrigerant-134a absorb energy in the form of heat transfer, as they vaporize in the evaporator causing a cooling effect in the region being cooled.

These are only a meager number of engineering applications, and the study of thermodynamics is relevant to the analysis of a much wider range of processes and applications not only in engineering, but also in other fields of science. Therefore, a careful study of this topic is required to improve the design and performance of energy-transfer systems.

2.2 Concept of Energy

The concept of energy was first introduced in mechanics by Newton when he hypothesized about kinetic and potential energies. However, the emergence of energy as a unifying concept in physics was not adopted until the middle of the 19^th century and was considered one of the major scientific achievements in that century. The concept of energy is so familiar to us today that it is intuitively obvious, yet we have difficulty in defining it exactly. Energy is a scalar quantity that can not be observed directly but can be recorded and evaluated by indirect measurements. The absolute value of energy of system is difficult to measure, whereas its energy change is rather easy to calculate. In our life the examples for energy are endless. The sun is the major source of the earth's energy. It emits a spectrum of energy that travels across space as electromagnetic radiation. Energy is also associated with the structure of matter and can be released by chemical and atomic reactions. Throughout history, the emergence of civilizations has been characterized by the discovery and effective application of energy to society's needs.

2.3 Forms of Energy

Energy manifests itself in many forms, which are either internal or transient, and energy can be converted from one form to another. In thermodynamic analysis, the forms of energy can be classified into two groups:

• The macroscopic forms of energy are those where a system possesses as a whole with respect to some outside reference frame such as kinetic and potential energies. For example, the macroscopic energy of an upmoving object changes with velocity and elevation. The macroscopic energy of a system is related to motion and the influence of some external effects such as gravity, magnetism, electricity and surface tension. The energy that a system possesses as a result of its motion relative to some reference frame is called kinetic energy. The energy that a system has as a result of its elevation in a gravitational field is called potential energy. Kinetic energy refers to the energy possessed by the system because of its overall motion, either translational or rotational. The word "overall" is italicized because the kinetic energy to which we refer is the kinetic energy of the entire system, not the kinetic energy of the molecules in the system. If the system is a gas, the kinetic energy is the energy due to the macroscopic flow of the gas, not the motion of individual molecules. The potential energy of a system is the sum of the gravitational, centrifugal, electrical, and magnetic potential energies. To illustrate using gravitational potential energy, a one-kilogram mass, 100 m above the ground, clearly has a greater potential energy than the same kilogram mass on the ground. That potential energy can be converted into other forms of energy, such as kinetic energy, if the mass is allowed to fall freely. Kinetic and potential energy depend on the environment in which the system exists. In particular, the potential energy of a system depends on the choice of a zero level. For example, if the ground level is considered to be at zero potential energy, then the potential energy of the mass at 100 m above the ground will have a positive potential energy equal to the mass (1 kg) multiplied by the gravitational constant (g = 9.807 m/s² at sea level) and the height above the ground (100 m). Its potential energy will be 980.7 (kgm²)/s² = 980.7 Newton-meters (Nm), that is, 980.7 J. The datum plane for potential energy can be chosen arbitrarily. If it had been chosen at 100 m above the ground level, the potential energy of the mass would have been zero. Of course, the difference in potential energy between the mass at 100 m and the mass at ground level is the same independent of the datum plane.
• The microscopic forms of energy are those related to the molecular structure of a system and the degree of the molecular activity, and they are independent of outside reference frames. The sum of all the microscopic forms of energy is called the internal energy of a system. The internal energy of a system depends on the inherent qualities, or properties, of the materials in the system, such as composition and physical form, as well as the environmental variables (temperature, pressure, electric field, magnetic field, etc.). Internal energy can have many forms, including, sensible and latent (i.e., thermal), chemical, nuclear, electrical, mechanical, magnetic, and surface energy. For example, a spring that is compressed has a higher internal energy (mechanical energy) than a spring that is not compressed, because the compressed spring can do some work on changing (expanding) to the uncompressed state. As another example, consider two identical vessels, each containing hydrogen and oxygen. In the first, the gases are contained in the elemental form, pure hydrogen and pure oxygen in a ratio of 2:1. In the second, the identical number of atoms is contained, but in the form of water. One can appreciate that the internal energy of the first is different from the second. A spark set off in the first container will result in a violent release of energy. The same will not be true in the second. Clearly, the internal energy present differs in these two situations. Any energy balance will have to take this difference into account.

The science of thermodynamics is built on the concept of equilibrium states and the postulate that the change in the value of thermodynamic quantities, such as internal energy, between two equilibrium states of a system does not depend on the thermodynamic path the system took to get between the two states. The change is defined by the final and beginning equilibrium states of that system. This means that the internal energy change of a system is determined by a knowledge of all the parameters that specify the system in its final state and in its initial state. The parameters are pressure, temperature, magnetic field, surface area, mass, and so on. If a system changes from a state labeled 1 to a state labeled 2, the change in internal energy (ΔU) will be (U₂ -U₁), the internal energy in the final state less the internal energy in the initial state. The difference does not depend on how the system proceeded from state 1 to state 2. The internal energy thus is referred to as a state or point function, since it is a function of the state of the system only, and not the history of the process.

On the question of thermal energy, it is intuitive that the internal energy of a system increases as its temperature is increased: We know that we have to add energy to a bar of iron to raise its temperature. The form of internal energy of a material that is related to its temperature is called sensible thermal energy, and the form of energy related to the change of phase is called latent thermal energy. The sensible and latent thermal energy (usually referred to as heat in daily life) can be transferred to or from a system due to a temperature difference. Therefore, heat transfer is thermal energy in transition.

2.4 The First law of Thermodynamics (FLT)

The FLT stands for the first law of the conservation of energy. This is stated as energy can be neither created nor destroyed; it just changes form. The FLT defines internal energy as a state function and provides a formal statement of the conservation of energy. However, it provides no information about the direction in which processes can spontaneously occur, that is, the reversibility aspects of thermodynamic processes. For example, it cannot say how cells can perform work while existing in an isothermal environment. It gives no information about the inability of any thermodynamic process to convert heat into mechanical work with full efficiency, or any insight into why mixtures cannot spontaneously separate or unmix themselves. An experimentally derived principle to characterize the availability of energy is required to do this. This is precisely the role of the second law of thermodynamics that we will explain later.

2.5 FLT vs Energy

The total energy E represents the sum of all forms of energy a system possesses, and the change in the energy content of a system during a process is expressed as ∆E_system. In the absence of electrical, magnetic, surface, etc effects, the total energy in that case can be expressed as the sum of the internal, kinetic, and potential energies as

E = U + KE + PE and ∆E_system = ∆U + ∆KE + ∆PE

(1)

Energy can be transferred to or from a system in three forms: heat Q, work W, and mass flow m. Energy interactions are recognized at the system boundary as they cross it, and they represent the energy gained or lost by a system during a process. Then the FLT or energy balance for any system undergoing any kind of process can be expressed as

(2)

That is, the net change (increase or decrease) in the total energy of the system during a process is equal to the difference between the total energy entering and the total energy leaving the system during that process. This relation can also be expressed per unit mass, differential, and rate forms as

e_in − e_out = Δe_system

(3)

δE_in −δE_out = dE_system or δe_in − δe_out = de_system

(4)

(5)

The only two forms of energy interactions associated with a fixed mass or closed system are heat transfer and work.

For a closed system undergoing a cycle, the initial and final states are identical and thus ∆E_system = E₂ − E₁ = 0. Then the energy balance for a cycle simplifies to E_in − E_out = 0 or E_in = E_out. Noting that a closed system does not involve any mass flow across its boundaries, the energy balance for a cycle can be expressed in terms of heat and work interactions as $W_{net,out}=Q_{net,in} \text{or} {\stackrel{.}{W}}_{net,out}={\stackrel{.}{Q}}_{net,in}$. That is, the net work output during a cycle is equal to net heat input for a cycle.

For a control volume that involves a fluid stream at pressure P, the fluid upstream acts like a piston, doing boundary work Pv per unit mass of fluid to maintain flow. For convenience, the flow work and internal energy are combined into enthalpy, h = u + Pv, which represents the microscopic forms of energy for a flowing fluid (as opposed to non-fluig fluid in a container). Then the energy transfer by mass flowing into or out of a system per unit mass of the fluid stream can be expressed as

h_tot = h + ke + pe

Energy balance for an adiabatic steam turbine with negligible kinetic and potential energies, for example, can be expressed as $\stackrel{.}{m}{h}_1={\stackrel{.}{W}}_{out}+\stackrel{.}{m}{h}_2$ where 1 is the inlet state of steam, 2 is the exit state, $\stackrel{.}{m}$ is the mass flow rate, and ${\stackrel{.}{W}}_{out}$ is the power output.

3. Entropy

3.1 Introduction

Within the past 50 years our view of Nature has changed drastically. Classical science emphasized equilibrium and stability. Now we see fluctuations, instability, evolutionary processes on all levels from chemistry and biology to cosmology. Everywhere we observe irreversible processes in which time symmetry is broken. The distinction between reversible and irreversible processes was first introduced in thermodynamics through the concept of "entropy".

In the modern context, the formulation of entropy is fundamental for understanding thermodynamic aspects of self-organization, evolution of order and life that we see in Nature. When a system is isolated, energy increase will be zero. In this case the entropy of the system will continue to increase due to irreversible processes and reach the maximum possible value, which is the state of thermodynamic equilibrium. In the state of equilibrium, all irreversible processes cease. When a system begins to exchange entropy with the exterior then, in general, it is driven away from equilibrium, and the entropy producing irreversible processes begins to operate. The exchange of entropy is due to exchange of heat and matter. The entropy flowing out of an adiabatic system is always larger than the entropy flowing into the system, the difference arising due to entropy produced by irreversible processes within the system. As we shall see in the following chapters, systems that exchange entropy with their exterior do not simply increase the entropy of the exterior, but may undergo dramatic spontaneous transformations to "self-organization." The irreversible processes that produce entropy create these organized states. Such self-organized states range from convection patterns in fluids to life. Irreversible processes are the driving forces that create this order.

Much of the internal energy of a substance is randomly distributed as kinetic energy at the molecular and sub molecular levels and as energy associated with attractive or repulsive forces between molecular and sub molecular entities, which are moving closer together or further apart in relation to their mean separation. This energy is sometimes described as being 'disordered' as it is not accessible as work at the macroscopic level in the same way as is the kinetic energy or gravitational potential energy that an entire system possesses owing to its velocity or position in the gravitational field. Although energy is the capacity to do work, it is not possible directly to access the minute quantities of disordered energy possessed at a given instant by the various modes of energy possession of the entities so as to yield mechanical shaft work on the macroscopic scale. The term 'disorder' refers to the lack of information about exactly how much energy is associated at any moment with each mode of energy possession of each molecular or sub molecular entity within the system.

At the molecular and sub molecular level there is also 'ordered energy' associated with attractive or repulsive forces between entities that have fixed mean relative positions. Part of this energy is, in principle, accessible as work at the macroscopic level under very special conditions, which are beyond the scope of this manuscript. Temperature is the property that determines whether a system that is in equilibrium will experience any decrease or increase in its disordered energy if it is brought into contact with another system that is in equilibrium. If the systems do not have the same temperature, disordered energy will be redistributed from the system at the higher temperature to the one at the lower temperature. There is then less information about precisely where that energy resides, as it is now dispersed over the two systems.

Heat transfer to a system increases the disordered energy of the system. Heat transfer from a system reduces the disordered energy. Reversible heat transfer is characterized by both the amount of energy transferred to or from the system and the temperature level at which this occurs. The property entropy, whose change between states is defined as the integral of the ratio of the reversible heat transfer to the absolute temperature, is a measure of the state of disorder of the system. This 'state of disorder' is characterized by the amount of disordered energy and its temperature level. When reversible heat transfer occurs from one system to another, both systems have the same temperature and the increase in the disorder of one is exactly matched by the decrease in disorder of the other. When reversible adiabatic work is done on or by a system its ordered energy increases or decreases by exactly the amount of the work and the temperature level changes in a way that depends on the substances involved. Reversible work is characterized by the amount of energy transferred to or from the system, irrespective of the temperature of the system. Irreversible work, such as stirring work or friction work, involves a change in the disorder of the system and, like heat transfer to a system, has the effect of increasing the entropy.

3.2 Entropy Aspects

It is now important to introduce a new thermodynamic property, entropy, that is simply a measure of the amount of molecular disorder within a system. In this regard, a system possessing a high degree of molecular disorder (such as a high temperature gas) has a very high entropy value and vice versa. It is important to note that numerical values for specific entropy are commonly listed in thermodynamic tables along with values for specific volume, specific internal energy, and specific enthalpy. Therefore, entropy is known as the core of the second law thermodynamics. Here, we have to highlight the following facts:

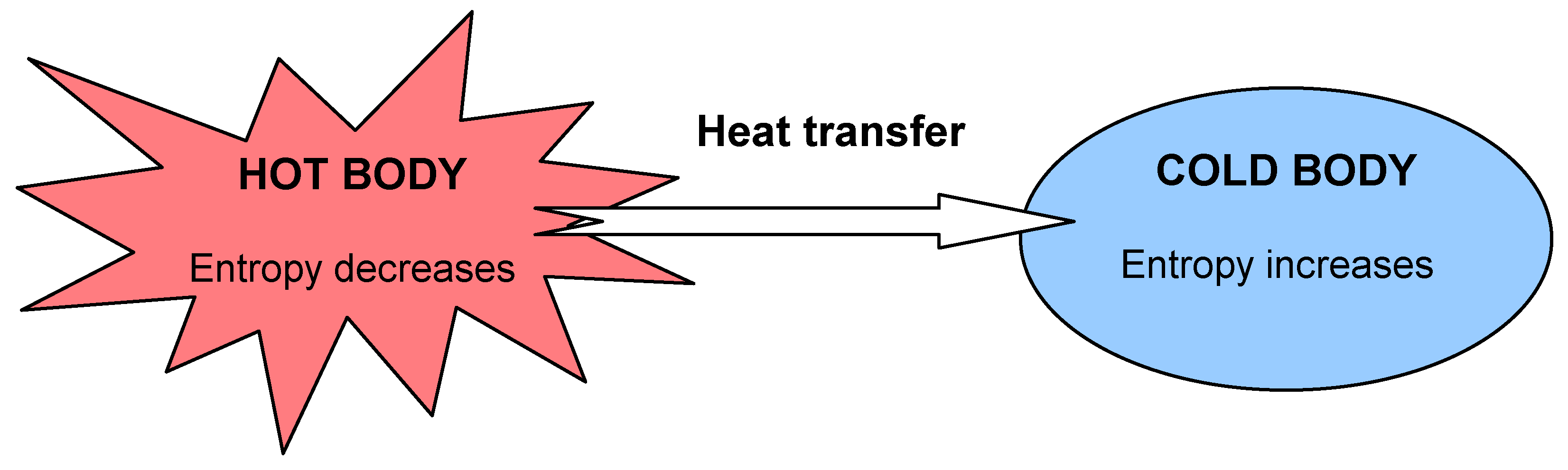
• The entropy of a system is a measure of the amount of molecular disorder within the system.
• A system can only generate, not destroy, entropy.
• The entropy of a system can be increased or decreased by energy transports across the system boundary.

Heat and work are mechanisms of energy transfer. They are measures of the change in the internal energy in one body as energy is transferred to it or from it to another. Work is accomplished by a force acting through a distance. Heat requires a difference in temperature for its transfer. The definition of heat energy can be broadened to include the energy stored in a hot gas as the average kinetic energy of randomly moving molecules. This description enabled us to understand the natural flow of heat energy from a hot to a cooler substance. The concept of random motion was translated into a notion of order and disorder. The key linkage of order/disorder with probability followed. Energy transfers or conversions are changes of the state of a system. The natural direction of a change in state of a system is from a state of low probability to one of higher probability. That is what probability means. And disordered states are more probable than ordered ones. Thus the natural direction of change of state of a system is from order to disorder. This is the "something" that is changing in all the energy transfers and conversions we have described. Finally, we gave that something a name-entropy. The entropy of a state of a system is proportional to (depends on) its probability. Thus the SLT can be expressed more broadly in terms of entropy in the following way:

In any transfer or conversion of energy within a closed system, the entropy of the system increases. The consequences of the second law can thus be stated positively as the spontaneous or natural direction of energy transfer or conversion is toward increasing entropy, or negatively as all energy transfers or conversions are irreversible. Or, in keeping with our paraphrasing of the FLT as "You can't get something for nothing," the SLT asserts: You can't even get all you pay for.

It is low-entropy energy sources that are being used up, and low-entropy energy is "useful" energy. The energy sources in the universe were rated on an entropy/usefulness scale from the zero-entropy, highly useful mechanical forms such as gravitational potential energy, which are easily converted to work, to the high-entropy, unusable heat of our surroundings.

In summary, this broader interpretation of the SLT suggests that real "energy conservation" should include the practice of thermodynamic economy. Each energy transfer or conversion, all else being equal, should be arranged so that the total change in entropy (entropy generation) is a minimum. This requires that energy sources be matched in entropy to energy end use.

3.3 Significance of Entropy

The "entropy" of the state of a system is a measure of the probability of its occurrence. States of low probability have low entropy; states of high probability have high entropy. With this definition we see, from the previous discussion and examples, that in any transfer or conversion of energy, because the spontaneous direction of the change of state of a closed system is from a less to a more probable state, the entropy of the system must increase. That is the broader statement we have been seeking for the second law, "In any energy transfer or conversion within an isolated closed system, the entropy of that system increases."

Energy conversions can proceed so that the entropy of a part of a system is decreased. Charging a storage battery, freezing ice cubes, and even the processes of life and growth are examples. In each of these examples, order has been won from disorder and entropy has decreased. If the total system is considered, however, the total effect has been an increase in disorder. To charge a battery we must provide energy above and beyond that necessary to re-form the chemical combinations in the battery plates. Some of this low-entropy electrical energy is changed into high-entropy heat energy in the current-carrying wires. In freezing ice we increase the order and thus decrease the entropy of the water in the ice cube trays by removing heat from it. The heat energy removed, however, has to flow into a substance that is at a lower temperature than the surroundings. Thus, the entropy and the disorder of this gas are increased. Moreover, we put low-entropy electrical energy into the refrigerator through the motor, and this energy is degraded to heat. The overall change in entropy is positive. In the life process, highly ordered structures are built from the much simpler structures of various chemicals, but to accomplish this, life takes in relatively low-entropy energy-sunlight and chemical energy-and gives off high-entropy heat energy. The entropy of the total system again increases. Figure 2 illustrates a heat transfer process from the entropy point of view.

Figure 2. Illustration of entropy increase and decrease for cold and hot bodies.

Figure 2. Illustration of entropy increase and decrease for cold and hot bodies.

We point out from Fig. 2 that during a heat transfer process, the net entropy increases. As a matter of fact, the increase in entropy of the cold body more than offsets the decrease in the entropy of the hot body. The SLT requires that the increase in entropy of the cold body be greater than the decrease in entropy of the hot body. The conclusion is that processes can occur only in the direction of increased overall entropy or molecular disorder. That is, the entire universe is getting more and more chaotic every day.

Another way of stating the consequence of the SLT is to say that all energy transfers or conversions are irreversible. They will go spontaneously in the direction of increasing entropy. They will not go spontaneously toward a state of lower entropy. For example, in a power plant some of the losses, as we have said earlier, can be minimized, but none of them can be eliminated. Entropy must increase. The usual mechanism is for some low-entropy energy to be converted, through friction or electrical resistance, for instance, or through leakage of high-temperature, low-entropy heat energy and its degradation to high-entropy heat energy at the lower environmental temperature.

3.4 Carnot's Contribution

The final understanding and statement of the SLT was the result of a sometimes brilliant but more often tedious set of theoretical and experimental investigations over a hundred or so years. One of the most brilliant contributions was made early on by a young French engineer, Sadi Carnot, in the nineteenth century. Carnot, studying the early steam engines, was able to abstract from the pumping pistons and spinning wheels the basic property that the conversion of heat energy into mechanical work requires a difference of temperature. The purpose of a heat engine, as he described it, is to take heat from a high-temperature source, convert some of this to mechanical work, and then reject the rest of the heat energy to a lower-temperature source (or "heat reservoir" as we call it). Carnot described heat engines in a crude analogy to waterwheels. The energy available for conversion in a waterwheel is the gravitational energy contained in water as it flows from some height (behind a dam or from a mountain lake) down through the wheel. The amount of energy available depends on the difference in height-the "head" as it is called-between the source and the pool below the wheel. The energy available to a heat engine depends on the "temperature head." Just as a high dam can provide more energy than a low one, a large temperature difference can provide more energy to be converted by a heat engine than can a small temperature difference. In the example of a heat engine, the high-temperature reservoir would be the hot steam coming from the power plant furnace. The low-temperature reservoir to which the engine (in our example, the steam turbine) rejects the unconverted energy is the condenser cooled by circulating water. The important temperature difference is thus the difference in temperature between the steam-which is usually at about 625°C- and the water in the condenser-which is typically at the environment temperature of about 25°C. The "temperature head" in this example would therefore be 600°C. Carnot's brilliant explanation of this basic property of heat engines thus led immediately toward the second law. Once energy is in the form of heat energy, we can never hope to convert all of it back into mechanical energy. Some heat energy will always remain in the exhaust.

3.5 The Second Law of Thermodynamics (SLT)

Although a spontaneous process can proceed only in a definite direction, the FLT gives no information about direction; it merely states that when one form of energy is converted into another, identical quantities of energy are involved regardless of feasibility of the process. In this regard, events could be envisioned that would not violate the FLT, e.g., transfer of a certain quantity of heat from a low-temperature body to a high-temperature body, without expenditure of work. However, the reality shows that this is impossible and FLT becomes inadequate in picturizing the complete energy transfer. Furthermore, experiments indicated that when energy in the form of heat is transferred to a system, only a portion of heat can be converted into work.

The SLT establishes the difference in quality between different forms of energy and explains why some processes can spontaneously occur, whereas other can not. It indicated a trend of change and is usually expressed as an inequality. The SLT has been confirmed by experimental evidences like other physical laws of nature.

The SLT defines the fundamental physical quantity entropy as a randomized energy state unavailable for direct conversion to work. It also states that all spontaneous processes, both physical and chemical, proceed to maximize entropy, that is, to become more randomized and to convert energy into a less available form. A direct consequence of fundamental importance is the implication that at thermodynamic equilibrium the entropy of a system is at a relative maximum; that is, no further increase in disorder is possible without changing by some external means (such as adding heat) the thermodynamic state of the system. A basic corollary of the SLT is the statement that the sum of the entropy changes of a system and that of its surroundings must always be positive, that is, the universe (the sum of all systems and surroundings) is constrained to become forever more disordered and to proceed toward thermodynamic equilibrium with some absolute maximum value of entropy. From a biological standpoint this is certainly a reasonable concept, since unless gradients in concentration and temperature are forcibly maintained by the consumption of energy, organisms proceed spontaneously toward the biological equivalent of equilibrium-death.

The SLT is quite general. However, when intermolecular forces are long range, as in the case of particles interacting through gravitation, there are difficulties because our classification into extensive variables (proportional to volume) and intensive variables (independent of volume) does not apply. The total energy is no longer proportional to the volume. Fortunately gravitational forces are very weak as compared to the short range intermolecular forces. It is only on the astrophysical scale that this problem becomes important. The generality of the SLT gives us a powerful means to understand the thermodynamic aspects of real systems through the usage of ideal systems. A classic example is Planck's analysis of radiation in thermodynamic equilibrium with matter (blackbody radiation) in which Planck considered idealized simple harmonic oscillators interacting with radiation. Planck considered simple harmonic oscillators not merely because they are good approximations of molecules but because the properties of radiation in thermal equilibrium with matter are universal, regardless of the particular nature of the matter with which the radiation interacts. The conclusions one arrives at using idealized oscillators and the laws of thermodynamics must also be valid for all other forms of matter, however complex.

What makes this new statement of the SLT valuable as a guide to energy policy is the relationship between entropy and the usefulness of energy. Energy is most useful to us when we can get it to flow from one substance to another, e.g., to warm a house and we can use it to do work. Useful energy thus must have low entropy so that the SLT will allow transfer or conversions to occur spontaneously.

3.6 SLT Statements

Although there are various formulations of the SLT, two of them are better known such as the Clausius statement and the Kelvin-Planck statement.

• The Clausius statement. It is impossible for a system to transfer heat from a lower temperature reservoir to a higher temperature reservoir. Simply, heat transfer can only occur spontaneously in the direction of temperature decrease. For example, we can not construct a refrigerator that operates without any work input.
• The Kelvin-Planck statement. It is impossible for a system to receive a given amount of heat from a high-temperature reservoir and provide an equal amount of work output. While a system converting work to an equivalent energy transfer as heat is possible, a device converting heat to an equivalent energy transfer as work is impossible. For example, we can not build a heat engine that has a thermal efficiency of 100%.

3.7 The Clausius Inequality

It is a mathematical statement of the second law as a precursor to the definition of a difference in a property known as entropy. It was first stated by the German physicist R.J.E. Clausius (known as one of the founders of thermodynamics) and is expressed as

∮(δQ/T) ≤ 0

(6)

where the cyclic integral symbol ∮ shows the integration should be done over the entire cycle, and the sign of heat transfer is determined with respect to the system (positive if to the system, and negative if from the system). The cyclic integral of δQ/T is always less than or equal to zero. If it is equal to zero, it is for a system undergoing or containing only reversible processes (or cycles). If it is less than zero, it is for a system undergoing or containing only irreversible processes (or cycles).

The inequality given above can be eliminated by

S_gen = −∮(δQ/T)

(7)

where the quantity S_gen is the entropy generation associated with a cycle as a measure of the irreversibilities which occur during the cycle. It can be summarized as follows:

• S_gen = ΔS_total = ΔS_sys + ΔS_surr = 0 for a reversible process.
• S_gen = ΔS_total = ΔS_sys + ΔS_surr > 0 for an irreversible process.

It is important to note that for a reversible process:

ΔS_sys = (Q/T)_rev and ΔS_surr = - (Q/T)_rev

(8)

and for an irreversible process:

ΔS_sys > (Q/T)_irr

(9)

due to entropy generation within the system as a result of internal irreversibilities. Hence, although the change in entropy of the system and surroundings may individually increase, decrease, or remain constant, the total entropy change or the total entropy generation can not be less than zero for any process.

3.8 UsefulRelationships

It is important to list some useful relations and Tds equations for any process of a pure substance, assuming the absence of electricity, magnetism, solid distortion effects, and surface tension. Therefore, we list four equations and highlight their implications and restrictions as follows:

• δq = du + δw: This is a statement of the FLT and is applicable to any simple compressible closed system.
• δq = du + pdv: This is a statement of the FLT and is restricted to reversible processes of a closed system only.
• Tds = du + δw: This is a combined statement of the FLT and SLT (with Tds = δq).
• Tds = du + pdv: This is a combined statement of the FLT and SLT and is valid for all processes between equilibrium states.

4. Exergy

4.1 Introduction

A very important class of problems in engineering thermodynamics concerns systems or substances that can be modelled as being in equilibrium or stable equilibrium, but that are not in mutual stable equilibrium with the surroundings. For example, within the earth there are reserves of fuels that are not in mutual stable equilibrium with the atmosphere and the sea. The requirements of mutual chemical equilibrium are not met. Any system at a temperature above or below that of the environment is not in mutual stable equilibrium with the environment. In this case the requirements of mutual thermal equilibrium are not met. It is found that any lack of mutual stable equilibrium between a system and the environment can be used to produce work. The SLT allows the maximum work that could be produced to be determined.

The exergy of a system is defined as the maximum shaft work that could be done by the composite of the system and a specified reference environment that is assumed to be infinite, in equilibrium, and ultimately to enclose all other systems. Typically, the environment is specified by stating its temperature, pressure and chemical composition. Exergy is not simply a thermodynamic property, but rather is a co-property of a system and the reference environment. The term exergy comes from the Greek words ex and ergon, meaning from and work: the exergy of a system can be increased if work is done on it. The following are some terms found in the literature that are equivalent to or nearly equivalent to exergy: available energy, essergy, utilizable energy, available work, availability.

Exergy has the characteristic that it is conserved only when all processes of the system and the environment are reversible. Exergy is destroyed whenever an irreversible process occurs. When an exergy analysis is performed on a plant such as an entire power station, a chemical processing plant or a refrigeration plant, the thermodynamic imperfections can be quantified as exergy destruction, which is wasted work or wasted potential for the production of work. Like energy, exergy can be transferred or transported across the boundary of a system. For each type of energy transfer or transport there is a corresponding exergy transfer or transport. In particular, exergy analysis takes into account the different thermodynamic values of work and heat. The exergy transfer associated with shaft work is equal to the shaft work. The exergy transfer associated with heat transfer, however, depends on the temperature level at which it occurs in relation to the temperature of the environment.

4.2 Exergy Aspects

It is also important to illustrate some meanings of exergy by the following simple examples:

• A system in complete equilibrium with its environment does not have any exergy. No difference appears in temperature, pressure, or concentration etc. for running any processes.
• The more a system deviates from the environment, the more exergy it carries. Hot water has a higher content of exergy during the winter than it has on a hot summer day. A block of ice carries hardly any exergy in winter while it does in summer.
• When the energy loses its quality, it results in exergy destroyed. The exergy is the part of the energy which is useful in the society and therefore has an economic value and is worth taking care of.
• Almost all energy, converted in the thin layer on the earth’s surface, where life can be found, derives from the sun. Sunlight, rich in exergy, reaches the earth. A lot of it is reflected but the energy absorbed on the earth is converted and finally leaves the earth as heat radiation with no exergy relative to the earth. The net exergy absorbed by the earth is consequently gradually destroyed but during this destruction it manages to drive the water/wind system and the life on earth. The green plants absorb exergy from the sunlight and convert it via photosynthesis into chemical exergy. The chemical exergy then passes through different food chains in the ecosystems. On every tropical level exergy is consumed and micro-organisms live on the last level in this food chain. There exists no waste.
• A concentrated deposit of mineral ‘contrasts’ with the environment and this contrast increases with the concentration of the mineral. The mineral is thus a carrier of exergy. When the mineral is mined the exergy content of the mineral is kept constant, and if it is enriched the exergy content increases. A poor deposit of mineral contains less exergy and can accordingly be utilised only through a larger input of external exergy. Today this substitution of exergy often comes from exergy forms such as coal and oil. When a concentrated mineral is dispersed the exergy content is decreased (item 3).
• An apparent difficulty in the definition of exergy is that it depends on the environment. This difficulty could, however, be solved through conventions, one could define a ‘standard environment’ with a given chemical composition at a certain temperature and pressure. A possible standard environment for global use could, for instance, be a standard atmosphere, a standard sea and a standard bed-rock. One principal problem is, however, that these systems are not in equilibrium with each other. Sometimes one should, in addition to this, use local standards depending on the season (item 2).
• An engineer designing a system is expected to aim for the highest possible technical efficiency at a minimum cost under the prevailing technical, economic and legal conditions, but also with regard to ethical, ecological and social consequences. Exergy is a concept that makes this work a great deal easier. Thus, exergetics offers a unique insight where losses and possible improvements can be determined, and Life Cycle Exergy Analysis (LCEA) is suggested as a method to better meet environmental conditions.

Before getting into details of the linkages between energy and exergy, exergy and the environment, energy and sustainable development, we provide some key points to highlight the importance of the exergy and its utilization:

• It is a primary tool in best addressing the impact of energy resource utilization on the environment.
• It is an effective method using the conservation of mass and conservation of energy principles together with the second law of thermodynamics for the design and analysis of energy systems.
• It is a suitable technique for furthering the goal of more efficient energy-resource use, for it enables the locations, types, and true magnitudes of wastes and losses to be determined.
• It is an efficient technique revealing whether or not and by how much it is possible to design more efficient energy systems by reducing the inefficiencies in existing systems.
• It is a key component in obtaining sustainable development.

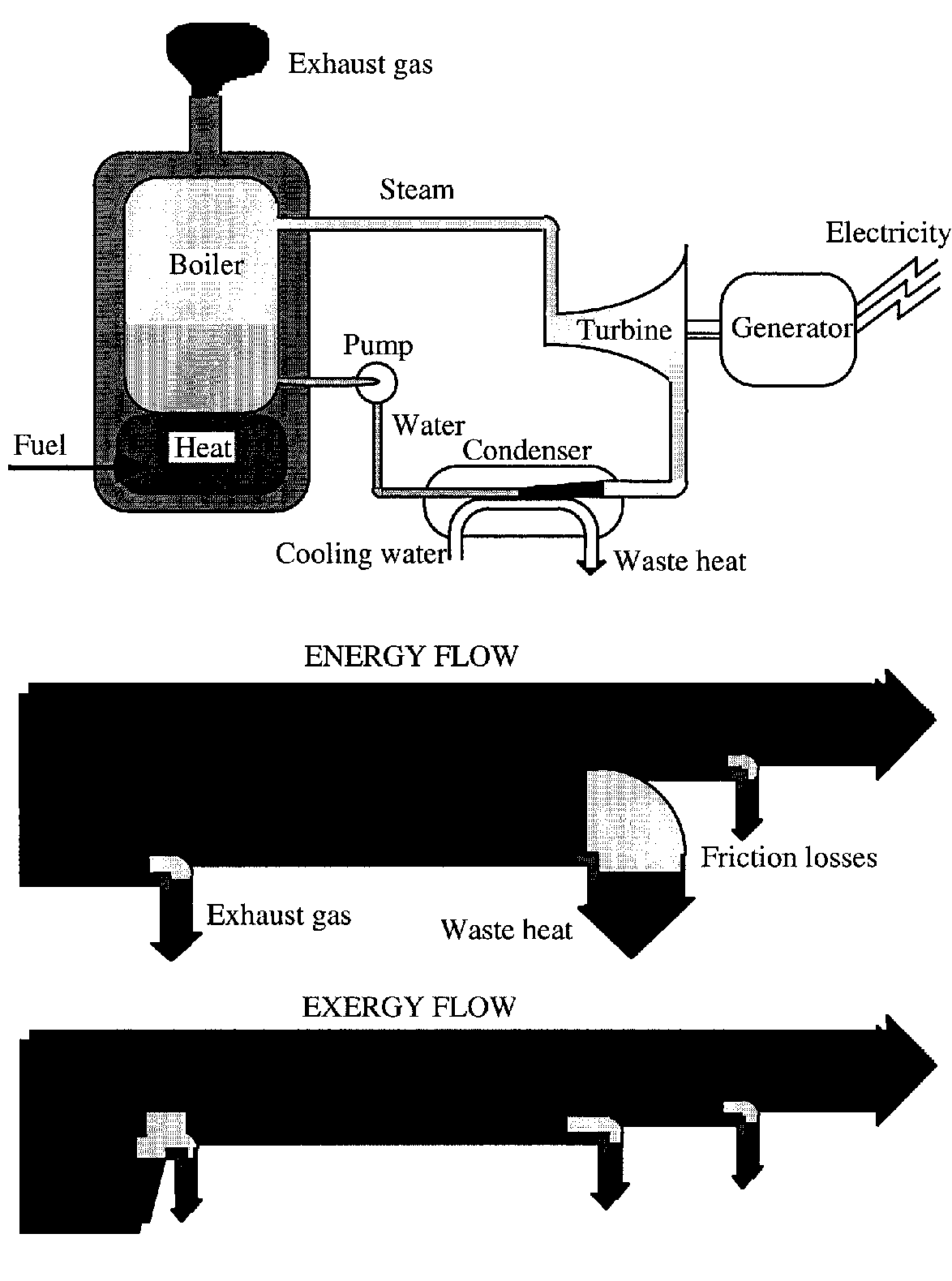
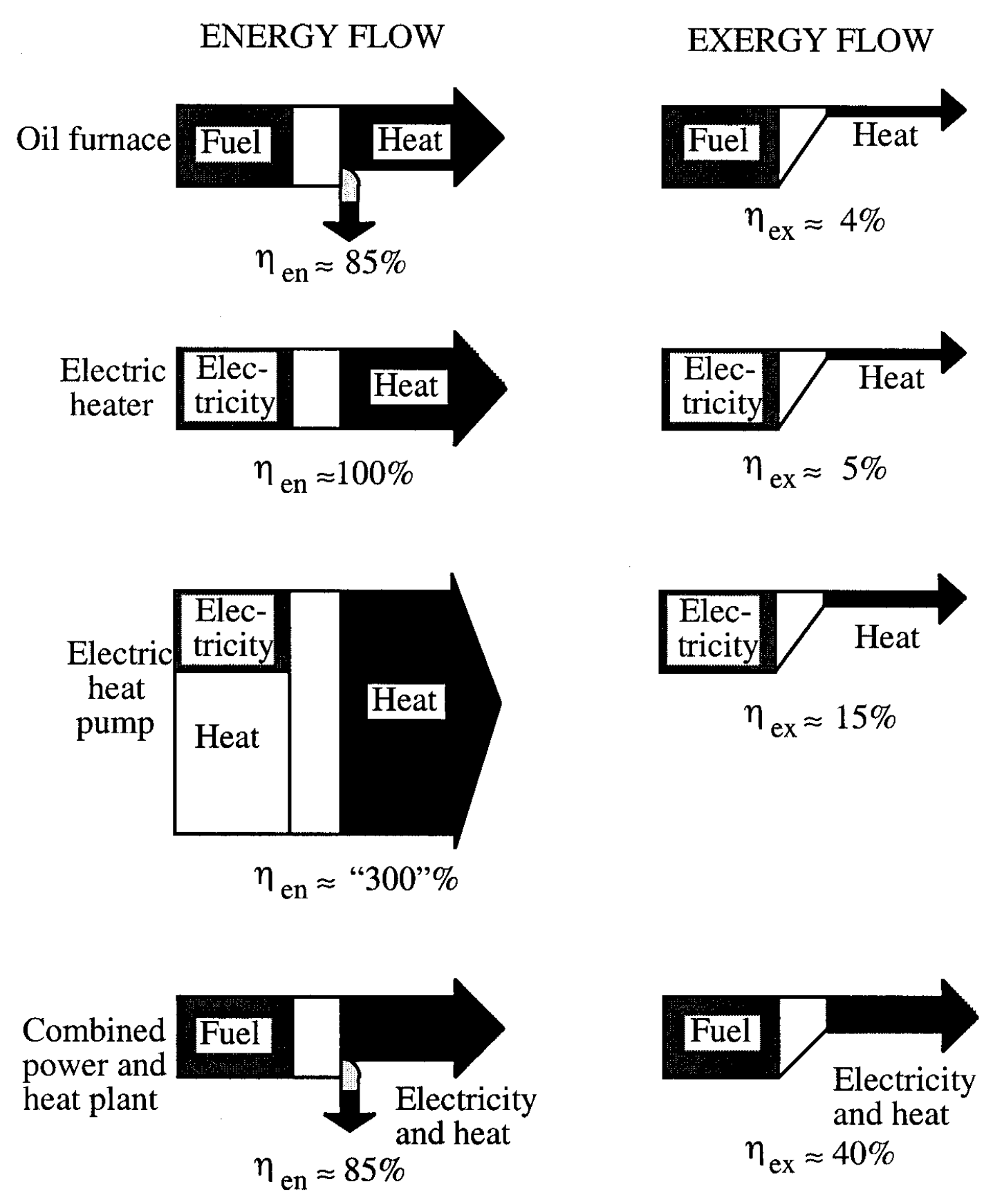
4.3 Exergy vs Energy

The traditional method of assessing the energy disposition of an operation involving the physical or chemical processing of materials and products with accompanying transfer and/or transformation of energy is by the completion of an energy balance. This balance is apparently based on the FLT. In this balance, information on the system is employed to attempt to reduce heat losses or enhance heat recovery. However, from such a balance no information is available on the degradation of energy, occurring in the process and to quantify the usefulness or quality of the heat content in various streams leaving the process as products, wastes, or coolants.

The exergy method of analysis overcomes the limitations of the FLT. The concept of exergy is based on both FLT and SLT. Exergy analysis can clearly indicate the locations of energy degradation in a process that may lead to improved operation or technology. It can also quantify the quality of heat in a reject stream. So, the main aim of exergy analysis is to identify the causes and to calculate the true magnitudes of exergy losses. Table 1 presents a general comparison of both energy and exergy.

Table 1. Comparison of energy and exergy.

ENERGY

EXERGY

is dependent on the parameters of matter or energy flow only, and independent of the environment parameters. has the values different from zero (equal to mc 2 upon Einstein’s equation). is governed by the FLT for all the processes. is limited by the SLT for all processes (incl. reversible ones). is motion or ability to produce motion. is always conserved in a process, so can neither be destroyed or produced. is a measure of quantity only.

is dependent both on the parameters of matter or energy flow and on the environment parameters. is equal to zero (in dead state by equilibrium with the environment). is governed by the FLT for reversible processes only (in irreversible processes it is destroyed partly or completely). is not limited for reversible processes due to the SLT. is work or ability to produce work. is always conserved in a reversible process, but is always consumed in an irreversible process. is a measure of quantity and quality due to entropy.

Table 1. Comparison of energy and exergy.

ENERGY

EXERGY

is dependent on the parameters of matter or energy flow only, and independent of the environment parameters. has the values different from zero (equal to mc 2 upon Einstein’s equation). is governed by the FLT for all the processes. is limited by the SLT for all processes (incl. reversible ones). is motion or ability to produce motion. is always conserved in a process, so can neither be destroyed or produced. is a measure of quantity only.

is dependent both on the parameters of matter or energy flow and on the environment parameters. is equal to zero (in dead state by equilibrium with the environment). is governed by the FLT for reversible processes only (in irreversible processes it is destroyed partly or completely). is not limited for reversible processes due to the SLT. is work or ability to produce work. is always conserved in a reversible process, but is always consumed in an irreversible process. is a measure of quantity and quality due to entropy.

To begin with, we must distinguish between exergy and energy in order to avoid any confusion with the traditional energy-based methods of thermal system analysis and design. Energy flows into and out of a system via mass flow, heat transfer, and work (e.g., shafts, piston rods). Energy is conserved, not destroyed: this is the statement made by the FLT. Exergy is an entirely different concept. It represents quantitatively the "useful" energy, or the ability to do work-the work content-of the great variety of streams (mass, heat, work) that flow through the system. The first attribute of the property "exergy" is that it makes it possible to compare on a common basis interactions (inputs, outputs) that are quite different in a physical sense. Another benefit is that by accounting for all the exergy streams of the system it is possible to determine the extent to which the system destroys exergy. The destroyed exergy is proportional to the generated entropy. In actual systems, exergy is always destroyed, partially or totally: this is the statement made by the SLT. The destroyed exergy, or the generated entropy is responsible for the less-than-theoretical efficiency of the system.

Example-I: for Difference Between Energy and Exergy Description

The exergy concept is today extensively used within the steam power engineering, where energy forms of different qualities are dealt with. It is shown here that for hot steam, district heating and waste heat the quality index, i.e. the exergy in relation to the energy content, becomes lower and lower. This must be taken into account by those engineers who work with these different energy forms. Let us examine how a power plant works. The upper part of Fig. 3 is the schematic of a basic power plant, in this case a condensing power plant, where the combustion of oil or coal takes place. It could also illustrate a nuclear power plant, where uranium is used instead for supplying heat. The heat produced is used to boil water under high pressure in a large boiler, in principle a large pressure-cooker (steam production unit). The steam is supplied to a turbine, where the energy of the steam is converted into rotation of the turbine shaft. At the other end of the shaft, an electric generator is located, producing electricity. The electricity is then supplied to the consumer to accomplish various tasks.

Figure 3. The energy- and exergy flow through a condensing power plant [1,2].

Figure 3. The energy- and exergy flow through a condensing power plant [1,2].

When the steam passed through the turbine it transmitted exergy to the electric generator. After the turbine, the steam is chilled in a condenser to water, and brought back to the boiler. This cooling is necessary to optimize the power transmission in the turbine, since the turbine can work with maximal difference in pressure when the steam is condensed immediately after passing through it. The chemical energy in oil and coal, or the nuclear energy in uranium, is thus transformed into electrical energy, but not without losses. The losses are great in a power plant, no less than about 40%, and in a nuclear power plant they are no less than about 70%. Counting the total system, from the preparation of the energy raw material to the finishing treatment of the waste products, there are even greater losses.

Let us now see what happens to the losses in the power plant itself. In the bottom part of Fig. 3 there are two diagrams of flows, so-called Sankey-diagrams [1]. In the top diagram, the width of the flow is proportional to the energy content for the respective energy form, in the bottom diagram, the width is proportional to the exergy content. The first thing we notice is that the widths of the inflows and outflows in the two diagrams are almost equal. This is due to the fact that both the inflows and the outflows are very high quality energy forms. The quality indexes for the energy forms in question lie between 90% and 100%. For electrical energy the exergy content is as large as the energy content. The losses in the two diagrams are, however, quite different. At first we have losses in the furnace. The fuel is here converted into heat. In an oil or coal fueled power plant we get a flame temperature of about two thousand degrees (°C). In a nuclear power plant the temperature is instead a few hundred degrees (°C). The heat is then transmitted through heat exchangers to boiling water. The pressure is high, with the result that the water does not boil until it reaches a temperature of a few hundred degrees. Through the walls of the furnace, and through pipes, heat is transmitted to the environment, where it is lost. Heat is also discharged with the exhaust gases, to keep the chimney of an oil and coal power plant free from condensed water. These furnace losses represent only a small percentage of the total energy conversion. We see, however, from the exergy diagram that something drastic happens. At this point, more than one third of the exergy is lost. We also see that it is lost in the process itself, i.e. only a very small part of the lost exergy leaves the power plant. The exergy flow just becomes narrower. Large quantities of entropy are created. This is due to the fact that the steam that leaves the boiler has a lower temperature and pressure than should be physically possible. The reason for this is limitations in the fatigue strength of the components included in the process, principally in the boiler and the turbine blades. In a nuclear power plant, more than half the exergy is lost at this stage of the process.

The width of the flows of thermal energy and thermal exergy as hot steam in Fig. 3, show the greatest difference between energy and exergy flow. This is also a completely different view of how the losses in the process arise. In a diagram of energy flows, the losses are heaviest in the condenser. A great deal of the energy is lost in the condenser through waste heat in the cooling water. Waste heat is, however, heat at a very low temperature and therefore energy of a very low quality. This is clearly shown in the exergy diagram. The exergy content of the waste heat is just a small percentage of the energy content. To make it clearer we can picture the following process. Let us suppose that we convert the thermal energy in the waste heat into mechanical energy by an ideal process. From the waste heat, we would then only be able to convert that part of the energy content that corresponds to mechanical work, i.e. the exergy content. At such a conversion process the loss would be waste heat at the same temperature as the environment, i.e. with the exergy content equal to zero. It is by no means possible to attain more mechanical or electrical energy out of the thermal energy than what is determined by the thermal exergy. When changing from mechanical energy to electrical energy, both with an exergy content of 100%, small losses arise through friction. These losses are on the whole equally small in both diagrams. Part of the friction losses consists of mechanical fatigue, i.e., wearing out of shafts and bearings [2].

The conclusion we can draw from the diagrams will thus be that in the diagrams of energy flows, the heaviest losses appear in the condenser but from the exergy flow, the heaviest losses seem to happen already at the combustion in the boiler. We also see from the diagram of exergy flows that these losses in the boiler cannot be extracted. Thus, the exergy is used in the process itself. It is an inevitable “internal loss”, in the process and is dependent on the technical solutions available.

Example-II: Difference Between Energy and Exergy Description

The diagrams in Fig. 4 illustrate the differences between energy and exergy flows, and thereby efficiency, for 4 conversion systems: an oil furnace, electric heater, an electric heat pump and a combined power and heat plant. At the top we see the conversion of fuel into heat in an ordinary oil furnace. The energy efficiency is limited to about 85%, principally through stack losses. The low value of the exergy efficiency, about 4%, is, however, due to the fact that the fall in temperature when a thousand degree flame heats water to 60°C is not utilized. As we can see, electric heating has an energy efficiency of 100%. In the diagram for the electric heat pump we see that this is not a top limit of energy efficiency at the conversion of electricity into heat. A heat pump can, of course, also be run with fuels by connecting it to a combustion engine. The heat pump can also in this way take the place of an ordinary furnace for space heating. If the environment is ignored, the conversion of electrical energy or fuels into heat can be well over 100%. We see that in looking at exergy the picture becomes quite different. The exergy efficiency for electric heat is about 5% and for the heat pump 15% [2].

Figure 4. Energy and exergy efficiency for an oil furnace, an electric heater, an electric heat pump and a combined power and heat plant [2,3].

Figure 4. Energy and exergy efficiency for an oil furnace, an electric heater, an electric heat pump and a combined power and heat plant [2,3].

4.4 Interdisciplinary Nature of Exergy

Under the facts listed in Section 4.2, we earlier introduced a new concept and defined exergy as a distinct discipline, because of its interdisciplinary character as the confluence of energy, environment and sustainable development (Fig. 5). Energy production, transformation, transport and use have important impacts on the earth's environment. Energy and environment policies increasingly play a prominent role in relating to a broad range of local, regional and global environmental concerns.

Figure 5. The interdisciplinary triangle of exergy [4].

Figure 5. The interdisciplinary triangle of exergy [4].

4.5 Exergy Analysis

Exergy is defined as the maximum amount of work which can be produced by a system or a flow of matter or energy as it comes to equilibrium with a reference environment. Exergy is a measure of the potential of the system or flow to cause change, as a consequence of not being completely in stable equilibrium relative to the reference environment. Unlike energy, exergy is not subject to a conservation law (except for ideal, or reversible, processes). Rather, exergy is consumed or destroyed, due to irreversibilities in any real process. The exergy consumption during a process is proportional to the entropy created due to irreversibilities associated with the process [5,6,7,8,9,10].

For exergy analysis, the state of the reference environment, or the reference state, must be specified completely. This is commonly done by specifying the temperature, pressure and chemical composition of the reference environment. The results of exergy analyses, consequently, are relative to the specified reference environment, which in most applications is modelled after the actual local environment [5].

Exergy analysis is a method that uses the conservation of mass and conservation of energy principles together with the SLT for the analysis, design and improvement of energy and other systems. The exergy method is useful for furthering the goal of more efficient energy-resource use, for it enables the locations, types, and true magnitudes of wastes and losses to be determined. In general, more meaningful efficiencies are evaluated with exergy analysis rather than energy analysis, since exergy efficiencies are always a measure of the approach to the ideal case. Therefore, exergy analysis can reveal whether or not and by how much it is possible to design more efficient energy systems by reducing the inefficiencies in existing systems. Many engineers and scientists suggest that the thermodynamic performance of a process is best evaluated by performing an exergy analysis in addition to or in place of conventional energy analysis because exergy analysis appears to provide more insights and to be more useful in efficiency improvement efforts than energy analysis.

It is important to highlight that exergy analysis can lead to a substantially reduced rate in the use of natural resources and the environmental pollution by reducing the rate of discharge of waste products.

4.6 Exergy Models

Exergy is a measure of how far a certain system deviates from equilibrium with its environment and therefore, the following expressions can be written for exergy contained in a system.

• Ex = T₀(S_t,eq - S_t)

  (10)

where T₀ is the temperature of the environment and (S_t,eq - S_t) is the deviation from equilibrium of the negentropy (=minus the entropy) of the system and its environment, i.e., the total system. (‘eq’ denotes equilibrium with the environment.)

• Ex = U + P₀V – T₀S – Σ_i µ_i0n_i

  (11)

where U, V, S, and n_i denote extensive parameters of the system (energy, volume, entropy, and the number of moles of different chemical components) and P₀, T₀, and µ_i0 are intensive parameters of the environment (pressure, temperature, and chemical potential which also may include gravitational and electromagnetic potentials etc.). The subscript "o" denotes conditions of the reference environment. It is evident from this equation that the exergy of a system is zero when it is in equilibrium with the reference environment (i.e., when T = T_o, p = p_o, and μ_k = μ_ko for all k).

• Ex = (U – U_eq) + P₀(V – V_eq ) – T₀ (S – S_eq ) – Σ_i µ_i0(n_i – n_ieq)

  (12)

where on the right side easily determined quantities appear. It is thus an easy task to determine the exergy content of a given system in a given environment. For a substance which has an exergy content deriving only from its concentration the following relation holds:

• Ex = RT₀nln(c/c₀)

  (13)

where n is the number of moles of the substance, R is the gas constant, T₀ is the temperature of the environment, c is concentration of the substance in the material considered, and c₀ = concentration of the substance in the environment.

For materials like inert gases or other not chemically active materials this concept of exergy is applicable. The chemically reacting materials receive an additional exergy contribution from the change in the chemical potential. The exergy content in a material can thus be summarized by the following formula:

• Ex = n[µ – µ₀ + RT₀ln(c/c₀)]

  (14)

where µ₀ is chemical potential for the material in its reference state, i.e. in equilibrium with the environment. The chemical potential values for most materials can be found in a tabular form in some reference books.

4.7 Definition of Environment

It is noted that the natural environment does not possess the theoretical characteristics of a reference environment. The natural environment is not in equilibrium, and its intensive properties vary spatially and temporally. Many chemical reactions in the natural environment are blocked because the transport mechanisms necessary to reach equilibrium are too slow at ambient conditions. Thus, the exergy of the natural environment is not zero, as work could be obtained if it were to come to equilibrium. In developing reference-environment models for exergy analysis, a compromise is often made between the theoretical requirements of the reference environment and the actual behavior of the natural environment.

Several reference-environment models have been proposed. The most significant classes of these are described below [4,5,6]:

• Natural-environment-subsystem models: These models attempt to simulate realistically subsystems of the natural environment. This model consists of saturated moist air and liquid water in phase equilibrium. An extension of that model was proposed to allow sulphur-containing materials to be analyzed. The temperature and pressure of this reference environment (Table 2) are normally taken to be 25°C and 1 atm, respectively, and the chemical composition is taken to consist of air saturated with water vapor, and the following condensed phases at 25°C and 1 atm: water (H₂O), gypsum (CaSO₄•2H₂O), and limestone (CaCO₃). The stable configurations of C, O and N respectively are taken to be those of CO₂, O₂ and N₂ as they exist in air saturated with liquid water at T₀ and P₀ (the temperature and pressure for the reference environment); of hydrogen is taken to be in the liquid phase of water saturated with air at T₀ and P₀; and of S and Ca respectively are taken to be those of CaSO₄•2H₂O and CaCO₃ at T₀ and P₀.
• Reference-substance models: With this model, a "reference substance" is selected for every chemical element and assigned zero exergy. This is the model in which the reference substances are selected as the most valueless substances found in abundance in the natural environment. The criterion for selecting such reference substances is consistent with the notion of simulating the natural environment, but is primarily economic in nature, and is vague and arbitrary with respect to the selection of reference substances. Part of this environment is the composition of moist air, including N₂, O₂, CO₂, H₂O and the noble gases; gypsum (for sulphur) and limestone (for calcium). This model is not similar to the natural environment. Consequently absolute exergies evaluated with this model do not relate to the natural environment, and can not be used rationally to evaluate efficiencies or environmental impact.

Table 2. A reference-environment model.

T0 = 25°C = 298.15 K
P0 = 1 aim
Composition:	(i) Atmospheric air saturated with H2O at T0 and P0 (having the following composition):
		Air Constituents	Mole Fraction
		N2	0.7567
		O2	0.2035
		H2O	0.0303
		Ar	0.0091
		CO2	0.0003
		H2	0.0001
	(ii) The following condensed phases at T0 and P0:
		Water (H2O)
		Limestone (CaCO3)
		Gypsum (CaSO4•2H2O)

Table 2. A reference-environment model.

T0 = 25°C = 298.15 K
P0 = 1 aim
Composition:	(i) Atmospheric air saturated with H2O at T0 and P0 (having the following composition):
		Air Constituents	Mole Fraction
		N2	0.7567
		O2	0.2035
		H2O	0.0303
		Ar	0.0091
		CO2	0.0003
		H2	0.0001
	(ii) The following condensed phases at T0 and P0:
		Water (H2O)
		Limestone (CaCO3)
		Gypsum (CaSO4•2H2O)

• Equilibrium and constrained-equilibrium models: It is the model in which all the materials present in the atmposphere, oceans and a layer of the crust of the earth are pooled together and an equilibrium composition is calculated for a given temperature. The selection of the thickness of crust considered is subjective and is intended to include all materials accessible to technical processes. Thicknesses varying from 1 m to 1000 m, and a temperature of 25°C were considered. For all thicknesses, the model differed significantly from the natural environment. Exergy values obtained using these environments are significantly dependent on the thickness of crust considered, and represent the absolute maximum amount of work obtainable from a material. Since there is no technical process available which can obtain this work from materials, this equilibrium model does not give meaningful exergy values when applied to the analysis of real processes. Its modified version of the equilibrium environment was proposed later in which the calculation of an equilibrium composition excludes the possibility of the formation of nitric acid (HNO₃) and its compounds. That is, all chemical reactions in which these substances are formed are in constrained equilibrium, and all other reactions are in unconstrained equilibrium. When a thickness of crust of 1 m and temperature of 25°C are used, the model is similar to the natural environment.
• Process-dependent models: This is the model which contains only components that participate in the process being examined in a stable equilibrium composition at the temperature and pressure of the natural environment. This model is dependent on the process examined, and is not general. Exergies evaluated for a specific process-dependent model are relevant only to the process. They can not rationally be compared with exergies evaluated for other process-dependent models or used in environmental assessments.

An understanding of the relations between exergy and the environment may reveal the fundamental patterns and forces that affect and underlie changes in the environment, and help researchers to deal better with environmental damage.

4.8 Exergy Efficiencies

Here, we introduce another concept of SLT efficiency, referring to the exergy eficiency and to show its use in assessing the efficiency or energy utilization. Engineers make frequent use of efficiencies to gauge the performance of devices and the effectiveness of processes. Many of these expressions are based on energy-they are FLT efficiencies. Also useful are measures of performance that take into account limitations imposed by the second law. Efficiencies of this type are called here SLT efficiencies.

To illustrate the idea of a performance parameter having to do with the SLT and to contrast it with an analogous energy-based efficiency, consider a control volume at steady-state for which the energy and availability equations can be written, respectively, as

(Energy in) = (Energy out in product) + (Energy loss)

(15)

(Availability in) = (Availability out in product) + (Availability loss) + (Availability destruction)

(16)

In these equations, the term product might refer to shaft work or electricity developed, a certain heat transfer, some desired combination of heat and work, or possibly a particular exit stream (or streams). Losses are understood to include such things as waste heat and slack gases vented to thc surroundings without use. The destruction term in the availability equation refers to availability destruction due to internal irreversibilities. From either viewpoint, energy or availability, a gauge of how effectively the input is converted to the product is the ratio (product/input), that is

η= Energy out in product/Energy in = 1 - [Loss/Input]

(17)

ψ = Availability out in product/Availability in = 1 - [(Loss + Destruction)/Input]

(18)

Here, the exergy efficiency ψ frequently gives a finer understanding of performance than η. In computing η, the same weight is assigned to energy whether it becomes shaft work or a stream of low temperature fluid. Also, it centers attention on reducing 'losses" to improve efficiency. The parameter ψ weights energy flows by accounting for each in terms of availability. It stresses that both losses and internal irreversibilities need to be dealt with to improve performance. In many cases it is the irreversibilities that are more significant and the more difficult to deal with.

Efficiency equations each define a class of efficiencies because a judgment has to be made about what is the product, what is counted as a loss, and even what is regarded as the input. Different decisions about these lead to different efficiency expressions within the class.

Other kinds of second law efficiency expressions also appear in the literature. One of these, appropriate only for devices at steady-state, is calculated as the ratio of the sum of the availability exiting to the sum of the availability entering. Another class of second law efficiencies is composed of task efficiencies.

5. Illustrative Examples

Next we provide four illustrative examples on (i) entropy generation during heat transfer processes, (ii) entropy generation in a wall, (iii) entropy generation associated with heat transfer and finally (iv) a sensible energy storage system. These examples will highlight the importance of these concepts and show the facts in thermal engineering applications.

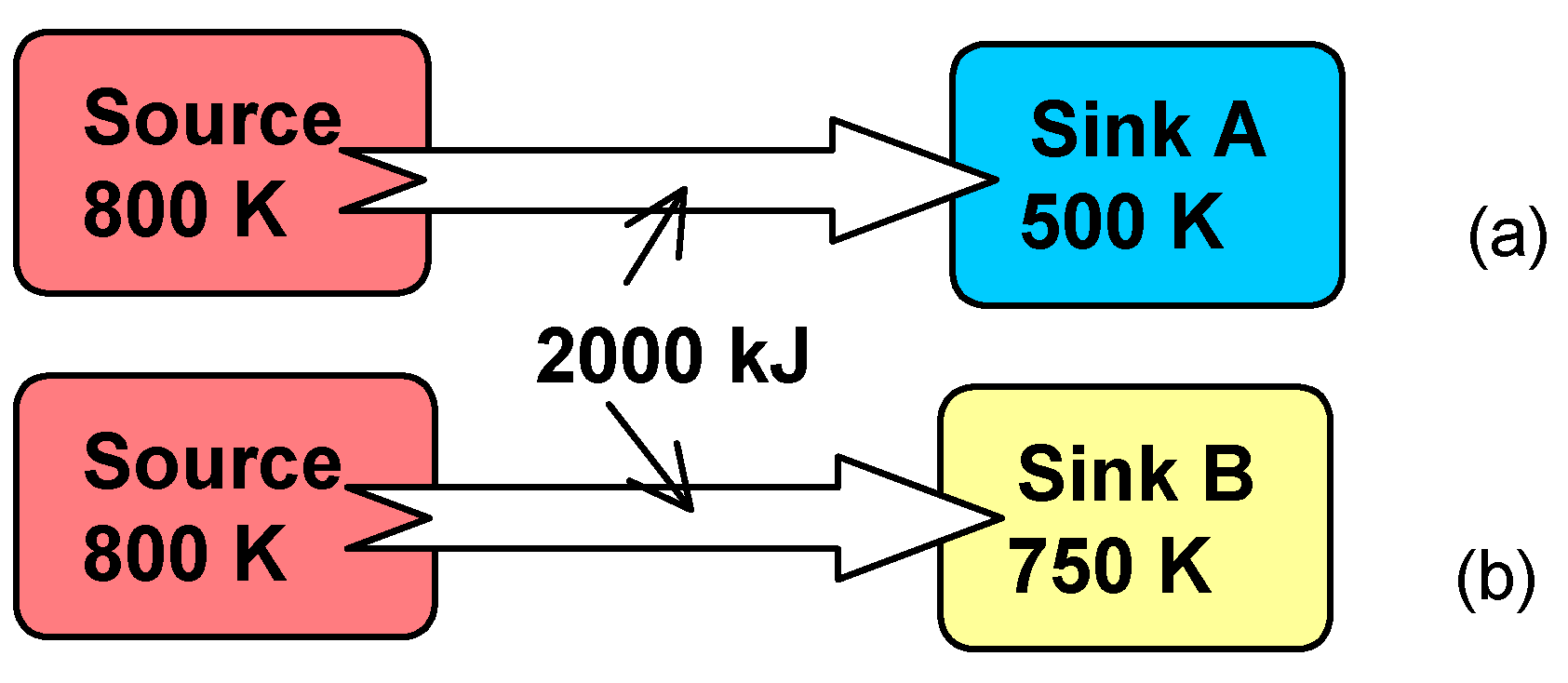
5.1 Illustrative Example 1

A heat source at 800 K loses 2000 kJ of heat to a sink at (a) 500 K and (b) 750 K. Determine which heat transfer process is more irreversible [10].

Solution: A sketch of the reservoirs is shown in Fig. 6. Both cases involve heat transfer through a finite temperature difference, and therefore both are irreversible. The magnitude of the irreversibility associated with each process can be determined by calculating the total entropy change for each case. The total entropy change for a heat transfer process involving two reservoirs (a source and a sink) is the sum of the entropy changes of each reservoir since the two reservoirs form an adiabatic system.

Or do they? The problem statement gives the impression that the two reservoirs are in direct contact during the heat transfer process. But this cannot be the case since the temperature at a point can have only one value, and thus it cannot be 800 K on one side of the point of contact and 500 K on the other side. In other words, the temperature function cannot have a jump discontinuity. Therefore, it is reasonable to assume that the two reservoirs are separated by a partition through which the temperature drops from 800 K on one side to 500 K (or 750 K) on the other. Therefore, the entropy change of the partition should also be considered when evaluating the total entropy change for this process. However, considering that entropy is a property and the values of properties depend on the state of a system, we can argue that the entropy change of the partition is zero since the partition appears to have undergone a steady process and thus experienced no change in its properties at any point. We base this argument on the fact that the temperature on both sides of the partition and thus throughout remained constant during this process. Therefore, we are justified to assume that ΔS_partition = 0 since the entropy (as well as the energy) content of the partition remained constant during this process. Since each reservoir undergoes an internally reversible, isothermal process, the entropy change for each reservoir can be determined from ΔS = Q/T₀ where T₀ is the constant absolute temperature of the system and Q is the heat transfer for the internally reversible process.

(a)

For the heat transfer process to a sink at 500 K:

ΔS_source = Q_source/T_source = -2000 kJ/800 K = -2.5 kJ/K

ΔS_sink = Q_source/T_source = 2000 kJ/500 K = +4.0 kJ/K

and

S_gen = ΔS_total = ΔS_source + ΔS_sink = (-2.5 + 4.0) kJ/K = +1.5 kJ/K

Therefore, 1.5 kJ/K of entropy is generated during this process. Noting that both reservoirs have undergone internally reversible processes, the entire entropy generation took place in the partition.

(b)

Repeating the calculations in part (a) for a sink temperature of 750 K, we obtain

ΔS_source = -2.5 kJ/K

ΔS_sink = +2.7 kJ/K

and

S_gen = ΔS_total = (-2.5 + 2.7) kJ/K = +0.2 kJ/K

The total entropy change for the process in part (b) is smaller, and therefore it is less irreversible. This is expected since the process in (b) involves a smaller temperature difference and thus a smaller irreversibility.

Discussion: The irreversibilities associated with both processes could be eliminated by operating a Carnot heat engine between the source and the sink. For this case it can be shown that ΔS_total = 0.

Figure 6. Schematic for the example on entropy generation during heat transfer processes.

Figure 6. Schematic for the example on entropy generation during heat transfer processes.

5.2 Illustrative Example 2

Consider steady heat transfer through a 5-m×6–m brick wall of a house of thickness 30 cm. On a day when the temperature of the outdoors is 0°C, the house is maintained at 27°C. The temperatures of the inner and outer surfaces of the brick wall are measured to be 20°C and 5°C, respectively, and the rate of heat transfer through the wall is 1035 W. Determine the rate of entropy generation in the wall, and the rate of total entropy generation associated with this heat transfer process [10].

Solution: We first take the wall as the system (Fig. 7). This is a closed system since no mass crosses the system boundary during the process. We note that the entropy change of the wall is zero during this process since the state and thus the entropy of the wall do not change anywhere in the wall. Heat and entropy are entering from one side of the wall, and leaving from the other side.

Assumptions: (i) The process is steady, and thus the rate of heat transfer through the wall is constant. (ii) Heat transfer through the wall is one-dimensional.

Analysis: The rate form of the entropy balance for the wall simplifies to

$${\left(\stackrel{\cdot }{Q}/T\right)}_{in}-{\left(\stackrel{\cdot }{Q}/T\right)}_{out}+\stackrel{\cdot }{S_{gen}}=0\Rightarrow \text{(1035 W/293 K)}-\text{(1035 W/278 K) }+\stackrel{\cdot }{S_{gen}}=0\Rightarrow \stackrel{\cdot }{S_{gen}}=\underset{\_}{\underset{\_}{0.191\text{ W/K}}}$$

Therefore, the rate of entropy generation in the wall is 0.191 W/K.

Note that entropy transfer by heat at any location is Q/T at that location, and the direction of entropy transfer is the same as the direction of heat transfer.

To determine the rate of total entropy generation during this heat transfer process, we extend the system to include the regions on both sides of the wall that experience a temperature change. Then one side of the system boundary becomes room temperature while the other side becomes the temperature of the outdoors. The entropy balance for this extended system (system immediate surroundings) will be the same as that given above, except the two boundary temperatures will be 300 and 273 K instead of 293 and 278 K, respectively. Then the rate of total entropy generation becomes

$$\text{(1035 W/300 K)}-\text{(1035 W/273 K) }+{\stackrel{\cdot }{S}}_{gen,total}=0\Rightarrow {\stackrel{\cdot }{S}}_{gen,total}=\underset{\_}{\underset{\_}{0.341\text{ W/K}}}$$

Discussion: Note that the entropy change of this extended system is also zero since the state of air does not change at any point during the process. The differences between the two entropy generations is 0.150 W/K, and it represents the entropy generated in the air layers on both sides of the wall. The entropy generation in this case is entirely due to irreversible heat transfer through a finite temperature difference.

Figure 7. Schematic for the example on entropy generation in a wall.

Figure 7. Schematic for the example on entropy generation in a wall.

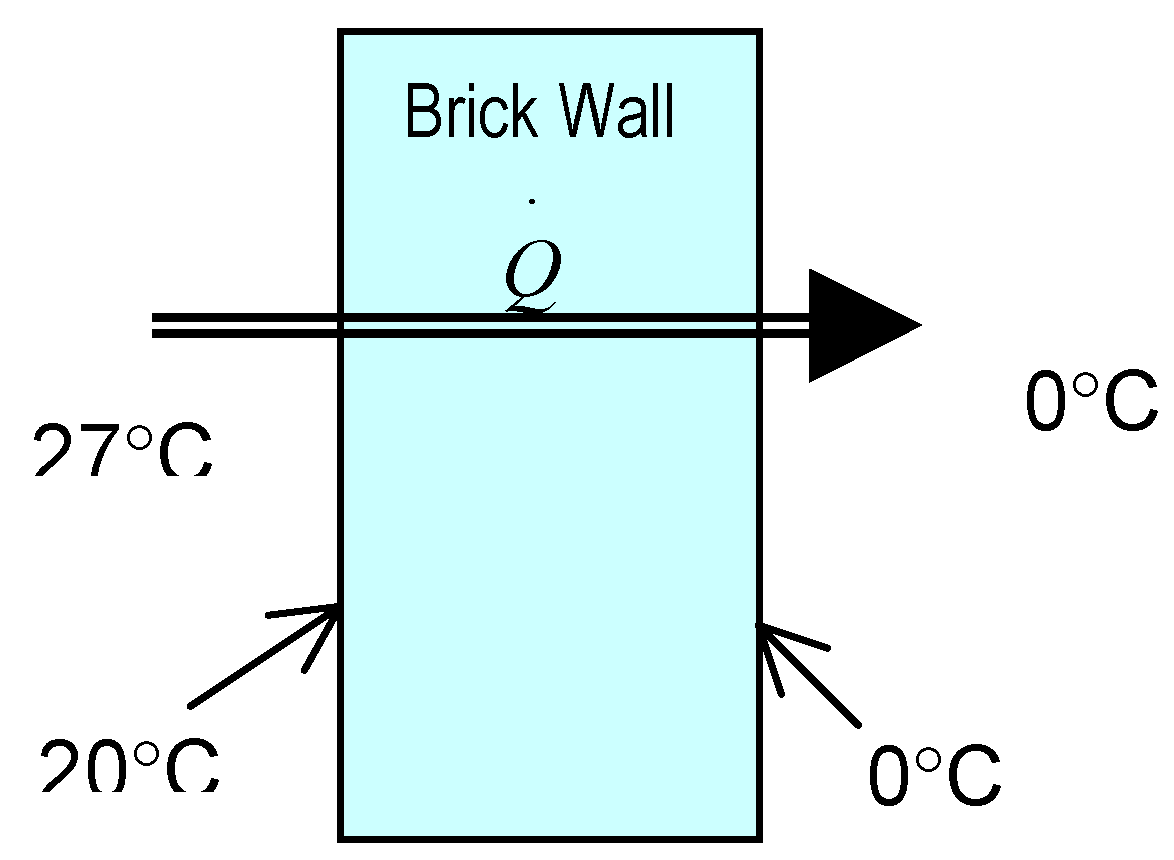
5.3 Illustrative Example 3

Consider a frictionless piston-cylinder device contains a saturated liquid–vapor mixture of water at 100°C. During a constant-pressure process, 600 kJ of heat is transferred to the surrounding air at 25°C. As a result, part of the water vapor contained in the cylinder condenses. Determine (a) the entropy change of the water and (b) the total entropy generation during this heat transfer process [10].

Solution: We first take the water in the cylinder as the system (Fig. 8). This is a closed system since no mass crosses the system boundary during the process. We note that the pressure and thus the temperature of water in the cylinder remain constant during this process. Also, the entropy of the system decreases the process because of heat loss.

Assumptions: (i) There are no irreversibilities involved within the system boundaries, and thus the process is internally reversible. (ii) The water temperature remains constant at 100°C everywhere, including the boundaries.

Analysis: (a) Noting that water undergoes an internally reversible isothermal process, its entropy change can be determined from

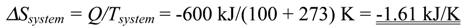
(b)

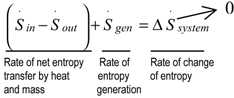
To determine the total entropy generation during this process, we consider the extended system, which includes the water, the piston-cylinder device, and the region immediately outside the system that experiences a temperature change so that the entire boundary of the extended system is at the surrounding temperature of 25°C. The entropy balance for this extended system (system immediate surroundings) yields

The entropy generation in this case is entirely due to irreversible heat transfer through a finite temperature difference.

Note that the entropy change of this extended system is equivalent to the entropy change of water since the piston-cylinder device and the immediate surroundings do not experience any change of state at any point, and thus any change in any property, including entropy.

Discussion For the sake of argument, consider the reverse process (i.e., the transfer of 600 kJ of heat from the surrounding air at 25°C to saturated water at 100°C) and see if the increase of entropy principle can detect the impossibility of this process. This time, heat transfer will be to the water (heat gain instead of heat loss), and thus the entropy change of water will be +1.61 kJ/K. Also, the entropy transfer at the boundary of the extended system will have the same magnitude but opposite direction. This will result in an entropy generation of -0.4 kJ/K. The negative sign for the entropy generation indicates that the reverse process is impossible.

To complete the discussion, let us consider the case where the surrounding air temperature is a differential amount below 100°C (say 99.999…9°C) instead of being 25°C. This time, heat transfer from the saturated water to the sur-rounding air will take place through a differential temperature difference rendering this process reversible. It can be shown that S_gen = 0 for this process.

Remember that reversible processes are idealized processes, and they can be approached but never reached in reality.

Figure 8. Schematic for the example on entropy generation associated with heat transfer [10].

Figure 8. Schematic for the example on entropy generation associated with heat transfer [10].

Further Discussion on Entropy Generation Associated with a Heat Transfer Process:

In the example above it is determined that 0.4 kJ/K of entropy is generated during the heat transfer process, but it is not clear where exactly the entropy generation takes place, and how. To pinpoint the location of entropy generation, we need to be more precise about the description of the system, its surroundings, and the system boundary.

In that example, we assumed both the system and the surrounding air to be isothermal at 100°C and 25°C, respectively. This assumption is reasonable if both fluids are well mixed. The inner surface of the wall must also be at 100°C while the outer surface is at 25°C since two bodies in physical contact must have the same temperature at the point of contact. Considering that entropy transfer with heat transfer Q through a surface at constant temperature T is Q/T, the entropy transfer from the water into the wall is Q/T_sys = 1.61 kJ/K. Likewise, entropy transfer from the outer surface of the wall into the surrounding air is Q/T_surr = 2.01 kJ/K. Obviously, entropy in the amount of (2.01 − 1.61) = 0.4 kJ/K is generated in the wall, as illustrated in Fig. 9b.

Identifying the location of entropy generation enables us to determine whether a process is internally reversible. A process is internally reversible if no entropy is generated within the system boundaries. Therefore, the heat transfer process discussed in the example above is internally reversible if the inner surface of the wall is taken as the system boundary, and thus the system excludes the container wall. If the system boundary is taken to be the outer surface of the container wall, then the process is no longer internally reversible since the wall, which is the site of entropy generation, is now part of the system.

For thin walls, it is very tempting to ignore the mass of the wall and to regard the wall as the boundary between the system and the surroundings. This seemingly harmless choice hides the site of the entropy generation from view and is a source of confusion. The temperature in this case drops suddenly from T_sys to T_surr at the boundary surface, and confusion arises as to which temperature to use in the relation Q/T for entropy transfer at the boundary.

Note that if the system and the surrounding air are not isothermal as a result of insufficient mixing, then part of the entropy generation will occur in both the system and the surrounding air in the vicinity of the wall, as shown in Fig. 9c.

Figure 9. Schematic representation of entropy generation during a heat transfer process through a finite temperature difference [10].

Figure 9. Schematic representation of entropy generation during a heat transfer process through a finite temperature difference [10].

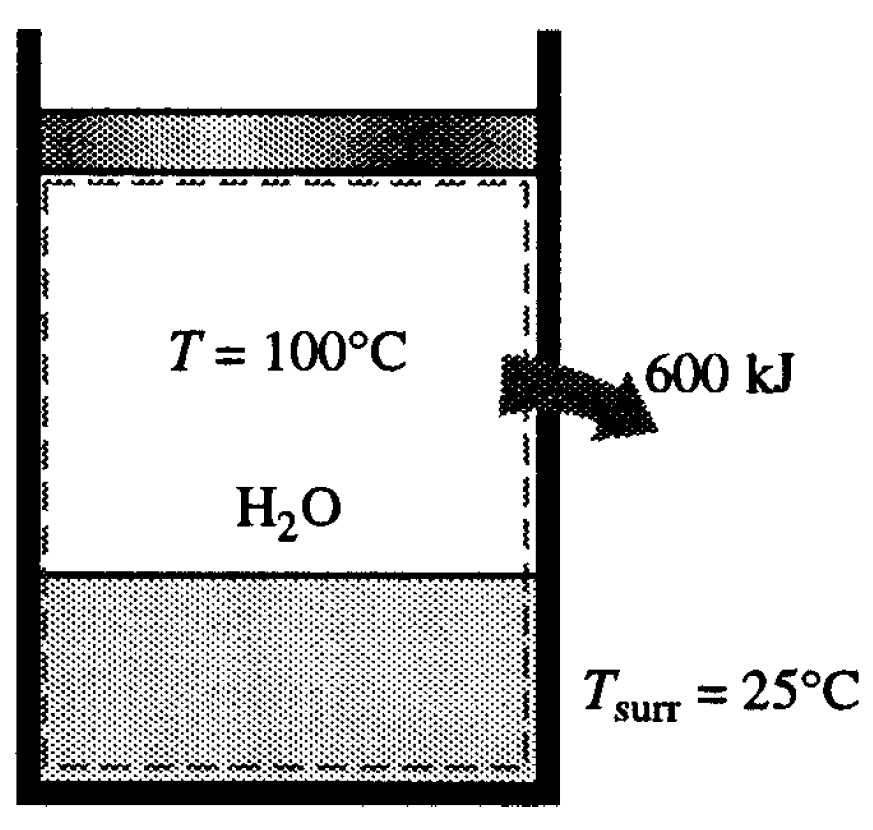
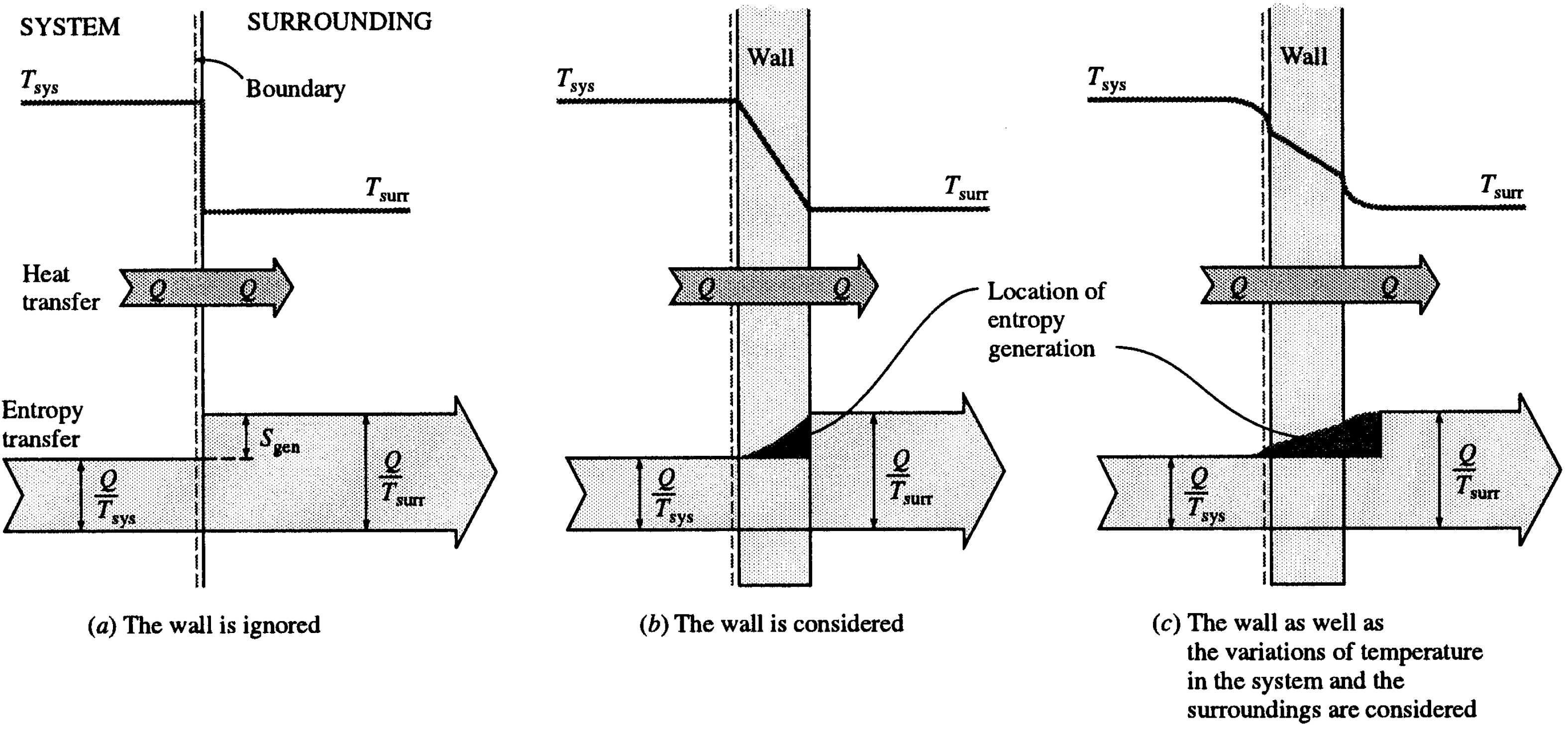
5.4 Illustrative Example 4

In this example, we consider a sensible energy storage (SES) system encompassing three processes such as charging, storing and discharging (Figure 10) in order to distinguish energy and exergy concepts clearly, and highlight the importance of exergy as a potential tool for practical thermodynamic systems.

1) Consider two SES systems, X and Y, in an environment at a temperature of 25°C. Each one receives 104,650 kJ of heat from a stream of 500 kg of water, which is cooled from 80 to 30°C. Therefore, the heat input to each of the storage unit during the charging period is

Q_; = m_i c_pΔT = 500 x 4.186 x (80 ‑ 30) = 104,650 kJ

For the system X:

After one day, heat in the amount of 94,185 kJ is recovered during the discharging period from the storage system X by a stream of 4500 kg of water being heated from 30 to 35°C. That is,

Q_o = m_o cp ΔT = 4500 x 4.186 x (35 ‑ 30) = 94,185 kJ

Therefore, the energy efficiency for SES system X becomes

η_x = Q_o/Q_i = 94,185/104,650 = 0.90

Heat rejection to the surroundings during storage is:

Q_r = Q_; – Q_o = 104,650 – 94,185 = 10,465 kJ

For the system Y:

For the storage system Y, the heat recovered during discharging, the energy efficiency and the heat rejection to the surrounding can be evaluated in a similar way. In this regard, the storage system Y stores the heat for 90 days, after which an energy quantity of 94 185 kJ is recovered during the discharging period by heating a stream of 500 kg of water from 30 to 75°C, with the resulting energy efficiency of the storage cycle as follows:

Q_o = m_o cp ΔT = 500 x 4.186 x (75 ‑ 30) = 94,185 kJ

Thus, the energy efficiency for SES system Y can be found as same as the storage X.

η_{x =} Q_o/Q_i = 94 185/104 650 = 0.90

The value of heat rejection to the surroundings during storage is:

Q_r = Q_; – Q_o = 104 650 – 94 185 = 10,465 kJ

It is useful to mention that the ability of storing sensible heat in a given tank (or container) strongly depends at the same time on the value for the material of ρc_p.

As a result, both storage systems have the same energy efficiency when calculated by considering the first‑law of thermodynamics, but storage system Y, which stores the heat for 90 days rather than one day, and which returns the heat at the much more useful temperature of 75 rather than 35°C, gives a considerable high performance. It is clear that a more perceptive measure of comparison than that provided by the energy efficiency of the storage cycle is needed if the true usefulness of a SES is to be assessed and a rational basis for the optimization of its economic value established. Therefore, it is necessary to introduce the exergy efficiency which is a measure of the effectiveness of the SES system. An efficiency defined simply as the percentage of the total energy stored in a system which can be recovered ignores the quality (availability) of the recovered energy, and so cannot provide a measure of ideal performance as mentioned earlier. It is obvious that the exergy efficiency definition provides a better measure.

2) Consider the aforementioned example of SES systems X and Y. For the corresponding cases, an exergy analysis is conducted below. The exergy efficiencies can easily be obtained using the equations listed in Table 3. The exergy change during the charging period can be obtained as

A_i = m_jc_p[(T₁– T₂) – T₀(ln(T₁/T₂)] = 500 x 4.186 x [(353 ‑ 303) – 298 x (In(353/303)] = 9386.88 kJ

For the system X:

The exergy change during the discharging period for the storage system X can be calculated as follows:

A_o = m_oc_p[(T₁– T₂) – T₀(ln(T₁/T₂)] = 4500 x 4.186 x [(308 ‑ 303) ‑ 298 x(In(308/303)] = 2310.18 kJ

Therefore, the exergy efficiency for storage X becomes

ψ_x = A_o/A_i = 2310.18/9386.88 = 0.25

For the system Y:

As mentioned earlier, heat is recovered from the storage after 90 days by a stream of 500 kg of water entering at 30°C and leaving at 75°C. The exergy change and efficiency of storage system Y can be obtained as follows:

Figure 10. Schematic of three subprocesses of a sensible energy storage system.

Figure 10. Schematic of three subprocesses of a sensible energy storage system.

A_o = m_oc_p[(T₁– T₂) – T₀(ln(T₁/T₂)] = 500 x 4.186 x [(348 ‑ 303) ‑ 298 x (In(348/303)] = 7819.52 kJ

ψ_y = A_o/A_i = 7819.52/9386.88 = 0.83

As a result, it can be seen in the example that for both storage systems the energy efficiencies became the same as 90% despite having two different storage periods. It means that the first law of thermodynamics is not sufficient to distinguish these two separate SES systems running on two different storage periods. This requirement brings exergy forefront as a more capable tool. For this reason, the distinction can easily be made between two storage systems (X and Y) by using exergy analysis, resulting in two different exergy efficiencies as 25% for the system X and 83% for the system Y. This is due to Y having the advantage over SES system X, because of the higher temperature and thus greater availability content. This example gives some practical illustrations of the more abstract concepts discussed before and highlights the importance of understanding and considering the exergy, rather than energy in which exergy is more effective and more efficient tool for the performance analysis of SES systems. The results are reliable for energy storage systems

To summarize, some intuitive advantages of exergy analysis can be listed as follows:

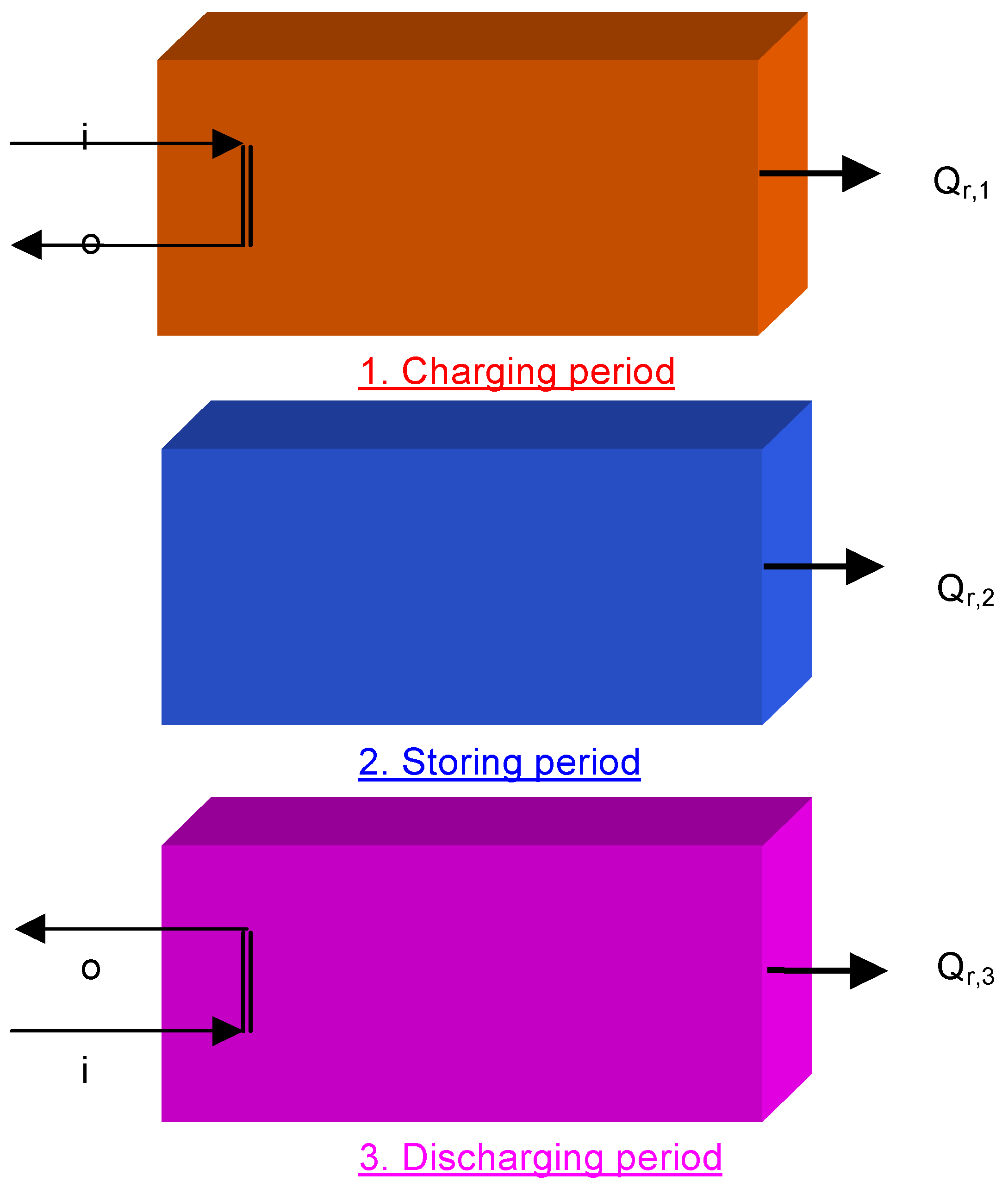
• It provides more proper accounting of the loss of availability of heat in SES system using the conservation of mass and energy principles together with the second law of thermodynamics for the goals of design and analysis.
• It gives more meaningful and useful information than energy analysis regarding the efficiency, losses and performance of SES systems.
• It is more correct reflecting the thermodynamic and economic values of the operation of SES systems.
• It is an efficient technique revealing whether or not and by how much it is possible to design more efficient SES systems by reducing the inefficiencies in the existing units.

6. Conclusions

In a broader perspective (except for the zeroth and third law of thermodynamics), we can define the thermodynamics as a science of energy, exergy, and entropy. Apparently, the FLT refers to the energy analysis which only identifies losses of work and potential improvements or the effective use of resources, e.g., in an adiabatic throttling process. However, the SLT, i.e., exergy analysis takes the entropy portion into consideration by including irreversibilities. During the past decade exergy related studies have received considerable attention from various disciplines ranging from chemical engineering to mechanical engineering, from environmental engineering to ecology and so on. As a consequence of this, recently, international exergy community has expanded greatly.