The thermodynamic basis for the constancy of the speed of light[
47] provides the starting point for a thermodynamic basis for Einstein’s Special Theory of Relativity[
9] with its space-time metric[
23] and quantum mechanics[
2]. The starting point in this chain of logic is the adoption of generalizations of the classical thermodynamic laws and their use to define the mechanical entropy, (mentropy), and arrive at the maximum mentropy principal for isolated mechanical systems. The ability of these laws to require the constancy of the speed of light displays their connection to relativistic theories. However, this article will display the logic through the development of mechanics. There will be numerous points in this logic where one could branch off on interesting and useful topics. See the Logic Flow chart in
Figure 1. This article will stay strictly on the track of presenting the logic from the adopted laws through relativistic mechanics to quantum mechanics.
The basic laws may be restated here for clarity.
1 First Law (Conservation of Energy)
The concept of conservation of energy is fundamental to all branches of physics and is the beginning of the basis of thermodynamics and mechanics. In terms of generalized coordinates or independent variables, the notion of work, or mechanical energy, is considered linear forms of the type
where the forces
Fi may be functions of the velocities (
dqi/dt =
ui) as well as the coordinates
qi and the summation convention is used. The line integral
then represents the work done along the path
C by the generalized forces.
A system may acquire energy by other means in addition to the work terms; such energy acquisition is denoted
. The system energy, which represents the energy possessed by the system, is considered to be
With these concepts, then the First Law, which is the generalized Law of Conservation of Energy, has the form
Positive
is taken as energy added to the system by means other than through the work terms and
Fi is taken as the component of the generalized force acting on the system which caused displacement
dqi.
2 Second Law
There are processes, or motions, that satisfy the First Law but are not observed in nature. The purpose of the Second Law is to incorporate such experimental facts into the model of dynamics. The statement of the Second Law is made using the axiomatic statement provided by the Greek mathematician Carathéodory[
2], who presented an axiomatic development of the Second Law of thermodynamics that may be applied to a system of any number of variables. The Second Law may then be stated as follows:
In the neighborhood (however close) of any equilibrium state of a system of any number of dynamic coordinates, there exist states that cannot be reached by reversible E-conservative ( = 0) processes or motions.
When the variables are thermodynamic variables, the E-conservative processes are known as adiabatic processes.
A reversible process, or motion, is one that is performed in such a way that, at the conclusion of the process, both the system and the local surroundings may be restored to their initial states without producing any change in the rest of the universe.
3 Mentropy and Geometry
It was previously shown that the Second Law guarantees the existence of an integrating factor for the First Law where the integrating factor is a function of only the speed[
47]. The Second Law also requires that the mentropy must be maximized for an isolated system for which
= 0. This principle becomes a variational principle for isolated systems. A metric may be obtained by considering the stability conditions when
q and
S are taken as the independent variables. For example, consider the terms of second order in small displacements beginning with the general condition
Choose
U =
U(
q, S), which, because of the identity
φdS =
sU −
Fdq
is a natural choice for the independent variables, and expand
δU in powers of the
δq and
δS
The inequality (2) then shows that in Equation (3),
Retaining only the second order terms, the criterion of stability is that a quadratic differential form be positive definite;
Adopting this quadratic form as the metric of a general system whose variables are held fixed, we may then write this metric as
where the summation convention is used and
with
q0 ≡
S/F0, the scaled mentropy for dimensional correctness.
Thus, the stability conditions provide a metric in the four-dimensional manifold of spacementropy. The arc length
s in the space-mechanical entropy manifold may be parameterized by choosing
ds ≡
u0dt ≡
cdt, where
u0 ≡
c is the unique velocity appearing in the integrating factor of the second postulate. There are two reasons for choosing the unique velocity. First, it is the only well-defined velocity we have thus far. Secondly, we may look ahead to the metric of the Special Theory of Relativity. The metric may now be written as
Now suppose the systems considered are restricted to only
E-conservative systems. Then the principle of increasing mentropy may be imposed in the form of the variational principle
In order to use this variation principle, Eqn. (5) may be expanded, solved for (
dq0) and squared to arrive at the quadratic form
where
with
uα ≡
dqα/dt.
By defining
x0 ≡
ct, xα =
qα;
α = 1, 2, 3, then Eqn. (6) may be written as
where
f ≡
h00. This metric obviously reduces, in the Euclidean limit of constant coefficients, to the metric of Minkowski’s space-time manifold of Special Relativity[
23]. It is interesting to note that in the metric of Eqn. (6) the difference in the sign on the time and space elements of the metric come from the fact that the stability conditions are given in terms of space and mentropy while the variational principle was taken to be the Mentropy Principle. In this fashion the Second Law guarantees the limiting aspect found in Einstein’s Special Theory of Relativity.
In his General Theory of Relativity, Einstein assumed the space-time manifold to be Riemannian[
11]. However, this assumption involves the a priori assumption that the scalar product be invariant. This assumption was later questioned by Weyl in his generalization of geometry[
37]. From the viewpoint that the adopted postulates should contain the other theories within them then it becomes desirable to determine whether or not these postulates specify the geometry of the (
dq0)
2 space-time manifold. More particularly do the adopted postulates lead to a geometry includes the geometry of current theories? To arrive at a more general geometry would not be a limitation for it would certainly include the others.
Recalling Eqn. (7), we can define
Now the Second Law guarantees the existence of the function mentropy and that
dq0 be a perfect differential; therefore
where
≡
∂q0/∂xi. Then the exactness of
dq0 is stated by
By defining the parallel displacement of a vector to be
and using Eqns. (10) and (11) it may be seen that the connections must be symmetrical, or
This result should not be taken to mean that only symmetric connections need to be considered. Rather it means that given the ’s that maximize (dq0)2, then the connections are symmetrical. However, since a variational principle must be used to determine the ’s, then both symmetric and antisymmetrical connections will have to be considered.
In Weyl’s generalization of geometry he found it necessary to assume the symmetry of the connections. He proved a theorem showing that the symmetry of the connections guaranteed the existence of a local Euclidean limiting manifold and used this theorem in support of the symmetry assumption. Here we find that the Second Law requires that the connections formed by the solution coefficients must be symmetrical thus guaranteeing, through Weyl’s theorem, the existence of a local Euclidean geometry within the Dynamic Theory.
Suppose now we consider whether the order of differentiating the change in mentropy makes any difference. This means that we must use symmetric connections since the actual change in mentropy will be determined by the metric coefficients that generate a maximum. Knowing that the change in mentropy is a total derivative provides the knowledge that the mentropy space must be Reimannian.
It may be shown that the requirement that the change in mentropy be a total derivative also requires that the difference in the order of differentiation
must vanish.
This is the necessary and sufficient condition that the differential mentropy change may be transferred from an initial point to all points of the space in a manner that is independent of the path.
The distinguishing features of Riemannian geometry is the invariance of the scalar product under a vector transplantation. Therefore to determine whether the (
dq0)
2 space is a Riemannian space, consider the vector
ξi and
. Now since
ξi =
gijξj and
then
Or, since
and
then
Thus the change in the covariant and the contravariant vectors are given by
Now consider the change in the scalar product
ξiηi. Then
Renaming the indices in the second term yields
Thus the geometry of the (
dq0)
2 manifold is Riemannian.
Next consider the question of what is the geometry of the (
dσ)
2 space? Equation (8) shows that we may write (
dσ)
2 =
f(
dq0)
2, which is reminiscent of Weyl’s generalized geometry. Further we have
Then in the sigma space an arbitrary vector
ξi would have a length
ℓ given by the self-scalar product
where
l is the length of the vector in the mentropy space.
If we differentiate Eqn. (13), we have
However, in the mentropy space the length of the vector is unchanged under parallel displacement so that
Comparing Eqn. (14) with the definition of the parallel displacement of a vector, Eqn. (11), we find that
plays a role similar to that of the connections
the definition of parallel displacement of a vector. Therefore we shall define the change in the length of a vector under displacement to be
This is the same definition Weyl made in his generalization of geometry. However, there is a difference in the way it was obtained. Weyl chose this definition in analogy with the connections Γ and the definition then led to the second more general metric. In this theory the fundamental laws lead us to two metrics and Eqn. (14) for the change in the length of a vector under displacement. Therefore, we have no choice. Eqn. (14) is a derived equation and Eqn. (15) only renames the logarithmic derivative.
Using Eqn. (15) we may obtain, in general,
Renaming the various summation indices, rearranging terms, and using the length of a vector, we obtain
Since this must hold for arbitrary choice of
ξi and
dxk, we conclude that
This is the same system of linear equations for the connections of a Reimannian space except that the inhomogeneous term
gijs has now to be replaced by
gijk − 2
gijφk. Therefore the same linear algebra as before leads to
where
is the usual Christoffel symbol of the second kind.
Now, since the mentropy space is Riemannian, then in the mentropy space we have
and
and the length
of a vector is unchanged under parallel displacement. However, the same displacement law in the sigma space, with metric
, leads to the relation
Thus ±(1
/2)(
∂ ln
f/∂xk) plays the role of
φk in Eqn. (15). It follows then that the ordinary connections
constructed from
are equal to the more general connections
constructed according to Eqn. (16) from
gij and
φk = (1
/2)(
∂ ln
f/∂xk):
This can also be seen by direct computation from Eqn. (15) and
We may interpret the change of metric from
gij to
by Eqn. (19) as a change of scale for the length at every point of the Riemannian manifold by the variable gauge factor
f. This transformation is called a gauge transformation, and
φk called a gauge vector field.
The generalized geometry thus separates the problem of measurement of angles from that of measurement of length. For instance, the angle between the two vectors
ξi and
ηi at a given point of the space is measured by the ratio
This ratio does not change under the gauge transformation Eqn. (19). The gauge transformation is therefore an angle-preserving, or conformal, change of metric. On the other hand, the length of vectors will change under Eqn. (19) according to Eqn. (14). Thus the metric tensor
determines angles, while one needs also the gauge vector
φk to measure length.
Considering the sigma space, which is characterized by the tensor field
and gauge vector
. The same argument as before shows that we may, without changing the intrinsic geometric properties of vector fields, replace the geometric quantities by use of a scalar field
f as follows:
That is, in the new metric, vectors will have the same law of affine transplantation and the angle between different vectors at the same point of the manifold will be preserved, but the local lengths of a vector will be changed according to
Thus the general Weyl geometry of the sigma space admits also a conformal gauge transformation.
4 Quantum Mechanics
In 1927 F. London derived quantum principles from Weyl’s geometry[
21]. However, the results of his work made it difficult to define length as a real number and because of this Weyl later interpreted the mathematical formalism of his unified theory as connected with transplanting a state vector of a quantum theoretical system.
Suppose that we consider an isolated, or E-
conservative, system so that
= 0. Then, because of the Second Law
dq0 ≥ 0 which is the principle of increasing mentropy. Then certainly (
dq0)
2 ≥ 0 and also, since (
dq0)
2 =
f(
dσ)
2, then
f(
dσ)
2 ≥ 0. However, if
f < 0, then (
dσ)
2 < 0 since it is the product that must remain greater than, or equal to, zero. In this case
But
and
which implies that the element of arc (
dσ) is given by
where (
dσ)
0 is some initial value of the element of arc.
Now suppose an equilibrium, or reversible, state is desired so that
dq0 = 0. Thus, the desired condition is a null trajectory of the (
dq0)
2 manifold. Then, if
f ≠ 0, the desired condition is also a null trajectory of the (
dσ)
2 manifold. This implies that
d(
dσ) = 0 or (
dσ) = (
dσ)
0, so that
which is satisfied only if
where
N is an integer. This is the quantum condition London introduced.
To illustrate how this condition arises from this approach, suppose a description of a hydrogen atom is desired. A hydrogen atom is in a stable condition and, if isolated, satisfies the conditions = 0 and dq0 = 0. These conditions along with f ≠ 0 establish the quantization of the integral in Eqn. (21). To show how the Dynamic Theory removes from London’s work the difficulty of defining length as a real number, consider an elementary presentation of London’s.
Suppose the field of a proton to be given by
Equality of forces for the simple case of circular motion requires that
Thus the period is given by
T = 2
πr/v and the velocity by
Now
so that
solving for the radius shows that the allowed radii
1 are
By choosing
where
h is Planck’s constant, then the possible radii become
which are the Bohr radii.
The imaginary
α1 presented the difficulty, in London’s work, of defining length as a real number. Here real distance, or length, may be defined, and properly should be, in the (
dq0) manifold. Recalling that the definition of the potentials is
it may easily be seen that if
f < 0, then
φk becomes imaginary as does the length of arc in the (
dσ)
2 manifold since the length of arc is given by
However, the arc length in the (
dq0)
2 manifold is real since
dq0 ≥ 0 by the Second Law.
It should be noted that the conditions for quantization are not restricted to = 0, dq0 = 0 , and f < 0 as used here. Any set of conditions which results in the final element of arc (dσ) being equal to the initial element of arc (dσ)0 results in quantum conditions. It is particularly significant to note that the quantization involves only forces which may be described in terms of the ”distance curvature” and does not involve forces describable by a vector curvature. Thus interpreting the gauge potentials φk to be electromagnetic potentials provides quantum effects for electromagnetic forces.
Here, again, is a distinction between curved and Euclidean manifolds, though here it appears slightly different. Isomentropic systems require quantization. However, this quantization depends upon the existence of a gauge function and appropriate restrictive conditions. Thus a curved space may exhibit quantum effects but only if the curvature is accompanied by a gauge function or a distance curvature.
Thus this theory, through London’s quantization, not only supports the contention that ”God does not play with dice all the time” but, further, may supply the answer to the question, ”What is waving in the wave function?” London showed that the wave function is directly related to the element of the arc length in the sigma manifold. Therefore the ”waving” is the tendency of this element of arc length to increase and decrease around a closed path. Using the calculus of complex variables, the quantum number becomes the order, or multiplicity of the zero of (dσ). This may also be stated in terms of null trajectories. Einstein’s null trajectory was the path light travels and remains so here. However, this is the zeroth order null trajectory. The remaining null trajectories for the complex arc length are given, as London showed, by the equations of Quantum Mechanics.
5 Conclusions
The following are among those conclusions that may be made from the forgoing:
1. The thermodynamic laws require Einstein’s postulate concerning the constancy of the speed of light,
2. The thermodynamic laws provide a metric through the stability conditions that lead to the space-time manifold of Einstein’s Special Theory of Relativity when the mentropy principle is used,
3. The thermodynamic laws require not one, but two manifolds for a complete description of an event and the theory requires that one be a Riemannian and the other be a Weyl space,
4. The thermodynamic laws require that the equations of Schrödinger’s quantum Mechanics be used for stable isomentropic states and that these quantum states are null trajectories in a Weyl space, and
5. Neither the Special Theory of Relativity nor Weyl’s Quantum Principles are the primitive concepts they are currently thought to be.
6 Non-Singular Gauge Potential
Weyl first proposed his gauge factor in his 1918 attempt to embed electromagnetism into geometry[
36]. Schrödinger noticed that for a large number of systems satisfying the Bohr-Sommerfeld quantization conditions, the exponent of the non-integrable Weyl factor
became quantized[
31]. He also showed that, if the unit of quantization was taken to be imaginary with a magnitude of Planck’s constant, then the Weyl factor was unity. London showed that the Weyl factor was proportional to the Schrödinger wave function and that, if one knew the gauge potentials appearing in the exponent of the Weyl factor and asked what paths are allowed if the exponent were to remain quantized, the paths allowed were those given by Shrödinger wave mechanics[
20]. Though London’s reinterpretation was tentative, Weyl seized upon it and presented a formulation in a 1929 paper that is considered a classic, was complete and went further to propose that electromagnetism could be
derived from the gauge potential[
38]. In this paper, Weyl introduced a special case of Noether’s theorem, which displayed the analogy between energy-momentum and electromagnetic conservation laws and, thereby, made the result familiar to physicists in the context of field theory.
Many scientists have engaged in gauge theory research as a result of this initial work. These researchers have given numerous invaluable contributions to the field. However, the synopsis above is sufficient to display that the basis of quantum gauge theory began with the concept of quantized motion. London showed that the solutions to Shrödinger’s wave equation determined the paths that were allowed, while Weyl’s gauge factor remained unity and its exponent quantized. This provided a description of quantized paths or motion.
The exponent of the gauge factor may be thought of as having three parts: an integrand (which are the gauge potentials), a path (which is given by the differentials) and an integral value (the result of integrating the integrand over the path). Thus, while London showed that the equations of quantum mechanics gave the paths allowed by a quantized exponent provided the gauge potentials were known, another question may be put to the exponent with equal expectations with regard to the descriptions of physical phenomena.
Particles exhibit quantized potentials, and it is the interactions of a particle with electromagnetic fields that establishes the identity of a particle. If this identity is to persist in time and through movement in space, the identifying gauge potentials must be independent of this motion. Consider the question of what gauge potentials are allowed which are independent of the path and satisfy the quantum condition of the exponent? The gauge potentials sought must satisfy where the i on the right hand side indicates an imaginary value and the summation convention is to be applied to the j’s, Here N has been used to distinguish the gauge potential quantum number from the previous orbital or path, quantum number, n. If the gauge potentials are to be independent of the dxj then all of the path elements may be chosen to be zero except a single arbitrary dxj. Therefore, the gauge potentials must satisfy the condition that , where now the summation convention is not used and each gauge potential is quantized by the value Nj.
When φ0 is identified with the electrostatic potential, as is done in quantum mechanics, the quantum number, N0, quantizes the charge of the electrostatic potential. Therefore, the same quantum condition that Schrödinger, London, and Weyl used to quantize the paths allowed by a unity scale factor also quantizes the gauge potentials allowed for the particles! One of the first results of this quantization of electric charge may be seen when using Weyl’s derivation of the electromagnetic fields. Fields which are given as ∂jφk − ∂kφj = Fjk are quantized by a difference in the gauge potential quantum numbers. Quantized gauge fields may have negative quantum numbers even if all gauge potential quantum numbers are positive.
Further, since these fields must satisfy Maxwell’s field equations, the dependence of the gauge potentials upon space may be determined using the technique of seeking a solution that is the product of functions of the independent variables. When this assumed solution is tried in the Maxwell equation ∇ • B = 0, and the variables are separated, the differential equation for the radial dependence of the quantized, particle gauge potential is found to be where fr is the unknown function of radius, r. The solution to the differential equation is the nonsingular function where the subscript in the exponent indicates that the exponent depends upon the particle’s gauge potential quantum numbers and may, therefore, be different for different particles.
Forces of interaction between two particles which are the negative slopes of this type of nonsingular potential, given the same λN for each particle, change their sign when the separation r equals λN, since force is proportional to . Therefore, particles, which have repulsive long-range interactions, must have attractive short-range interactions.
Particles with different λN will have forces that do not obey Newton’s third law as the force on one particle due to the presence of a second particle will vanish when the separation equals λ2. While the force on the second particle due to the presence of the first particle will vanish as at a separation of λ1.
Consequences of such interactions are worked out below and appear to have no need for renormalization, as might be expected of a non-singular potential. Also, the interactions between unlike particles,
, must be solved as a two-particle system which appears to reduce to well-known bilinear forms[
4,
27,
51,
33,
34] upon applying appropriate restrictive assumptions, such as all motion is assumed to be motion
about the center of mass or all motion is assumed to be
of the center of mass.
7 Using Newton’s Equations of Motion
A non-singular, electrostatic potential of the form
, where the
λ may be different for each particle, would not satisfy Newton’s third law concerning equal and opposite forces for all separations,
r, and would necessitate revisiting all of the equations of motion concerning the interaction of unlike particles. An investigation of the equations of motion may start with the well-known change of coordinates which allows one the see the motion about the center of mass,
where the small
r’s represent vectors to each body, or between the bodies, and the capital
R represents the vector to the center of mass of the two bodies. Of course the inverse transformations associated with the transformation contained in Equations (26) exist and are the usual ones associated with the center of mass (COM) approach.
By using the COM approach and writing the low velocity limit of the equations of motion (EOM), we find
where the superscripts
i and
e represent internal and external forces respectively and theˆdenotes a unit vector. By using the standard definition for the total mass,
M =
m1 +
m2, and the reduced mass,
µ = (
m1m2)
/M and setting all external forces to zero, Equations (23) may be put into the form
The EOM of Equations (24) display the effect of Newton’s Third Law on the two-body problem. Should Newton’s Third Law hold in both magnitude and direction then the first equation shows that the force on the COM vanishes while the two forces, which must remain separate when Newton’s Third Law does not hold, becomes a single-force statement without any reference to the mass of the bodies. Further, the first equation gives the motion OF the COM while the second equation gives the motion ABOUT the COM.
Many other conclusions might be pointed out concerning Equations (24). However, it may be of more interest to specialize the forces appearing in the EOM to those of the electric forces between electrically charged particles that exhibit the non-singular potential above. These forces have two traits that have important consequences. First, they depend only upon the separation of the two bodies. That is, the magnitude of the forces depend upon the separation distance, while the direction of the forces are on a line between the bodies. This means that they have ”central force” properties. Secondly, they are the result of taking the gradient of a potential. They are not, however, conservative forces in the classical sense for that would include the assumption of Newton’s Third Law.
Though the following presentation will use symbols of general forces it may be useful to display here the functional dependence of the forces that the non-singular potentials produce. The force on body one due to the presence of body two is
while the force on body two due to the presence of body one is
Equations (25) and (26) exhibit the property that at large separations they approximately obey Newton’s Third Law, but as the separation approaches the larger of the λ’s they begin to severely depart from Newton’s Third Law. Therefore, these two forces cannot be combined into a single central force as is done in classical mechanics, nor can their potentials be combined into a single potential.
Additionally, these forces display the attribute of central forces since they each have the form
One of the attributes of central forces is a constant angular momentum since the torque is
Therefore,
From Equation (29) it may be seen that since the total angular momentum must be a constant, then both the vectors
r and
v must lie in a fixed plane perpendicular to the angular momentum,
L.
The total angular momentum about the origin is given by
Then, using the EOM, Equations (23), with vanishing external forces,
Equation (31) may be written in terms of the COM coordinates to find
By using the forces given by Equations (25) and (26) then Equation (32) becomes
from which it may be seen that there are two ways for the change in total angular momentum to vanish. The first is that
λ1 =
λ2 and the second is for the COM to be on the line defined by the two bodies. This requires that, for two distinctly different bodies, their motion must have a total angular momentum that is constant with respect to some point in the plane determined by the positions of the two bodies and this point may be taken as the origin. Further, both bodies must be on a line with the angle
θ, or
θ +
π, in this plane. The significance of this is that Equation (32) requires that, not only must the total angular momentum be constant in time, but so must the angular momentum
ABOUT, and
OF, the COM.
By using this result together with the EOM, Equations (23) and (24), with the force laws, Equations (25) and (26), the Conservation of Energy, and transferring to the cylindrical coordinates typical of motion for central forces, it may be shown that the energy, which is a constant of the low velocity motion, becomes
where
K +
V is the energy of
ABOUT the COM and
Kc +
Vc is the energy
OF the COM. In Equation (34), the parts are given by:
where
k = (
Z1Z2e2)
/(4
πε0).
Now one may assume circular orbits for both the COM and motion about the COM and assume that both orbits have quantized angular momentum to obtain an expanded Bohr model of the two-body problem, which may be shown to be
with
nθ being the quantum number for the motion about the COM and
nc being the quantum number of the motion of the COM and the functions of lambdas are given by the definitions
By putting Equations (37) in this form, it is easy to see that the vanishing of the lambdas reduces Equation (36) to the classical energy equation of Bohr’s theory.
The first-order approximation to the Bohr energy levels may be found by assuming that
λ1 = 0 and
λ2 is very small compared to
r in Equations (35) and (37). Keeping only terms of the first order of
λ2/r negative cube roots are avoided and yields the first approximation of the energy as
For the atomic hydrogen atom ionization energy a
λ2 of 1 fermi produces a prediction of the energy level that is approximately 2×10
−5 different from Bohr’s model. Comparing this to the statement of experimental error of 5 × 10
−5 makes it important to redo the ionization energy with reduced experimental error[
16].
8 Using Schrödinger’s Wave Equation
An expanded Schrödinger-like wave equation may be developed using similar assumptions that Schrödinger used[
32]. To be consistent with the energy expression of Equation (34), the de-Broglie relations for motion about the COM and for motion of the COM must be used. When this is done, and the required linear behavior and free system limit is met, the resulting wave equation ends up being
The time-independent, expanded wave equation in cylindrical coordinates is then
where the potentials are those in Equations (35).
The estimate of the difference in prediction between the Bohr energy levels and the similar predictions of the non-singular potentials was 2 × 10−5 . In order to compare the energy levels with the Schrödinger energy levels the potentials of Equations (35) should be used in Equation (40).
The vector equation of Equation (40) may be solved by the method of separation of variables. First, by trying a solution of the form, , one finds that Equation (40) separates into two sets of three equations each where one set depends upon (r, θ, φ) and the other set depends upon (R, Θ, Φ). The separation constant, Ec, is related to the COM kinetic energy.
The two sets of three equations may be separated further by trying and . The solutions for ΨΘ and ΨΦ are identical to the solutions for Ψθ and Ψφ respectively with the separation constants mL and L corresponding to the separation constants and .
The equation for Ψ
r becomes
Recognizing the potential difficulties of obtaining solutions with both
V(
r) and
Vc(
r) having transcendental terms, an investigation of the influence of the non-singular potentials may be conducted by assuming
and
.
Following the method of solving Schrödinger’s time-independent equation, the following definitions:
and
together with the trial solution,
requires that two relations must be met; namely
and
In order to satisfy
s ≥ 0,
where
Further, the series will terminate if
γ −
δ =
n is an integer. The solution may then be put into the form
The COM radial equation has no potential terms and is
This equation has a Bessel function solution of the form
This solution does not fully establish the value of
Ec. This value can be determined, but is not done here, by considering that Equation (33) requires that
.
9 Using Relativistic Quantum Mechanics
To obtain a Lorentz covariant EOM, one must begin with a Lorentz covariant relation between energy and momentum[
7,
25]. In special relativity, the energy,
E, momentum,
p, and rest mass,
m, of a free particle are connected by the relation
Defining the four quantities
and the corresponding quantities
shows that the quantity
PµPµ is a Lorentz scalar. Using the summation convention, Equation (41) becomes
For two free particles taken together as a system, the energy, momentum and mass should all be additive, that is
For the two particle, free system, Equation (46) becomes
or
Equation (43) leads to a free system Klein-Gordon equation of the form
as the 2-particle, free system Klein-Gordon equation.
Equation (44) allows us to use natural units where the units of action and the speed of light may be set to unity.
Standard procedure of relativistic quantum mechanics allows one to seek a wave equation of the form
where
H is the system Hamiltonian.
A necessary (but not sufficient) condition that Equation (45) be Lorentz covariant is that the Hamiltonian,
H, be linear in the spatial derivatives. When the Hamiltonian of the two body system is
For free particles, there is no distinction between the
α’s and
β’s, and the system’s Hamiltonian would be given by
when there is no interaction between the particles.
The properties of the
α’s and
β would then be the same as developed classically or
In the x-representation, the Hamiltonian equation becomes
where Ψ(
x) =
< x|
> .The two independent particle, free system Hamiltonain obeys the free system relativistic energymomentum equation, but the requirement of Lorentz covariance has not yet been imposed on the system.
Multiply Equation (47) on the left by the matrix
β and remembering that the total Hamiltonian in Equation (46) is the sum of the Hamiltonian of each particle, results in
Equation (48) may also be written as
where
.
All inertial observers must agree on Equation (49). Now the properties of the matrices are the same as in the classical case in that
and
Just as under the Lorentz transformation,
each component of a vector transforms into a linear combination of all components, also require that each component of the wave function transforms into a linear combination of all four components; i.e.,
where the symbol
means ”transform under a Lorentz transformation into...”.
S must be a 4 × 4 matrix. An inverse transformation is required to exist or
S−1S =
SS−1 =
I.
Now if Equation (49) is to be Lorentz covariant we must require that
where
so that the primed and unprimed inertial observers agree on the form of the Hamiltonian.
To obtain Equation (50) from (49) one must write
and
Putting these into Equation (53) gives
Multiplying on the left by
S then gives
which would be identical to Equation (54) if
and
The Lorentz transformation should be the same for both particles so that and then the spinor transformation is identical to the classical case for each particle and each leads to the same condition that must be imposed on the S matrix in order that the two particle Dirac equation be Lorentz covariant.
Notice that, by considering the two particles as a system, the total system angular momentum includes the total angular momentum of both particles and is to be conserved.
Now consider the situation where the two particles making up the system interact with each other with forces which do not only obey Newton’s Third Law yet neither body interacts with system’s surroundings.
Therefore, consider the substitution
in the two particle, non-interacting, free system Hamiltonian. In the x-representation, this becomes
so that the Equation (49) becomes
Equation (51) may also be written
where
is the transpose of
.
When e1 is the electric charge of the first particle, e2 is the electric charge of the second particle, A1 is the potential of the first particle, and A2 is the potential of the second particle, then Equations (51) and (52) should describe the interaction between the two bodies making up the system which does not have any interactions with its surroundings.
Consider the problem to be separated into the motion of the COM and the motion about the COM. Then subscript 1 ⇒ r, θ, φ with A1µ(r, θ, φ) and A2µ(r, θ, φ) and subscript 2 ⇒ R, Θ, Φ.
Recalling that one of the requirements on the free system Hamiltonian was that its solutions also be solutions of the free system Klein-Gordon equation, it should be of some interest to see whether or not the solutions of Equation (52) are also solutions of the corresponding Klein-Gordon equation. Since the Klein-Gordon equation is a second-order differential equation, whereas the Hamiltonian is of first-order, it will be necessary to operate on the latter with first order differential operators in order to cast it into a form similar to the Klein-Gordon equation. If we operate on the left of Equation (52) with the operator
we obtain
The corresponding Klein-Gordon equation comes from Equation (44) with the substitution
∂µ →
∂µ −
eAµ. Then we would have
We notice that in Equation (53) we have
where
which may be shown to be
. But
Now let
, then look at
Therefore, Equation (55) gives us
.
On the other hand
σij = −2
iSk (
i, j, k cyclic), but with two particles in the system this should be written
Putting Equations (54-56) into Equation (53) we find
or
Most of the terms involving the matrices σµν vanish. This is because the scalar product of a symmetric and an anti-symmetric tensor vanishes. That is, if Sµν and Tµν satisfy Sµν = Sνµ, Tµν = −Tνµ then SµνTµν = 0.
In Equation (57), the quantity
σµν is anti-symmetric under interchange of
µ and
ν. The terms involving −
ie1∂1µA2νσµνΨ(
x) = −
ie1σµνΨ(
x)(
∂1µA2ν) −
ie1A2ν∂1µσµνΨ(
x) are also antisymmetric. Now let us write out the coefficient of
σµν in Equation (57):
Obviously the terms
, and
are symmetric so they may be dropped. Combining terms leads to
The terms −(
∂1µ∂2ν +
∂2µ∂1ν) and
e1e2(
A2µA1ν +
A1µA2ν) are symmetric under an interchange of
µ and
ν. The following is left
Using
leads to
In the last four terms the coefficients of
σµν are symmetric in an interchange of
µ and
ν so only the first two terms remain. These may be written in symmetric and anti-symmetric form since
Only the anti-symmetric part will survive. Rewriting Equation (57) as
Defining
this may be written as
Equation (58) appears to be a very interesting equation. Typically the fields
Fµν =
∂µAν −
∂νAµ are identified as the electromagnetic field and the result is the Klein-Gordon equation with fields. Here the derivatives and gauge potentials are mixed so care must be taken when interpreting the terms. Also remember
or this may be written as
.
Notice that should both particles have spin ±1/2 the total system spin, which is S = S1 + S2 = SθIθ, must take on the values −1, 0, or 1, similar to the values allowed for isospin. A system with three spin 1/2 particles would take on values of −3/2, −1/2, 1/2, or = 3/2.
Perhaps Equation (58) may best be understood by considering the motion ABOUT the COM and the motion OF the COM as being our two motions. Further, consider the two particle system for which the potentials of Equations (35), hold. Now consider the two extremes of, first, the motion OF the COM is small compared to the motion ABOUT the COM. This would be the case when the particle separation is large compared to the larger of the λ’s. In this case it may be seen that, in Equation (35), the COM potential vanishes, and the remaining potential about the COM approaches the classical electrostatic potential. Further, Equation (52) collapses to the classical Dirac equation for the motion of a particle in the field of another. Next, consider the case when the particle separation is of the order of the two λ’s and the motion ABOUT the COM may be neglected. In this case the potential ABOUT the COM is being driven to zero by the exponents while the potential of the COM is becoming dominant. Notice that the potentials at large separations produce a dominant negative potential, as in the hydrogen atom. Separations of the order of the λ’s produce a very sharp positive potential which returns to zero as the separations become less than the smaller of the λ’s. This sets up the condition whereby the COM may be trapped in a positive energy well from which it may escape through tunneling.
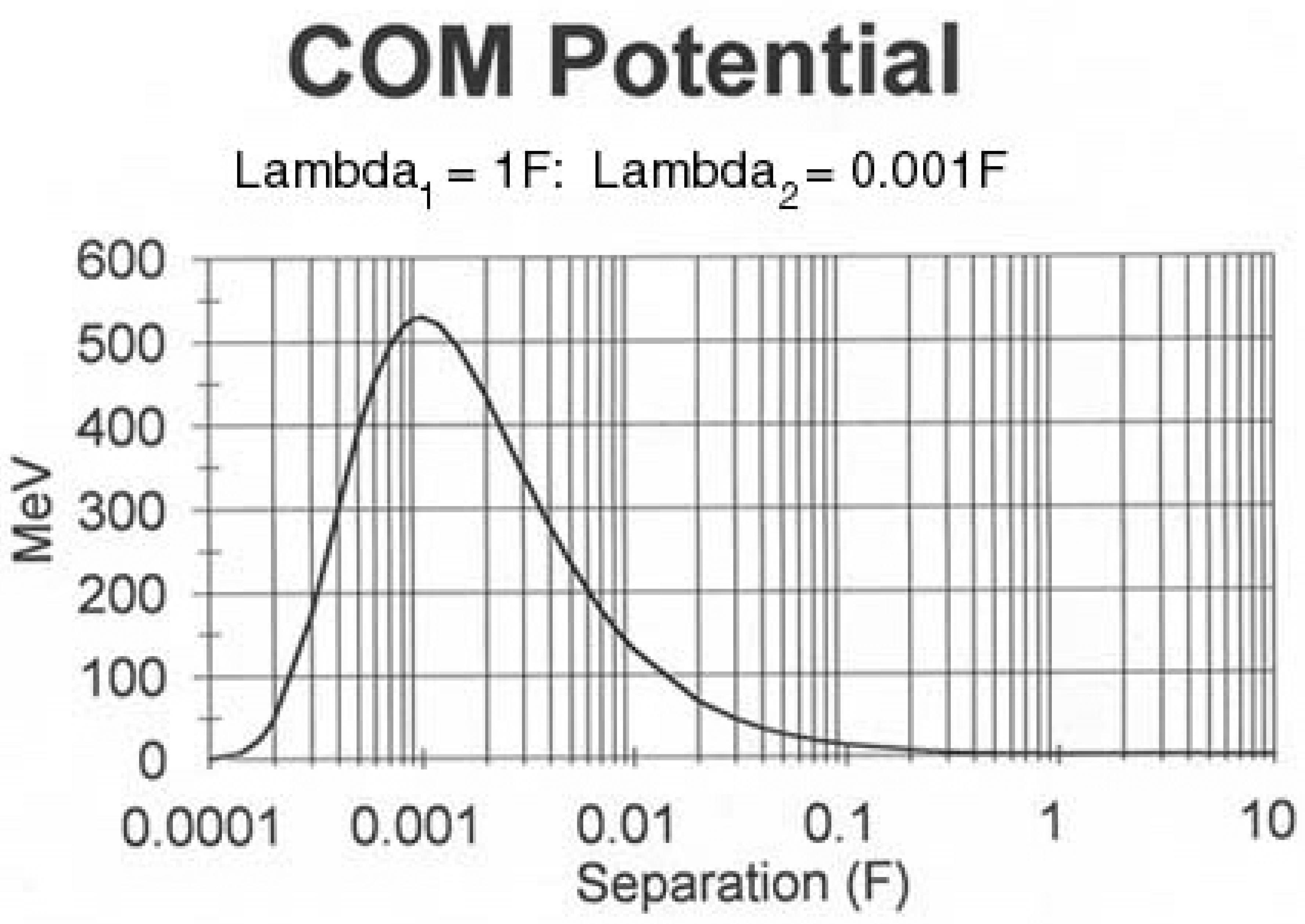
In order to see this conclusion, consider the plot of the potential of the center of mass in Equation (39),
Vc in
Figure 2.
Consider the extension of the above to a system of three particles interacting yet having no outside fields influencing their motions. This would lead to the three momenta
or
with the definition
, where
θ,
β, and
γ are cyclic. Then Equation (52) may be written
where
θ,
β, and
γ are cyclic. By defining
Equation (58) becomes
where
θ,
β,
κ, and
η range from 1 to 3 and
θ,
β, and
η are cyclic.
Equation (60) represents the Klein-Gordon equation for three particles when one particle is different from the other two. However, for three like particles it remains valid, but has some terms that vanish due to the equal and opposite forces.
The extension to N particles should follow readily and would provide for solving the internal motions of a system made up of N particles interacting relativistically with each other in the absence of external forces. The discussion of the two-particle system above led to the conclusion that when, all motion is taken to be motion OF the COM, the potential well formed was a positive energy well which would allow the calculation of the lifetime of the state. This would argue that an N-particle system, for which the COM is required to move, that any bound state of the COM might also be trapped in a positive energy well. The lifetimes of these states would then be subject to calculation.
10 Gauge Fields and Gravity
The preceeding sections have shown how the Dynamic Theory, through Weyl’s quantum principle, leads to a non-singular electrostatic potential. A unification of the electromagnetic and the nuclear forces was then required by this non-singular potential. Further, it should be noted that the only geometry that has been discussed was related to Weyl’s geometrical gauge function. A geometrical gauge function produces gauge forces but does not produce, or is not produced by, a Riemannian curvature. Therefore, the gauge forces discussed in the previous sections cannot incorporate gravitational forces that are described by a Riemannian curvature.
However, the first and second laws that provide the basis for the predictions of the previous sections are not limited to a specific number of work terms. They would provide an equally powerful and consistent basis for a five dimensional theory as for one in four dimensions. This sections briefly displays the use of the laws in a five dimensional space and shows how a restriction on a manifold with only gauge forces can lead to forces described by a Riemannian curvature.
Several researchers used an extension into five dimensions in their search to unify the electromagnetic, nuclear and gravitational forces[
18,
35,
26,
15,
14,
8,
22]. However, in each of these attempts, the real world was thought to be described in the four dimensions of space and time and the fifth dimension was used in order to get additional degrees of freedom to work with in their search for the unifying field. On the other hand, numerous researchers used the basis of quantum mechanics in their research into the unification of the various forces of Nature[
36,
31,
20,
38]. Neither approach has produced the desired unification.
Consider combining these two areas of research in the following manner. Let a five-dimensional manifold have some physical reality in all five dimensions. The first four are the four of space and time as used in Einstein’s General Theory of Relativity. The physical manifestation of the fifth dimension is to be learned during this investigation. Whatever the fifth dimension turns out to be, requiring it to be conserved will embed a four-dimensional hypersurface into the five-dimensional manifold.
The starting point of this investigation is the exponent of the non-integrable Weyl factor
. The quantum principle requires this exponent to be quantized as in
where the
i on the right hand side indicates an imaginary value and the summation convention is to be applied to the
j’s. Here the indices are to be considered to range from 0 to 4, with 0, (1, 2, 3) and 4 representing time, space and the new fifth dimension respectively. Just as Weyl showed the gauge fields may be derived from these gauge potentials and the components of the 5-dimensional field tensor may be written in matrix form as
For simplicity, all the field components may be set to zero except for the
V0 component. The surface field tensor will be given
where
for
i = 0, 1, 2, 3 and
. The space indices,
i, j, k range over 0, 1, 2, 3, 4 while the surface indices
α, β, η, ν only take on values of 0, 1, 2, 3. The surface metric is found from
where
.
The space energy-momentum tensor for matter under the influence of gauge fields is given by
![]()
and may be written in terms of the surface metric as
![]()
since
![]()
![]()
is the statement required by the conservation of the fifth dimension.
The surface energy-momentum tensor may now be found within the space tensor and written
![]()
. The form of this expression for the surface energy-momentum tensor suggests writing
which, of course, look like the field equations of Einstein’s General Theory of Relativity, when Equations (61) are taken to be Einstein’s field equations,
where
κ is the gravitational constant. Then the field
V0, which is the only non-zero field component considered, must be related to the gravitational field and the fifth gauge potential must be related to the gravitational potential. Therefore, the physical reality of the fifth dimension is gravitating mass or its equivalent, mass.
11 The Gravitational Schrödinger’s Equation
The preceding section showed that the conservation of mass embeds a four dimensional hypersurface within a five dimensional manifold of space, time and mass. It was also shown that the description of the surface must obey Einstein’s equations of his General theory of Relativity. A description may also be obtained from the surrounding five dimensional manifold. Weyl’s Gauge Principle has been applied to the four dimensional, non-integrable manifold to specify a description of motion for which the gauge is a constant. The same may be done in five dimensions. In the case where the electrostatic potential is taken to be zero, a non-zero, non-singular gravitational potential may be left which has the same dependence upon radial distance as the electrostatic potential previously discussed. Then Weyl’s Principle applies to this potential when integrable paths are desired and it should be no surprise that the same logical approach produces a gravitational Schrödinger-like equation where the only differences are the use of the gravitational potential and a gravitational unit of action.
When this is done, and the required linear behavior and free system limit is met, the resulting gravitational wave equation ends up being
The time-independent, expanded wave equation in cylindrical coordinates is then
where the potentials are gravitational potentials of the same form as the electrostatic potentials in Equations (35).
The vector equation of Equation (63) may be solved, just as before, by the method of separation of variables. First, by trying a solution of the form, , one finds that Equation (63) separates into two sets of three equations each where one set depends upon (r, θ, φ) and the other set depends upon (R, Θ, Φ). The separation constant, Ec, is related to the COM kinetic energy.
The two sets of three equations may be separated further by trying and . The solutions for ΨΘ and ΨΦ are identical to the solutions for Ψθ and Ψφ respectively with the separation constants mL and L corresponding to the separation constants and .
The equation for Ψ
r becomes
Recognizing the possible difficulties of obtaining solutions with both
V(
r) and
Vc(
r) having transcendental terms, an investigation of the influence of the non-singular potentials may be conducted by assuming
and
.
Following the method, previously used for solving Schrödinger’s time-independent equation, the following definitions:
and
together with the trial solution,
requires that two relations must be met; namely
and
In order to satisfy
s ≥ 0,
where
Further, the series will terminate if
γ −
δ =
n is an integer. The solution may then be put into the form
The COM radial equation has no potential terms and is
This equation has a Bessel function solution of the form
This solution does not fully establish the value of
Ec. This value can be determined, but is not done here, by considering that Equation (33) requires that
.
11.1 Limiting Case Solutions
In the limit where
λ1 =
λ2 = 0, it may easily be seen that the above solution collapses back to a solution for the gravitational problem just as the solution for the electrostatic case. That is, in solving the Ψ
φ(
φ) equation, we shall find that the equation has acceptable solutions only for certain values of m
l. Using these values of m
l in the equation for Ψ
θ(
θ), it turns out that this equation has acceptable solutions only for certain values of
l. With these values of
l in the equation for Ψ
r(
r), this equation is found to have acceptable solutions only for certain values of the total energy,
E; that is, the energy of the gravitational orbits is quantized! In exactly the same manner as in the atomic case, the angular momentum and the energy are both quantized functions. This fact allows one to write
These equations provide the elliptical solutions familar to planet orbits. There the semi-major axis is given by and the eccentricity may be found as . From the expression for the eccentricity, one may anticipate that this property of planetary orbits will not be quantized.
For the quantum numbers n, l and ml, there are many possible quantum states to find the planetary orbits to be in. The solar system with all the planets and comets may also be considered as a multi-planet system with all the similar potential relations between the planets as has been seen for the multi-electron atoms. Here there is an increased complexity and richness of possibilities in the differing properties of each planet. These solutions may allow classifying stars in the universe as the atoms are now classified; that is, there may be a periodic table of stars.
Those who have not read of the data supporting the quantization of the solar system may wish to look in Dr. Halton Arp’s book ”Seeing Red” published by Apeiron (1998). The quantized orbits of the planets, taken individually as a single planet system, would show quantized semimajor axis as . If the experimental value of an for the Earth is taken with the Earth’s quantum number, 5, then the value of the gravitational unity of action for the solar system would be J-sec.
The red shifts due to the five dimensional, time dependent, non-singular gravitational potentials has been worked out[
48]. When these are taken to be quantized potentials, one finds the red shifts must exhibit different types of quantization. The quantized red shift relation is
where the subscript
r refers to conditions and time of photon reception and the subscript
e denotes the conditions of the photon emission.
There are now two types of quantization and both may be put into the form of ratios as
![]()
for the quantization associated with the graviational potential where the red shifted light is received, and
![]()
for the quantization of the gravitational potential where the red shifted light is emitted. For the cases where
and
there is some simplification of these ratios. In the limit of a very dense emitter close to the point of reception, one obtains
![]()
. One should expect that a non-singular gravitational potential will have a maximum gravitational potential that can be obtained. Then X would be given by the maximum allowed exponent. On the other hand, suppose one looks at the low red shift limit, where the distance between the emitter and the point of reception dominates. Then one finds
![]()
. From this expression it is easy to see that a cluster of emitters at roughly the same distance will display a quantized red shift according to that distance.
Arp discusses red shift quantization at 72 km/sec periodicity, 32.5 periodicity and quantization such that . The first two might be distance quantization while the later might be the quantized red shifts from emitters near maximum gravitational density.
12 Light Quanta
The presentation to this point has shown how the Dynamic Theory offers a new view of dynamic mechanical systems. Questions naturally arise concerning the predictive ability of the theory that may not be completely answered in the sections above. This section presents an example of how the theory provides new approaches to old problems. The problem chosen is the century old apparent theoretical dichotomy between the wave and particle description of light.
The concept of a photon started with Einstein’s light quanta.[
9] The concept has been the subject of many articles since 1905. The name photon was first introduced by Lewis 21 years later.[
19] However, both Planck’s[
28] and Einstein’s derivations of the famous relation between energy and frequency,
ϵ =
hν, came from studies of radiation in thermal equilibrium with a system described by statistical thermodynamics. In 1917 Einstein wrote, ‘The properties of elementary processes required by [his momentum fluctuation relation] make it seem almost inevitable to formulate a truly quantized theory of radiation.’[
12] Einstein was not, and never would be satisfied, with his and others, inability to obtain such a theory. In 1924, after the experimental evidence of the Compton Effect provided proof of the quantization of light, he wrote, ‘There are therefore now two theories of light, both indispensable, and—as one must admit today despite twenty years of tremendous effort on the part of theoretical physicists—without any logical connection.’[
13]
Weyl’s quantum principle may be used to derive Maxwell’s electromagnetic field equations.[
38] These, in turn, may be used to derive the electromagnetic wave equations. At the same time the quantum principle requires that the gauge potentials be quantized since
where
and there is no summation over the j’s. The radial electrostatic dependence may be investigated by considering N
o to be nonzero and N
x=N
y=N
z=0. The concept of a photon, as a particle, is one that is electrically neutral. The wave description allows the discussion of polarization such that an electromagnetic wave traveling along the x axis may have its electric field directed along the y axis. Then, consider N
o=N
x=N
z=0. The quantum principle requires that the y component of the gauge (vector) potential be quantized, as
where the dependence upon x and t was chosen to be sure that the electric field, given by
, satisfies the wave equations. This expression may be used to find the average value of the Poynting vector, or
. The average value of the square of electric field, over one cycle, is given by
.
Therefore, Now a quantum of light for which N=1 would have an energy flow of I = hν when . Einstein’s energy relation, for a single light quantum passing through a unit area, is then ϵ = hν.
13 Conclusions
The first result displayed was that the quantum principle requires the gauge potentials of particles to be quantized in integer steps. This quantization leads to non-singular gauge potentials, which may be different for different particles. These results argue that the quantum principle provides more information than previously tapped. The appearance of non-singular potentials removes the problems requiring renormalization.
Section VII points out that while the description of two different particles, interacting through their gauge potentials, may not be reduced to a problem of a single particle in an electric field fixed in space, the two-particle problem is solvable.
Section VIII displays a method for solving the Schrödinger wave equation extended so as to describe the interaction between two different particles. Further, this section evaluates the firstorder deviation in the energy predictions between the classical and the non-singular potentials and determines this value to be within the experimental error of past energy experiments.
Section IX presents a relativistic approach to the gauge interactions between unlike particles. The equations for the two-particle system appear as generalizations of the equations currently used in the electro-weak theories. The total spin of the two-particle system appears to play a role identical to that of isospin.
When the three-particle system is addressed, the resulting equations appear as generalizations of the Su(3) group. Again, the total spin plays a role identical to isospin.
There are many possible conclusions these results may support. The more obvious ones might be:
1) the phenomena currently allocated to description by weak nuclear forces may be described by the difference between the non-singular potentials of the particles,
2) the strong force may be due to the non-singular nature of the potentials and not due to an independent force, and
3) isospin is simply the total spin of an n-particle system.
Section X points out that a 5-dimensional gauge field may be described by a 4-dimensional curved surface embedded into the 5-dimensional manifold by an appropriate restriction. The 5-dimensional gauge field in a manifold of space-time-mass derived from the gauge principle, may have a 4-dimensional hypersurface embedded into in by the conservation of mass. On the hypersurface, Einstein’s gravitational field equations must be satisfied. Therefore, there exists three ways of describing phenomena on the hypersurface:
1) a gauge field description from the 5-D manifold of space-time-mass with the restriction of conservation of mass,
2) a geometric surface description using tangents to the surface to form the surface metric (the first fundamental quadratic form of the surface), and
3) a geometric surface description using the normal to the surface to form the surface metric (the second fundamental quadratic form of the surface).
The use of the quantum principle to determine the quantized particle gauge potentials and their non-singular character argues that the weak and strong nuclear forces are the result of this non-singular character. It further argues that the gravitational field is a gauge field linked to the electromagnetic field in a 5-dimensional manifold of space-time-mass, but, when conservation of mass is imposed, it may be described by the geometry of the 4-D hypersurface of space-time, embedded into the 5-D manifold by the conservation of mass.
A photon may be defined as a gauge vector potential with the quantum number set to unity and which satisfies the wave equation. Further, the light quanta comes from Weyl’s quantum principle which also provides the basis for radiation and needs no connection to statistics or thermodynamics. Weyl’s quantum principle provides the logical connection that Einstein was trying to find.
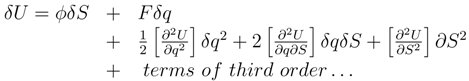

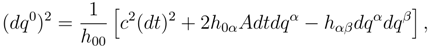


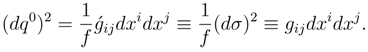

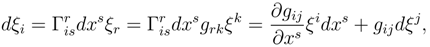


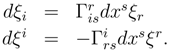
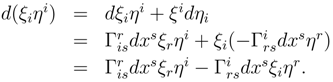
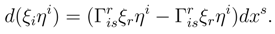
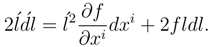

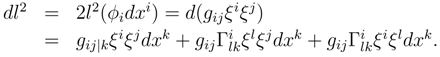
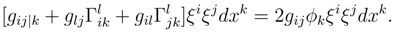
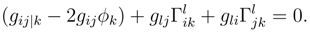
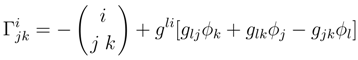
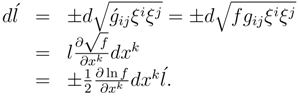

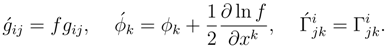
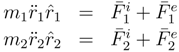



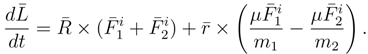
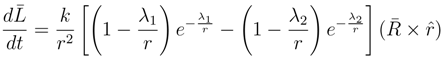
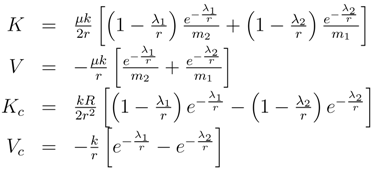

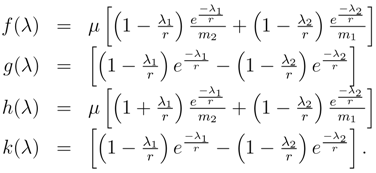





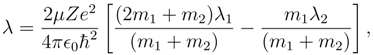
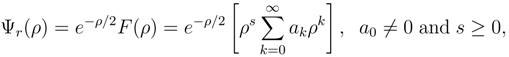
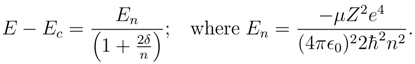
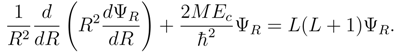
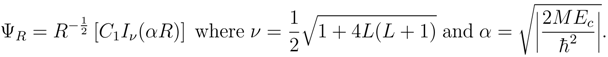

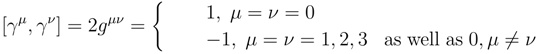


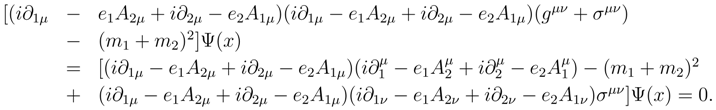
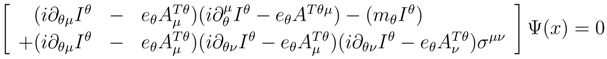

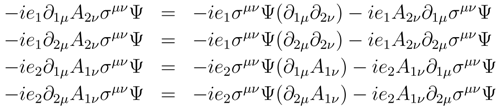

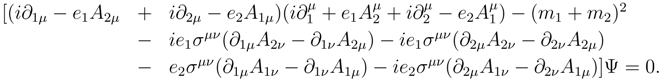

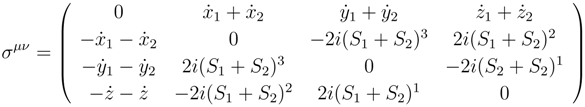
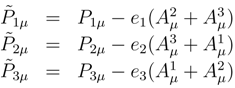
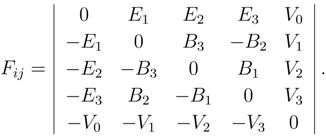
 and may be written in terms of the surface metric as
and may be written in terms of the surface metric as 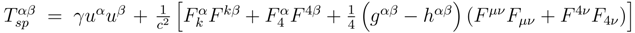 since
since 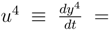
 is the statement required by the conservation of the fifth dimension.
is the statement required by the conservation of the fifth dimension. . The form of this expression for the surface energy-momentum tensor suggests writing
. The form of this expression for the surface energy-momentum tensor suggests writing
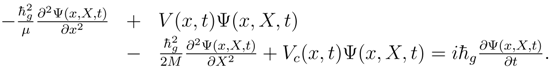

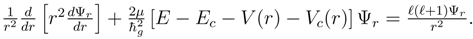
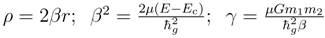
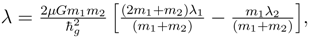
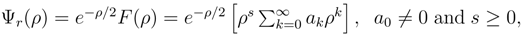
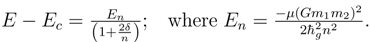
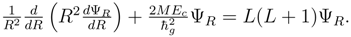
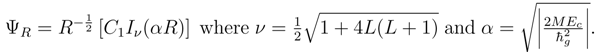

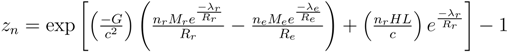
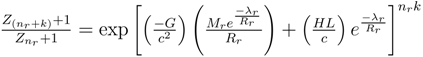 for the quantization associated with the graviational potential where the red shifted light is received, and
for the quantization associated with the graviational potential where the red shifted light is received, and 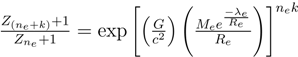 for the quantization of the gravitational potential where the red shifted light is emitted. For the cases where and there is some simplification of these ratios. In the limit of a very dense emitter close to the point of reception, one obtains
for the quantization of the gravitational potential where the red shifted light is emitted. For the cases where and there is some simplification of these ratios. In the limit of a very dense emitter close to the point of reception, one obtains 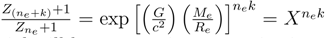 . One should expect that a non-singular gravitational potential will have a maximum gravitational potential that can be obtained. Then X would be given by the maximum allowed exponent. On the other hand, suppose one looks at the low red shift limit, where the distance between the emitter and the point of reception dominates. Then one finds
. One should expect that a non-singular gravitational potential will have a maximum gravitational potential that can be obtained. Then X would be given by the maximum allowed exponent. On the other hand, suppose one looks at the low red shift limit, where the distance between the emitter and the point of reception dominates. Then one finds  . From this expression it is easy to see that a cluster of emitters at roughly the same distance will display a quantized red shift according to that distance.
. From this expression it is easy to see that a cluster of emitters at roughly the same distance will display a quantized red shift according to that distance.