Quantum Computing for Transport Network Optimization
Abstract
1. Introduction
2. Bus Route Optimization Model
2.1. Classical Model of Bus Route Optimization
2.2. QUBO Model and CIM
3. Experiment
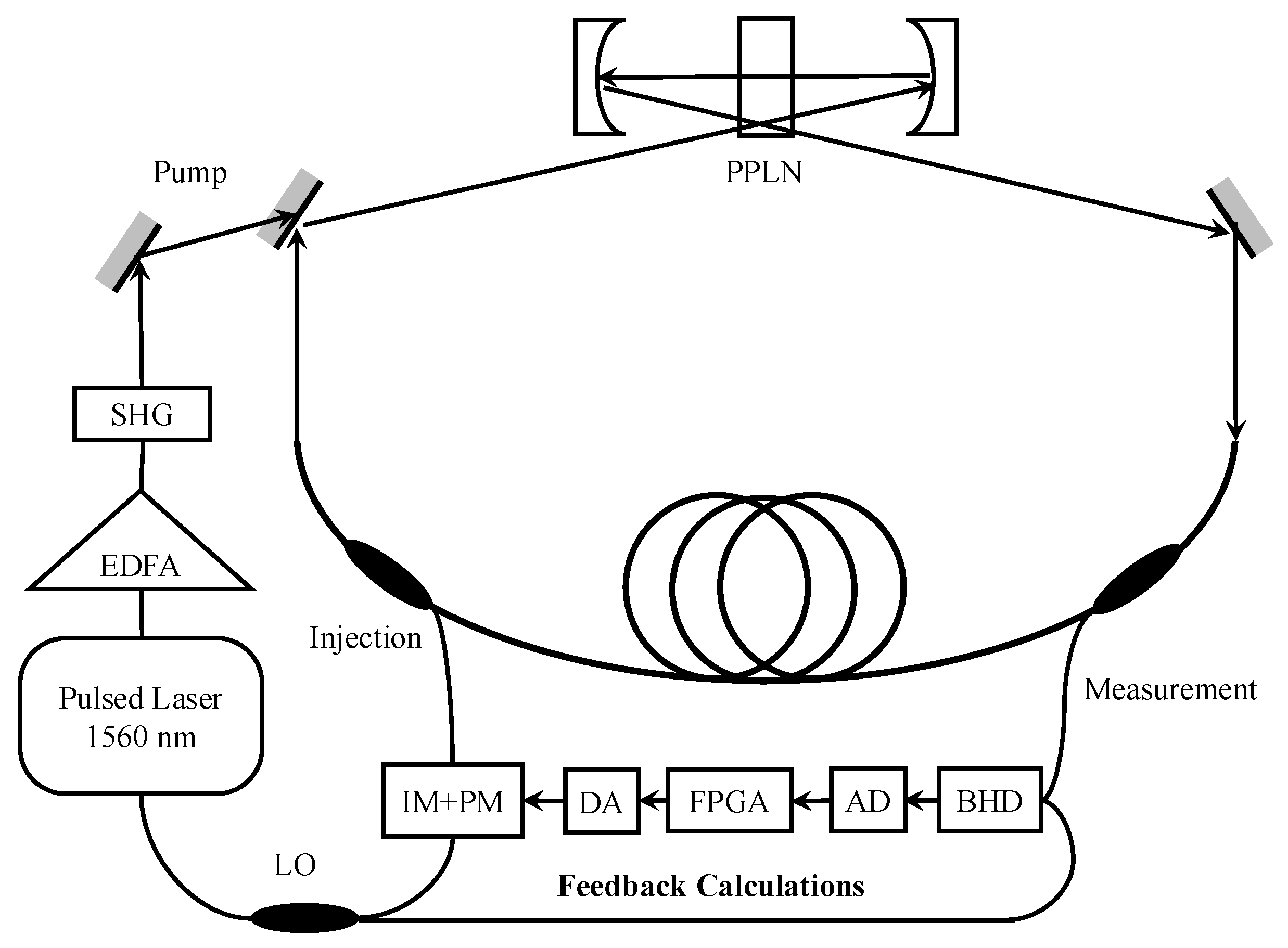
3.1. The Principle of CIM Solving Optimization Problems
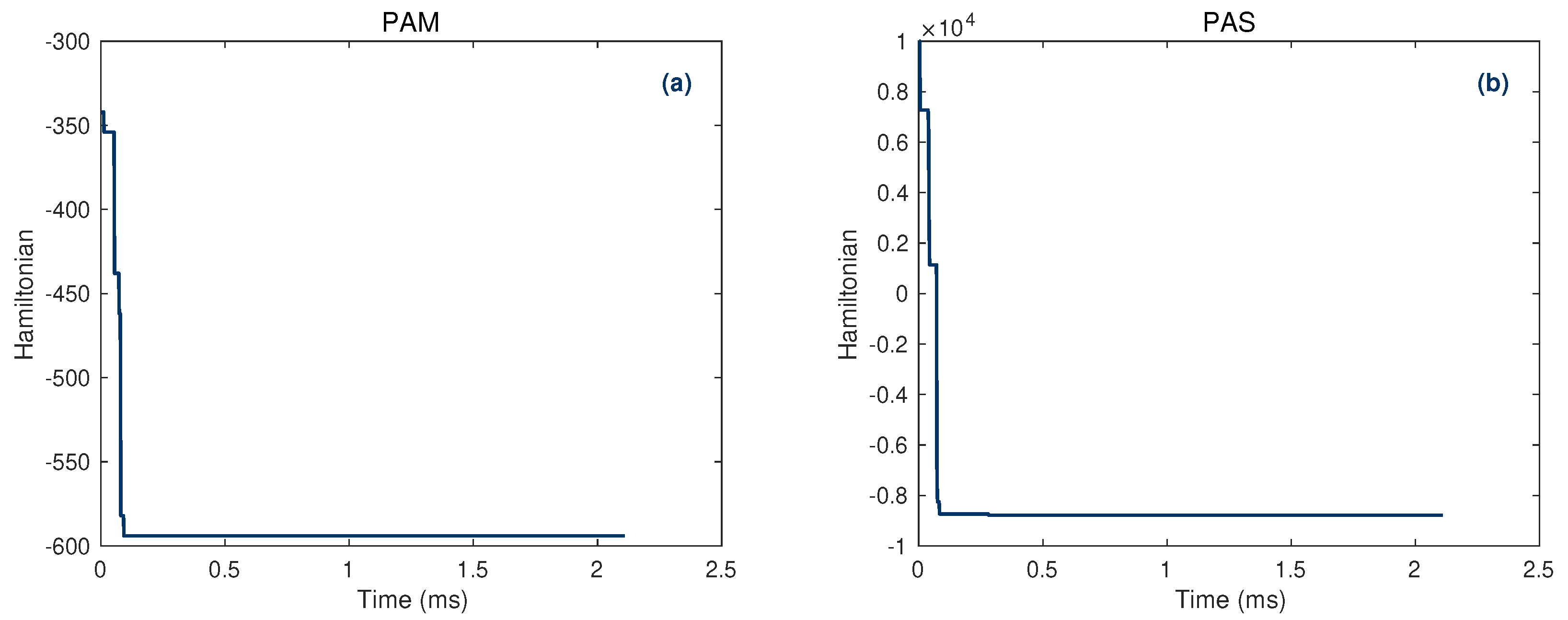
3.2. Experimental Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CIM | Coherent Ising Machine |
| BRO | Bus Route Optimization |
| QUBO | Quadratic Unconstrained Binary Optimization |
| TND | Transport Network Design |
| SA | Simulated Annealing |
Appendix A. The Chosen Routes and Pseudocode
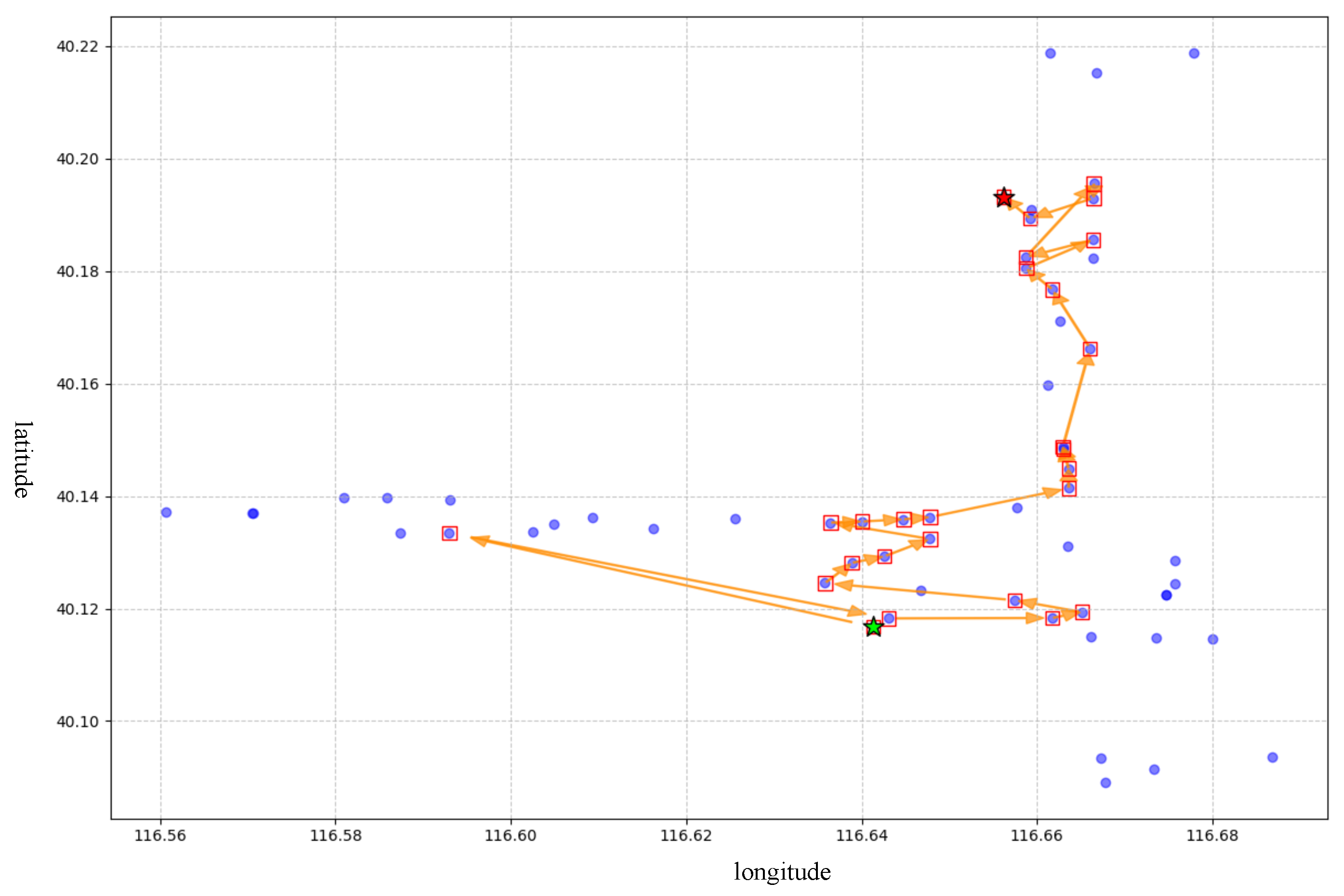
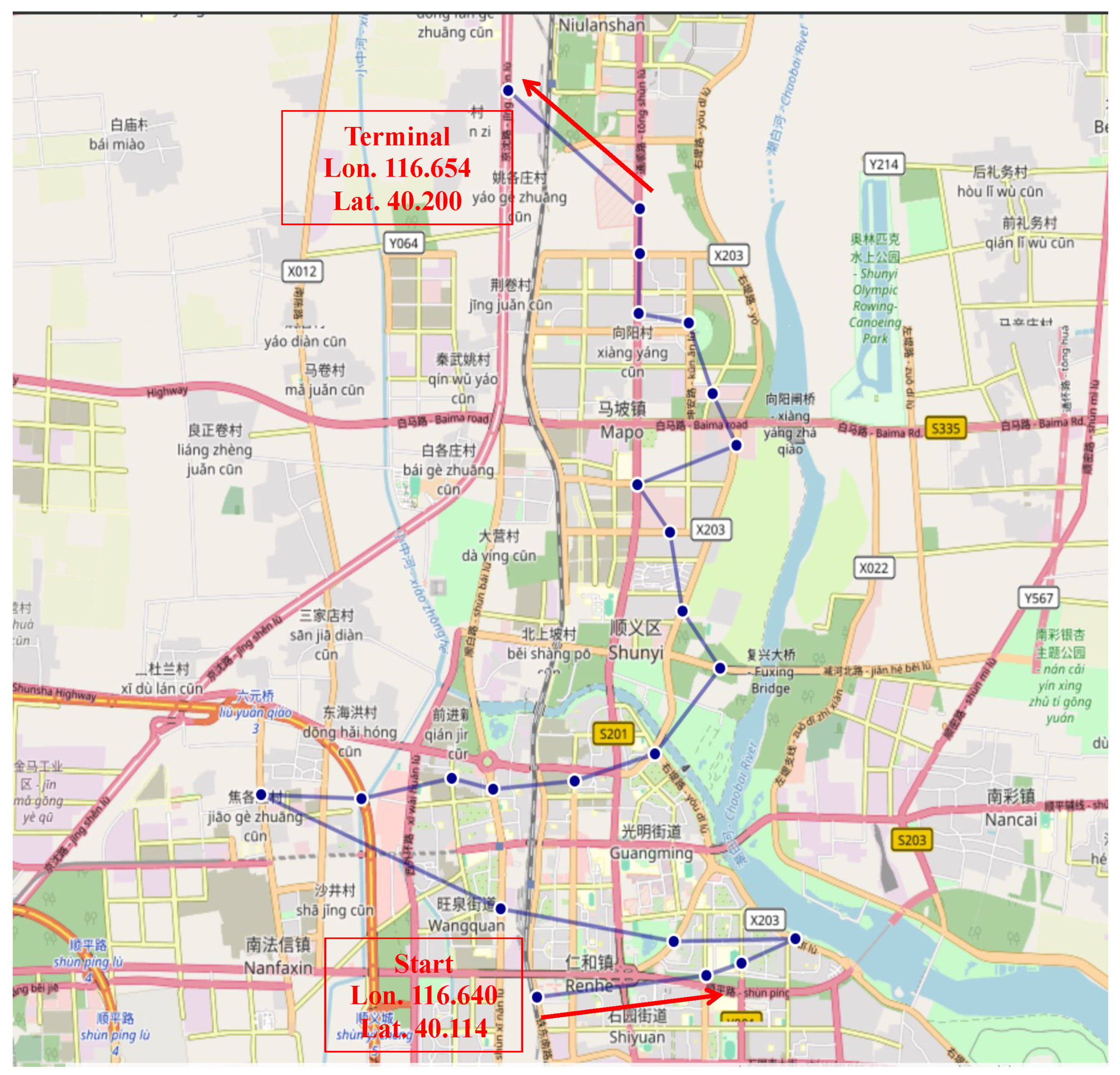

| Algorithm A1 Two-Stage Pipeline: OR-Tools + Gurobi, Simulated Annealing or Tabu search |
|
References
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Boixo, S.; Isakov, S.V.; Smelyanskiy, V.N.; Babbush, R.; Ding, N.; Jiang, Z.; Bremner, M.J.; Martinis, J.M.; Neven, H. Characterizing quantum supremacy in near-term devices. Nat. Phys. 2018, 14, 595–600. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- King, A.D.; Nocera, A.; Rams, M.M.; Dziarmaga, J.; Wiersema, R.; Bernoudy, W.; Raymond, J.; Kaushal, N.; Heinsdorf, N.; Harris, R.; et al. Beyond-classical computation in quantum simulation. Science 2025, 388, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Gilyén, A.; Su, Y.; Low, G.H.; Wiebe, N. Quantum singular value transformation and beyond: Exponential improvements for quantum matrix arithmetics. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, Phoenix, AZ, USA, 23–26 June 2019; pp. 193–204. [Google Scholar]
- Zhuang, Y.; Azfar, T.; Wang, Y.; Sun, W.; Wang, X.; Guo, Q.; Ke, R. Quantum computing in intelligent transportation systems: A survey. Chain 2024, 1, 138–149. [Google Scholar] [CrossRef]
- Wang, S.; Pei, Z.; Wang, C.; Wu, J. Shaping the future of the application of quantum computing in intelligent transportation system. Intell. Converg. Netw. 2021, 2, 259–276. [Google Scholar] [CrossRef]
- Bentley, C.D.; Marsh, S.; Carvalho, A.R.; Kilby, P.; Biercuk, M.J. Quantum computing for transport optimization. arXiv 2022, arXiv:2206.07313. [Google Scholar] [CrossRef]
- Dixit, V.V.; Niu, C. Quantum computing for transport network design problems. Sci. Rep. 2023, 13, 12267. [Google Scholar] [CrossRef]
- Ceder, A.; Wilson, N.H. Bus network design. Transp. Res. Part Methodol. 1986, 20, 331–344. [Google Scholar] [CrossRef]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 1989, 36. [Google Scholar]
- Farahani, R.Z.; Miandoabchi, E.; Szeto, W.Y.; Rashidi, H. A review of urban transportation network design problems. Eur. J. Oper. Res. 2013, 229, 281–302. [Google Scholar] [CrossRef]
- Guihaire, V.; Hao, J.K. Transit network design and scheduling: A global review. Transp. Res. Part Policy Pract. 2008, 42, 1251–1273. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Delgado, F.; Giesen, R.; Muñoz, J.C. Planning, operation, and control of bus transport systems: A literature review. Transp. Res. Part Methodol. 2015, 77, 38–75. [Google Scholar] [CrossRef]
- Cleophas, C.; Cottrill, C.; Ehmke, J.F.; Tierney, K. Collaborative urban transportation: Recent advances in theory and practice. Eur. J. Oper. Res. 2019, 273, 801–816. [Google Scholar] [CrossRef]
- Tong, L.C.; Zhou, L.; Liu, J.; Zhou, X. Customized bus service design for jointly optimizing passenger-to-vehicle assignment and vehicle routing. Transp. Res. Part Emerg. Technol. 2017, 85, 451–475. [Google Scholar] [CrossRef]
- Honjo, T.; Sonobe, T.; Inaba, K.; Inagaki, T.; Ikuta, T.; Yamada, Y.; Kazama, T.; Enbutsu, K.; Umeki, T.; Kasahara, R.; et al. 100,000-spin coherent Ising machine. Sci. Adv. 2021, 7, eabh0952. [Google Scholar] [CrossRef]
- Inagaki, T.; Haribara, Y.; Igarashi, K.; Sonobe, T.; Tamate, S.; Honjo, T.; Marandi, A.; McMahon, P.L.; Umeki, T.; Enbutsu, K.; et al. A coherent Ising machine for 2000-node optimization problems. Science 2016, 354, 603–606. [Google Scholar] [CrossRef]
- McMahon, P.L.; Marandi, A.; Haribara, Y.; Hamerly, R.; Langrock, C.; Tamate, S.; Inagaki, T.; Takesue, H.; Utsunomiya, S.; Aihara, K.; et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 2016, 354, 614–617. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Marandi, A.; Wen, K.; Byer, R.L.; Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. 2013, 88, 063853. [Google Scholar] [CrossRef]
- Hamerly, R.; Inagaki, T.; McMahon, P.L.; Venturelli, D.; Marandi, A.; Onodera, T.; Ng, E.; Langrock, C.; Inaba, K.; Honjo, T.; et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci. Adv. 2019, 5, eaau0823. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Wang, Z.; Huang, Z.; Cai, D.; Jia, B.; Cao, C.; Ma, Y.; Wei, H.; Wen, K.; Qian, L. Optical experimental solution for the multiway number partitioning problem and its application to computing power scheduling. Sci. China Physics, Mech. Astron. 2023, 66, 290313. [Google Scholar] [CrossRef]
- Zha, J.; Su, J.; Li, T.; Cao, C.; Ma, Y.; Wei, H.; Huang, Z.; Qian, L.; Wen, K.; Zhang, J. Encoding molecular docking for quantum computers. J. Chem. Theory Comput. 2023, 19, 9018–9024. [Google Scholar] [CrossRef]
- Li, W.; Wang, C.; Wei, H.; Hou, S.; Cao, C.; Pan, C.; Ma, Y.; Wen, K. Unified sparse optimization via quantum architectures and hybrid techniques. Quantum Sci. Technol. 2025, 10, 025059. [Google Scholar] [CrossRef]
- Huang, Y.; Li, W.; Pan, C.; Hou, S.; Lu, X.; Cui, C.; Wen, J.; Xu, J.; Cao, C.; Ma, Y.; et al. Quantum computing for mimo beam selection problem: Model and optical experimental solution. In Proceedings of the GLOBECOM 2023-2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 8–12 December 2023; IEEE: New York, NY, USA, 2023; pp. 5463–5468. [Google Scholar]
- Li, W.; Wang, C.; Zhu, H.; Gao, Q.; Ma, Y.; Wei, H.; Wen, K. Quantum-Classical Hybrid Quantized Neural Network. arXiv 2025, arXiv:2506.18240. [Google Scholar] [CrossRef]
- Kepaptsoglou, K.; Karlaftis, M. Transit route network design problem. J. Transp. Eng. 2009, 135, 491–505. [Google Scholar] [CrossRef]
- Bubeck, S.; Jiang, Q.; Lee, Y.T.; Li, Y.; Sidford, A. Near-optimal method for highly smooth convex optimization. In Proceedings of the Conference on Learning Theory, PMLR, Phoenix, AZ, USA, 25–28 June 2019; pp. 492–507. [Google Scholar]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Benoit, A.; Asef, P. Navigating Intelligence: A Survey of Google OR-Tools and Machine Learning for Global Path Planning in Autonomous Vehicles. Adv. Intell. Syst. 2024, 6, 2300840. [Google Scholar] [CrossRef]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef]
- Mohseni, N.; McMahon, P.L.; Byrnes, T. Ising machines as hardware solvers of combinatorial optimization problems. Nat. Rev. Phys. 2022, 4, 363–379. [Google Scholar] [CrossRef]
- Tang, L.; Yang, C.; Wen, K.; Wu, W.; Guo, Y. Quantum computing for several AGV scheduling models. Sci. Rep. 2024, 14, 12205. [Google Scholar] [CrossRef]
- Boettcher, S. Deep reinforced learning heuristic tested on spin-glass ground states: The larger picture. Nat. Commun. 2023, 14, 5658. [Google Scholar] [CrossRef] [PubMed]
- Glover, F.; Kochenberger, G.; Du, Y. A tutorial on formulating and using QUBO models. arXiv 2018, arXiv:1811.11538. [Google Scholar]
- Bowles, J.; Dauphin, A.; Huembeli, P.; Martinez, J.; Acín, A. Quadratic unconstrained binary optimization via quantum-inspired annealing. Phys. Rev. Appl. 2022, 18, 034016. [Google Scholar] [CrossRef]
- Guerreschi, G.G. Solving quadratic unconstrained binary optimization with divide-and-conquer and quantum algorithms. arXiv 2021, arXiv:2101.07813. [Google Scholar]
- Jiang, J.R.; Chu, C.W. Classifying and benchmarking quantum annealing algorithms based on quadratic unconstrained binary optimization for solving NP-hard problems. IEEE Access 2023, 11, 104165–104178. [Google Scholar] [CrossRef]
- Oshiyama, H.; Ohzeki, M. Benchmark of quantum-inspired heuristic solvers for quadratic unconstrained binary optimization. Sci. Rep. 2022, 12, 2146. [Google Scholar] [CrossRef] [PubMed]
- Boettcher, S. Analysis of the relation between quadratic unconstrained binary optimization and the spin-glass ground-state problem. Phys. Rev. Res. 2019, 1, 033142. [Google Scholar] [CrossRef]
- Wolsey, L.A.; Nemhauser, G.L. Integer and Combinatorial Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Beijing Qboson Quantum Technology Co. Ltd. Kaiwu SDK. 2025. Available online: https://platform.qboson.com (accessed on 7 May 2025).
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2025. Available online: https://docs.gurobi.com/projects/optimizer/en/current/index.html (accessed on 20 August 2025).
- Pincus, M. A Monte Carlo method for the approximate solution of certain types of constrained optimization problems. Oper. Res. 1970, 18, 1225–1228. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt Jr, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Fan, W.; Machemehl, R.B. Using a simulated annealing algorithm to solve the transit route network design problem. J. Transp. Eng. 2006, 132, 122–132. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.Z.; Jin, P.H.; Wu, S.H.; Yao, B.Z. Transit route network design-maximizing direct and transfer demand density. Transp. Res. Part Emerg. Technol. 2012, 22, 58–75. [Google Scholar] [CrossRef]
- Queiroz, M.; Sörensen, K. Evaluating a Simulated Annealing metaheuristic for the Heterogeneous On-Demand Bus Routing Problem with a novel experimental setup. Comput. Oper. Res. 2025, 107116. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Osaba, E.; Villar-Rodriguez, E.; Oregi, I.; Moreno-Fernandez-de Leceta, A. Focusing on the Hybrid Quantum Computing—Tabu Search Algorithm: New Results on the Asymmetric Salesman Problem; Association for Computing Machinery: New York, NY, USA, 2021. [Google Scholar]
- Goto, H.; Tatsumura, K.; Dixon, A.R. Combinatorial optimization by simulating adiabatic bifurcations in nonlinear Hamiltonian systems. Sci. Adv. 2019, 5, eaav2372. [Google Scholar] [CrossRef] [PubMed]
- Mücke, S.; Gerlach, T.; Piatkowski, N. Optimum-preserving QUBO parameter compression. Quantum Mach. Intell. 2025, 7, 1. [Google Scholar] [CrossRef]
- OpenStreetMap contributors. OpenStreetMap. 2025. Available online: https://www.openstreetmap.org (accessed on 22 August 2025).
| S | Set of candidate stations for the new bus route |
| E | Set of all stations |
| W | Set of OD pairs |
| A | Set of adjacent stations |
| Binary variable indicating whether the path from station i to station j is selected (i and j are adjacent stations). | |
| Number of passenger demands with origin station i and destination station j | |
| Constant indicating whether stations i and j are adjacent stations. If the distance between them is below a certain threshold, ; otherwise, . | |
| Path length between stations i and j | |
| Constant. indicates that station can reach target station via existing bus routes. Otherwise, . Note that . |
| PAM | CIM | Gurobi | SA | Tabu |
|---|---|---|---|---|
| Average Runtime ± SD (ms) | 0.19 ± 0.16 | 1.17 ± 0.32 | 69.57 ± 6.26 | 73.86 ± 8.01 |
| Time-saving ratio (%) | 84.06 | 99.73 | 99.75 | |
| Success Probability (%) | 100 | 100 | 53.3 | 16.7 |
| PAS | CIM | Gurobi | SA | Tabu |
|---|---|---|---|---|
| Average Runtime ± SD (ms) | 1.71 ± 1.50 | 999.87 ± 14.67 | 77.18 ± 8.89 | 121.42 ± 9.08 |
| Time-saving ratio (%) | 99.83 | 97.79 | 98.60 | |
| Optimality Gap (%) | 0.07 | 0 | 1.63 | 0.70 |
| Success Probability (%) | 10 | 100 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, J.; Liu, Z.; Bai, Y.; Wang, Y.; Gao, Q.; Ma, Y.; Zheng, C.; Wen, K. Quantum Computing for Transport Network Optimization. Entropy 2025, 27, 953. https://doi.org/10.3390/e27090953
Ju J, Liu Z, Bai Y, Wang Y, Gao Q, Ma Y, Zheng C, Wen K. Quantum Computing for Transport Network Optimization. Entropy. 2025; 27(9):953. https://doi.org/10.3390/e27090953
Chicago/Turabian StyleJu, Jiangwei, Zhihang Liu, Yuelin Bai, Yong Wang, Qi Gao, Yin Ma, Chao Zheng, and Kai Wen. 2025. "Quantum Computing for Transport Network Optimization" Entropy 27, no. 9: 953. https://doi.org/10.3390/e27090953
APA StyleJu, J., Liu, Z., Bai, Y., Wang, Y., Gao, Q., Ma, Y., Zheng, C., & Wen, K. (2025). Quantum Computing for Transport Network Optimization. Entropy, 27(9), 953. https://doi.org/10.3390/e27090953







