Mutual Information and Quantum Coherence in Minimum Error Discrimination of N Pure Equidistant Quantum States
Abstract
1. Introduction
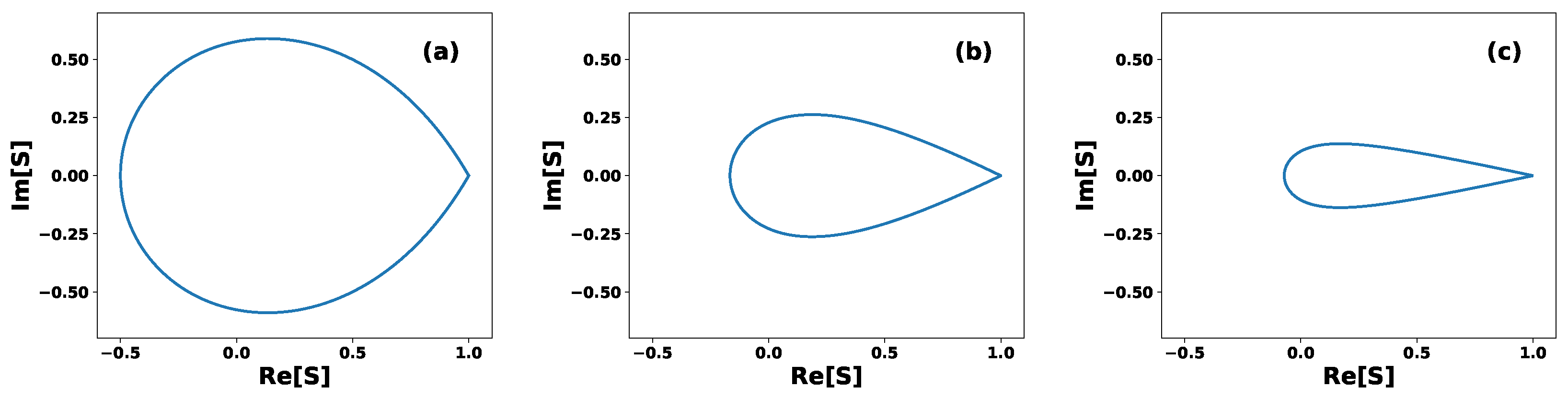
2. Equidistant States
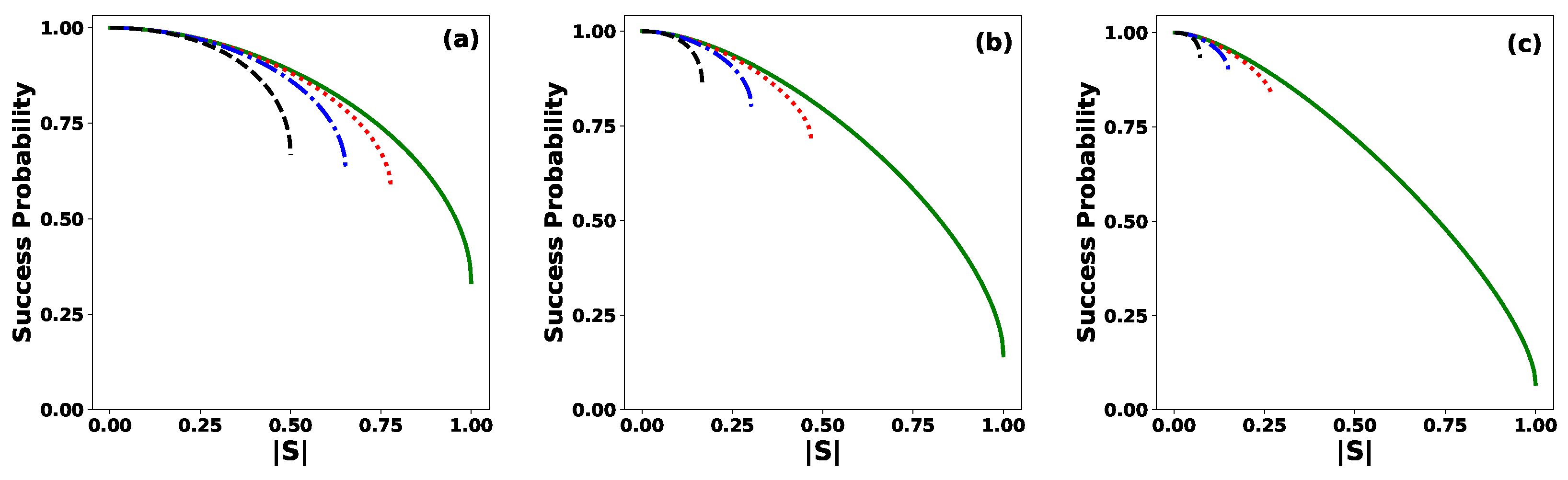
3. Minimum Error Discrimination
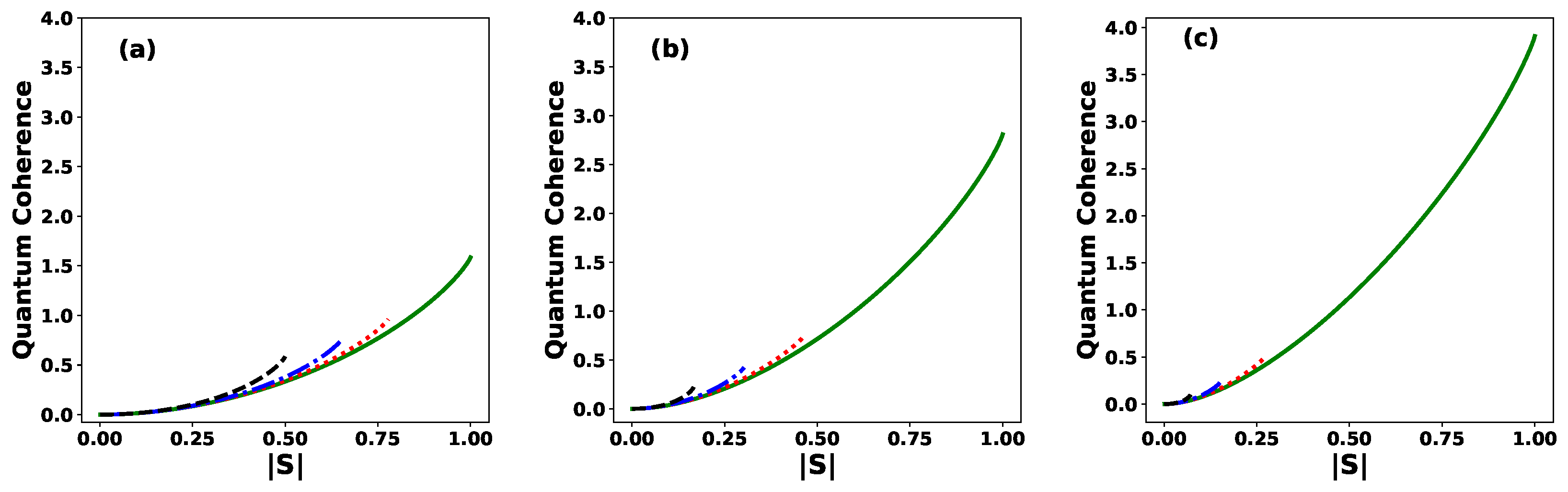
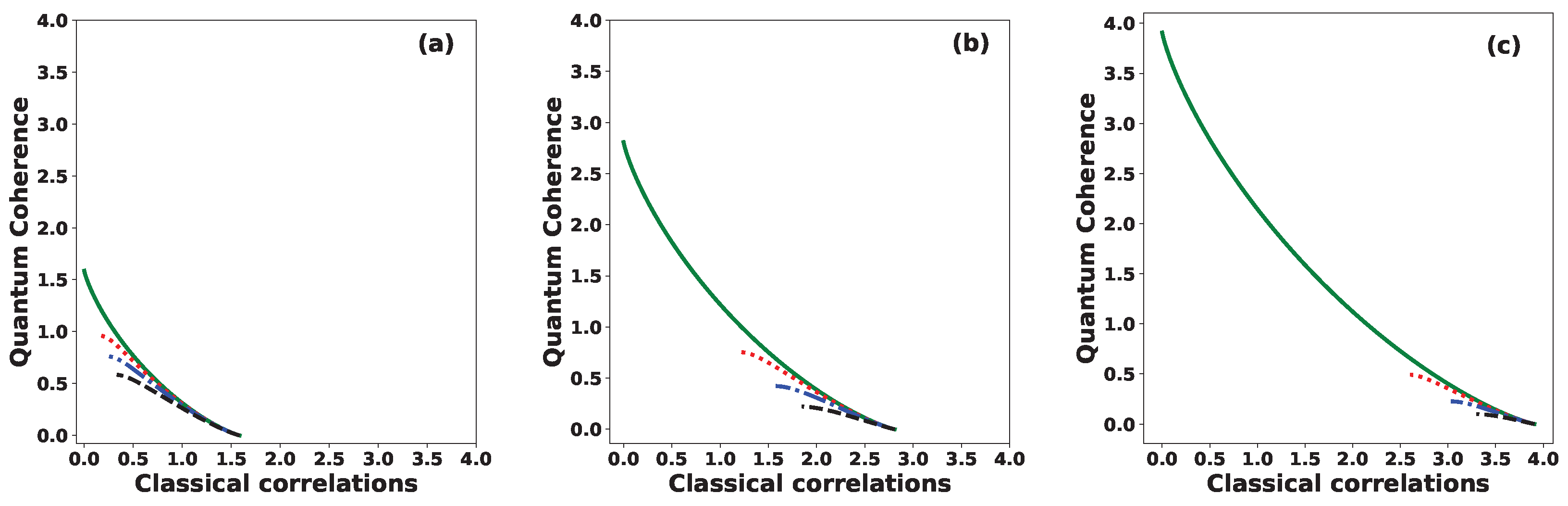
4. Quantum Coherence
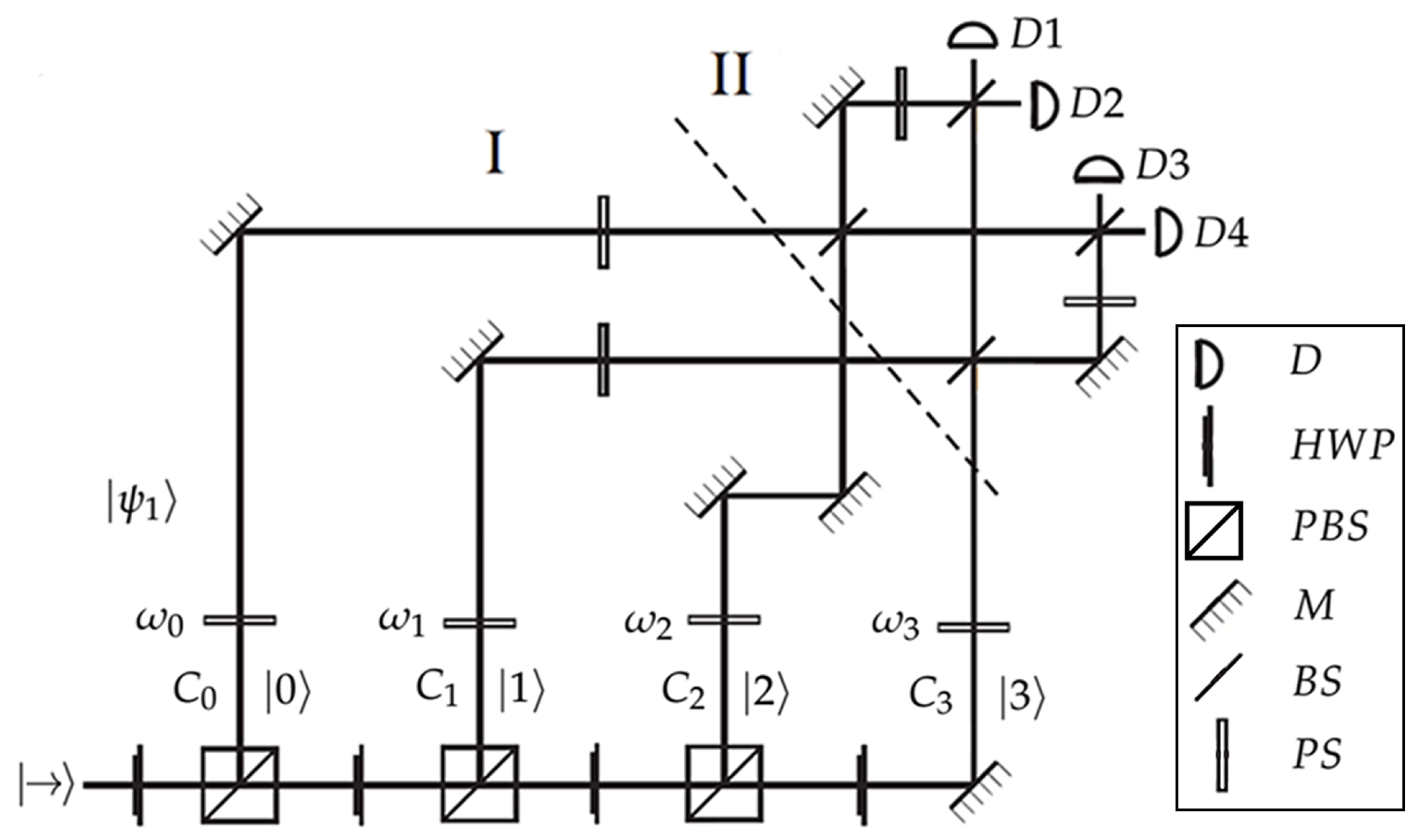
5. Channel Without Entanglement
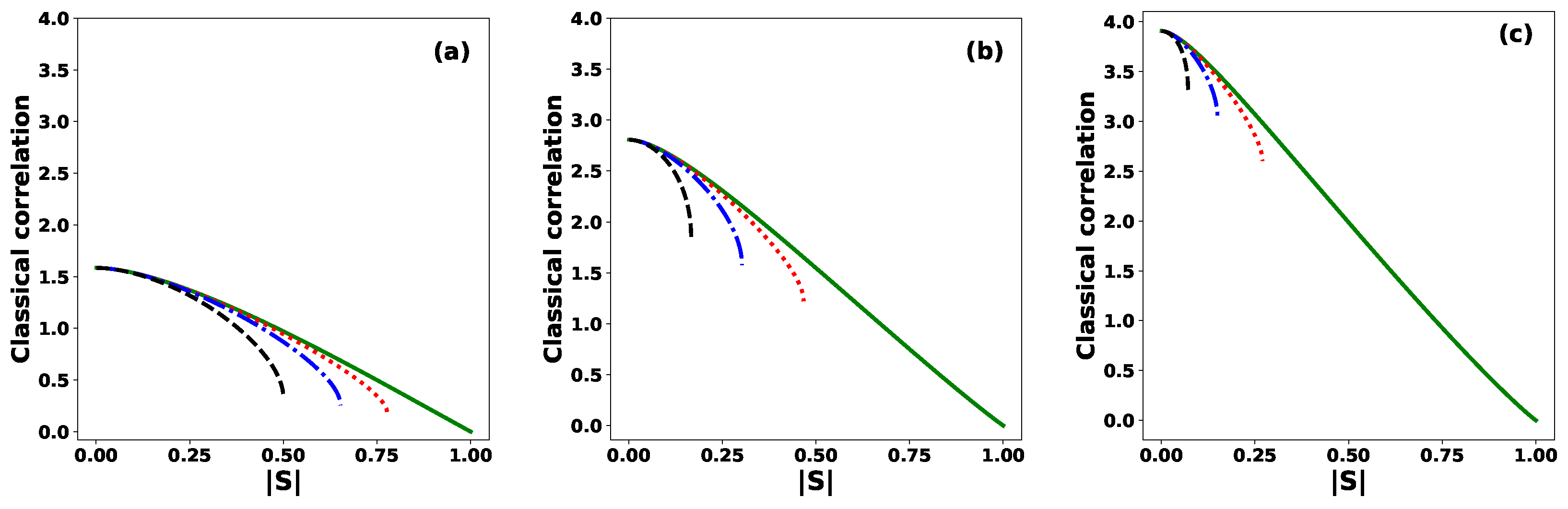
6. Classical Correlations and Quantum Discord
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Vallone, G.; Bacco, D.; Dequal, D.; Gaiarin, S.; Luceri, V.; Bianco, G.; Villoresi, P. Experimental Satellite Quantum Communications. Phys. Rev. Lett. 2015, 115, 040502. [Google Scholar] [CrossRef]
- Bergou, J.; Hillery, M. Introduction to the Theory of Quantum Information Processing; Springer Science + Business Media: New York, NY, USA, 2013. [Google Scholar]
- Barnett, S.M.; Croke, S. Quantum State Discrimination. Adv. Opt. Photonics 2009, 1, 238–278. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. Theor. Comput. Sci. 1984, 560, 175–179. [Google Scholar] [CrossRef]
- Holevo, A.S. Statistical Decision Theory for Quantum Systems. J. Multivar. Anal. 1973, 3, 337–394. [Google Scholar] [CrossRef]
- Yuen, H.P.; Kennedy, R.S.; Lax, M. Optimum testing of multiple hypothesis in quantum detection theory. IEEE Trans. Inf. Theory 1975, 21, 125. [Google Scholar] [CrossRef]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Dall’Arno, M.; D’Ariano, G.M.; Sacchi, M.F. Informational power of quantum measurements. Phys. Rev. A 2011, 83, 062304. [Google Scholar] [CrossRef]
- Sasaki, M.; Barnett, S.; Jozsa, R.; Osaki, M.; Hirota, O. Accessible information and optimal strategies for real symmetrical quantum sources. Phys. Rev. A 1999, 59, 3325. [Google Scholar] [CrossRef]
- Levitin, L.B. Optimal quantum measurements for two pure and mixed states. In Quantum Communications and Measurement; Belavkin, V.P., Hirota, O., Hudson, R.L., Eds.; Plenum: New York, NY, USA, 1995; pp. 439–448. [Google Scholar]
- Clarke, R.B.M.; Kendon, V.M.; Chefles, A.; Barnett, S.M.; Riis, E.; Sasaki, M. Experimental realization of optimal detection strategies for overcomplete states. Phys. Rev. A 2001, 64, 012303. [Google Scholar] [CrossRef]
- Nakahira, K.; Kato, K.; Usuda, T.S. Generalized quantum state discrimination problems. Phys. Rev. A 2015, 91, 052304. [Google Scholar] [CrossRef]
- Jiménez, O.; Solís-Prosser, M.A.; Neves, L.; Delgado, A. Quantum Discord, Thermal Discord, and Entropy Generation in the Minimum Error Discrimination Strategy. Entropy 2019, 21, 263. [Google Scholar] [CrossRef]
- Jiménez, O.; Solís-Prosser, M.A.; Neves, L.; Delgado, A. Mutual Information and Quantum Discord in Quantum State Discrimination with a Fixed Rate of Inconclusive Outcomes. Entropy 2021, 23, 73. [Google Scholar] [CrossRef]
- Suzuki, J.; Assad, S.M.; Englert, B. Accessible information about quantum states: An open optimization problem. In Mathematics of Quantum Computation and Quantum Technology, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Ban, M.; Kurokawa, K.; Momose, R.; Hirota, O. Optimun Measurements for Discrimination Among Symmetric Quantum States and Parameter Estimation. Int. J. Theor. Phys. 1997, 36, 1269–1288. [Google Scholar] [CrossRef]
- Barnett, S. Minimum-error discrimination between multiply symmetric states. Phys. Rev. A 2001, 64, 030303(R). [Google Scholar] [CrossRef]
- Chou, C.L.; Hsu, L.Y. Minimum-error discrimination between symmetric mixed quantum states. Phys. Rev. A 2003, 68, 042305. [Google Scholar] [CrossRef]
- Jafarizadeh, M.A.; Sufiani, R.; Khiavi, Y.M. Minimum error discrimination between similarity-transformed quantum states. Phys. Rev. A 2011, 84, 012102. [Google Scholar] [CrossRef]
- Bae, J. Structure of minimum-error quantum state discrimination. New J. Phys. 2013, 15, 073037. [Google Scholar] [CrossRef]
- Varga, A.; Adam, P.; Bergou, J.A. Maximum information measurement for qubit states. Sci. Rep. 2024, 14, 11888. [Google Scholar] [CrossRef] [PubMed]
- Shor, P. On the number of elements needed in a POVM attaining the accessible information. arXiv 2000, arXiv:quant-ph/0009077. [Google Scholar] [CrossRef]
- Oreshkov, O.; Calsamiglia, J.; Muñoz-Tapia, R.; Bagan, E. Optimal signal states for quantum detectors. New J. Phys. 2011, 13, 073032. [Google Scholar] [CrossRef]
- Ban, M.; Osaki, M.; Hirota, O. Upper bound of the accessible information and lower bound of the Bayes cost in quantum signal-detection processes. Phys. Rev. A 1996, 54, 2718. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Caves, C.M. Ensamble-Dependent Bounds for Accessible Information in Quantum Mechanics. Phys. Rev. Lett. 1994, 73, 3047. [Google Scholar] [CrossRef]
- Roa, L.; Delgado, A.; Fuentes-Guridi, I. Optimal conclusive teleportation of quantum states. Phys. Rev. A 2003, 68, 022310. [Google Scholar] [CrossRef]
- Neves, L.; Solís-Prosser, M.A.; Delgado, A.; Jiménez, O. Quantum teleportation via maximum-confidence quantum measurements. Phys. Rev. A 2012, 85, 062322. [Google Scholar] [CrossRef]
- Delgado, A.; Roa, L.; Retamal, J.C.; Saavedra, C. Entanglement swapping via quantum state discrimination. Phys. Rev. A 2005, 71, 012303. [Google Scholar] [CrossRef]
- Solís-Prosser, M.A.; Delgado, A.; Jiménez, O.; Neves, L. Deterministic and probabilistic entanglement swapping of nonmaximally entangled states assisted by optimal quantum state discrimination. Phys. Rev. A 2014, 89, 012337. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Barnett, S.M.; Chefles, A. Three-state quantum cryptography. J. Mod. Opt. 2000, 47, 507. [Google Scholar] [CrossRef]
- Pati, A.K.; Parashar, P.; Agrawal, P. Probabilistic superdense coding. Phys. Rev. A 2005, 72, 012329. [Google Scholar] [CrossRef]
- Barnett, S.M.; Riis, E. Experimental demonstration of polarization discrimination at the Helstrom bound. J. Mod. Opt. 1997, 44, 1061. [Google Scholar] [CrossRef] [PubMed]
- Waldherr, G.; Dada, A.C.; Neumann, P.; Jelezko, F.; Andersson, E.; Wrachtrup, J. Distinguishing between Nonorthogonal Quantum States of a Single Nuclear Spin. Phys. Rev. Lett. 2012, 109, 180501. [Google Scholar] [CrossRef] [PubMed]
- Solís-Prosser, M.A.; Fernandes, M.F.; Jiménez, O.; Delgado, A.; Neves, L. Experimental Minimum-Error Quantum-State Discrimination in High Dimensions. Phys. Rev. Lett. 2017, 118, 100501. [Google Scholar] [CrossRef] [PubMed]
- Berta, M.; Christandl, M.; Colbeck, R.; Renes, J.; Renner, R. The uncertaincy principle in the presence of quantum memory. Nat. Phys. 2010, 6, 659–662. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J. Generalized Entropic Uncertaincy Relations. Phys. Rev. Lett. 1988, 60, 1103. [Google Scholar] [CrossRef]
- Coles, P.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic Uncertaincy Relations and their Applications. Rev. Mod. Phys. 2017, 89, 015002. [Google Scholar] [CrossRef]
- Roa, L.; Hermann-Avigliano, C.; Salazar, R.; Klimov, A.B. Conclusive discrimination among N equidistant pure states. Phys. Rev. A 2011, 84, 014302. [Google Scholar] [CrossRef]
- Paiva-Sánchez, C.; Burgos-Inostroza, E.; Jiménez, O.; Delgado, A. Quantum tomography via equidistant states. Phys. Rev. A 2010, 82, 032115. [Google Scholar] [CrossRef]
- Jiménez, O.; Roa, L.; Delgado, A. Probabilistic cloning of equidistant states. Phys. Rev. A 2010, 82, 022328. [Google Scholar] [CrossRef]
- Raynal, P.; Lütkenhaus, N.; Van Enk, S.J. Reduction theorems for optimal unambiguous state discrimination of density matrices. Phys. Rev. A 2003, 68, 022308. [Google Scholar] [CrossRef]
- Jiménez, O.; Sánchez-Lozano, X.; Burgos-Inostroza, E.; Delgado, A.; Saavedra, C. Experimental scheme for unambiguous discrimination of linearly independent symmetric states. Phys. Rev. A 2007, 76, 062107. [Google Scholar] [CrossRef]
- Solís-Prosser, M.A.; Delgado, A.; Jiménez, O.; Neves, L. Parametric separation of symmetric pure quantum states. Phys. Rev. A 2016, 93, 012337. [Google Scholar] [CrossRef]
- Bromley, T.R.; Cianciaruso, M.; Adesso, G. Frozen Quantum Coherence. Phys. Rev. Lett. 2015, 114, 210401. [Google Scholar] [CrossRef]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, O.; Solís-Prosser, M.A.; Delgado, A.; Neves, L. Quantum resources for assisted optimal state discrimination. Phys. Rev. Res. 2024, 6, 043303. [Google Scholar] [CrossRef]
- Melo, L.F.; Jiménez, O.; Neves, L. Coherence based on positive operator-valued measures for standard and concatenated quantum state discrimination with inconclusive results. Phys. Rev. A 2025, 111, 012403. [Google Scholar] [CrossRef]
- Yuan, X.; Zhou, H.; Cao, Z.; Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 2015, 92, 022124. [Google Scholar] [CrossRef]
- Bischof, F.; Kampermann, H.; Bruß, D. Quantifying coherence with respect to general quantum measurements. Phys. Rev. A 2021, 103, 032429. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R.; Oppenheim, J.; Sen(De), A.; Sen, U.; Synak-Radtke, B. Local versus nonlocal information in quantum-information theory: Formalism and phenomena. Phys. Rev. A 2005, 71, 062307. [Google Scholar] [CrossRef]
- Namkung, M.; Kwon, Y. Optimal sequential state discrimination between two mixed quantum states. Phys. Rev. A 2017, 96, 022318. [Google Scholar] [CrossRef]
- Solís-Prosser, M.A.; Jiménez, O.; Delgado, A.; Neves, L. Enhanced discrimination of high-dimensional quantum states by concatenated optimal measurement strategies. Quantum Sci. Technol. 2022, 7, 015017. [Google Scholar] [CrossRef]
- Groisman, B.; Popescu, S.; Winter, A. Quantum, classical, and total amount of correlations in a quantum state. Phys. Rev. A 2005, 72, 032317. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Dahlsten, O.; Renner, R.; Rieper, E.; Vedral, V. Inadequacy of von Neumann entropy for characterizing extractable work. New J. Phys. 2011, 13, 053015. [Google Scholar] [CrossRef]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Zwolak, M.; Zurek, W.H. Complementarity of quantum discord and classically accessible information. Sci. Rep. 2013, 3, 1729. [Google Scholar] [CrossRef]
- Herderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Gen. 2001, 34, 6899. [Google Scholar] [CrossRef]
- Huang, Y. Quantum discord for two-qubit X states: Analytical formula with very small worst-case error. Phys. Rev. A 2013, 88, 014302. [Google Scholar] [CrossRef]
- Namkung, M.; Chang, J.; Shin, J.; Kwon, Y. Revisiting Quantum Discord for Two-Qubit X States: The Error Bound to an Analytical Formula. Int. J. Theor. Phys. 2015, 54, 3340–3349. [Google Scholar] [CrossRef]
- Ali, M.; Rau, A.; Alber, G. Quantum discord for two-qubit X states. Phys. Rev. A 2010, 82, 069902. [Google Scholar] [CrossRef]
- Fields, D.; Bergou, J.; Hillery, M.; Santra, S.; Malinovsky, V. Optimal unambiguous discrimination of Bell-like states with linear optics. Phys. Rev. A 2022, 106, 023706. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez, O. Mutual Information and Quantum Coherence in Minimum Error Discrimination of N Pure Equidistant Quantum States. Entropy 2025, 27, 863. https://doi.org/10.3390/e27080863
Jiménez O. Mutual Information and Quantum Coherence in Minimum Error Discrimination of N Pure Equidistant Quantum States. Entropy. 2025; 27(8):863. https://doi.org/10.3390/e27080863
Chicago/Turabian StyleJiménez, Omar. 2025. "Mutual Information and Quantum Coherence in Minimum Error Discrimination of N Pure Equidistant Quantum States" Entropy 27, no. 8: 863. https://doi.org/10.3390/e27080863
APA StyleJiménez, O. (2025). Mutual Information and Quantum Coherence in Minimum Error Discrimination of N Pure Equidistant Quantum States. Entropy, 27(8), 863. https://doi.org/10.3390/e27080863






