A Guiding Principle for Quantum State Discrimination in the Real-Spectrum Phase of P-Pseudo-Hermitian Systems
Abstract
1. Introduction
2. Two-State Discrimination in P-Pseudo-Hermitian and PT-Symmetric Systems
2.1. QSD Using a P-Pseudo-Hermitian Hamiltonian
2.2. QSD Using a PT-Symmetric Hamiltonian
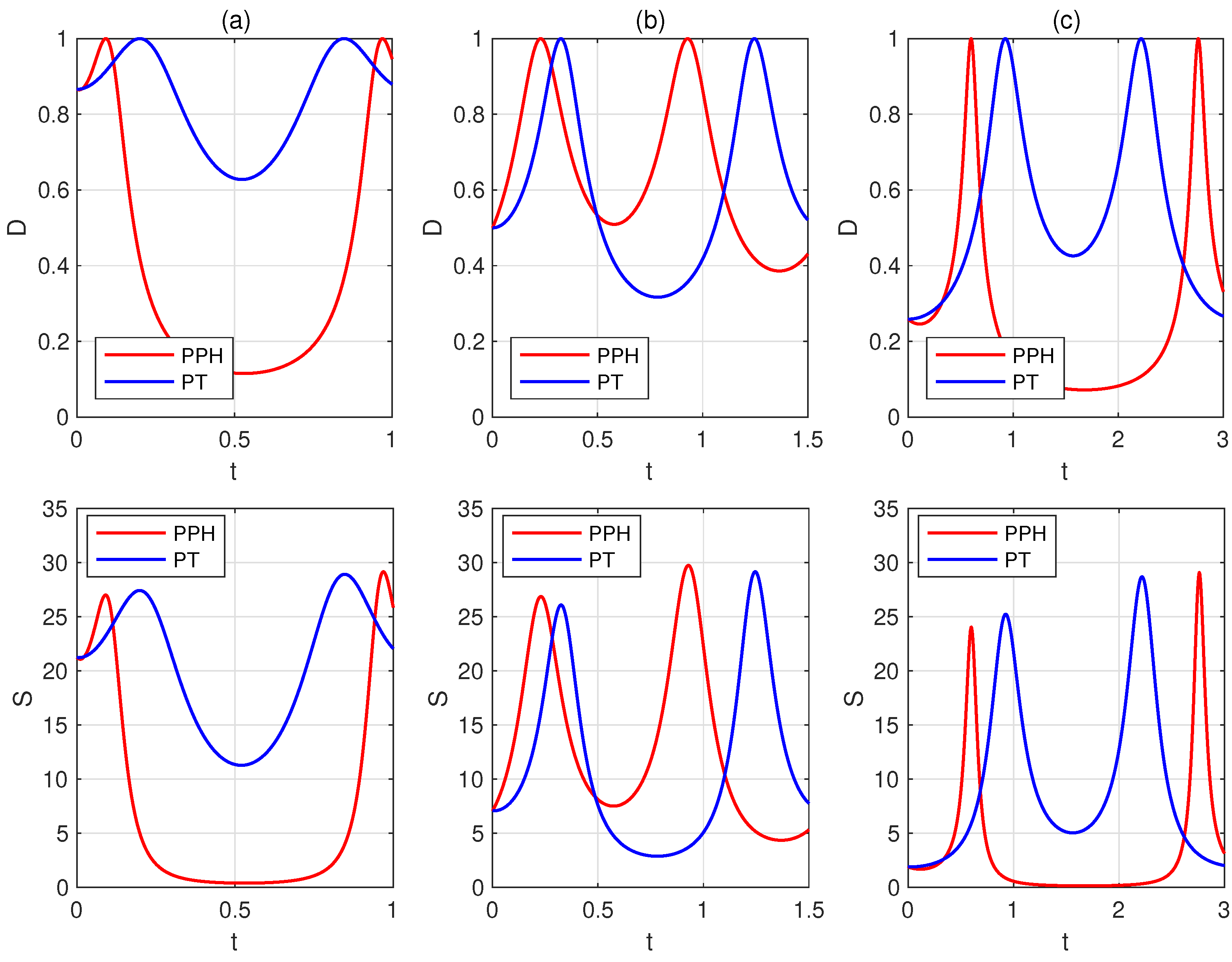
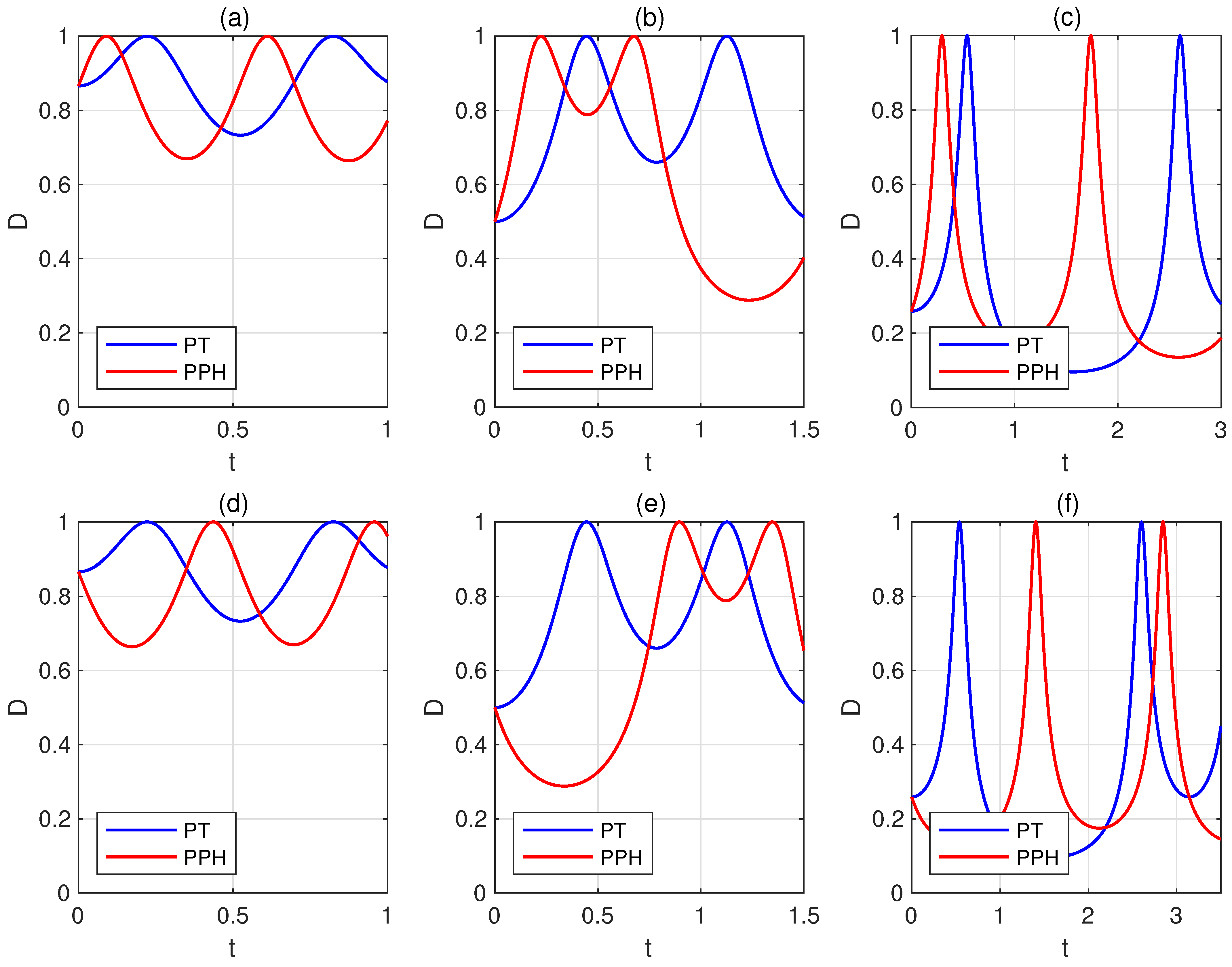
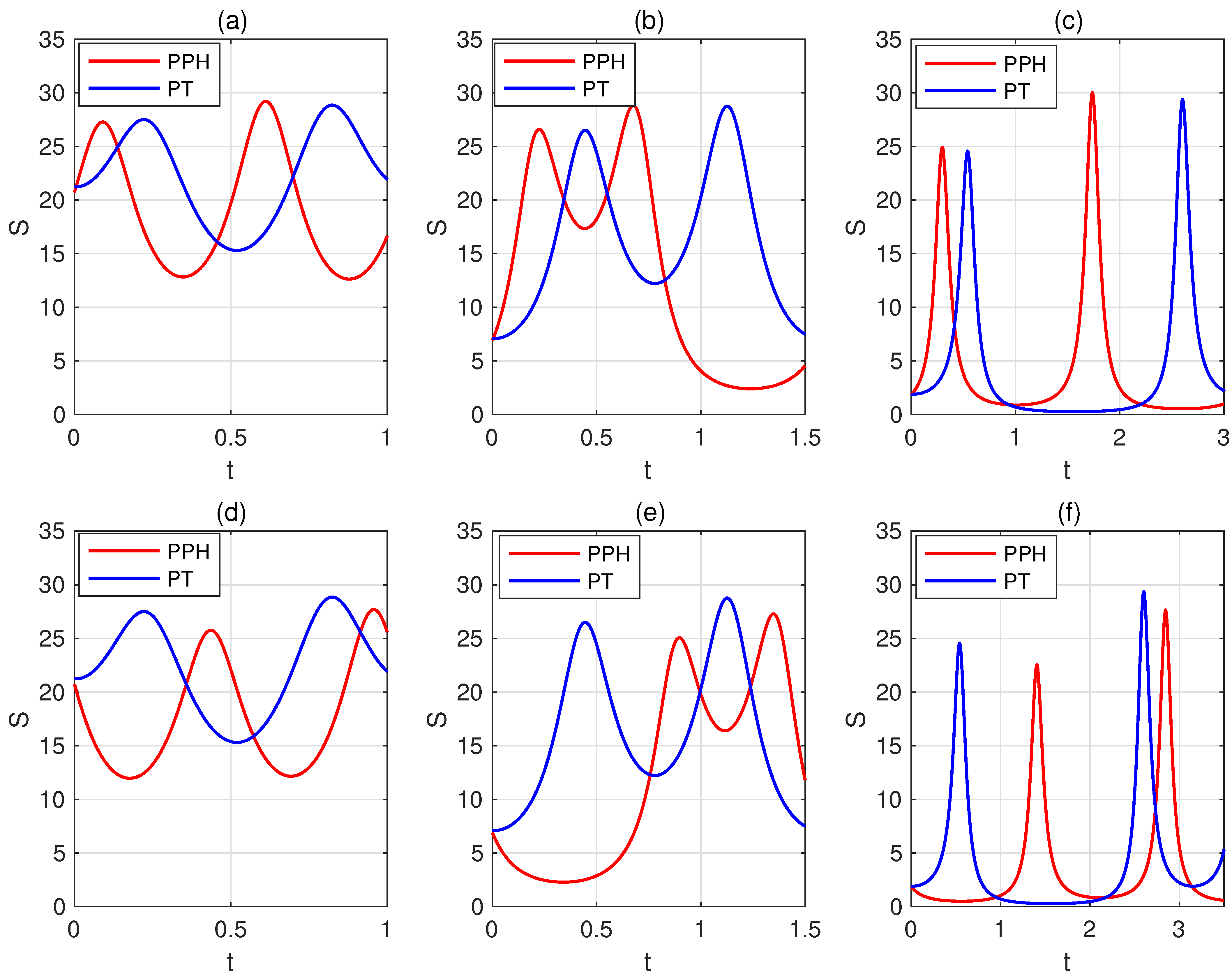
3. The Time Required for the Two Systems to Evolve and into Orthogonal Ones
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| QSD | quantum state discrimination |
| NH | non-Hermitian |
| NISQ | noisy intermediate-scale quantum |
Appendix A. Details About QSD in P-Pseudo-Hermitian Systems
Appendix B. Proof of the Comparison of Evolution Times Between the Two Systems
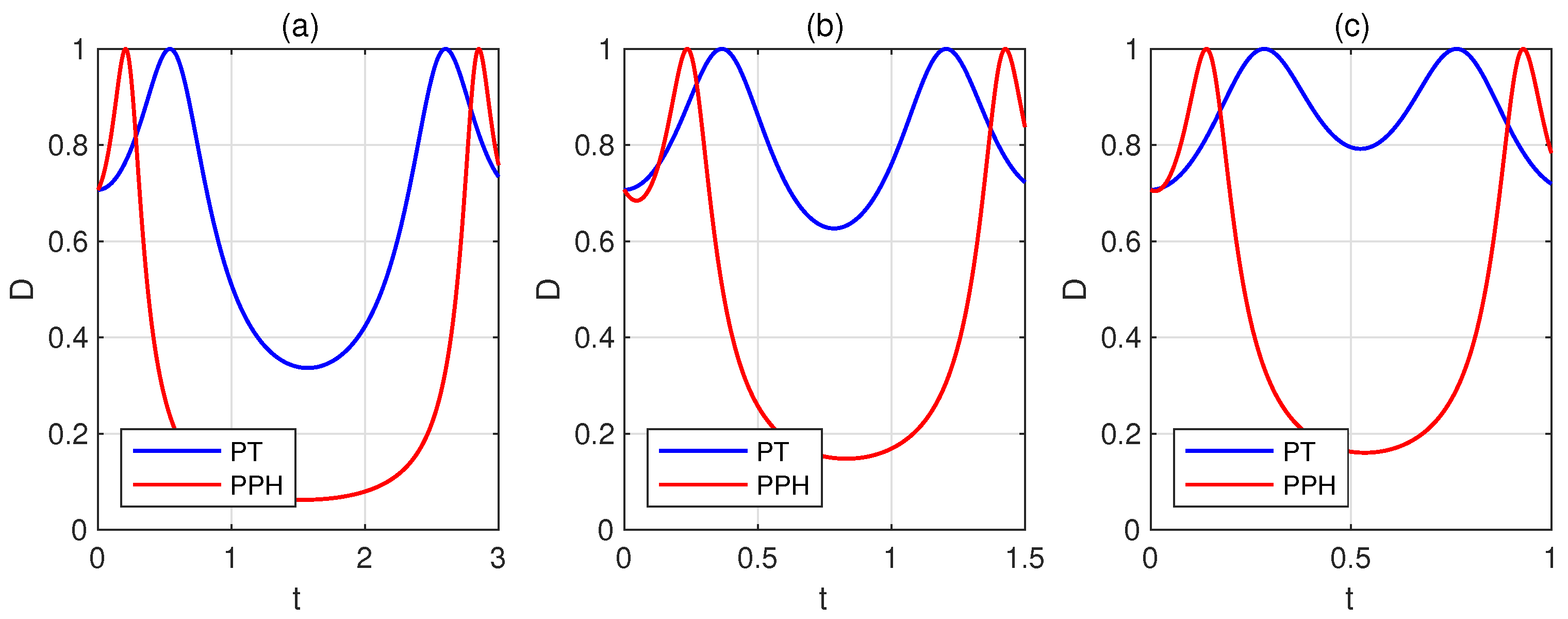
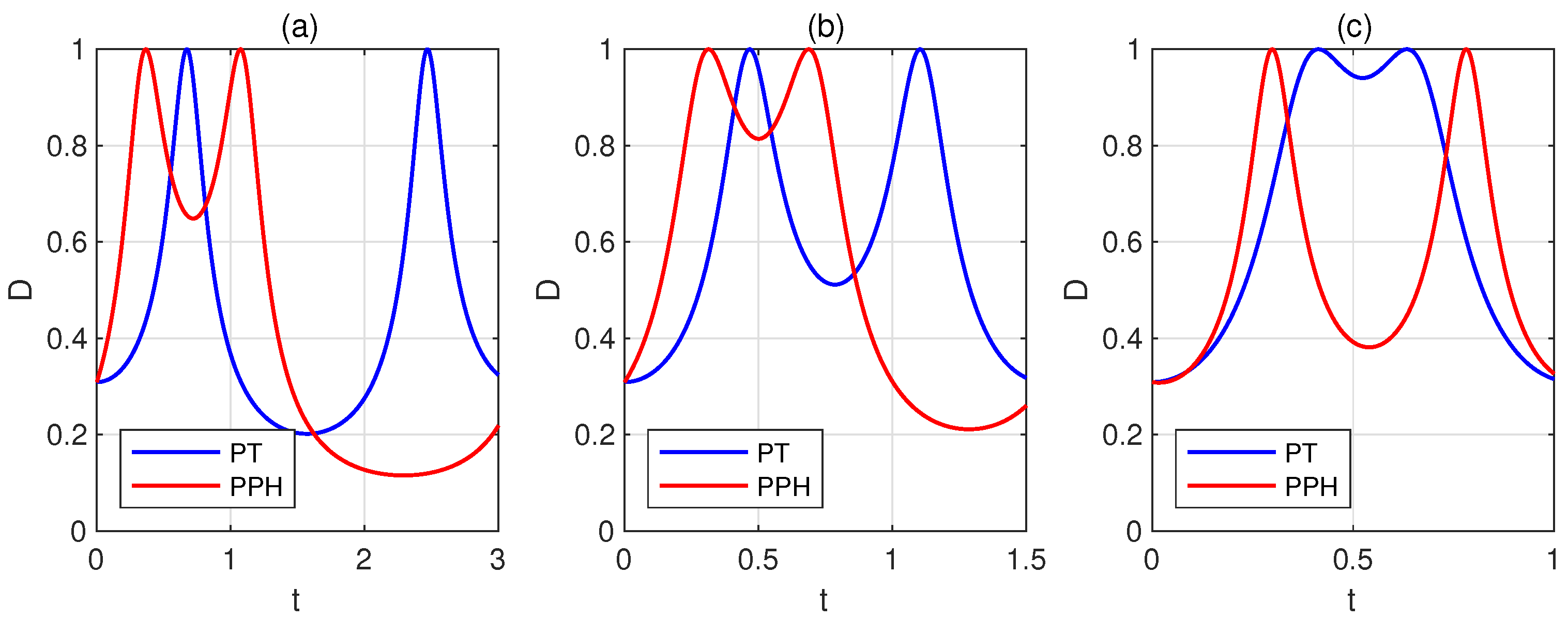
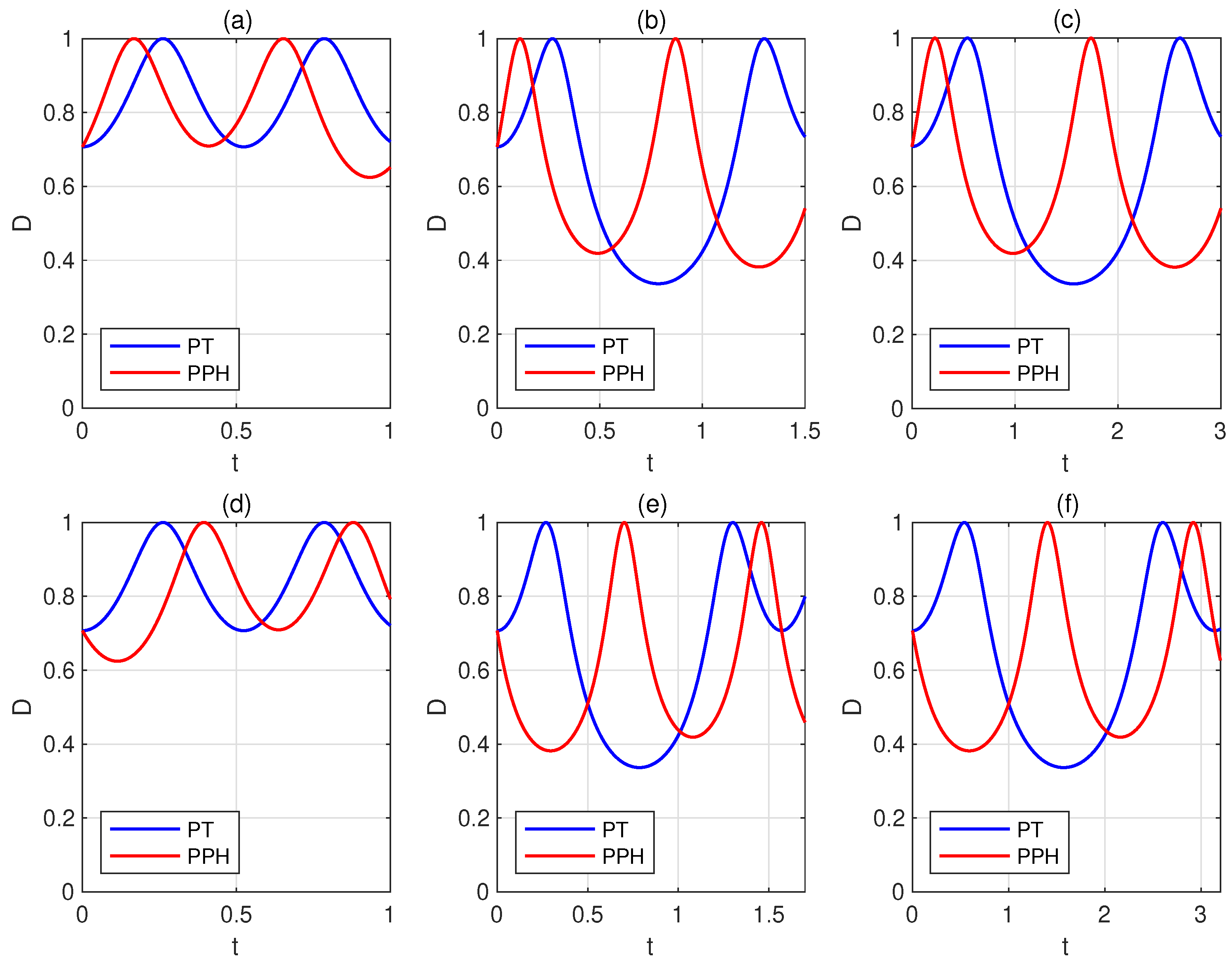
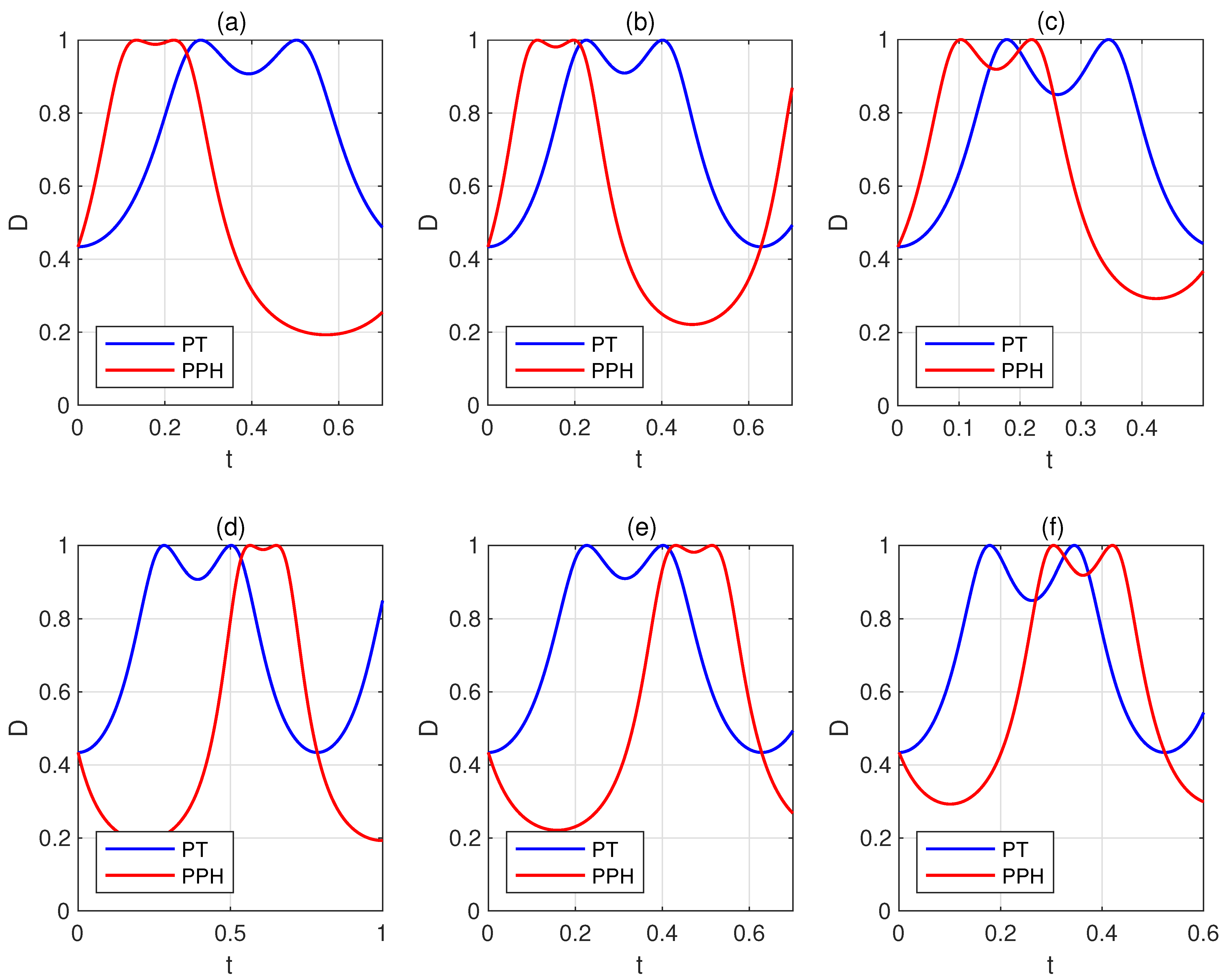
Appendix C. Further Numerical Simulations



References
- Barnett, S.M.; Croke, S. Quantum state discrimination. Adv. Opt. Photonics 2009, 1, 238–278. [Google Scholar] [CrossRef]
- Bae, J.; Kwek, L.C. Quantum state discrimination and its applications. J. Phys. A Math. Theor. 2015, 48, 083001. [Google Scholar] [CrossRef]
- Pusey, M.F.; Barrett, J.; Rudolph, T. On the reality of the quantum state. Nat. Phys. 2012, 8, 475–478. [Google Scholar] [CrossRef]
- Bennett, C.H. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–12 December 1984. [Google Scholar]
- Abrams, D.S.; Lloyd, S. Nonlinear quantum mechanics implies polynomial-time solution for NP-complete and P problems. Phys. Rev. Lett. 1998, 81, 3992. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. An update on quantum cryptography. In Advances in Cryptology; Workshop on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1984; pp. 475–480. [Google Scholar]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Helstrom, C.W. Quantum detection and estimation theory. J. Stat. Phys. 1969, 1, 231–252. [Google Scholar] [CrossRef]
- Holevo, A.S. Statistical decision theory for quantum systems. J. Multivar. Anal. 1973, 3, 337–394. [Google Scholar] [CrossRef]
- Solís-Prosser, M.; Fernandes, M.; Jiménez, O.; Delgado, A.; Neves, L. Experimental minimum-error quantum-state discrimination in high dimensions. Phys. Rev. Lett. 2017, 118, 100501. [Google Scholar] [CrossRef] [PubMed]
- Clarke, R.B.; Chefles, A.; Barnett, S.M.; Riis, E. Experimental demonstration of optimal unambiguous state discrimination. Phys. Rev. A 2001, 63, 040305. [Google Scholar] [CrossRef]
- Mohseni, M.; Steinberg, A.M.; Bergou, J.A. Optical realization of optimal unambiguous discrimination for pure and mixed quantum states. Phys. Rev. Lett. 2004, 93, 200403. [Google Scholar] [CrossRef]
- Agnew, M.; Bolduc, E.; Resch, K.J.; Franke-Arnold, S.; Leach, J. Discriminating single-photon states unambiguously in high dimensions. Phys. Rev. Lett. 2014, 113, 020501. [Google Scholar] [CrossRef]
- Ivanovic, I.D. How to differentiate between non-orthogonal states. Phys. Lett. A 1987, 123, 257–259. [Google Scholar] [CrossRef]
- Dieks, D. Overlap and distinguishability of quantum states. Phys. Lett. A 1988, 126, 303–306. [Google Scholar] [CrossRef]
- Peres, A. How to differentiate between non-orthogonal states. Phys. Lett. A 1988, 128, 19. [Google Scholar] [CrossRef]
- Jaeger, G.; Shimony, A. Optimal distinction between two non-orthogonal quantum states. Phys. Lett. A 1995, 197, 83–87. [Google Scholar] [CrossRef]
- Clarke, R.B.; Kendon, V.M.; Chefles, A.; Barnett, S.M.; Riis, E.; Sasaki, M. Experimental realization of optimal detection strategies for overcomplete states. Phys. Rev. A 2001, 64, 012303. [Google Scholar] [CrossRef]
- Christodoulides, D.; Yang, J. (Eds.) Parity-Time Symmetry and Its Applications; Springer: Singapore, 2018; Volume 280. [Google Scholar]
- Özdemir, Ş.K.; Rotter, S.; Nori, F.; Yang, L. Parity–time symmetry and exceptional points in photonics. Nat. Mater. 2019, 18, 783–798. [Google Scholar] [CrossRef]
- Croke, S. PT-symmetric Hamiltonians and their application in quantum information. Phys. Rev. A 2015, 91, 052113. [Google Scholar] [CrossRef]
- Kawabata, K.; Ashida, Y.; Ueda, M. Information retrieval and criticality in parity-time-symmetric systems. Phys. Rev. Lett. 2017, 119, 190401. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, K.; Zhan, X.; Bian, Z.; Kawabata, K.; Ueda, M.; Yi, W.; Xue, P. Observation of critical phenomena in parity-time-symmetric quantum dynamics. Phys. Rev. Lett. 2019, 123, 230401. [Google Scholar] [CrossRef]
- Wang, Y.T.; Li, Z.P.; Yu, S.; Ke, Z.J.; Liu, W.; Meng, Y.; Yang, Y.Z.; Tang, J.S.; Li, C.F.; Guo, G.C. Experimental investigation of state distinguishability in parity-time symmetric quantum dynamics. Phys. Rev. Lett. 2020, 124, 230402. [Google Scholar] [CrossRef]
- Fang, Y.L.; Zhao, J.L.; Zhang, Y.; Chen, D.X.; Wu, Q.C.; Zhou, Y.H.; Yang, C.P.; Nori, F. Experimental demonstration of coherence flow in PT-and anti-PT-symmetric systems. Commun. Phys. 2021, 4, 223. [Google Scholar] [CrossRef]
- Wang, W.C.; Zhou, Y.L.; Zhang, H.L.; Zhang, J.; Zhang, M.C.; Xie, Y.; Wu, C.W.; Chen, T.; Ou, B.Q.; Wu, W.; et al. Observation of PT-symmetric quantum coherence in a single-ion system. Phys. Rev. A 2021, 103, L020201. [Google Scholar] [CrossRef]
- Zheng, C. Quantum simulation of PT-arbitrary-phase–symmetric systems. Europhys. Lett. 2022, 136, 30002. [Google Scholar] [CrossRef]
- Zheng, C. Quantum simulation of τ-anti-pseudo-Hermitian two-level systems. Chin. Phys. B 2022, 31, 100301. [Google Scholar] [CrossRef]
- Zheng, C. Duality quantum simulation of a general parity-time-symmetric two-level system. Europhys. Lett. 2018, 123, 40002. [Google Scholar] [CrossRef]
- Wen, J.; Zheng, C.; Kong, X.; Wei, S.; Xin, T.; Long, G. Experimental demonstration of a digital quantum simulation of a general PT-symmetric system. Phys. Rev. A 2019, 99, 062122. [Google Scholar] [CrossRef]
- Gao, W.C.; Zheng, C.; Liu, L.; Wang, T.J.; Wang, C. Experimental simulation of the parity-time symmetric dynamics using photonic qubits. Opt. Express 2020, 29, 517–526. [Google Scholar] [CrossRef]
- Wen, J.; Zheng, C.; Ye, Z.; Xin, T.; Long, G. Stable states with nonzero entropy under broken PT symmetry. Phys. Rev. Res. 2021, 3, 013256. [Google Scholar] [CrossRef]
- Wang, P.; Jin, L.; Song, Z. Berry curvature inside a PT-symmetry protected exceptional surface. Phys. Rev. B 2024, 109, 115406. [Google Scholar] [CrossRef]
- Li, C.; Jin, L.; Song, Z. Coalescing Majorana edge modes in non-Hermitian PT-symmetric Kitaev chain. Sci. Rep. 2020, 10, 6807. [Google Scholar]
- Chu, Y.; Liu, Y.; Liu, H.; Cai, J. Quantum sensing with a single-qubit pseudo-Hermitian system. Phys. Rev. Lett. 2020, 124, 020501. [Google Scholar] [CrossRef]
- Ryu, J.W.; Han, J.H.; Yi, C.H.; Park, H.C.; Park, M.J. Pseudo-Hermitian topology in multiband non-Hermitian systems. Phys. Rev. A 2025, 111, 042205. [Google Scholar] [CrossRef]
- Jin, L.; Song, Z. Symmetry-protected scattering in non-Hermitian linear systems. Chin. Phys. Lett. 2021, 38, 024202. [Google Scholar] [CrossRef]
- Xu, H.; Jin, L. Pseudo-Hermiticity protects the energy-difference conservation in the scattering. Phys. Rev. Res. 2023, 5, L042005. [Google Scholar] [CrossRef]
- Jin, L. Unitary scattering protected by pseudo-hermiticity. Chin. Phys. Lett. 2022, 39, 037302. [Google Scholar] [CrossRef]
- Zhang, S.; He, T.; Jin, L. Localization dynamics at the exceptional point of non-hermitian creutz ladder. Chin. Phys. Lett. 2024, 41, 027201. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Song, Z. Dynamic magnetization in non-Hermitian quantum spin systems. Phys. Rev. B 2020, 101, 224301. [Google Scholar] [CrossRef]
- Hosseiny, S.M.; Jahromi, H.R.; Farajollahi, B.; Amniat-Talab, M. Technique for studying the coalescence of eigenstates and eigenvalues in non-Hermitian systems. Front. Phys. 2025, 20, 014201. [Google Scholar] [CrossRef]
- Sablevice, E.; Millington, P. Poincaré symmetries and representations in pseudo-Hermitian quantum field theory. Phys. Rev. D 2024, 109, 065012. [Google Scholar] [CrossRef]
- Starkov, G.A. Interplay of pseudo-Hermitian symmetries and degenerate manifolds in the eigenspectrum of non-Hermitian systems. arXiv 2024, arXiv:2402.07690. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; OUP Oxford: Oxford, UK, 2002. [Google Scholar]
- Barreiro, J.T.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An open-system quantum simulator with trapped ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef]
- Hu, Z.; Xia, R.; Kais, S. A quantum algorithm for evolving open quantum dynamics on quantum computing devices. arXiv 2019, arXiv:1904.00910. [Google Scholar] [CrossRef]
- Del Re, L.; Rost, B.; Kemper, A.; Freericks, J. Driven-dissipative quantum mechanics on a lattice: Simulating a fermionic reservoir on a quantum computer. Phys. Rev. B 2020, 102, 125112. [Google Scholar] [CrossRef]
- Viyuela, O.; Rivas, A.; Gasparinetti, S.; Wallraff, A.; Filipp, S.; Martín-Delgado, M.A. Observation of topological Uhlmann phases with superconducting qubits. Npj Quantum Inf. 2018, 4, 10. [Google Scholar] [CrossRef]
- Del Re, L.; Rost, B.; Foss-Feig, M.; Kemper, A.; Freericks, J. Robust measurements of n-point correlation functions of driven-dissipative quantum systems on a digital quantum computer. Phys. Rev. Lett. 2024, 132, 100601. [Google Scholar] [CrossRef]
- Schlimgen, A.W.; Head-Marsden, K.; Sager, L.M.; Narang, P.; Mazziotti, D.A. Quantum simulation of open quantum systems using a unitary decomposition of operators. Phys. Rev. Lett. 2021, 127, 270503. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having P T symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S.; Meisinger, P.N. PT-symmetric quantum mechanics. J. Math. Phys. 1999, 40, 2201–2229. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Caldeira, J.; Günther, U.; Meister, B.K.; Samsonov, B.F. PT-symmetric quantum state discrimination. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2013, 371, 20120160. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.X.; Zhang, Y.; Zhao, J.L.; Wu, Q.C.; Fang, Y.L.; Yang, C.P.; Nori, F. Quantum state discrimination in a PT-symmetric system. Phys. Rev. A 2022, 106, 022438. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F.; Meister, B.K. Faster than Hermitian quantum mechanics. Phys. Rev. Lett. 2007, 98, 040403. [Google Scholar] [CrossRef]
- Carlini, A.; Hosoya, A.; Koike, T.; Okudaira, Y. Time-optimal quantum evolution. Phys. Rev. Lett. 2006, 96, 060503. [Google Scholar] [CrossRef]
- Lam, M.R.; Peter, N.; Groh, T.; Alt, W.; Robens, C.; Meschede, D.; Negretti, A.; Montangero, S.; Calarco, T.; Alberti, A. Demonstration of quantum brachistochrones between distant states of an atom. Phys. Rev. X 2021, 11, 011035. [Google Scholar] [CrossRef]
- Zheng, C.; Hao, L.; Long, G.L. Observation of a fast evolution in a parity-time-symmetric system. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120053. [Google Scholar] [CrossRef]
- Assis, P.E.; Fring, A. The quantum brachistochrone problem for non-Hermitian Hamiltonians. J. Phys. A Math. Theor. 2008, 41, 244002. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Lee, T.; Wick, G. Negative metric and the unitarity of the S-matrix. Nucl. Phys. B 1969, 9, 209–243. [Google Scholar] [CrossRef]
- Konotop, V.V.; Yang, J.; Zezyulin, D.A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J. Math. Phys. 2002, 43, 205–214. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT-symmetry. II. A complete characterization of non-Hermitian Hamiltonians with a real spectrum. J. Math. Phys. 2002, 43, 2814–2816. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT-symmetry III: Equivalence of pseudo-Hermiticity and the presence of antilinear symmetries. J. Math. Phys. 2002, 43, 3944–3951. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudounitary operators and pseudounitary quantum dynamics. J. Math. Phys. 2004, 45, 932–946. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Two-component formulation of the Wheeler–DeWitt equation. J. Math. Phys. 1998, 39, 4499–4512. [Google Scholar] [CrossRef][Green Version]
- Ghatak, A.; Mandal, B.P. Entangled quantum state discrimination using a pseudo-Hermitian system. J. Phys. A Math. Theor. 2012, 45, 355301. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Gao, X.; Liu, Z.; Li, H.; Wen, J.; Zheng, C. A Guiding Principle for Quantum State Discrimination in the Real-Spectrum Phase of P-Pseudo-Hermitian Systems. Entropy 2025, 27, 836. https://doi.org/10.3390/e27080836
Dong Q, Gao X, Liu Z, Li H, Wen J, Zheng C. A Guiding Principle for Quantum State Discrimination in the Real-Spectrum Phase of P-Pseudo-Hermitian Systems. Entropy. 2025; 27(8):836. https://doi.org/10.3390/e27080836
Chicago/Turabian StyleDong, Qinliang, Xueer Gao, Zhihang Liu, Hui Li, Jingwei Wen, and Chao Zheng. 2025. "A Guiding Principle for Quantum State Discrimination in the Real-Spectrum Phase of P-Pseudo-Hermitian Systems" Entropy 27, no. 8: 836. https://doi.org/10.3390/e27080836
APA StyleDong, Q., Gao, X., Liu, Z., Li, H., Wen, J., & Zheng, C. (2025). A Guiding Principle for Quantum State Discrimination in the Real-Spectrum Phase of P-Pseudo-Hermitian Systems. Entropy, 27(8), 836. https://doi.org/10.3390/e27080836






