Robust Unsupervised Feature Selection Algorithm Based on Fuzzy Anchor Graph
Abstract
1. Introduction
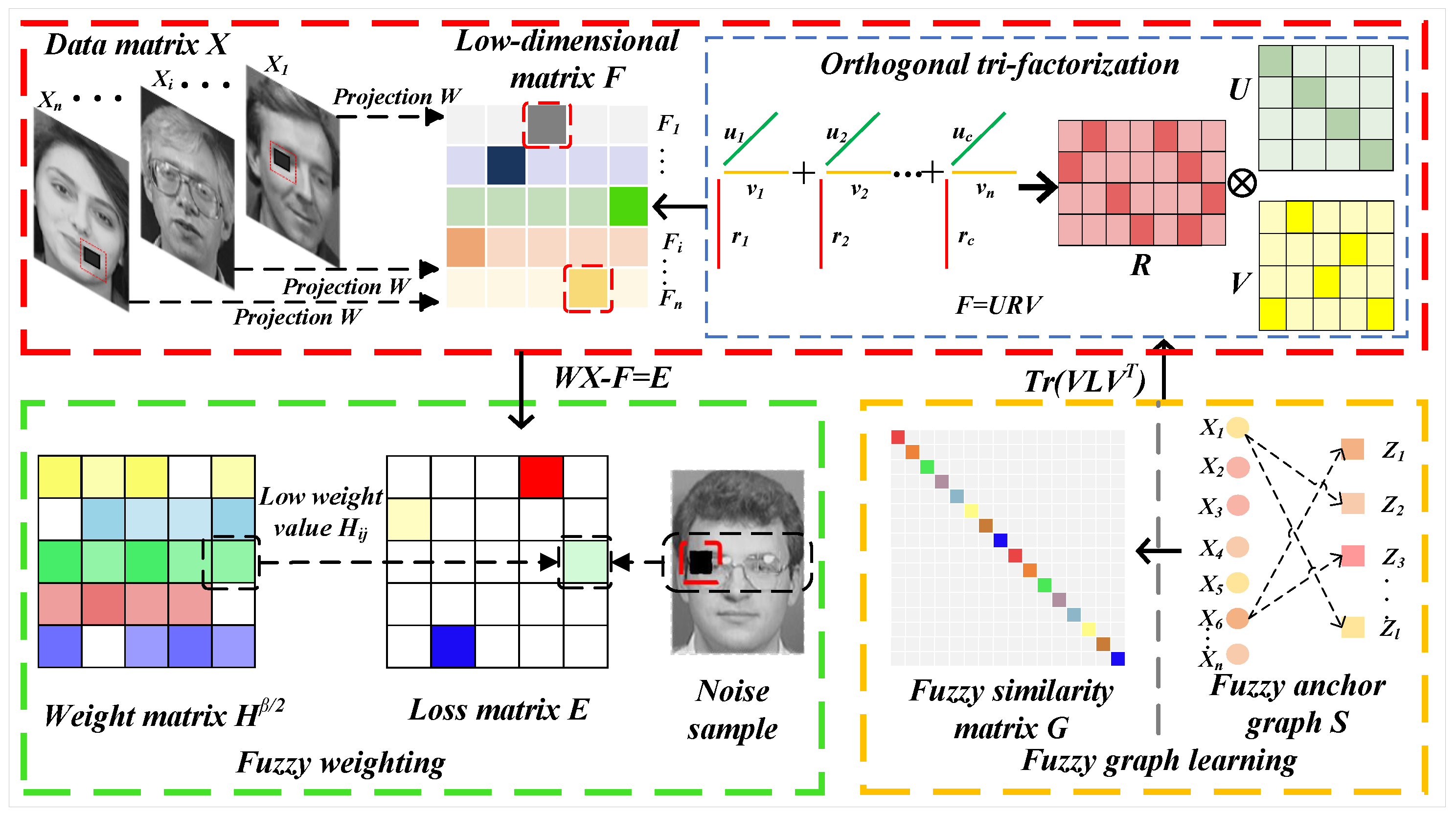
- This paper proposes a novel fuzzy neighborhood representation mechanism that captures uncertain node–cluster relationships through probabilistic membership distributions. Unlike traditional rigid neighborhood graphs, our approach enables soft cluster assignments while significantly reducing computational complexity from to through efficient anchor approximation. This innovation provides more accurate modeling of real-world data ambiguity while maintaining computational efficiency.
- To effectively handle feature redundancy and noise interference, we develop an adaptive fuzzy weighting system incorporated in the residual term. The system employs a learnable matrix with exponential scaling to dynamically adjust feature importance during optimization. Furthermore, we introduce orthogonal tri-factorization to enforce independence among cluster centers through rigorous orthogonal constraints, which enhances solution stability and prevents degenerate cases common in traditional approaches.
- We present a comprehensive optimization framework with detailed computational complexity analysis. Extensive experiments demonstrate that our method achieves significant speed improvements compared with eight state-of-the-art methods. The proposed approach consistently shows superior clustering performance and stronger noise resistance across various real-world and artificially noised datasets, validating its practical effectiveness.
2. Related Work
2.1. UFS Based on Adaptive Graph and Robust Loss (MFALBS)
2.2. UFS Based on Dual Fuzzy Graph and Orthogonal Basis Clustering (DFGOC)
2.3. UFS Based on the Exponential Weighting (LLSRFS)
3. Proposed Method
3.1. Notations
3.2. Problem Formulation
- Relaxes the strict orthogonality requirements.
- Preserves the independence of cluster centers.
- Maintains the discriminative power of features.
3.3. Optimization Procedure
3.3.1. Update H
3.3.2. Update Rules for V, U, R, and W
| Algorithm 1: Robust unsupervised feature selection based on the fuzzy anchor graph. |
| Input: Data matrix ; the number of clusters c; the number of neighbors k; parameters ; the maximum number of iterations T; the number of feature selection p. Output: Feature subset Initialization: Matrix and ; the iteration times ; Laplacian matrix . While not converged or Update by using (27); Update by using (33); Update by using (34); Update by using (35); Update by using (36); Update t by: ; EndWhile Calculate the evaluation scores for all the features according to . In descending order, we select the top p features to form a feature subset . |
3.4. Complexity Analysis
- Weight matrix updates scale as .
- Matrix optimization involves .
- Centroid matrix refinement shows complexity.
- Rotation matrix adjustment requires operations.
- Projection matrix learning contributes complexity.
4. Experiment Results and Analysis
4.1. Clustering Experiments
4.1.1. Experiment Preparation
- SUP [33]: This method combined feature selection and extraction by employing sparse projection matrices and purification matrices to effectively remove redundant information.
- UFS2 [34]: A unified learning approach is employed, embedding a binary feature selection vector into K-means, which allows for precise feature selection and avoids the suboptimal issues of traditional methods that select features before clustering.
- VCSDFS [35]: As an unsupervised feature selection method based on variance distance, it excludes features that differ significantly from the original set and selects a more discriminative subset.
- DHBWSL [36]: This method improves feature selection performance by leveraging dual high-order graph learning and Boolean weight adaptive learning to capture the local geometric structures in both data and feature spaces.
- UDS2FS [37]: To seek the discriminative subspace, through maximizing interclass divergence and minimizing within-class divergence, UDS2FS utilized soft label information to guide this process.
- LRPFS [38]: This method assigns attribute scores to samples through latent learning to enhance the ability to discriminate against outliers.
- RAFG [39]: By employing an adaptive graph to capture clustering distributions and applying norm constraints and norm regularization, noise and irrelevant features are able to be reduced.
- BGLR [40]: Addressing feature redundancy and computational complexity by selecting anchors based on sample variance, an adaptive anchor graph was constructed with norm constraints, applying to provide a discriminative feature subset with low redundancy regularization.
4.1.2. Clustering Results and Analysis
4.2. Noise Test
4.3. Ablation Study
4.4. Convergence Analysis
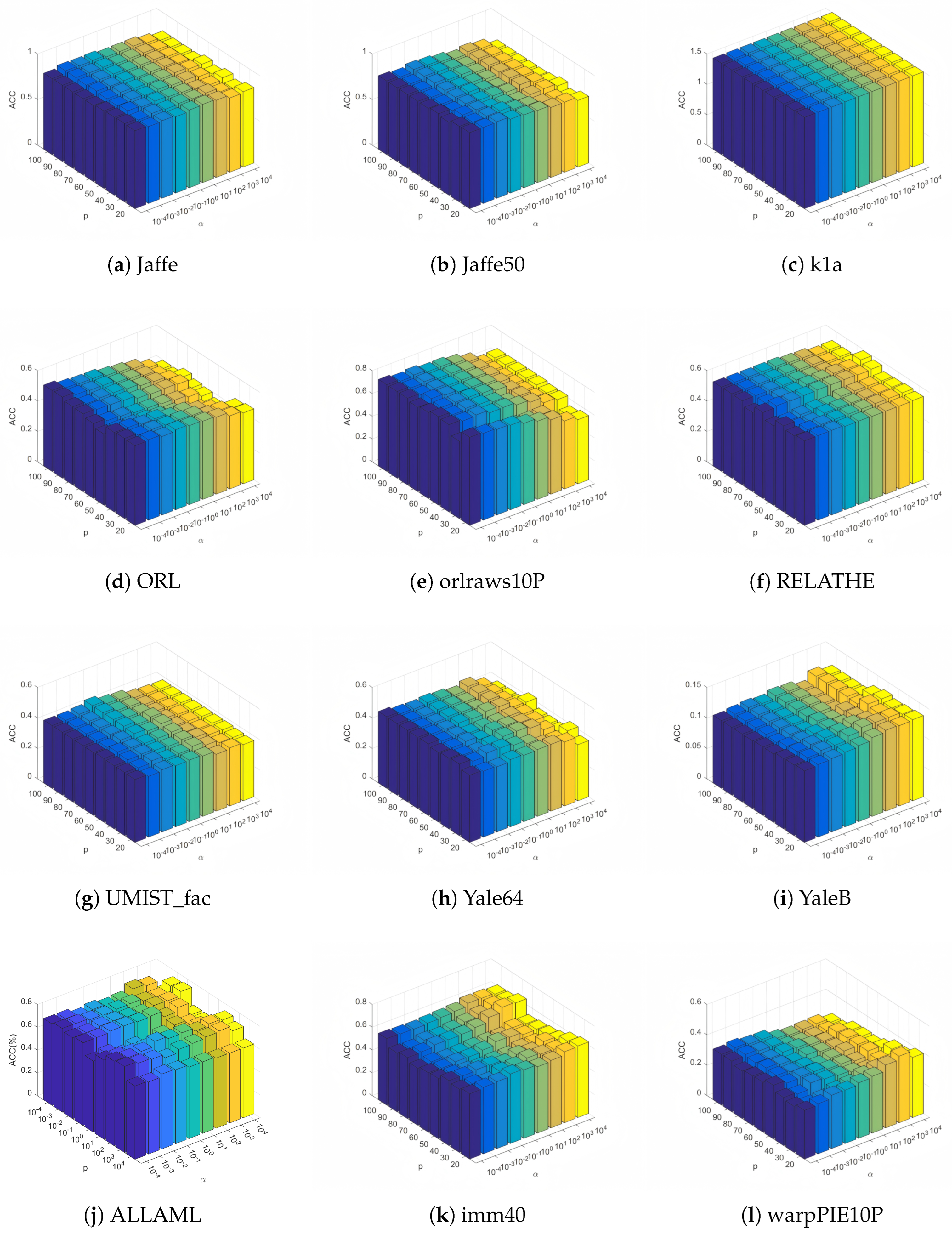
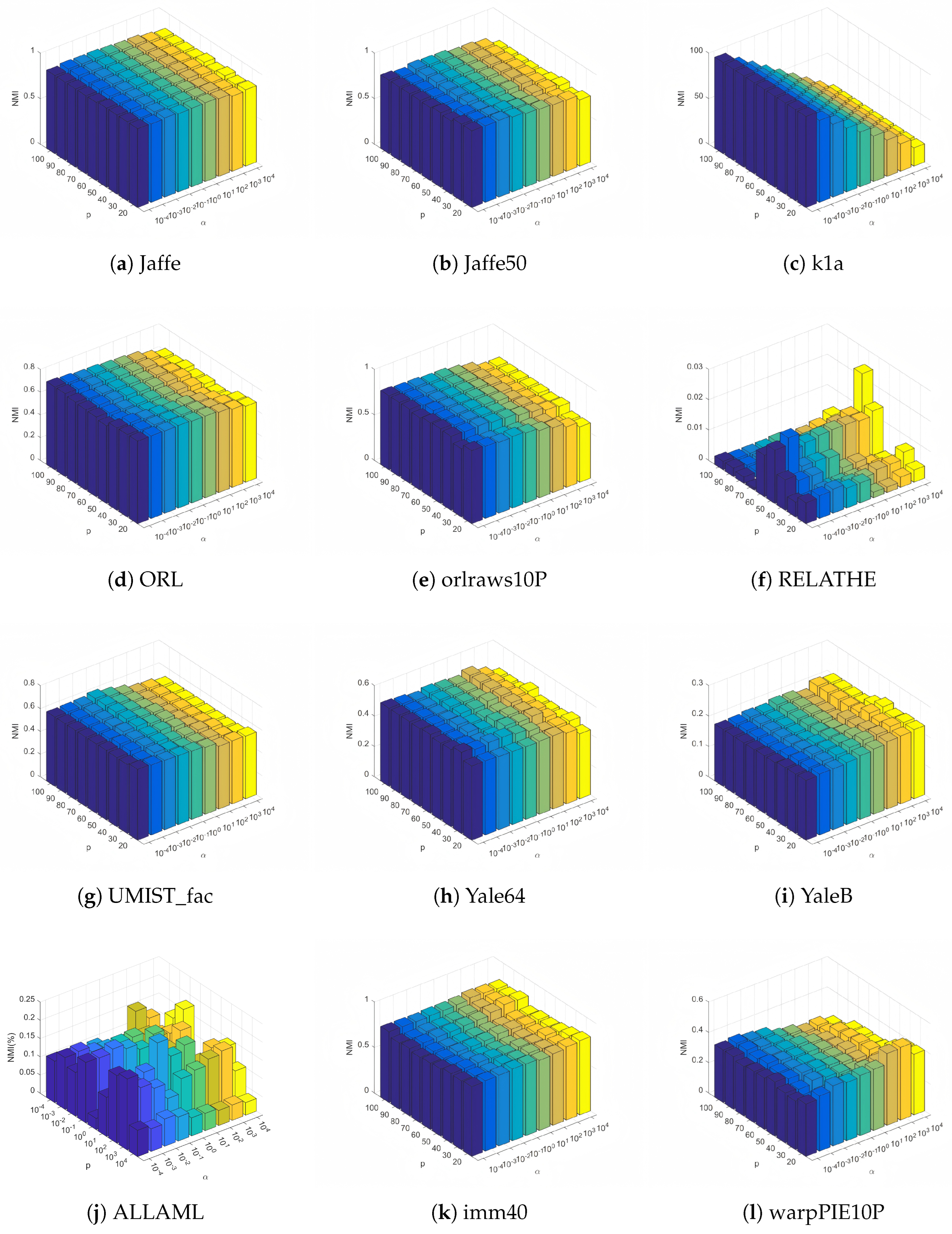
4.5. Parameter Sensitivity Analysis
4.6. Intuitive Validation of Fuzzy Anchor Graph Structure
4.7. Effectiveness Experiment of Feature Selection
4.8. T-SNE Visualization Experiment
4.9. Calculation Time Analysis
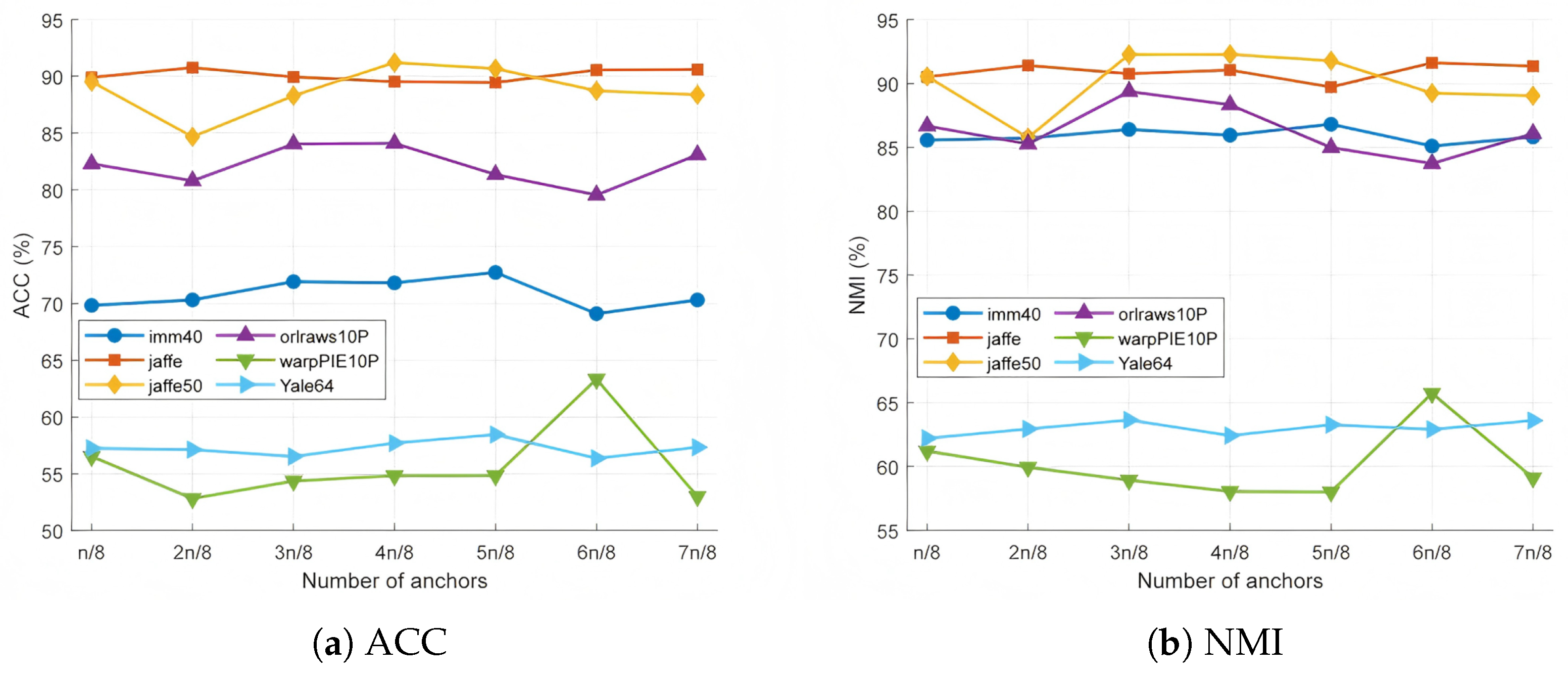
4.10. Analysis of Parameters of Fuzzy Anchor Graph
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jin, L.; Zhang, L.; Zhao, L. Feature selection based on absolute deviation factor for text classification. Inf. Process. Manag. 2023, 60, 103251. [Google Scholar] [CrossRef]
- Wang, H.; Hong, M. Supervised Hebb rule based feature selection for text classification. Inf. Process. Manag. 2019, 56, 167–191. [Google Scholar] [CrossRef]
- Wang, D.; Wang, L.; Chen, W.; Wang, H.; Liang, C. Unsupervised multi-view feature selection based on weighted low-rank tensor learning and its application in multi-omics datasets. Eng. Appl. Artif. Intell. 2025, 143, 110041. [Google Scholar] [CrossRef]
- Ileberi, E.; Sun, Y.; Wang, Z. A machine learning based credit card fraud detection using the GA algorithm for feature selection. J. Big Data 2022, 9, 24. [Google Scholar] [CrossRef]
- Li, Y.; Hu, L.; Gao, W. Multi-label feature selection with high-sparse personalized and low-redundancy shared common features. Inf. Process. Manag. 2024, 61, 103633. [Google Scholar] [CrossRef]
- Moslemi, A.; Jamshidi, M. Unsupervised feature selection using sparse manifold learning: Auto-encoder approach. Inf. Process. Manag. 2025, 62, 103923. [Google Scholar] [CrossRef]
- Samareh-Jahani, M.; Saberi-Movahed, F.; Eftekhari, M.; Aghamollaei, G.; Tiwari, P. Low-redundant unsupervised feature selection based on data structure learning and feature orthogonalization. Expert Syst. Appl. 2024, 240, 122556. [Google Scholar] [CrossRef]
- Sun, M.; Li, F.; Han, H. Fractal autoencoder with redundancy regularization for unsupervised feature selection. Sci. China Inf. Sci. 2025, 68, 122103. [Google Scholar] [CrossRef]
- Guo, Z.; Shen, Y.; Yang, T.; Li, Y.-J.; Deng, Y.; Qian, Y. Semi-supervised feature selection based on fuzzy related family. Inf. Sci. 2024, 652, 119660. [Google Scholar] [CrossRef]
- Liao, H.; Chen, H.; Yin, T.; Horng, S.-J.; Li, T. Adaptive orthogonal semi-supervised feature selection with reliable label matrix learning. Inf. Process. Manag. 2024, 61, 103727. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, J.; Wang, Z.; Zhang, C.; Yang, J.; Wang, Y.; Sheng, W.; Ding, W. Semi-supervised multi-view feature selection with adaptive similarity fusion and learning. Pattern Recognit. 2025, 159, 111159. [Google Scholar] [CrossRef]
- Saberi-Movahed, F.; Rostami, M.; Berahmand, K.; Karami, S.; Tiwari, P.; Oussalah, M.; Band, S.S. Dual regularized unsupervised feature selection based on matrix factorization and minimum redundancy with application in gene selection. Knowl.-Based Syst. 2022, 256, 109884. [Google Scholar] [CrossRef]
- Chen, H.; Nie, F.; Wang, R.; Li, X. Unsupervised feature selection with flexible optimal graph. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 2014–2027. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Sun, H.; Hao, S. Adaptive dictionary and structure learning for unsupervised feature selection. Inf. Process. Manag. 2022, 59, 102931. [Google Scholar] [CrossRef]
- Assadi, H.N.; Kyanfar, F.; Saberi-Movahed, F.; Salemi, A. Bilinear Self-Representation for Unsupervised Feature Selection with Structure Learning. Neurocomputing 2025, 625, 129557. [Google Scholar] [CrossRef]
- Xu, S.; Xie, X.; Cao, Z. Graph–Regularized Consensus Learning and Diversity Representation for unsupervised multi-view feature selection. Knowl.-Based Syst. 2025, 311, 113043. [Google Scholar] [CrossRef]
- Li, Y.; Hu, L.; Gao, W. Multi-label feature selection via robust flexible sparse regularization. Pattern Recognit. 2023, 134, 109074. [Google Scholar] [CrossRef]
- Moslemi, A.; Ahmadian, A. Dual regularized subspace learning using adaptive graph learning and rank constraint: Unsupervised feature selection on gene expression microarray datasets. Comput. Biol. Med. 2023, 167, 107659. [Google Scholar] [CrossRef]
- Huang, P.; Yang, X. Unsupervised feature selection via adaptive graph and dependency score. Pattern Recognit. 2022, 127, 108622. [Google Scholar] [CrossRef]
- Ma, Z.; Wei, Y.; Huang, Y.; Wang, J. Unsupervised feature selection based on minimum-redundant subspace learning with self-weighted adaptive graph. Digit. Signal Process. 2024, 155, 104738. [Google Scholar] [CrossRef]
- Bai, H.; Huang, M.; Zhong, P. Precise feature selection via non-convex regularized graph embedding and self-representation for unsupervised learning. Knowl.-Based Syst. 2024, 296, 111900. [Google Scholar] [CrossRef]
- Xie, X.; Cao, Z.; Sun, F. Joint learning of graph and latent representation for unsupervised feature selection. Appl. Intell. 2023, 53, 25282–25295. [Google Scholar] [CrossRef]
- Tang, C.; Zheng, X.; Zhang, W.; Liu, X.; Zhu, X.; Zhu, E. Unsupervised feature selection via multiple graph fusion and feature weight learning. Sci. China Inf. Sci. 2023, 66, 152101. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, X.; Chen, J.; Wang, P.; Liu, X.; Tian, J. Robust graph regularized unsupervised feature selection. Expert Syst. Appl. 2018, 96, 64–76. [Google Scholar] [CrossRef]
- Song, X. Self-representation with adaptive loss minimization via doubly stochastic graph regularization for robust unsupervised feature selection. Int. J. Mach. Learn. Cybern. 2025, 16, 661–685. [Google Scholar] [CrossRef]
- Nie, F.; Wu, D.; Wang, R.; Li, X. Self-weighted clustering with adaptive neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3428–3441. [Google Scholar] [CrossRef] [PubMed]
- Shang, R.; Kong, J.; Wang, L.; Zhang, W.; Wang, C.; Li, Y.; Jiao, L. Unsupervised feature selection via discrete spectral clustering and feature weights. Neurocomputing 2023, 517, 106–117. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Gu, Z.; Wei, J.-M.; Liu, J. Unsupervised feature selection by learning exponential weights. Pattern Recognit. 2024, 148, 110183. [Google Scholar] [CrossRef]
- Huang, P.; Kong, Z.; Xie, M.; Yang, X. Robust unsupervised feature selection via data relationship learning. Pattern Recognit. 2023, 142, 109676. [Google Scholar] [CrossRef]
- Song, X. Robust unsupervised feature selection based on matrix factorization with adaptive loss via bi-stochastic graph regularization. Appl. Intell. 2025, 55, 55. [Google Scholar] [CrossRef]
- Li, D.; Chen, H.; Mi, Y.; Luo, C.; Horng, S.-J.; Li, T. Dual space-based fuzzy graphs and orthogonal basis clustering for unsupervised feature selection. Pattern Recognit. 2024, 155, 110683. [Google Scholar] [CrossRef]
- Miao, J.; Zhao, J.; Yang, T.; Tian, Y.; Shi, Y.; Xu, M. Robust sparse orthogonal basis clustering for unsupervised feature selection. Expert Syst. Appl. 2025, 274, 126890. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Nie, F.; Li, X. Joint feature selection and extraction with sparse unsupervised projection. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3071–3081. [Google Scholar] [CrossRef]
- Chang, H.; Guo, J.; Zhu, W. Rethinking embedded unsupervised feature selection: A simple joint approach. IEEE Trans. Big Data 2022, 9, 380–387. [Google Scholar] [CrossRef]
- Karami, S.; Saberi-Movahed, F.; Tiwari, P.; Marttinen, P.; Vahdati, S. Unsupervised feature selection based on variance–covariance subspace distance. Neural Netw. 2023, 166, 188–203. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Ma, J.; Ma, Z.; Huang, Y. Subspace learning for dual high-order graph learning based on boolean weight. Entropy 2025, 27, 107. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Peng, Y.; Nie, F.; Kong, W. Soft Label Guided Unsupervised Discriminative Sparse Subspace Feature Selection. J. Classif. 2024, 41, 129–157. [Google Scholar] [CrossRef]
- Ma, Z.; Huang, Y.; Li, H.; Wang, J. Unsupervised feature selection with latent relationship penalty term. Axioms 2023, 13, 6. [Google Scholar] [CrossRef]
- Jiang, K.; Cao, T.; Zhu, L.; Sun, Q. Adaptive and flexible ℓ1-norm graph embedding for unsupervised feature selection. Appl. Intell. 2024, 54, 11732–11751. [Google Scholar] [CrossRef]
- Xiang, L.; Chen, H.; Yin, T.; Horng, S.-J.; Li, T. Unsupervised feature selection based on bipartite graph and low-redundant regularization. Knowl.-Based Syst. 2024, 302, 112379. [Google Scholar] [CrossRef]









| Notation | Description |
|---|---|
| Data matrix of size | |
| Projection matrix of size | |
| Clustering indicates matrix of size | |
| Auxiliary matrix of size | |
| Clustering center matrix of size | |
| Fuzzy anchor graph matrix of size | |
| Fuzzy weighting matrix of size | |
| Fuzzy similarity matrix of size | |
| Degree matrix of size | |
| Laplacian matrix of size | |
| Identity matrix of size | |
| Frobenius norm of matrix | |
| Trace of matrix | |
| ⊙ | Element multiplication of matrix |
| Vector of all ones of size |
| Dataset | Size | Dimensionality | Class | Type |
|---|---|---|---|---|
| ORL | 400 | 1024 | 40 | Face image |
| YaleB | 2414 | 1024 | 38 | Face image |
| imm40 | 240 | 1024 | 40 | Face image |
| ALLAML | 72 | 7219 | 2 | Biological |
| warpPIE10P | 210 | 2420 | 10 | Face image |
| Jaffe | 213 | 676 | 10 | Face image |
| orlraws10P | 100 | 10,304 | 10 | Face image |
| RELATHE | 1427 | 4322 | 2 | Text |
| Jaffe50 | 213 | 1024 | 10 | Face image |
| Yale64 | 165 | 4096 | 15 | Face image |
| UMIST_fac | 575 | 1024 | 20 | Face image |
| kla | 2340 | 1326 | 6 | Text |
| Datasets | SUP | UFS2 | VCSDFS | DHBWSL | UDS2FS | LRPFS | RAFG | BGLR | FWFGFS |
|---|---|---|---|---|---|---|---|---|---|
| ORL | 52.98 ± 2.69 | 41.07 ± 1.67 | 50.53 ± 2.11 | 56.05 ± 2.45 | 50.55 ± 2.20 | 47.57 ± 2.38 | 54.43 ± 2.16 | 53.55 ± 2.09 | 56.37 ± 3.00 |
| (100) | (100) | (60) | (100) | (30) | (90) | (100) | (100) | (100) | |
| YaleB | 12.58 ± 0.48 | 22.36 ± 1.28 | 10.03 ± 0.34 | 17.56 ± 0.35 | 10.39 ± 0.58 | 16.21 ± 0.37 | 9.41 ± 0.21 | 13.09 ± 0.45 | 22.62 ± 0.98 |
| (30) | (80) | (50) | (20) | (30) | (20) | (40) | (20) | (40) | |
| imm40 | 57.35 ± 2.61 | 55.45 ± 2.34 | 45.68 ± 2.53 | 53.83 ± 2.02 | 52.27 ± 2.08 | 60.29 ± 3.25 | 59.60 ± 3.41 | 55.18 ± 3.05 | 71.81 ± 2.61 |
| (70) | (80) | (100) | (90) | (100) | (40) | (20) | (70) | (30) | |
| ALLAML | 70.34 ± 0.81 | 71.92 ± 0.02 | 85.69 ± 0.12 | 89.35 ± 0.94 | 78.37 ± 0.75 | 76.11 ± 2.14 | 74.65 ± 1.85 | 74.79 ± 0.51 | 90.62 ± 1.95 |
| (30) | (20) | (30) | (20) | (20) | (100) | (100) | (90) | (20) | |
| warpPIE10P | 26.61 ± 1.17 | 50.69 ± 3.04 | 28.16 ± 1.67 | 42.11 ± 2.98 | 37.97 ± 2.57 | 33.88 ± 1.83 | 52.50 ± 2.43 | 26.95 ± 1.55 | 54.83 ± 2.58 |
| (60) | (50) | (60) | (90) | (90) | (20) | (20) | (30) | (40) | |
| Jaffe | 86.03 ± 5.09 | 76.12 ± 6.61 | 83.00 ± 4.15 | 89.41 ± 4.18 | 84.69 ± 5.51 | 80.02 ± 5.86 | 85.39 ± 4.01 | 88.94 ± 6.23 | 89.53 ± 5.45 |
| (70) | (100) | (80) | (60) | (20) | (100) | (100) | (90) | (70) | |
| orlraws10P | 76.45 ± 4.53 | 55.70 ± 2.40 | 66.85 ± 4.90 | 82.45 ± 4.33 | 67.90 ± 5.34 | 67.65 ± 4.59 | 80.30 ± 4.02 | 75.75 ± 4.71 | 84.10 ± 4.19 |
| (20) | (100) | (90) | (50) | (20) | (60) | (90) | (100) | (90) | |
| RELATHE | 54.66 ± 0.02 | 54.75 ± 0.18 | 54.65 ± 0.03 | 59.55 ± 0.12 | 59.00 ± 0.02 | 59.09 ± 0.05 | 55.18 ± 0.49 | 54.66 ± 0.14 | 59.67 ± 1.12 |
| (100) | (60) | (100) | (70) | (50) | (60) | (80) | (100) | (30) | |
| Jaffe50 | 81.97 ± 5.22 | 62.74 ± 3.10 | 73.23 ± 3.57 | 79.92 ± 4.48 | 77.93 ± 6.42 | 81.50 ± 2.76 | 84.64 ± 5.12 | 82.69 ± 4.03 | 91.22 ± 5.20 |
| (100) | (100) | (50) | (100) | (80) | (100) | (100) | (100) | (100) | |
| Yale64 | 52.66 ± 3.31 | 41.09 ± 3.08 | 46.39 ± 1.97 | 44.96 ± 3.91 | 47.51 ± 2.85 | 41.15 ± 1.73 | 55.00 ± 4.30 | 52.21 ± 3.00 | 57.69 ± 3.23 |
| (90) | (90) | (30) | (100) | (20) | (80) | (100) | (90) | (90) | |
| UMIST_fac | 45.67 ± 2.24 | 47.65 ± 2.05 | 46.16 ± 2.15 | 47.98 ± 3.59 | 48.20 ± 2.14 | 50.15 ± 3.02 | 51.24 ± 3.41 | 45.36 ± 1.73 | 51.87 ± 3.15 |
| (100) | (50) | (90) | (60) | (40) | (100) | (50) | (40) | (60) | |
| k1a | 32.81 ± 2.01 | 59.31 ± 0.01 | 33.88 ± 0.38 | 42.66 ± 0.29 | 38.26 ± 0.49 | 59.35 ± 0.23 | 59.18 ± 0.02 | 34.65 ± 1.53 | 59.35 ± 0.02 |
| (70) | (20) | (40) | (70) | (20) | (30) | (20) | (20) | (30) |
| Datasets | SUP | UFS2 | VCSDFS | DHBWSL | UDS2FS | LRPFS | RAFG | BGLR | FWFGFS |
|---|---|---|---|---|---|---|---|---|---|
| ORL | 73.27 ± 1.60 | 62.50 ± 0.97 | 70.95 ± 1.06 | 74.78 ± 1.21 | 70.40 ± 1.41 | 69.05 ± 1.28 | 73.49 ± 1.26 | 73.07 ± 1.33 | 74.87 ± 1.49 |
| (100) | (100) | (60) | (40) | (30) | (90) | (90) | (100) | (100) | |
| YaleB | 20.57 ± 0.66 | 36.17 ± 0.54 | 14.48 ± 0.54 | 28.13 ± 0.48 | 16.22 ± 0.81 | 25.99 ± 0.26 | 15.01 ± 0.23 | 22.55 ± 0.49 | 33.26 ± 0.62 |
| (30) | (80) | (50) | (20) | (20) | (20) | (40) | (20) | (40) | |
| imm40 | 77.31 ± 1.27 | 75.68 ± 1.47 | 68.70 ± 1.27 | 74.22 ± 1.18 | 72.84 ± 1.15 | 78.40 ± 1.36 | 78.34 ± 1.18 | 74.74 ± 1.48 | 85.95 ± 1.07 |
| (70) | (70) | (80) | (30) | (100) | (40) | (40) | (20) | (30) | |
| ALLAML | 12.51 ± 0.99 | 11.23 ± 2.53 | 37.86 ± 2.55 | 47.92 ± 3.88 | 15.58 ± 0.88 | 18.42 ± 2.75 | 16.76 ± 4.33 | 16.52 ± 0.62 | 53.51 ± 2.41 |
| (30) | (90) | (30) | (20) | (20) | (100) | (20) | (90) | (30) | |
| warpPIE10P | 26.17 ± 1.93 | 54.73 ± 1.95 | 25.19 ± 1.66 | 45.49 ± 3.03 | 41.81 ± 2.21 | 26.29 ± 1.94 | 55.13 ± 1.48 | 26.45 ± 2.29 | 58.06 ± 2.36 |
| (60) | (70) | (60) | (90) | (90) | (30) | (50) | (40) | (40) | |
| Jaffe | 89.04 ± 2.77 | 78.59 ± 3.66 | 83.84 ± 2.29 | 90.32 ± 2.54 | 87.80 ± 2.92 | 82.24 ± 3.90 | 87.89 ± 1.91 | 90.70 ± 3.68 | 91.05 ± 2.93 |
| (70) | (100) | (80) | (70) | (20) | (100) | (30) | (90) | (30) | |
| orlraws10P | 80.22 ± 1.82 | 64.69 ± 1.69 | 70.64 ± 3.23 | 85.46 ± 2.34 | 73.31 ± 4.16 | 69.12 ± 2.09 | 82.51 ± 2.48 | 80.48 ± 2.73 | 88.32 ± 2.74 |
| (20) | (100) | (90) | (50) | (20) | (100) | (90) | (100) | (90) | |
| RELATHE | 0.08 ± 0.02 | 0.33 ± 0.14 | 0.08 ± 0.02 | 7.04 ± 1.72 | 2.19 ± 0.21 | 5.47 ± 0.06 | 0.64 ± 0.03 | 0.27 ± 0.13 | 7.07 ± 0.32 |
| (100) | (80) | (100) | (60) | (50) | (20) | (30) | (30) | (100) | |
| Jaffe50 | 82.59 ± 2.81 | 70.06 ± 2.65 | 71.33 ± 2.56 | 79.51 ± 2.66 | 83.22 ± 3.52 | 83.20 ± 2.15 | 84.77 ± 2.65 | 82.57 ± 2.32 | 92.27 ± 3.32 |
| (40) | (100) | (50) | (100) | (80) | (100) | (90) | (40) | (80) | |
| Yale64 | 57.54 ± 2.43 | 47.33 ± 2.64 | 50.07 ± 1.44 | 50.58 ± 3.02 | 54.56 ± 1.68 | 46.07 ± 2.18 | 60.22 ± 2.86 | 56.05 ± 2.79 | 62.43 ± 1.98 |
| (90) | (90) | (30) | (100) | (20) | (80) | (100) | (90) | (100) | |
| UMIST_fac | 65.19 ± 1.62 | 62.65 ± 1.50 | 63.51 ± 1.64 | 67.23 ± 2.28 | 63.03 ± 1.62 | 66.55 ± 1.28 | 69.39 ± 1.44 | 64.54 ± 1.69 | 69.87 ± 1.26 |
| (70) | (80) | (90) | (60) | (70) | (100) | (80) | (60) | (60) | |
| k1a | 8.45 ± 0.24 | 0.32 ± 0.22 | 8.00 ± 0.06 | 8.77 ± 0.42 | 8.10 ± 0.09 | 1.97 ± 0.31 | 1.88 ± 0.25 | 8.28 ± 0.28 | 1.04 ± 0.38 |
| (70) | (80) | (40) | (70) | (20) | (40) | (20) | (20) | (90) |
| Datasets | Original Dataset | Data Type | Noise Type and Level |
|---|---|---|---|
| OR_8 | ORL | Face image | Blocknoise () |
| OR_12 | ORL | Face image | Blocknoise () |
| OR_16 | ORL | Face image | Blocknoise () |
| imm40_8 | imm40 | Face image | Blocknoise () |
| imm40_12 | imm40 | Face image | Blocknoise () |
| imm40_16 | imm40 | Face image | Blocknoise () |
| Datasets | SUP | UFS2 | VCSDFS | DHBWSL | UDS2FS | LRFGS | RAFG | BGLR | FWFGFS |
|---|---|---|---|---|---|---|---|---|---|
| OR_8 | 52.45 ± | 40.67 ± | 49.90 ± | 50.97 ± | 49.80 ± | 48.26 ± | 53.38 ± | 52.31 ± | 55.15 ± |
| 2.62 (100) | 1.40 (100) | 2.11 (60) | 2.08 (80) | 2.15 (40) | 2.80 (100) | 1.96 (100) | 2.83 (100) | 2.07 (60) | |
| OR_12 | 51.58 ± | 40.52 ± | 49.30 ± | 50.75 ± | 48.00 ± | 47.40 ± | 53.28 ± | 52.21 ± | 53.43 ± |
| 3.15 (100) | 1.26 (100) | 2.34 (100) | 2.91 (100) | 1.72 (40) | 2.28 (100) | 2.56 (90) | 2.19 (100) | 2.88 (100) | |
| OR_16 | 51.28 ± | 40.76 ± | 49.20 ± | 50.38 ± | 47.71 ± | 45.62 ± | 53.38 ± | 51.78 ± | 53.95 ± |
| 2.54 (100) | 2.15 (100) | 1.83 (100) | 2.33 (80) | 2.03 (50) | 2.04 (100) | 2.87 (90) | 2.02 (100) | 2.12 (60) | |
| imm40_8 | 66.77 ± | 53.54 ± | 43.27 ± | 50.77 ± | 57.31 ± | 59.50 ± | 59.87 ± | 51.45 ± | 70.14 ± |
| 3.14 (90) | 2.75 (70) | 2.11 (20) | 3.08 (90) | 2.95 (100) | 3.29 (40) | 3.39 (60) | 2.46 (60) | 3.84 (20) | |
| imm40_12 | 57.12 ± | 53.14 ± | 40.14 ± | 52.37 ± | 57.37 ± | 55.41 ± | 63.60 ± | 54.18 ± | 68.18 ± |
| 2.48 (60) | 2.36 (100) | 2.09 (20) | 2.03 (30) | 1.73 (90) | 3.42 (100) | 2.84 (20) | 2.34 (50) | 3.00 (20) | |
| imm40_16 | 55.66 ± | 53.14 ± | 38.85 ± | 50.89 ± | 47.06 ± | 50.83 ± | 59.54 ± | 52.04 ± | 69.66 ± |
| 2.89 (50) | 2.33 (20) | 1.92 (100) | 3.26 (30) | 2.63 (20) | 2.02 (100) | 3.42 (70) | 3.10 (50) | 2.81 (20) |
| Datasets | SUP | UFS2 | VCSDFS | DHBWSL | UDS2FS | LRFGS | RAFG | BGLR | FWFGFS |
|---|---|---|---|---|---|---|---|---|---|
| OR_8 | 72.48 ± | 62.08 ± | 69.93 ± | 71.84 ± | 69.67 ± | 68.52 ± | 72.76 ± | 72.21 ± | 73.41 ± |
| 1.52 (100) | 1.31 (100) | 1.37 (100) | 1.31 (80) | 1.17 (30) | 1.55 (100) | 1.30 (100) | 1.74 (100) | 1.19 (70) | |
| OR_12 | 71.94 ± | 61.47 ± | 69.23 ± | 70.81 ± | 68.10 ± | 67.62 ± | 72.79 ± | 71.81 ± | 72.80 ± |
| 1.69 (100) | 0.91 (100) | 1.38 (100) | 1.56 (80) | 1.14 (40) | 1.37 (100) | 1.41 (90) | 1.60 (100) | 1.75 (80) | |
| OR_16 | 71.13 ± | 61.18 ± | 69.90 ± | 70.50 ± | 68.41 ± | 68.75 ± | 72.56 ± | 71.43 ± | 72.74 ± |
| 1.65 (100) | 1.02 (100) | 1.59 (100) | 1.48 (80) | 1.17 (30) | 1.35 (100) | 1.23 (100) | 1.15 (100) | 1.27 (80) | |
| imm40_8 | 82.75 ± | 73.87 ± | 66.68 ± | 72.61 ± | 77.31 ± | 78.30 ± | 78.51 ± | 72.79 ± | 85.76 ± |
| 1.43 (90) | 1.58 (70) | 1.66 (100) | 1.22 (30) | 1.48 (100) | 1.62 (40) | 1.19 (40) | 1.01 (60) | 1.42 (30) | |
| imm40_12 | 77.99 ± | 74.21 ± | 64.25 ± | 73.92 ± | 77.15 ± | 74.38 ± | 80.27 ± | 74.06 ± | 83.47 ± |
| 1.13 (60) | 1.14 (90) | 1.20 (20) | 1.21 (30) | 1.45 (100) | 1.87 (100) | 1.43 (20) | 1.29 (50) | 1.36 (20) | |
| imm40_16 | 77.89 ± | 73.42 ± | 63.10 ± | 73.04 ± | 69.90 ± | 70.78 ± | 78.33 ± | 72.72 ± | 84.76 ± |
| 1.03 (50) | 1.05 (20) | 1.50 (100) | 1.46 (30) | 1.33 (20) | 1.41 (100) | 1.30 (40) | 1.37 (50) | 1.26 (20) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Ma, Z.; Ma, J.; Li, H. Robust Unsupervised Feature Selection Algorithm Based on Fuzzy Anchor Graph. Entropy 2025, 27, 827. https://doi.org/10.3390/e27080827
Yan Z, Ma Z, Ma J, Li H. Robust Unsupervised Feature Selection Algorithm Based on Fuzzy Anchor Graph. Entropy. 2025; 27(8):827. https://doi.org/10.3390/e27080827
Chicago/Turabian StyleYan, Zhouqing, Ziping Ma, Jinlin Ma, and Huirong Li. 2025. "Robust Unsupervised Feature Selection Algorithm Based on Fuzzy Anchor Graph" Entropy 27, no. 8: 827. https://doi.org/10.3390/e27080827
APA StyleYan, Z., Ma, Z., Ma, J., & Li, H. (2025). Robust Unsupervised Feature Selection Algorithm Based on Fuzzy Anchor Graph. Entropy, 27(8), 827. https://doi.org/10.3390/e27080827





