Enhancing Prediction by Incorporating Entropy Loss in Volatility Forecasting
Abstract
1. Introduction
2. Materials and Methods
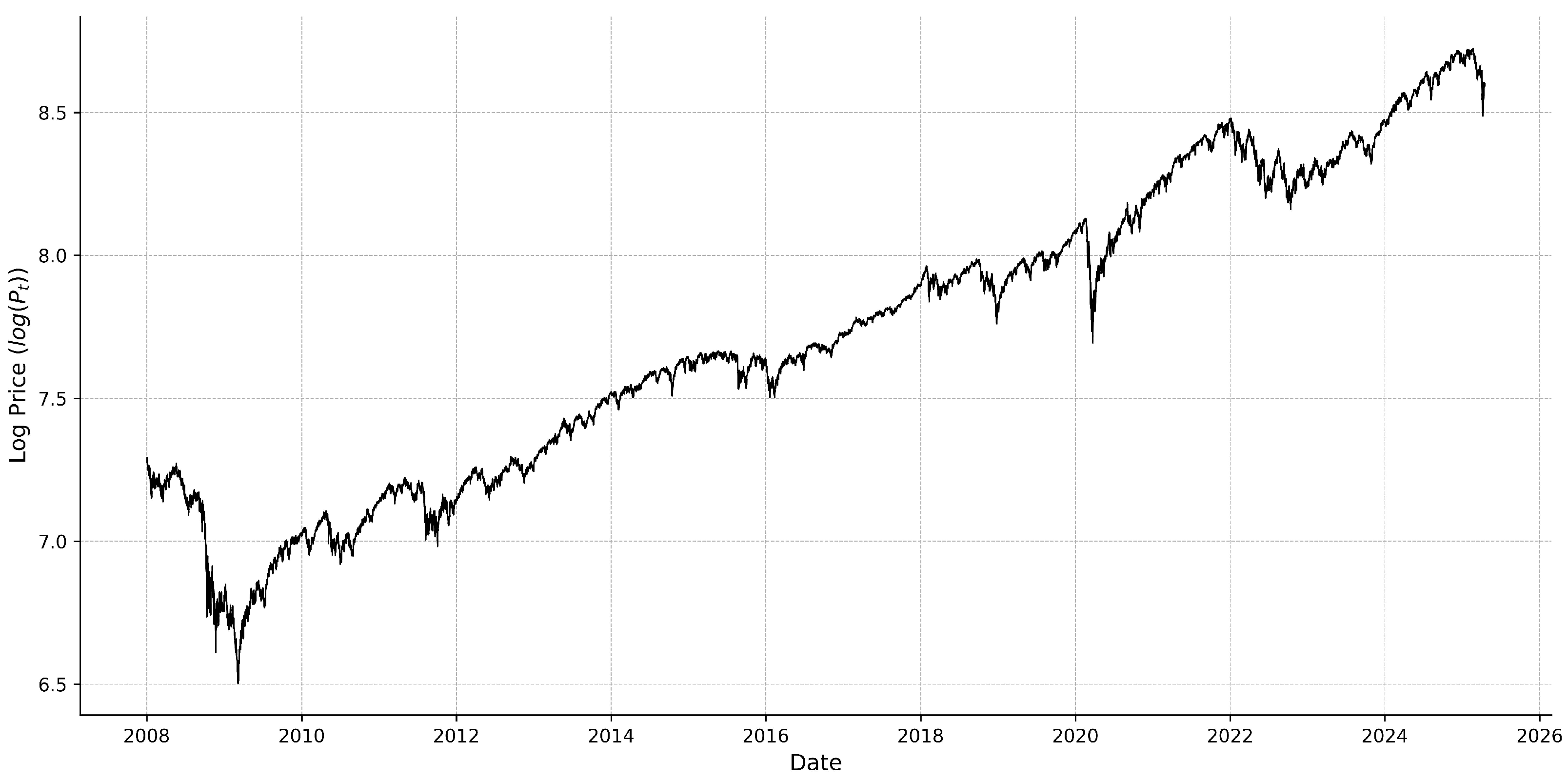
2.1. Data Description
- Datetime: indicating the timestamp of the 5 min subinterval of the values (e.g., “2008-01-02 09:35:00”);
- Open: the opening price at the beginning of a 5 min subinterval (e.g., “1470.17”);
- High: the highest price reached within a 5 min subinterval (e.g., “1470.17”);
- Low: the lowest price reached within a 5 min subinterval (e.g., “1467.88”);
- Close: the closing price at the end of the 5 min subinterval (e.g., “1469.49”).
- Last-minute updates or new information, such as macroeconomic announcements and earnings reports;
- Herding behavior or panic selling, plausibly caused by changes in investor sentiment [53];
- Changes in market liquidity and trading intensity reinforce price volatility, particularly during periods of stress [54].
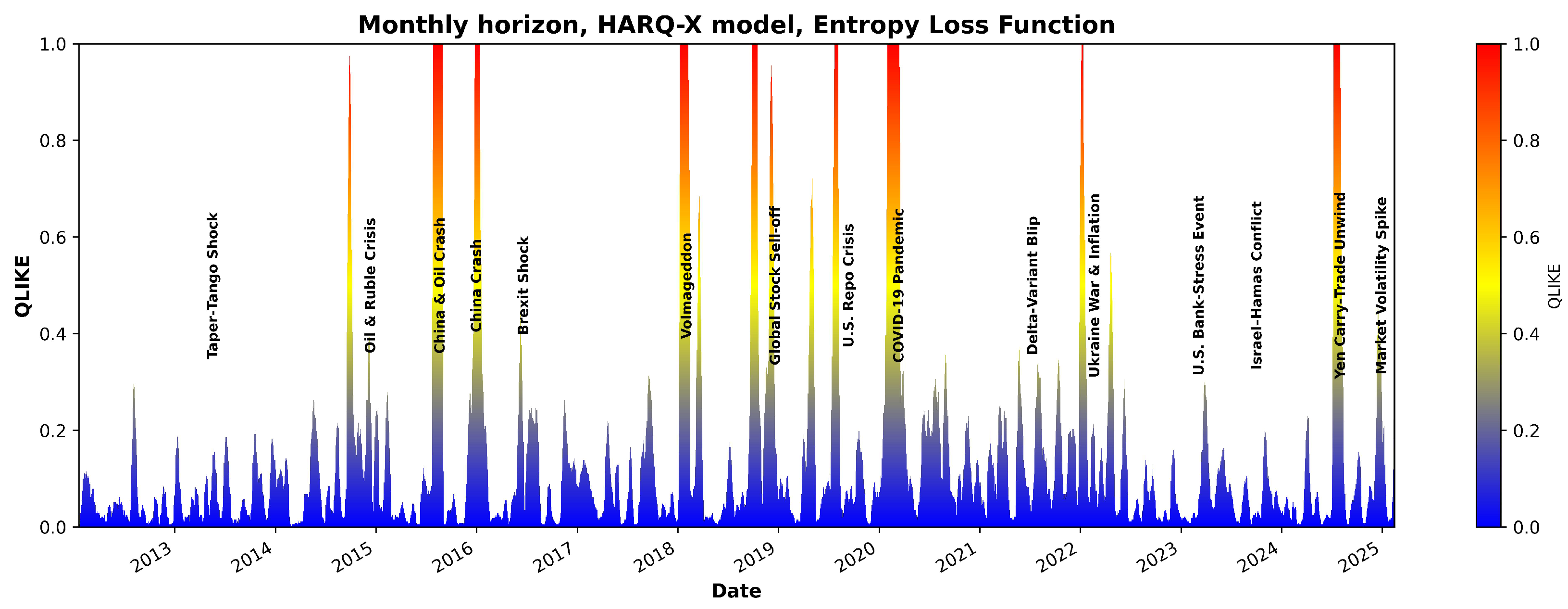
- The great financial crisis in 2008–2009.
- The European sovereign debt crisis in 2010–2012.
- The “Taper Tantrum” in 2013.
- The Chinese stock market turmoil and oil price crash in 2015–2016.
- The U.S.–China trade war in 2018.
- The COVID-19 pandemic in 2020.
- Inflation, aggressive rate hikes, and the Russia–Ukraine war in 2022. A combination of factors created a bear market for most of 2022:
- -
- High inflation;
- -
- Monetary tightening;
- -
- Russia–Ukraine conflict.
- The U.S. regional banking crisis and Israel–Hamas conflict in 2023.
- The Artificial Intelligence (AI) boom in 2023–2025.
- Weakening corporate outlook, political uncertainty, and Israel–Iran 12-day war in 2025.
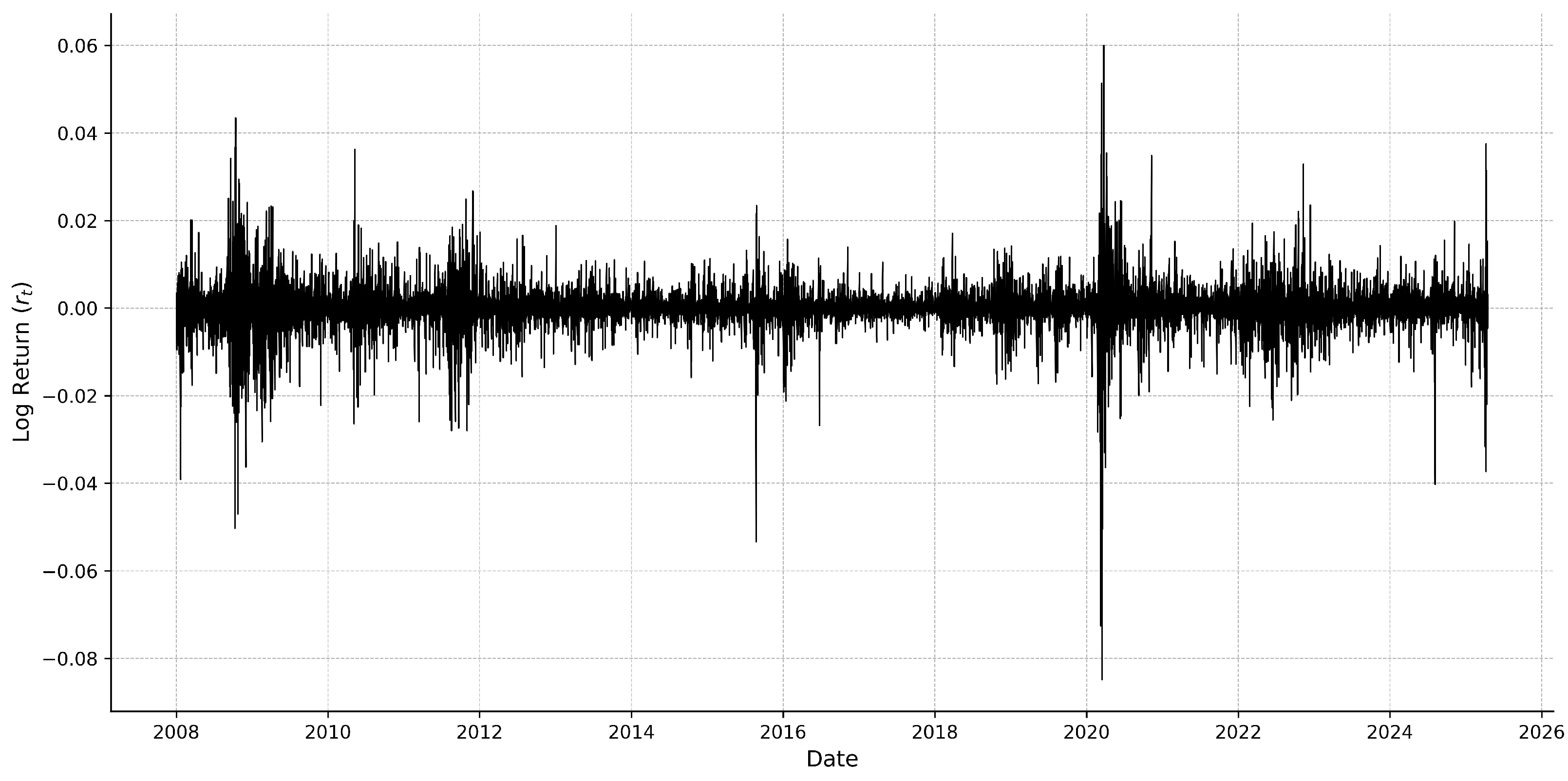
2.2. Return and Realized Measure Construction
2.3. Stochastic Modeling of Log Price Dynamics
- = 0—the starting point is always equal to zero.
- With probability 1, the function is continuous over the period t.
- The process has stationary, independent increments.
- The increment follows a NORMAL (0 t) distribution.
2.3.1. Classical Approach: Geometric Brownian Motion (GBM)
2.3.2. Generalized Approach: Stochastic Volatility Models
2.4. Heterogeneous Autoregressive-Type Model Specifications
2.4.1. Heterogeneous Autoregressive Model of Realized Volatility
2.4.2. Heterogeneous Autoregressive Model of Realized Quarticity
2.5. HAR Model Estimation and Evaluation
2.5.1. Ordinary Least Squares
2.5.2. Weighted Least Squares
2.5.3. Least Absolute Deviations
2.5.4. Robust Regression Models
2.5.5. Entropy Loss Function
2.5.6. Summary
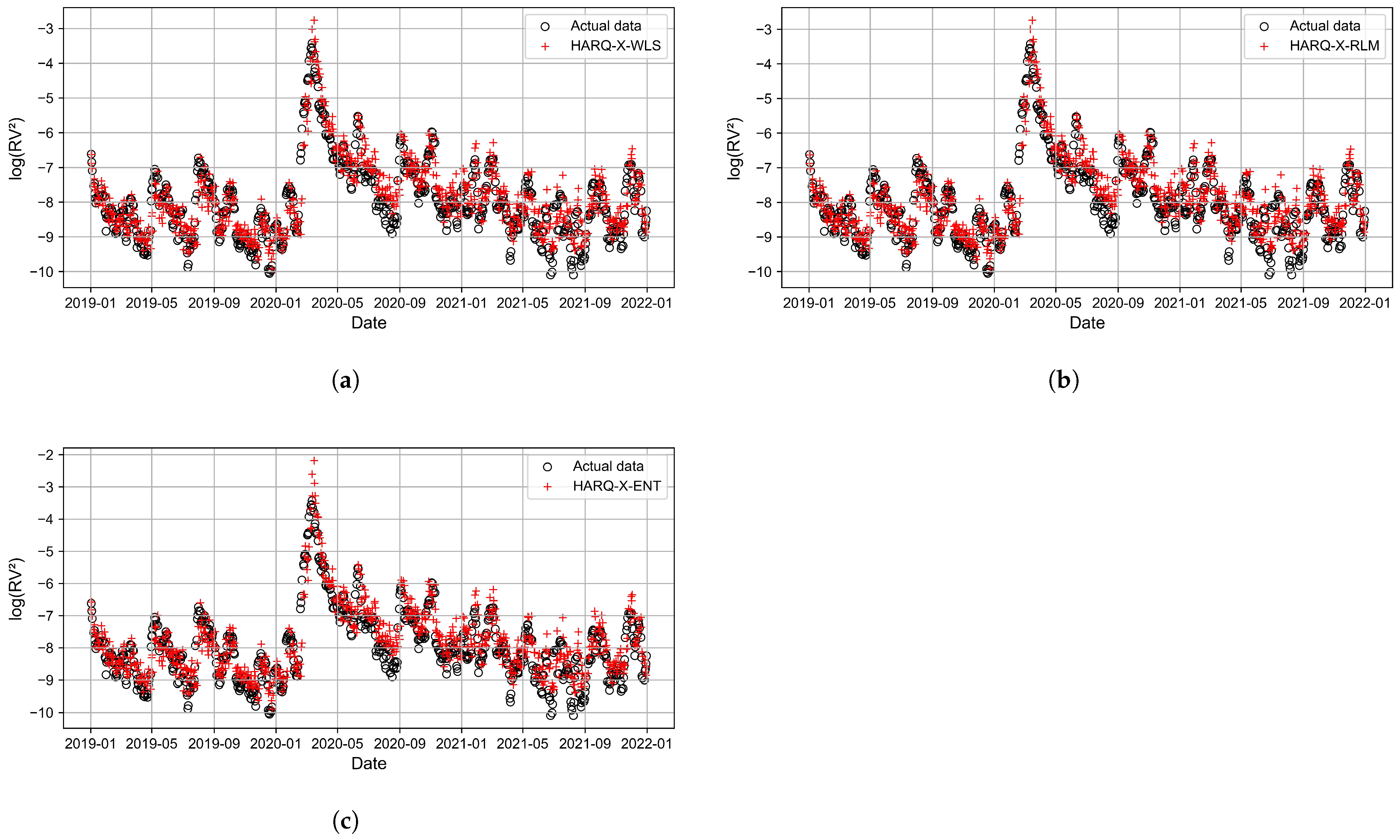
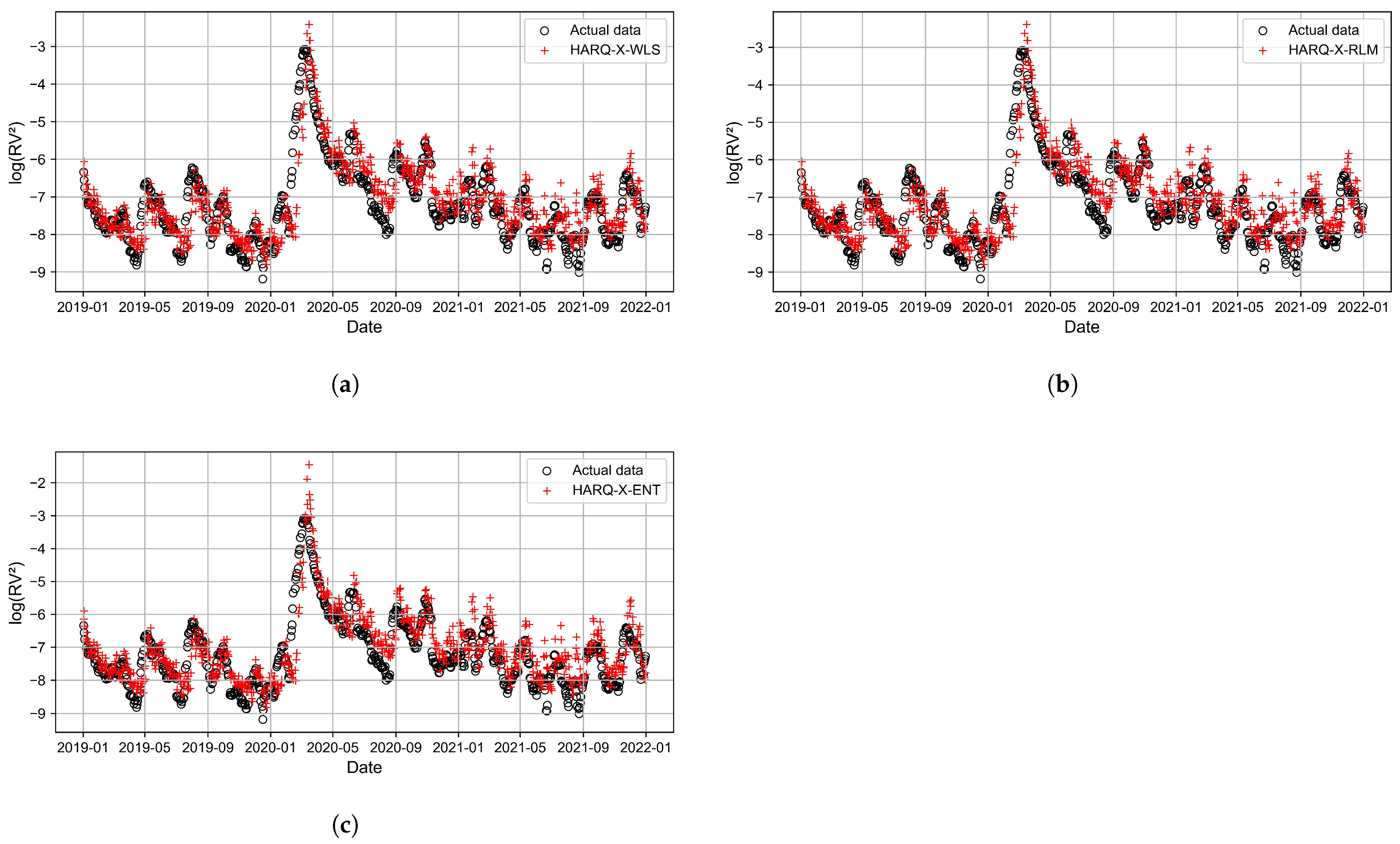
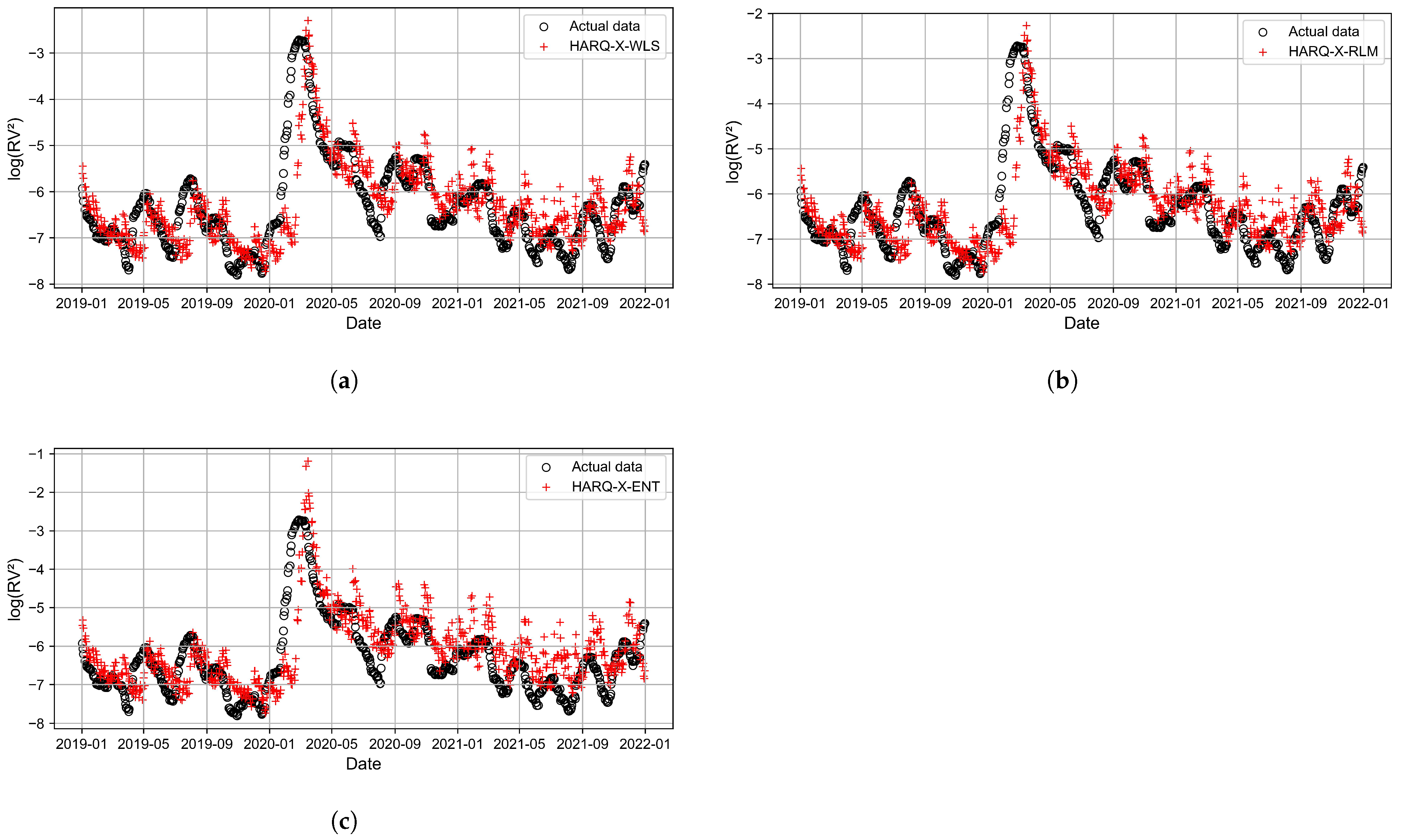
2.6. Forecast Design
2.6.1. Rolling Window Forecasting
2.6.2. Forecasting Targets
2.7. Evaluation Metrics
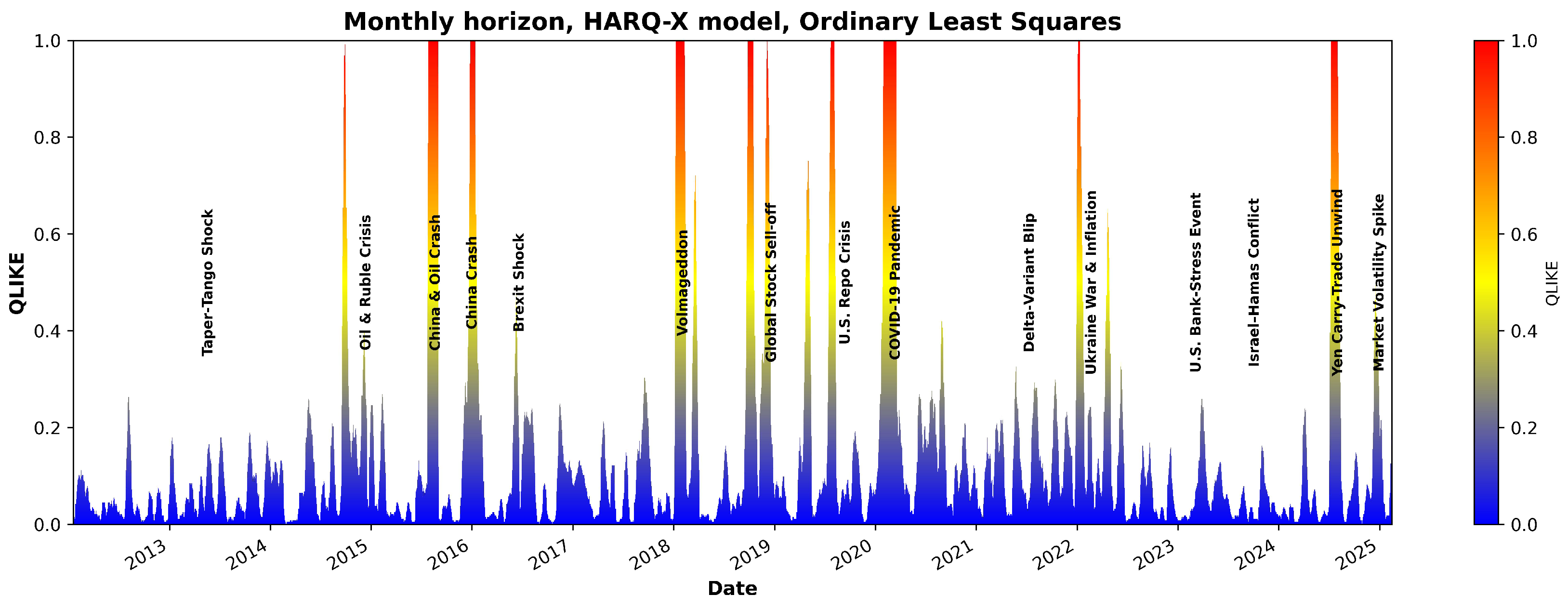
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARCH | Autoregressive Conditional Heteroskedasticity |
| ARIMA | Autoregressive Integrated Moving Average |
| Bi-RNN | Bidirectional Recurrent Neural Network |
| CNN | Convolutional Neural Network |
| ECON | Economics |
| EGARCH | Exponential Generalized Autoregressive Conditional Heteroskedasticity |
| ELF | Entropy Loss Function |
| ESN | Echo State Neural Network |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| GBM | Geometric Brownian Motion |
| GBP | (GRU–BiRNN–PSO) |
| GJR-GARCH | Glosten–Jagannathan–Runkle Generalized Autoregressive Conditional Heteroskedasticity |
| GRU | Gated Recurrent Unit |
| HAR | Heterogeneous Autoregressive |
| HARQ | Heterogeneous Autoregressive model with Realized Quarticity |
| HAR-RV | Heterogeneous Autoregressive model of Realized Volatility |
| HAR-RV-CJ | Heterogeneous Autoregressive model of Realized Variance with Continuous and Jump components |
| HARQ-X | Heterogeneous Autoregressive Model with realized Quarticity and Exogenous Variables |
| IQ | Integrated Quarticity |
| LAD | Least Absolute Deviation |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LSTM | Long Short-Term Memory |
| LST-HAR | Logistic Smooth Transition HAR |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MT-GARCH | Multi-Task Generalized Autoregressive Conditional Heteroskedasticity |
| MTL-GARCH | Multi-Task Learning Generalized |
| NARX | Nonlinear Autoregressive with Exogenous Input |
| NBEATSx | Neural Basis Expansion Analysis for Time Series with Exogenous Variables |
| NLP | Natural Language Processing |
| OLS | Ordinary Least Squares |
| PCA | Principal Component Analysis |
| PSO | Particle Swarm Optimization |
| QLIKE | Quasi-Likelihood Loss |
| RF | Random Forest |
| RLM | Robust Linear Model |
| RQ | Realized Quarticity |
| RV | Realized Variance |
| SPX | Standard & Poor’s 500 |
| SV | Stochastic Volatility |
| SVM | Support Vector Machine |
| TCN | Temporal Convolutional Network |
| V-HAR | Vector HAR |
| VIX | Chicago Board Options Exchange Volatility |
| VMD | Variational Mode Decomposition |
| WLS | Weighted Least Squares |
References
- Cambridge Dictionary. Volatility. 2025. Available online: https://dictionary.cambridge.org/dictionary/english/volatility (accessed on 3 May 2025).
- Correia, M.; Kang, J.; Richardson, S. Asset volatility. Rev. Account. Stud. 2018, 23, 37–94. [Google Scholar] [CrossRef]
- Schwert, G.W. Why Does Stock Market Volatility Change Over Time? J. Financ. 1989, 44, 1115–1153. [Google Scholar] [CrossRef]
- Chou, R.Y.; Chou, H.; Liu, N. Range Volatility: A Review of Models and Empirical Studies. In Handbook of Financial Econometrics and Statistics; Lee, C.F., Lee, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 2029–2050. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Nelson, D.B. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 1991, 59, 347–370. [Google Scholar] [CrossRef]
- Pilbeam, K.; Langeland, K.N. Forecasting exchange rate volatility: GARCH models versus implied volatility forecasts. Int. Econ. Econ. Policy 2015, 12, 127–142. [Google Scholar] [CrossRef]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T. Answering the Skeptics: Yes, Standard Volatility Models do Provide Accurate Forecasts. Int. Econ. Rev. 1998, 39, 885–905. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Econometric Analysis of Realized Volatility and its Use in Estimating Stochastic Volatility Models. J. R. Stat. Soc. Ser. Stat. Methodol. 2002, 64, 253–280. [Google Scholar] [CrossRef]
- Poon, S.H.; Granger, C.W.J. Forecasting Volatility in FInancial Markets: A Review. J. Econ. Lit. 2003, 41, 478. [Google Scholar] [CrossRef]
- Gatheral, J.; Thibault, J.; Rosenbaum, M. Volatility is rough. Quant. Financ. 2018, 18, 933–949. [Google Scholar] [CrossRef]
- Ulugbode, M.A.; Shittu, O.I. Transition E-Garch Model for Modeling and Forecasting Volatility of Equity Stock Returns in Nigeria Stock Exchange. Int. J. Res. Innov. Soc. Sci. (IJRISS) 2024, VII, 2120–2134. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Labys, P. Modeling and Forecasting Realized Volatility. Econometrica 2003, 71, 579–625. [Google Scholar] [CrossRef]
- Corsi, F. A Simple Approximate Long-Memory Model of Realized Volatility. J. Financ. Econom. 2009, 7, 174–196. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X. Roughing It Up: Including Jump Components in the Measurement, Modeling, and Forecasting of Return Volatility. Rev. Econ. Stat. 2007, 89, 701–720. [Google Scholar] [CrossRef]
- Patton, A.J.; Sheppard, K. Good Volatility, Bad Volatility: Signed Jumps and the Persistence of Volatility. Rev. Econ. Stat. 2015, 97, 683–697. [Google Scholar] [CrossRef]
- Prokopczuk, M.; Symeonidis, L.; Wese Simen, C. Do Jumps Matter for Volatility Forecasting? Evidence from Energy Markets. J. Futur. Mark. 2016, 36, 758–792. [Google Scholar] [CrossRef]
- Kambouroudis, D.S.; McMillan, D.G.; Tsakou, K. Forecasting Stock Return Volatility: A Comparison of GARCH, Implied Volatility, and Realized Volatility Models. J. Futur. Mark. 2016, 36, 1127–1163. [Google Scholar] [CrossRef]
- Bollerslev, T.; Patton, A.J.; Quaedvlieg, R. Exploiting the errors: A simple approach for improved volatility forecasting. J. Econom. 2016, 192, 1–18. [Google Scholar] [CrossRef]
- Qu, H.; Chen, W.; Niu, M.; Li, X. Forecasting realized volatility in electricity markets using logistic smooth transition heterogeneous autoregressive models. Energy Econ. 2016, 54, 68–76. [Google Scholar] [CrossRef]
- Cubadda, G.; Guardabascio, B.; Hecq, A. A vector heterogeneous autoregressive index model for realized volatility measures. Int. J. Forecast. 2017, 33, 337–344. [Google Scholar] [CrossRef]
- Clements, A.; Preve, D.P.A. A Practical Guide to harnessing the HAR volatility model. J. Bank. Financ. 2021, 133, 106285. [Google Scholar] [CrossRef]
- Li, Z.C.; Xie, C.; Wang, G.J.; Zhu, Y.; Zeng, Z.J.; Gong, J. Forecasting global stock market volatilities: A shrinkage heterogeneous autoregressive (HAR) model with a large cross-market predictor set. Int. Rev. Econ. Financ. 2024, 93, 673–711. [Google Scholar] [CrossRef]
- Michael, N.; Mihai, C.; Howison, S. Options-driven volatility forecasting. Quant. Financ. 2025, 25, 443–470. [Google Scholar] [CrossRef]
- Luong, C.; Dokuchaev, N. Forecasting of Realised Volatility with the Random Forests Algorithm. J. Risk Financ. Manag. 2018, 11, 61. [Google Scholar] [CrossRef]
- Bucci, A. Realized Volatility Forecasting with Neural Networks. J. Financ. Econom. 2020, 18, 502–531. [Google Scholar] [CrossRef]
- Zhang, C.X.; Li, J.; Huang, X.F.; Zhang, J.S.; Huang, H.C. Forecasting stock volatility and value-at-risk based on temporal convolutional networks. Expert Syst. Appl. 2022, 207, 117951. [Google Scholar] [CrossRef]
- Ge, W.; Lalbakhsh, P.; Isai, L.; Lenskiy, A.; Suominen, H. Neural Network-Based Financial Volatility Forecasting: A Systematic Review. ACM Comput. Surv. 2022, 55, 14:1–14:30. [Google Scholar] [CrossRef]
- Zahid, S.; Saleem, H.M.N. Stock Volatility Prediction Using Machine Learning during COVID-19. Stat. Comput. Interdiscip. Res. 2023, 5, 99–119. [Google Scholar] [CrossRef]
- Christensen, K.; Siggaard, M.; Veliyev, B. A Machine Learning Approach to Volatility Forecasting. J. Financ. Econom. 2023, 21, 1680–1727. [Google Scholar] [CrossRef]
- Souto, H.G.; Moradi, A. Introducing NBEATSx to realized volatility forecasting. Expert Syst. Appl. 2024, 242, 122802. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Cucuringu, M.; Qian, Z. Volatility Forecasting with Machine Learning and Intraday Commonality*. J. Financ. Econom. 2024, 22, 492–530. [Google Scholar] [CrossRef]
- Mensah, N.; Agbeduamenu, C.O.; Obodai, T.N.; Adukpo, T.K. Leveraging Machine Learning Techniques to Forecast Market Volatility in the U.S. EPRA Int. J. Econ. Bus. Manag. Stud. (EBMS) 2025, 12, 76–85. [Google Scholar]
- Lolic, M. Tree-Based Methods of Volatility Prediction for the S&P 500 Index. Computation 2025, 13, 84. [Google Scholar] [CrossRef]
- Beg, K. Comparative Analysis of Machine Learning Models for Sectoral Volatility Prediction in Financial Markets. J. Inf. Syst. Eng. Manag. 2025, 10, 837–846. [Google Scholar] [CrossRef]
- Mansilla-Lopez, J.; Mauricio, D.; Narváez, A. Factors, Forecasts, and Simulations of Volatility in the Stock Market Using Machine Learning. J. Risk Financ. Manag. 2025, 18, 227. [Google Scholar] [CrossRef]
- Monfared, S.A.; Enke, D. Volatility Forecasting Using a Hybrid GJR-GARCH Neural Network Model. Procedia Comput. Sci. 2014, 36, 246–253. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Fadic, A.; Minutolo, M.C. Volatility forecast using hybrid Neural Network models. Expert Syst. Appl. 2014, 41, 2437–2442. [Google Scholar] [CrossRef]
- Yang, R.; Yu, L.; Zhao, Y.; Yu, H.; Xu, G.; Wu, Y.; Liu, Z. Big data analytics for financial Market volatility forecast based on support vector machine. Int. J. Inf. Manag. 2020, 50, 452–462. [Google Scholar] [CrossRef]
- Trierweiler Ribeiro, G.; Alves Portela Santos, A.; Cocco Mariani, V.; dos Santos Coelho, L. Novel hybrid model based on echo state neural network applied to the prediction of stock price return volatility. Expert Syst. Appl. 2021, 184, 115490. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Yang, Y.; Zhou, K.; Kumar, M. Dynamic Prediction Model of Financial Asset Volatility Based on Bidirectional Recurrent Neural Networks. J. Organ. End User Comput. (JOEUC) 2024, 36, 1–23. [Google Scholar] [CrossRef]
- Mishra, A.K.; Renganathan, J.; Gupta, A. Volatility forecasting and assessing risk of financial markets using multi-transformer neural network based architecture. Eng. Appl. Artif. Intell. 2024, 133, 108–223. [Google Scholar] [CrossRef]
- Brini, A.; Toscano, G. SpotV2Net: Multivariate intraday spot volatility forecasting via vol-of-vol-informed graph attention networks. Int. J. Forecast. 2025, 41, 1093–1111. [Google Scholar] [CrossRef]
- Hu, N.; Yin, X.; Yao, Y. A novel HAR-type realized volatility forecasting model using graph neural network. Int. Rev. Financ. Anal. 2025, 98, 103881. [Google Scholar] [CrossRef]
- Li, H.; Huang, X.; Luo, F.; Zhou, D.; Cao, A.; Guo, L. Revolutionizing agricultural stock volatility forecasting: A comparative study of machine learning and HAR-RV models. J. Appl. Econ. 2025, 28, 2454081. [Google Scholar] [CrossRef]
- Kumar, S.; Rao, A.; Dhochak, M. Hybrid ML models for volatility prediction in financial risk management. Int. Rev. Econ. Financ. 2025, 98, 103915. [Google Scholar] [CrossRef]
- Wang, S.; Bai, Y.; Ji, T.; Fu, K.; Wang, L.; Lu, C.T. Stock Movement and Volatility Prediction from Tweets, Macroeconomic Factors and Historical Prices. In Proceedings of the 2023 IEEE International Conference on Big Data (BigData), Sorrento, Italy, 15–18 December 2023; pp. 1863–1872. [Google Scholar] [CrossRef]
- Shi, M.X.; Chen, C.C.; Huang, H.H.; Chen, H.H. Enhancing Volatility Forecasting in Financial Markets: A General Numeral Attachment Dataset for Understanding Earnings Calls. In Proceedings of the 13th International Joint Conference on Natural Language Processing and the 3rd Conference of the Asia-Pacific Chapter of the Association for Computational Linguistics (Volume 2: Short Papers); Park, J.C., Arase, Y., Hu, B., Lu, W., Wijaya, D., Purwarianti, A., Krisnadhi, A.A., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2023; pp. 37–42. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Yang, L.; Zhang, Y.; Dong, R. NLP-Based Analysis of Annual Reports: Asset Volatility Prediction and Portfolio Strategy Application. In Proceedings of the 32nd Irish Conference on Artificial Intelligence and Cognitive Science, CEUR Workshop Proceedings, Dublin, Ireland, 9–10 December 2024; Volume 3910, pp. 228–240. [Google Scholar]
- Baker, M.; Wurgler, J. Investor Sentiment in the Stock Market. J. Econ. Perspect. 2007, 21, 129–151. [Google Scholar] [CrossRef]
- Chordia, T.; Roll, R.; Subrahmanyam, A. Evidence on the speed of convergence to market efficiency. J. Financ. Econ. 2005, 76, 271–292. [Google Scholar] [CrossRef]
- Liu, L.Y.; Patton, A.J.; Sheppard, K. Does anything beat 5-min RV? A comparison of realized measures across multiple asset classes. J. Econom. 2015, 187, 293–311. [Google Scholar] [CrossRef]
- Andersen, T.G.; Tim, B.; Francis X, D.; Labys, P. The Distribution of Realized Exchange Rate Volatility. J. Am. Stat. Assoc. 2001, 96, 42–55. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S.E. Brownian Motion and Stochastic Calculus, 2nd ed.; Number 113 in Graduate texts in mathematics; Springer: New York, NY, USA, 1996. [Google Scholar]
- Szczypińska, A.; Piotrowski, E.W.; Makowski, M. Deterministic risk modelling: Newtonian dynamics in capital flow. Phys. A Stat. Mech. Its Appl. 2025, 665, 130499. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Comte, F.; Renault, E. Long memory in continuous-time stochastic volatility models. Math. Financ. 1998, 8, 291–323. [Google Scholar] [CrossRef]
- Zwanzig, R. Memory Effects in Irreversible Thermodynamics. Phys. Rev. 1961, 124, 983–992. [Google Scholar] [CrossRef]
- Müller, U.A.; Dacorogna, M.M.; Davé, R.D.; Olsen, R.B.; Pictet, O.V.; von Weizsäcker, J.E. Volatilities of different time resolutions—Analyzing the dynamics of market components. J. Empir. Financ. 1997, 4, 213–239. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 6th ed.; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Vera, J.F.; Heiser, W.J.; Murillo, A. Global Optimization in Any Minkowski Metric: A Permutation-Translation Simulated Annealing Algorithm for Multidimensional Scaling. J. Classif. 2007, 24, 277–301. [Google Scholar] [CrossRef]
- De Nolasco Santos, F.; D’Antuono, P.; Noppe, N.; Weijtjens, W.; Devriendt, C. Minkowski logarithmic error: A physics-informed neural network approach for wind turbine lifetime assessment. In Proceedings of the ESANN 2022 Proceedings, Bruges, Belgium, 5–7 October 2022; pp. 357–362. [Google Scholar] [CrossRef]
- Urniezius, R.; Survyla, A.; Paulauskas, D.; Bumelis, V.A.; Galvanauskas, V. Generic estimator of biomass concentration for Escherichia coli and Saccharomyces cerevisiae fed-batch cultures based on cumulative oxygen consumption rate. Microb. Cell Factories 2019, 18, 190. [Google Scholar] [CrossRef]
- Urniezius, R.; Survyla, A. Identification of Functional Bioprocess Model for Recombinant E. coli Cultivation Process. Entropy 2019, 21, 1221. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]






| Datetime | Open | High | Low | Close |
|---|---|---|---|---|
| 2008-01-02 09:35:00 | 1470.17 | 1470.17 | 1467.88 | 1469.49 |
| 2008-01-02 09:40:00 | 1469.78 | 1471.71 | 1469.39 | 1471.22 |
| 2008-01-02 09:45:00 | 1471.56 | 1471.77 | 1470.69 | 1470.78 |
| 2008-01-02 09:50:00 | 1470.28 | 1471.06 | 1470.1 | 1470.74 |
| 2008-01-02 09:55:00 | 1470.81 | 1470.81 | 1468.42 | 1469.37 |
| Interval Length () | Subintervals per Day | Notes |
|---|---|---|
| 1 min | 390 | Ultra-high frequency |
| 2 min | 195 | |
| 3 min | 130 | |
| 5 min | 78 | Standard for RV computation |
| 10 min | 39 | |
| 15 min | 26 | Lower frequency, less detail |
| 30 min | 13 | |
| 60 min (1 h) | 6.5 | Usually rounded to 6 or 7 |
| 195 min | 2 | Half-day intervals |
| 390 min | 1 | One daily observation (EOD) |
| OLS | LAD | WLSRQ | RLM p = 2.1 | RLM p = 1.3 | ELF = 0.1 | |
|---|---|---|---|---|---|---|
| Daily horizon | ||||||
| QLIKE | 0.342028 | 0.345926 | 0.342150 | 0.341260 | 0.345827 | 0.321536 |
| MAE | 0.579774 | 0.579553 | 0.579665 | 0.579930 | 0.579114 | 0.580111 |
| MSE | 0.541348 | 0.541339 | 0.541206 | 0.541537 | 0.540675 | 0.541350 |
| Weekly horizon | ||||||
| QLIKE | 0.166367 | 0.177811 | 0.166370 | 0.165485 | 0.173596 | 0.165114 |
| MAE | 0.384559 | 0.382425 | 0.384370 | 0.385148 | 0.382333 | 0.385893 |
| MSE | 0.251494 | 0.255576 | 0.251327 | 0.251533 | 0.253271 | 0.251493 |
| Biweekly horizon | ||||||
| QLIKE | 0.227243 | 0.248310 | 0.227262 | 0.227243 | 0.241540 | 0.223707 |
| MAE | 0.423649 | 0.421023 | 0.423434 | 0.424573 | 0.420693 | 0.426678 |
| MSE | 0.318779 | 0.326519 | 0.318584 | 0.318715 | 0.322992 | 0.318777 |
| Monthly horizon | ||||||
| QLIKE | 0.370091 | 0.436770 | 0.370073 | 0.365128 | 0.413238 | 0.359545 |
| MAE | 0.464938 | 0.459841 | 0.464795 | 0.467163 | 0.458579 | 0.473115 |
| MSE | 0.397698 | 0.419242 | 0.397519 | 0.397602 | 0.409113 | 0.397699 |
| OLS | LAD | WLSRQ | RLM p = 2.1 | RLM p = 1.3 | ELF = 0.1 | |
|---|---|---|---|---|---|---|
| Daily horizon | ||||||
| QLIKE | 0.308979 | 0.323848 | 0.308999 | 0.307671 | 0.319208 | 0.306458 |
| MAE | 0.543546 | 0.542170 | 0.5434 | 0.543920 | 0.541912 | 0.544287 |
| MSE | 0.478849 | 0.481396 | 0.478685 | 0.479025 | 0.479668 | 0.479030 |
| Weekly horizon | ||||||
| QLIKE | 0.155273 | 0.165662 | 0.155253 | 0.154416 | 0.162043 | 0.154245 |
| MAE | 0.366248 | 0.364350 | 0.366114 | 0.366870 | 0.364036 | 0.367386 |
| MSE | 0.231442 | 0.235199 | 0.231280 | 0.231505 | 0.233154 | 0.231651 |
| Biweekly horizon | ||||||
| QLIKE | 0.218227 | 0.239794 | 0.218224 | 0.216364 | 0.233033 | 0.215052 |
| MAE | 0.543546 | 0.542170 | 0.5434 | 0.543920 | 0.541912 | 0.544287 |
| MSE | 0.301743 | 0.309658 | 0.301538 | 0.301734 | 0.305979 | 0.302221 |
| Monthly horizon | ||||||
| QLIKE | 0.366199 | 0.431019 | 0.366162 | 0.361283 | 0.409767 | 0.356297 |
| MAE | 0.458733 | 0.453891 | 0.458593 | 0.460855 | 0.452515 | 0.466573 |
| MSE | 0.389303 | 0.409066 | 0.389112 | 0.389269 | 0.400158 | 0.390595 |
| OLS | LAD | WLSRQ | RLM p = 2.1 | RLM p = 1.3 | ELF = 0.1 | ELF = 0.01 | |
|---|---|---|---|---|---|---|---|
| Daily horizon | |||||||
| QLIKE | 0.278937 | 0.290429 | 0.278922 | 0.277805 | 0.287298 | 0.276995 | 0.268285 |
| MAE | 0.522870 | 0.523373 | 0.522898 | 0.523026 | 0.522701 | 0.523440 | 0.526647 |
| MSE | 0.446430 | 0.448930 | 0.446519 | 0.446398 | 0.447735 | 0.446812 | 0.449631 |
| Weekly horizon | |||||||
| QLIKE | 0.132194 | 0.138245 | 0.132158 | 0.131710 | 0.136197 | 0.131713 | 0.129863 |
| MAE | 0.345263 | 0.339749 | 0.345213 | 0.346180 | 0.340703 | 0.346390 | 0.350214 |
| MSE | 0.204014 | 0.203218 | 0.203967 | 0.204422 | 0.202857 | 0.204676 | 0.206861 |
| Biweekly horizon | |||||||
| QLIKE | 0.190002 | 0.206361 | 0.189978 | 0.188780 | 0.200254 | 0.188493 | 0.184266 |
| MAE | 0.384005 | 0.376994 | 0.383951 | 0.385496 | 0.377558 | 0.386880 | 0.396262 |
| MSE | 0.265001 | 0.266835 | 0.264918 | 0.265749 | 0.264141 | 0.267138 | 0.274253 |
| Monthly horizon | |||||||
| QLIKE | 0.337472 | 0.381946 | 0.337457 | 0.333633 | 0.367668 | 0.331365 | 0.319398 |
| MAE | 0.427724 | 0.417575 | 0.427714 | 0.430771 | 0.417262 | 0.437475 | 0.469005 |
| MSE | 0.353712 | 0.362413 | 0.353673 | 0.354721 | 0.356853 | 0.360805 | 0.389078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urniezius, R.; Petrauskas, R.; Vaitkus, V.; Karimov, J.; Brazauskas, K.; Repsyte, J.; Kacerauskiene, E.; Harms, T.; Dargiene, J.; Ezerskis, D. Enhancing Prediction by Incorporating Entropy Loss in Volatility Forecasting. Entropy 2025, 27, 806. https://doi.org/10.3390/e27080806
Urniezius R, Petrauskas R, Vaitkus V, Karimov J, Brazauskas K, Repsyte J, Kacerauskiene E, Harms T, Dargiene J, Ezerskis D. Enhancing Prediction by Incorporating Entropy Loss in Volatility Forecasting. Entropy. 2025; 27(8):806. https://doi.org/10.3390/e27080806
Chicago/Turabian StyleUrniezius, Renaldas, Rytis Petrauskas, Vygandas Vaitkus, Javid Karimov, Kestutis Brazauskas, Jolanta Repsyte, Egle Kacerauskiene, Torsten Harms, Jovita Dargiene, and Darius Ezerskis. 2025. "Enhancing Prediction by Incorporating Entropy Loss in Volatility Forecasting" Entropy 27, no. 8: 806. https://doi.org/10.3390/e27080806
APA StyleUrniezius, R., Petrauskas, R., Vaitkus, V., Karimov, J., Brazauskas, K., Repsyte, J., Kacerauskiene, E., Harms, T., Dargiene, J., & Ezerskis, D. (2025). Enhancing Prediction by Incorporating Entropy Loss in Volatility Forecasting. Entropy, 27(8), 806. https://doi.org/10.3390/e27080806







