Low-Complexity Automorphism Ensemble Decoding of Reed-Muller Codes Using Path Pruning
Abstract
1. Introduction
- From the perspective of polar codes, we investigate information set partitioning of RM codes based on the Plotkin construction. Leveraging a uniform partitioning of the factor graph permutation group (FGPG), which is a subgroup of the full automorphism group of RM codes, we prove that the subcode-based information set partitioning exhibits permutation invariance (PI) between any two automorphisms from the same subgroup of the FGPG. Additionally, we demonstrate that, for the AED of RM codes that uses automorphisms only from the FGPG, the PI property makes it possible for the SC or SCL constituent decoders to generate identical partial information bit estimates, resulting in a notable subcode estimate convergence (SEC) phenomenon during decoding.
- We propose a subcode-based partial constituent metric (SPCM) to detect the SEC in the AED that employs the SC or SCL constituent decoders. We prove that under both theoretical and implementation-friendly forms, the SPCMs of SC (or SCL) constituent decoders that use automorphisms from the same subgroup of the FGPG are identical once SEC occurs. Furthermore, we find that the intensity of SEC can serve as a runtime noise level indicator for the corrupted codeword, where a strong SEC typically indicates a high redundancy of the decoding capacity in the AED. Based on this observation, we develop an SEC-aided path pruning method for AED, which allows only a few constituent decoders to continue decoding when the intensity of SEC exceeds a preset threshold.
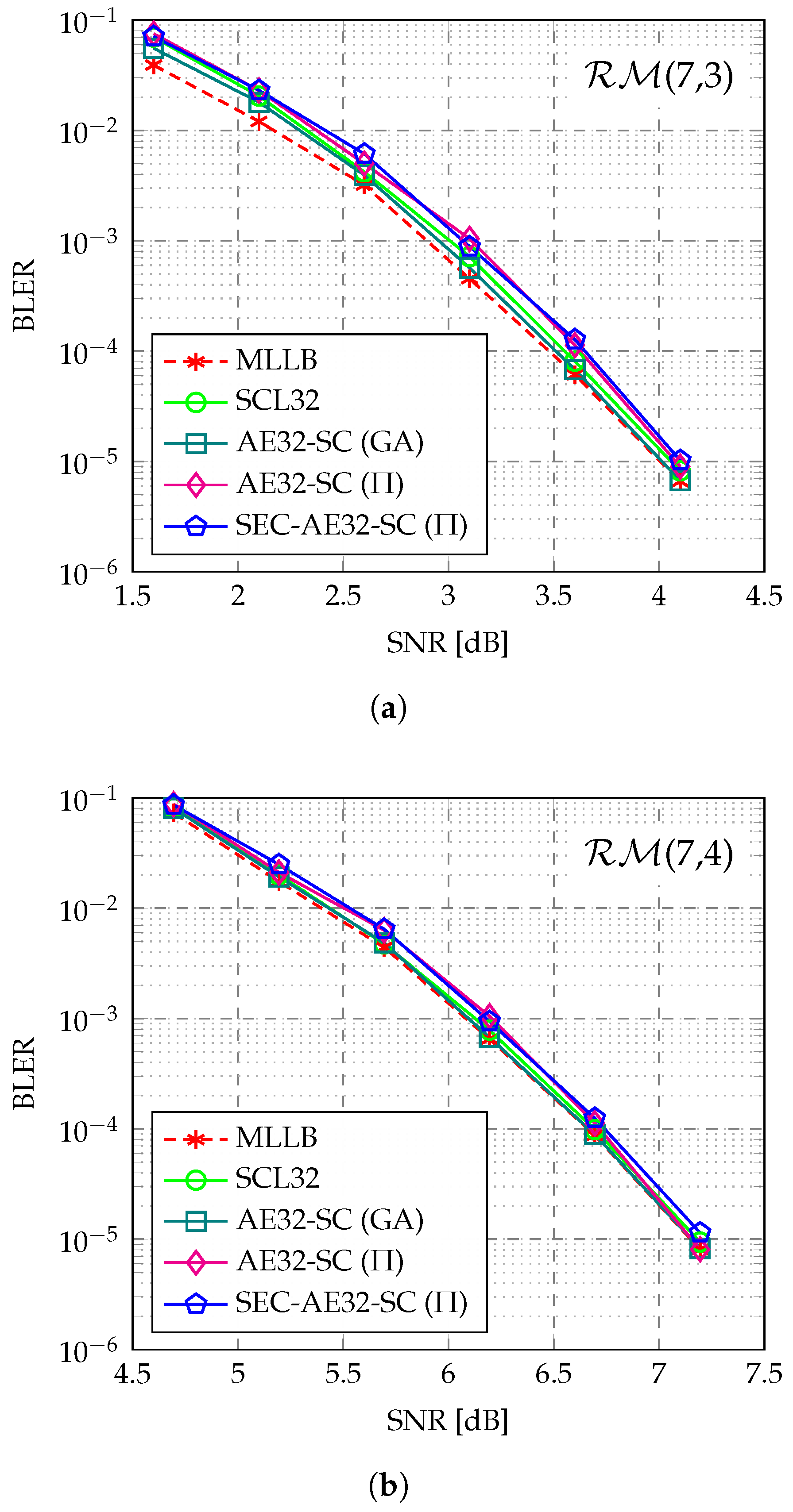
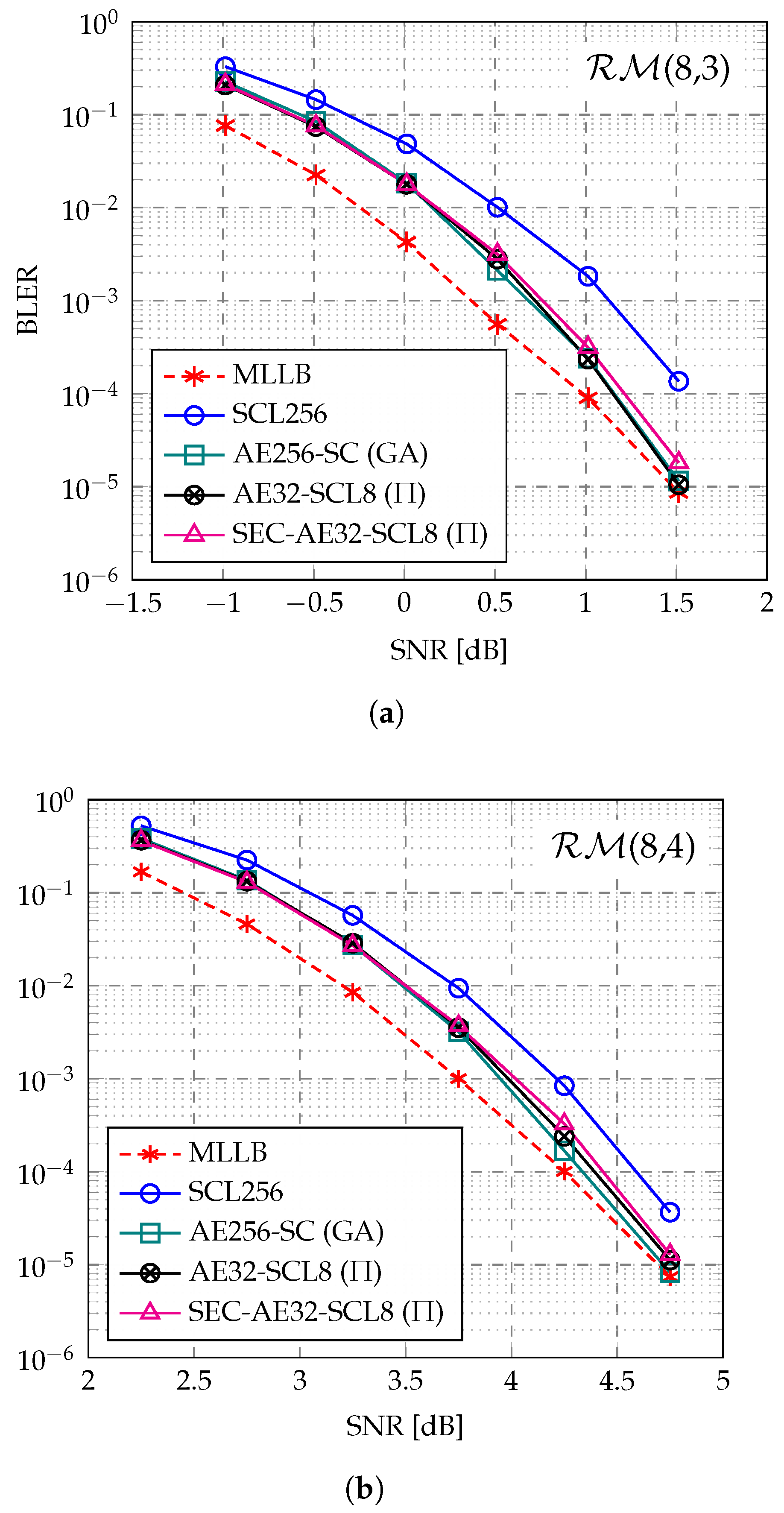
- The block error rate (BLER) and decoding complexity of the proposed SEC-aided AED (SEC-AED) are extensively evaluated across multiple short RM codes, covering different code lengths and rates. The numerical results demonstrate that the proposed SEC-AED incurs negligible BLER degradation to the AED, maintaining near ML performance for RM decoding. Additionally, at a low target BLER of around , our proposed SEC-AED achieves complexity reductions of up to 43.5% and 67.6% under fully parallel and partially parallel implementations, respectively. The SEC-aided path pruning technique can serve as an efficient power-reduction technology in the hardware-based low-latency AED for RM codes.
2. Preliminaries
2.1. Notations
2.2. Definition of RM Codes via Hadamard Transforms
2.3. SC and SCL Decoding
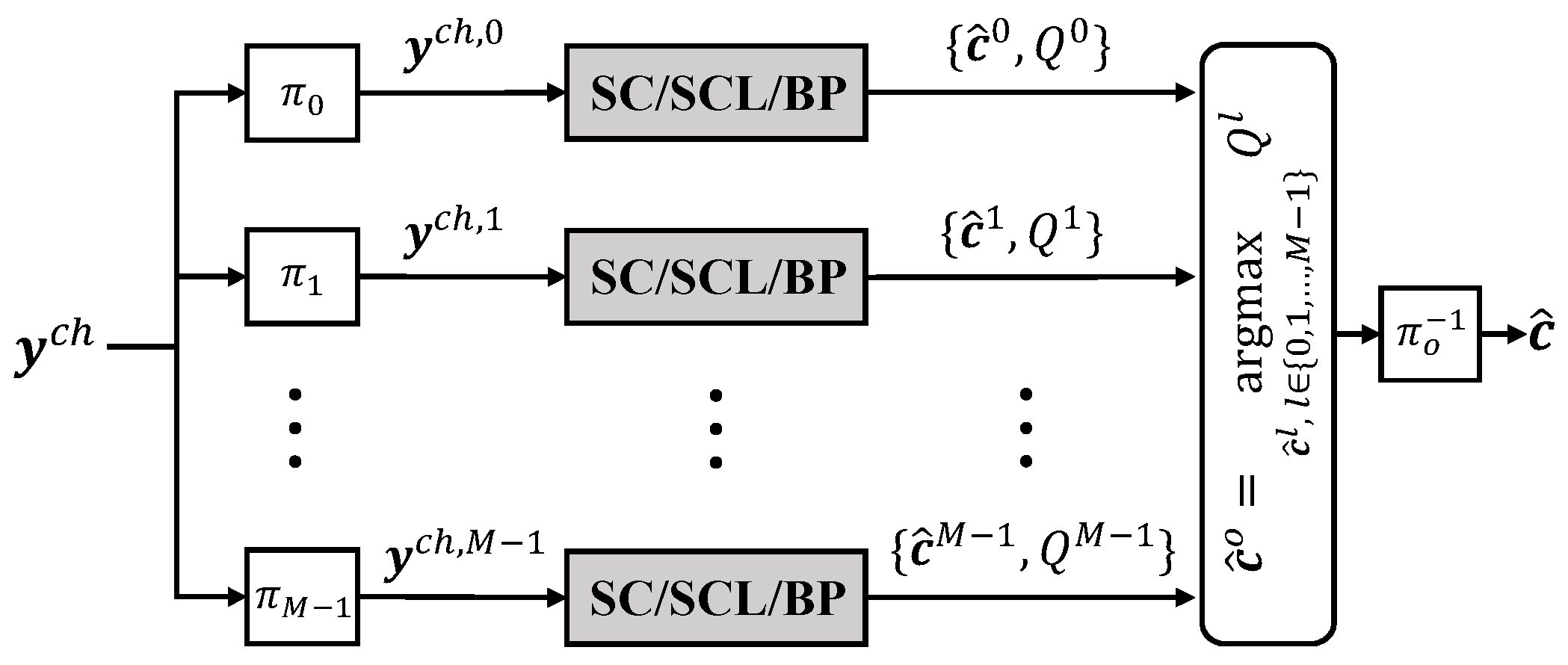
2.4. Automorphism Ensemble Decoding
2.5. SC- and SCL-Based AED Using Factor Graph Permutation Group
3. Subcode Estimate Convergence-Aided Path Pruning
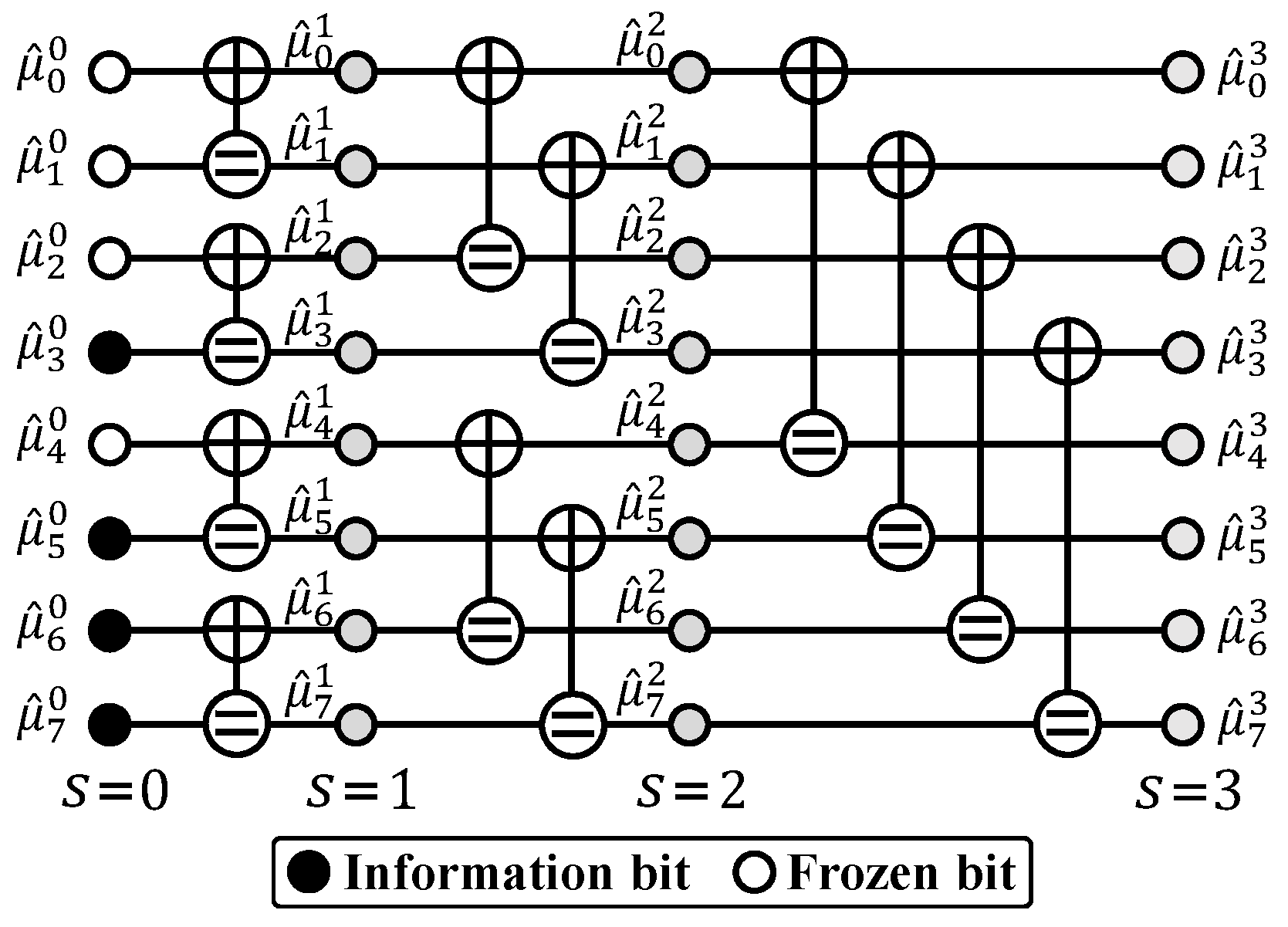
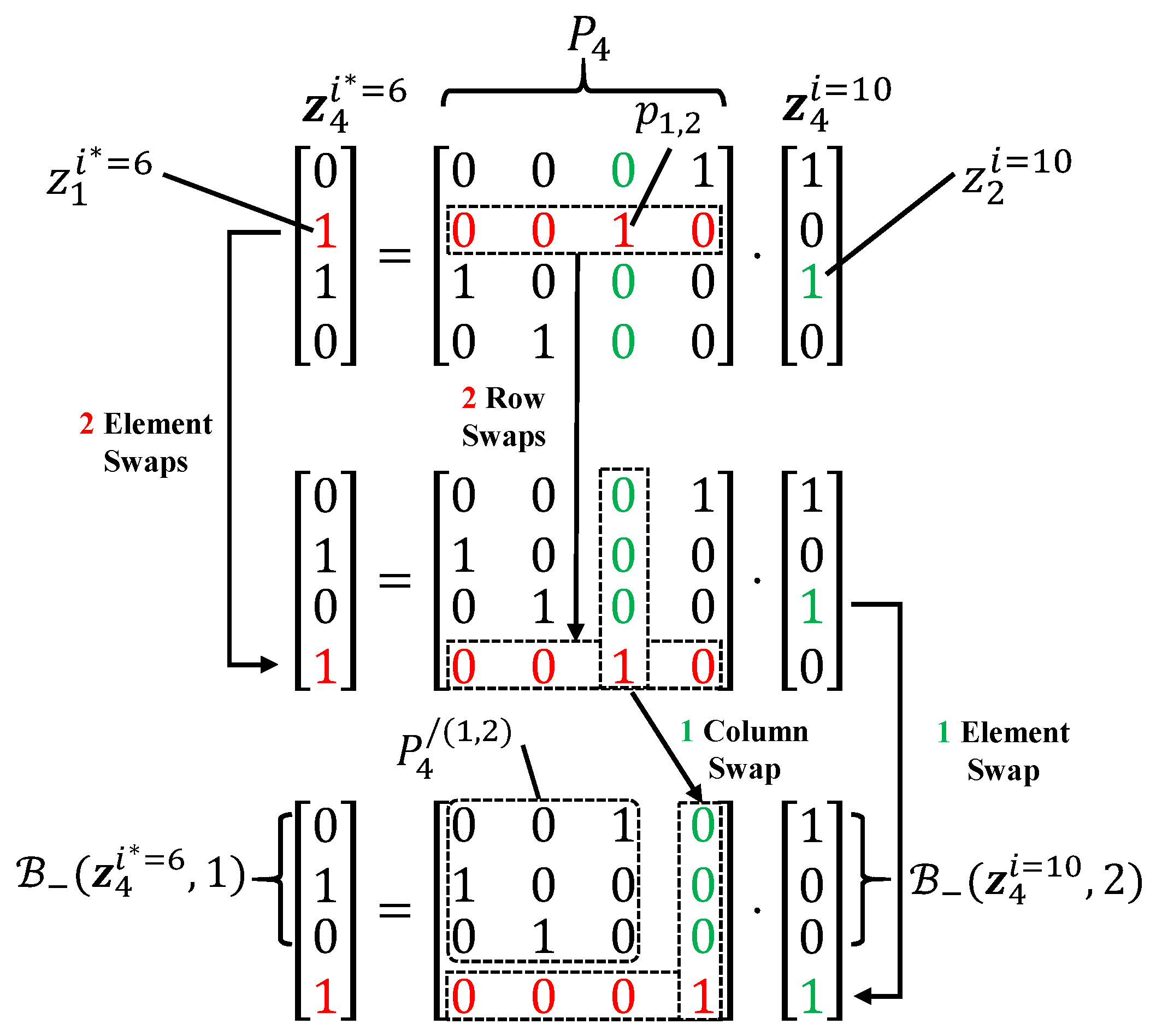
3.1. Subcode-Based Partitioning of Information Set
3.2. Permutation Invariance of Information Set Partitioning
3.3. Subcode-Based Partial Constituent Metric Convergence
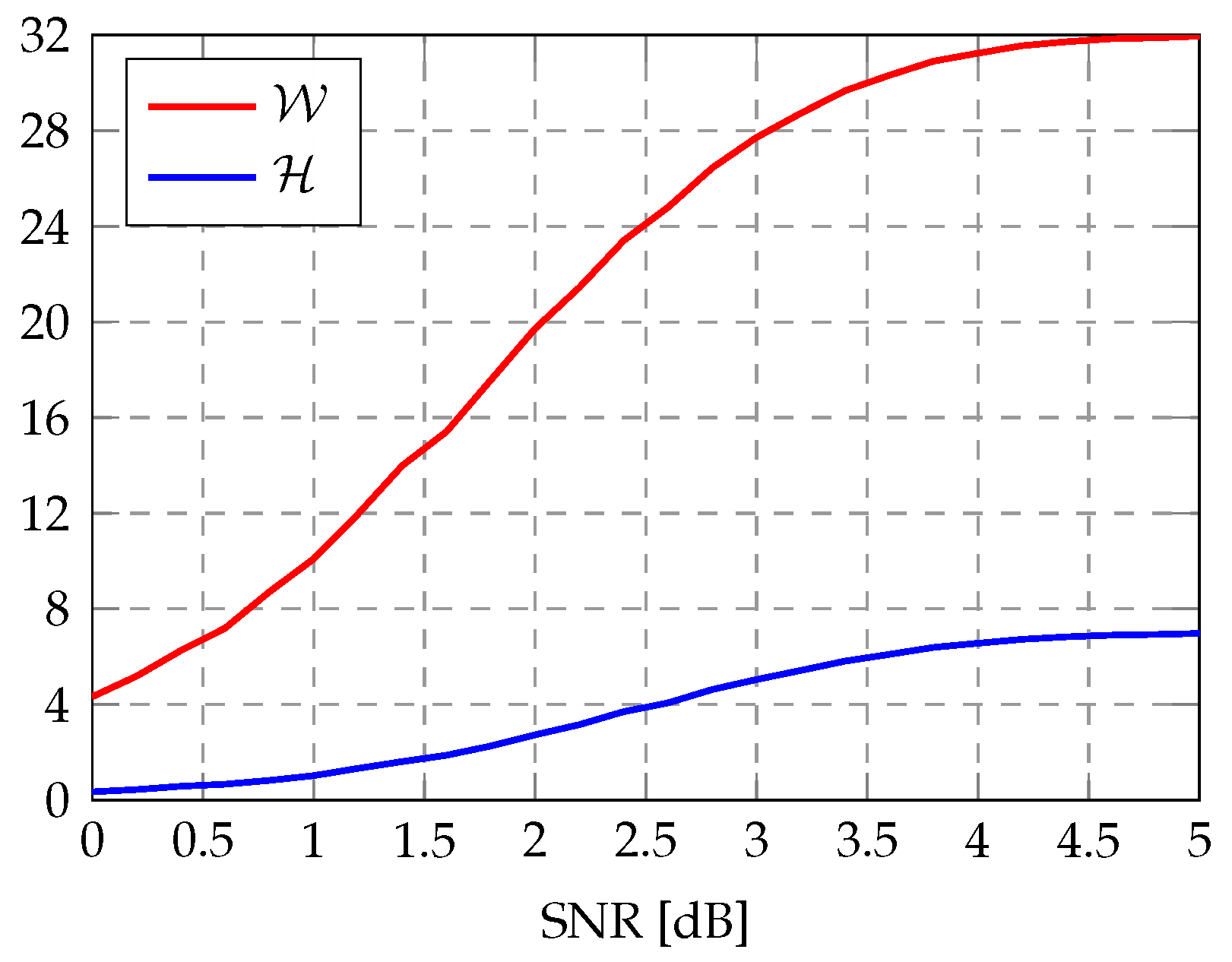
3.4. Subcode Estimate Convergence-Aided Path Pruning

3.5. Complexity of SEC-Aided AE Decoding
4. Experimental Results and Discussion
4.1. Error-Correction Performance
4.2. Complexity
4.3. Practical Relevance
4.4. Extensibility
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, F.; Yu, F.R.; Zhang, H.; Li, X.; Ji, H.; Leung, V.C.M. Enabling Massive IoT Toward 6G: A Comprehensive Survey. IEEE Internet Things J. 2021, 8, 11891–11915. [Google Scholar] [CrossRef]
- Muller, D.E. Application of Boolean Algebra to Switching Circuit Design and to Error Detection. Trans. IRE Prof. Group Electron. Comput. 1954, 3, 6–12. [Google Scholar] [CrossRef]
- Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Kudekar, S.; Kumar, S.; Mondelli, M.; Pfister, H.D.; Şaşoǧlu, E.; Urbanke, R.L. Reed-Muller Codes Achieve Capacity on Erasure Channels. IEEE Trans. Inf. Theory 2017, 63, 4298–4316. [Google Scholar] [CrossRef]
- Abbe, E.; Shpilka, A.; Wigderson, A. Reed-Muller Codes for Random Erasures and Errors. IEEE Trans. Inf. Theory 2015, 61, 5229–5252. [Google Scholar] [CrossRef]
- Reeves, G.; Pfister, H.D. Reed–Muller Codes on BMS Channels Achieve Vanishing Bit-Error Probability for all Rates Below Capacity. IEEE Trans. Inf. Theory 2024, 70, 920–949. [Google Scholar] [CrossRef]
- Arikan, E. A Survey of Reed-Muller Codes from Polar Coding Perspective. In Proceedings of the 2010 IEEE Information Theory Workshop on Information Theory (ITW), Cairo, Egypt, 6–8 January 2010; pp. 1–5. [Google Scholar]
- Mondelli, M.; Hassani, S.H.; Urbanke, R.L. From Polar to Reed-Muller Codes: A Technique to Improve the Finite-Length Performance. IEEE Trans. Commun. 2014, 62, 3084–3091. [Google Scholar] [CrossRef]
- Yue, C.; Miloslavskaya, V.; Shirvanimoghaddam, M.; Vucetic, B.; Li, Y. Efficient Decoders for Short Block Length Codes in 6G URLLC. IEEE Commun. Mag. 2023, 61, 84–90. [Google Scholar] [CrossRef]
- Be’ery, Y.; Snyders, J. Optimal Soft Decision Block Decoders Based on Fast Hadamard Transform. IEEE Trans. Inf. Theory 1986, 32, 355–364. [Google Scholar] [CrossRef]
- Reed, I. A class of multiple-error-correcting codes and the decoding scheme. Trans. IRE. Prof. Group Electron. Comput. 1954, 4, 38–49. [Google Scholar] [CrossRef]
- Sidel’nikov, V.M.; Pershakov, A.S. Decoding of Reed–Müller codes with a large number of errors. Probl. Peredachi Informatsii 1992, 28, 80–94. [Google Scholar]
- Sakkour, B. Decoding of Second Order Reed-Muller Codes with a Large Number of Errors. In Proceedings of the 2005 IEEE Information Theory Workshop (ITW), Rotorua, New Zealand, 29 August–1 September 2005; pp. 176–178. [Google Scholar]
- Dumer, I. Recursive decoding and its performance for low-rate Reed-Muller codes. IEEE Trans. Inf. Theory 2004, 50, 811–823. [Google Scholar] [CrossRef]
- Dumer, I.; Shabunov, K. Soft-decision decoding of Reed-Muller codes: Recursive lists. IEEE Trans. Inf. Theory 2006, 52, 1260–1266. [Google Scholar] [CrossRef]
- Santi, E.; Hager, C.; Pfister, H.D. Decoding Reed-Muller Codes Using Minimum-Weight Parity Checks. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 1296–1300. [Google Scholar]
- Ye, M.; Abbe, E. Recursive Projection-Aggregation Decoding of Reed-Muller Codes. IEEE Trans. Inf. Theory 2020, 66, 4948–4965. [Google Scholar] [CrossRef]
- Hashemipour-Nazari, M.; Nardi-Dei, A.; Goossens, K.; Balatsoukas-Stimming, A. Hardware Implementation of Projection-Aggregation Decoders for Reed-Muller Codes. IEEE Trans. Circuits Syst. I Reg. Papers, 2024; early access. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. List Decoding of Polar Codes. IEEE Trans. Inf. Theory 2015, 61, 2213–2226. [Google Scholar] [CrossRef]
- Han, S.; Kim, B.; Chung, J.; Ha, J. Improved Automorphism Ensemble Decoder for Polar Codes. IEEE Commun. Lett. 2024, 28, 1750–1754. [Google Scholar] [CrossRef]
- Geiselhart, M.; Elkelesh, A.; Ebada, M.; Cammerer, S.; Brink, S.T. Automorphism Ensemble Decoding of Reed-Muller Codes. IEEE Trans. Commun. 2021, 69, 6424–6438. [Google Scholar] [CrossRef]
- MacWilliams, F.J.; Sloane, N.J.A. The Theory of Error-Correcting Codes; North-Holland: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Pillet, C.; Sagitov, I.; Bioglio, V.; Giard, P. Shortened Polar Codes Under Automorphism Ensemble Decoding. IEEE Commun. Lett. 2024, 28, 773–777. [Google Scholar] [CrossRef]
- Tian, K.; Sun, H.; Liu, Y.; Liu, R. Quasi-Optimal Path Convergence-Aided Automorphism Ensemble Decoding of Reed–Muller Codes. Entropy 2025, 27, 424. [Google Scholar] [CrossRef]
- Ivanov, K.; Urbanke, R. Improved decoding of second-order Reed-Muller codes. In Proceedings of the 2019 IEEE Information Theory Workshop (ITW), Visby, Sweden, 25–28 August 2019; pp. 1–5. [Google Scholar]
- Alamdar-Yazdi, A.; Kschischang, F.R. A Simplified Successive-Cancellation Decoder for Polar Codes. IEEE Commun. Lett. 2011, 15, 1378–1380. [Google Scholar] [CrossRef]
- Sarkis, G.; Giard, P.; Vardy, A.; Thibeault, C.; Gross, W.J. Fast Polar Decoders: Algorithm and Implementation. IEEE J. Sel. Areas Commun. 2014, 32, 946–957. [Google Scholar] [CrossRef]
- Sarkis, G.; Giard, P.; Vardy, A.; Thibeault, C.; Gross, W.J. Fast List Decoders for Polar Codes. IEEE J. Sel. Areas Commun. 2016, 34, 318–328. [Google Scholar] [CrossRef]
- Hanif, M.; Ardakani, M. Fast Successive-Cancellation Decoding of Polar Codes: Identification and Decoding of New Nodes. IEEE Commun. Lett. 2017, 21, 2360–2363. [Google Scholar] [CrossRef]
- Ren, Y.; Kristensen, A.T.; Shen, Y.; Balatsoukas-Stimming, A.; Zhang, C.; Burg, A. A Sequence Repetition Node-Based Successive Cancellation List Decoder for 5G Polar Codes: Algorithm and Implementation. IEEE Trans. Signal Process. 2022, 70, 5592–5607. [Google Scholar] [CrossRef]
- Kamenev, M.; Kameneva, Y.; Kurmaev, O.; Maevskiy, A. A New Permutation Decoding Method for Reed-Muller Codes. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 26–30. [Google Scholar]
- Balatsoukas-Stimming, A.; Parizi, M.B.; Burg, A. LLR-Based Successive Cancellation List Decoding of Polar Codes. IEEE Trans. Signal Process. 2015, 63, 5165–5179. [Google Scholar] [CrossRef]
- Condo, C. Input-Distribution-Aware Successive Cancellation List Decoding of Polar Codes. IEEE Commun. Lett. 2021, 25, 1510–1514. [Google Scholar] [CrossRef]
- Doan, N.; Hashemi, S.A.; Mondelli, M.; Gross, W.J. On the Decoding of Polar Codes on Permuted Factor Graphs. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Abbe, E.; Shpilka, A.; Ye, M. Reed-Muller Codes: Theory and Algorithms. IEEE Trans. Inf. Theory 2021, 67, 3251–3277. [Google Scholar] [CrossRef]
- Bioglio, V.; Land, I.; Pillet, C. Group Properties of Polar Codes for Automorphism Ensemble Decoding. IEEE Trans. Inf. Theory 2023, 69, 3731–3747. [Google Scholar] [CrossRef]
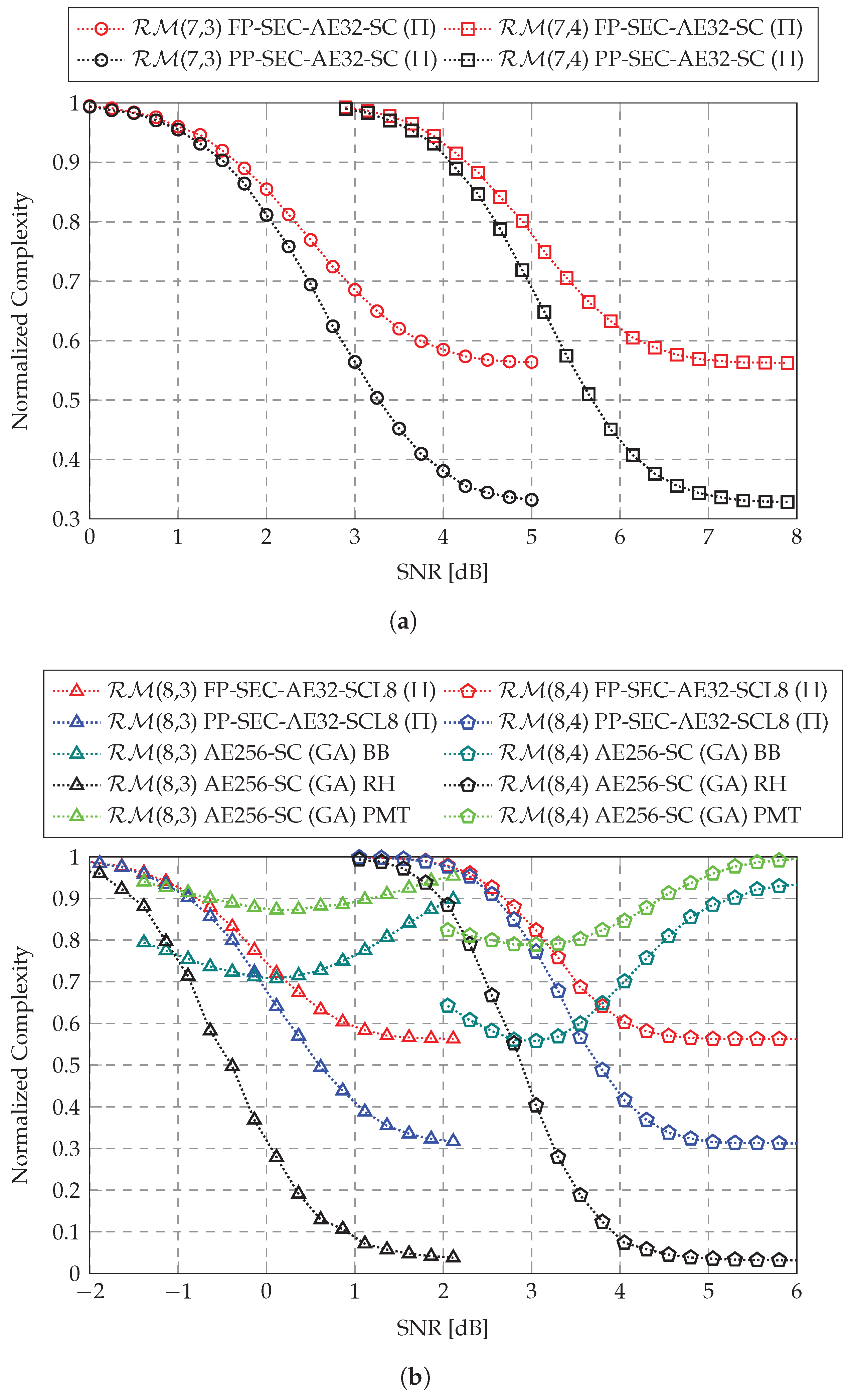
| Code | N | K | R | M | SNR [dB] | FP | PP | |
|---|---|---|---|---|---|---|---|---|
| (7,3) | 128 | 64 | 32 | SC | 58.5% | 38.1% | ||
| (7,4) | 128 | 99 | 32 | SC | 56.5% | 33.6% | ||
| (8,3) | 256 | 93 | 32 | SCL8 | 56.7% | 33.6% | ||
| (8,4) | 256 | 163 | 32 | SCL8 | 56.5% | 32.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, K.; Liu, R.; Lu, Z. Low-Complexity Automorphism Ensemble Decoding of Reed-Muller Codes Using Path Pruning. Entropy 2025, 27, 808. https://doi.org/10.3390/e27080808
Tian K, Liu R, Lu Z. Low-Complexity Automorphism Ensemble Decoding of Reed-Muller Codes Using Path Pruning. Entropy. 2025; 27(8):808. https://doi.org/10.3390/e27080808
Chicago/Turabian StyleTian, Kairui, Rongke Liu, and Zheng Lu. 2025. "Low-Complexity Automorphism Ensemble Decoding of Reed-Muller Codes Using Path Pruning" Entropy 27, no. 8: 808. https://doi.org/10.3390/e27080808
APA StyleTian, K., Liu, R., & Lu, Z. (2025). Low-Complexity Automorphism Ensemble Decoding of Reed-Muller Codes Using Path Pruning. Entropy, 27(8), 808. https://doi.org/10.3390/e27080808









