Order Lot Sizing: Insights from Lattice Gas-Type Model
Abstract
1. Introduction
2. Literature Review
3. Methodology
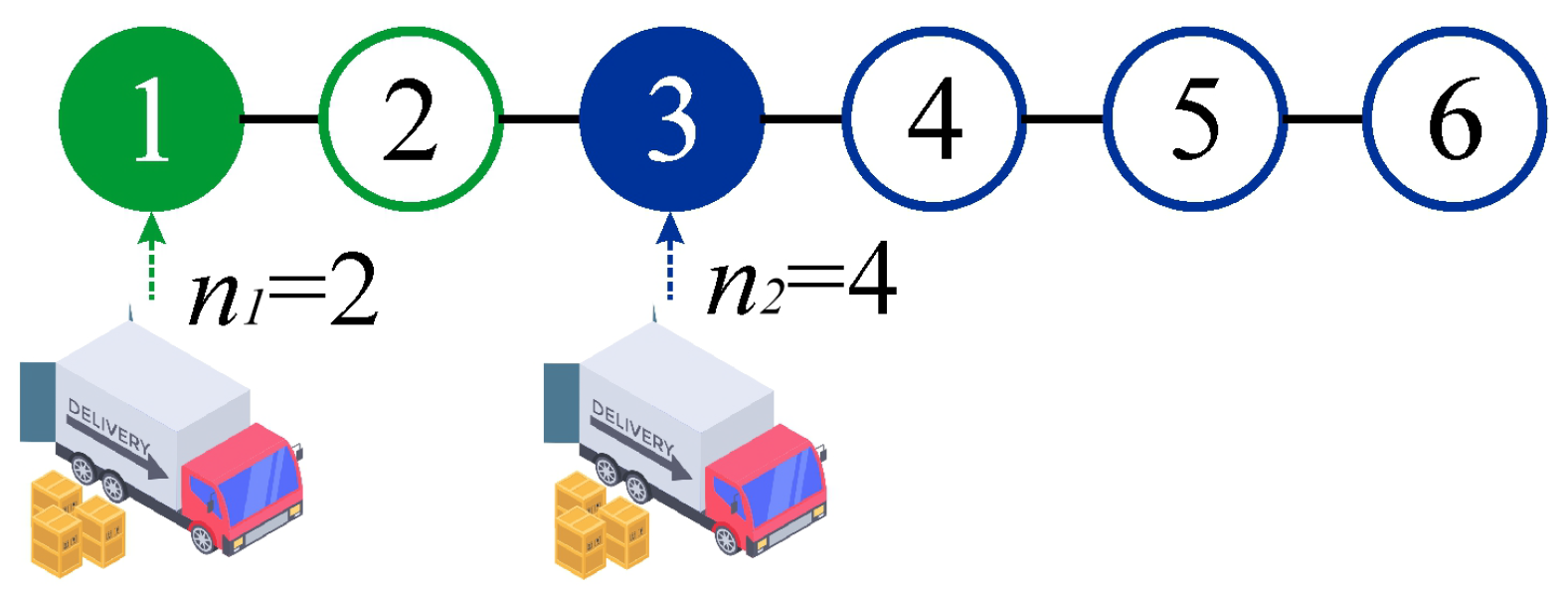
3.1. Lot-Sizing Model: Basic Definitions
3.2. Equivalence Between Lot-Sizing Model and Lattice Gas Model
3.3. Cluster Approximation
3.4. Summary of the Modeling Process
- (1)
- Select the specific lot-sizing problem to be studied.
- (2)
- Based on the selected problem in step (1), choose the corresponding equivalent lattice gas model. An example is shown in Table 1 for the single-item lot-sizing model considered in this work. Other problems, such as multi-item lot-sizing or cases involving variable material requirements per period, will require a different definition of lateral interactions and a modified number of adsorbed components.
- (3)
- Apply cluster approximation. To do this, the factor must be obtained using a computational algorithm that explores all possible configurations. In our case, a C++ code developed by the authors was used to count all possible arrangements of N orders over a planning horizon of length M. Once is determined, the grand partition function is computed, from which all relevant statistical properties can be derived.
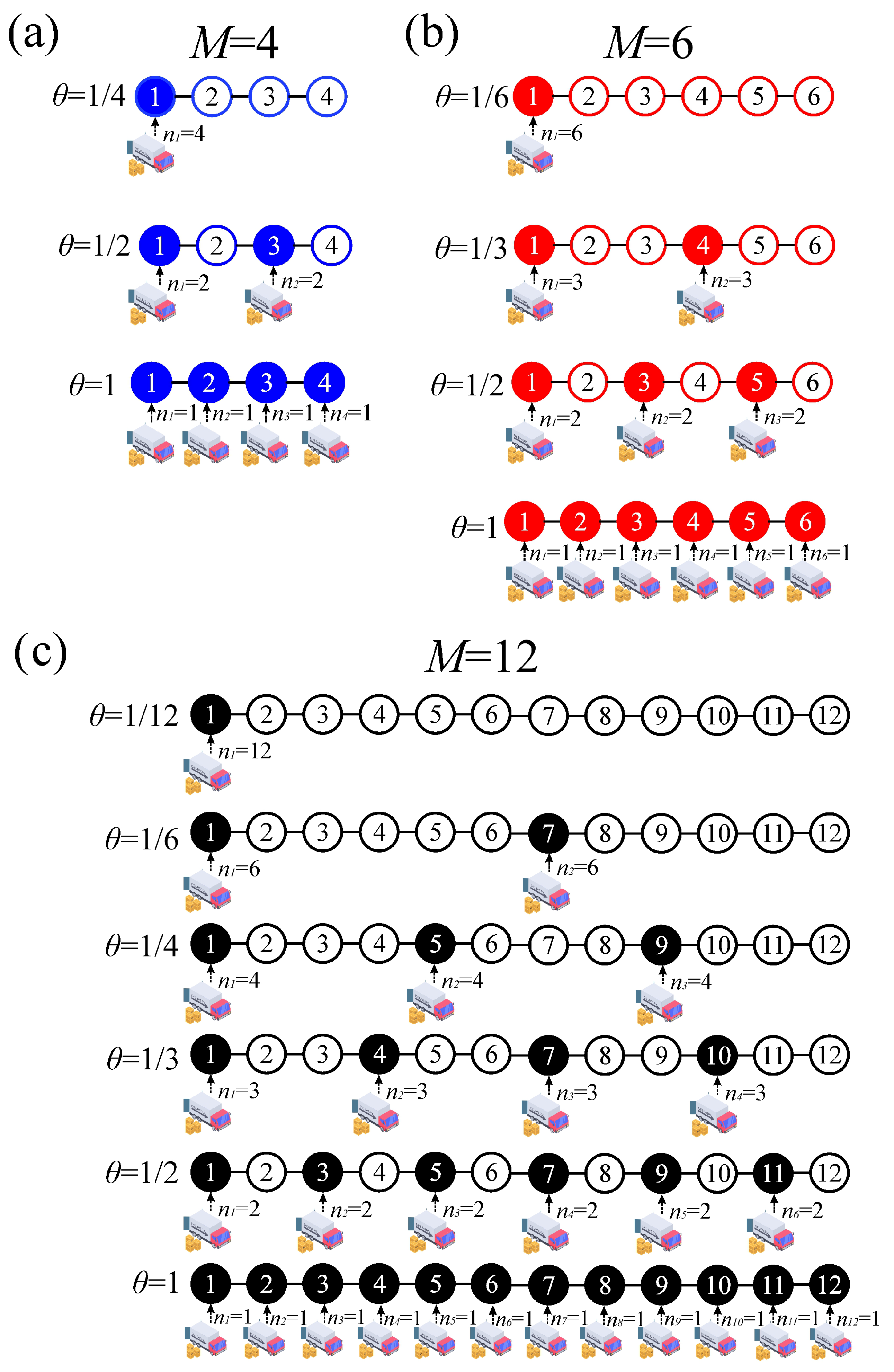
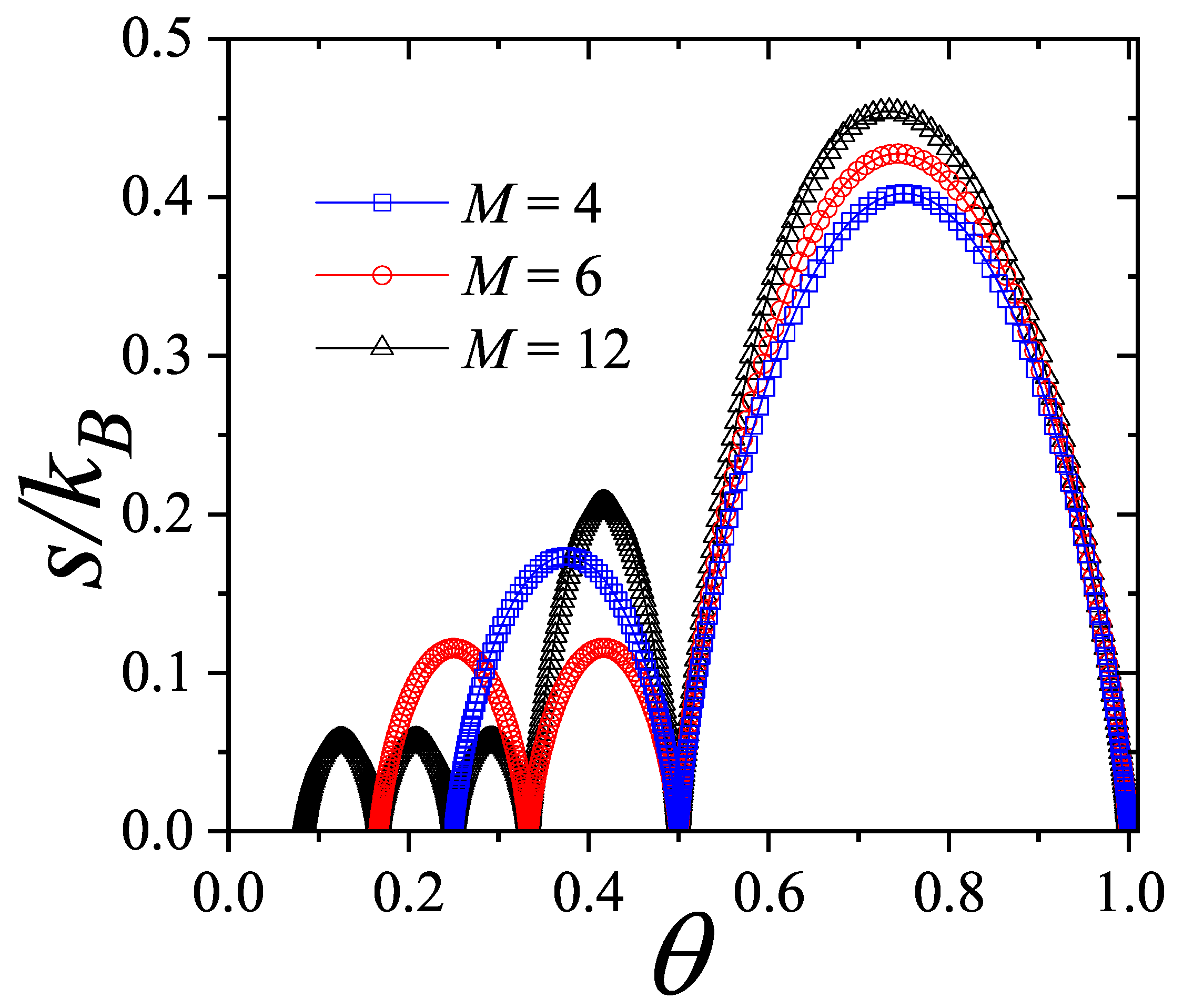
4. Results
5. Conclusions
- Optimal strategies emerge from thermodynamic principles: We demonstrated that optimal supply policies naturally arise from the minimization of a free energy function, mirroring the principle used to determine equilibrium states in physical systems. This insight opens a promising research avenue at the intersection of statistical physics and supply chain optimization.
- Accurate cost prediction through cluster approximation: Using cluster approximation techniques, we confirmed that crucial metrics, such as total cost and order distributions, can be predicted with high accuracy, aligning closely with known exact solutions [25].
- Configurational entropy as a complexity metric: Our analysis highlights the role of configurational entropy as a measure of complexity and robustness in inventory strategies, introducing a novel and meaningful decision-making metric. Specifically, for the physical model described in Ref. [25], which consists of a one-dimensional mechanical system of point particles connected by elastic elements, the optimal strategy to minimize the total cost for a given N corresponds to a configuration in which all springs have equal length (constant ), resulting in zero net force on each particle. Within the framework of the lattice gas model, this exact result is consistent with the structures inferred from the curves of configurational entropy as a function of coverage.
- A powerful analytical tool for supply planning: As a corollary of the above results, we showed that the theoretical machinery developed for studying adsorption and magnetism via lattice gas models offers a simple yet powerful tool for identifying optimal strategies in supply planning. This is a particularly valuable contribution, as it introduces to supply chain management a rich set of analytical tools from statistical physics. As a concrete example, we demonstrated that cluster approximation theory not only reveals the structure of optimal strategies but is especially effective due to the discrete nature of the planning horizon M.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. One-Dimensional Lattice Gas of Interacting k-mers
References
- Ferdian, R.; Halim, A.H. Dynamic Lot Sizing Model for Retailers with Multi Suppliers, Quantity Discounts, and Capacity Constraints That Consider Advance Demand Informations. Int. J. Prod. Manag. Eng. 2024, 12, 158–168. [Google Scholar] [CrossRef]
- Bindewald, V.; Dunke, F.; Nickel, S. Comparison of Different Approaches to Multistage Lot Sizing with Uncertain Demand. Int. Trans. Oper. Res. 2023, 30, 3771–3800. [Google Scholar] [CrossRef]
- Kania, A.; Afsar, B.; Miettinen, K.; Sipilä, J. DESMILS: A Decision Support Approach for Multi-Item Lot Sizing Using Interactive Multiobjective Optimization. J. Intelli. Manuf. 2023, 35, 1373–1387. [Google Scholar] [CrossRef]
- Tremblet, D.; Thevenin, S.; Dolgui, A. Constraint Learning Approaches to Improve the Approximation of the Capacity Consumption Function in Lot-Sizing Models. Eur. J. Oper. Res. 2025, 322, 679–692. [Google Scholar] [CrossRef]
- Purnomo, A.; Syafrianita, S. Incorporating Time Value of Money into Lot-Sizing Decisions for Improved Supply Chain Performance. J. Sys. Manag. Sci. 2024, 14, 514–532. [Google Scholar] [CrossRef]
- Chotayakul, S.; Punyangarm, V. A Fuzzy Approach to Determine Production Lot Size for Capacitated Single-Stage Production Process with Fuzzy Demand. J. Adv. Dev. Eng. Sci. 2024, 14, 16–29. [Google Scholar]
- Segerstedt, A.; Abdul-Jalbar, B.; Samuelsson, B. Reformulated Silver-Meal and Similar Lot Sizing Techniques. Axioms 2023, 12, 661. [Google Scholar] [CrossRef]
- Chowdhury, N.T.; Baki, M.F.; Azab, A. A Modeling and Hybridized Decomposition Approach for the Multi-Level Capacitated Lot-Sizing Problem with Setup Carryover, Backlogging, and Emission Control. Oper. Res. Forum 2024, 5, 68. [Google Scholar] [CrossRef]
- Rohaninejad, M.; Vahedi-Nouri, B.; Hanzálek, Z.; Tavakkoli-Moghaddam, R. An Integrated Lot-Sizing and Scheduling Problem in a Reconfigurable Manufacturing System under Workforce Constraints. Int. J. Prod. Res. 2023, 62, 3994–4013. [Google Scholar] [CrossRef]
- Woarawichai, C.; Naenna, T. Solving inventory lot-sizing with supplier selec tion under alternative quantity discounts and vehicle capacity. Int. J. Logist. Syst. Manag. 2018, 30, 179–194. [Google Scholar] [CrossRef]
- Bahroun, M.; Harbi, S.; Bouchriha, H. A new approach for ordering decision under uncertainties: A case study in the retail supply chain. Int. J. Logist. Syst. Manag. 2019, 32, 392–413. [Google Scholar] [CrossRef]
- Randa, A.C.; Dogru, M.K.; Iyigun, C.; Özen, U. Heuristic methods for the capacitated stochastic lot-sizing problem under the static-dynamic uncertainty strategy. Comput. Oper. Res. 2019, 109, 89–101. [Google Scholar] [CrossRef]
- Tai, P.; Huyen, P.; Buddhakulsomsiri, J. A novel modeling approach for a capacitated (s,t) inventory system with backlog under stochastic discrete demand and lead time. Int. J. Ind. Eng. Comput. 2021, 12, 1–14. [Google Scholar] [CrossRef]
- Chen, Z.; Rossi, R. A cash constrained single item stochastic lot-sizing problem. IFAC-PapersOnLine 2019, 52, 1479–1483. [Google Scholar] [CrossRef]
- Goyal, S.K. Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1985, 36, 335–338. [Google Scholar] [CrossRef]
- Sanchez-Varretti, F.O.; Garcia, G.D.; Pasinetti, P.M.; Ramirez-Pastor, A.J. Adsorption of binary mixtures on two-dimensional surfaces: Theory and Monte Carlo simulations. Adsorption 2014, 20, 855–862. [Google Scholar] [CrossRef]
- Sanchez-Varretti, F.O.; Bulnes, F.M.; Ramirez-Pastor, A.J. A cluster-exact approximation study of the adsorption of binary mixtures on heterogeneous surfaces. Appl. Surf. Sci. 2016, 387, 268–273. [Google Scholar] [CrossRef]
- De La Cruz Feliz, N.M.; Longone, P.J.; Sanchez-Varretti, F.O.; Bulnes, F.M.; Ramirez-Pastor, A.J. Cluster approximation applied to multisite-occupancy adsorption: Configurational entropy of the adsorbed phase for dimers and trimers on triangular lattices. Phys. Chem. Chem. Phys. 2023, 25, 14942–14954. [Google Scholar] [CrossRef] [PubMed]
- Longone, P.J.; Sanchez-Varretti, F.O.; Bulnes, F.M.; Ramirez-Pastor, A.J. Lattice-gas model of methane and carbon dioxide sI clathrate hydrates: A comprehensive study using analytical cluster approximation and Monte Carlo simulations. Phys. Rev. E 2024, 110, 064103-15. [Google Scholar] [CrossRef] [PubMed]
- Lebrecht, W.; Centres, P.M.; Ramirez-Pastor, A.J. Analytical approximation of the site percolation thresholds for monomers and dimers on two-dimensional lattices. Physica A 2019, 516, 133–143. [Google Scholar] [CrossRef]
- Vogel, E.E.; Vargas, P.; Saravia, G.; Valdes, J.; Ramirez-Pastor, A.J.; Centres, P.M. Thermodynamics of Small Magnetic Particles. Entropy 2017, 19, 499. [Google Scholar] [CrossRef]
- Riccardo, J.J.; Riccardo, J.L.; Ramirez-Pastor, A.J.; Pasinetti, P.M. Multiple Exclusion Statistics. Phys. Rev. Lett. 2019, 123, 020602. [Google Scholar] [CrossRef] [PubMed]
- Riccardo, J.J.; Pasinetti, P.M.; Ramirez-Pastor, A.J.; Riccardo, J.L. Exclusion statistics for structured particles on topologically correlated states. I. Single species lattice gases. Phys. Rev. E 2025, 111, 014122-13. [Google Scholar] [CrossRef] [PubMed]
- Riccardo, J.J.; Pasinetti, P.M.; Ramirez-Pastor, A.J.; Riccardo, J.L. Exclusion statistics for structured particles on topologically correlated states. II. Multicomponent lattice gases. Phys. Rev. E 2025, 111, 014123-19. [Google Scholar] [CrossRef] [PubMed]
- Tobares, T.D.; Mieras, M.M.; Sanchez-Varretti, F.O.; Iguain, J.L.; Ramirez-Pastor, A.J. A Physical Model Approach to Order Lot Sizing. arXiv 2025, arXiv:2502.06856v1. [Google Scholar]
- Harris, F.W. How many parts to make at once. Factory. Mag. Manag. 1913, 10, 135–136. [Google Scholar] [CrossRef]
- Wilson, R.H. A scientific routine for stock control. Harv. Bus. Rev. 1934, 13, 116–118. [Google Scholar]
- DeMatteis, J.J. An economic lot-sizing technique: I the part-period algorithm. HIBM Sys. J. 1968, 7, 30–38. [Google Scholar] [CrossRef]
- Wagner, H.M.; Whitin, T.M. Dynamic Version of the Economic Lot Size Model. Manag. Sci. 1958, 5, 89–96. [Google Scholar] [CrossRef]
- Silver, E.A.; Meal, H.C. A heuristic for selecting lot size quantities for the case of a deterministic time-varying demand rate and discrete opportunities for replenishment. Prod. Inventory Manag. 1973, 14, 64–74. [Google Scholar]
- Glover, F. Tabu Search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Hernandez, W.; Suer, G.A. Genetic algorithms in lot sizing decisions. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 2280–2286. [Google Scholar] [CrossRef]
- Hoseini Shekarabi, S.A.; Gharaei, A.; Karimi, M. Modelling and optimal lot-sizing of integrated multi-level multi-wholesaler supply chains under the shortage and limited warehouse space: Generalised outer approximation. Int. J. Syst. Sci. Oper. Logist. 2019, 6, 237–257. [Google Scholar] [CrossRef]
- Jeenanunta, C.; Kongtarat, V.; Buddhakulsomsiri, J. A simulation-optimisation approach to determine optimal order-up-to level for inventory system with long lead time. Int. J. Logist. Syst. Manag. 2021, 38, 253–276. [Google Scholar] [CrossRef]
- Wisniewski, T.; Szymanski, R. Simulation-based optimisation of replenishment policy in supply chains. Int. J. Logist. Syst. Manag. 2021, 38, 135–150. [Google Scholar] [CrossRef]
- Tobares, T.D.; Mieras, M.M.; Palma, R.R.; Sanchez-Varretti, F.O. Theoretical relationship between the cluster size of orders in the materials requirement planning. Int. J. Logist. Syst. Manag. 2023, 46, 27–46. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Tang, O. Simulated Annealing in Lot Sizing Problems. Int. J. Prod. Econ. 2004, 88, 173–181. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, P.; Alejo-Reyes, A.; Cuevas, E.; Mendoza, A. A Modified Simulated Annealing (MSA) Algorithm to Solve the Supplier Selection and Order Quantity Allocation Problem with Non-Linear Freight Rates. Axioms 2023, 12, 459. [Google Scholar] [CrossRef]
- Slama, I.; Ben-Ammar, O.; Dolgui, A.; Masmoudi, F. Genetic Algorithm and Monte Carlo Simulation for a Stochastic Capacitated Disassembly Lot-Sizing Problem under Random Lead Times. Comput. Ind. Eng. 2021, 159, 107468. [Google Scholar] [CrossRef]
- Drechsler, F.S. Decision trees and the second law. Oper. Res. Q. 1968, 19, 409–419. [Google Scholar] [CrossRef]
- Tyler, G.W. A thermodynamic model of manpower systems. J. Oper. Res. Soc. 1989, 40, 137–139. [Google Scholar] [CrossRef]
- Whewell, R. Turning up the heat under the supply-chain. Logist. Focus 1997, 5, 18–22. [Google Scholar]
- Chen, W.-H. Business process management: A thermodynamics perspective. J. Appl. Manag. Stud. 1999, 8, 241–257. [Google Scholar]
- Tseng, K.-J. Application of thermodynamics on product life cycle. J. Am. Acad. Bus. 2004, 4, 464–470. [Google Scholar]
- Nuwayhid, R.Y.; Jaber, M.Y.; Rosen, M.A.; Sassine, G.P. On the thermodynamic treatment of diffusion-like economic commodity flow. Int. J. Exergy 2006, 3, 103–117. [Google Scholar] [CrossRef]
- Bruyn, P.; Huysmans, P.; Mannaert, H.; Verelst, J. Understanding Entropy Generation during the Execution of Business Process Instantiations: An Illustration from Cost Accounting. Lect. Notes Bus. Inf. Process. 2013, 146, 103–117. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Nuwayhid, R.Y.; Rosen, M.A. Price-driven economic order systems from a thermodynamic point of view. Int. J. Prod. Res. 2004, 42, 5167–5184. [Google Scholar] [CrossRef]
- Jaber, M.Y. Lot sizing with permissible delay in payments and entropy cost. Comput. Ind. Eng. 2007, 52, 78–88. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M.; Moualek, I. Lot sizing with learning, forgetting and entropy cost. Int. J. Prod. Econ. 2009, 118, 19–25. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. The effects of learning and forgetting on the optimal lot size quantity of intermittent production runs. Prod. Plan. Control. 1998, 9, 20–27. [Google Scholar] [CrossRef]
- Castellano, D. Stochastic Reorder Point-Lot Size (r,Q) Inventory Model under Maximum Entropy Principle. Entropy 2016, 18, 16. [Google Scholar] [CrossRef]
- You, M.; Xiao, Y.; Zhang, S.; Zhou, S.; Yang, P.; Pan, X. Modeling the Capacitated Multi-Level Lot-Sizing Problem under Time-Varying Environments and a Fix-and-Optimize Solution Approach. Entropy 2019, 21, 377. [Google Scholar] [CrossRef] [PubMed]
- Miller, G.W.; Knaebel, K.S.; Ikels, K.G. Equilibria of nitrogen, oxygen, argon, and air in molecular sieve 5A. AIChE J. 1987, 33, 194–201. [Google Scholar] [CrossRef]
- Hill, T.L. An Introduction to Statistical Thermodynamics; Addison-Wesley: Reading, PA, USA, 1960. [Google Scholar]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Dover Publications Inc.: New York, NY, USA, 2007. [Google Scholar]
- Friedli, S.; Velenik, Y. Statistical Mechanics of Lattice Systems: A Concrete Mathematical Introduction; Cambridge University Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ramirez-Pastor, A.J.; Aligia, A.; Romá, F.; Riccardo, J.L. Multisite-Occupancy Adsorption and Surface Diffusion of Linear Adsorbates in Low Dimensions: Rigorous Results for a Lattice Gas Model. Langmuir 2000, 16, 5100–5105. [Google Scholar] [CrossRef]
- Romá, F.; Ramirez-Pastor, A.J. Statistical thermodynamics of adsorbates with nonsymmetrical lateral interactions. Phys. Rev. E 2004, 69, 036124. [Google Scholar] [CrossRef] [PubMed]
- Aligia, A.A. One-dimensional oxygen ordering in YBa2Cu3O7−δ. Phys. Rev. B 1993, 47, 15308–15311. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, R. A Theory of Cooperative Phenomena. Phys. Rev. B 1951, 81, 988–1003. [Google Scholar] [CrossRef]
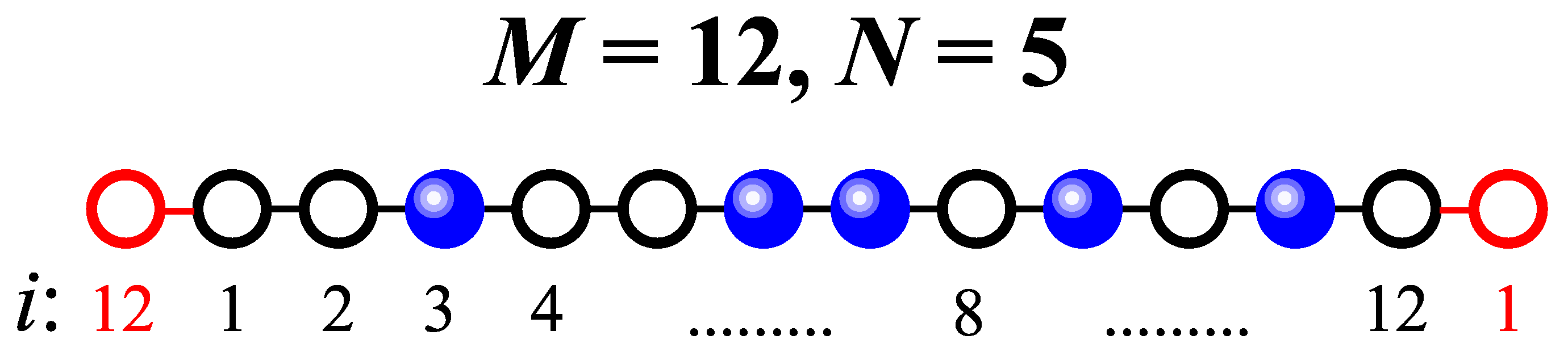


| Lot-Sizing Model | Lattice Gas Model |
|---|---|
| M, planing horizon | M, lattice size |
| N, number of orders | N, number of adsorbed particles |
| , ordering cost | , effective chemical potential, adsorbate–adsorbent interaction |
| , holding cost | adsorbate–adsorbate interaction |
| N | M = 4 | M = 6 | M = 12 |
|---|---|---|---|
| 1 | 15 (0.25) | 25 () | 55 () |
| 2 | 5 (0.50) | 10 () | 25 () |
| 3 | … | 5 (0.50) | 15 (0.25) |
| 4 | … | … | 10 () |
| 6 | … | … | 5 (0.50) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mieras, M.M.; Tobares, T.D.; Sanchez-Varretti, F.O.; Ramirez-Pastor, A.J. Order Lot Sizing: Insights from Lattice Gas-Type Model. Entropy 2025, 27, 774. https://doi.org/10.3390/e27080774
Mieras MM, Tobares TD, Sanchez-Varretti FO, Ramirez-Pastor AJ. Order Lot Sizing: Insights from Lattice Gas-Type Model. Entropy. 2025; 27(8):774. https://doi.org/10.3390/e27080774
Chicago/Turabian StyleMieras, Margarita Miguelina, Tania Daiana Tobares, Fabricio Orlando Sanchez-Varretti, and Antonio José Ramirez-Pastor. 2025. "Order Lot Sizing: Insights from Lattice Gas-Type Model" Entropy 27, no. 8: 774. https://doi.org/10.3390/e27080774
APA StyleMieras, M. M., Tobares, T. D., Sanchez-Varretti, F. O., & Ramirez-Pastor, A. J. (2025). Order Lot Sizing: Insights from Lattice Gas-Type Model. Entropy, 27(8), 774. https://doi.org/10.3390/e27080774







