On the Rate-Distortion Theory for Task-Specific Semantic Communication
Abstract
1. Introduction
- (1)
- We propose a novel taks-specific semantic communication architecture that generalizes traditional rate-distortion theory by incorporating a general divergence metrics to quantify semantic distance.
- (2)
- We derive the closed-form expressions for the semantic rate-distortion functions under Gaussian semantic sources, specifically for Wasserstein distance, KL divergence, and reverse KL divergence, revealing fundamental tradeoffs among transmission rate, distortion, and semantic distance.
- (3)
- Extensive experiments are conducted on image-based semantic communication systems for both generation and classification tasks. Our results suggest that the proposed framework significantly outperforms traditional MSE-based approaches, with reverse KL divergence demonstrating superior perceptual quality in generation tasks and KL divergence achieving higher classification accuracy.
2. Background and Preliminary
3. System Model and Problem Formulation
3.1. System Model
3.2. Problem Formulation
- (1)
- MSE Distortion: This corresponds to the signal-level distortion measured by the average squared difference of energy between the source and reconstructed signal, defined as . Denote by the maximum MSE distortion level that can be tolerated by the destination user. We can write the following constraint:
- (2)
- Task-relevant Semantic Distance: This corresponds to the task-specific distribution divergence that measures the semantic dissimilarity between the semantic source and its recovery. Generally speaking, different tasks require different divergence metrics and have different maximum tolerable levels of the recovered signal. For example, KL divergence has been commonly used for signal classification [10,21] and Wasserstein distance has often been adopted for signal generation [11]. In addition to the standard distribution divergence, some novel metrics for measuring the perceptual quality of specific types of signals, such as image and video, including Inception score [22] and SSIM [23], can also be included in our framework. Let be the set of supported tasks. Let and be the task-specific (semantic) distance metric and the maximum tolerable level for task m. We can write the following constraint on the task-relevant semantic distance:
4. Theoretical Results
4.1. Classification Task
4.2. Generation Task
4.3. SRD Function for Gaussian Sources
5. Experimental Results
5.1. Experimental Setups
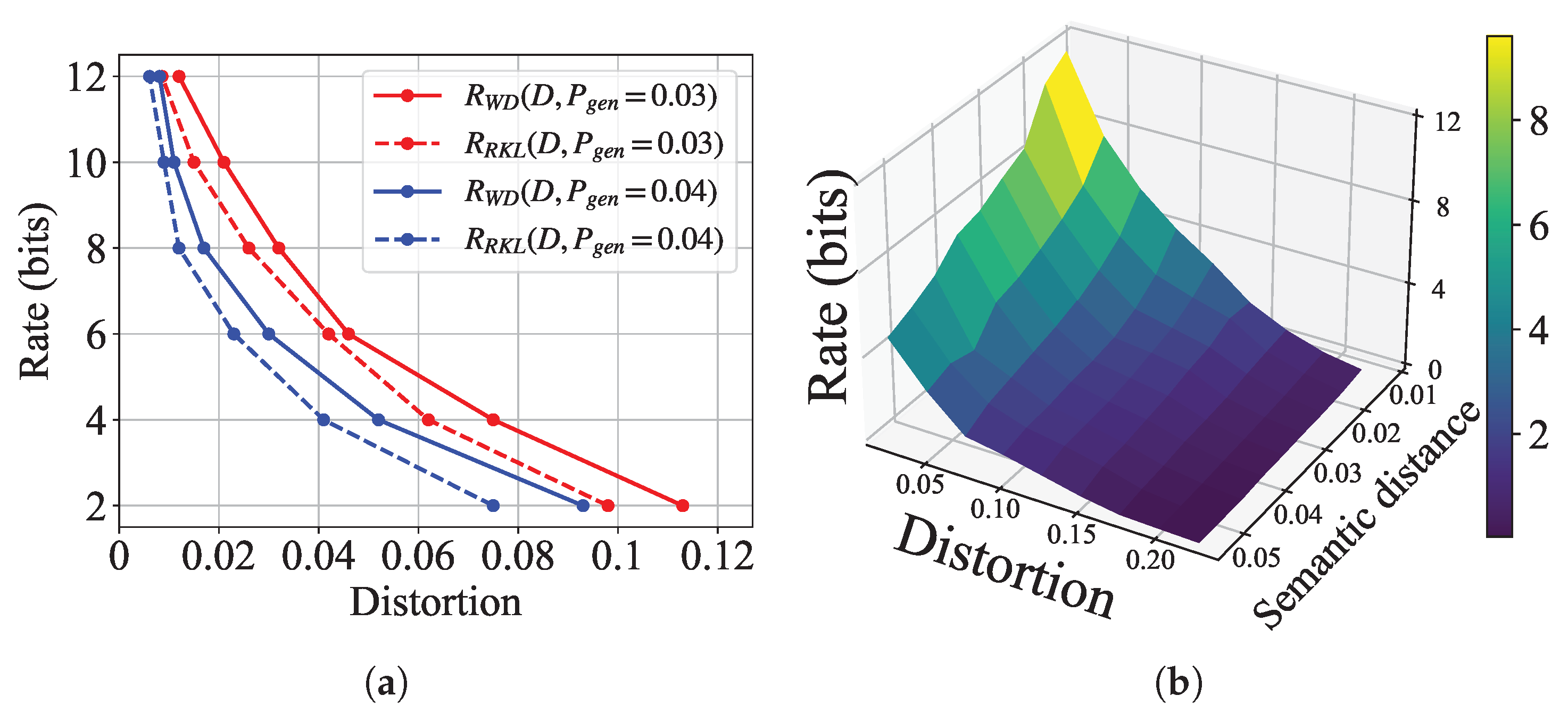
5.2. Results for Generation Tasks
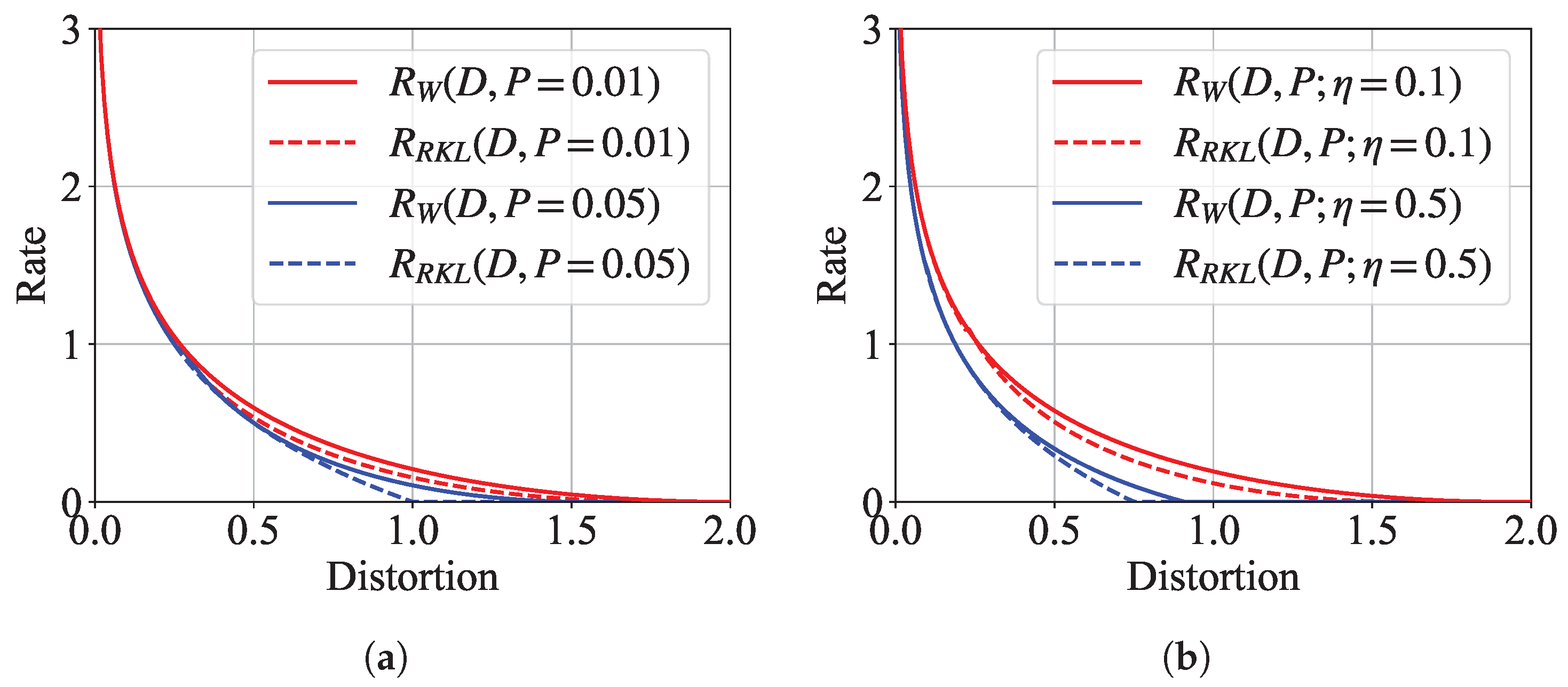
5.2.1. Achievable Rates Under Different Distance Measures
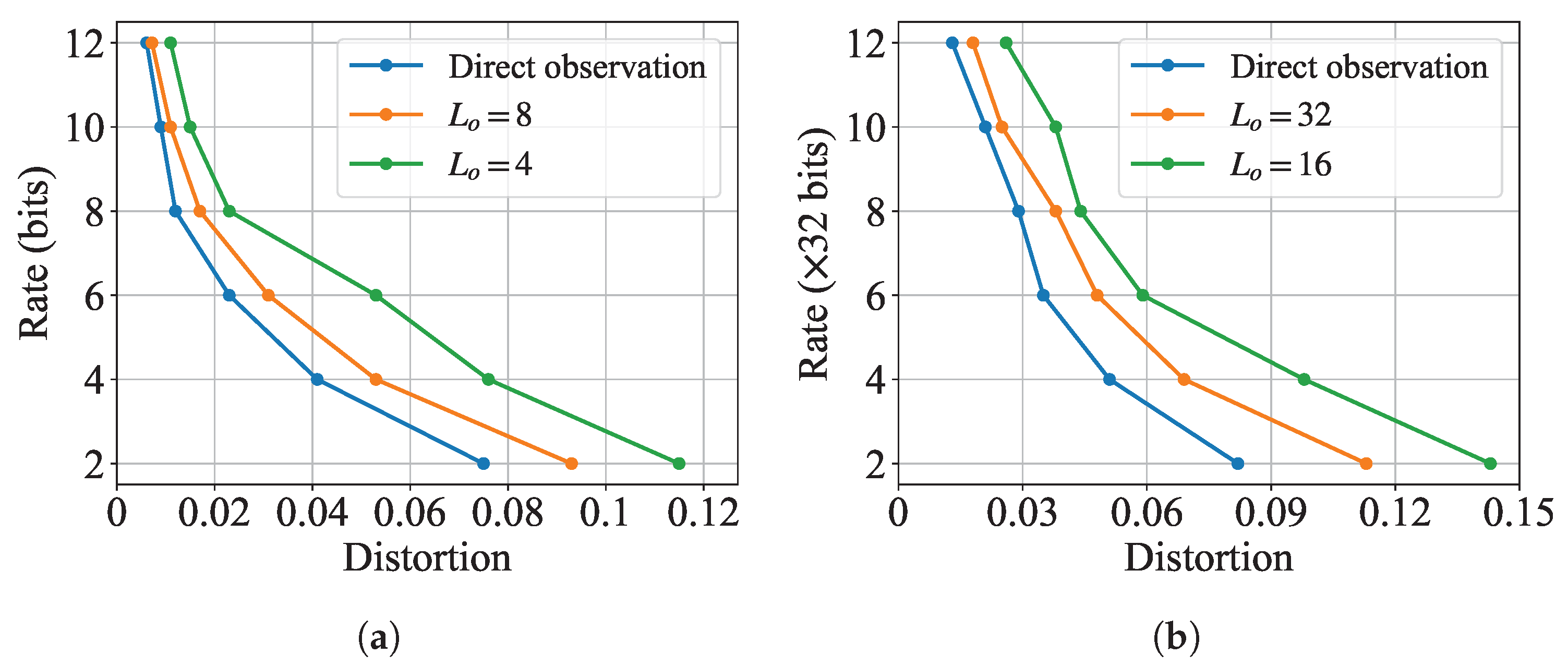
5.2.2. Impact of Indirect Observation
5.2.3. Impact of Side Information
5.2.4. Perceptual Quality Under Different Divergences
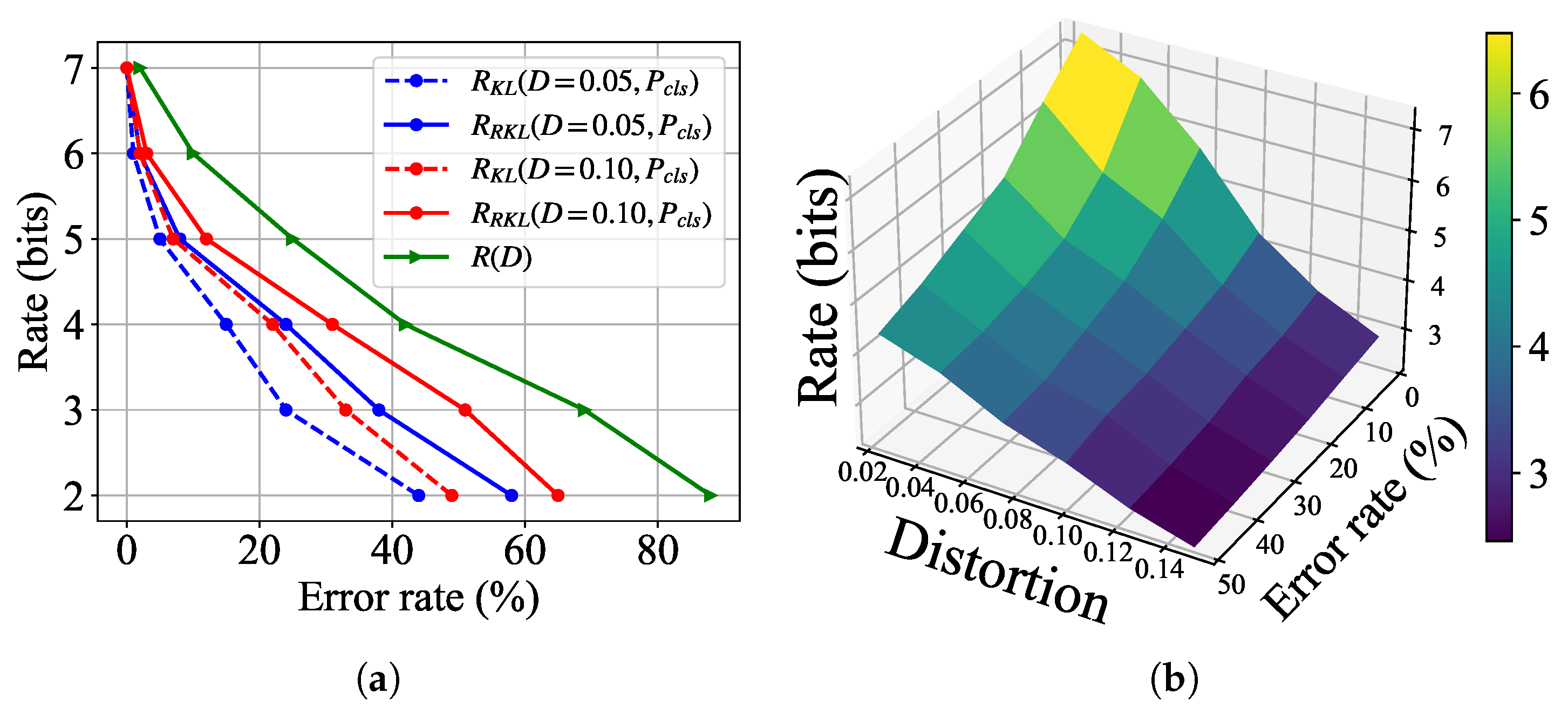
5.3. Results for Classification Tasks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorems 1 and 2
References
- Shi, G.; Xiao, Y.; Li, Y.; Xie, X. From semantic communication to semantic-aware networking: Model, architecture, and open problems. IEEE Commun. Mag. 2021, 59, 44–50. [Google Scholar] [CrossRef]
- Chai, J.; Xiao, Y.; Shi, G.; Saad, W. Rate-distortion-perception theory for semantic communication. In Proceedings of the 2023 IEEE 31st International Conference on Network Protocols (ICNP), Reykjavik, Iceland, 10–13 October 2023; pp. 1–6. [Google Scholar]
- Xiao, Y.; Sun, Z.; Shi, G.; Niyato, D. Imitation learning-based implicit semantic-aware communication networks: Multi-layer representation and collaborative reasoning. IEEE J. Sel. Areas Commun. 2023, 41, 639–658. [Google Scholar] [CrossRef]
- Xiao, Y.; Liao, Y.; Li, Y.; Shi, G.; Poor, H.V.; Saad, W.; Debbah, M.; Bennis, M. Reasoning over the air: A reasoning-based implicit semantic-aware communication framework. IEEE Trans. Wireless Commun. 2024, 23, 3839–3855. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, X.; Li, Y.; Shi, G.; Başar, T. Rate-distortion theory for strategic semantic communication. In Proceedings of the 2022 IEEE Information Theory Workshop (ITW), Mumbai, India, 1–9 November 2022; pp. 279–284. [Google Scholar]
- Weaver, W. Recent contributions to the mathematical theory of communication. ETC Rev. Gen. Semant. 1949, 10, 261–281. [Google Scholar]
- Xie, H.; Qin, Z.; Li, G.Y.; Juang, B.H. Deep learning enabled semantic communication systems. IEEE Trans. Signal Process. 2021, 69, 2663–2675. [Google Scholar] [CrossRef]
- Zhang, H.; Shao, S.; Tao, M.; Bi, X.; Letaief, K.B. Deep learning-enabled semantic communication systems with task-unaware transmitter and dynamic data. IEEE J. Sel. Areas Commun. 2022, 41, 170–185. [Google Scholar] [CrossRef]
- Gündüz, D.; Wigger, M.A.; Tung, T.-Y.; Zhang, P.; Xiao, Y. Joint source–channel coding: Fundamentals and recent Progress in practical designs. Proc. IEEE 2024, 1–32. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Blau, Y.; Michaeli, T. The perception-distortion tradeoff. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6228–6237. [Google Scholar]
- Blau, Y.; Michaeli, T. Rethinking lossy compression: The rate-distortion-perception tradeoff. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 675–685. [Google Scholar]
- Wagner, A.B. The rate-distortion-perception tradeoff: The role of common randomness. arXiv 2022, arXiv:2202.04147. [Google Scholar]
- Niu, X.; Gündüz, D.; Bai, B.; Han, W. Conditional Rate-distortion-perception trade-Off. arXiv 2023, arXiv:2305.09318. [Google Scholar]
- Zhang, G.; Qian, J.; Chen, J.; Khisti, A. Universal rate-distortion-perception representations for lossy compression. Adv. Neural Inf. Process. Syst. 2021, 34, 11517–11529. [Google Scholar] [CrossRef]
- Serra, G.; Stavrou, P.A.; Kountouris, M. Computation of rate-distortion-perception function under f-divergence perception constraints. In Proceedings of the 2023 IEEE International Symposium on Information Theory (ISIT), Taipei, Taiwan, 25–30 June 2023; pp. 531–536. [Google Scholar]
- Serra, G.; Stavrou, P.A.; Kountouris, M. Alternating minimization schemes for computing rate-distortion-perception functions with f-divergence perception constraint. arXiv 2024, arXiv:2408.15015. [Google Scholar]
- Serra, G.; Stavrou, P.A.; Kountouris, M. On the computation of the Gaussian rate-distortion-perception function. IEEE J. Sel. Areas Inf. Theory 2024, 5, 314–330. [Google Scholar] [CrossRef]
- Sourla, M.V.; Serra, G.; Stavrou, P.A.; Kountouris, M. Analyzing α-divergence in Gaussian rate-distortion-perception theory. In Proceedings of the IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 10–13 September 2024; pp. 856–860. [Google Scholar]
- Minka, T.P. Expectation propagation for approximate Bayesian inference. arXiv 2013, arXiv:1301.2294. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training GANs. In Proceedings of the NIPS 2016 Workshop on Interpretable Machine Learning for Complex Systems, Barcelona, Spain, 9 December 2016; pp. 2234–2242. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wan, N.; Li, D.; Hovakimyan, N. f-divergence variational inference. Adv. Neural Inf. Process. Syst. 2020, 33, 17370–17379. [Google Scholar]
- Beran, R. Minimum Hellinger distance estimates for parametric models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
- Novello, N.; Tonello, A.M. f-Divergence based classification: Beyond the use of cross-entropy. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Jeong, M.; Cardone, M.; Dytso, A. Demystifying the optimal performance of multi-class classification. Adv. Neural Inf. Process. Syst. 2023, 36, 31638–31664. [Google Scholar]
- Witsenhausen, H. Indirect rate distortion problems. IEEE Trans. Inf. Theory 2003, 26, 518–521. [Google Scholar] [CrossRef]
- Liu, J.; Shao, S.; Zhang, W.; Poor, H.V. An indirect rate-distortion characterization for semantic sources: General model and the case of gaussian observation. IEEE Trans. Commun. 2022, 70, 5946–5959. [Google Scholar] [CrossRef]
- Zhang, M.; Bird, T.; Habib, R.; Xu, T.; Barber, D. Variational f-divergence minimization. arXiv 2019, arXiv:1907.11891. [Google Scholar]
- Wyner, A.D. The rate-distortion function for source coding with side information at the decoder\3-II: General sources. Inf. Control 1978, 38, 60–80. [Google Scholar] [CrossRef]
- Englesson, E.; Azizpour, H. Generalized Jensen-Shannon divergence loss for learning with noisy labels. In Proceedings of the NeurIPS 2021 Competitions and Demonstrations Track, Online, 6–14 December 2021; pp. 30284–30297. [Google Scholar]
- Dieng, A.B.; Tran, D.; Ranganath, R.; Paisley, J.; Blei, D. Variational Inference via χ Upper Bound Minimization. In Proceedings of the NIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]




| Divergence | Source | SI | Work | |
|---|---|---|---|---|
| TV | Bernoulli | ✗ | [13] | |
| WD | Gaussian | ✗ | [16] | |
| WD, KL, RKL | Gaussian | Equations (15)–(17) | ✔ | Proposed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, J.; Zhu, H.; Xiao, Y.; Shi, G.; Zhang, P. On the Rate-Distortion Theory for Task-Specific Semantic Communication. Entropy 2025, 27, 775. https://doi.org/10.3390/e27080775
Chai J, Zhu H, Xiao Y, Shi G, Zhang P. On the Rate-Distortion Theory for Task-Specific Semantic Communication. Entropy. 2025; 27(8):775. https://doi.org/10.3390/e27080775
Chicago/Turabian StyleChai, Jingxuan, Huixiang Zhu, Yong Xiao, Guangming Shi, and Ping Zhang. 2025. "On the Rate-Distortion Theory for Task-Specific Semantic Communication" Entropy 27, no. 8: 775. https://doi.org/10.3390/e27080775
APA StyleChai, J., Zhu, H., Xiao, Y., Shi, G., & Zhang, P. (2025). On the Rate-Distortion Theory for Task-Specific Semantic Communication. Entropy, 27(8), 775. https://doi.org/10.3390/e27080775






