Comparative Analysis of Robust Entanglement Generation in Engineered XX Spin Chains
Abstract
1. Introduction
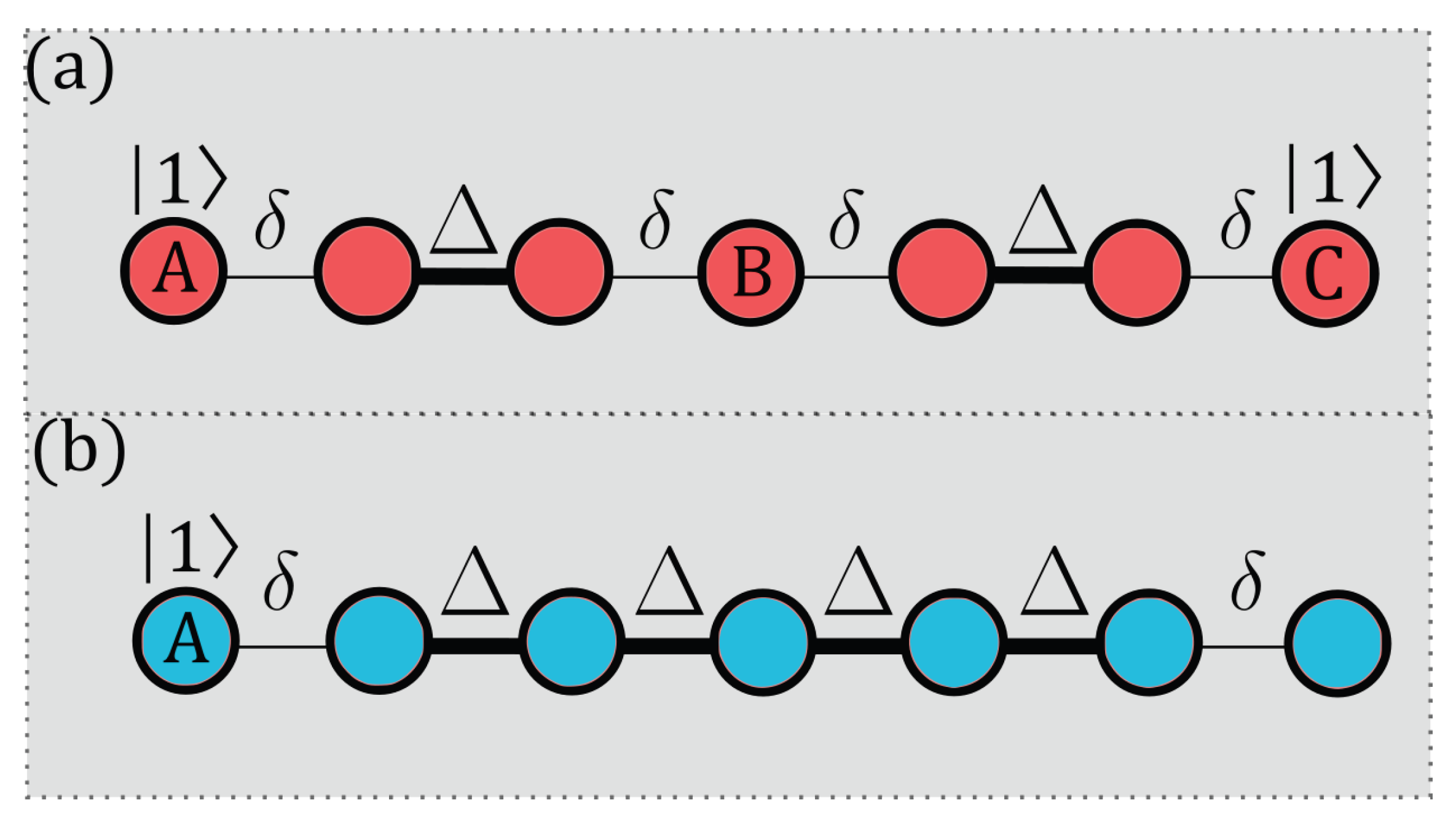
2. Model and Methods
Entanglement Generation Protocols
3. Results
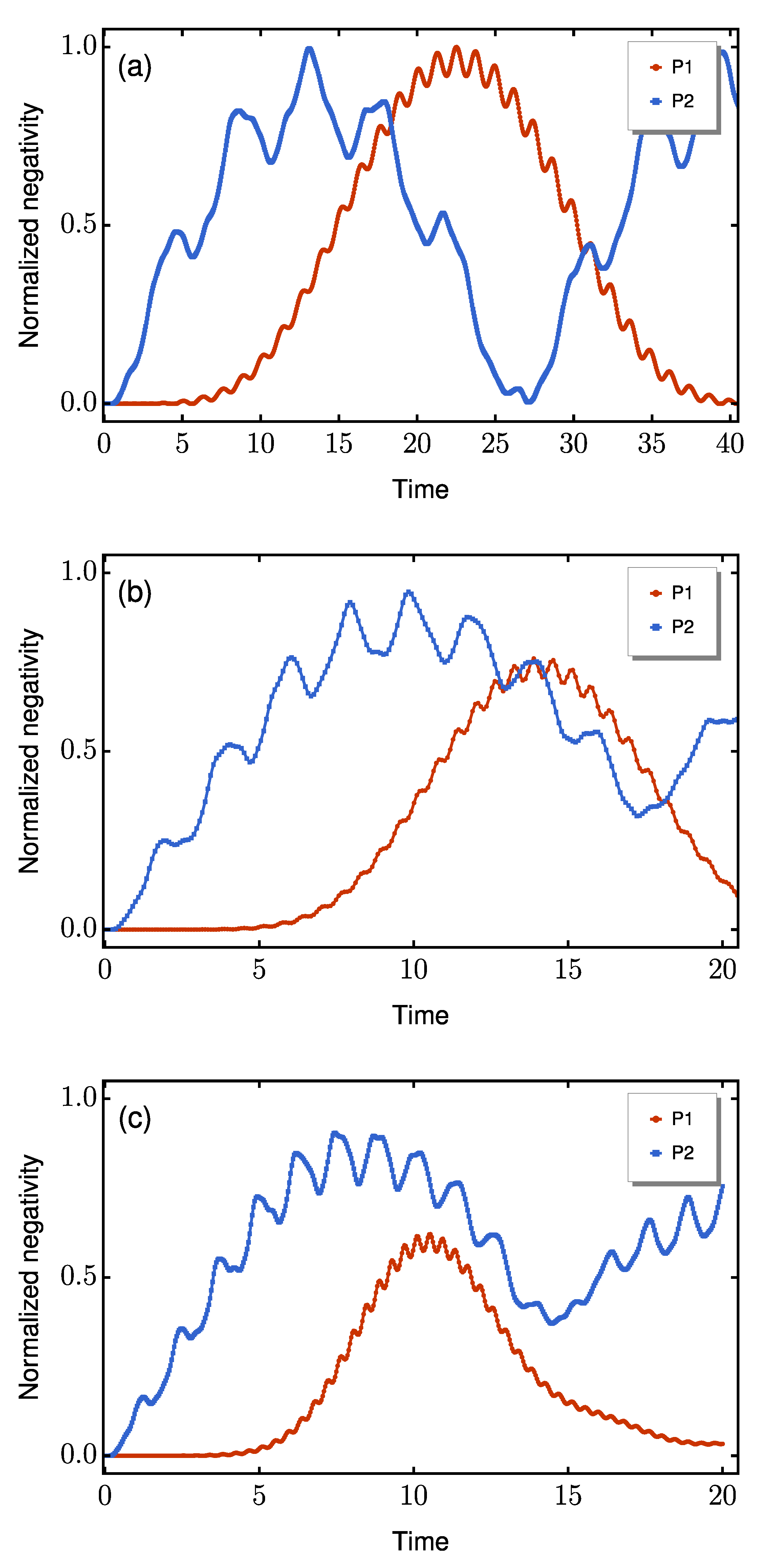
3.1. Benchmark Without Noise: Dynamics in Pristine Chains
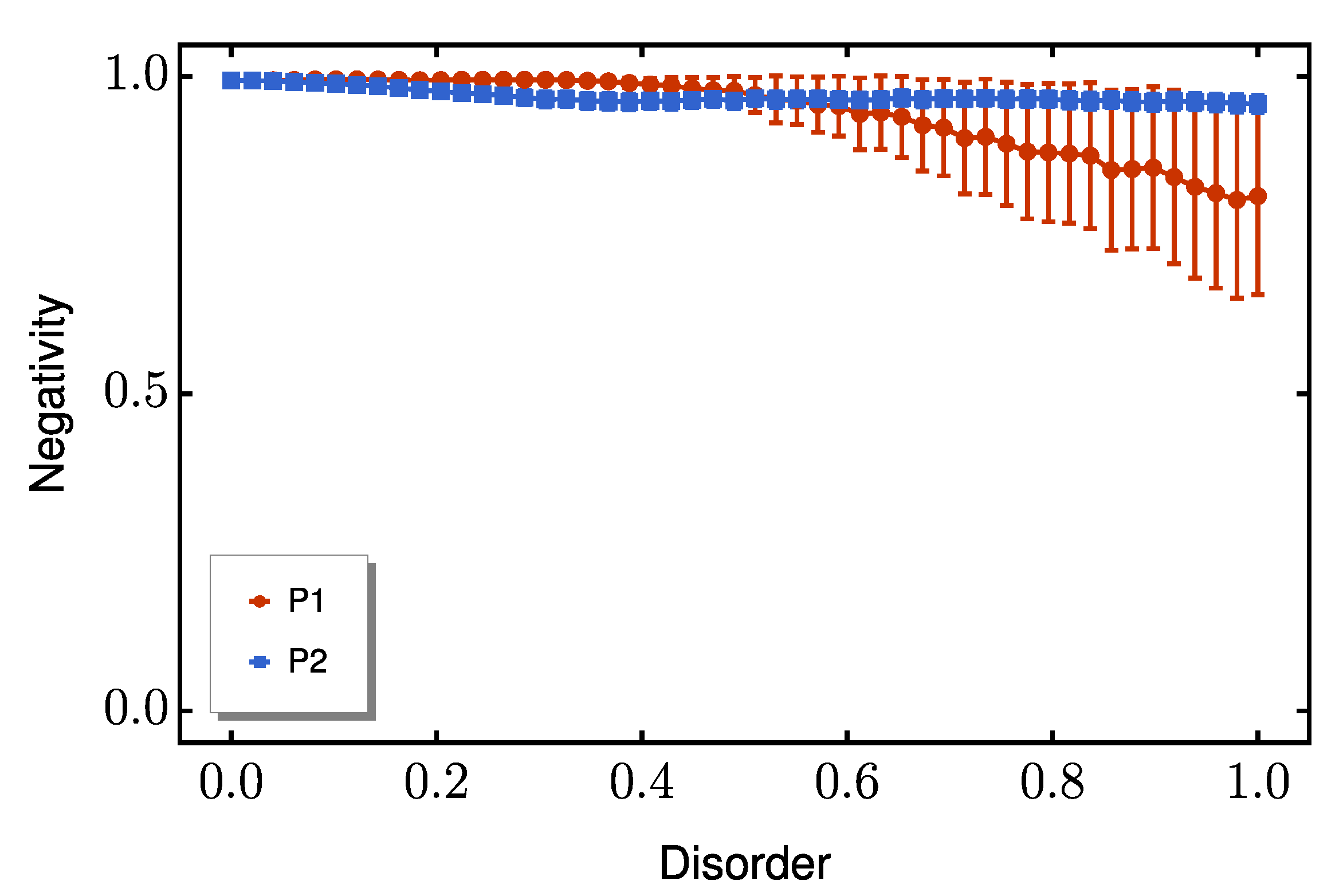
3.2. Robustness of the Spin-1/2 Protocol
3.3. Resistance to Dephasing
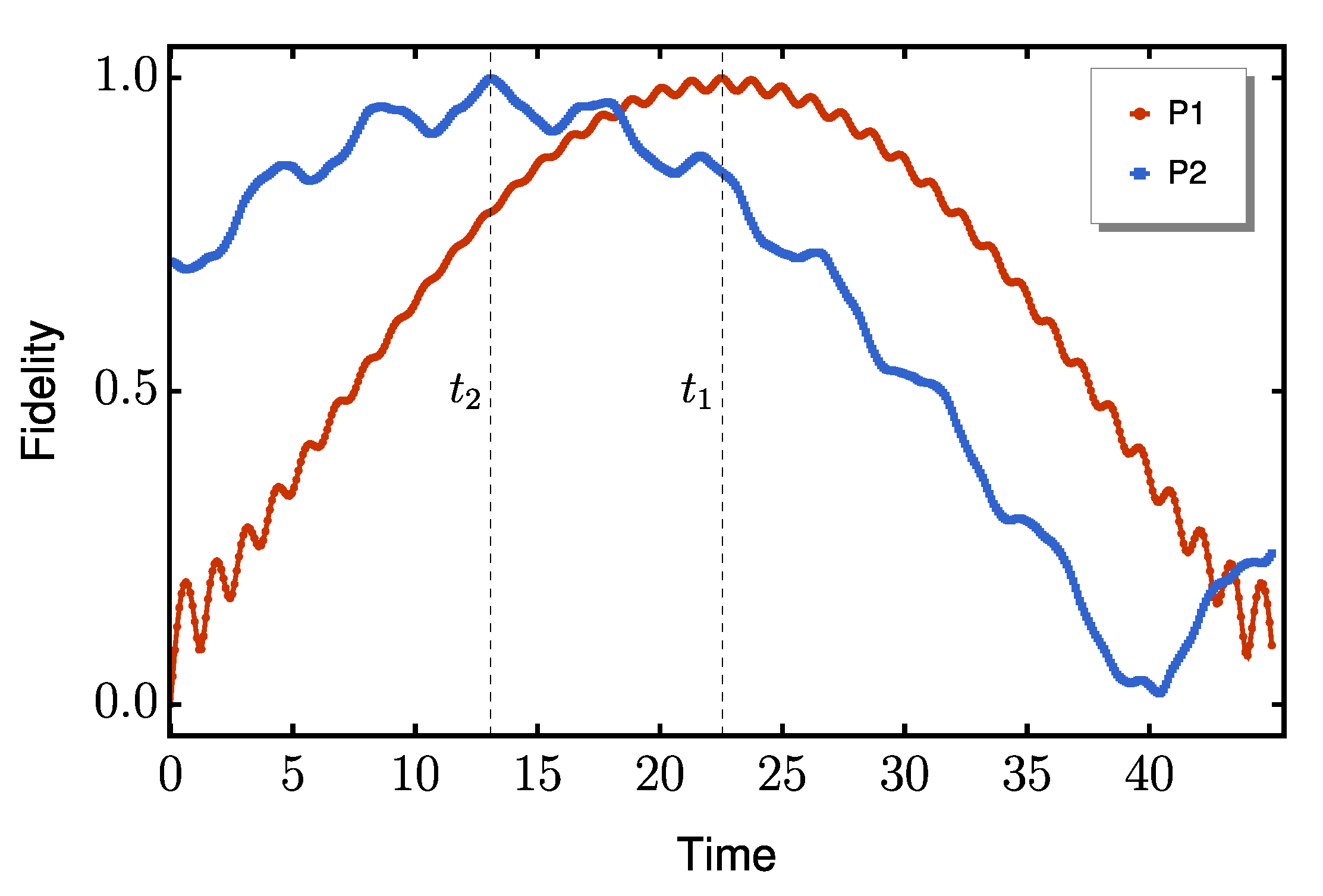
3.4. Non-Markovian Effects
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Effective Dynamics
Appendix A.1. Effective Dispersive Hamiltonian for Protocol 2
Appendix A.2. Trimer Approximation in the Strong Dimerization Regime
References
- Acín, A.; Bloch, I.; Buhrman, H.; Calarco, T.; Eichler, C.; Eisert, J.; Esteve, D.; Gisin, N.; Glaser, S.J.; Jelezko, F.; et al. The quantum technologies roadmap: A European community view. New J. Phys. 2018, 20, 080201. [Google Scholar] [CrossRef]
- Chitambar, E.; Gour, G. Quantum resource theories. Rev. Mod. Phys. 2019, 91, 025001. [Google Scholar] [CrossRef]
- Takeda, S.; Mizuta, T.; Fuwa, M.; van Loock, P.; Furusawa, A. Deterministic quantum teleportation of photonic quantum bits by a hybrid technique. Nature 2013, 500, 315–318. [Google Scholar] [CrossRef] [PubMed]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum Metrology. Phys. Rev. Lett. 2006, 96, 010401. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Mattle, K.; Weinfurter, H.; Zeilinger, A.; Sergienko, A.V.; Shih, Y. New High-Intensity Source of Polarization-Entangled Photon Pairs. Phys. Rev. Lett. 1995, 75, 4337. [Google Scholar] [CrossRef] [PubMed]
- Hucul, D.; Inlek, I.V.; Vittorini, G.; Crocker, C.; Debnath, S.; Clark, S.M.; Monroe, C. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 2015, 11, 37. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef] [PubMed]
- Bose, S. Quantum communication through spin chain dynamics: An introductory overview. Contemp. Phys. 2007, 48, 13. [Google Scholar] [CrossRef]
- Nikolopoulos, G.M.; Petrosyan, D.; Lambropoulos, P. Electron wavepacket propagation in a chain of coupled quantum dots. J. Phys. Condens. Matter 2004, 16, 4991. [Google Scholar] [CrossRef]
- Kay, A. Perfect, efficient, state transfer and its application as a constructive tool. Int. J. Quantum Inf. 2010, 8, 641. [Google Scholar] [CrossRef]
- D’Amico, I. Quantum Information and Quantum Computation: Theory and Experiments; Nova Science Publishers: Hauppauge, NY, USA, 2007. [Google Scholar] [CrossRef][Green Version]
- Tejada, J.; Chudnovsky, E.M.; del Barco, E.; Hernandez, J.M.; Spiller, T.P. Magnetic qubits as hardware for quantum computers. Nanotechnology 2001, 12, 181. [Google Scholar] [CrossRef]
- Twamley, J. Quantum-cellular-automata quantum computing with endohedral fullerenes. Phys. Rev. A 2003, 67, 052318. [Google Scholar] [CrossRef]
- Bose, S. Quantum Communication through an Unmodulated Spin Chain. Phys. Rev. Lett. 2003, 91, 207901. [Google Scholar] [CrossRef]
- Christandl, M.; Datta, N.; Ekert, A.; Landahl, A.J. Perfect State Transfer in Quantum Spin Networks. Phys. Rev. Lett. 2004, 92, 187902. [Google Scholar] [CrossRef]
- Osborne, T.J.; Nielsen, M.A. Entanglement in a simple quantum phase transition. Phys. Rev. A 2002, 66, 032110. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517. [Google Scholar] [CrossRef]
- Alsulami, A.H.; D’Amico, I.; Estarellas, M.P.; Spiller, T.P. Unitary Design of Quantum Spin Networks for Robust Routing, Entanglement Generation, and Phase Sensing. Adv. Quantum Technol. 2022, 5, 2200013. [Google Scholar] [CrossRef]
- Yung, M.-H.; Bose, S. Perfect state transfer, effective gates, and entanglement generation in engineered bosonic and fermionic networks. Phys. Rev. A 2005, 71, 032310. [Google Scholar] [CrossRef]
- Estarellas, M.P.; D’Amico, I.; Spiller, T.P. Robust quantum entanglement generation and generation-plus-storage protocols with spin chains. Phys. Rev. A 2017, 95, 042335. [Google Scholar] [CrossRef]
- Venuti, L.C.; Boschi, C.D.E.; Roncaglia, M. Long-Distance Entanglement in Spin Systems. Phys. Rev. Lett. 2006, 96, 247206. [Google Scholar] [CrossRef]
- Venuti, L.C.; Giampaolo, S.M.; Illuminati, F.; Zanardi, P. Long-distance entanglement and quantum teleportation in XX spin chains. Phys. Rev. A 2007, 76, 052328. [Google Scholar] [CrossRef]
- Giampaolo, S.M.; Illuminati, F. Long-distance entanglement and quantum teleportation in coupled-cavity arrays. Phys. Rev. A 2009, 80, 050301. [Google Scholar] [CrossRef]
- Nikolopoulos, G.M.; Petrosyan, D.; Lambropoulos, P. Coherent electron wavepacket propagation and entanglement in array of coupled quantum dots. Europhys. Lett. 2004, 65, 297. [Google Scholar] [CrossRef]
- Nikolopoulos, G.M.; Jex, I. Quantum State Transfer and Network Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Agarwal, K.D.; Haldar, S.K.; De, A.S. Creating two-qudit maximally entangled quantum link through bulk. arXiv 2024, arXiv:2408.07649. [Google Scholar]
- Dell’Anna, F.; Pradhan, S.; Boschi, C.D.E.; Ercolessi, E. Quantum Fisher information and multipartite entanglement in spin-1 chains. Phys. Rev. B 2023, 108, 144414. [Google Scholar] [CrossRef]
- Refael, G.; Moore, J.E. Entanglement entropy of the random s = 1 Heisenberg chain. Phys. Rev. B 2007, 76, 024419. [Google Scholar] [CrossRef]
- Wilkinson, K.N.; Estarellas, M.P.; Spiller, T.P.; D’amico, I. Rapid and Robust generation of Einstein–Podolsky–Rosen pairs with Spin Chains. Quantum Inf. Comput. 2018, 18, 247. [Google Scholar] [CrossRef]
- Estarellas, M.P.; D’Amico, I.; Spiller, T.P. Topologically protected localised states in spin chains. Sci. Rep. 2017, 7, 42904. [Google Scholar] [CrossRef] [PubMed]
- Huo, M.X.; Li, Y.; Song, Z.; Sun, C.P. The Peierls distorted chain as a quantum data bus for quantum state transfer. Europhys. Lett. 2008, 84, 30004. [Google Scholar] [CrossRef]
- Neto, G.; de Ponte, M.; Moussa, M.H.Y. Nonlocal dissipative tunneling for high-fidelity quantum-state transfer between distant parties. Phys. Rev. A 2012, 85, 052303. [Google Scholar] [CrossRef]
- Yao, N.Y.; Jiang, L.; Gorshkov, A.V.; Gong, Z.-X.; Zhai, A.; Duan, L.-M.; Lukin, M.D. Robust Quantum State Transfer in Random Unpolarized Spin Chains. Phys. Rev. Lett. 2011, 106, 040505. [Google Scholar] [CrossRef] [PubMed]
- Paganelli, S.; Lorenzo, S.; Apollaro, T.J.; Plastina, F.; Giorgi, G.L. Routing quantum information in spin chains. Phys. Rev. A 2013, 87, 062309. [Google Scholar] [CrossRef]
- Almeida, G.M.A.; de Moura, F.A.B.F.; Lyra, M.L. Entanglement generation between distant parties via disordered spin chains. Quantum Inf. Process. 2019, 18, 41. [Google Scholar] [CrossRef]
- Rivas, Á.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Shrikant, U.; Mandayam, P. Quantum non-Markovianity: Overview and recent developments. Front. Quantum Sci. Technol. 2023, 2, 1134583. [Google Scholar] [CrossRef]
- Imamog, A. Stochastic wave-function approach to non-Markovian systems. Phys. Rev. A 1994, 50, 3650. [Google Scholar] [CrossRef]
- Garraway, B.M. Nonperturbative decay of an atomic system in a cavity. Phys. Rev. A 1997, 55, 2290. [Google Scholar] [CrossRef]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C.L. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217. [Google Scholar] [CrossRef]
- Wang, X.; Bayat, A.; Schirmer, S.G.; Bose, S. Robust entanglement in antiferromagnetic Heisenberg chains by single-spin optimal control. Phys. Rev. A 2010, 81, 032312. [Google Scholar] [CrossRef]
- Galve, F.; Zueco, D.; Reuther, G.M.; Kohler, S.; Hänggi, P. Creation and manipulation of entanglement in spin chains far from equilibrium. Eur. Phys. J. Spec. Top. 2010, 180, 237–246. [Google Scholar] [CrossRef]
- Alkurtass, B.; Bayat, A.; Sodano, P.; Bose, S.; Johannesson, H. Ballistic entanglement cloud after a boundary quench. Phys. Rev. Res. 2025, 7, 013268. [Google Scholar] [CrossRef]
- Bayat, A.; Bose, S.; Johannesson, H. (Eds.) Entanglement in Spin Chains: From Theory to Quantum Technology Applications; Quantum Science and Technology; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Manzano, D. A short introduction to the Lindblad master equation. AIP Adv. 2020, 10, 025106. [Google Scholar] [CrossRef]
- Martinis, J.M.; Nam, S.; Aumentado, J.; Urbina, C. Rabi Oscillations in a Large Josephson-Junction Qubit. Phys. Rev. Lett. 2002, 89, 117901. [Google Scholar] [CrossRef] [PubMed]
- Schreier, J.A.; Houck, A.A.; Koch, J.; Schuster, D.I.; Johnson, B.R.; Chow, J.M.; Gambetta, J.M.; Majer, J.; Frunzio, L.; Devoret, M.H.; et al. Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 2008, 77, 180502. [Google Scholar] [CrossRef]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042. [Google Scholar] [CrossRef]
- Schindler, P.; Barreiro, J.T.; Monz, T.; Nebendahl, V.; Nigg, D.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Blatt, R. A quantum information processor with trapped ions. New J. Phys. 2013, 15, 123012. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V.; Damski, B.; Sen, A.; Sen, U. Ultracold atomic gases in optical lattices: Mimicking condensed matter physics and beyond. Adv. Phys. 2007, 56, 243–379. [Google Scholar] [CrossRef]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Vicenti, J.I. Lower bounds on concurrence and separability conditions. Phys. Rev. A 2007, 75, 052320. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M.; Cirac, J.I. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys. 2009, 5, 633–636. [Google Scholar] [CrossRef]
- Lin, Y.; Gaebler, J.; Reiter, F.; Tan, T.; Bowler, R.; Sørensen, A.; Leibfried, D.; Wineland, D. Dissipative production of a maximally entangled steady state of two quantum bits. Nature 2013, 504, 415–418. [Google Scholar] [CrossRef] [PubMed]
- Dias, J.; Wächtler, C.W.; Nemoto, K.; Munro, W.J. Entanglement generation between distant spins via quasilocal reservoir engineering. Phys. Rev. Res. 2023, 5, 043295. [Google Scholar] [CrossRef]
- Kurpiers, P.; Magnard, P.; Walter, T.; Royer, B.; Pechal, M.; Heinsoo, J.; Salathé, Y.; Akin, A.; Storz, S.; Besse, J.-C.; et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 2018, 558, 264–267. [Google Scholar] [CrossRef] [PubMed]
- Bahri, Y.; Vosk, R.; Altman, E.; Vishwanath, A. Localization and topology protected quantum coherence at the edge of hot matter. Nat. Commun. 2015, 6, 7341. [Google Scholar] [CrossRef]
- Klimov, A.B.; Romero, J.L.; Delgado, J.; Soto, L.L.S.N. Master equations for effective Hamiltonians. J. Opt. B Quantum Semiclass. Opt. 2002, 5, 34. [Google Scholar] [CrossRef]
- Lee, C.-W.; Noh, C.; Kim, J. Effective formalism for open-quantum-system dynamics: Time-coarse-graining approach. Phys. Rev. A 2018, 97, 012102. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Müller, C.; Lisenfeld, J.; Shnirman, A.; Poletto, S. Interacting two-level defects as sources of fluctuating high-frequency noise in superconducting circuits. Phys. Rev. B 2015, 92, 035442. [Google Scholar] [CrossRef]
- Cywin, Ł.; Witzel, W.M.; Sarma, S.D. Pure quantum dephasing of a solid-state electron spin qubit in a large nuclear spin bath coupled by long-range hyperfine-mediated interactions. Phys. Rev. B 2009, 79, 245314. [Google Scholar] [CrossRef]
- Tanimura, Y. Stochastic Liouville, Langevin, Fokker–Planck, and Master Equation Approaches to Quantum Dissipative Systems. J. Phys. Soc. Jpn. 2006, 75, 082001. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. Classical counterexamples to Bell’s inequalities. Phys. Rev. A 2002, 65, 042106. [Google Scholar] [CrossRef]
- Diósi, L.; Gisin, N.; Strunz, W.T. Non-Markovian quantum state diffusion. Phys. Rev. A 1998, 58, 1699. [Google Scholar] [CrossRef]
- Chin, A.W.; Rivas, Á.; Huelga, S.F.; Plenio, M.B. Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials. J. Math. Phys. 2010, 51, 092109. [Google Scholar] [CrossRef]
- Blais, A.; Grimsmo, A.L.; Girvin, S.M.; Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 2021, 93, 025005. [Google Scholar] [CrossRef]
- Chikkaraddy, R.; de Nijs, B.; Benz, F.; Barrow, S.J.; Scherman, O.A.; Rosta, E.; Demetriadou, A.; Fox, P.; Hess, O.; Baumberg, J.J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. [Google Scholar] [CrossRef] [PubMed]
- Leghtas, Z.; Touzard, S.; Pop, I.M.; Kou, A.; Vlastakis, B.; Petrenko, A.; Sliwa, K.M.; Narla, A.; Shankar, S.; Hatridge, M.J.; et al. Method for universal detection of two-photon polarization entanglement. Phys. Rev. A 2015, 91, 032315. [Google Scholar] [CrossRef]
- Jia, D.; Sakharwade, N. Tensor products of process matrices with indefinite causal structure. Phys. Rev. A 2018, 97, 032110. [Google Scholar] [CrossRef]
- Tamascelli, D.; Smirne, A.; Huelga, S.F.; Plenio, M.B. Efficient Simulation of Finite-Temperature Open Quantum Systems. Phys. Rev. Lett. 2019, 123, 090402. [Google Scholar] [CrossRef]
- Keup, C.; Kühn, T.; Dahmen, D.; Helias, M. Transient Chaotic Dimensionality Expansion by Recurrent Networks. Phys. Rev. X 2021, 11, 021064. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005. [Google Scholar] [CrossRef]
- de Moraes Neto, G.; de Ponte, M.; Moussa, M.H.Y. Colored channels for high-fidelity information transfer and processing between remote multi-branch quantum circuits. Europhys. Lett. 2013, 103, 43001. [Google Scholar] [CrossRef]
- Grimaudo, R.; de Castro, A.S.M.; Messina, A.; Valenti, D. Spin-Chain-Star Systems: Entangling Multiple Chains of Spin Qubits. Fortschr. Phys. 2022, 70, 2200042. [Google Scholar] [CrossRef]
- de Moraes Neto, G.; Teizen, V.; Montenegro, V.; Vernek, E. Steady many-body entanglements in dissipative systems. Phys. Rev. A 2017, 96, 062313. [Google Scholar] [CrossRef]
- Monroe, C.; Campbell, W.C.; Duan, L.-M.; Gong, Z.-X.; Gorshkov, A.V.; Hess, P.W.; Islam, R.; Kim, K.; Linke, N.M.; Pagano, G.; et al. Programmable quantum simulations of spin systems with trapped ions. Rev. Mod. Phys. 2021, 93, 025001. [Google Scholar] [CrossRef]
- Mei, Q.-X.; Wang, B.-Z.; Yang, T.; Chen, Y.; Wu, J.; Wang, P.; Zhang, X.; Tan, T.; Qiao, Y.; Cui, J.-M.; et al. Experimental Realization of the Rabi-Hubbard Model with Trapped Ions. Phys. Rev. Lett. 2022, 128, 160504. [Google Scholar] [CrossRef] [PubMed]
- Zueco, D.; Reuther, G.M.; Kohler, S.; Hänggi, P. Qubit-oscillator dynamics in the dispersive regime: Analytical theory beyond the rotating-wave approximation. Phys. Rev. A 2009, 80, 033846. [Google Scholar] [CrossRef]


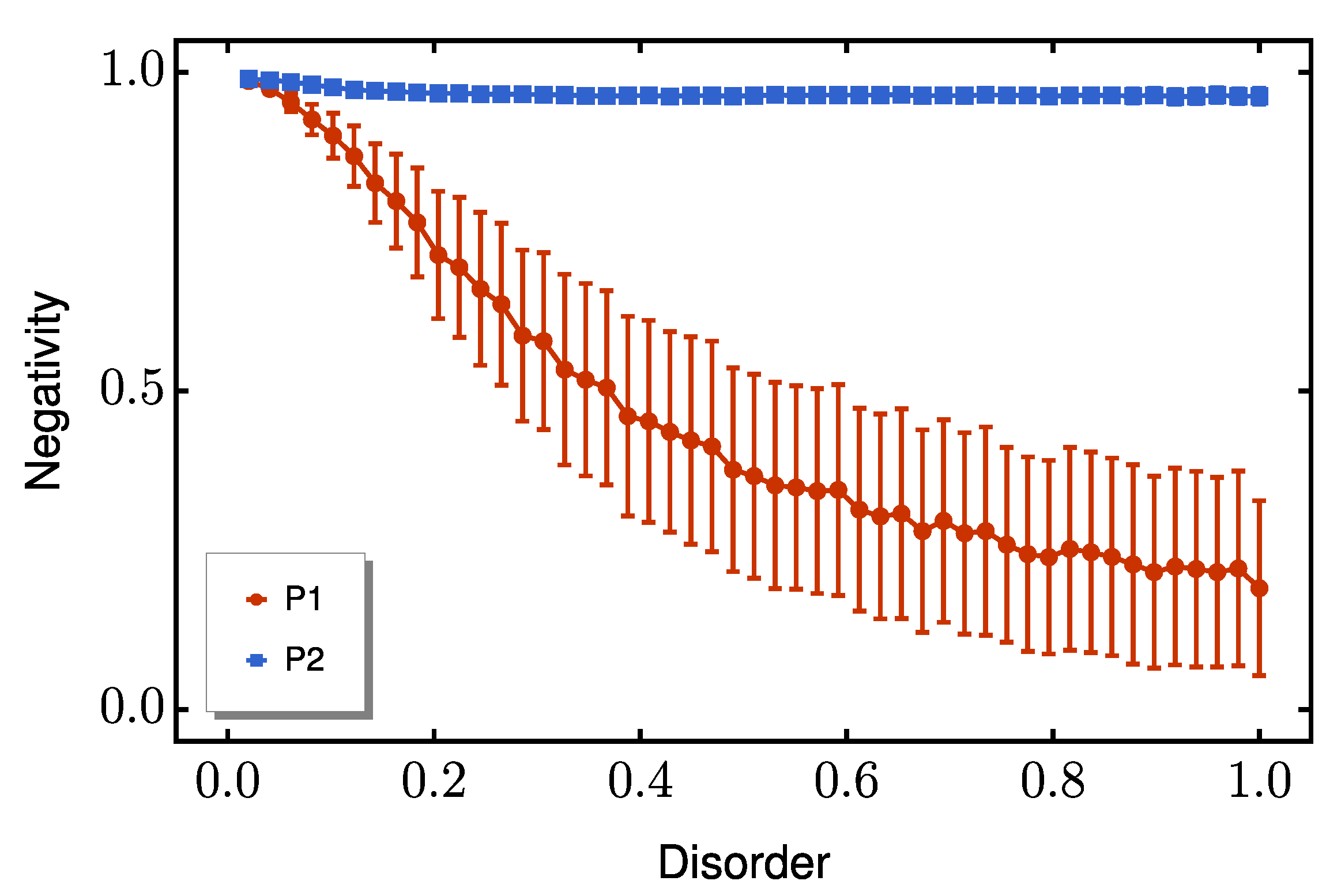

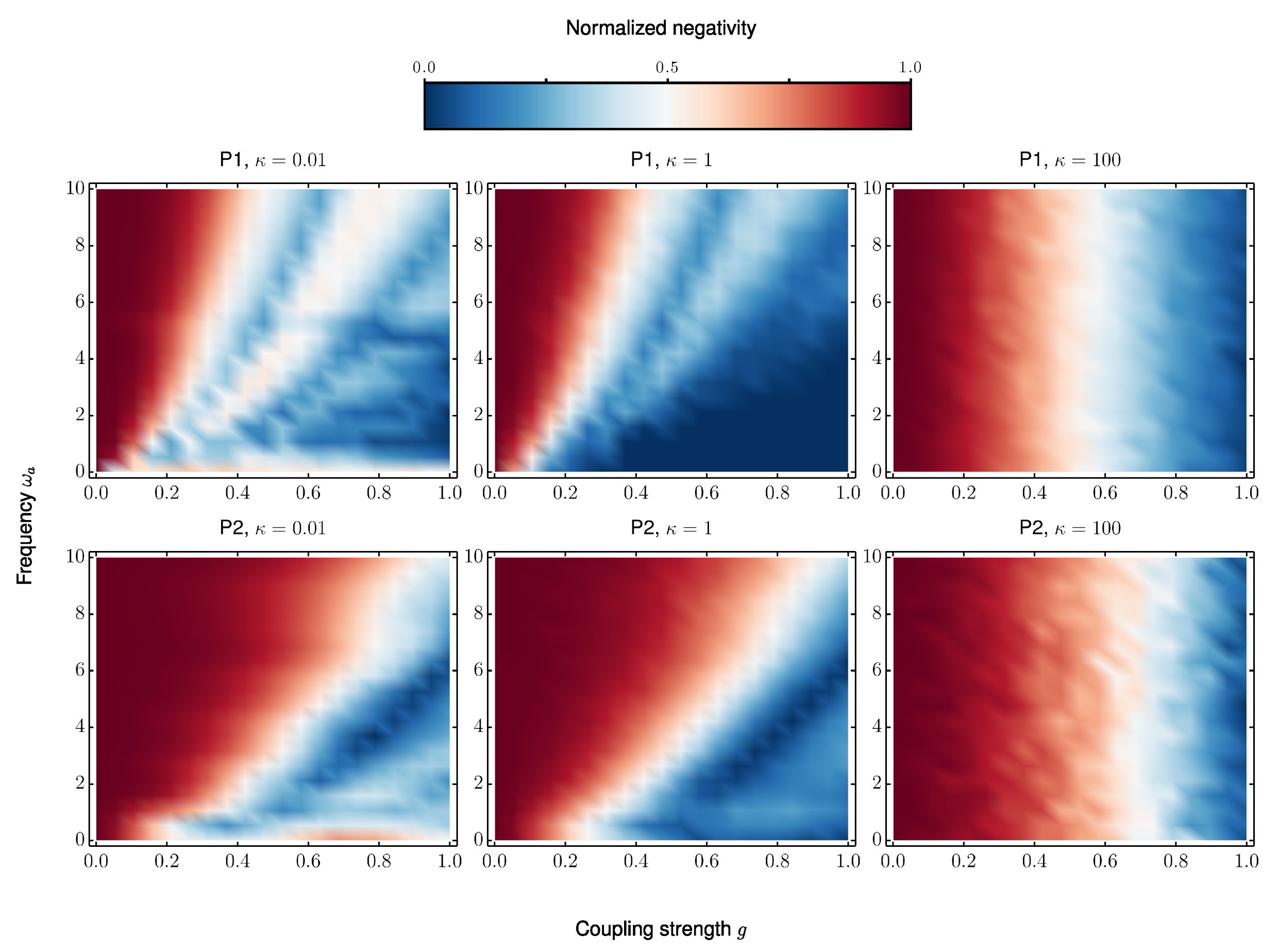
| Spin | B | ||||
|---|---|---|---|---|---|
| 1 | 22.50 | 1 | 13 | 3.7 | |
| 1 | 0.75 | 13.9 | 0.94 | 9.8 | 2.9 |
| 0.62 | 10.54 | 0.9 | 7.45 | 4.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soares, E.K.; de Moraes Neto, G.D.; Andrade, F.M. Comparative Analysis of Robust Entanglement Generation in Engineered XX Spin Chains. Entropy 2025, 27, 764. https://doi.org/10.3390/e27070764
Soares EK, de Moraes Neto GD, Andrade FM. Comparative Analysis of Robust Entanglement Generation in Engineered XX Spin Chains. Entropy. 2025; 27(7):764. https://doi.org/10.3390/e27070764
Chicago/Turabian StyleSoares, Eduardo K., Gentil D. de Moraes Neto, and Fabiano M. Andrade. 2025. "Comparative Analysis of Robust Entanglement Generation in Engineered XX Spin Chains" Entropy 27, no. 7: 764. https://doi.org/10.3390/e27070764
APA StyleSoares, E. K., de Moraes Neto, G. D., & Andrade, F. M. (2025). Comparative Analysis of Robust Entanglement Generation in Engineered XX Spin Chains. Entropy, 27(7), 764. https://doi.org/10.3390/e27070764







