Enhancing Robustness of Variational Data Assimilation in Chaotic Systems: An α-4DVar Framework with Rényi Entropy and α-Generalized Gaussian Distributions
Abstract
1. Introduction
2. Methods
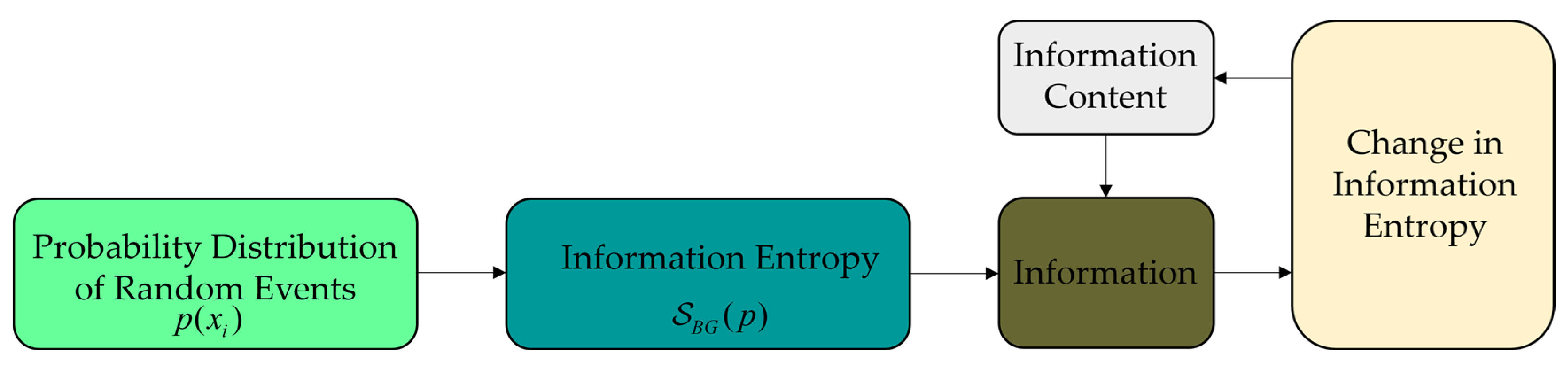
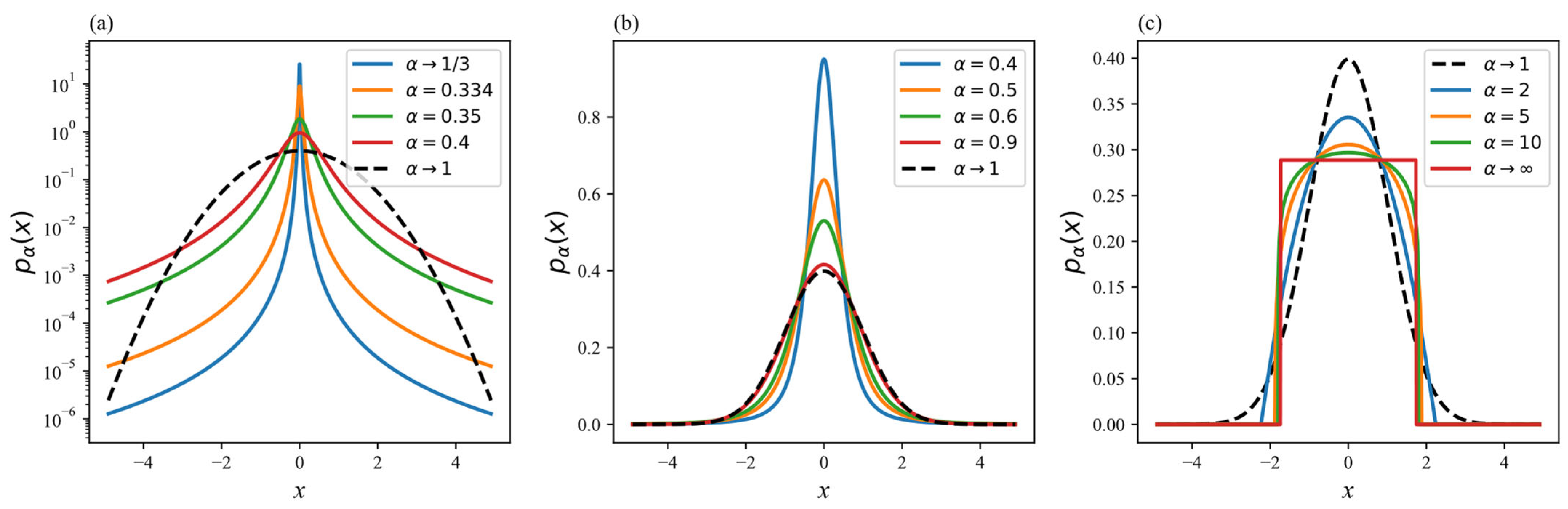
2.1. Rényi Entropy and the α-Generalized Gaussian Distribution
2.2. Non-Gaussian Nonlinear Data Assimilation Method Based on the α-Generalized Gaussian Distribution
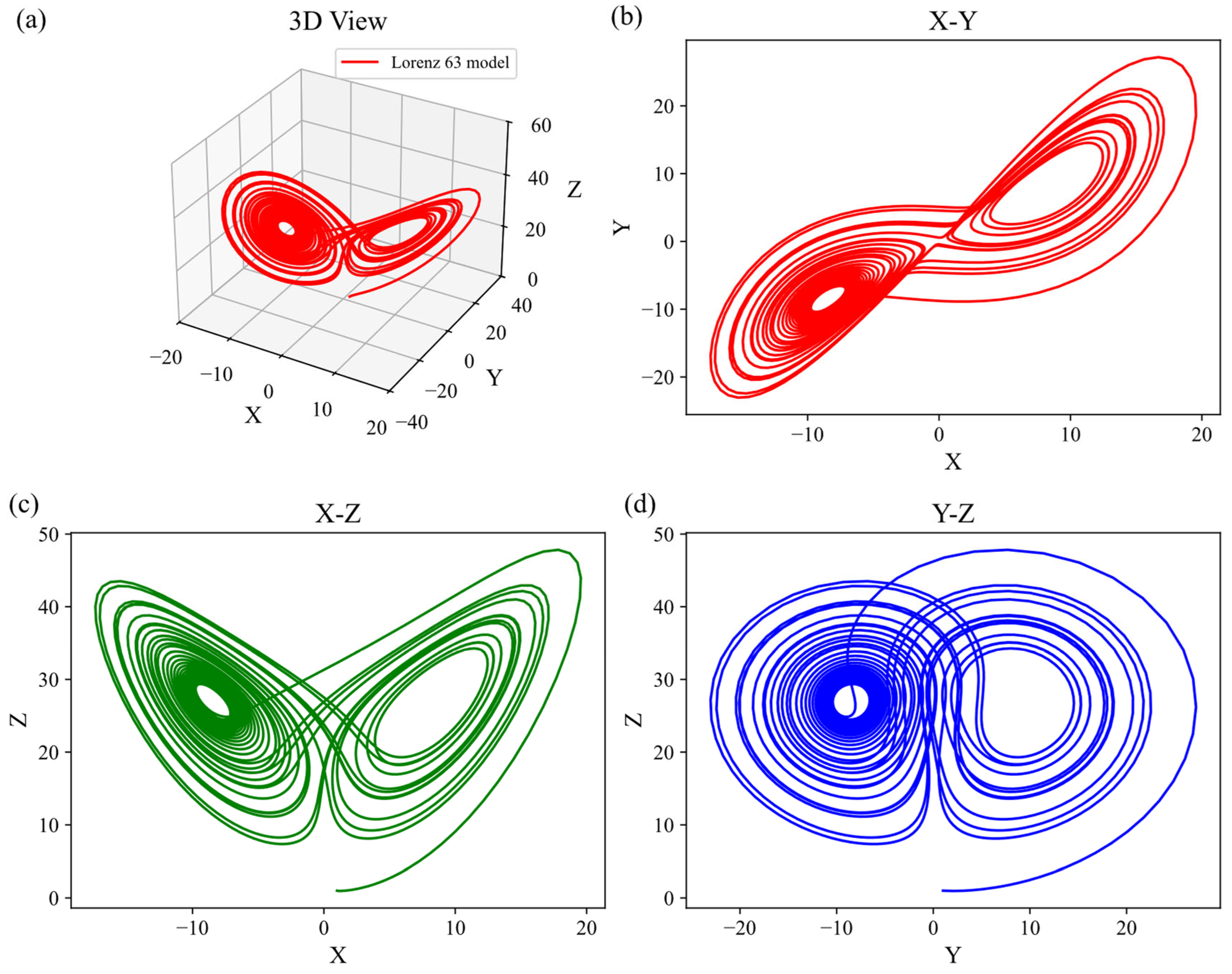
2.3. Lorenz-63 Model
3. Results
3.1. Comparative Experiments of Traditional 4DVar and α-4DVar Under Error-Free Observation Conditions in Lorenz-63
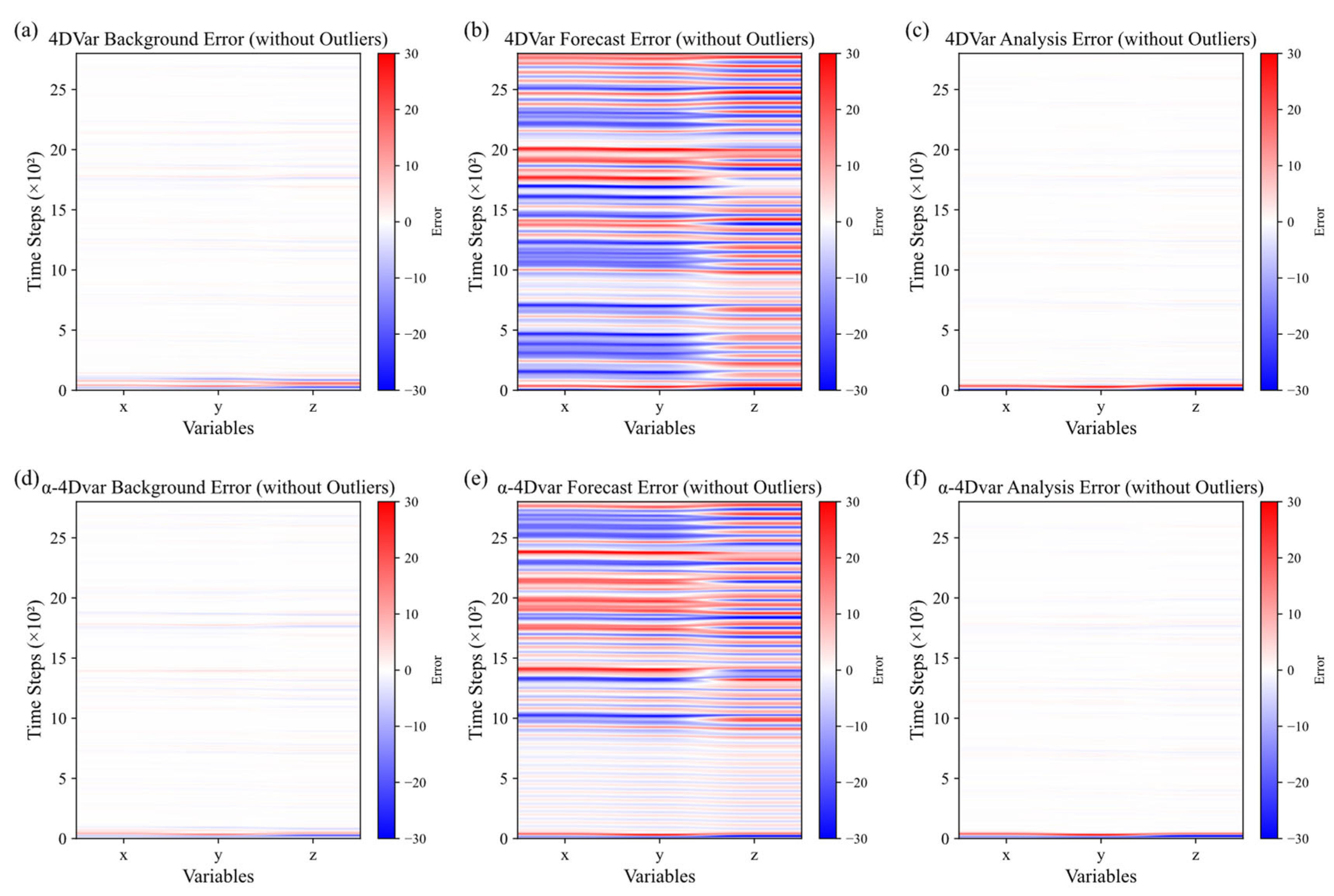
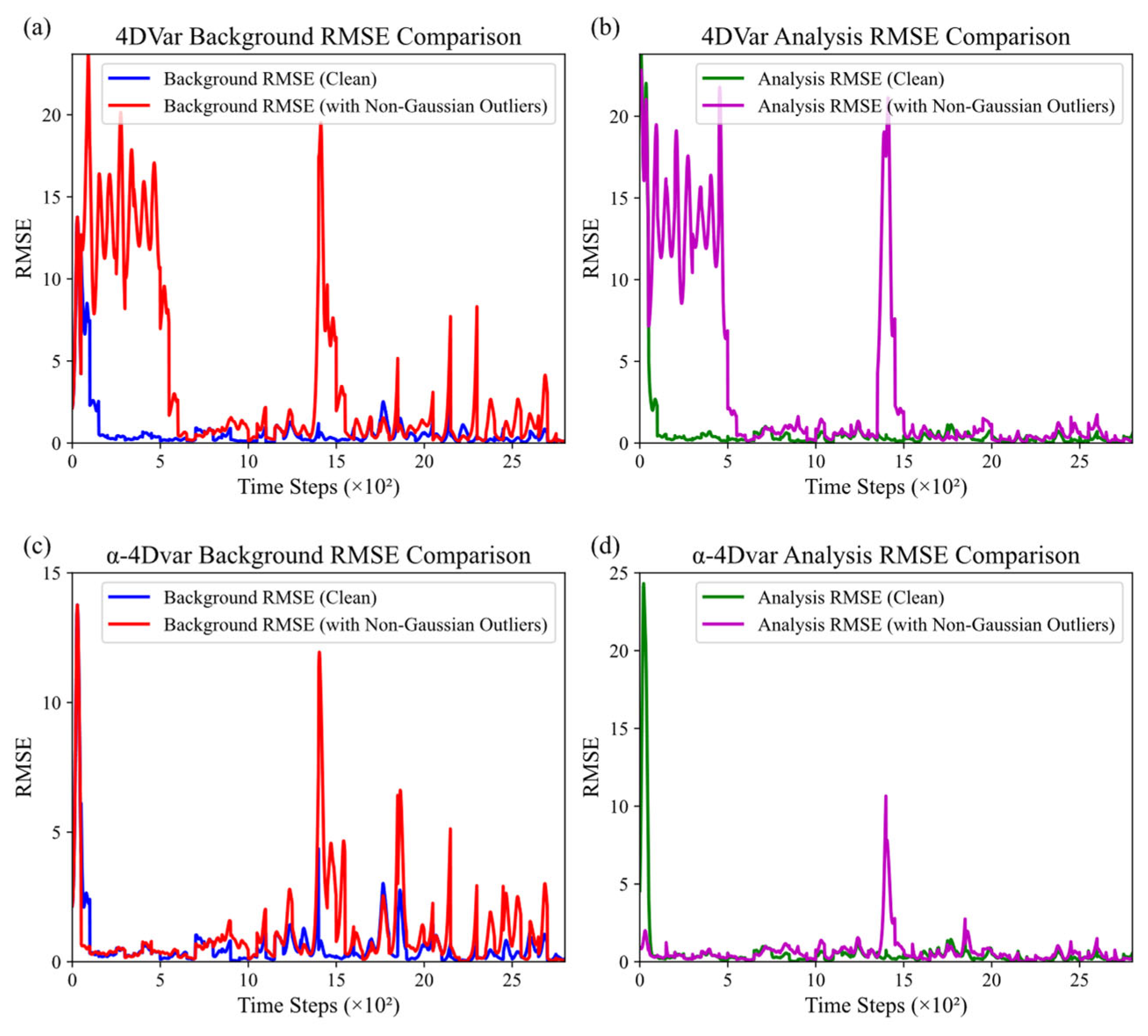
3.2. Comparative Experiments of Traditional 4DVar and α-4DVar Under Gaussian and Non-Gaussian Errors in Lorenz-63
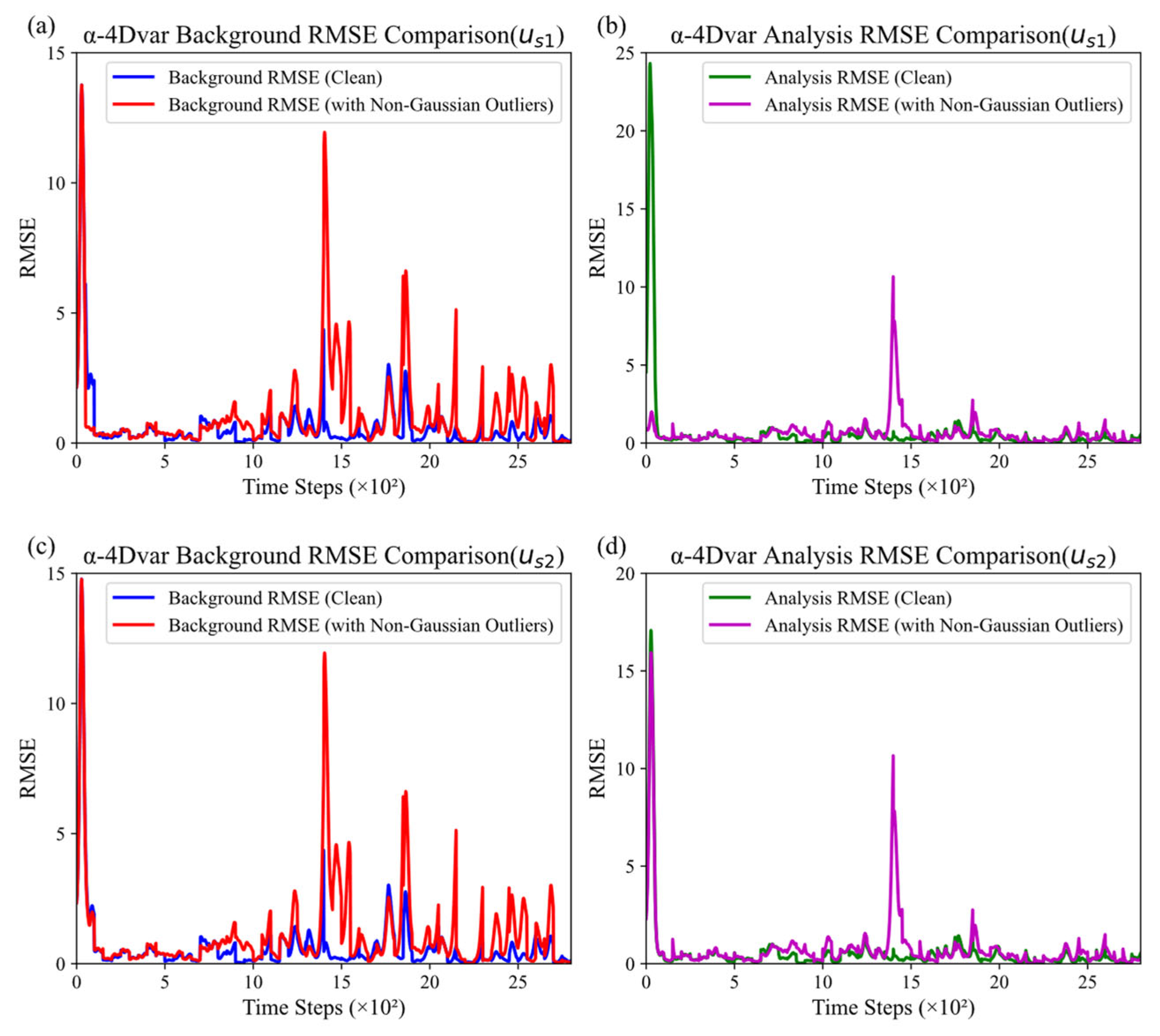
3.3. Comparative Experiments of α-4DVar with Different Initial Guesses in Lorenz-63
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 4DVar | Four-dimensional variational data assimilation |
| RMSE | Root mean square error |
| GNSS | Global navigation satellite system |
| WRFDA | Weather Research and Forecasting Data Assimilation |
| BGS | Boltzmann–Gibbs–Shannon entropy |
| ODEs | Ordinary differential equations |
| GGD | Generalized Gaussian distribution |
References
- Wang, H.; Yuan, S.; Liu, Y.; Li, Y. Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection. Remote Sens. 2022, 14, 5980. [Google Scholar] [CrossRef]
- Potthast, R.; Vobig, K.; Blahak, U.; Simmer, C. Data Assimilation of Nowcasted Observations. Mon. Weather Rev. 2022, 150, 969–980. [Google Scholar] [CrossRef]
- Bai, W.; Wang, G.; Huang, F.; Sun, Y.; Du, Q.; Xia, J.; Wang, X.; Meng, X.; Hu, P.; Yin, C.; et al. Review of Assimilating Spaceborne Global Navigation Satellite System Remote Sensing Data for Tropical Cyclone Forecasting. Remote Sens. 2025, 17, 118. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.; Yu, H.; Wu, K.; Lang, S.; Xu, Y. Comparison of Wave Spectrum Assimilation and Significant Wave Height Assimilation Based on Chinese-French Oceanography Satellite Observations. Remote Sens. Environ. 2024, 305, 114085. [Google Scholar] [CrossRef]
- Li, S.; Hu, H.; Fang, C.; Wang, S.; Xun, S.; He, B.; Wu, W.; Huo, Y. Hyperspectral Infrared Atmospheric Sounder (HIRAS) Atmospheric Sounding System. Remote Sens. 2022, 14, 3882. [Google Scholar] [CrossRef]
- Zalesny, V.; Agoshkov, V.; Shutyaev, V.; Parmuzin, E.; Zakharova, N. Numerical Modeling of Marine Circulation with 4D Variational Data Assimilation. J. Mar. Sci. Eng. 2020, 8, 503. [Google Scholar] [CrossRef]
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data Assimilation in the Geosciences: An Overview of Methods, Issues, and Perspectives. Wiley Interdiscip. Rev.-Clim. Chang. 2018, 9, e535. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Qi, Z. Remote Sensing Data Assimilation in Crop Growth Modeling from an Agricultural Perspective: New Insights on Challenges and Prospects. Agronomy 2024, 14, 1920. [Google Scholar] [CrossRef]
- Bonavita, M.; Arcucci, R.; Carrassi, A.; Dueben, P.; Geer, A.J.; Le Saux, B.; Longepe, N.; Mathieu, P.-P.; Raynaud, L. Machine Learning for Earth System Observation and Prediction. Bull. Am. Meteorol. Soc. 2021, 102, E710–E716. [Google Scholar] [CrossRef]
- Dong, R.; Leng, H.; Zhao, J.; Song, J.; Liang, S. A Framework for Four-Dimensional Variational Data Assimilation Based on Machine Learning. Entropy 2022, 24, 264. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Hou, Y.; Qi, P. Altimeter Significant Wave Height Data Assimilation in the South China Sea Using Ensemble Optimal Interpolation. Chin. J. Oceanol. Limnol. 2015, 33, 1309–1319. [Google Scholar] [CrossRef]
- El Serafy, G.Y.H.; Schaeffer, B.A.; Neely, M.-B.; Spinosa, A.; Odermatt, D.; Weathers, K.C.; Baracchini, T.; Bouffard, D.; Carvalho, L.; Conmy, R.N.; et al. Integrating Inland and Coastal Water Quality Data for Actionable Knowledge. Remote Sens. 2021, 13, 2899. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Sun, Z.; Jiang, X.; Zeng, J.; Liu, R. Kalman Filter and Its Application in Data Assimilation. Atmosphere 2023, 14, 1319. [Google Scholar] [CrossRef]
- Chorin, A.; Morzfeld, M.; Tu, X. Implicit Particle Filters for Data Assimilation. Commun. Appl. Math. Comput. Sci. 2010, 5, 221–240. [Google Scholar] [CrossRef]
- Mack, J.; Arcucci, R.; Molina-Solana, M.; Guo, Y.-K. Attention-Based Convolutional Autoencoders for 3D-Variational Data Assimilation. Comput. Meth. Appl. Mech. Eng. 2020, 372, 113291. [Google Scholar] [CrossRef]
- Rao, V.; Sandu, A. A Time-Parallel Approach to Strong-Constraint Four-Dimensional Variational Data Assimilation. J. Comput. Phys. 2016, 313, 583–593. [Google Scholar] [CrossRef]
- Galanis, G.; Louka, P.; Katsafados, P.; Pytharoulis, I.; Kallos, G. Applications of Kalman Filters Based on Non-Linear Functions to Numerical Weather Predictions. Ann. Geophys. 2006, 24, 2451–2460. [Google Scholar] [CrossRef]
- Peng, W.; Weng, F.; Ye, C. The Impact of MERRA-2 and CAMS Aerosol Reanalysis Data on FengYun-4B Geostationary Interferometric Infrared Sounder Simulations. Remote Sens. 2025, 17, 761. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, Z.; Tang, Y. On Oceanic Initial State Errors in the Ensemble Data Assimilation for a Coupled General Circulation Model. J. Adv. Model. Earth Syst. 2022, 14, e2022MS003106. [Google Scholar] [CrossRef]
- Bonaduce, A.; Storto, A.; Cipollone, A.; Raj, R.P.; Yang, C. Exploiting Enhanced Altimetry for Constraining Mesoscale Variability in the Nordic Seas and Arctic Ocean. Remote Sens. 2025, 17, 684. [Google Scholar] [CrossRef]
- Sun, L.; Seidou, O.; Nistor, I.; Liu, K. Review of the Kalman-Type Hydrological Data Assimilation. Hydrol. Sci. J. 2016, 61, 2348–2366. [Google Scholar] [CrossRef]
- Bai, X.; Qin, Z.; Li, J.; Zhang, S.; Wang, L. The Impact of Spatial Dynamic Error on the Assimilation of Soil Moisture Retrieval Products. Remote Sens. 2025, 17, 239. [Google Scholar] [CrossRef]
- Zhou, H.; Geng, G.; Yang, J.; Hu, H.; Sheng, L.; Lou, W. Improving Soil Moisture Estimation via Assimilation of Remote Sensing Product into the DSSAT Crop Model and Its Effect on Agricultural Drought Monitoring. Remote Sens. 2022, 14, 3187. [Google Scholar] [CrossRef]
- Wei, H.; Huang, Y.; Hu, F.; Zhao, B.; Guo, Z.; Zhang, R. Motion Estimation Using Region-Level Segmentation and Extended Kalman Filter for Autonomous Driving. Remote Sens. 2021, 13, 1828. [Google Scholar] [CrossRef]
- Mahfouz, S.; Mourad-Chehade, F.; Honeine, P.; Farah, J.; Snoussi, H. Target Tracking Using Machine Learning and Kalman Filter in Wireless Sensor Networks. IEEE Sens. J. 2014, 14, 3715–3725. [Google Scholar] [CrossRef]
- Huang, S.X.; Han, W.; Wu, R.S. Theoretical Analyses and Numerical Experiments of Variational Assimilation for One-Dimensional Ocean Temperature Model with Techniques in Inverse Problems. Sci. China Ser. D-Earth Sci. 2004, 47, 630–638. [Google Scholar] [CrossRef]
- Islam, T.; Srivastava, P.K.; Kumar, D.; Petropoulos, G.P.; Dai, Q.; Zhuo, L. Satellite Radiance Assimilation Using a 3DVAR Assimilation System for Hurricane Sandy Forecasts. Nat. Hazards 2016, 82, 845–855. [Google Scholar] [CrossRef][Green Version]
- Rohm, W.; Guzikowski, J.; Wilgan, K.; Kryza, M. 4DVAR Assimilation of GNSS Zenith Path Delays and Precipitable Water into a Numerical Weather Prediction Model WRF. Atmos. Meas. Tech. 2019, 12, 345–361. [Google Scholar] [CrossRef]
- Shen, F.; Min, J.; Li, H.; Xu, D.; Shu, A.; Zhai, D.; Guo, Y.; Song, L. Applications of Radar Data Assimilation with Hydrometeor Control Variables within the WRFDA on the Prediction of Landfalling Hurricane IKE (2008). Atmosphere 2021, 12, 853. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Su, Q.; Chai, X.; Lu, J.; Ni, W.; Duan, B.; Ren, K. Accurate Initial Field Estimation for Weather Forecasting with a Variational Constrained Neural Network. npj Clim. Atmos. Sci. 2024, 7, 223. [Google Scholar] [CrossRef]
- He, J.; Shi, Y.; Zhou, B.; Wang, Q.; Ma, X. Variational Quality Control of Non-Gaussian Innovations and Its Parametric Optimizations for the GRAPES m3DVAR System. Front. Earth Sci. 2023, 17, 620–631. [Google Scholar] [CrossRef]
- Jardak, M.; Talagrand, O. Ensemble Variational Assimilation as a Probabilistic Estimator—Part 1: The Linear and Weak Non-Linear Case. Nonlinear Process. Geophys. 2018, 25, 565–587. [Google Scholar] [CrossRef]
- Bocquet, M.; Pires, C.; Wu, L. Beyond Gaussian Statistical Modeling in Geophysical Data Assimilation. Mon. Weather Rev. 2010, 138, 2997–3023. [Google Scholar] [CrossRef]
- Chan, M.-Y.; Anderson, J.L.; Chen, X. An Efficient Bi-Gaussian Ensemble Kalman Filter for Satellite Infrared Radiance Data Assimilation. Mon. Weather Rev. 2020, 148, 5087–5104. [Google Scholar] [CrossRef]
- Hou, T.; Kong, F.; Chen, X.; Lei, H.; Hu, Z. Evaluation of Radar and Automatic Weather Station Data Assimilation for a Heavy Rainfall Event in Southern China. Adv. Atmos. Sci. 2015, 32, 967–978. [Google Scholar] [CrossRef]
- Tavolato, C.; Isaksen, L. On the Use of a Huber Norm for Observation Quality Control in the ECMWF 4D-Var. Q. J. R. Meteorol. Soc. 2015, 141, 1514–1527. [Google Scholar] [CrossRef]
- Shataer, S.; Lawless, A.S.; Nichols, N.K. Conditioning of Hybrid Variational Data Assimilation. Numer. Linear Algebra Appl. 2024, 31, e2534. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, H. A Big Data-Driven Nonlinear Least Squares Four-Dimensional Variational Data Assimilation Method: Theoretical Formulation and Conceptual Evaluation. Earth Space Sci. 2019, 6, 1430–1439. [Google Scholar] [CrossRef]
- Haben, S.A.; Lawless, A.S.; Nichols, N.K. Conditioning of Incremental Variational Data Assimilation, with Application to the Met Office System. Tellus Ser. A-Dyn. Meteorol. Oceanol. 2011, 63, 782–792. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, J. Generalised Variational Assimilation of Cloud-Affected Brightness Temperature Using Simulated Hyper-Spectral Atmospheric Infrared Sounder Data. Adv. Space Res. 2014, 54, 49–58. [Google Scholar] [CrossRef]
- Van Loon, S.; Fletcher, S.J. Foundations for Universal Non-Gaussian Data Assimilation. Geophys. Res. Lett. 2023, 50, e2023GL105148. [Google Scholar] [CrossRef]
- Heusler, S.; Duer, W.; Ubben, M.S.; Hartmann, A. Aspects of Entropy in Classical and in Quantum Physics. J. Phys. A-Math. Theor. 2022, 55, 404006. [Google Scholar] [CrossRef]
- Clark, D.K. The Mechanical Theory of Heat. J. Frankl. Inst. 1860, 70, 163–169. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Malyarenko, A.; Mishura, Y.; Ralchenko, K.; Rudyk, Y.A.; Cacciari, I. Properties of Various Entropies of Gaussian Distribution and Comparison of Entropies of Fractional Processes. Axioms 2023, 12, 1026. [Google Scholar] [CrossRef]
- Harremoes, P. Entropy Inequalities for Lattices. Entropy 2018, 20, 784. [Google Scholar] [CrossRef] [PubMed]
- Rényi, A. On Measures of Entropy and Information. In Contributions to the Theory of Statistics, Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Los Angeles, CA, USA, 20 June–30 July 1960; University of California Press: Oakland, CA, USA, 1961; Volume 4.1, pp. 547–562. [Google Scholar]
- Da Silva, S.L.E.F.; Dos Santos Lima, G.Z.; De Araújo, J.M.; Corso, G. Extensive and Nonextensive Statistics in Seismic Inversion. Phys. A Stat. Mech. Its Appl. 2021, 563, 125496. [Google Scholar] [CrossRef]
- Fathi Hafshejani, S.; Gaur, D.; Dasgupta, A.; Benkoczi, R.; Gosala, N.R.; Iorio, A. A Hybrid Quantum Solver for the Lorenz System. Entropy 2024, 26, 1009. [Google Scholar] [CrossRef] [PubMed]
- Elsheikh, A.H.; Hoteit, I.; Wheeler, M.F. A Nested Sampling Particle Filter for Nonlinear Data Assimilation. Q. J. R. Meteorol. Soc. 2014, 140, 1640–1653. [Google Scholar] [CrossRef]
- Jin, L.; Liu, Z.; Li, L. Prediction and Identification of Nonlinear Dynamical Systems Using Machine Learning Approaches. J. Ind. Inf. Integr. 2023, 35, 100503. [Google Scholar] [CrossRef]
- Alqhtani, M.; Khader, M.M.; Saad, K.M. Numerical Simulation for a High-Dimensional Chaotic Lorenz System Based on Gegenbauer Wavelet Polynomials. Mathematics 2023, 11, 472. [Google Scholar] [CrossRef]


| Method | Assimilation Steps | Consumed Time(G) | Consumed Time(NG) |
|---|---|---|---|
| 4DVar | 2800 | 16.83 s | 17.96 s |
| α-4DVar (α = 0.9) | 2800 | 20.04 s | 23.45 s |
| Time Increment | \ | 19.1% | 30.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Cao, X.; Peng, K.; Zhou, M.; Guo, Y. Enhancing Robustness of Variational Data Assimilation in Chaotic Systems: An α-4DVar Framework with Rényi Entropy and α-Generalized Gaussian Distributions. Entropy 2025, 27, 763. https://doi.org/10.3390/e27070763
Luo Y, Cao X, Peng K, Zhou M, Guo Y. Enhancing Robustness of Variational Data Assimilation in Chaotic Systems: An α-4DVar Framework with Rényi Entropy and α-Generalized Gaussian Distributions. Entropy. 2025; 27(7):763. https://doi.org/10.3390/e27070763
Chicago/Turabian StyleLuo, Yuchen, Xiaoqun Cao, Kecheng Peng, Mengge Zhou, and Yanan Guo. 2025. "Enhancing Robustness of Variational Data Assimilation in Chaotic Systems: An α-4DVar Framework with Rényi Entropy and α-Generalized Gaussian Distributions" Entropy 27, no. 7: 763. https://doi.org/10.3390/e27070763
APA StyleLuo, Y., Cao, X., Peng, K., Zhou, M., & Guo, Y. (2025). Enhancing Robustness of Variational Data Assimilation in Chaotic Systems: An α-4DVar Framework with Rényi Entropy and α-Generalized Gaussian Distributions. Entropy, 27(7), 763. https://doi.org/10.3390/e27070763






