Quantum Error Mitigation in Optimized Circuits for Particle-Density Correlations in Real-Time Dynamics of the Schwinger Model
Abstract
1. Introduction
2. Lattice QED in One Spatial Dimension
- A convenient basis of the edge space is represented by the electric field eigenstates , satisfying , with and ;
- The gauge connection acts on this basis as a cyclic permutation: and ;
- The lattice counterpart of the Gauss law which fixes the admissible states is given bywhich must be valid at all sites x and at any time.
3. Classical–Quantum Embedding
4. Digital Circuit for Unitary Evolution and Green Functions

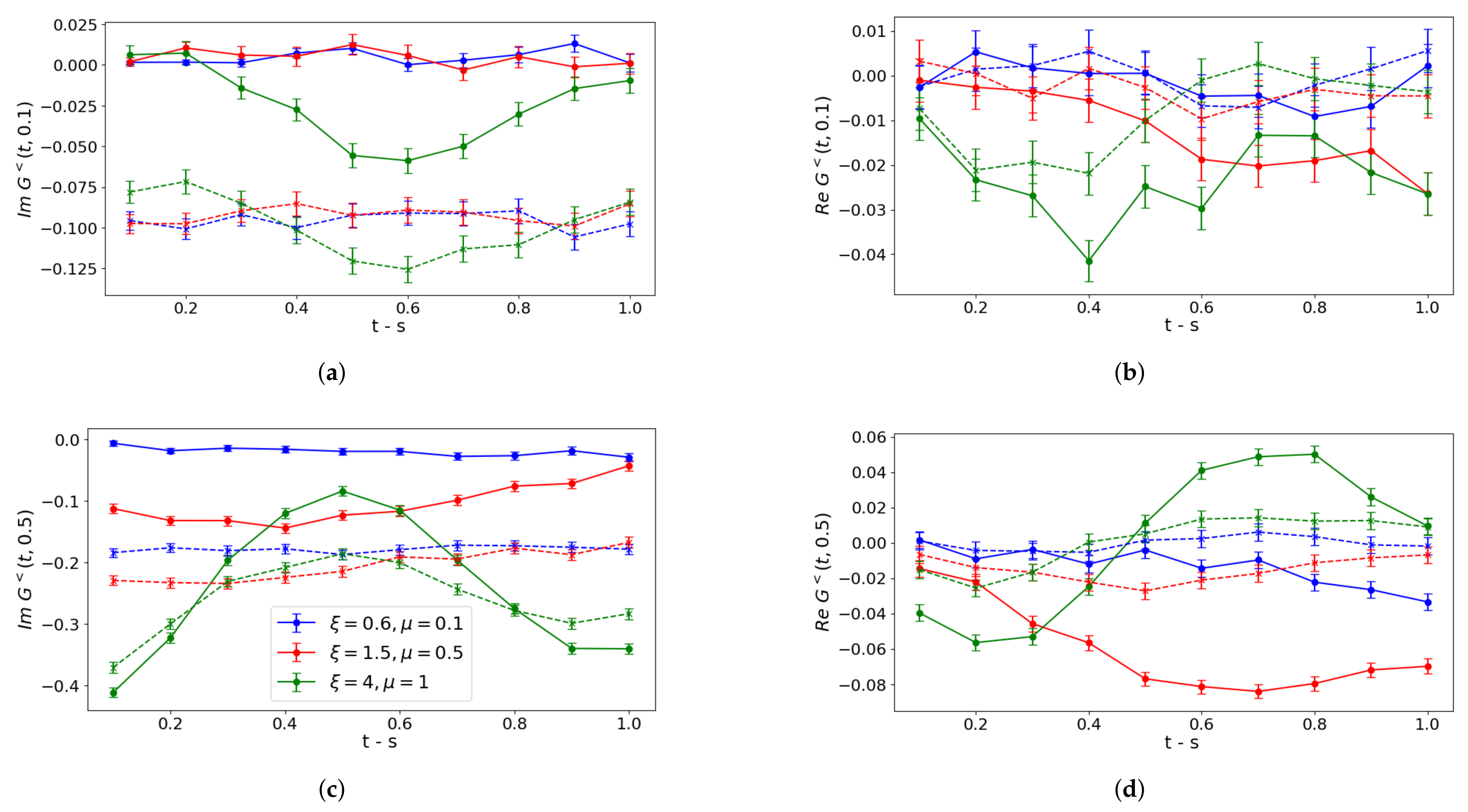
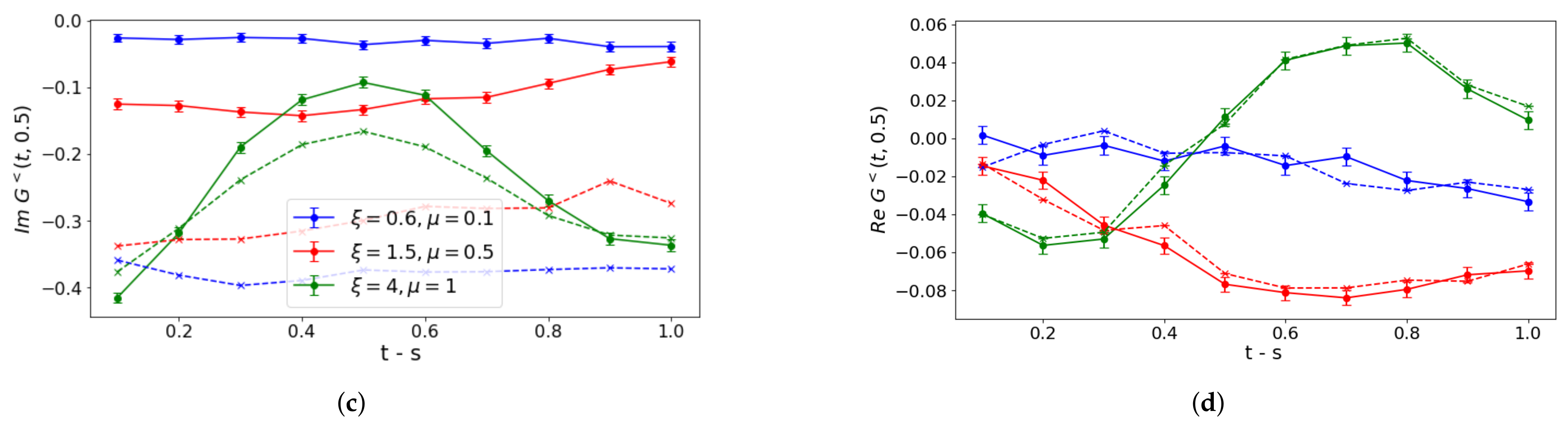
5. Implementation on IBM Quantum Platform
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NISQ | noise intermediate-scale quantum |
| QED | quantum electrodynamics |
| DQPT | dynamical quantum phase transition |
| T-REx | twirled readout error extinction |
| ZNE | zero noise extrapolation |
Appendix A. Basis of the Gauge-Invariant Subspace
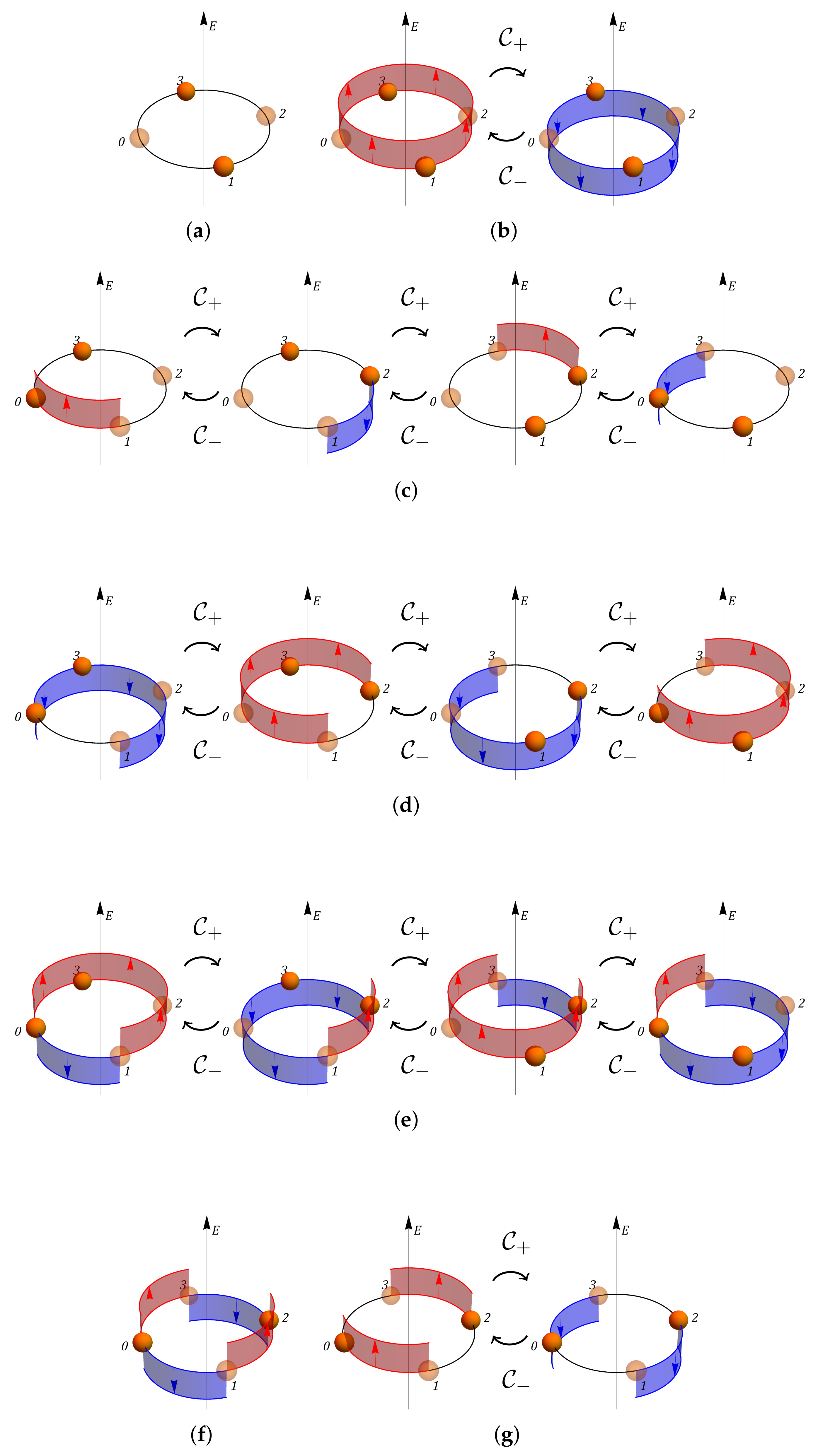
- Panels (a,b) show the Dirac vacuum, corresponding to the two even sites being empty and the two odd sites being filled, with the three possible total background fields, which are completely fixed by the value of the electric field on the edge joining the sites 0 and 1: the state with zero electric field background is a fixed point with respect to , while the other two states with non-zero electric field background give one orbit.
- Panels (c,d,e) show the 12 one-meson states, corresponding to occupying one even and one odd site, the three panels corresponding to the orbits of the three possible configurations obtained from the three possible Dirac vacuum configurations, respectively, by moving a particle from site 2 to site 3;
- Panels (f,g) show the two-meson states, corresponding to the two even sites being filled and the two odd sites being empty and the three possible total field configurations, the two states with represent an orbit, while the state with is a fixed point.
- subspace with :
- subspace with :
- subspace with :
- subspace with :
Appendix B. Optimal Permutation
Appendix C. General Procedure for Classical–Quantum Embedding
- Step 1: Store a list of possible site configurations for all even and odd sites. This is a total of six configurations each for both even and odd sites due to the following:
- -
- Each site, represented as x, can be filled or empty;
- -
- For either value of occupancy, the link to the right, represented as , can take three possible values of electric field. The link to the left, , is fixed by Gauss’ law.
- Step 2: Place sites one after the other, following the pattern even–odd–even–odd… ensuring that the values of the common links match.
- Step 3: Impose periodic boundary conditions: .
- Step 4: Eliminate the configurations that do not correspond to the right total number of particles (in our case, half filling). After this step, we obtain the basis states which are best represented as a dictionary, with each site mapping to its occupancy (0 or 1), and each link mapping to a element representing the electric field on that link (with values ).
- Step 5: Arrange states into multiplets under translation and charge conjugation symmetries and isolate the multiplet containing the vacuum state. This multiplet corresponds to the sector and evolves independently of the other blocks.
- Step 6: Find the Hamiltonian matrix elements in this multiplet. Embed this matrix into a -dimensional space, where M is the lowest such value the matrix can be embedded into. This gives the number of needed qubits.
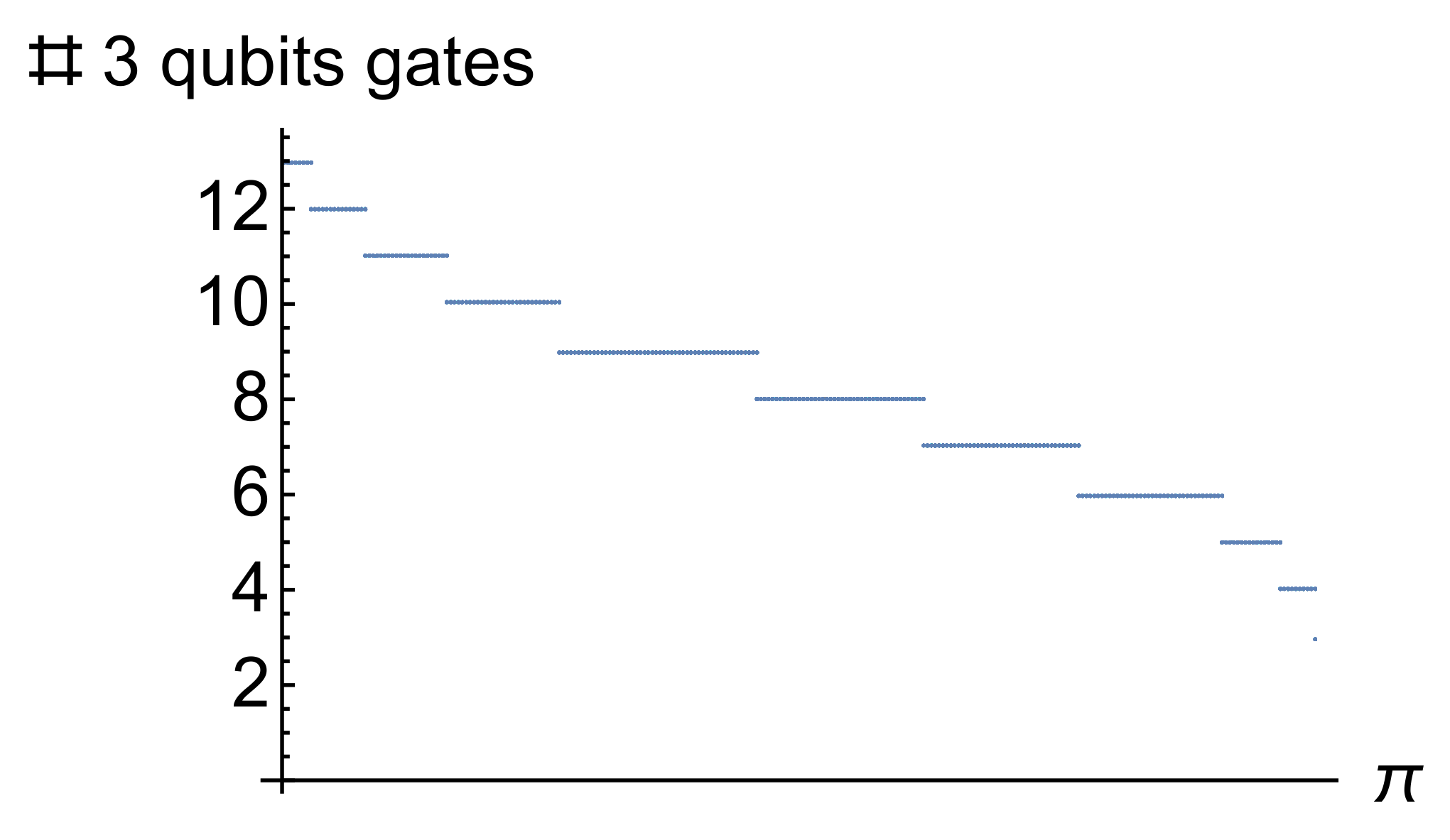
- Step 7: Find an optimal permutation of the basis states such that the number of higher-qubit gates in the Pauli gate expansion of is minimized.
- Step 8: Use the Pauli gate expansion of the Hamiltonian in the optimized encoding to construct the Trotter steps in the time evolution.
- We define the objective function aswhere is the set of M-qubit Pauli gates. This simply counts the number of such gates in the decomposition of the Hamiltonian .
- Start with an initial configuration of the Hamiltonian and store .
- We choose a “neighborhood” of a configuration of to be the set of configurations related to it by a single swap of two indices: row row j, column column j. For a -dimensional system, the dimension of each neighborhood scales as .
- Go to a locally optimal configuration in this neighborhood, according to some heuristic choice; calculate the objective function for the new configuration and update .
- Continue until cannot be improved any further.
| L | System Size M | M-Qubit Gates in Optimal Permutation | Runtime |
|---|---|---|---|
| 2 | 4 | 2 | s |
| 4 | 8 | 3 | s |
| 6 | 16 | 8 | s |
| 8 | 64 | 123 | s |
Appendix D. Digital Circuit for Trotter Evolution
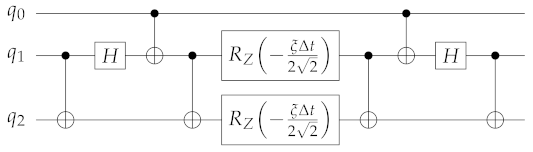
- Single-qubit gates are related to the coefficients with . They can implemented by the circuitwhich is endowed with a high average fidelity.
- Two-qubit gates can be grouped in three different operators. The first one contains the terms corresponding to the coefficients and is represented by the circuitThe second operator contains the terms corresponding to the coefficients and is given by the circuitFinally the third operator, which contains the terms with the coefficient , corresponds to the circuitHere, the abundance of controlled gates causes a decreasing average fidelity with respect to the single-qubits gates case.
- Three-qubit gates are grouped in two different operators, where the first one contains the terms with coefficients and is given by the circuitwhile the second contains the terms with coefficients and is implemented by the circuit
Appendix E. The Circuit of Mach–Zender Interferometer

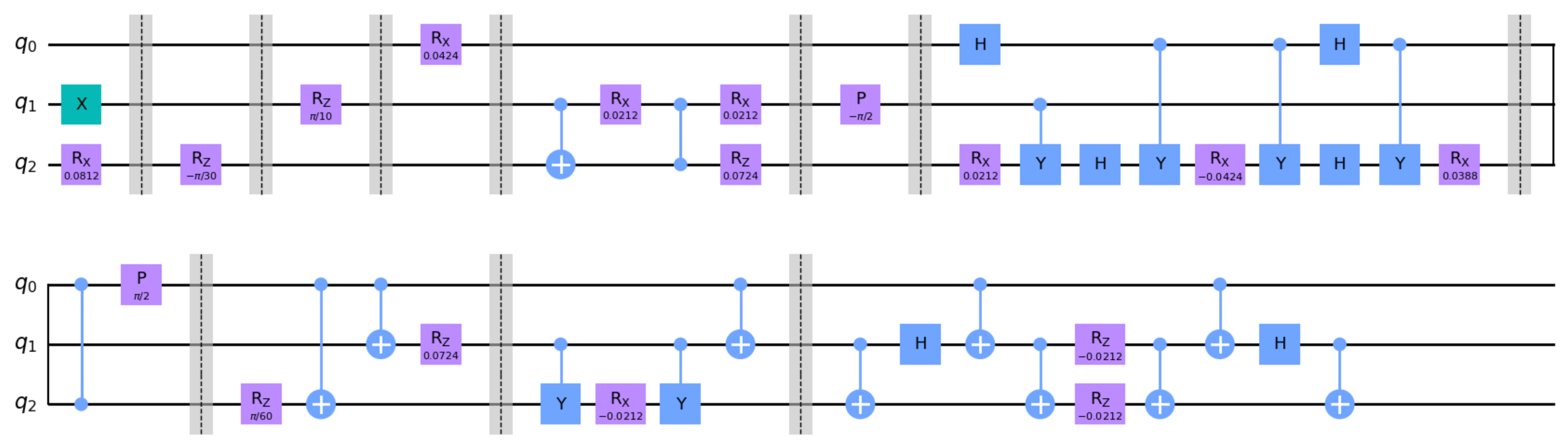
Appendix F. T-REx and ZNE Mitigation Schemes
References
- Bañuls, M.C.; Blatt, R.; Catani, J.; Celi, A.; Cirac, J.I.; Dalmonte, M.; Fallani, L.; Jansen, K.; Lewenstein, M.; Montangero, S.; et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D 2020, 74, 165. [Google Scholar] [CrossRef]
- Di Meglio, A.; Jansen, K.; Tavernelli, I.; Alexandrou, C.; Arunachalam, S.; Bauer, C.W.; Borras, K.; Carrazza, S.; Crippa, A.; Croft, V.; et al. Quantum Computing for High-Energy Physics: State of the Art and Challenges. PRX Quantum 2024, 5, 037001. [Google Scholar] [CrossRef]
- Ayral, T.; Louvet, T.; Zhou, Y.; Lambert, C.; Stoudenmire, E.M.; Waintal, X. Density-Matrix Renormalization Group Algorithm for Simulating Quantum Circuits with a Finite Fidelity. Phys. Rev. X Quantum 2023, 4, 020304. [Google Scholar] [CrossRef]
- Schwinger, J. Gauge Invariance and Mass. II. Phys. Rev. 1962, 128, 2425–2429. [Google Scholar] [CrossRef]
- Turner, C.J.; Michailidis, A.A.; Abanin, D.A.; Serbyn, M.; Papić, Z. Quantum scarred eigenstates in a Rydberg atom chain: Entanglement, breakdown of thermalization, and stability to perturbations. Phys. Rev. B 2018, 98, 155134. [Google Scholar] [CrossRef]
- Notarnicola, S.; Collura, M.; Montangero, S. Real-time-dynamics quantum simulation of (1+1)-dimensional lattice QED with Rydberg atoms. Phys. Rev. Res. 2020, 2, 013288. [Google Scholar] [CrossRef]
- Desaules, J.Y.; Banerjee, D.; Hudomal, A.; Papić, Z.; Sen, A.; Halimeh, J.C. Weak ergodicity breaking in the Schwinger model. Phys. Rev. B 2023, 107, L201105. [Google Scholar] [CrossRef]
- Halimeh, J.C.; Homeier, L.; Schweizer, C.; Aidelsburger, M.; Hauke, P.; Grusdt, F. Stabilizing lattice gauge theories through simplified local pseudogenerators. Phys. Rev. Res. 2022, 4, 033120. [Google Scholar] [CrossRef]
- Damme, M.V.; Lang, H.; Hauke, P.; Halimeh, J.C. Reliability of lattice gauge theories in the thermodynamic limit. Phys. Rev. B 2023, 107, 035153. [Google Scholar] [CrossRef]
- Halimeh, J.C.; Barbiero, L.; Hauke, P.; Grusdt, F.; Bohrdt, A. Robust quantum many-body scars in lattice gauge theories. Quantum 2023, 7, 1004. [Google Scholar] [CrossRef]
- Halimeh, J.C.; Hauke, P. Stabilizing Gauge Theories in Quantum Simulators: A Brief Review. arXiv 2022. [Google Scholar] [CrossRef]
- Kent, B.; Racz, S.; Shashi, S. Scrambling in quantum cellular automata. Phys. Rev. B 2023, 107, 144306. [Google Scholar] [CrossRef]
- Mueller, N.; Carolan, J.A.; Connelly, A.; Davoudi, Z.; Dumitrescu, E.F.; Yeter-Aydeniz, K. Quantum Computation of Dynamical Quantum Phase Transitions and Entanglement Tomography in a Lattice Gauge Theory. PRX Quantum 2023, 4, 030323. [Google Scholar] [CrossRef]
- Heyl, M. Scaling and Universality at Dynamical Quantum Phase Transitions. Phys. Rev. Lett. 2015, 115, 140602. [Google Scholar] [CrossRef]
- Heyl, M. Dynamical quantum phase transitions: A review. Rep. Prog. Phys. 2018, 81, 054001. [Google Scholar] [CrossRef]
- Van Damme, M.; Zache, T.V.; Banerjee, D.; Hauke, P.; Halimeh, J.C. Dynamical quantum phase transitions in spin-S U(1) quantum link models. Phys. Rev. B 2022, 106, 245110. [Google Scholar] [CrossRef]
- Van Damme, M.; Desaules, J.Y.; Papić, Z.; Halimeh, J.C. Anatomy of Dynamical Quantum Phase Transitions. Phys. Rev. Res. 2023, 5, 033090. [Google Scholar] [CrossRef]
- Osborne, J.; McCulloch, I.P.; Halimeh, J.C. Probing Confinement Through Dynamical Quantum Phase Transitions: From Quantum Spin Models to Lattice Gauge Theories. arXiv 2023. [Google Scholar] [CrossRef]
- Pedersen, S.P.; Zinner, N.T. Lattice gauge theory and dynamical quantum phase transitions using noisy intermediate-scale quantum devices. Phys. Rev. B 2021, 103, 235103. [Google Scholar] [CrossRef]
- Jensen, R.B.; Pedersen, S.P.; Zinner, N.T. Dynamical quantum phase transitions in a noisy lattice gauge theory. Phys. Rev. B 2022, 105, 224309. [Google Scholar] [CrossRef]
- Muschik, C.; Heyl, M.; Martinez, E.; Monz, T.; Schindler, P.; Vogell, B.; Dalmonte, M.; Hauke, P.; Blatt, R.; Zoller, P. U(1) Wilson lattice gauge theories in digital quantum simulators. New J. Phys. 2017, 19, 103020. [Google Scholar] [CrossRef]
- Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664. [Google Scholar] [CrossRef]
- Martinez, E.A.; Muschik, C.A.; Schindler, P.; Nigg, D.; Erhard, A.; Heyl, M.; Hauke, P.; Dalmonte, M.; Monz, T.; Zoller, P.; et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 2016, 534, 516–519. [Google Scholar] [CrossRef] [PubMed]
- Klco, N.; Dumitrescu, E.F.; McCaskey, A.J.; Morris, T.D.; Pooser, R.C.; Sanz, M.; Solano, E.; Lougovski, P.; Savage, M.J. Quantum-classical computation of Schwinger model dynamics using quantum computers. Phys. Rev. A 2018, 98, 032331. [Google Scholar] [CrossRef]
- Schweizer, C.; Grusdt, F.; Berngruber, M.; Barbiero, L.; Demler, E.; Goldman, N.; Bloch, I.; Aidelsburger, M. Floquet approach to ℤ2 lattice gauge theories with ultracold atoms in optical lattices. Nat. Phys. 2019, 15, 1168. [Google Scholar] [CrossRef]
- Yang, B.; Sun, H.; Ott, R.; Wang, H.Y.; Zache, T.V.; Halimeh, J.C.; Yuan, Z.S.; Hauke, P.; Pan, J.W. Observation of gauge invariance in a 71-site Bose–Hubbard quantum simulator. Nature 2020, 587, 392. [Google Scholar] [CrossRef]
- Willsch, D.; Rieger, D.; Winkel, P.; Willsch, M.; Dickel, C.; Krause, J.; Ando, Y.; Lescanne, R.; Leghtas, Z.; Bronn, N.T.; et al. Observation of Josephson harmonics in tunnel junctions. Nat. Phys. 2024, 20, 815–821. [Google Scholar] [CrossRef]
- Marchegiani, G.; Amico, L.; Catelani, G. Quasiparticles in Superconducting Qubits with Asymmetric Junctions. PRX Quantum 2022, 3, 040338. [Google Scholar] [CrossRef]
- Connolly, T.; Kurilovich, P.D.; Diamond, S.; Nho, H.; Bøttcher, C.G.L.; Glazman, L.I.; Fatemi, V.; Devoret, M.H. Coexistence of Nonequilibrium Density and Equilibrium Energy Distribution of Quasiparticles in a Superconducting Qubit. Phys. Rev. Lett. 2024, 132, 217001. [Google Scholar] [CrossRef]
- Krause, J.; Marchegiani, G.; Janssen, L.; Catelani, G.; Ando, Y.; Dickel, C. Quasiparticle effects in magnetic-field-resilient three-dimensional transmons. Phys. Rev. Appl. 2024, 22, 044063. [Google Scholar] [CrossRef]
- Yelton, E.; Larson, C.P.; Iaia, V.; Dodge, K.; La Magna, G.; Baity, P.G.; Pechenezhskiy, I.V.; McDermott, R.; Kurinsky, N.A.; Catelani, G.; et al. Modeling phonon-mediated quasiparticle poisoning in superconducting qubit arrays. Phys. Rev. B 2024, 110, 024519. [Google Scholar] [CrossRef]
- Fischer, P.B.; Catelani, G. Nonequilibrium quasiparticle distribution in superconducting resonators: Effect of pair-breaking photons. SciPost Phys. 2024, 17, 070. [Google Scholar] [CrossRef]
- McEwen, M.; Miao, K.C.; Atalaya, J.; Bilmes, A.; Crook, A.; Bovaird, J.; Kreikebaum, J.M.; Zobrist, N.; Jeffrey, E.; Ying, B.; et al. Resisting High-Energy Impact Events through Gap Engineering in Superconducting Qubit Arrays. Phys. Rev. Lett. 2024, 133, 240601. [Google Scholar] [CrossRef] [PubMed]
- Iaia, V.; Ku, J.; Ballard, A.; Larson, C.P.; Yelton, E.; Liu, C.H.; Patel, S.; McDermott, R.; Plourde, B.L.T. Phonon downconversion to suppress correlated errors in superconducting qubits. Nat. Commun. 2022, 13, 6425. [Google Scholar] [CrossRef]
- Pomarico, D.; Cosmai, L.; Facchi, P.; Lupo, C.; Pascazio, S.; Pepe, F.V. Dynamical Quantum Phase Transitions of the Schwinger Model: Real-Time Dynamics on IBM Quantum. Entropy 2023, 25, 608. [Google Scholar] [CrossRef]
- Tancara, D.; Fredes, J.; Norambuena, A. Quantum kernels for classifying dynamical singularities in a multiqubit system. Quantum Sci. Technol. 2024, 9, 035046. [Google Scholar] [CrossRef]
- Gustafson, E.; Dreher, P.; Hang, Z.; Meurice, Y. Indexed improvements for real-time trotter evolution of a (1+1) field theory using NISQ quantum computers. Quantum Sci. Technol. 2021, 6, 045020. [Google Scholar] [CrossRef]
- Huffman, E.; Vera, M.G.; Banerjee, D. Toward the real-time evolution of gauge-invariant ℤ2 and U(1) quantum link models on noisy intermediate-scale quantum hardware with error mitigation. Phys. Rev. D 2022, 106, 094502. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Tran, M.C.; Zhu, Y.; Green, A.M.; Alderete, C.H.; Davoudi, Z.; Linke, N.M. Digital Quantum Simulation of the Schwinger Model and Symmetry Protection with Trapped Ions. Phys. Rev. X Quantum 2022, 3, 020324. [Google Scholar] [CrossRef]
- Javanmard, Y.; Liaubaite, U.; Osborne, T.J.; Santos, L. Quantum simulation of dynamical phase transitions in noisy quantum devices. arXiv 2022. [Google Scholar] [CrossRef]
- Farrell, R.C.; Illa, M.; Ciavarella, A.N.; Savage, M.J. Scalable Circuits for Preparing Ground States on Digital Quantum Computers: The Schwinger Model Vacuum on 100 Qubits. PRX Quantum 2024, 5, 020315. [Google Scholar] [CrossRef]
- Hidalgo, L.; Draper, P. Quantum simulations for strong-field QED. Phys. Rev. D 2024, 109, 076004. [Google Scholar] [CrossRef]
- Filippov, S.; Leahy, M.; Rossi, M.A.C.; García-Pérez, G. Scalable tensor-network error mitigation for near-term quantum computing. arXiv 2023. [Google Scholar] [CrossRef]
- Fischer, L.E.; Leahy, M.; Eddins, A.; Keenan, N.; Ferracin, D.; Rossi, M.A.C.; Kim, Y.; He, A.; Pietracaprina, F.; Sokolov, B.; et al. Dynamical simulations of many-body quantum chaos on a quantum computer. arXiv 2024. [Google Scholar] [CrossRef]
- Endo, S.; Kurata, I.; Nakagawa, Y.O. Calculation of the Green’s function on near-term quantum computers. Phys. Rev. Res. 2020, 2, 033281. [Google Scholar] [CrossRef]
- Libbi, F.; Rizzo, J.; Tacchino, F.; Marzari, N.; Tavernelli, I. Effective calculation of the Green’s function in the time domain on near-term quantum processors. Phys. Rev. Res. 2022, 4, 043038. [Google Scholar] [CrossRef]
- Rizzo, J.; Libbi, F.; Tacchino, F.; Ollitrault, P.J.; Marzari, N.; Tavernelli, I. One-particle Green’s functions from the quantum equation of motion algorithm. Phys. Rev. Res. 2022, 4, 043011. [Google Scholar] [CrossRef]
- van den Berg, E.; Minev, Z.K.; Temme, K. Model-free readout-error mitigation for quantum expectation values. Phys. Rev. A 2022, 105, 032620. [Google Scholar] [CrossRef]
- Giurgica-Tiron, T.; Hindy, Y.; LaRose, R.; Mari, A.; Zeng, W.J. Digital zero noise extrapolation for quantum error mitigation. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020; pp. 306–316. [Google Scholar] [CrossRef]
- Ercolessi, E.; Facchi, P.; Magnifico, G.; Pascazio, S.; Pepe, F.V. Phase transitions in ℤn gauge models: Towards quantum simulations of the Schwinger-Weyl QED. Phys. Rev. D 2018, 98, 074503. [Google Scholar] [CrossRef]
- Kogut, J.; Susskind, L. Hamiltonian formulation of Wilson’s lattice gauge theories. Phys. Rev. D 1975, 11, 395. [Google Scholar] [CrossRef]
- Notarnicola, S.; Ercolessi, E.; Facchi, P.; Marmo, G.; Pascazio, S.; Pepe, F.V. Discrete Abelian gauge theories for quantum simulations of QED. J. Phys. A: Math. Theor. 2015, 48, 30FT01. [Google Scholar] [CrossRef]
- Sjöqvist, E.; Pati, A.K.; Ekert, A.; Anandan, J.S.; Ericsson, M.; Oi, D.K.L.; Vedral, V. Geometric Phases for Mixed States in Interferometry. Phys. Rev. Lett. 2000, 85, 2845. [Google Scholar] [CrossRef] [PubMed]
- Carollo, A.; Fuentes-Guridi, I.; Santos, M.F.; Vedral, V. Geometric Phase in Open Systems. Phys. Rev. Lett. 2003, 90, 160402. [Google Scholar] [CrossRef] [PubMed]
- IBM Quantum. 2024. Available online: https://quantum-computing.ibm.com/ (accessed on 10 April 2025).
- Pomarico, D. Multiscale Entanglement Renormalization Ansatz: Causality and Error Correction. Dynamics 2023, 3, 33. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 4 ed.; The MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Ekert, A.K.; Alves, C.M.; Oi, D.K.L.; Horodecki, M.; Horodecki, P.; Kwek, L.C. Direct Estimations of Linear and Nonlinear Functionals of a Quantum State. Phys. Rev. Lett. 2002, 88, 217901. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pomarico, D.; Pandey, M.; Cioli, R.; Dell’Anna, F.; Pascazio, S.; Pepe, F.V.; Facchi, P.; Ercolessi, E. Quantum Error Mitigation in Optimized Circuits for Particle-Density Correlations in Real-Time Dynamics of the Schwinger Model. Entropy 2025, 27, 427. https://doi.org/10.3390/e27040427
Pomarico D, Pandey M, Cioli R, Dell’Anna F, Pascazio S, Pepe FV, Facchi P, Ercolessi E. Quantum Error Mitigation in Optimized Circuits for Particle-Density Correlations in Real-Time Dynamics of the Schwinger Model. Entropy. 2025; 27(4):427. https://doi.org/10.3390/e27040427
Chicago/Turabian StylePomarico, Domenico, Mahul Pandey, Riccardo Cioli, Federico Dell’Anna, Saverio Pascazio, Francesco V. Pepe, Paolo Facchi, and Elisa Ercolessi. 2025. "Quantum Error Mitigation in Optimized Circuits for Particle-Density Correlations in Real-Time Dynamics of the Schwinger Model" Entropy 27, no. 4: 427. https://doi.org/10.3390/e27040427
APA StylePomarico, D., Pandey, M., Cioli, R., Dell’Anna, F., Pascazio, S., Pepe, F. V., Facchi, P., & Ercolessi, E. (2025). Quantum Error Mitigation in Optimized Circuits for Particle-Density Correlations in Real-Time Dynamics of the Schwinger Model. Entropy, 27(4), 427. https://doi.org/10.3390/e27040427