Robust Fractional Low Order Adaptive Linear Chirplet Transform and Its Application to Fault Analysis
Abstract
1. Introduction
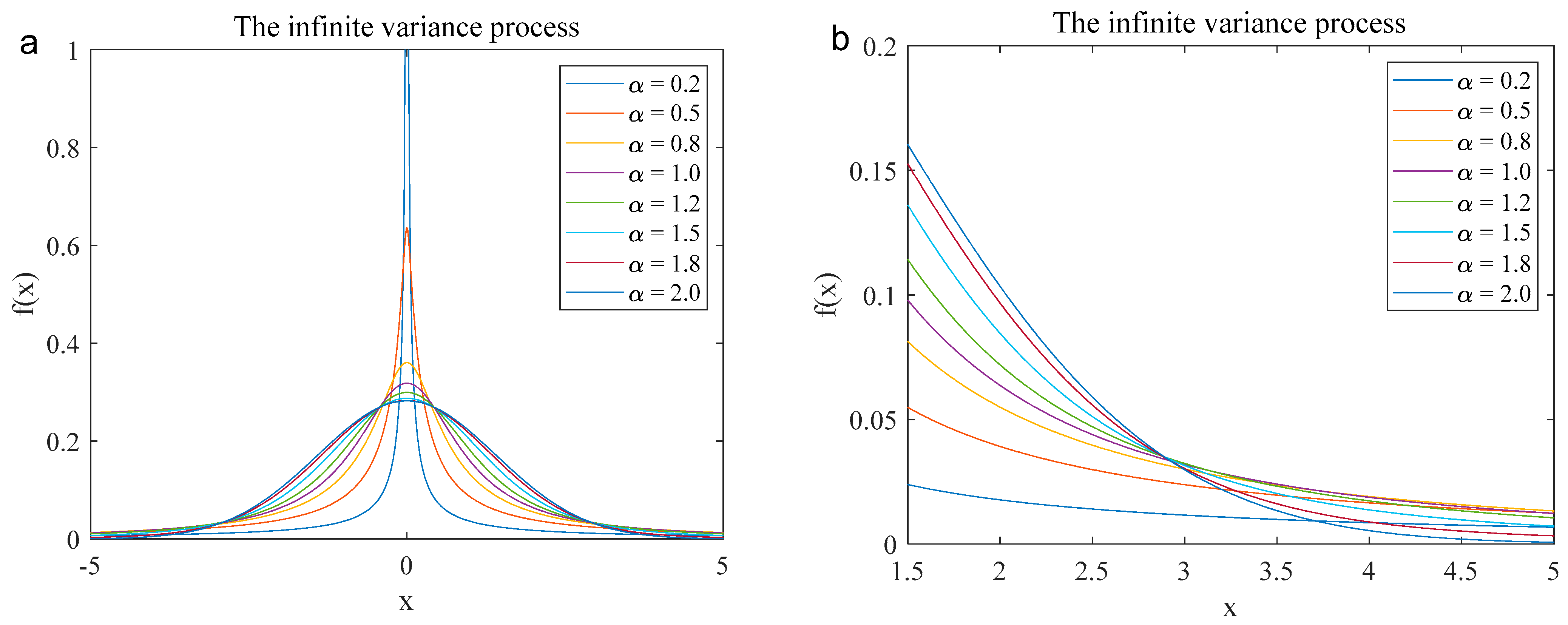
2. Novel Statistical Model for the Mechanical Vibration Signals
2.1. Novel Statistical Model
2.2. Novel Statistical Model for the Mechanical Vibration Signals
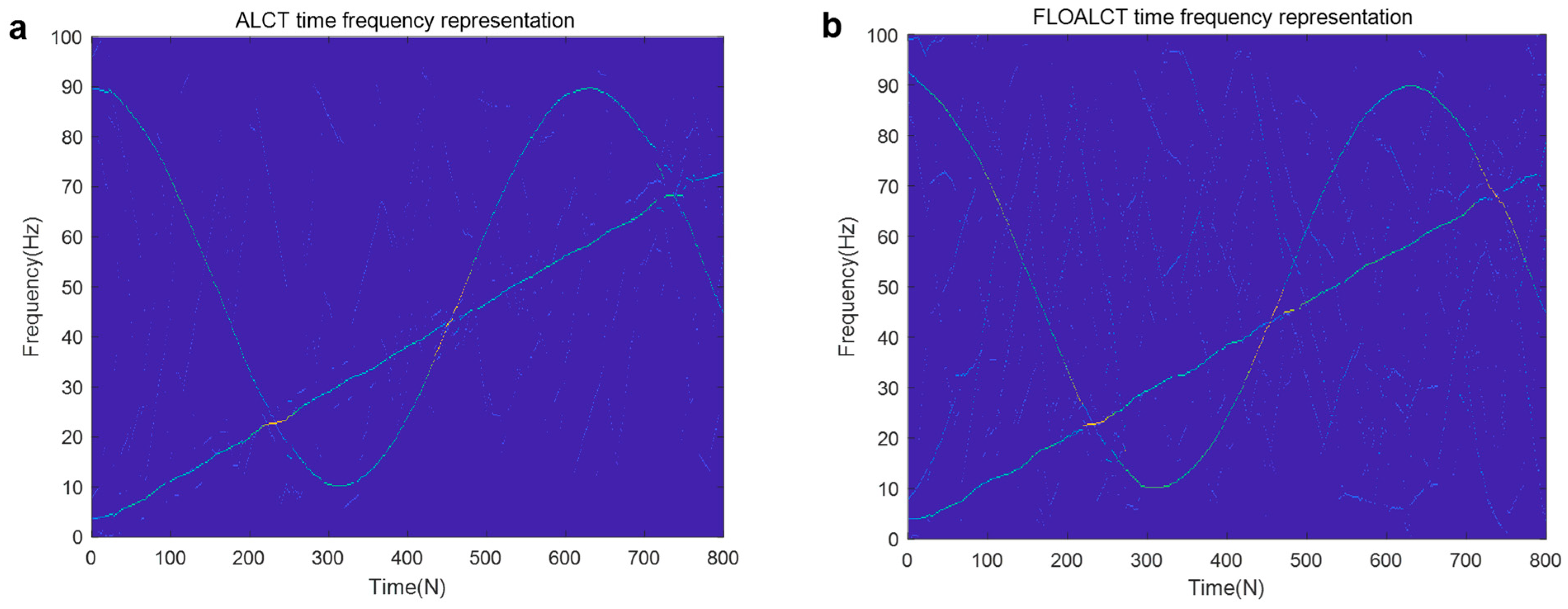
3. Robust FLOALCT Time Frequency Representation
3.1. FLOALCT TFR Method
3.1.1. Principle
| Algorithm 1. FLOALCT algorithm for multi-component signals |
| 1: Initialization phase and parameter setting. Including normalized window and p-order moment parameter et al. 2: Calculate fractional p-order moment of the signal . 3: Chirplet basis generation. Including chirp rate range, time axis for window and chirplet kernels. 4: Iterative component extraction: set initial residual , . 5: While > threshold. 6: Compute FLOLCT of residual using Formula (2). 7: Search for the peak in the time-frequency domain and extract the optimal parameter of the k-th component using Formula (14). 8: Generate TFR of the k-th component using Formula (15). 9: Compute reconstructed component. 10: Update residual . 11: n = n + 1. 12: End. 13: Reconstruct the k-th component of the original signal using Formulas (11) and (12). 14: Combine all components using Formula (13). |
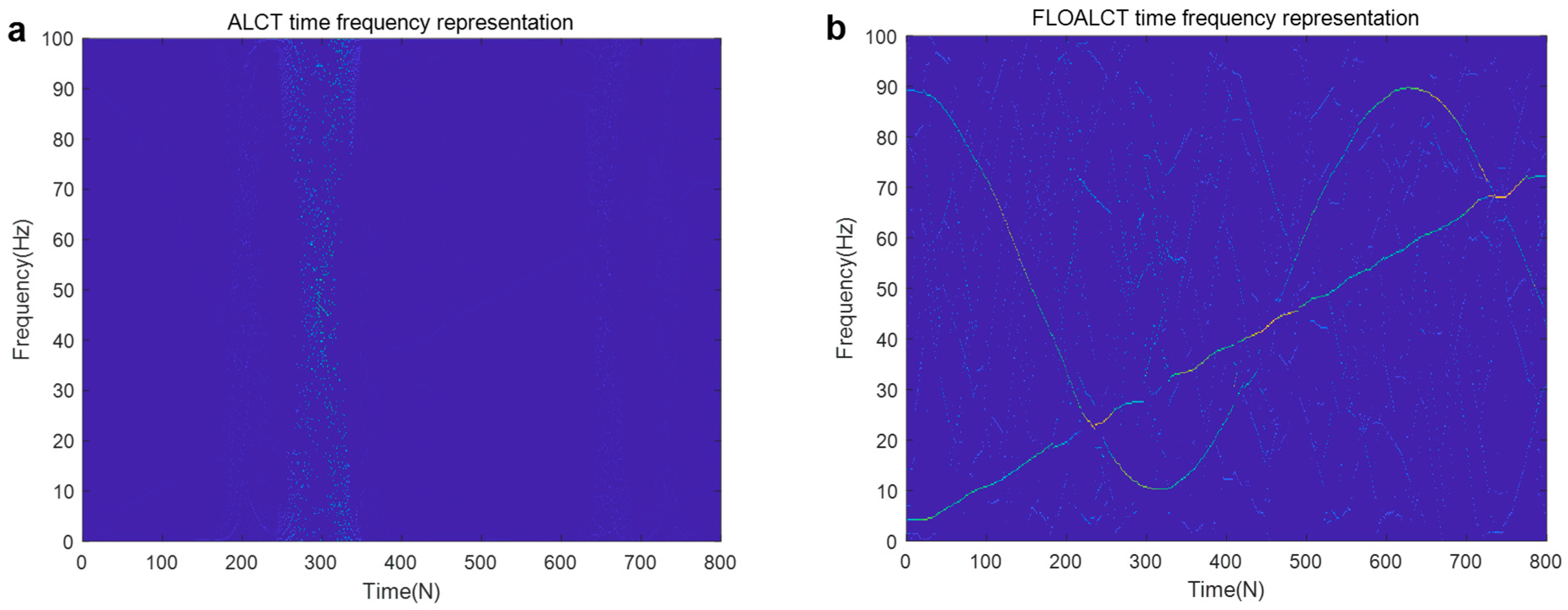
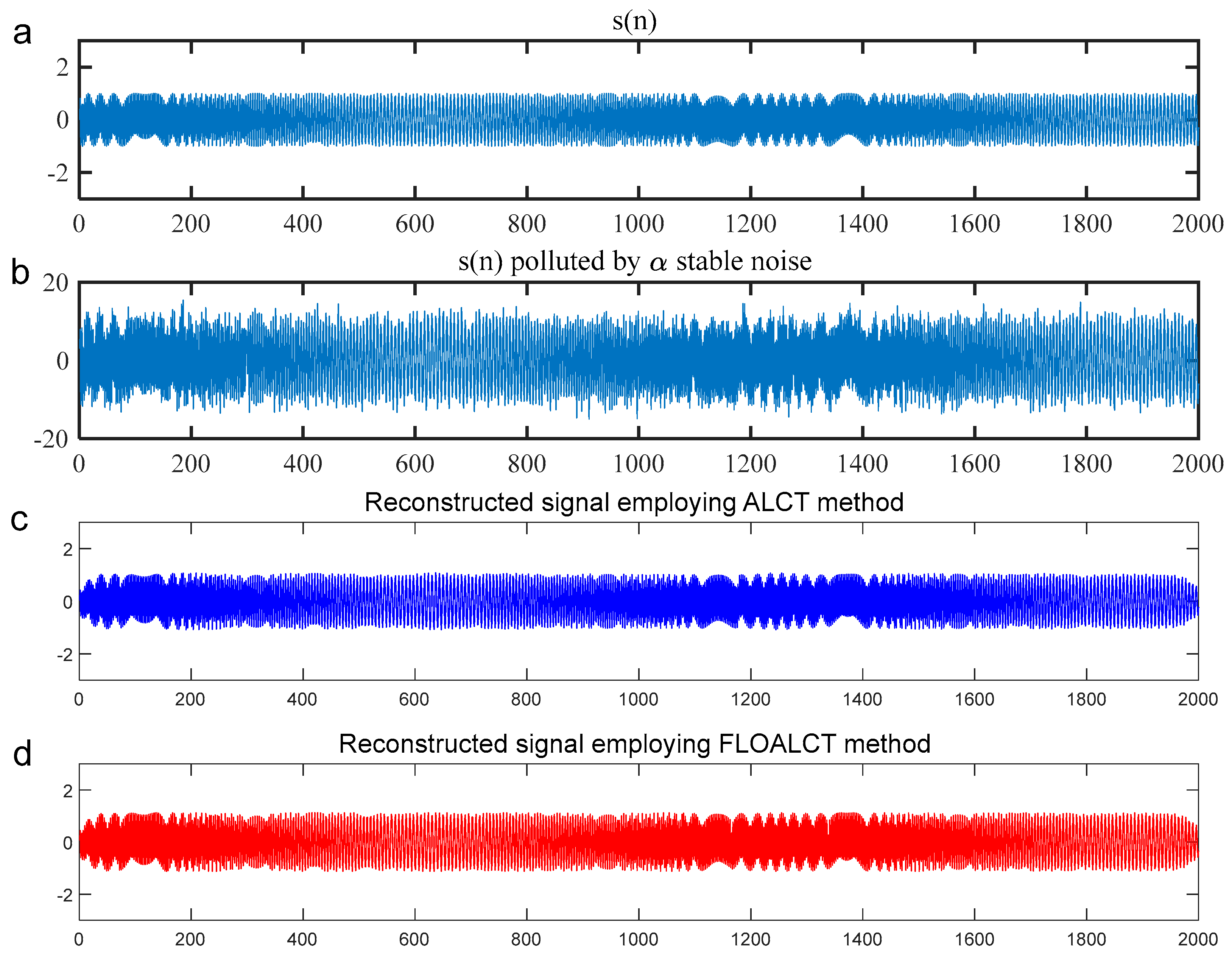
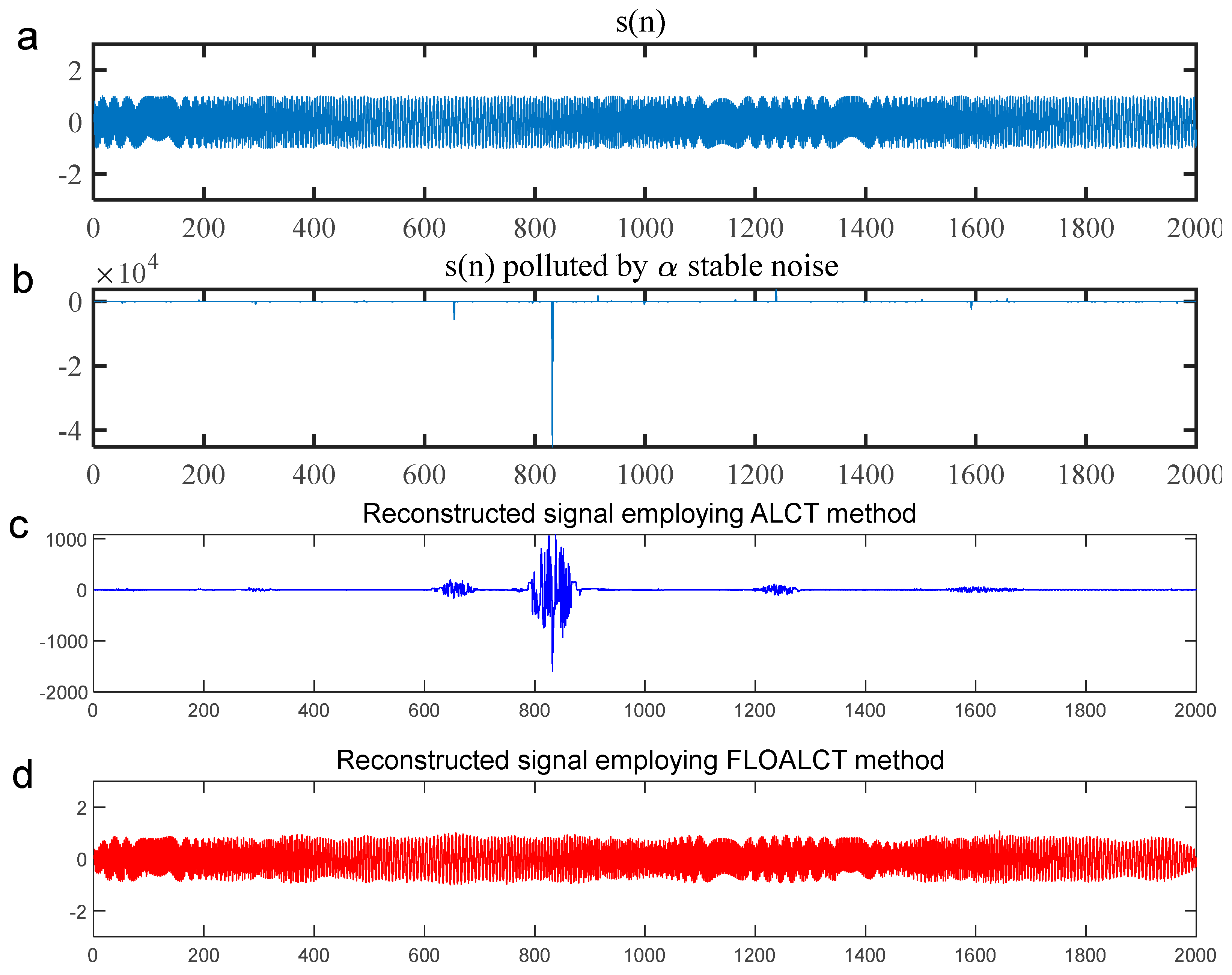
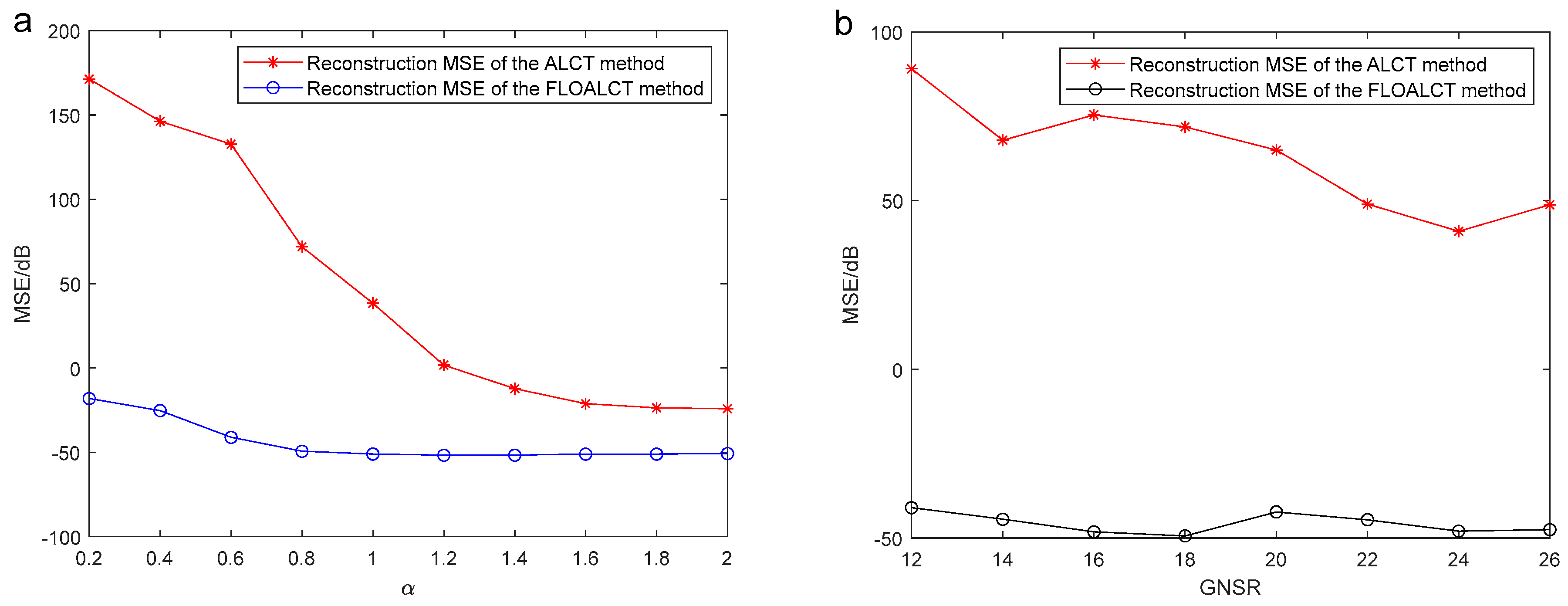
3.1.2. Application Review
3.1.3. Remarks
3.2. FLOASCT TFR Method
3.2.1. Principle
| Algorithm 2. FLOASCT algorithm |
| 1: Initialization including p-order moment parameter , time vector , frequency center point f_center, angle candidate set angle_candidates, et al. 2: Calculate fractional p-order moment of the signal using Formula (6). 3: Sliding window processing. 4: Multi-angle candidate. 5: For theta in angle candidates: 6: Calculate –: = −tan(theta)/(2*mean(f_center)). 7: Optimize parameters – (Gradient descent method). 8: Calculate adaptive chirp rate. 9: End for. 10: Construct kernel function according to Formula (24). 11: Calculate the energy concentration index of each candidate angle. 12: Calculate the sub-FLOASCTTFR using Formula (23). 13: Select the optimal TFR. 14: Output final time-frequency representation. |
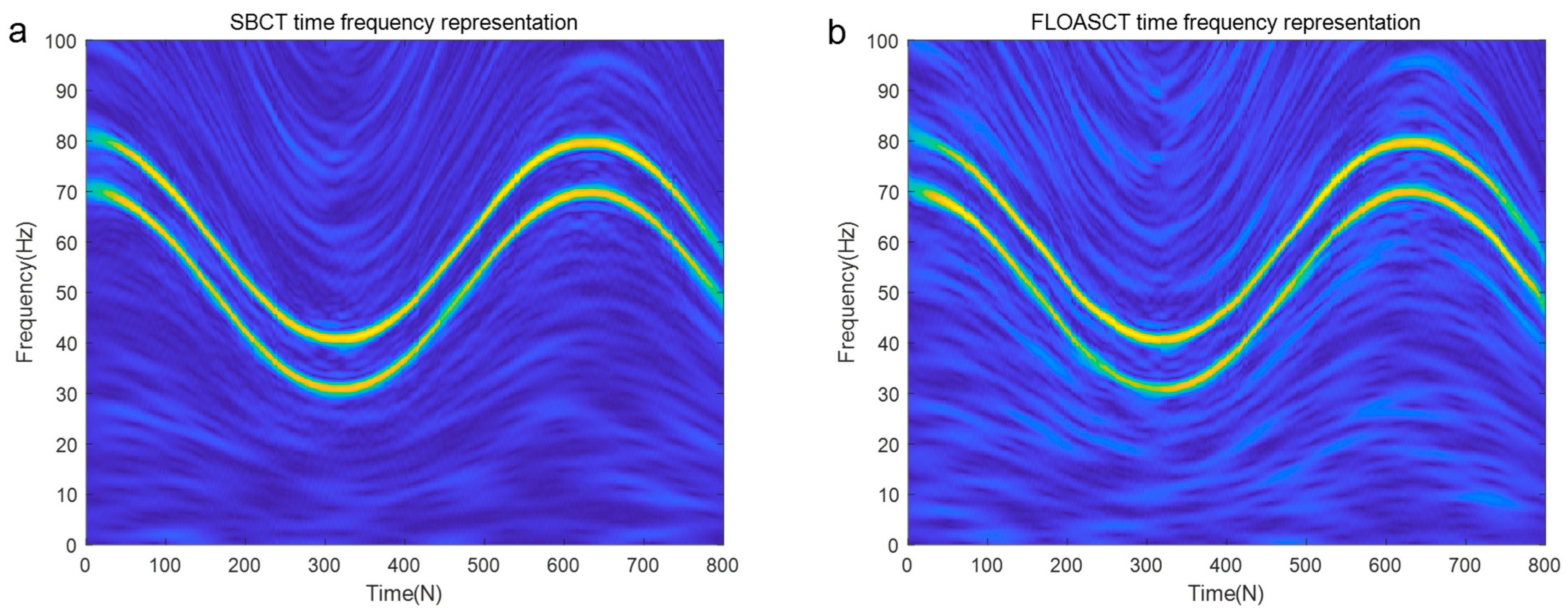
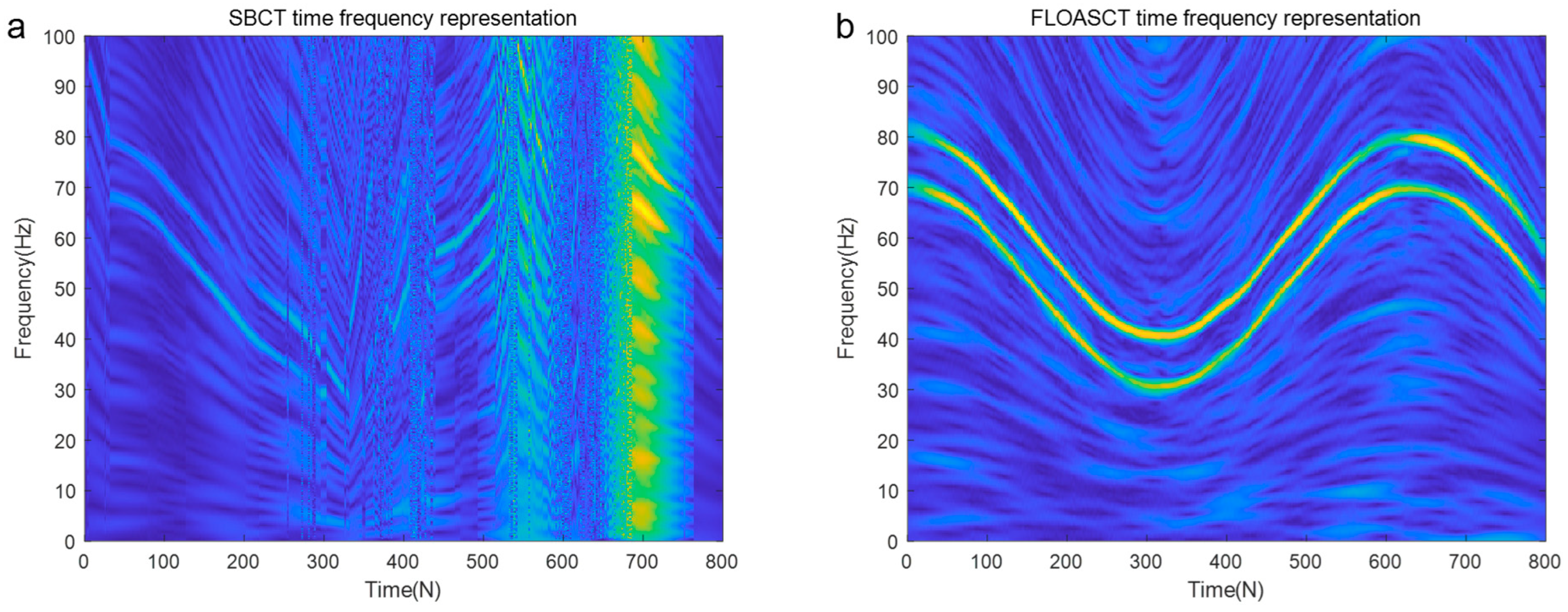
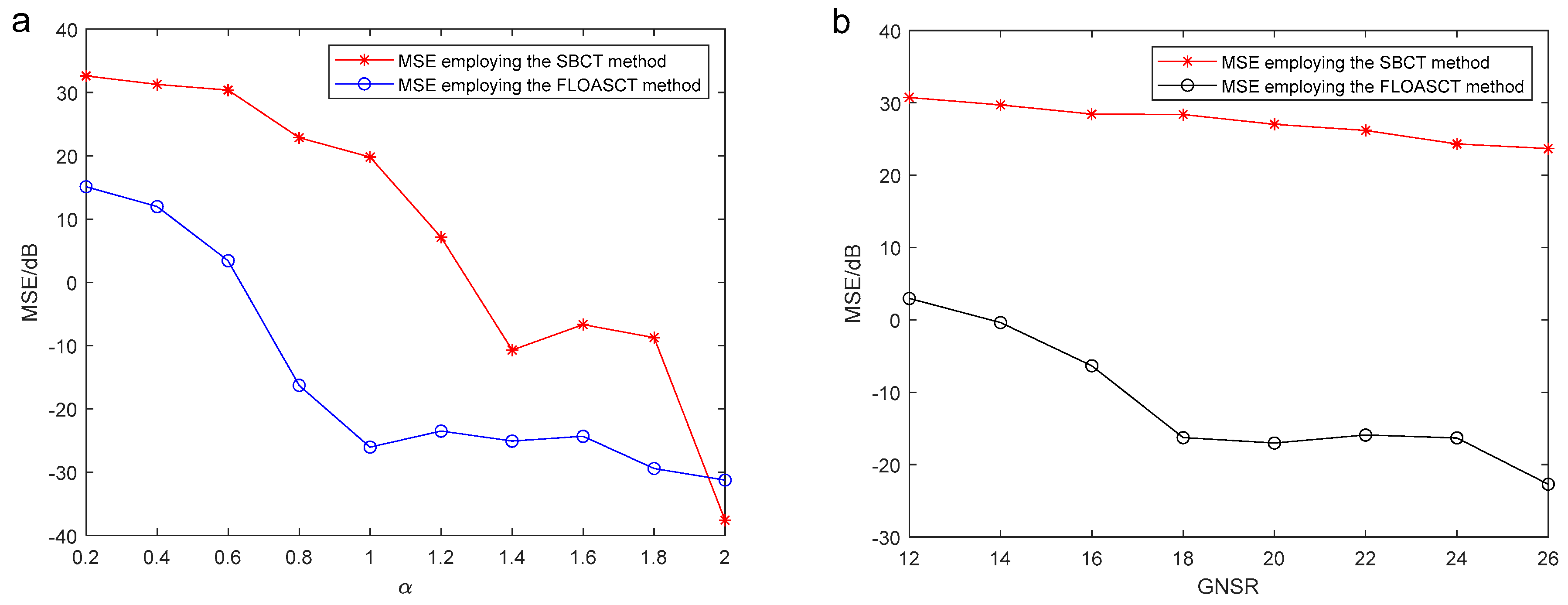
3.2.2. Application Review
3.2.3. Remarks
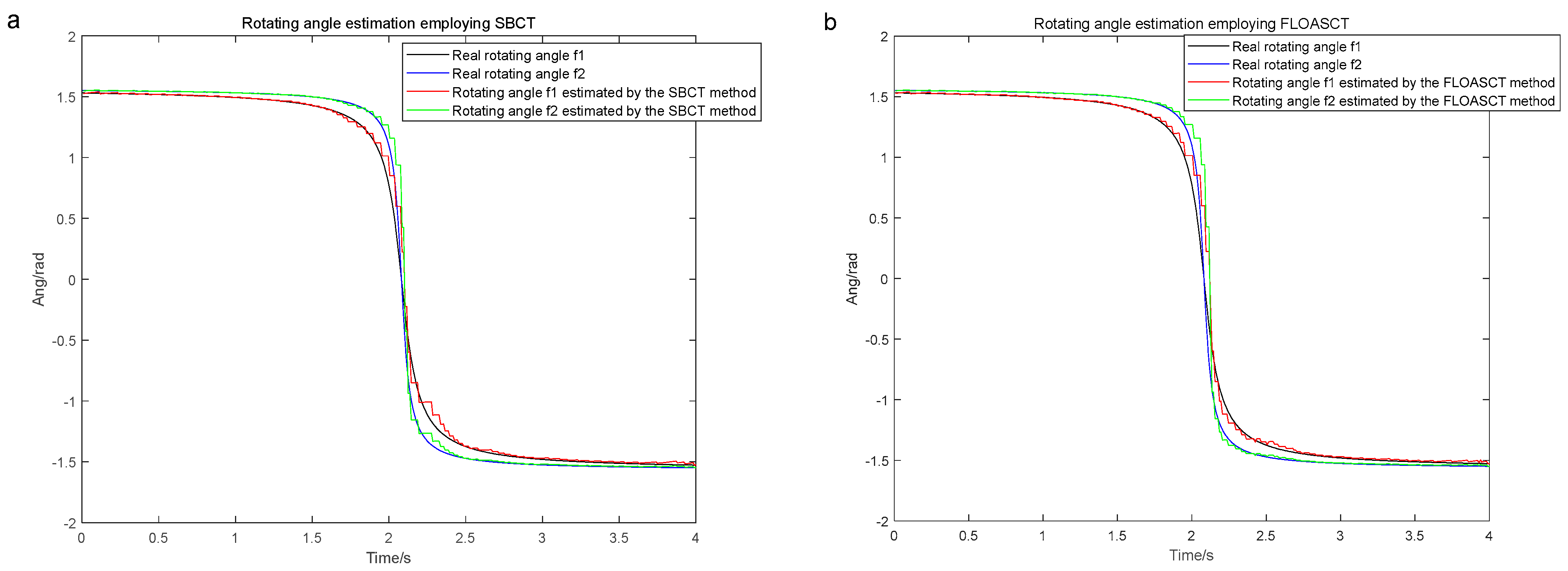
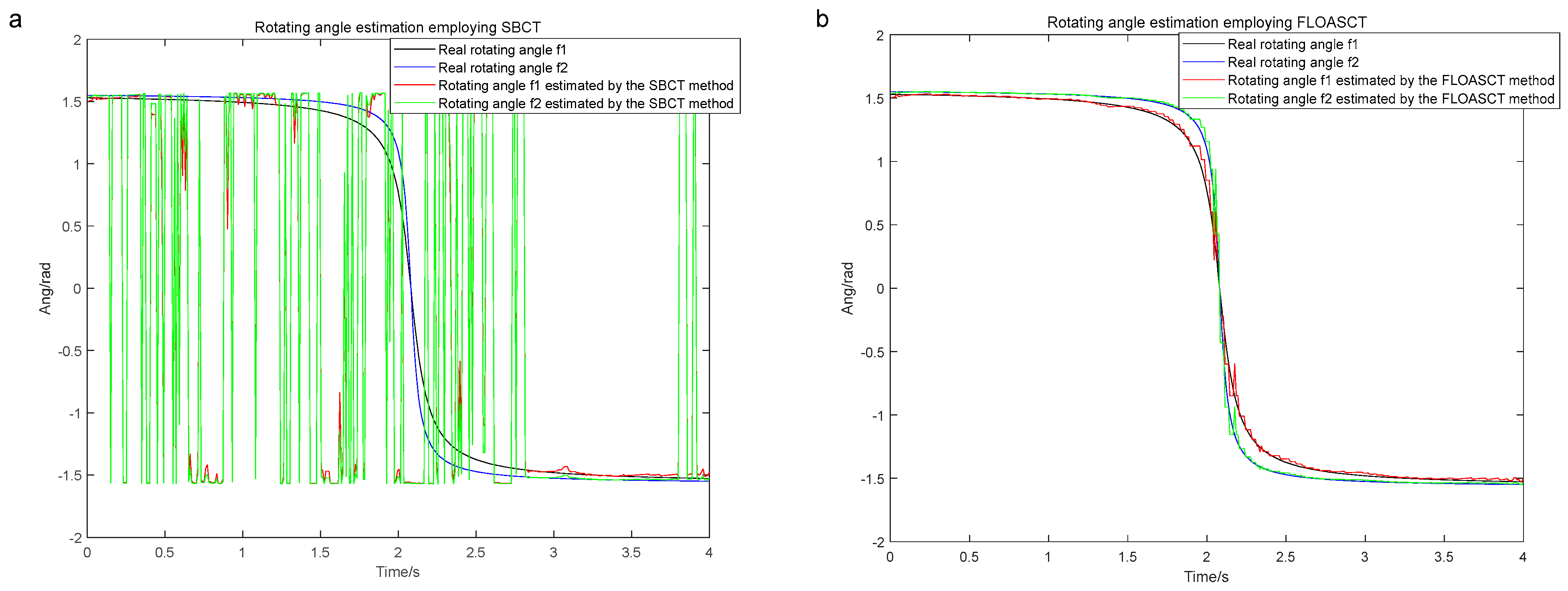
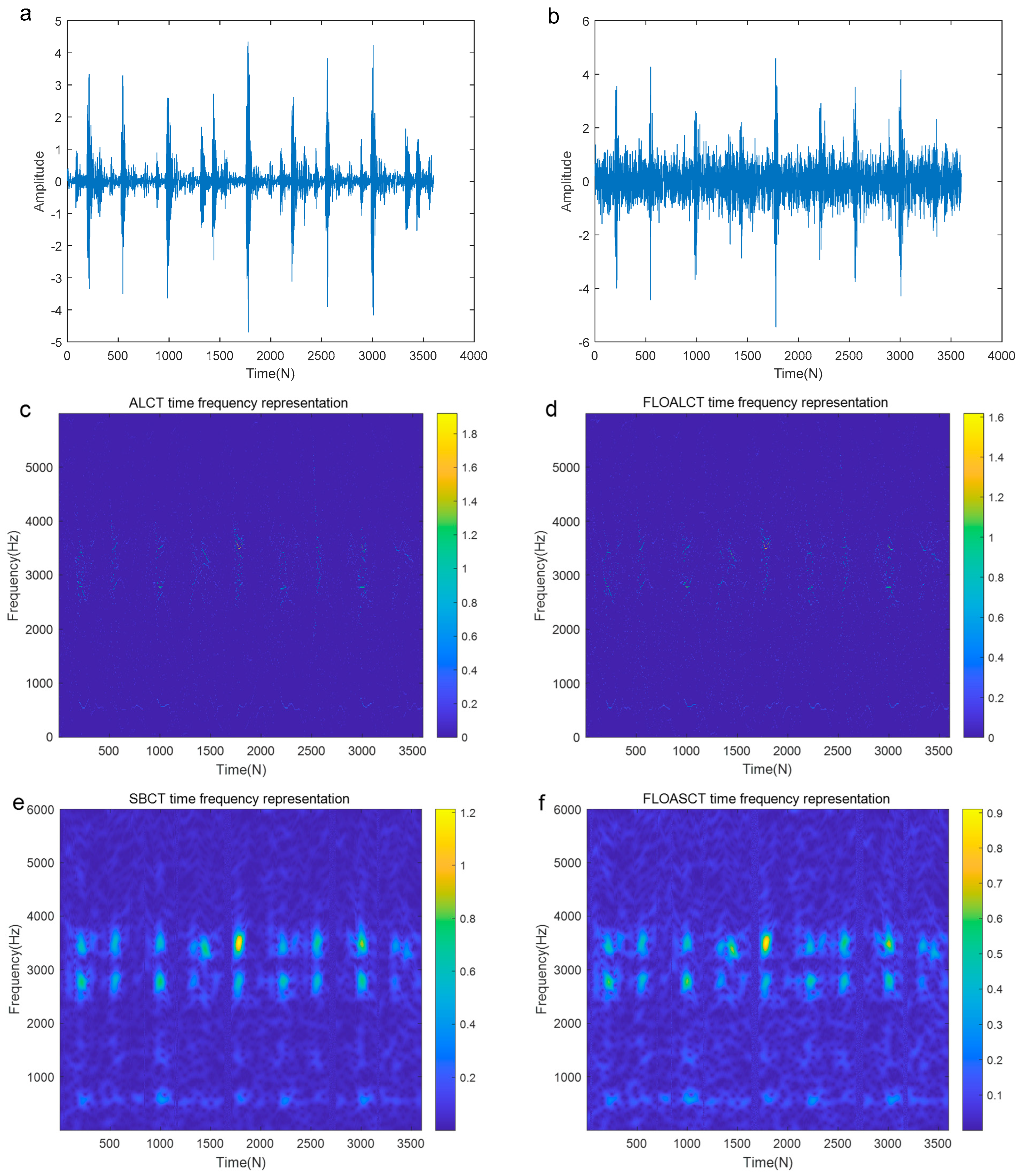
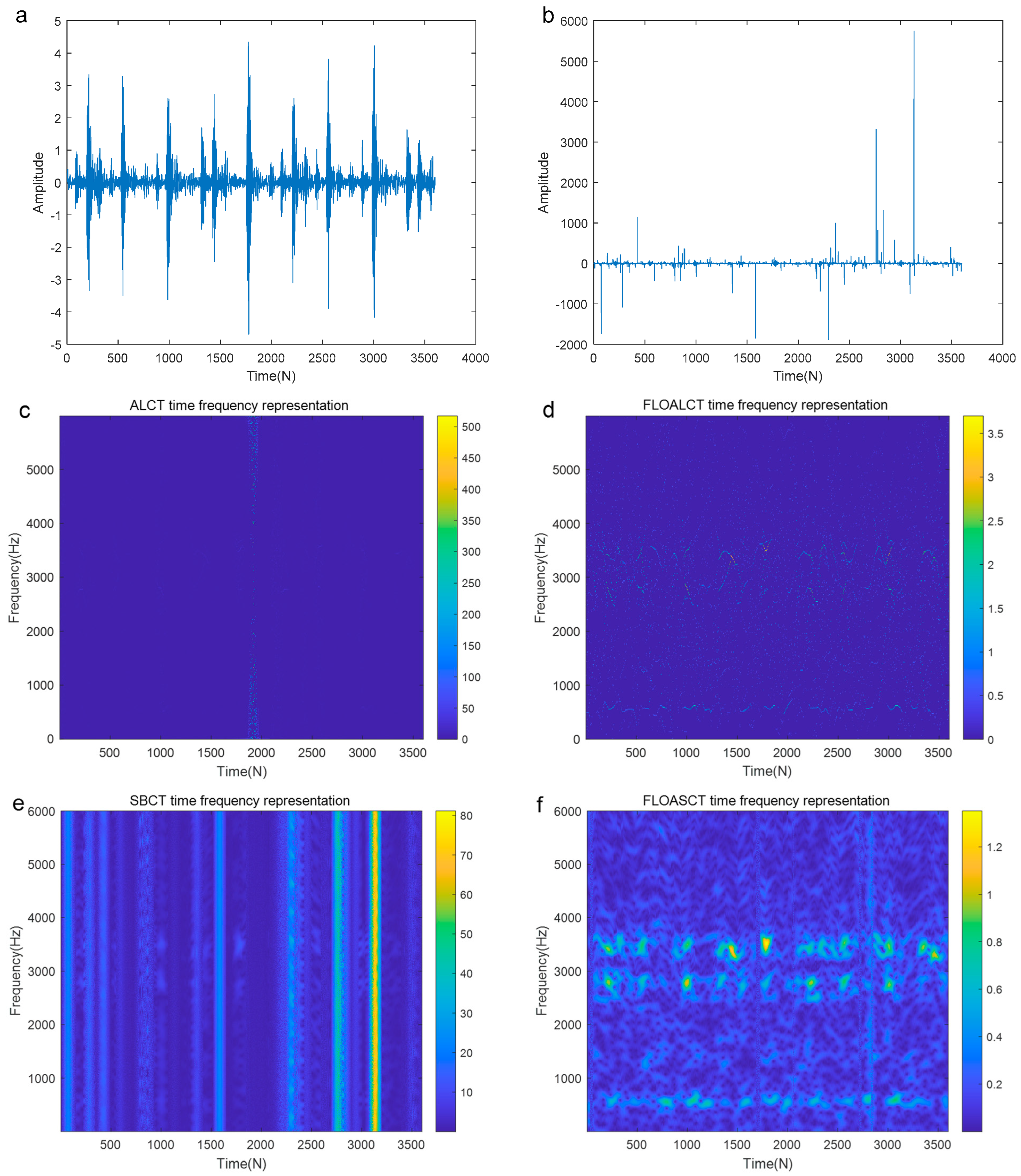
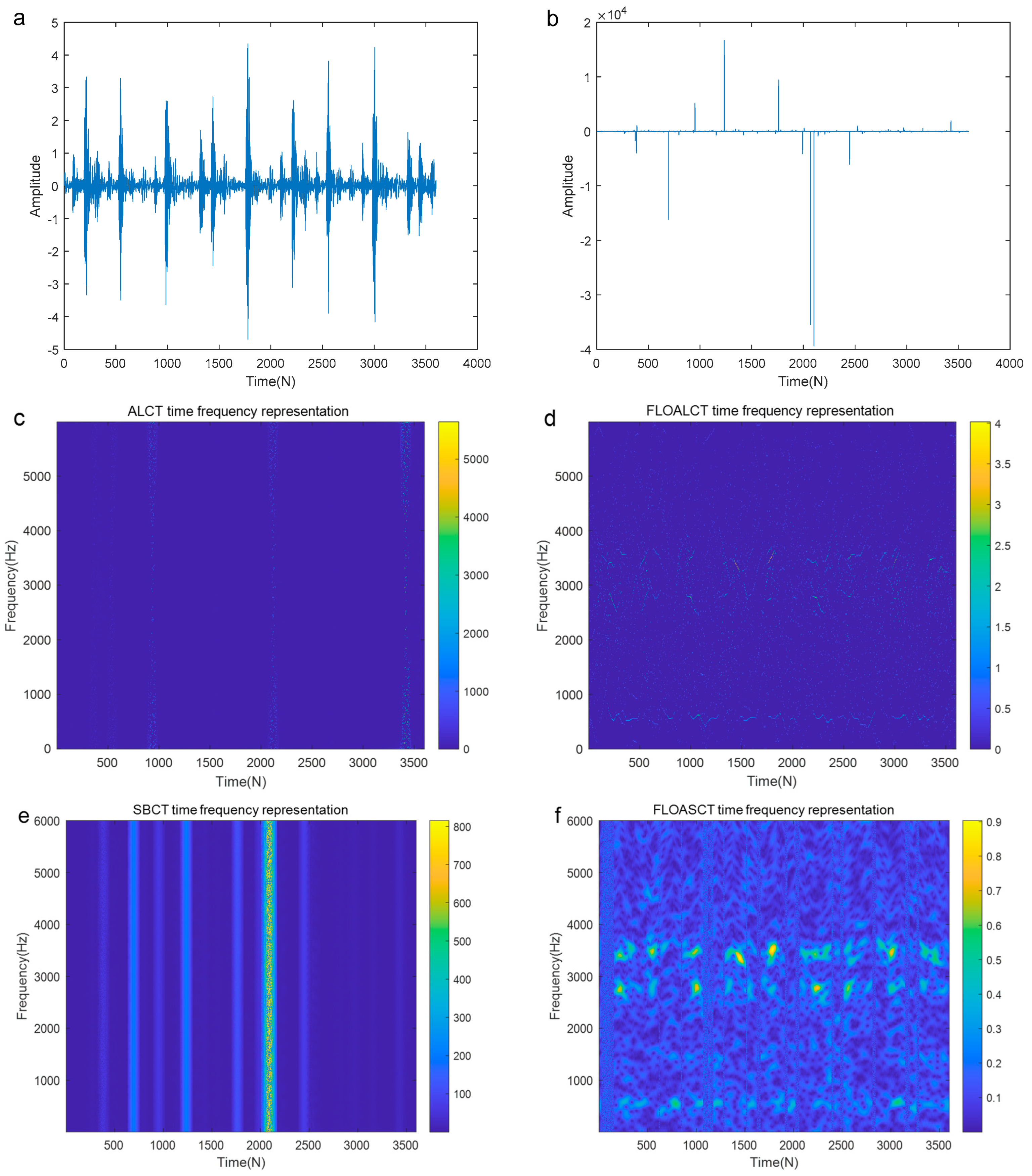
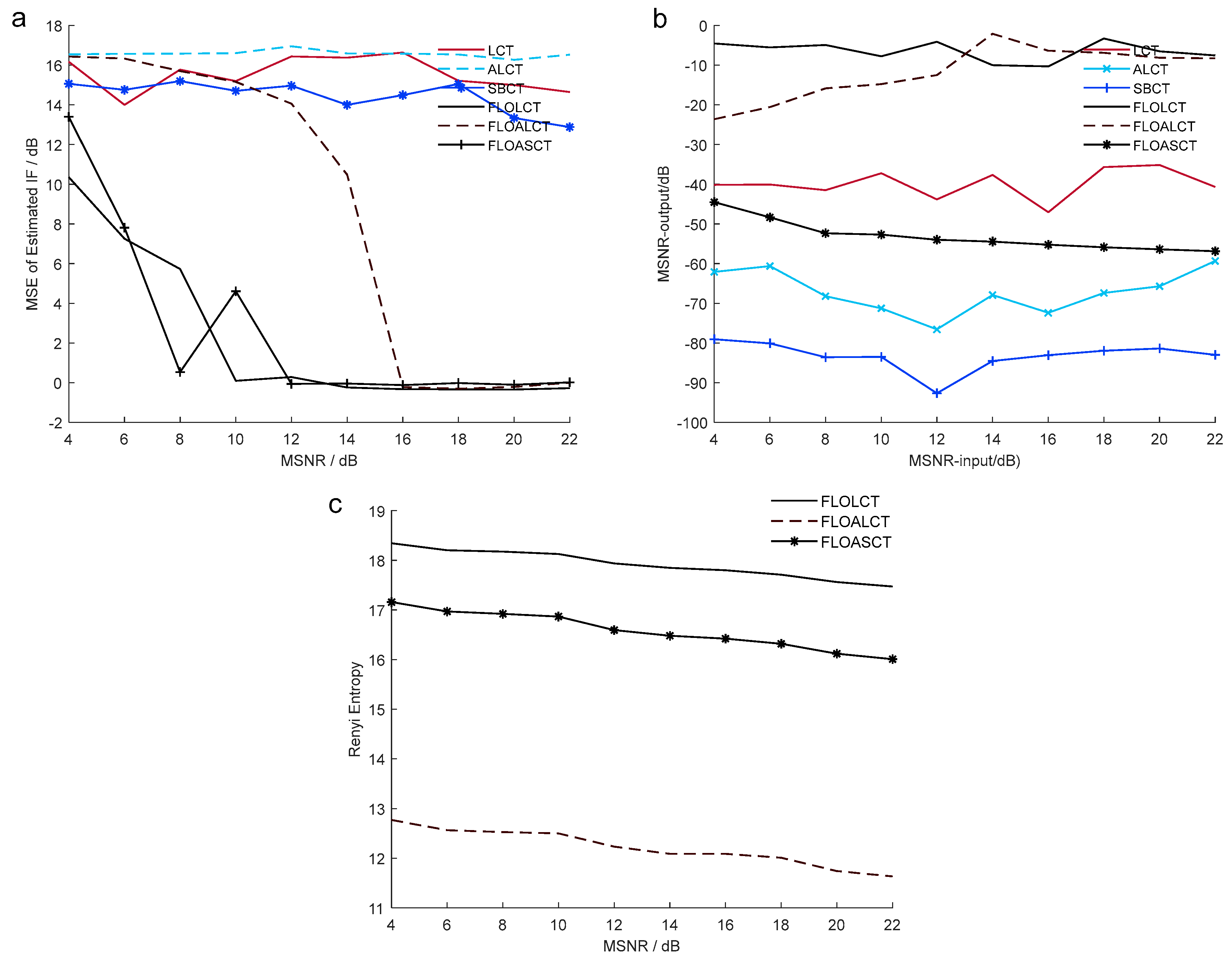
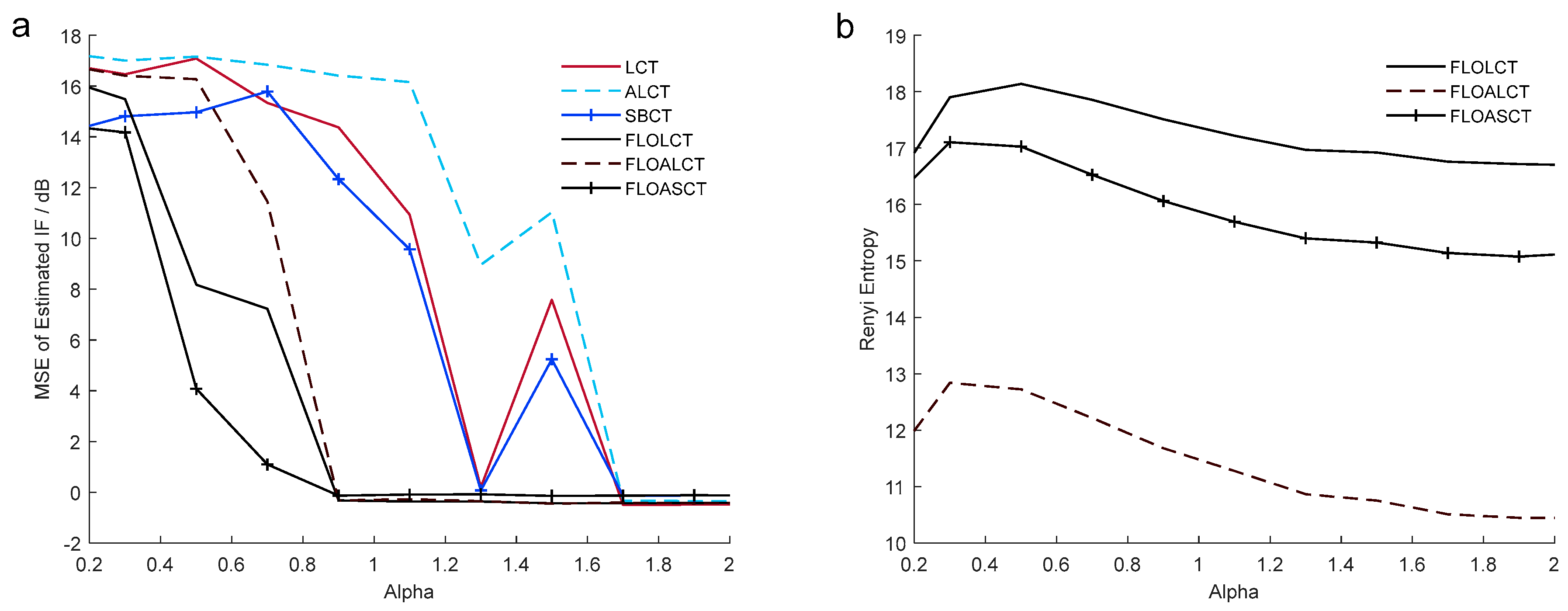
4. Application Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, W.H.; Chen, X.Y.; Cao, X.H.; Kong, Z.X.; Wang, L.; Li, G.Y.; Li, M.; Zhu, N.H.; Li, W. Compact Photonics-Assisted Short-Time Fourier Transform for Real-Time Spectral Analysis. J. Light. Technol. 2024, 42, 194–200. [Google Scholar] [CrossRef]
- Meng, P.F.; Li, T.F.; Zhou, K.; Tang, Z.R.; Zhu, G.Y.; Li, Z.R.; Cao, Y.T.; Zhang, H.Z.; Yin, Y.; Guo, J.K. A Novel Time-Frequency-Domain Reflectometry Location Method for Power Cable Defects Based on Synchrosqueezing Transform. IEEE Trans. Instrum. Meas. 2024, 73, 8004709. [Google Scholar] [CrossRef]
- Ukawa, C.; Yamashita, Y. Fault detection and identification method: 3D-CNN combined with continuous wavelet transform. Comput. Chem. Eng. 2024, 189, 108791. [Google Scholar] [CrossRef]
- Guo, Y.Z.; Wang, L.P.; Li, Y.; Guo, L.Z.; Meng, F.G. The Detection of Freezing of Gait in Parkinson’s Disease Using Asymmetric Basis Function TV-ARMA Time-Frequency Spectral Estimation Method. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2077–2086. [Google Scholar] [CrossRef]
- Wei, D.Y.; Shen, J.S. Multi-spectra synchrosqueezing transform. Signal Process. 2023, 207, 108940. [Google Scholar] [CrossRef]
- Tu, Q.Y.; Sheng, Z.C.; Fang, Y.; Nasir, A.A. Local maximum multisynchrosqueezing transform and its application. Digit. Signal Process. 2023, 140, 104122. [Google Scholar] [CrossRef]
- Correia, L.B.; Justo, J.F.; Angélico, B.A. Polynomial Adaptive Synchrosqueezing Fourier Transform: A method to optimize multiresolution. Digit. Signal Process. 2024, 150, 104526. [Google Scholar] [CrossRef]
- Bao, W.J.; Tu, X.T.; Li, F.C.; Huang, Y. Generalized Synchrosqueezing Transform: Algorithm and Applications. IEEE Trans. Instrum. Meas. 2023, 72, 3503511. [Google Scholar] [CrossRef]
- Xiong, H.Q.; An, B.Z.; Sun, B.Y.; Lu, J.Y. An Improved Synchrosqueezing S-Transform and Its Application in a GPR Detection Task. Sensors 2024, 24, 2981. [Google Scholar] [CrossRef]
- Chen, Y.M.; Li, J. 2D Second-Order Time-Frequency Synchrosqueezing Transform: For Non-stationary Signals Well-Localized Components Extraction and Separation. Circuits Syst. Signal Process. 2024, 43, 7894–7923. [Google Scholar] [CrossRef]
- Do-Duc, H.; Chau-Thanh, D.; Tran-Thai, S. A New Algorithm for Speech Feature Extraction Using Polynomial Chirplet Transform. Circuits Syst. Signal Process. 2024, 43, 2320–2340. [Google Scholar] [CrossRef]
- Liu, Y.; Xiang, H.; Jiang, Z.S.; Xiang, J.W. Iterative Synchrosqueezing-Based General Linear Chirplet Transform for Time-Frequency Feature Extraction. IEEE Trans. Instrum. Meas. 2023, 72, 3506711. [Google Scholar] [CrossRef]
- Guan, Y.P.; Liang, M.; Necsulescu, D.S. Velocity Synchronous Linea Chirplet Transform. IEEE Trans. Ind. Electron. 2019, 66, 6270–6280. [Google Scholar] [CrossRef]
- Sun, J.X.; Shu, Y.Q.; Li, J.Q.; Ge, Y.Q.; Chen, W.C. Optical Chirplet Transform for Observing Pulse Ultrafast Structures. ACS Photonics 2024, 11, 3441–3446. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, P.; Chen, X.P.; Song, Y.W.; Lan, P. Synchronous spline-kernelled Chirplet squeezing transform and its application for seismic data analysis. Digit. Signal Process. 2024, 154, 104686. [Google Scholar] [CrossRef]
- Yuan, P.P.; Zhao, Z.J.; Liu, Y.; Shen, Z.X. A combined spline chirplet transform and local maximum synchrosqueezing technique for structural instantaneous frequency identification. Smart Struct. Syst. 2024, 33, 201–215. [Google Scholar]
- Yuan, P.P.; Zhao, Z.J.; Ren, W.X. A combination of improved spline-kernelled chirplet transform and multi-synchrosqueezing technique for analyzing nonstationary signals and structural instantaneous frequency identification. Mech. Syst. Signal Process. 2024, 223, 111873. [Google Scholar] [CrossRef]
- Wang, J.G.; Tian, Y.; Dai, F.F.; Shen, Y.J.; Yang, Y.J.; Liu, Q.; Wu, Y.J. Local maximum synchrosqueezing reassigning chirplet transform and its application to gearbox fault diagnosis. Meas. Sci. Technol. 2024, 35, 086121. [Google Scholar] [CrossRef]
- Guan, Y.P.; Feng, Z.P. Adaptive Linear Chirplet Transform for Analyzing Signals With Crossing Frequency Trajectories. IEEE Trans. Ind. Electron. 2022, 69, 8396–8410. [Google Scholar] [CrossRef]
- López, C.; Moore, K.J. Enhanced adaptive linear chirplet transform for crossing frequency trajectories. J. Sound Vib. 2024, 578, 118358. [Google Scholar] [CrossRef]
- Yan, Z.; Jiao, J.P.; Xu, Y.G. Adaptive linear chirplet synchroextracting transform for time-frequency feature extraction of non-stationary signals. Mech. Syst. Signal Process. 2024, 220, 111700. [Google Scholar] [CrossRef]
- Li, M.F.; Wang, T.Y.; Chu, F.L.; Han, Q.K.; Qin, Z.Y.; Zuo, M.J. Scaling-Basis Chirplet Transform. IEEE Trans. Ind. Electron. 2021, 68, 8777–8788. [Google Scholar] [CrossRef]
- Hou, Y.T.; Wang, L.M.; Luo, X.L.; Han, X.C. Local maximum synchrosqueezes form scaling-basis chirplet transform. PLoS ONE 2022, 17, e0278223. [Google Scholar] [CrossRef] [PubMed]
- Kaur, M.; Upadhyay, R.; Kumar, V. A Hybrid Deep Learning Framework Using Scaling-Basis Chirplet Transform for Motor Imagery EEG Recognition in Brain-Computer Interface Applications. Int. J. Imaging Syst. Technol. 2024, 34, e23127. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Cui, L.L.; Chu, F.L. Synchro-Reassigning Scaling Chirplet Transform for Planetary Gearbox Fault Diagnosis. IEEE Sens. J. 2022, 22, 15248–15257. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Wang, H.H.; Cui, L.L. Frequency-chirprate synchrosqueezing-based scaling chirplet transform for wind turbine nonstationary fault feature time-frequency representation. Mech. Syst. Signal Process. 2024, 209, 111112. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Wang, H.H.; Huang, X.F.; Cui, L.L. Local Optimal Scaling Chirplet Transform for Processing Nonstationary Mechanical Vibration Signals. IEEE Trans. Instrum. Meas. 2024, 73, 3517109. [Google Scholar] [CrossRef]
- Sinha, P.; Paul, K.; Deb, S.; Vidyarthi, A.; Kilak, A.S.; Gupta, D. A New Approach to Detect Power Quality Disturbances in Smart Cities Using Scaling-Based Chirplet Transform with Strategically Placed Smart Meters. J. Circuits Syst. Comput. 2024, 33, 2450093. [Google Scholar] [CrossRef]
- Bajaj, A.; Kumar, S. The Investigation and Validation of the α-Stable Distribution Characteristics for Noises that Corrupt ECG Signals. Arab. J. Sci. Eng. 2024, 49, 16743–16770. [Google Scholar] [CrossRef]
- Hottovy, S.; Pagnini, G. Linear combinations of i.i.d. strictly stable variables with random coefficients and their application to anomalous diffusion processes. Phys. A Stat. Mech. Its Appl. 2024, 647, 129912. [Google Scholar] [CrossRef]
- Krutto, A.; Nost, T.H.; Thoresen, M. A heavy-tailed model for analyzing miRNA-seq raw read counts. Stat. Appl. Genet. Mol. Biol. 2024, 23, 20230016. [Google Scholar] [CrossRef] [PubMed]
- Shan, Z.B.; Yao, R.G.; Liu, X.S.; Liu, Y.Q. DOA estimation for acoustic vector sensor array based on fractional order cumulants sparse representation. Phys. Commun. 2024, 67, 102486. [Google Scholar] [CrossRef]
- Wang, H.; Deng, C.; Long, J.; Zhou, Y. Robust Fractional Low-Order Multiple Window STFT for Infinite Variance Process Environment. IET Signal Process. 2024, 2024, 7605121. [Google Scholar] [CrossRef]
- Long, J.; Deng, C.; Wang, H. Robust post-processing time frequency technology and its application to mechanical fault diagnosis. Sci. Rep. 2024, 14, 20456. [Google Scholar] [CrossRef]
- Jiangnan University Bearing Dataset. Available online: http://www.52phm.cn/datasets/bear/Bearing-data-set-of-Jiangnan-University.html (accessed on 27 June 2025).
- Li, W.T.; Zhang, Z.S.; Zhang, R. Newton Time-Reassigned Multi-Synchrosqueezing Wavelet Transform. IEEE Signal Process. Lett. 2024, 31, 2390–2394. [Google Scholar] [CrossRef]
- CWRU Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 27 June 2025).
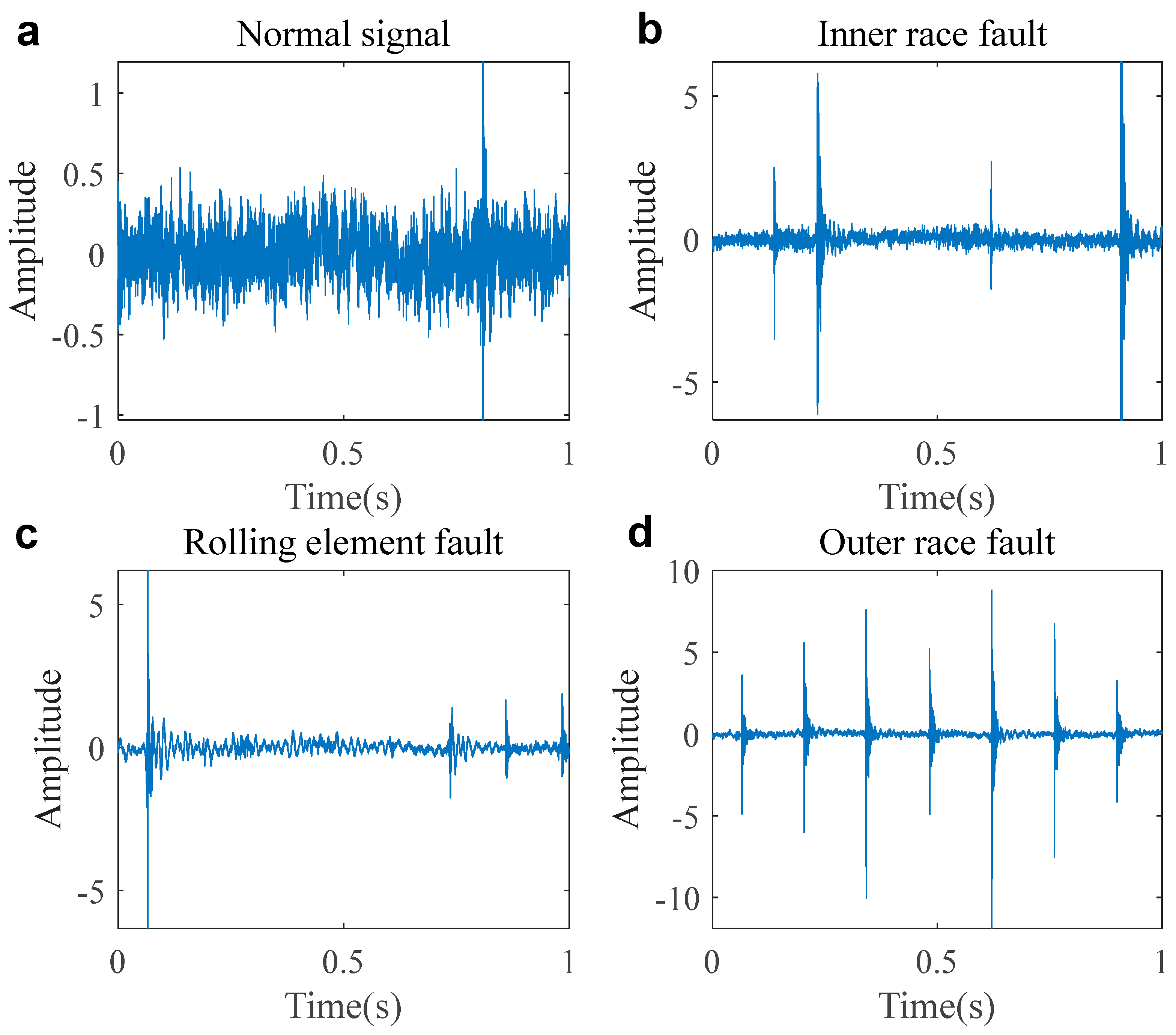
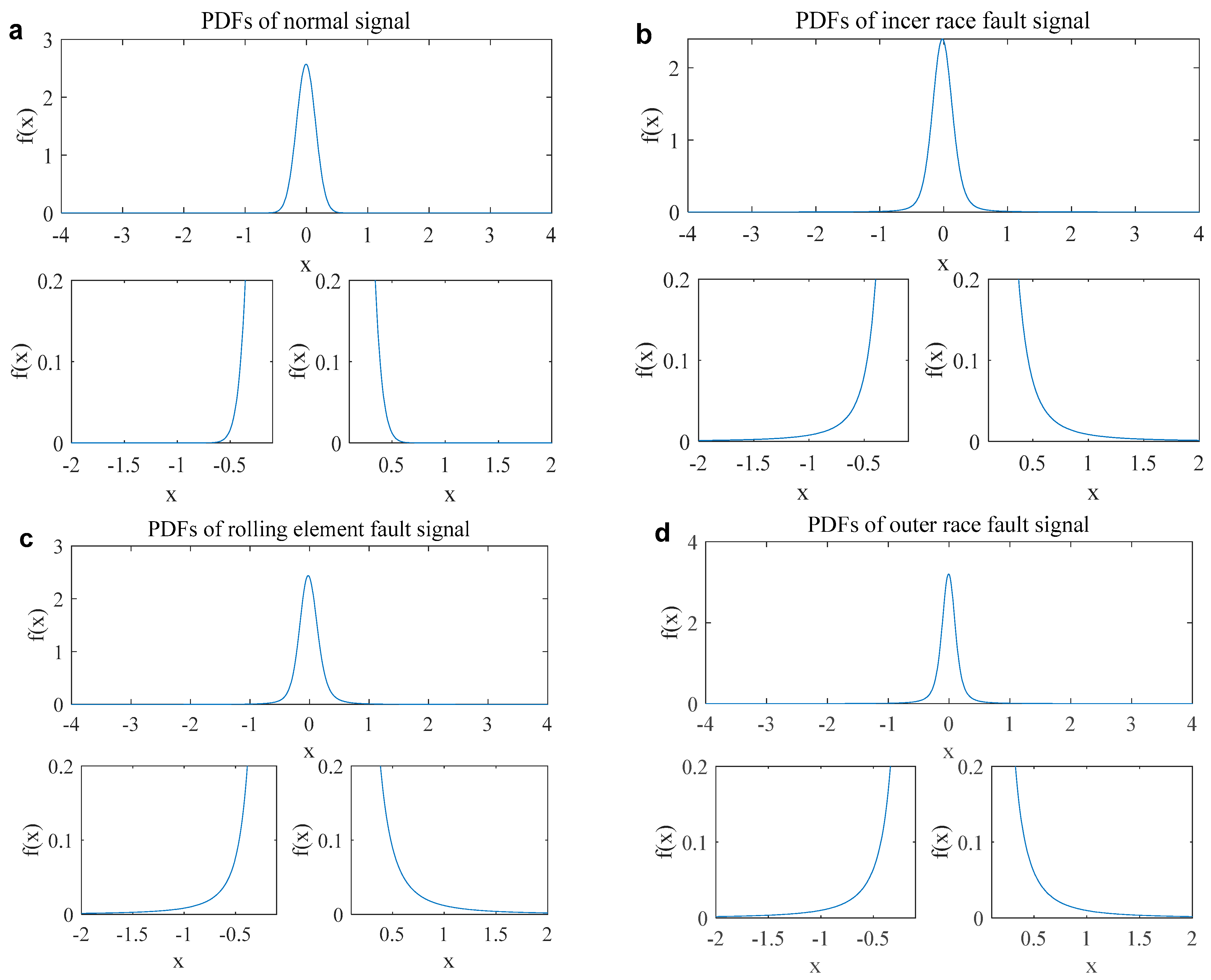
| Type | Infinite Variance Process Model Parameters | |||
|---|---|---|---|---|
| Normal signal | 2 | 0.3328 | 0.1097 | −0.0072 |
| Inner race fault | 1.6646 | 0.0976 | 0.1185 | −0.0127 |
| Rolling element fault | 1.5985 | 0.1968 | 0.1170 | −0.0025 |
| Outer race fault | 1.4639 | 0.0036 | 0.0900 | −0.0064 |
| Methods | FLOSTFT | FLOLCT | ALCT | FLOALCT | SBCT | FLOASCT |
|---|---|---|---|---|---|---|
| Computing Time (s) | 0.0835 | 0.1314 | 1.2164 | 1.5217 | 3.8218 | 3.8424 |
| Methods | Features | Deficiencies | Application Scenarios |
|---|---|---|---|
| FLOSTFT | Simple algorithm | Low time-frequency resolution | Early analysis for the mechanical fault signals |
| FLOLCT | High energy concentration cannot be achieved at every point in time | Constant chirp rate | Suitable for linear fault signal analysis |
| FLOALCT | Strong anti-interference ability, high time-frequency concentration | It has local time-frequency diffusion | Multicomponent fault signals with cross frequency trajectories |
| FLOASCT | High time-frequency concentration and strong adaptive ability without prior conditions | TFR indicates the existence of local blurring | Multicomponent fault signal with close frequency interval and large background noise |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, J.; Deng, C.; Wang, H.; Zhou, Y. Robust Fractional Low Order Adaptive Linear Chirplet Transform and Its Application to Fault Analysis. Entropy 2025, 27, 742. https://doi.org/10.3390/e27070742
Long J, Deng C, Wang H, Zhou Y. Robust Fractional Low Order Adaptive Linear Chirplet Transform and Its Application to Fault Analysis. Entropy. 2025; 27(7):742. https://doi.org/10.3390/e27070742
Chicago/Turabian StyleLong, Junbo, Changshou Deng, Haibin Wang, and Youxue Zhou. 2025. "Robust Fractional Low Order Adaptive Linear Chirplet Transform and Its Application to Fault Analysis" Entropy 27, no. 7: 742. https://doi.org/10.3390/e27070742
APA StyleLong, J., Deng, C., Wang, H., & Zhou, Y. (2025). Robust Fractional Low Order Adaptive Linear Chirplet Transform and Its Application to Fault Analysis. Entropy, 27(7), 742. https://doi.org/10.3390/e27070742





