Extended Blahut–Arimoto Algorithm for Semantic Rate-Distortion Function
Abstract
1. Introduction
- First, based on the synonymous mapping in SIT, the EBA algorithm is proposed by extending the classical BA algorithm to the semantic communication system. Similar to the BA algorithm, the EBA algorithm is also an iterative procedure that converges to the semantic RD function through alternating optimization of the transition and reconstruction distributions. The convergence is guaranteed by the convexity property of the semantic RD function, providing an efficient method for computing the semantic RD function for arbitrary discrete source models.
- Then, starting from a syntactic mapping, an optimization framework is developed for scenarios with unknown synonymous mappings. The framework combines the EBA algorithm with simulated annealing [26] to progressively merge syntactic symbols and identify the mapping with maximum synonymous number that satisfies objective constraints, enabling the discovery of optimal semantic representations that balance compression efficiency and distortion.
- Furthermore, by considering the semantic knowledge base (SKB) as a specific instance of synonymous mapping, the EBA algorithm provides a theoretical approach for analyzing and predicting the SKB size. Using the CUB dataset [27], experimental results indicate that increasing the SKB size directly improves semantic communication compression efficiency, thereby validating the critical role of SKB in enhancing transmission performance.
2. Preliminaries
2.1. Notation and Conventions
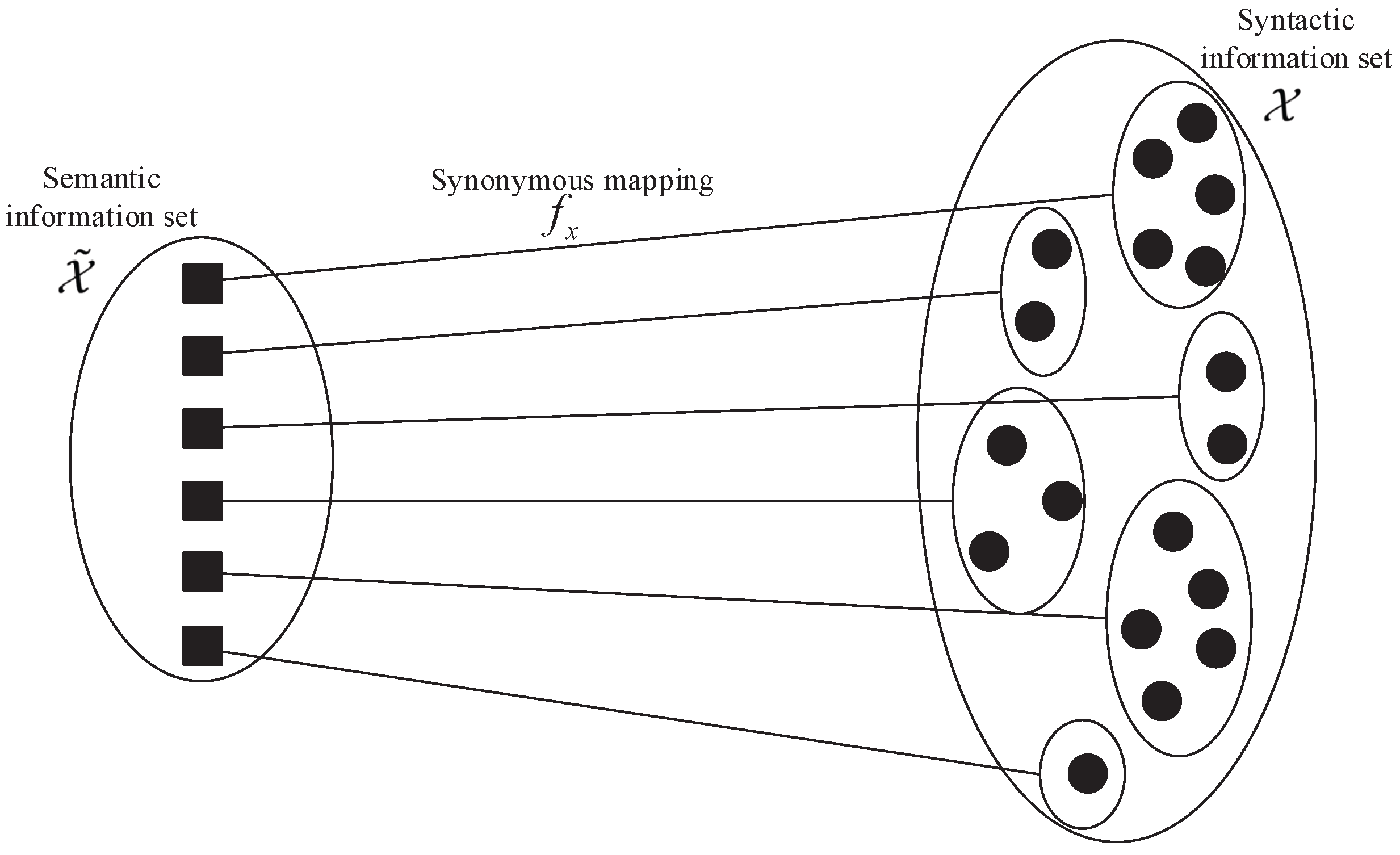
2.2. Semantic RD Function
2.3. BA Algorithm
3. Extended BA Algorithm
3.1. EBA Algorithm for the Semantic RD Function
| Algorithm 1: EBA algorithm for the semantic RD function. |
 |
3.2. EBA Algorithm for the Optimal Synonymous Mapping
| Algorithm 2: Optimization framework for finding the optimal synonymous mapping. |
 |
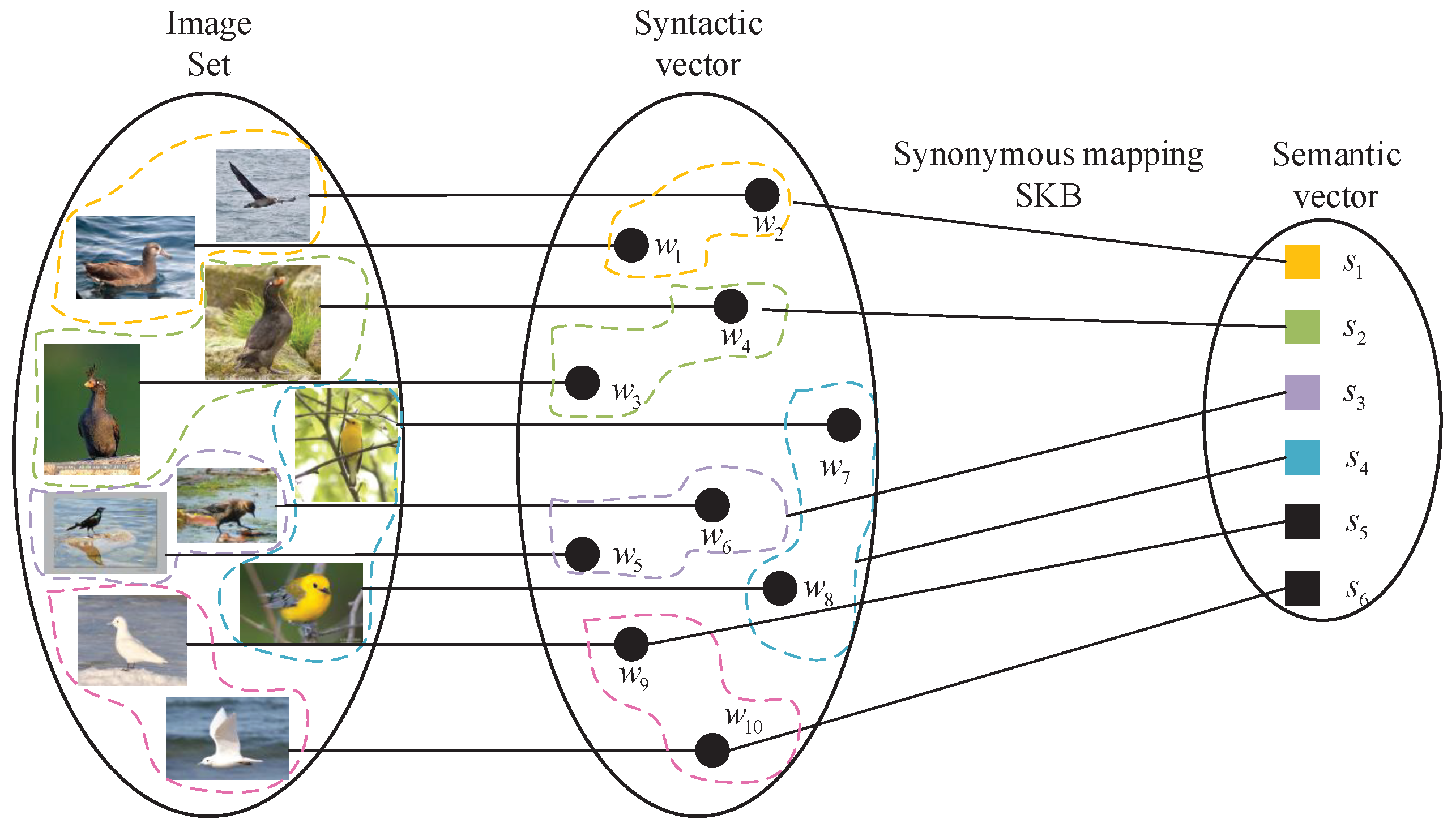
4. The Application to SKB
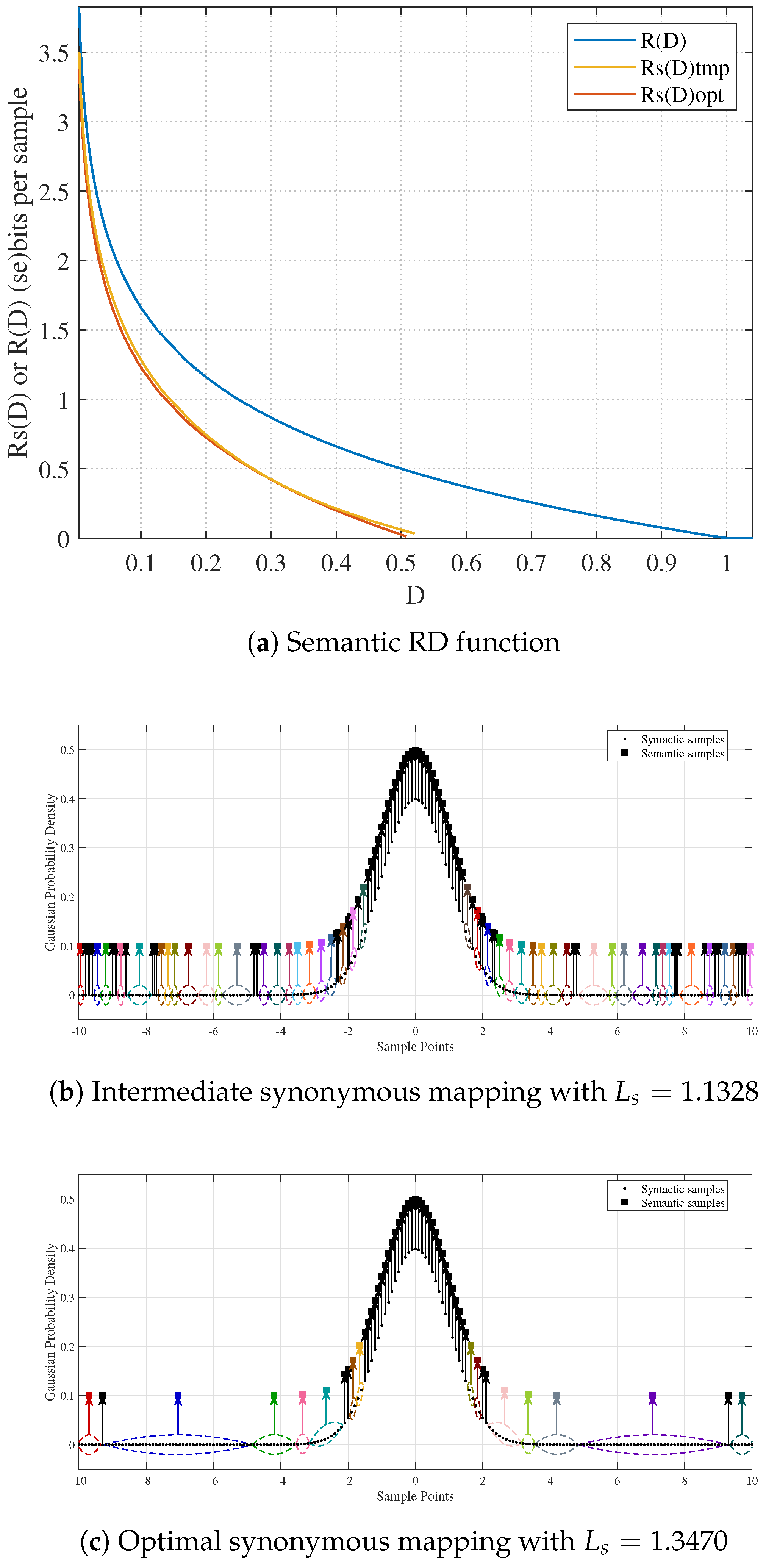
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BA | Blahut–Arimoto |
| CIT | classical information theory |
| CUB | CUB-200-2011 Birds |
| EBA | extended Blahut–Arimoto |
| RD | rate-distortion |
| SIT | semantic information theory |
| SKB | semantic knowledge base |
| SMSE | semantic mean squared error |
References
- Gündüz, D.; Qin, Z.; Aguerri, I.E.; Dhillon, H.S.; Yang, Z.; Yener, A.; Wong, K.K.; Chae, C.B. Beyond transmitting bits: Context, semantics, and task-oriented communications. IEEE J. Sel. Areas Commun. 2022, 41, 5–41. [Google Scholar] [CrossRef]
- Weaver, W. The mathematics of communication. In Communication Theory; Routledge: London, UK, 2017; pp. 27–38. [Google Scholar] [CrossRef]
- Farsad, N.; Rao, M.; Goldsmith, A. Deep learning for joint source-channel coding of text. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2326–2330. [Google Scholar]
- Xie, H.; Qin, Z.; Li, G.Y.; Juang, B.H. Deep learning enabled semantic communication systems. IEEE Trans. Signal Process. 2021, 69, 2663–2675. [Google Scholar] [CrossRef]
- Bourtsoulatze, E.; Kurka, D.B.; Gündüz, D. Deep joint source-channel coding for wireless image transmission. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 567–579. [Google Scholar] [CrossRef]
- Weng, Z.; Qin, Z. Semantic communication systems for speech transmission. IEEE J. Sel. Areas Commun. 2021, 39, 2434–2444. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Coding Theorems for a Discrete Source With a Fidelity CriterionInstitute of Radio Engineers, International Convention Record, vol. 7, 1959. In Claude E. Shannon: Collected Papers; IEEE Press: Piscataway, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Berger, T. Rate-distortion theory. In Wiley Encyclopedia of Telecommunications; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Arimoto, S. An algorithm for computing the capacity of arbitrary discrete memoryless channels. IEEE Trans. Inf. Theory 1972, 18, 14–20. [Google Scholar] [CrossRef]
- Blahut, R. Computation of channel capacity and rate-distortion functions. IEEE Trans. Inf. Theory 1972, 18, 460–473. [Google Scholar] [CrossRef]
- Dupuis, F.; Yu, W.; Willems, F.M. Blahut-Arimoto algorithms for computing channel capacity and rate-distortion with side information. In Proceedings of the International Symposium onInformation Theory, ISIT 2004, Chicago, IL, USA, 27 June–2 July 2004; p. 179. [Google Scholar]
- Lingyi, C.; Wu, S.; Ye, W.; Wu, H.; Zhang, W.; Wu, H.; Bo, B. A Constrained BA Algorithm for Rate-Distortion and Distortion-Rate Functions. Csiam Trans. Appl. Math. 2025, 6, 350–379. [Google Scholar] [CrossRef]
- Matz, G.; Duhamel, P. Information geometric formulation and interpretation of accelerated Blahut-Arimoto-type algorithms. In Proceedings of the Information Theory Workshop, San Antonio, TX, USA, 24–29 October 2004; pp. 66–70. [Google Scholar]
- Sayir, J. Iterating the Arimoto-Blahut algorithm for faster convergence. In Proceedings of the 2000 IEEE International Symposium on Information Theory (Cat. No. 00CH37060), Sorrento, Italy, 25–30 June 2000; p. 235. [Google Scholar]
- Yu, Y. Squeezing the Arimoto–Blahut algorithm for faster convergence. IEEE Trans. Inf. Theory 2010, 56, 3149–3157. [Google Scholar] [CrossRef]
- Rose, K. A mapping approach to rate-distortion computation and analysis. IEEE Trans. Inf. Theory 1994, 40, 1939–1952. [Google Scholar] [CrossRef]
- Stavrou, P.A.; Kountouris, M. The role of fidelity in goal-oriented semantic communication: A rate distortion approach. IEEE Trans. Commun. 2023, 71, 3918–3931. [Google Scholar] [CrossRef]
- Serra, G.; Stavrou, P.A.; Kountouris, M. Alternating Minimization Schemes for Computing Rate-Distortion-Perception Functions with f-Divergence Perception Constraints. arXiv 2024, arXiv:2408.15015. [Google Scholar]
- Serra, G.; Stavrou, P.A.; Kountouris, M. Computation of rate-distortion-perception function under f-divergence perception constraints. In Proceedings of the 2023 IEEE International Symposium on Information Theory (ISIT), Taipei, Taiwan, 25–30 June 2023; pp. 531–536. [Google Scholar]
- Li, D.; Huang, J.; Huang, C.; Qin, X.; Zhang, H.; Zhang, P. Fundamental limitation of semantic communications: Neural estimation for rate-distortion. J. Commun. Inf. Netw. 2023, 8, 303–318. [Google Scholar] [CrossRef]
- Liang, Z.; Niu, K.; Wang, C.; Xu, J.; Zhang, P. Synonymous Variational Inference for Perceptual Image Compression. arXiv 2025, arXiv:2505.22438. [Google Scholar]
- Niu, K.; Zhang, P. A mathematical theory of semantic communication. J. Commun. 2024, 45, 7–59. [Google Scholar] [CrossRef]
- Farquhar, S.; Kossen, J.; Kuhn, L.; Gal, Y. Detecting hallucinations in large language models using semantic entropy. Nature 2024, 630, 625–630. [Google Scholar] [CrossRef]
- Rose, K. Deterministic annealing for clustering, compression, classification, regression, and related optimization problems. Proc. IEEE 1998, 86, 2210–2239. [Google Scholar] [CrossRef]
- Wah, C.; Branson, S.; Welinder, P.; Perona, P.; Belongie, S. The Caltech-UCSD Birds-200–2011 Dataset; Tech. Rep. CNS-TR-2010-001; California Institute of Technology: Pasadena, CA, USA, 2011. [Google Scholar]
- Ren, J.; Zhang, Z.; Xu, J.; Chen, G.; Sun, Y.; Zhang, P.; Cui, S. Knowledge base enabled semantic communication: A generative perspective. IEEE Wirel. Commun. 2024, 31, 14–22. [Google Scholar] [CrossRef]
- Ni, F.; Wang, B.; Li, R.; Zhao, Z.; Zhang, H. Interplay of semantic communication and knowledge learning. In Wireless Semantic Communications: Concepts, Principles and Challenges; John Wiley & Sons: Hoboken, NJ, USA, 2025; pp. 87–108. [Google Scholar]
- Hello, N.; Di Lorenzo, P.; Strinati, E.C. Semantic communication enhanced by knowledge graph representation learning. In Proceedings of the 2024 IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 10–13 September 2024; pp. 876–880. [Google Scholar]
- Yi, P.; Cao, Y.; Kang, X.; Liang, Y.C. Deep learning-empowered semantic communication systems with a shared knowledge base. IEEE Trans. Wirel. Commun. 2023, 23, 6174–6187. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, H.; Xu, X.; Zhang, P.; Cui, S. Semantic knowledge base-enabled zero-shot multi-level feature transmission optimization. IEEE Trans. Wirel. Commun. 2023, 23, 4904–4917. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Liu, Y.; Sun, Y.; Niu, K.; Ma, N.; Cui, S.; Zhang, P. Extended Blahut–Arimoto Algorithm for Semantic Rate-Distortion Function. Entropy 2025, 27, 651. https://doi.org/10.3390/e27060651
Han Y, Liu Y, Sun Y, Niu K, Ma N, Cui S, Zhang P. Extended Blahut–Arimoto Algorithm for Semantic Rate-Distortion Function. Entropy. 2025; 27(6):651. https://doi.org/10.3390/e27060651
Chicago/Turabian StyleHan, Yuxin, Yang Liu, Yaping Sun, Kai Niu, Nan Ma, Shuguang Cui, and Ping Zhang. 2025. "Extended Blahut–Arimoto Algorithm for Semantic Rate-Distortion Function" Entropy 27, no. 6: 651. https://doi.org/10.3390/e27060651
APA StyleHan, Y., Liu, Y., Sun, Y., Niu, K., Ma, N., Cui, S., & Zhang, P. (2025). Extended Blahut–Arimoto Algorithm for Semantic Rate-Distortion Function. Entropy, 27(6), 651. https://doi.org/10.3390/e27060651





