Soft Classification in a Composite Source Model
Abstract
1. Introduction
1.1. Related Works
1.2. Contribution and Organization of Paper
- We characterize the classification rate–distortion function for general multi-class composite sources under classification distortion constraint only.
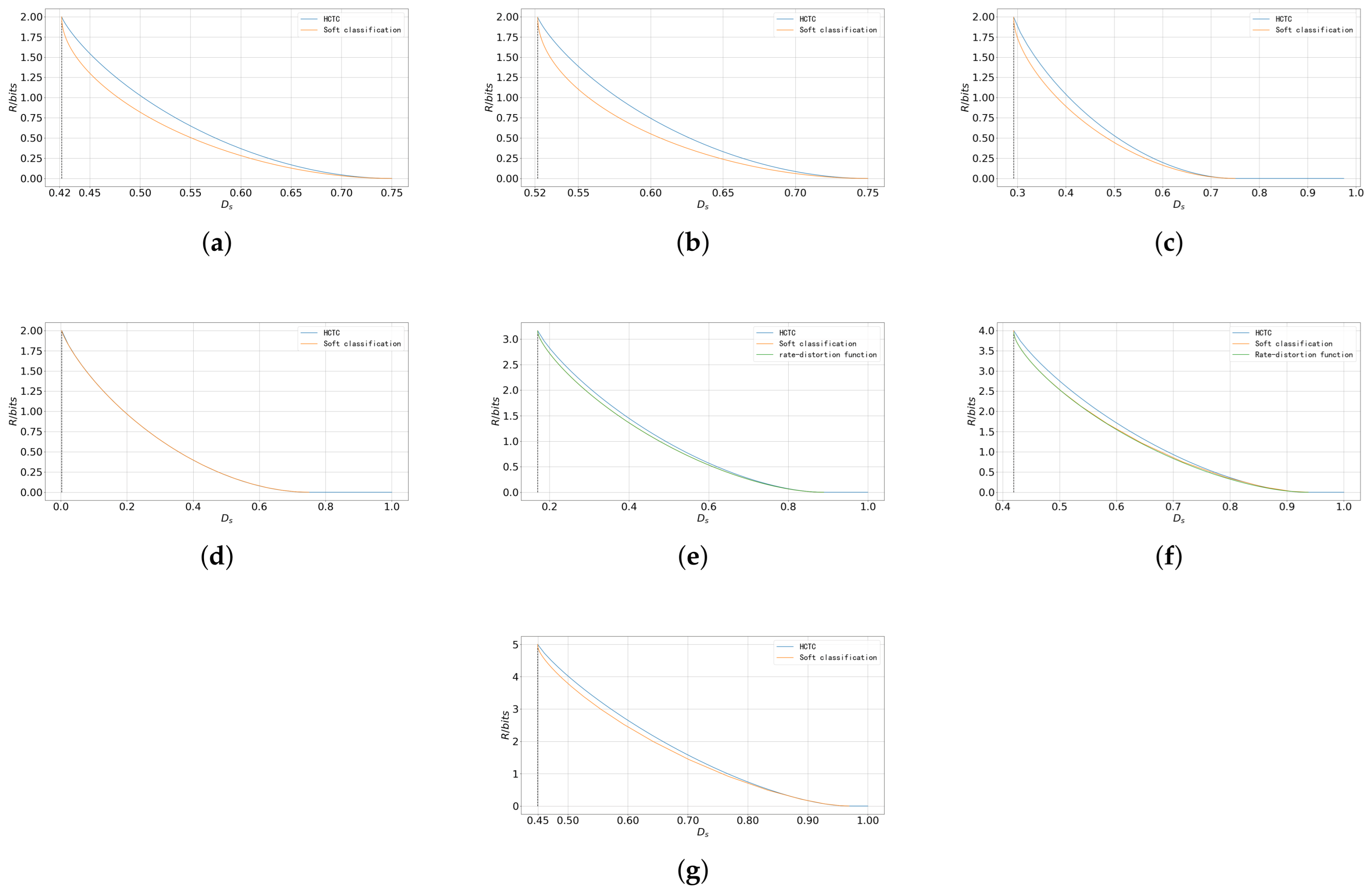
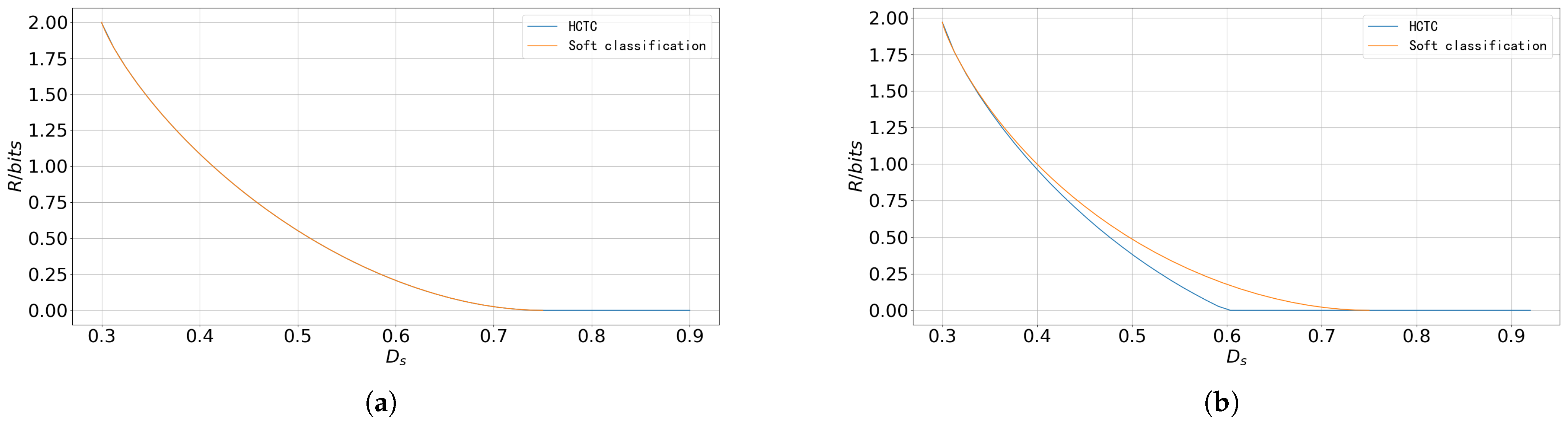
- Based on this setting, we study two schemes: the HCTC scheme and the soft classification scheme. We convert the rate–distortion performance of the HCTC scheme into the rate–distortion function of a discrete source. We also identify sufficient conditions for the rate–distortion optimality of both schemes and analyze the rate–distortion properties of the soft classification scheme. Our analysis shows that, by allowing only a small additional distortion compared to the minimum achievable distortion, the upper bound of the rate of the soft classification scheme can decrease rapidly. Through numerical results, we compare the performance of the two schemes and show that each has different strengths and weaknesses under different scenarios.
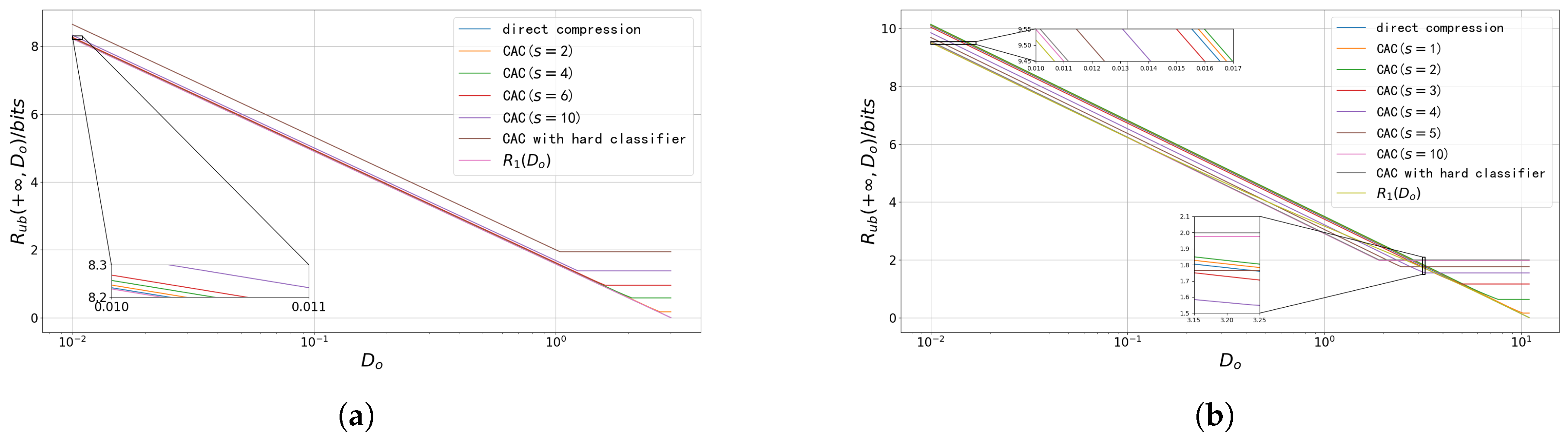
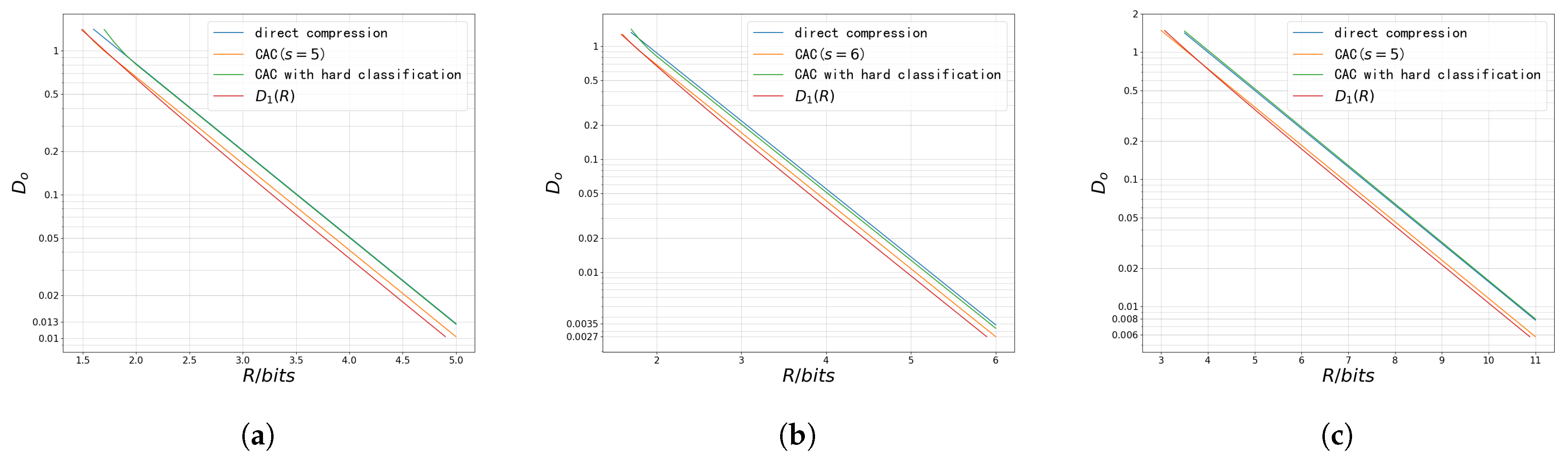
- When the reconstruction distortion is constrained, we derive an achievable upper bound of the reconstruction rate–distortion function and propose the CAC scheme using only Gaussian codebooks. Numerical results show that, with proper classification before compression, the rate–distortion performance of the CAC scheme can approach that of the scheme with a matched codebook. We also find that, under high-resolution conditions, the total bitrate of the CAC scheme can be minimized by separately optimizing the classifier and each sub-encoder.
2. Problem Formulation
3. Rate–Distortion Analysis for Classification in Composite Sources
3.1. Classification Rate–Distortion Function
3.2. Two Classification Schemes
3.2.1. Hard-Classify-Then-Compress
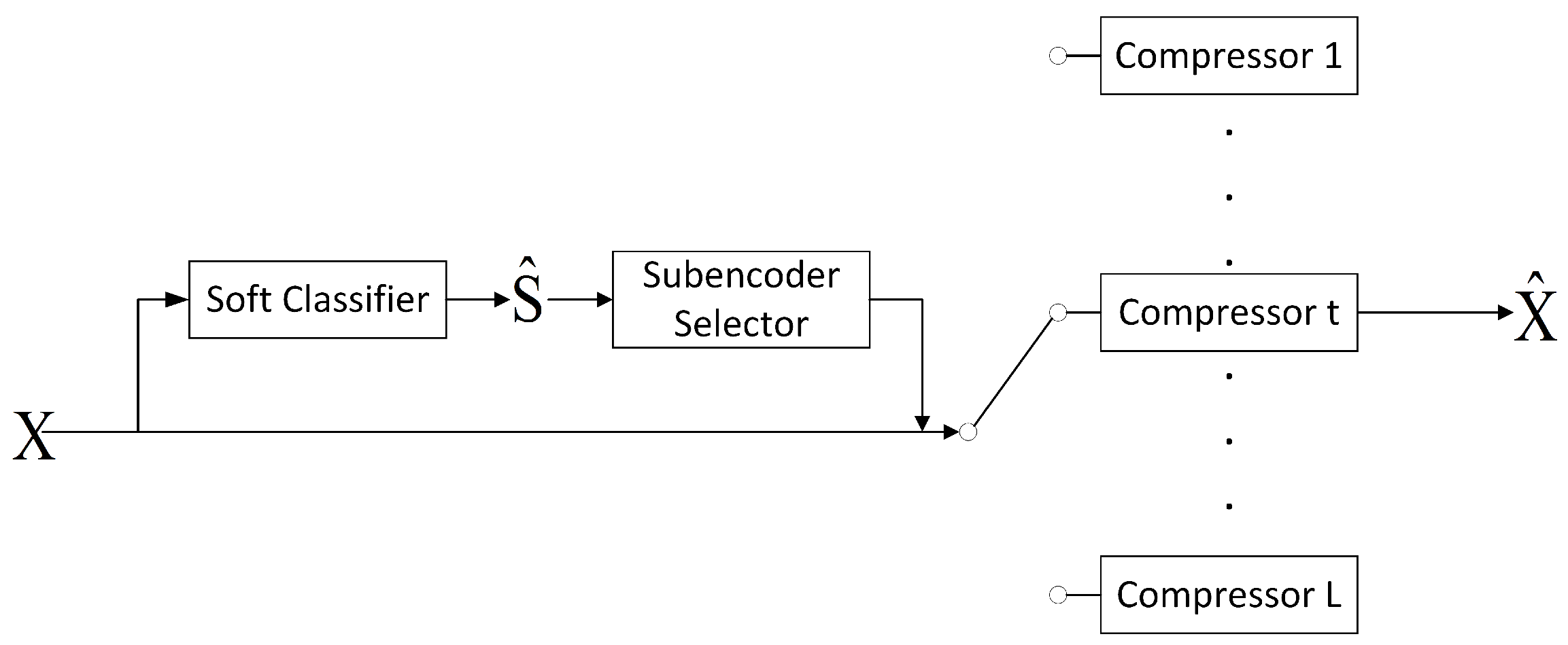
3.2.2. Symmetric Cases and Soft Classification
- The number of states is finite, and the observation space satisfies .
- The probability distributions of the sub-sources are distinct.
- .
- Let denote the mean of the t-th sub-source. There exists a point such that is equal for all t. For simplicity and without loss of generality, assume in the following discussion.
- For any two sub-sources indexed by a and b, there exists an orthonormal matrix H such that
- (1)
- .
- (2)
- specifically,
- (3)
- If , .
- Calculate the transition probabilities from observation X to the classification result using (20).
- Calculate the marginal distribution and the mutual information .
- , randomly generate a codebook containing i.i.d. sequences drawn according to . Each sequence is a codeword, indexed by .
- When encoding, select the codeword that is distortion typical [45] with . If there is more than one such , choose the one with the smallest index . If no such codeword exists for a given , encode it using .
- At the decoder, recover the sequence from the received index using the codebook . Due to the properties of the distortion-typical set, the rate–distortion pair is achievable for any .
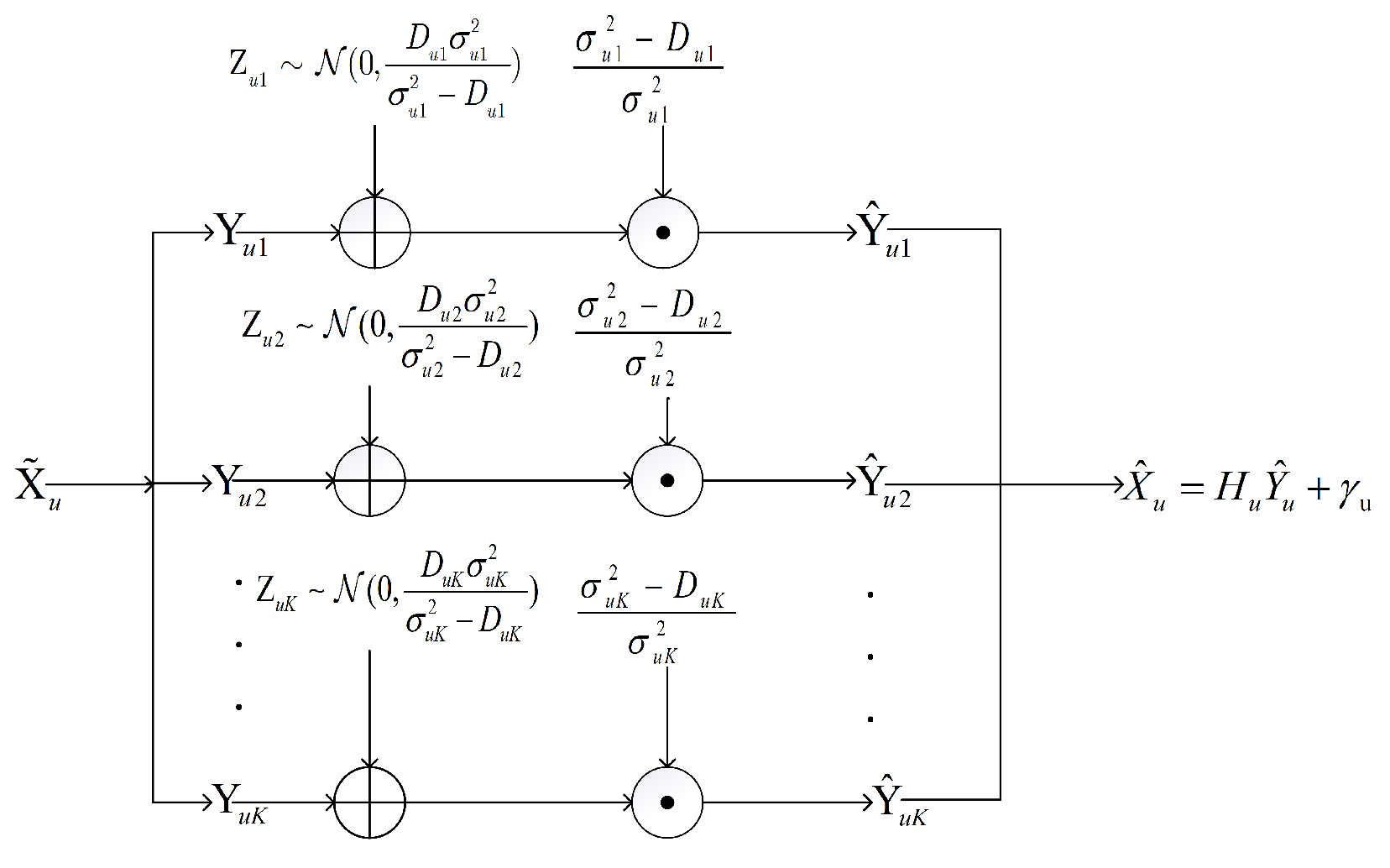
4. Classification-Aided Reconstruction of Composite Sources
- Select a distortion level D and perform the soft classification. Denote the result as .
- Encode X using the corresponding Gaussian encoder based on the soft classification result.
5. Numerical Result
5.1. Soft Classification and HCTC
5.2. Upper Bound of Reconstruction Rate–Distortion Function
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MSE | Mean-Squared Error |
| HCTC | Hard-Classify-Then-Compress |
| CAC | Classification-Aided-Compression |
| AWGN | Additive White Gaussian Noise |
| HMM | Hidden Markov Model |
| MCQ | Magnitude Classifying Quantization |
| GM | Gaussian Mixture |
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Corollary 1
Appendix D. Proof of Proposition 1
Appendix E. Proof of Proposition 2
Appendix F. Proof of Theorem 4
References
- Dobrushin, R.; Tsybakov, B. Information transmission with additional noise. IRE Trans. Inf. Theory 1962, 8, 293–304. [Google Scholar] [CrossRef]
- Wolf, J.; Ziv, J. Transmission of noisy information to a noisy receiver with minimum distortion. IEEE Trans. Inf. Theory 1970, 16, 406–411. [Google Scholar] [CrossRef]
- Berger, T. Rate Distortion Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Liu, J.; Zhang, W.; Poor, H.V. A Rate-Distortion Framework for Characterizing Semantic Information. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021; pp. 2894–2899. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, T.; Bai, B.; Han, W. The Estimation-Compression Separation in Semantic Communication Systems. In Proceedings of the 2022 IEEE Information Theory Workshop (ITW), Mumbai, India, 1–9 November 2022; pp. 315–320. [Google Scholar]
- Gerrish, A.; Schultheiss, P. Information rates of non-Gaussian processes. IEEE Trans. Inf. Theory 1964, 10, 265–271. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. IRE Nat. Conv. Rec 1959, 4, 1. [Google Scholar]
- Bar-Hillel, Y.; Carnap, R. Semantic information. Br. J. Philos. Sci. 1953, 4, 147–157. [Google Scholar] [CrossRef]
- Floridi, L. Outline of a Theory of Strongly Semantic Information. Minds Mach. 2004, 14, 197–221. [Google Scholar] [CrossRef]
- Bao, J.; Basu, P.; Dean, M.; Partridge, C.; Swami, A.; Leland, W.; Hendler, J.A. Towards a theory of semantic communication. In Proceedings of the 2011 IEEE Network Science Workshop, West Point, NY, USA, 22–24 June 2011; pp. 110–117. [Google Scholar] [CrossRef]
- Juba, B. Universal Semantic Communication; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Popovski, P.; Simeone, O.; Boccardi, F.; Gunduz, D.; Sahin, O. Semantic-Effectiveness Filtering and Control for Post-5G Wireless Connectivity. arXiv 2019, arXiv:1907.02441. [Google Scholar] [CrossRef]
- Kountouris, M.; Pappas, N. Semantics-Empowered Communication for Networked Intelligent Systems. IEEE Commun. Mag. 2021, 59, 96–102. [Google Scholar] [CrossRef]
- Seo, H.; Kang, Y.; Bennis, M.; Choi, W. Bayesian Inverse Contextual Reasoning for Heterogeneous Semantics- Native Communication. IEEE Trans. Commun. 2024, 72, 830–844. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Y.; Wang, Z.; You, L.; Pan, H.; Wang, F.; Cui, S. User Centric Semantic Communications. arXiv 2024, arXiv:2411.03127. [Google Scholar]
- Shlezinger, N.; Eldar, Y.C.; Rodrigues, M.R.D. Hardware-Limited Task-Based Quantization. IEEE Trans. Signal Process. 2019, 67, 5223–5238. [Google Scholar] [CrossRef]
- Ordentlich, O.; Polyanskiy, Y. Optimal Quantization for Matrix Multiplication. arXiv 2024, arXiv:2410.13780. [Google Scholar]
- Shlezinger, N.; van Sloun, R.J.G.; Huijben, I.A.M.; Tsintsadze, G.; Eldar, Y.C. Learning Task-Based Analog-to-Digital Conversion for MIMO Receivers. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 9125–9129. [Google Scholar] [CrossRef]
- Shlezinger, N.; Amar, A.; Luijten, B.; van Sloun, R.J.G.; Eldar, Y.C. Deep Task-Based Analog-to-Digital Conversion. IEEE Trans. Signal Process. 2022, 70, 6021–6034. [Google Scholar] [CrossRef]
- Lexa, M.A.; Johnson, D.H. Joint Optimization of Distributed Broadcast Quantization Systems for Classification. In Proceedings of the 2007 Data Compression Conference (DCC’07), Snowbird, UT, USA, 27–29 March 2007; pp. 363–374. [Google Scholar] [CrossRef]
- Dogahe, B.M.; Murthi, M.N. Quantization for classification accuracy in high-rate quantizers. In Proceedings of the 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 277–282. [Google Scholar] [CrossRef]
- Poor, H. Fine quantization in signal detection and estimation. IEEE Trans. Inf. Theory 1988, 34, 960–972. [Google Scholar] [CrossRef]
- Kipnis, A.; Rini, S.; Goldsmith, A.J. The Rate-Distortion Risk in Estimation From Compressed Data. IEEE Trans. Inf. Theory 2021, 67, 2910–2924. [Google Scholar] [CrossRef]
- Fontana, R. Universal codes for a class of composite sources (Corresp.). IEEE Trans. Inf. Theory 1980, 26, 480–482. [Google Scholar] [CrossRef]
- Liu, J.; Poor, H.V.; Song, I.; Zhang, W. A Rate-Distortion Analysis for Composite Sources Under Subsource-Dependent Fidelity Criteria. arXiv 2024, arXiv:2405.11818. [Google Scholar] [CrossRef]
- Liu, J.; Shao, S.; Zhang, W.; Poor, H.V. An Indirect Rate-Distortion Characterization for Semantic Sources: General Model and the Case of Gaussian Observation. IEEE Trans. Commun. 2022, 70, 5946–5959. [Google Scholar] [CrossRef]
- Witsenhausen, H. Indirect rate distortion problems. IEEE Trans. Inf. Theory 1980, 26, 518–521. [Google Scholar] [CrossRef]
- Liu, K.; Liu, D.; Li, L.; Ning, Y.; Li, H. Semantics-to-Signal Scalable Image Compression with Learned Revertible Representations. Int. J. Comput. Vis. 2021, 129, 2605–2621. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Schafer, R.W. Introduction to Digital Speech Processing. Found. Trends® Signal Process. 2007, 1, 1–194. [Google Scholar] [CrossRef]
- Kalveram, H.; Meissner, P. Itakura-saito clustering and rate distortion functions for a composite source model of speech. Signal Process. 1989, 18, 195–216. [Google Scholar] [CrossRef]
- Gibson, J.D.; Hu, J. Rate Distortion Bounds for Voice and Video. Found. Trends® Commun. Inf. Theory 2014, 10, 379–514. [Google Scholar] [CrossRef]
- Gibson, J. Rate distortion functions and rate distortion function lower bounds for real-world sources. Entropy 2017, 19, 604. [Google Scholar] [CrossRef]
- Rabiner, L. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Kingma, D.P. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Croitoru, F.A.; Hondru, V.; Ionescu, R.T.; Shah, M. Diffusion models in vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10850–10869. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Fei, Z.; Huang, L.; Zhang, W.; Zhao, B.; Guan, H.; Huang, Y. Failure Mode and Effects Analysis Method on the Air System of an Aircraft Turbofan Engine in Multi-Criteria Open Group Decision-Making Environment. Cybern. Syst. 2025, 1–32. [Google Scholar] [CrossRef]
- Popkov, Y.S.; Volkovich, Z.; Dubnov, Y.A.; Avros, R.; Ravve, E. Entropy “2”-Soft Classification of Objects. Entropy 2017, 19, 178. [Google Scholar] [CrossRef]
- Sharma, R.; Garg, P.; Dwivedi, R. A literature survey for fuzzy based soft classification techniques and uncertainty estimation. In Proceedings of the 2016 International Conference System Modeling & Advancement in Research Trends (SMART), Moradabad, India, 25–27 November 2016; pp. 71–75. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. Predicting individual pixel error in remote sensing soft classification. Remote Sens. Environ. 2017, 199, 401–414. [Google Scholar] [CrossRef]
- Weidmann, C.; Vetterli, M. Rate Distortion Behavior of Sparse Sources. IEEE Trans. Inf. Theory 2012, 58, 4969–4992. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Blahut, R. Computation of channel capacity and rate-distortion functions. IEEE Trans. Inf. Theory 1972, 18, 460–473. [Google Scholar] [CrossRef]
- Chen, L.; Wu, S.; Ye, W.; Wu, H.; Zhang, W.; Wu, H.; Bai, B. A constrained BA algorithm for rate-distortion and distortion-rate functions. arXiv 2023, arXiv:2305.02650. [Google Scholar]
- Yeung, R.W. A First Course in Information Theory; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
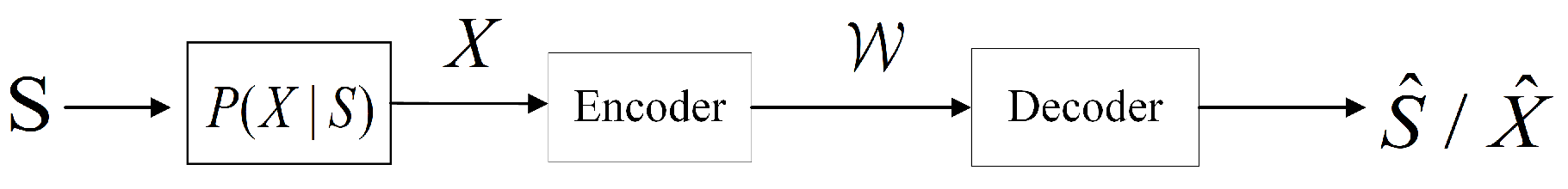
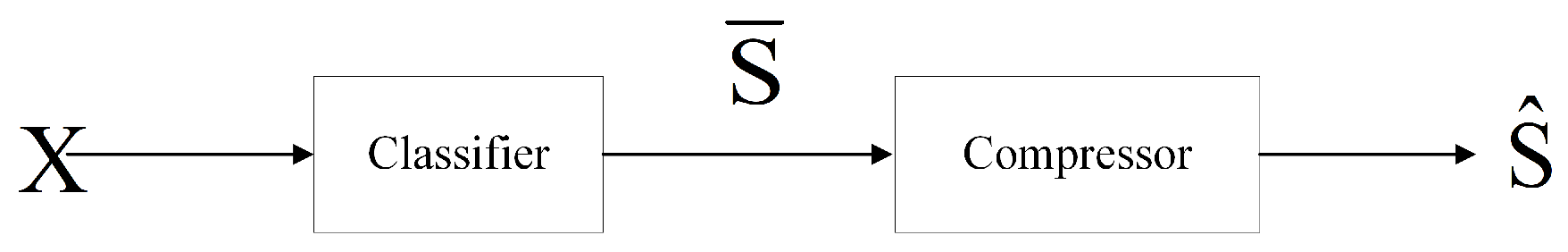





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Liu, J.; Zhang, W. Soft Classification in a Composite Source Model. Entropy 2025, 27, 620. https://doi.org/10.3390/e27060620
Cao Y, Liu J, Zhang W. Soft Classification in a Composite Source Model. Entropy. 2025; 27(6):620. https://doi.org/10.3390/e27060620
Chicago/Turabian StyleCao, Yuefeng, Jiakun Liu, and Wenyi Zhang. 2025. "Soft Classification in a Composite Source Model" Entropy 27, no. 6: 620. https://doi.org/10.3390/e27060620
APA StyleCao, Y., Liu, J., & Zhang, W. (2025). Soft Classification in a Composite Source Model. Entropy, 27(6), 620. https://doi.org/10.3390/e27060620






