Information Theory Meets Quantum Chemistry: A Review and Perspective
Abstract
1. Motivation
2. Brief Introduction to Information Theory
2.1. Shannon Entropy
My greatest concern was what to call it. I thought of calling it ‘information’, but the word was overly used, so I decided to call it ‘uncertainty’. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, “You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have an advantage [60].
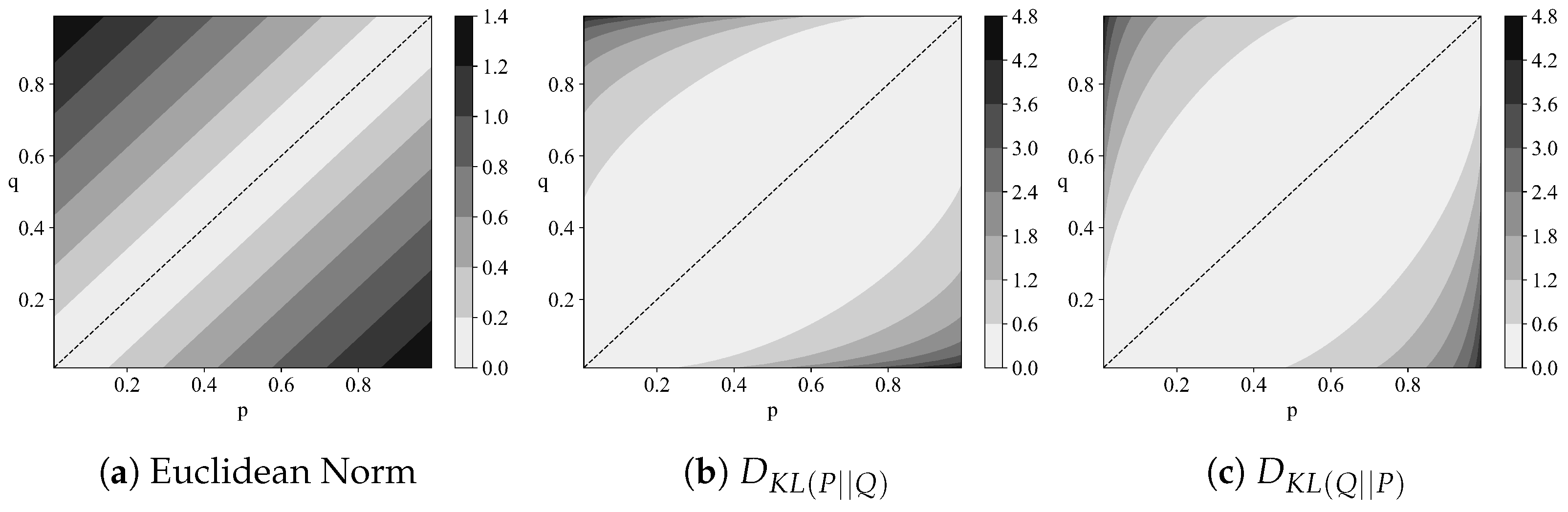
2.2. Relative Entropy
- Non-negativity:
- Identity of indiscernibles:
- Symmetry:
- Triangle inequality:
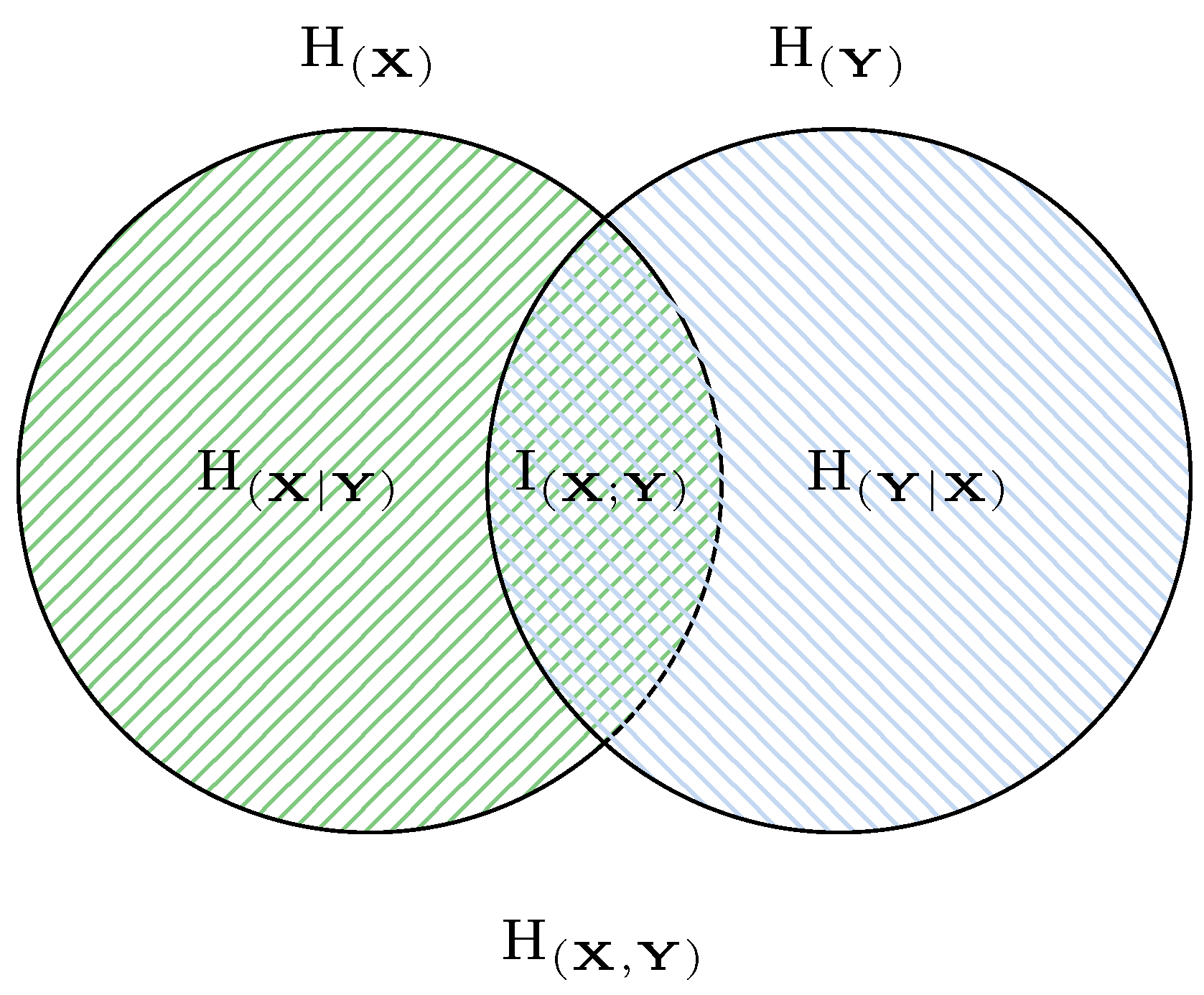
2.3. Bivariate Entropy
- The chain rule.
- Subadditivity.
- The relationship between different bivariate entropy,
3. Basic Ingredients of Information Theory in Quantum Chemistry: Reduced Density Matrix
3.1. Density Matrix and Reduced Density Matrix
3.2. 1-RDM and 2-RDM
3.3. 3-RDM and 4-RDM
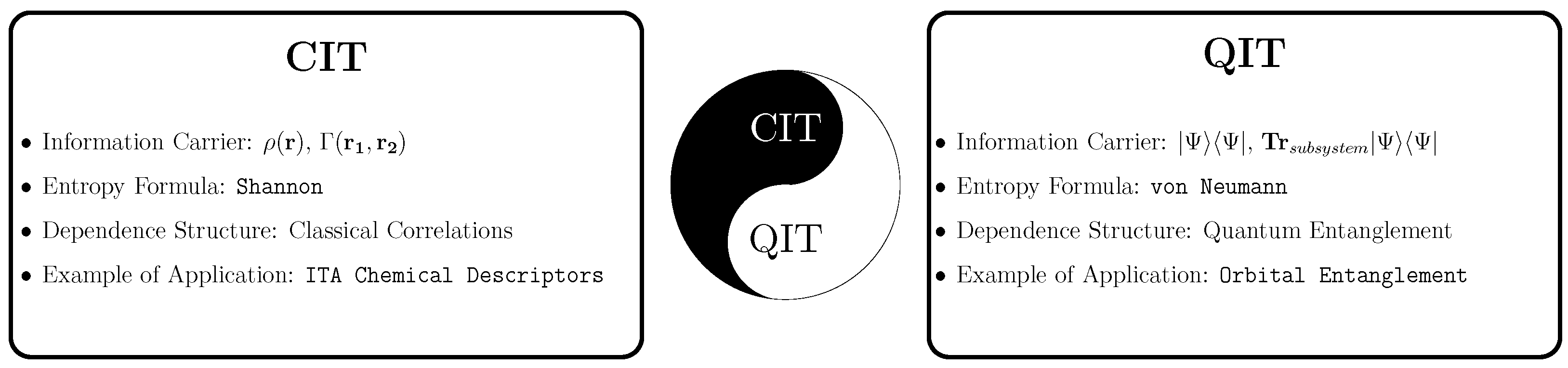
4. Classical Information Theory in Quantum Chemistry
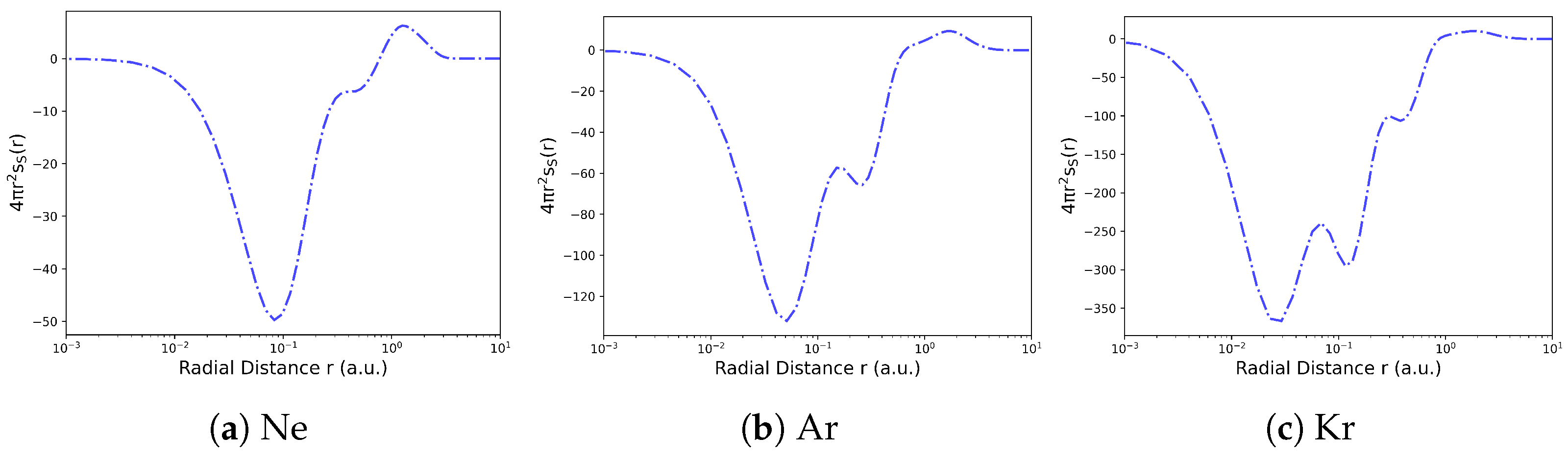
4.1. Electron Density in Position Space
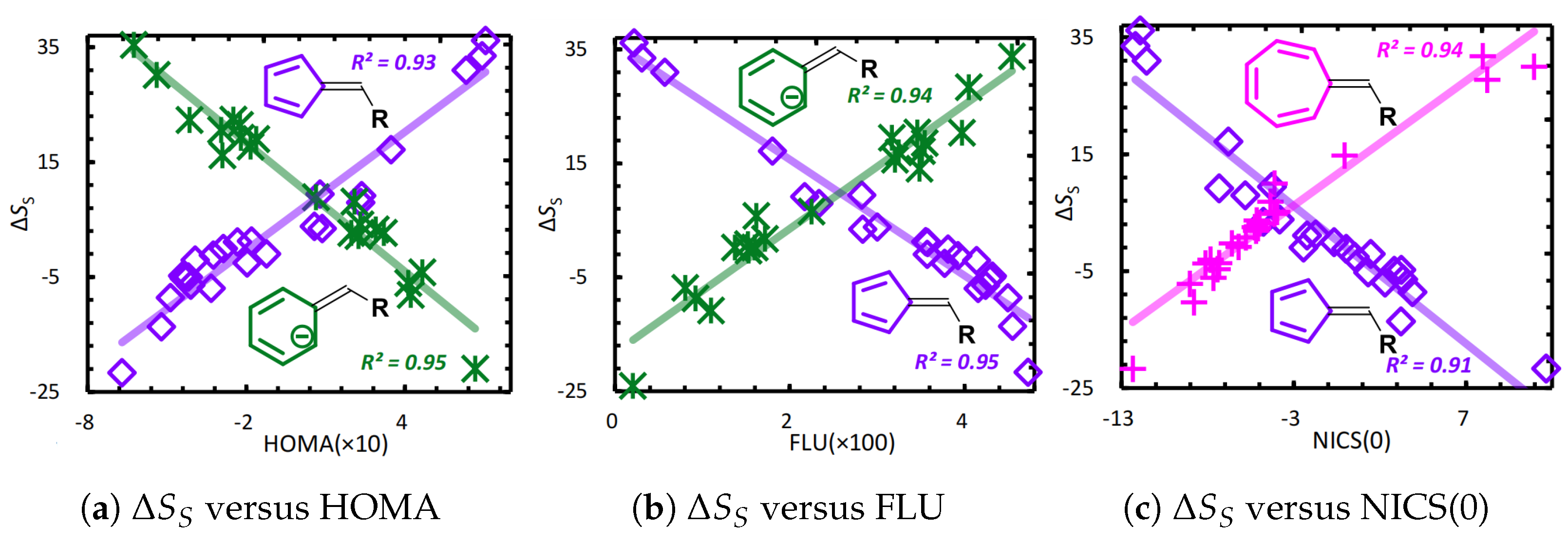
4.2. Information-Theoretic Approach Chemical Descriptors
Examples and Illustrations
- Global Descriptors: Assign a value to the entire system.
- Local Descriptors: Assign a value to each position in the system.
- Non-local Descriptors: Assign a value to each pair of positions in the system.
5. Quantum Information Theory in Quantum Chemistry
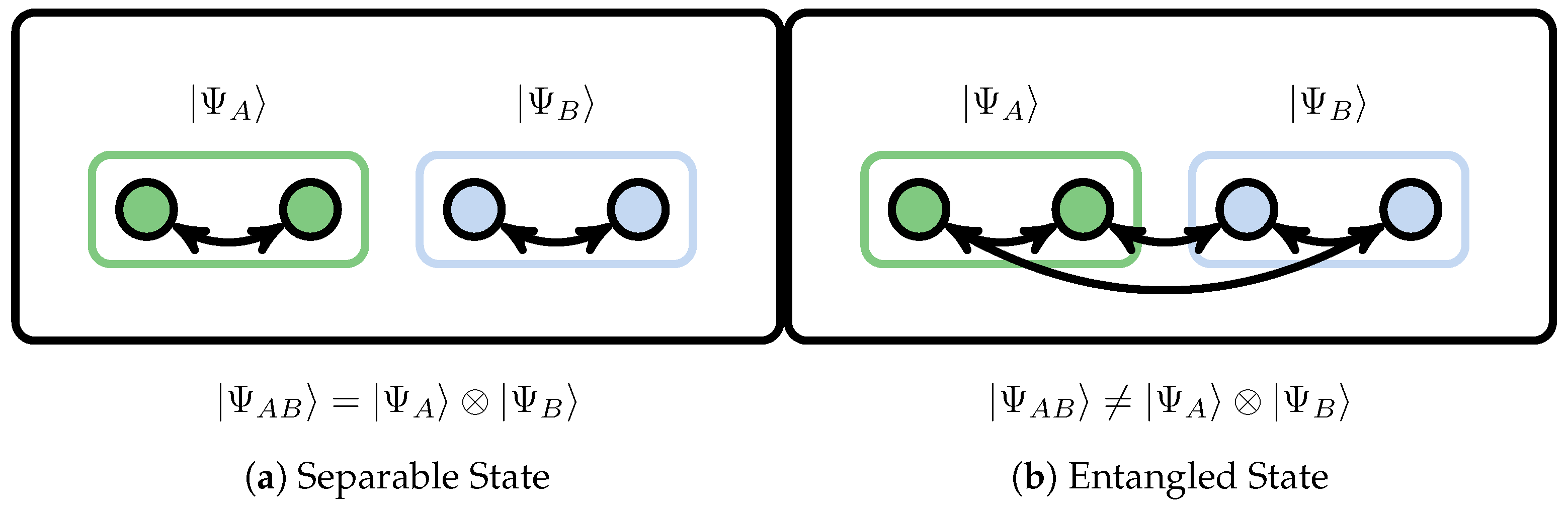
5.1. Bipartite Entanglement
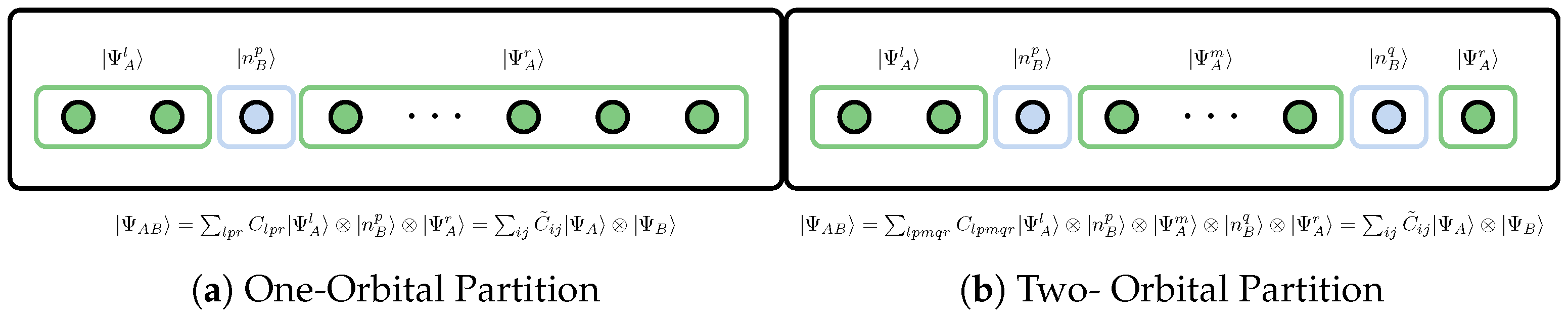
5.2. Orbital Reduced Density Matrix
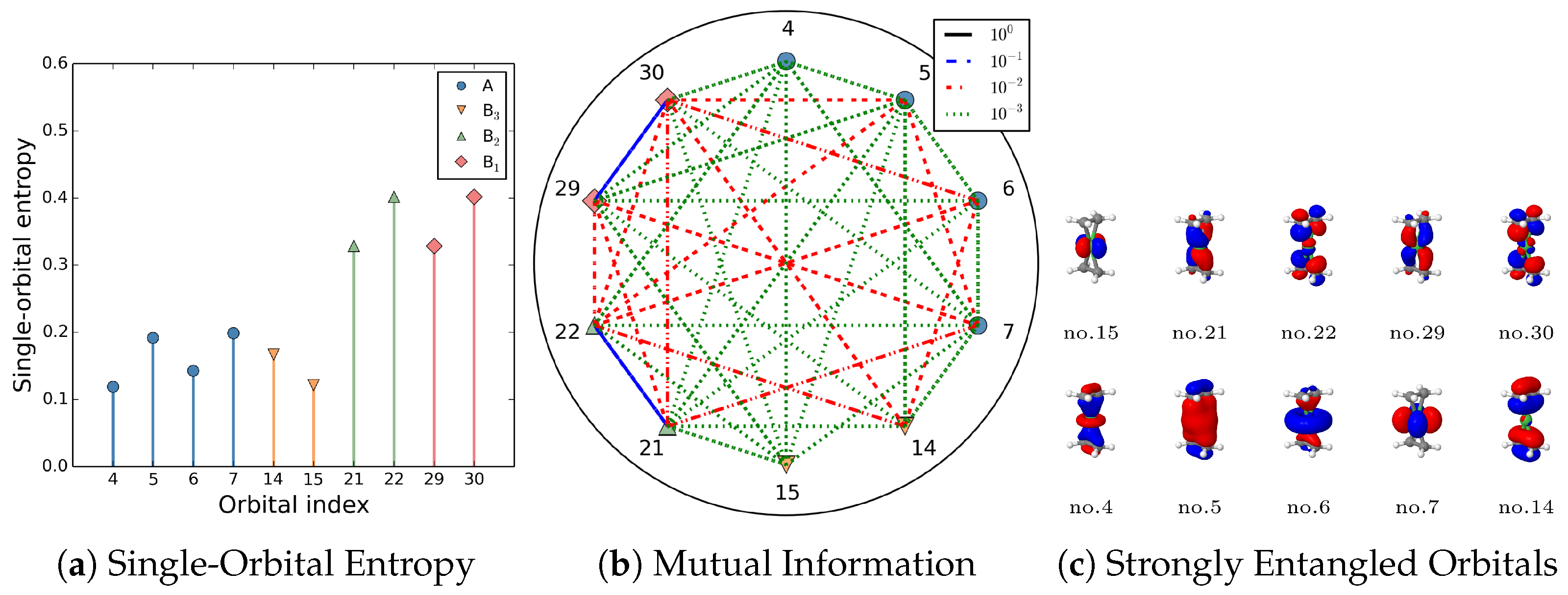
5.3. Orbital Entanglement
Examples and Illustrations
- Blue lines: Nondynamic correlated orbital pairs.
- Red lines: Static correlated orbitals.
- Green: Dynamic correlated orbitals.
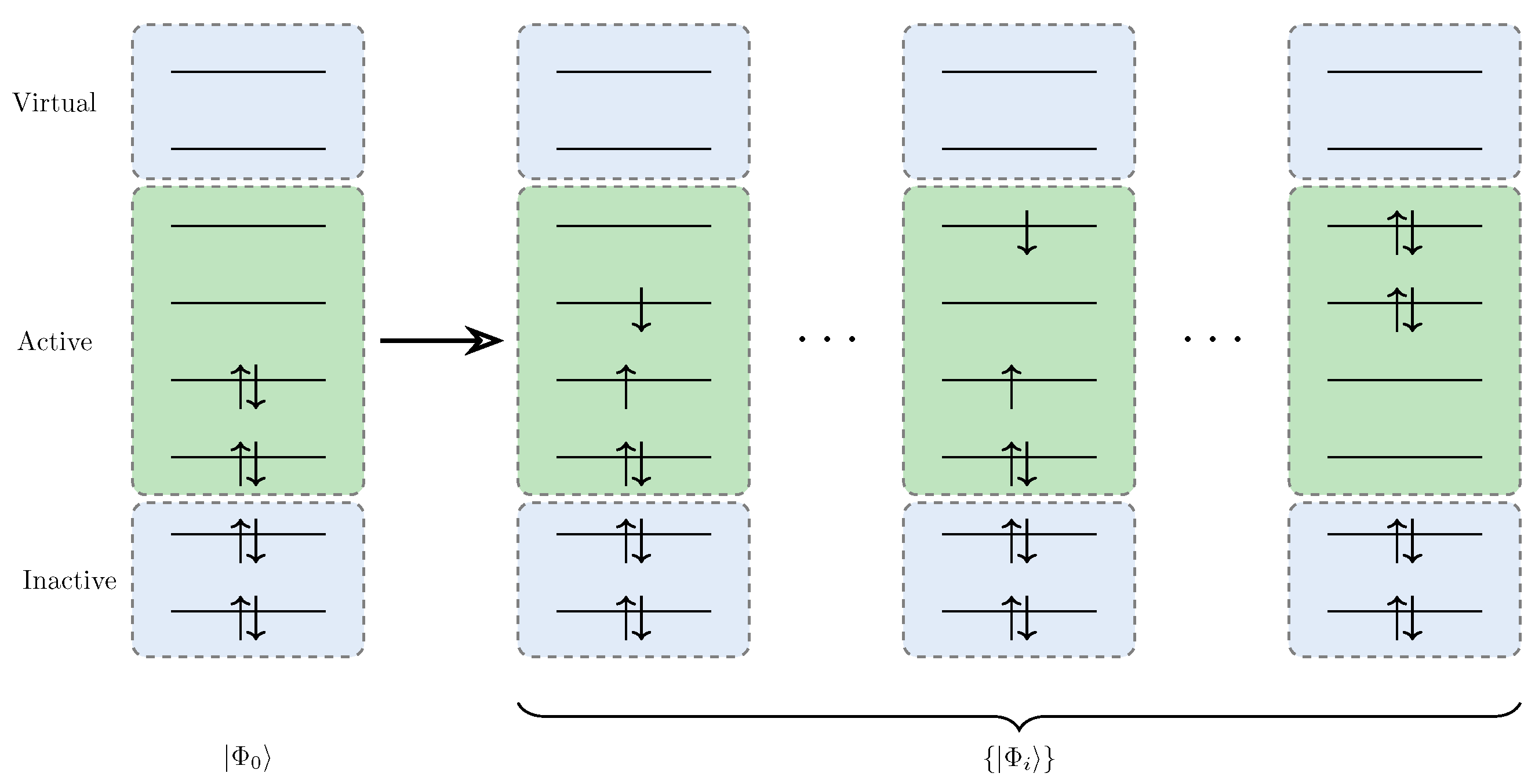
- Inactive space: Always doubly occupied.
- Active space: All the possible configurations are allowed.
- Virtual space: Always empty.
6. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Shannon entropy | |
| Relative entropy, Kullback–Leibler divergence | |
| Joint entropy | |
| Conditional entropy | |
| Mutual information | |
| Density matrix, Density operator | |
| k-Electron reduced density matrix with spin and spatial orbital | |
| Electron density at position | |
| Unit-normalized electron density (shape function) at position | |
| Pair-electron density at position and | |
| Unit-normalized pair-electron density at position and | |
| Shannon entropy with electron density | |
| Relative entropy with electron density | |
| Joint entropy with electron density | |
| Conditional entropy with electron density | |
| Mutual information with electron density | |
| k-Orbital reduced density matrix | |
| One-orbital entropy | |
| Orbital relative entropy | |
| Two-orbital entropy | |
| Orbital conditional entropy | |
| Orbital mutual information |
References
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Nyquist, H. Certain factors affecting telegraph speed. Bell Syst. Tech. J. 1924, 3, 324–346. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Ltd: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Witten, E. A mini-introduction to information theory. Riv. Nuovo Cim. 2020, 43, 187–227. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1995. [Google Scholar] [CrossRef]
- Helgaker, T.; Jørgensen, P.; Olsen, J. Molecular Electronic-Structure Theory; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Liu, S. Information-Theoretic Approach in Density Functional Reactivity Theory. Acta Phys.-Chim. Sin. 2016, 32, 98–118. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, Y.; He, X.; Li, Y.; Ayers, P.W.; Liu, S. Accurate and Efficient Prediction of Post-Hartree–Fock Polarizabilities of Condensed-Phase Systems. J. Chem. Theory Comput. 2023, 19, 6461–6470. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, Y.; He, X.; Ayers, P.W.; Liu, S. Efficient and accurate density-based prediction of macromolecular polarizabilities. Phys. Chem. Chem. Phys. 2023, 25, 2131–2141. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, Y.; Xu, E.; Liu, W.; Ayers, P.W.; Liu, S.; Chen, D. Fragment-Based Deep Learning for Simultaneous Prediction of Polarizabilities and NMR Shieldings of Macromolecules and Their Aggregates. J. Chem. Theory Comput. 2024, 20, 2655–2665. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, D.; Liu, S.; Rong, C.; Ayers, P.W. Why are information-theoretic descriptors powerful predictors of atomic and molecular polarizabilities. J. Mol. Model. 2024, 30, 361. [Google Scholar] [CrossRef]
- Rong, C.; Zhao, D.; He, X.; Liu, S. Development and Applications of the Density-Based Theory of Chemical Reactivity. J. Phys. Chem. Lett. 2022, 13, 11191–11200. [Google Scholar] [CrossRef]
- Liu, S. Identity for Kullback-Leibler divergence in density functional reactivity theory. J. Chem. Phys. 2019, 151, 141103. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Scholes, G.D. Foundations of Quantum Information for Physical Chemistry. J. Phys. Chem. Lett. 2024, 15, 4056–4069. [Google Scholar] [CrossRef] [PubMed]
- Materia, D.; Ratini, L.; Angeli, C.; Guidoni, L. Quantum Information reveals that orbital-wise correlation is essentially classical in Natural Orbitals. arXiv 2024, arXiv:2404.14093. [Google Scholar] [CrossRef] [PubMed]
- Aliverti-Piuri, D.; Chatterjee, K.; Ding, L.; Liao, K.; Liebert, J.; Schilling, C. What can quantum information theory offer to quantum chemistry? Faraday Discuss. 2024, 254, 76–106. [Google Scholar] [CrossRef]
- Nowak, A.; Legeza, O.; Boguslawski, K. Orbital entanglement and correlation from pCCD-tailored coupled cluster wave functions. J. Chem. Phys. 2021, 154, 084111. [Google Scholar] [CrossRef]
- Ding, L.; Mardazad, S.; Das, S.; Szalay, S.; Schollwöck, U.; Zimborás, Z.; Schilling, C. Concept of Orbital Entanglement and Correlation in Quantum Chemistry. J. Chem. Theory Comput. 2021, 17, 79–95. [Google Scholar] [CrossRef]
- Ratini, L.; Capecci, C.; Guidoni, L. Natural Orbitals and Sparsity of Quantum Mutual Information. J. Chem. Theory Comput. 2024, 20, 3535–3542. [Google Scholar] [CrossRef]
- Legeza, O.; Sòlyom, J. Optimizing the density-matrix renormalization group method using quantum information entropy. Phys. Rev. B 2003, 68, 195116. [Google Scholar] [CrossRef]
- Convy, I.; Huggins, W.; Liao, H.; Birgitta Whaley, K. Mutual information scaling for tensor network machine learning. Mach. Learn. Sci. Technol. 2022, 3, 015017. [Google Scholar] [CrossRef]
- Legeza, O.; Sólyom, J. Two-Site Entropy and Quantum Phase Transitions in Low-Dimensional Models. Phys. Rev. Lett. 2006, 96, 116401. [Google Scholar] [CrossRef]
- Szalay, S.; Pfeffer, M.; Murg, V.; Barcza, G.; Verstraete, F.; Schneider, R.; Legeza, O. Tensor product methods and entanglement optimization for ab initio quantum chemistry. Int. J. Quantum Chem. 2015, 115, 1342–1391. [Google Scholar] [CrossRef]
- Sears, S.B.; Parr, R.G.; Dinur, U. On the Quantum-Mechanical Kinetic Energy as a Measure of the Information in a Distribution. Isr. J. Chem. 1980, 19, 165–173. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Parr, R.G. Information theory, atoms in molecules, and molecular similarity. Proc. Natl. Acad. Sci. USA 2000, 97, 8879–8882. [Google Scholar] [CrossRef] [PubMed]
- Nalewajski, R.F.; Parr, R.G. Information Theory Thermodynamics of Molecules and Their Hirshfeld Fragments. J. Phys. Chem. A 2001, 105, 7391–7400. [Google Scholar] [CrossRef]
- Levine, R.D.; Bernstein, R.B. Energy disposal and energy consumption in elementary chemical reactions. Information theoretic approach. Acc. Chem. Res. 1974, 7, 393–400. [Google Scholar] [CrossRef]
- Procaccia, I.; Levine, R.D. The populations time evolution in vibrational disequilibrium: An information theoretic approach with application to HF. J. Chem. Phys. 1975, 62, 3819–3820. [Google Scholar] [CrossRef]
- Dinur, U.; Kosloff, R.; Levine, R.; Berry, M. Analysis of electronically nonadiabatic chemical reactions: An information theoretic approach. Chem. Phys. Lett. 1975, 34, 199–205. [Google Scholar] [CrossRef]
- Procaccia, I.; Levine, R.D. Vibrational energy transfer in molecular collisions: An information theoretic analysis and synthesis. J. Chem. Phys. 1975, 63, 4261–4279. [Google Scholar] [CrossRef]
- Levine, R.D.; Manz, J. The effect of reagent energy on chemical reaction rates: An information theoretic analysis. J. Chem. Phys. 1975, 63, 4280–4303. [Google Scholar] [CrossRef]
- Levine, R.D. Entropy and macroscopic disequilibrium. II. The information theoretic characterization of Markovian relaxation processes. J. Chem. Phys. 1976, 65, 3302–3315. [Google Scholar] [CrossRef]
- Levine, R.D. Information Theory Approach to Molecular Reaction Dynamics. Ann. Rev. Phys. Chem. 1978, 29, 59–92. [Google Scholar] [CrossRef]
- Slater, J.C. The Theory of Complex Spectra. Phys. Rev. 1929, 34, 1293–1322. [Google Scholar] [CrossRef]
- Hartree, D.R. Some Relations between the Optical Spectra of Different Atoms of the same Electronic Structure. II. Aluminium-like and Copper-like Atoms. Math. Proc. Camb. Phil. Soc. 1926, 23, 304–326. [Google Scholar] [CrossRef]
- Fock, V.A.Z. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148. [Google Scholar] [CrossRef]
- Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
- Koga, T.; Tatewaki, H.; Thakkar, A.J. Roothaan-Hartree-Fock wave functions for atoms with Z ≤ 54. Phys. Rev. A 1993, 47, 4510–4512. [Google Scholar] [CrossRef]
- Purvis, G.D.; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Shavitt, I. The history and evolution of configuration interaction. Mol. Phys. 1998, 94, 3–17. [Google Scholar] [CrossRef]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics: Theory and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Cooper, N.R.; Leese, M.R. Configuration interaction methods in molecular quantum chemistry. J. Mol. Struct.-Theochem. 2000, 94, 71–78. [Google Scholar]
- Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477–485. [Google Scholar] [CrossRef]
- Ahlrichs, R. Many body perturbation calculations and coupled electron pair models. Comput. Phys. Commun. 1979, 17, 31–45. [Google Scholar] [CrossRef]
- Bartlett, R.J. Many-body perturbation-theory and coupled cluster theory for electron correlation in molecules. Annu. Rev. Phys. Chem. 1981, 32, 359–401. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Asadchev, A.; Gordon, M.S. Fast and Flexible Coupled Cluster Implementation. J. Chem. Theory Comput. 2013, 9, 3385–3392. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Cremer, D. Møller–Plesset perturbation theory: From small molecule methods to methods for thousands of atoms. WIREs Comput. Mol. Sci. 2011, 1, 509–530. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1–20. [Google Scholar] [CrossRef]
- Engel, E.; Dreizler, R.M. Density Functional Theory: An Advanced Course; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Onicescu, O. Theorie de l’information energie informationelle. Comptes Rendus l’Acad. Sci. Ser. AB 1966, 263, 841–842. [Google Scholar]
- Rényi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Fisher, R.A. Theory of Statistical Estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat—Scholar’s Choice Edition; Creative Media Partners, LLC: Burbank, CA, USA, 2015. [Google Scholar]
- Accardi, L. Topics in quantum probability. Phys. Rep. 1981, 77, 169–192. [Google Scholar] [CrossRef]
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B Methodol. 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Liese, F.; Vajda, I. On divergences and informations in statistics and information theory. IEEE Trans. Inform. Theory 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Burago, D.; Burago, J.D.; Ivanov, S. A Course in Metric Geometry; American Mathematical Society: Providence, RI, USA, 2001. [Google Scholar]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Math. Proc. Camb. Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- Mazziotti, D.A. (Ed.) Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules, 1st ed.; Advances in Chemical Physics; Wiley: Hoboken, NJ, USA, 2007; Volume 134. [Google Scholar] [CrossRef]
- Gidopoulos, N.I.; Wilson, S.; Lipscomb, W.N.; Maruani, J.; Wilson, S. (Eds.) The Fundamentals of Electron Density, Density Matrix and Density Functional Theory in Atoms, Molecules and the Solid State; Progress in Theoretical Chemistry and Physics; Springer: Dordrecht, The Netherlands, 2003; Volume 14. [Google Scholar] [CrossRef]
- Absar, I. Reduced hamiltonian orbitals. II. Optimal orbital basis sets for the many-electron problem. Int. J. Quantum Chem. 1978, 13, 777–790. [Google Scholar] [CrossRef]
- Absar, I.; Coleman, A.J. Reduced hamiltonian orbitals. I. a new approach to the many-electron problem. Int. J. Quantum Chem. 2009, 10, 319–330. [Google Scholar] [CrossRef]
- Coleman, A.J.; Absar, I. Reduced hamiltonian orbitals. III. Unitarily invariant decomposition of hermitian operators. Int. J. Quantum Chem. 1980, 18, 1279–1307. [Google Scholar] [CrossRef]
- Mazziotti, D.A. Two-Electron Reduced Density Matrix as the Basic Variable in Many-Electron Quantum Chemistry and Physics. Chem. Rev. 2012, 112, 244–262. [Google Scholar] [CrossRef]
- Mazziotti, D.A. Parametrization of the two-electron reduced density matrix for its direct calculation without the many-electron wave function: Generalizations and applications. Phys. Rev. A 2010, 81, 062515. [Google Scholar] [CrossRef]
- Eugene DePrince III, A. Variational determination of the two-electron reduced density matrix: A tutorial review. WIREs Comput. Mol. Sci. 2024, 14, e1702. [Google Scholar] [CrossRef]
- Barcza, G.; Legeza, O.; Marti, K.H.; Reiher, M. Quantum-Information Analysis of Electronic States of Different Molecular Structures. Phys. Rev. A 2011, 83, 012508. [Google Scholar] [CrossRef]
- Szalay, S.; Barcza, G.; Szilvasi, T.; Veis, L.; Legeza, O. The Correlation Theory of the Chemical Bond. Sci. Rep. 2017, 7, 2237. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Kubo, R. Generalized Cumulant Expansion Method. J. Phys. Soc. Jpn. 1962, 17, 1100–1120. [Google Scholar] [CrossRef]
- Ziesche, P. Cumulant Expansions of Reduced Densities, Reduced Density Matrices, and Green’s Functions. In Many-Electron Densities and Reduced Density Matrices; Cioslowski, J., Ed.; Kluwer: New York, NY, USA, 2000; pp. 33–56. [Google Scholar]
- Alcoba, D.R.; Valdemoro, C. Family of modified-contracted Schrödinger equations. Phys. Rev. A 2001, 64, 062105. [Google Scholar] [CrossRef]
- Valdemoro, C.; Alcoba, D.R.; Tel, L.M.; Perez-Romero, E. Imposing Bounds on the High-Order Reduced Density Matrices Elements. Int. J. Quantum Chem. 2001, 85, 214–224. [Google Scholar] [CrossRef]
- Valdemoro, C. Spin-Adapted Reduced Hamiltonians 2. Total Energy and Reduced Density Matrices. Phys. Rev. A 1985, 31, 2123–2128. [Google Scholar] [CrossRef] [PubMed]
- Valdemoro, C. Spin-Adapted Reduced Hamiltonians. 1. Elementary Excitations. Phys. Rev. A 1985, 31, 2114–2122. [Google Scholar] [CrossRef] [PubMed]
- Mazziotti, D.A. Contracted Schrödinger equation: Determining quantum energies and two-particle density matrices without wave functions. Phys. Rev. A 1998, 57, 4219–4234. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Cumulant expansion of the reduced density matrices. J. Chem. Phys. 1999, 110, 2800–2809. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Irreducible Brillouin conditions and contracted Schrödinger equations for n-electron systems. II. Spin-free formulation. J. Chem. Phys. 2002, 116, 4787–4801. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Irreducible Brillouin conditions and contracted Schrödinger equations for n-electron systems. III. Systems of noninteracting electrons. J. Chem. Phys. 2004, 120, 7340–7349. [Google Scholar] [CrossRef]
- Mukherjee, D.; Kutzelnigg, W. Irreducible Brillouin conditions and contracted Schrödinger equations for n-electron systems. I. The equations satisfied by the density cumulants. J. Chem. Phys. 2001, 114, 2047–2061. [Google Scholar] [CrossRef]
- Nooijen, M.; Wladyslawski, M.; Hazra, A. Cumulant approach to the direct calculation of reduced density matrices: A critical analysis. J. Chem. Phys. 2003, 118, 4832–4848. [Google Scholar] [CrossRef]
- Levy, M. Universal Variational Functionals of Electron-Densities, 1st- Order Density-Matrices, and Natural Spin-Orbitals and Solution of the V-Representability Problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef]
- Kohn, W.; Becke, A.D.; Parr, R.G. Density Functional Theory of Electronic Structure. J. Phys. Chem. 1996, 100, 12974–12980. [Google Scholar] [CrossRef]
- Ayers, P.W. Axiomatic Formulations of the Hohenberg-Kohn Functional. Phys. Rev. A 2006, 73. [Google Scholar] [CrossRef]
- Ayers, P.W. Using classical many-body structure to determine electronic structure: An approach using k-electron distribution functions. Phys. Rev. A 2006, 74, 042502. [Google Scholar] [CrossRef]
- Ziesche, P. Attempts toward a pair density functional theory. Int. J. Quantum Chem. 1996, 60, 1361–1374. [Google Scholar] [CrossRef]
- Ziesche, P. Pair density functional theory—A generalized density functional theory. Phys. Lett. A 1994, 195, 213–220. [Google Scholar] [CrossRef]
- Nagy, Á. Spherically and system-averaged pair density functional theory. J. Phys. Chem. 2006, 125, 184104. [Google Scholar] [CrossRef]
- Nagy, Á. Time-Dependent Pair Density from the Principle of Minimum Fisher Information. J. Mol. Model. 2018, 24, 234. [Google Scholar] [CrossRef]
- Levy, M.; Ziesche, P. The pair density functional of the kinetic energy and its simple scaling property. J. Chem. Phys. 2001, 115, 9110–9112. [Google Scholar] [CrossRef]
- Ayers, P.W. Generalized Density Functional Theories Using the K-Electron Densities: Development of Kinetic Energy Functionals. J. Math. Phys. 2005, 46, 062107. [Google Scholar] [CrossRef]
- Cuevas-Saavedra, R.; Ayers, P.W. Coordinate scaling of the kinetic energy in pair density functional theory: A Legendre transform approach. Int. J. Quantum Chem. 2009, 109, 1699–1705. [Google Scholar] [CrossRef]
- Ayers, P.W.; Golden, S.; Levy, M. Generalizations of the Hohenberg-Kohn Theorem: I. Legendre Transform Constructions of Variational Principles for Density Matrices and Electron Distribution Functions. J. Chem. Phys. 2006, 124, 054101. [Google Scholar] [CrossRef]
- Ayers, P.W.; Davidson, E.R. Linear Inequalities for Diagonal Elements of Density Matrices. In Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2007; Chapter 16; pp. 443–483. [Google Scholar] [CrossRef]
- Keyvani, Z.A.; Shahbazian, S.; Zahedi, M. To What Extent are “Atoms in Molecules” Structures of Hydrocarbons Reproducible from the Promolecule Electron Densities? Chem. Eur. J. 2016, 22, 5003–5009. [Google Scholar] [CrossRef]
- Spackman, M.A.; Maslen, E.N. Chemical properties from the promolecule. J. Phys. Chem. 1986, 90, 2020–2027. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Act. 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. XVII. Spatial Partitioning of Charge Density. Isr. J. Chem. 1977, 16, 198–201. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Switka, E. Information Theoretic Approach to Molecular and Reactive Systems. Phys. Chem. Chem. Phys. 2002, 4, 4952–4958. [Google Scholar] [CrossRef]
- Nalewajski, R.F. Information Principles in the Theory of Electronic Structure. Chem. Phys. Lett. 2003, 372, 28–34. [Google Scholar] [CrossRef]
- Nagy, Á.; Romera, E. Relative Rényi entropy and fidelity susceptibility. Europhys. Lett. 2015, 109, 60002. [Google Scholar] [CrossRef]
- Nagy, Á. Relative information in excited-state orbital-free density functional theory. Int. J. Quantum Chem. 2020, 120, e26405. [Google Scholar] [CrossRef]
- Laguna, H.G.; Salazar, S.J.C.; Sagar, R.P. Entropic Kullback-Leibler Type Distance Measures for Quantum Distributions. Int. J. Quantum Chem. 2019, 119, e25984. [Google Scholar] [CrossRef]
- Borgoo, A.; Jaque, P.; Toro-Labbe, A.; Van Alsenoy, C.; Geerlings, P. Analyzing Kullback-Leibler Information Profiles: An Indication of Their Chemical Relevance. Phys. Chem. Chem. Phys. 2009, 11, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Bartolotti, L.J. Some remarks on the density functional theory of few-electron systems. J. Phys. Chem. 1983, 87, 2810–2815. [Google Scholar] [CrossRef]
- Ayers, P.W. Density per particle as a descriptor of Coulombic systems. Proc. Natl. Acad. Sci. USA 2000, 97, 1959–1964. [Google Scholar] [CrossRef] [PubMed]
- Ayers, P.W. Information Theory, the Shape Function, and the Hirshfeld Atom. Theor. Chem. Acc. 2006, 115, 370–378. [Google Scholar] [CrossRef]
- Ayers, P.W.; Cedillo, A. The Shape Function. In Chemical Reactivity Theory: A Density Functional View; Chattaraj, P.K., Ed.; Taylor and Francis: Boca Raton, FL, USA, 2009; Chapter 19; p. 269. [Google Scholar] [CrossRef]
- Noorizadeh, S.; Shakerzadeh, E. Shannon entropy as a new measure of aromaticity, Shannon aromaticity. Phys. Chem. Chem. Phys. 2010, 12, 4742–4749. [Google Scholar] [CrossRef]
- Yu, D. Studying on Aromaticity Using Information-Theoretic Approach in Density Functional Reactivity Theory. Ph.D. Thesis, Hunan Normal University, Changsha, China, 2019. [Google Scholar]
- Yu, D.; Stuyver, T.; Rong, C.; Alonso, M.; Lu, T.; De Proft, F.; Geerlings, P.; Liu, S. Global and local aromaticity of acenes from the information-theoretic approach in density functional reactivity theory. Phys. Chem. Chem. Phys. 2019, 21, 18195–18210. [Google Scholar] [CrossRef]
- Li, M.; Wan, X.; Rong, C.; Zhao, D.; Liu, S. Directionality and additivity effects of molecular acidity and aromaticity for substituted benzoic acids under external electric fields. Phys. Chem. Chem. Phys. 2023, 25, 27805–27816. [Google Scholar] [CrossRef]
- Rong, C.; Wang, B.; Zhao, D.; Liu, S. Information-theoretic approach in density functional theory and its recent applications to chemical problems. WIREs Comput. Mol. Sci. 2020, 10, e1461. [Google Scholar] [CrossRef]
- Liu, S. On the relationship between densities of Shannon entropy and Fisher information for atoms and molecules. J. Chem. Phys. 2007, 126, 191107. [Google Scholar] [CrossRef]
- Nalevajski, R.F. On phase/current components of entropy/information descriptors of molecular states. Mol. Phys. 2014, 112, 2587–2601. [Google Scholar] [CrossRef]
- Nalewajski, R. Phase/current information descriptors and equilibrium states in molecules. Int. J. Quantum Chem. 2014, 115, 1274–1288. [Google Scholar] [CrossRef]
- Nalewajski, R.F. Resultant Information Description of Electronic States and Chemical Processes. J. Phys. Chem. A 2019, 123, 9737–9752. [Google Scholar] [CrossRef]
- Nalewajski, R.F. Information-Theoretic Descriptors of Molecular States and Electronic Communications between Reactants. Entropy 2020, 22, 749. [Google Scholar] [CrossRef] [PubMed]
- Nalewajski, R.F. Information origins of the chemical bond: Bond descriptors from molecular communication channels in orbital resolution. Int. J. Quantum Chem. 2009, 109, 2495–2506. [Google Scholar] [CrossRef]
- Liu, S.; Rong, C.; Lu, T. Information Conservation Principle Determines Electrophilicity, Nucleophilicity, and Regioselectivity. J. Phys. Chem. A 2014, 118, 3698–3704. [Google Scholar] [CrossRef]
- Liu, S. Quantifying Reactivity for Electrophilic Aromatic Substitution Reactions with Hirshfeld Charge. J. Phys. Chem. A 2015, 119, 3107–3111. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of .pi.-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Matito, E.; Duran, M.; Solà, M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem. Phys. 2004, 122, 014109. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhao, D.; Liu, S.; Rong, C.; Ayers, P.W. Extending the information-theoretic approach from the (one) electron density to the pair density. J. Chem. Phys. 2025. accepted for publication. [Google Scholar]
- Sagar, R.P.; Guevara, N.L. Mutual information and correlation measures in atomic systems. J. Chem. Phys. 2005, 123, 044108. [Google Scholar] [CrossRef] [PubMed]
- Heinosaari, T.; Ziman, M. The Mathematical Language of Quantum Theory: From Uncertainty to Entanglement, 1st ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Ciarlet, P.G.; Lions, J.L. In Computational Chemistry: Reviews of Current Trends. In Computational Chemistry: Reviews of Current Trends; North-Holland: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics. IV, Analysis of Operators; Academic Press: London, UK, 1978. [Google Scholar]
- Yserentant, H. On the regularity of the electronic Schrödinger equation in Hilbert spaces of mixed derivatives. Numer. Math. 2004, 98, 731–759. [Google Scholar] [CrossRef]
- Islam, R.; Ma, R.; Preiss, P.M.; Eric Tai, M.; Lukin, A.; Rispoli, M.; Greiner, M. Measuring entanglement entropy in a quantum many-body system. Nature 2015, 528, 77–83. [Google Scholar] [CrossRef]
- Rissler, J.; Noack, R.M.; White, S.R. Measuring orbital interaction using quantum information theory. Chem. Phys. 2006, 323, 519–531. [Google Scholar] [CrossRef]
- Mazziotti, D.A. Entanglement, Electron Correlation, and Density Matrices, 1st ed.; Wiley: Hoboken, NJ, USA, 2007; Volume 134, pp. 493–535. [Google Scholar] [CrossRef]
- Boguslawski, K.; Tecmer, P.; Legeza, O.; Reiher, M. Entanglement Measures for Single- and Multireference Correlation Effects. J. Phys. Chem. Lett. 2012, 3, 3129–3135. [Google Scholar] [CrossRef]
- Boguslawski, K.; Tecmer, P. Orbital entanglement in quantum chemistry. Int. J. Quantum Chem. 2015, 115, 1289–1295. [Google Scholar] [CrossRef]
- Zhao, Y.; Boguslawski, K.; Tecmer, P.; Duperrouzel, C.; Barcza, G.; Legeza, O.; Ayers, P.W. Dissecting the bond-formation process of d 10-metal–ethene complexes with multireference approaches. Theor. Chem. Acc. 2015, 134, 120. [Google Scholar] [CrossRef]
- Duperrouzel, C.; Tecmer, P.; Boguslawski, K.; Barcza, G.; Örs, L.; Ayers, P.W. A quantum informational approach for dissecting chemical reactions. Chem. Phys. Lett. 2015, 621, 160–164. [Google Scholar] [CrossRef]
- Boguslawski, K.; Tecmer, P.; Legeza, O. Analysis of two-orbital correlations in wave functions restricted to electron-pair states. Phys. Rev. B 2016, 94, 155126. [Google Scholar] [CrossRef]
- Boguslawski, K.; Réal, F.; Tecmer, P.; Duperrouzel, C.; Pereira Gomes, A.S.; Legeza, Ö.; Ayers, P.W.; Vallet, V. On the multi-reference nature of plutonium oxides: PuO22+, PuO2, PuO3 and PuO2(OH)2. Phys. Chem. Chem. Phys. 2017, 19, 4317–4329. [Google Scholar] [CrossRef] [PubMed]
- Brandejs, J.; Veis, L.; Szalay, S.; Barcza, G.; Pittner, J.; Legeza, Ö. Quantum information-based analysis of electron-deficient bonds. J. Chem. Phys. 2019, 150, 204117. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.A.; Sarandy, M.S.; Lidar, D.A.; Sham, L.J. Linking entanglement and quantum phase transitions via density-functional theory. Phys. Rev. A 2006, 74, 052335. [Google Scholar] [CrossRef]
- Raghavachari, K.; Anderson, J.B. Electron Correlation Effects in Molecules. J. Phys. Chem. 1996, 100, 12960–12973. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef]
- White, S.R. Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 1993, 48, 10345–10356. [Google Scholar] [CrossRef]
- White, S.R.; Martin, R.L. Ab initio quantum chemistry using the density matrix renormalization group. J. Chem. Phys. 1999, 110, 4127–4130. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czech. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Fiedler, M. A property of eigenvectors of nonnegative symmetric matrices and its application to graph theory. Czech. Math. J. 1975, 25, 619–633. [Google Scholar] [CrossRef]
- Levine, B.G.; Durden, A.S.; Esch, M.P.; Liang, F.; Shu, Y. CAS without SCF—Why to use CASCI and where to get the orbitals. J. Chem. Phys. 2021, 154, 090902. [Google Scholar] [CrossRef] [PubMed]
- Stein, C.J.; Reiher, M. Automated Selection of Active Orbital Spaces. J. Chem. Theory Comput. 2016, 12, 1760–1771. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Knecht, S.; Schilling, C. Quantum Information-Assisted Complete Active Space Optimization (QICAS). J. Phys. Chem. Lett. 2023, 14, 11022–11029. [Google Scholar] [CrossRef] [PubMed]

| - | ||||
|---|---|---|---|---|
| - | 0 | 0 | 0 | |
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 |
| - | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | 1,1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 2,2 | 2,3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 3,2 | 3,3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 4,4 | 4,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 5,4 | 5,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 6,6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 7,7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8,8 | 8,9 | 8,10 | 8,11 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9,8 | 9,9 | 9,10 | 9,11 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10,8 | 10,9 | 10,10 | 10,11 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11,8 | 11,9 | 11,10 | 11,11 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12,12 | 12,13 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13,12 | 13,13 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14,14 | 14,15 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15,14 | 15,15 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16,16 |
| Correlation Effects | Intensity | a | |
|---|---|---|---|
| Nondynamic | Strong | >0.5 | ≈10−1 |
| Static | Medium | 0.5–0.1 | ≈10−1 |
| Dynamic | Weak | <0.1 | ≈10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhao, D.; Rong, C.; Liu, S.; Ayers, P.W. Information Theory Meets Quantum Chemistry: A Review and Perspective. Entropy 2025, 27, 644. https://doi.org/10.3390/e27060644
Zhao Y, Zhao D, Rong C, Liu S, Ayers PW. Information Theory Meets Quantum Chemistry: A Review and Perspective. Entropy. 2025; 27(6):644. https://doi.org/10.3390/e27060644
Chicago/Turabian StyleZhao, Yilin, Dongbo Zhao, Chunying Rong, Shubin Liu, and Paul W. Ayers. 2025. "Information Theory Meets Quantum Chemistry: A Review and Perspective" Entropy 27, no. 6: 644. https://doi.org/10.3390/e27060644
APA StyleZhao, Y., Zhao, D., Rong, C., Liu, S., & Ayers, P. W. (2025). Information Theory Meets Quantum Chemistry: A Review and Perspective. Entropy, 27(6), 644. https://doi.org/10.3390/e27060644







