Age of Information Minimization in Multicarrier-Based Wireless Powered Sensor Networks
Abstract
1. Introduction
1.1. Related Work
- Ref. [28] investigates a single-carrier system in contrast to this work, where we focus on a multicarrier system.
- Ref. [24] considers source nodes with embedded power supplies, whereas our work adopts WPT technology to energize these nodes.
- In contrast to the approach presented in [24], which aims to minimize the average total transmit power subject to per sensor AoI constraints, our work focuses on minimizing the long-term WAoI.
- In terms of optimization strategies, ref. [24] relies on conventional numerical methods. In contrast, our work pioneers a scheduling algorithm based on DRL. Moreover, while [28] employs the classical Deep Q-Network (DQN) algorithm, our research introduces a distinctly different DRL algorithm tailored to the specific challenges of our problem.
1.2. Contributions
- We formulate the problem of jointly optimizing subcarrier assignment, WET duration, and sensor sampling schedules to minimize the WAoI for diverse physical processes at the BS within a time-sensitive communication system. This is modeled as a multi-stage stochastic optimization problem, subject to energy causality constraints at the sensors.
- To address this optimization problem, we propose a novel dynamic control algorithm that integrates DRL and Lyapunov optimization techniques. Specifically, Lyapunov optimization is employed to decompose the multi-stage stochastic problem into a sequence of deterministic optimization problems, one for each time block. Subsequently, a DRL algorithm is utilized to determine the optimal scheduling decisions for each time block, with action exploration facilitated by a randomization policy.
- Extensive simulation results demonstrate the significant performance gains of our proposed algorithm in reducing the WAoI compared to benchmark algorithms, including the DQN, energy-based greedy, and AoI-based greedy schemes. Notably, our DRL algorithm exhibits good convergence performance and eliminates the need for a predefined upper limit for AoI values, unlike the DQN approach.
2. System Model and Problem Formulation
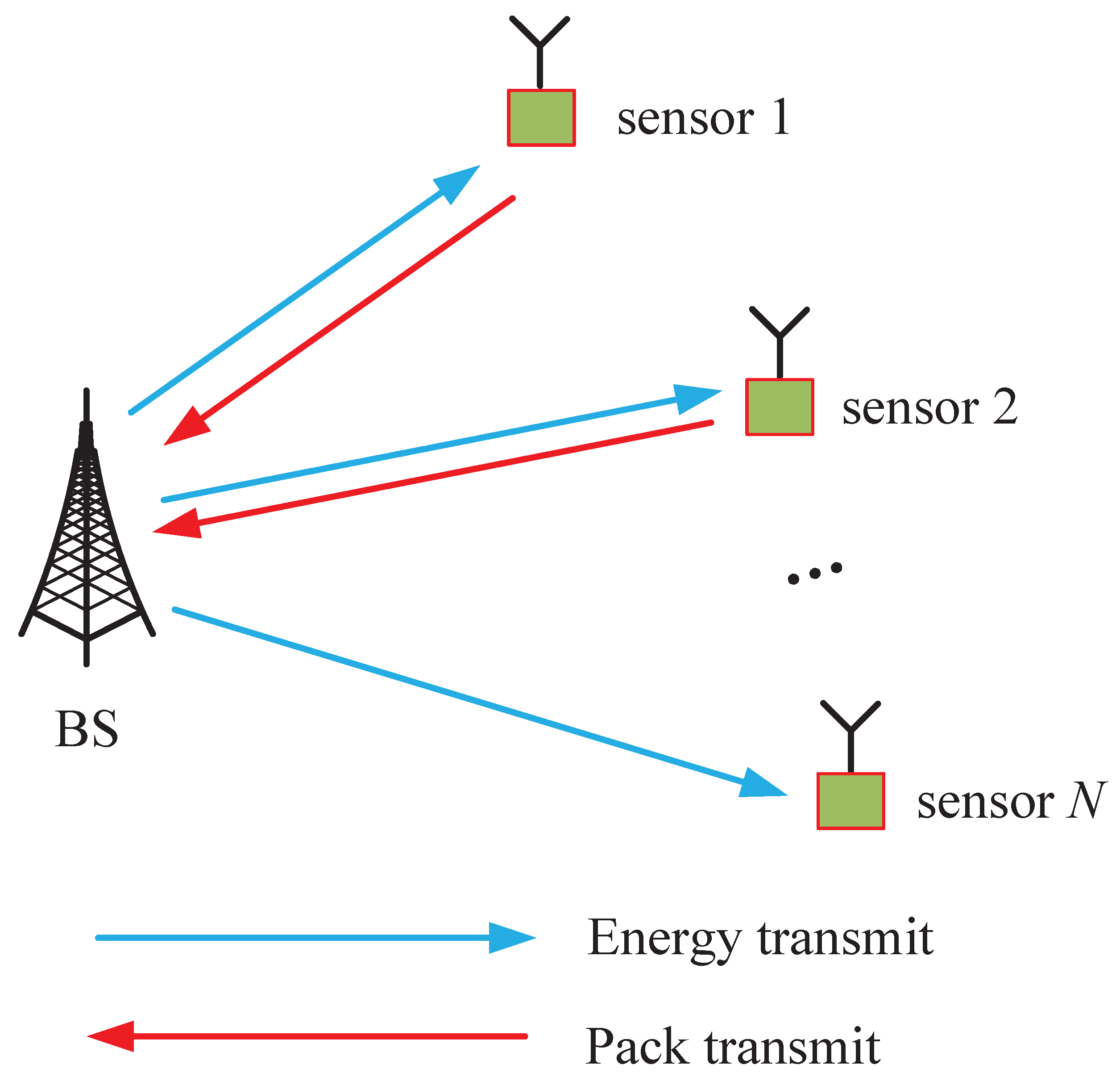
2.1. Network Model
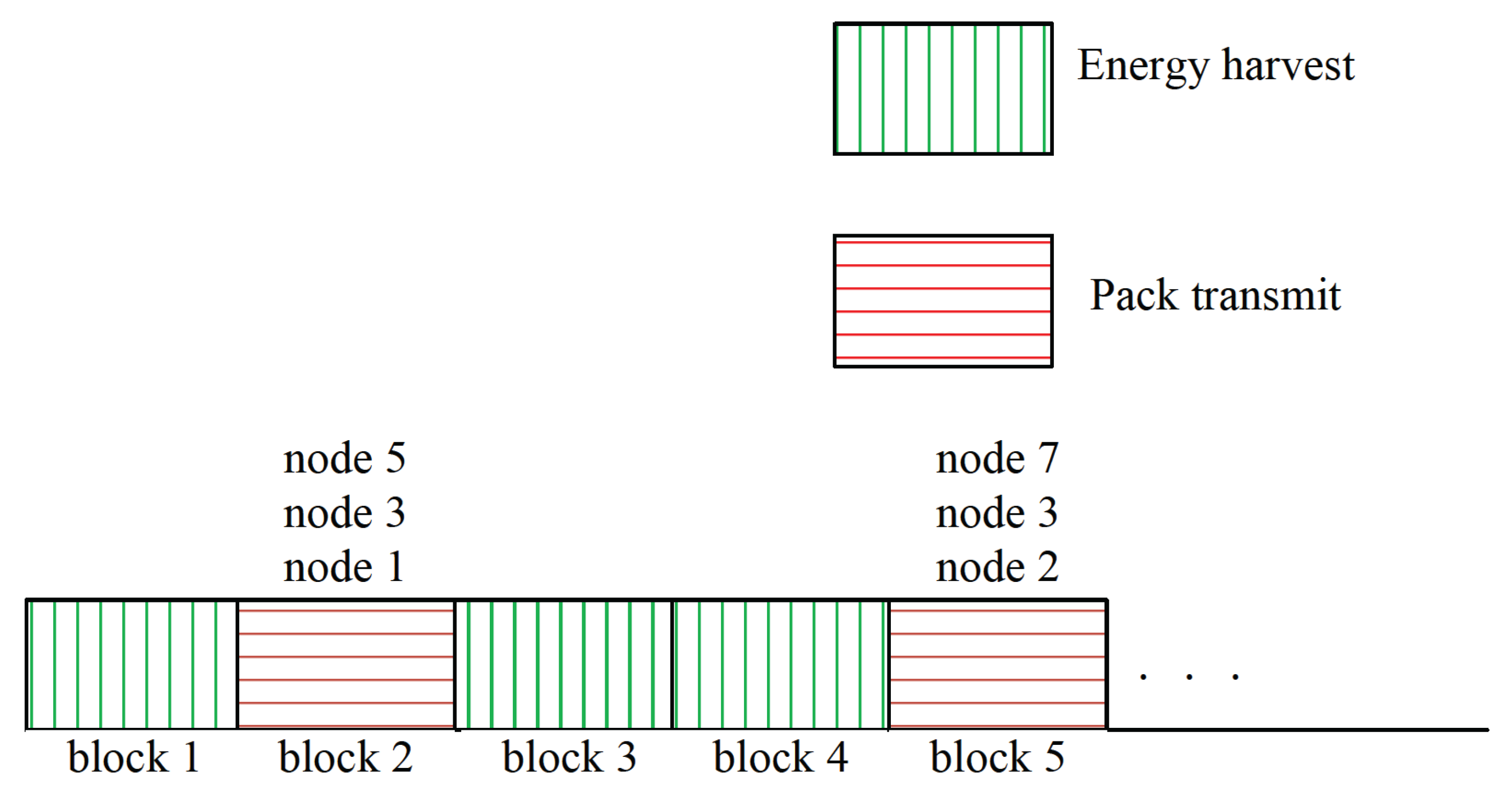
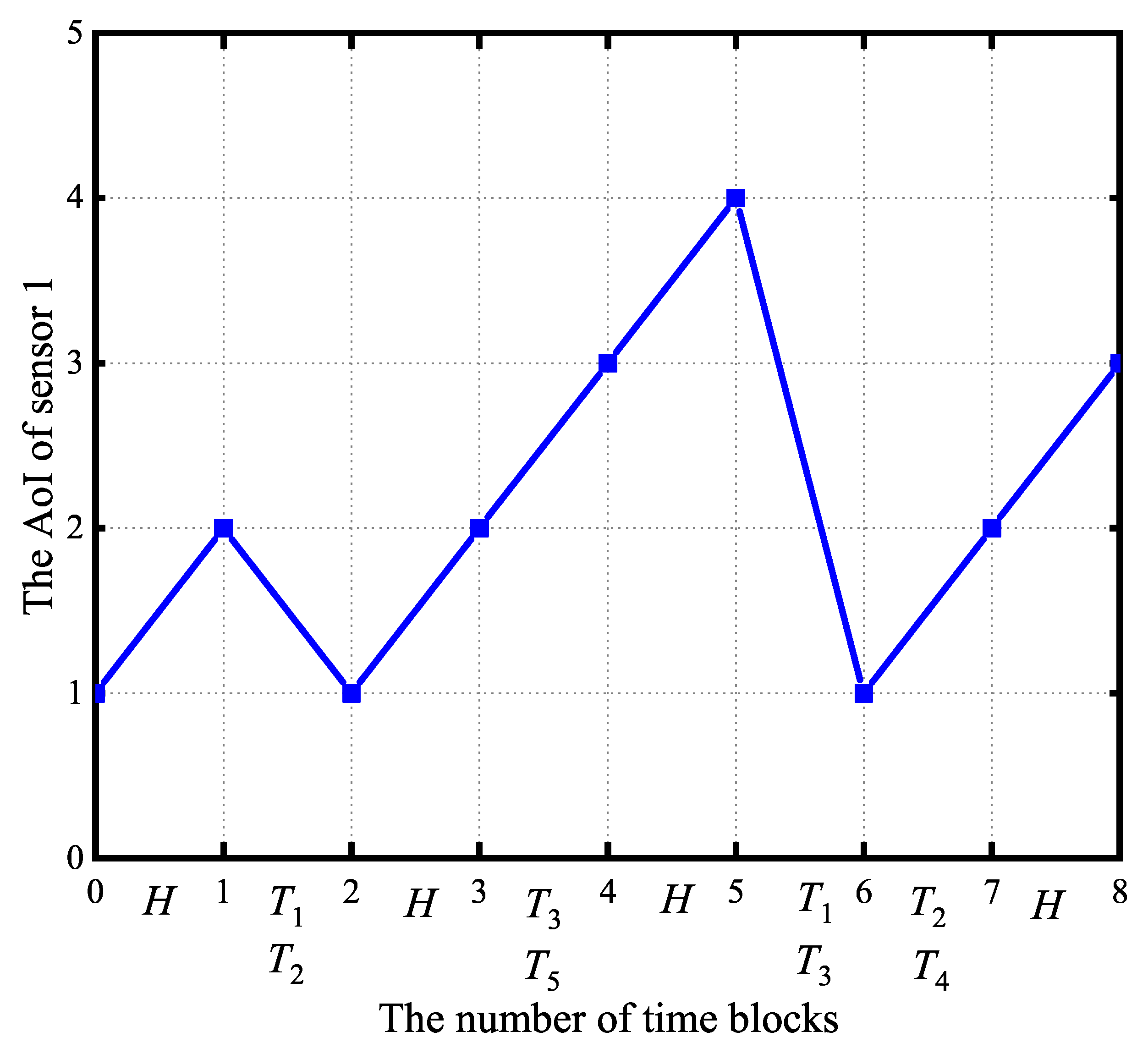
2.2. State and Action Spaces
2.3. Problem Formulation
3. The Decoupling Strategy for Multi-Stage Stochastic Optimization Based on Lyapunov Theory
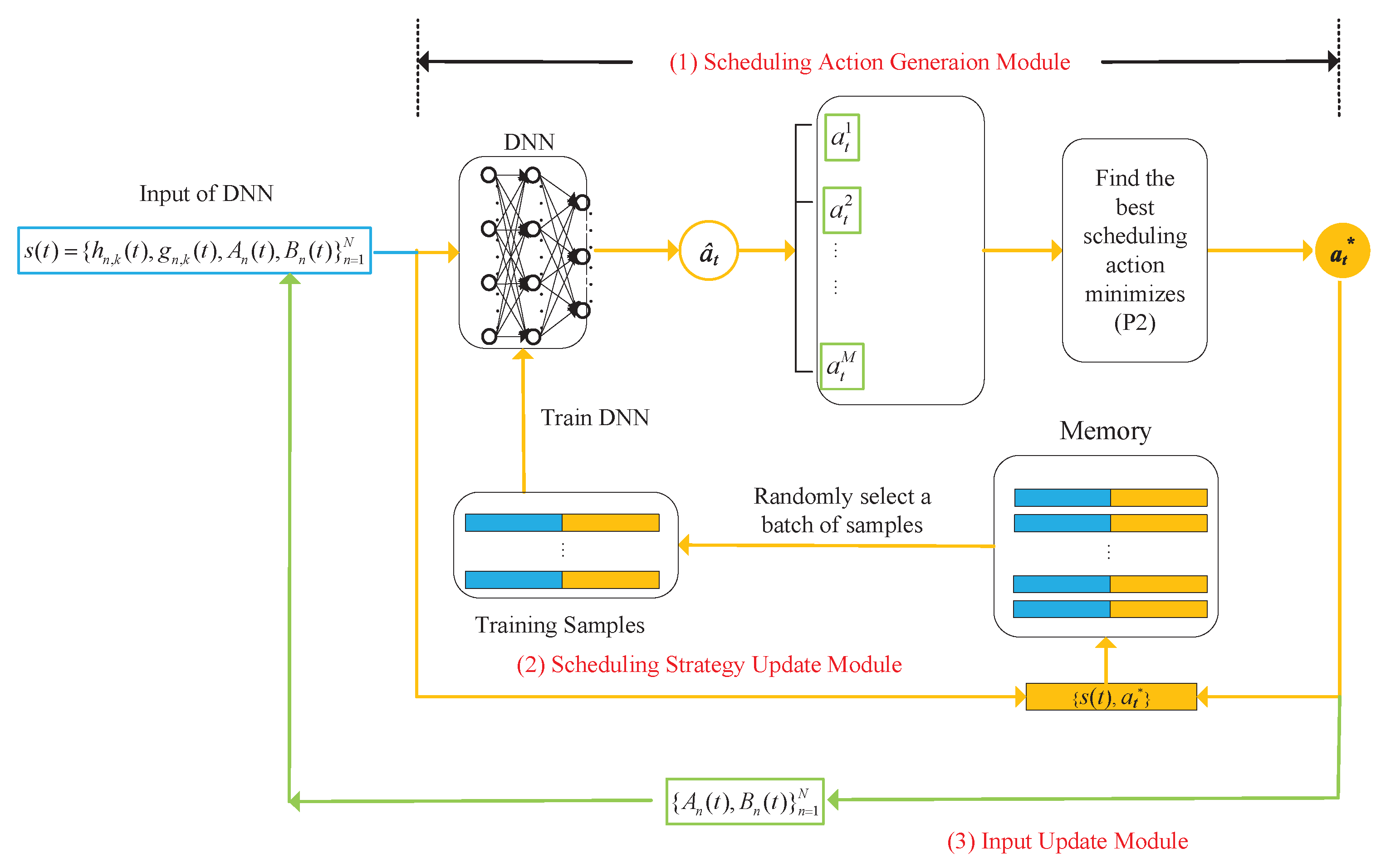
4. Lyapunov-Guided DRL for Online Scheduling Decisions
| Algorithm 1: LODR algorithm to solve the AoI minimization problem. |
 |
5. Performance Evaluation
5.1. Experimental Settings
5.2. Training Loss for LODR Algorithm
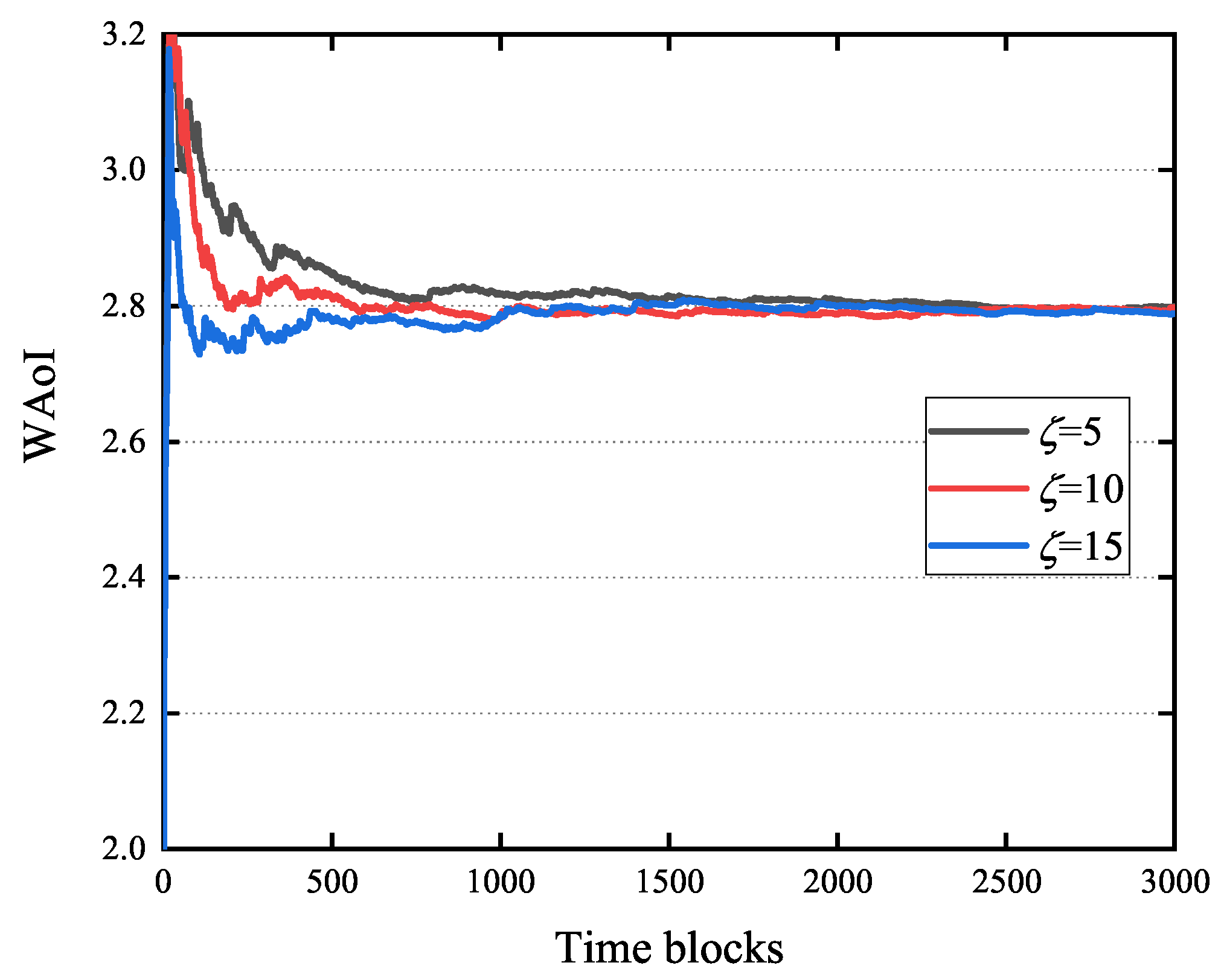
5.3. Impact of M and
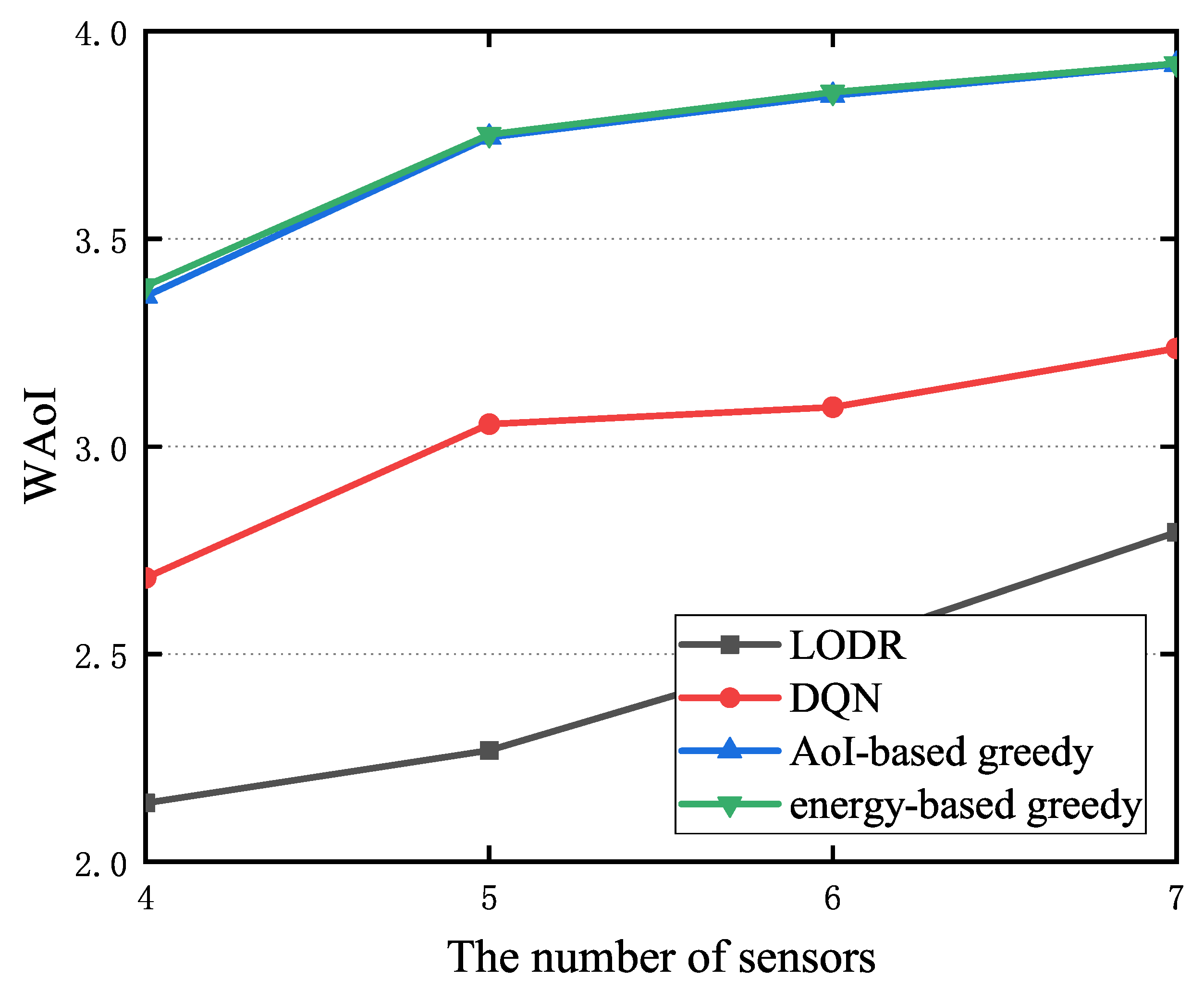
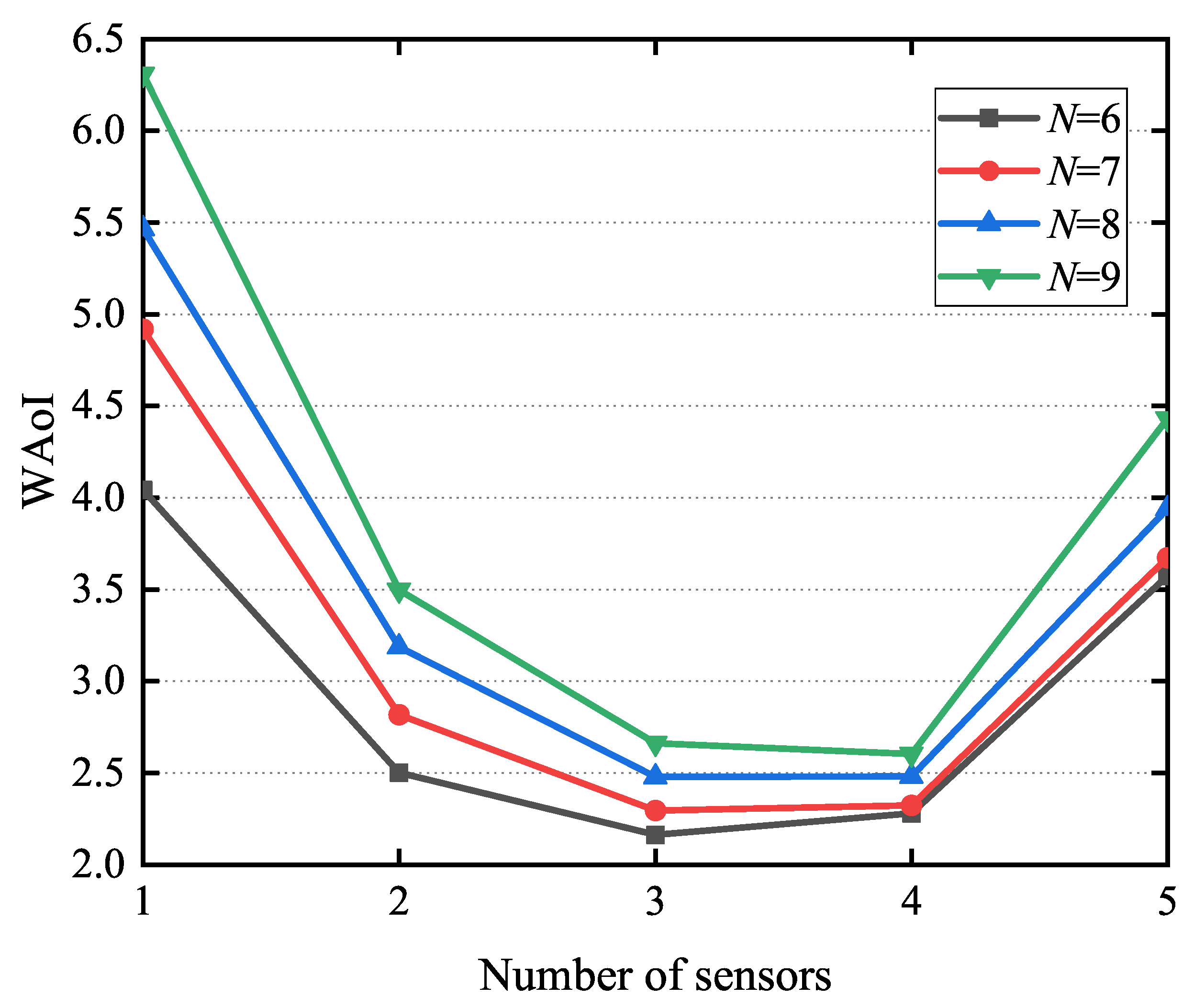
5.4. The WAoI of LODR
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AoI | Age of Information |
| WPSNs | Wireless powered sensor networks |
| WAoI | Long-term average weighted sum of Age of Information |
| RF | Radio frequency |
References
- Kosta, A.; Pappas, N.; Angelakis, V. Age information: A new concept, metric, tool. Found. Trends Netw. 2017, 12, 1–73. [Google Scholar] [CrossRef]
- Yates, R.D.; Kaul, S.K. The age of information: Real-time status updating by multiple sources. IEEE Trans. Inf. Theory 2019, 65, 1807–1827. [Google Scholar] [CrossRef]
- Sun, Y.; Kadota, I.; Talak, R.; Modiano, E. Age information: A new metric for information freshness. Synth. Lect. Commun. Netw. 2019, 12, 1–24. [Google Scholar]
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update. In Proceedings of the IEEE Conference Computer Communications (INFOCOM), Orlando, FL, USA, 25–30 March 2012; pp. 2731–2735. [Google Scholar]
- Feng, S.; Yang, J. Age of information minimization for an energy harvesting source With updating erasures: Without and with feedback. IEEE Trans. Commun. 2021, 69, 5091–5105. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Yates, R.D.; Kaul, S. Real-time status updating: Multiple sources. In Proceedings of the 2012 IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012; pp. 2666–2670. [Google Scholar]
- Kam, C.; Kompella, S.; Ephremides, A. Age of information under random updates. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 66–70. [Google Scholar]
- Huang, L.; Modiano, E. Optimizing age-of-information in a multiclass queueing system. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 1681–1685. [Google Scholar]
- Costa, M.; Codreanu, M.; Ephremides, A. On the age of information in status update systems with packet management. IEEE Trans. Inf. Theory 2016, 62, 1897–1910. [Google Scholar] [CrossRef]
- Chen, K.; Huang, L. Age-of-information in the presence of error. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 2579–2583. [Google Scholar]
- Barakat, B.; Keates, S.; Wassell, I.; Arshad, K. Is the zero-wait policy always optimum for information freshness (Peak Age) or throughput? IEEE Commun. Lett. 2019, 23, 987–990. [Google Scholar] [CrossRef]
- Kosta, A.; Pappas, N.; Ephremides, A.; Angelakis, V. Age and value of information: Non-linear age case. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 326–330. [Google Scholar]
- Hsu, Y.-P.; Modiano, E.; Duan, L. Scheduling algorithms for minimizing age of information in wireless broadcast networks with random arrivals. IEEE Trans. Mobile Comput. 2019, 19, 2903–2915. [Google Scholar] [CrossRef]
- Kadota, I.; Uysal-Biyikoglu, E.; Singh, R.; Modiano, E. Minimizing the age of information in broadcast wireless networks. In Proceedings of the 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 844–851. [Google Scholar]
- Chen, X.; Bidokhti, S.S. Benefits of coding on age of information in broadcast networks. In Proceedings of the 2019 IEEE Information Theory Workshop (ITW), Visby, Sweden, 25–28 August 2019. [Google Scholar]
- Bedewy, A.M.; Sun, Y.; Shroff, N.B. Optimizing data freshness, throughput, and delay in multi-server information-update systems. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 2569–2573. [Google Scholar]
- Talak, R.; Karaman, S.; Modiano, E. Minimizing age-of-information in multi-hop wireless networks. In Proceedings of the 2017 55th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 3–6 October 2017; pp. 486–493. [Google Scholar]
- Abd-Elmagid, M.A.; Pappas, N.; Dhillon, H.S. On the role of age of information in the Internet of Things. IEEE Commun. Mag. 2019, 57, 72–77. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Bai, B.; Dai, H. Age-optimal trajectory planning for UAV-assisted data collection. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Honolulu, HI, USA, 15–19 April 2018; pp. 553–558. [Google Scholar]
- Abd-Elmagid, M.A.; Dhillon, H.S. Average peak Age-of- Information minimization in UAV-assisted IoT networks. IEEE Trans. Veh. Technol. 2019, 68, 2003–2008. [Google Scholar] [CrossRef]
- Valehi, A.; Razi, A. Maximizing energy efficiency of cognitive wireless sensor networks with constrained age of information. IEEE Trans. Cognit. Commun. Netw. 2017, 3, 643–654. [Google Scholar] [CrossRef]
- Buyukates, B.; Soysal, A.; Ulukus, S. Age of information in two-hop multicast networks. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 513–517. [Google Scholar]
- Moltafet, M.; Leinonen, M.; Codreanu, M.; Pappas, N. Power minimization for Age of information constrained dynamic control in wireless sensor networks. IEEE Trans. Commun. 2022, 70, 419–432. [Google Scholar] [CrossRef]
- Abdel-Aziz, M.K.; Liu, C.-F.; Samarakoon, S.; Bennis, M.; Saad, W. Ultra-reliable low-latency vehicular networks: Taming the age of information tail. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Tang, H.; Wang, J.; Wang, J.; Song, L.; Song, J.; Song, J. Minimizing age of information with power constraints: Multiuser opportunistic scheduling in multi-state time-varying channels. IEEE J. Sel. Areas Commun. 2020, 38, 854–868. [Google Scholar] [CrossRef]
- Arafa, A.; Yang, J.; Ulukus, S.; Poor, H.V. Age-minimal transmission for energy harvesting sensors with finite batteries: Online policies. IEEE Trans. Inf. Theory 2020, 66, 534–556. [Google Scholar] [CrossRef]
- Abd-Elmagid, M.A.; Dhillon, H.S.; Pappas, N. A reinforcement learning framework for optimizing Age of information in RF-powered communication systems. IEEE Trans. Commun. 2020, 68, 4747–4760. [Google Scholar] [CrossRef]
- Arafa, A.; Ulukus, S. Timely updates in energy harvesting two-Hop networks: Offline and online policies. IEEE Trans. Wirel. Commun. 2019, 18, 4017–4030. [Google Scholar] [CrossRef]
- Leng, S.; Yener, A. Age of information minimization for an energy harvesting cognitive radio. IEEE Trans. Cognit. Commun. Netw. 2019, 5, 427–439. [Google Scholar] [CrossRef]
- Hu, H.; Xiong, K.; Qu, G.; Ni, Q.; Fan, P.; Letaief, K.B. AoI-minimal trajectory planning and data collection in UAV-assisted wireless powered IoT networks. IEEE Internet Things J. 2021, 8, 1211–1223. [Google Scholar] [CrossRef]
- Sun, Y.; Uysal-Biyikoglu, E.; Yates, R.D.; Koksal, C.E.; Shroff, N.B. Update or wait: How to keep your data fresh. IEEE Trans. Inf. Theory 2017, 3, 7492–7508. [Google Scholar] [CrossRef]
- Neely, M.J. Stochastic network optimization with application to communication and queueing systems. In Synthesis Lectures on Communication Networks; Morgan and Claypool: Belmont, MA, USA, 2010; Volume 3, pp. 1–211. [Google Scholar]
- Georgiadis, L.; Neely, M.J.; Tassiulas, L. Resource allocation and cross-layer control in wireless networks. Found. Trends Netw. 2006, 1, 1–144. [Google Scholar] [CrossRef]
- Bi, S.; Huang, L.; Wang, H.; Zhang, Y.-J.A. Lyapunov-guided deep reinforcement learning for stable online computation offloading in mobile-edge computing networks. IEEE Trans. Wirel. Commun. 2021, 20, 7519–7537. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Letaief, K.B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices. IEEE J. Sel. Areas Commun. 2016, 34, 3590–3605. [Google Scholar] [CrossRef]
- Lin, L.-J. Reinforcement Learning for Robots Using Neural Networks; School of Computer Science, Carnegie Mellon University: Pittsburgh, PA, USA, 1993; Tech. Rep. CMU-CS-93-103. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjel, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]






| Layers | Number of Neurons | Activation Function |
|---|---|---|
| Input layer | / | |
| Hidden layer 1 | 120 | ReLU |
| Hidden layer 2 | 80 | ReLU |
| HOutput layer | Sigmoid |
| Simulation Parameter | Values |
|---|---|
| Learning rate | 0.01 |
| Training interval | 10 |
| Memory size | 1024 |
| Batch size | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Xia, J.; Zhang, S.; Yu, X. Age of Information Minimization in Multicarrier-Based Wireless Powered Sensor Networks. Entropy 2025, 27, 603. https://doi.org/10.3390/e27060603
Sun J, Xia J, Zhang S, Yu X. Age of Information Minimization in Multicarrier-Based Wireless Powered Sensor Networks. Entropy. 2025; 27(6):603. https://doi.org/10.3390/e27060603
Chicago/Turabian StyleSun, Juan, Jingjie Xia, Shubin Zhang, and Xinjie Yu. 2025. "Age of Information Minimization in Multicarrier-Based Wireless Powered Sensor Networks" Entropy 27, no. 6: 603. https://doi.org/10.3390/e27060603
APA StyleSun, J., Xia, J., Zhang, S., & Yu, X. (2025). Age of Information Minimization in Multicarrier-Based Wireless Powered Sensor Networks. Entropy, 27(6), 603. https://doi.org/10.3390/e27060603





