Scaling Laws in Language Families
Abstract
1. Introduction
2. Materials and Methods
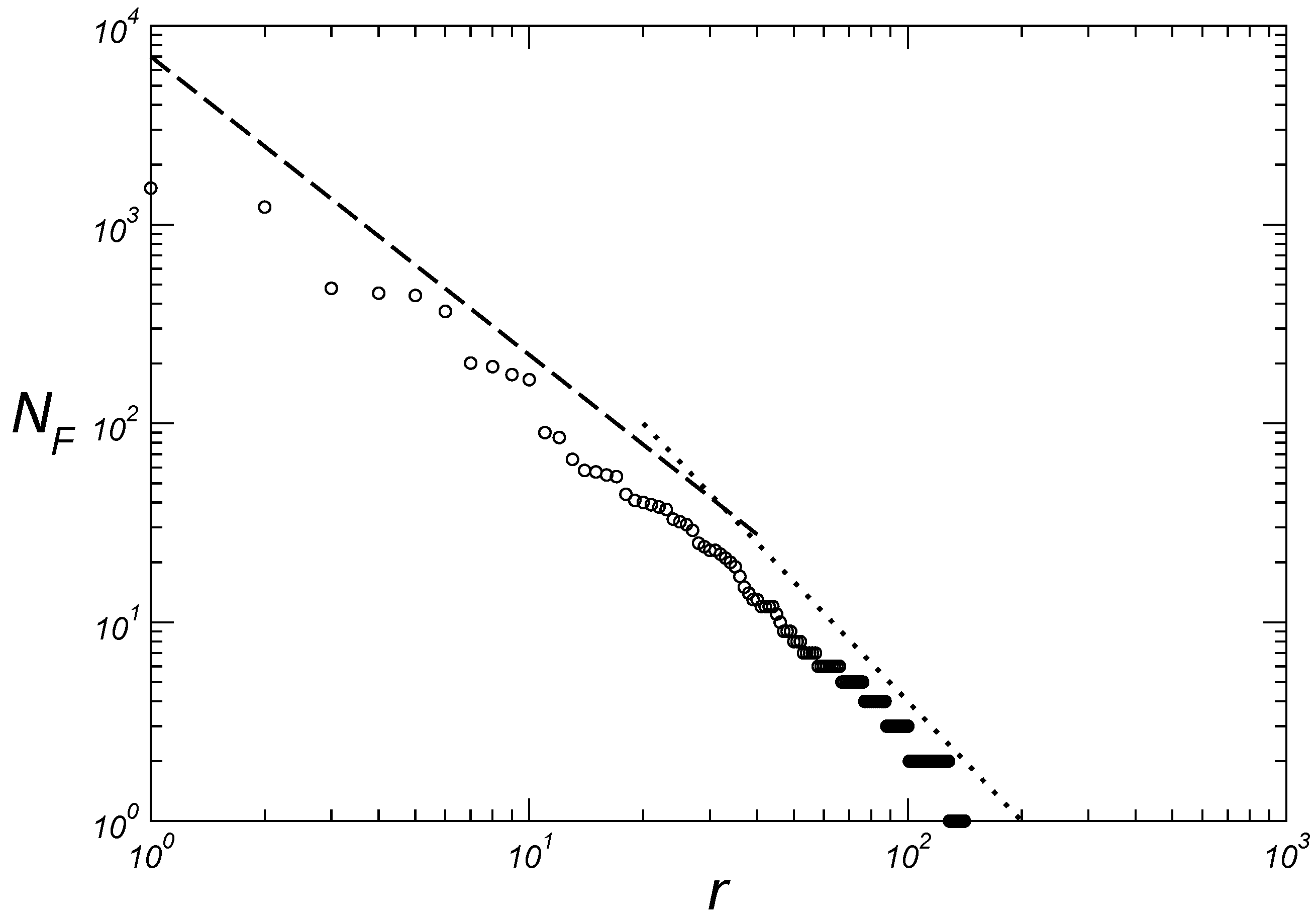
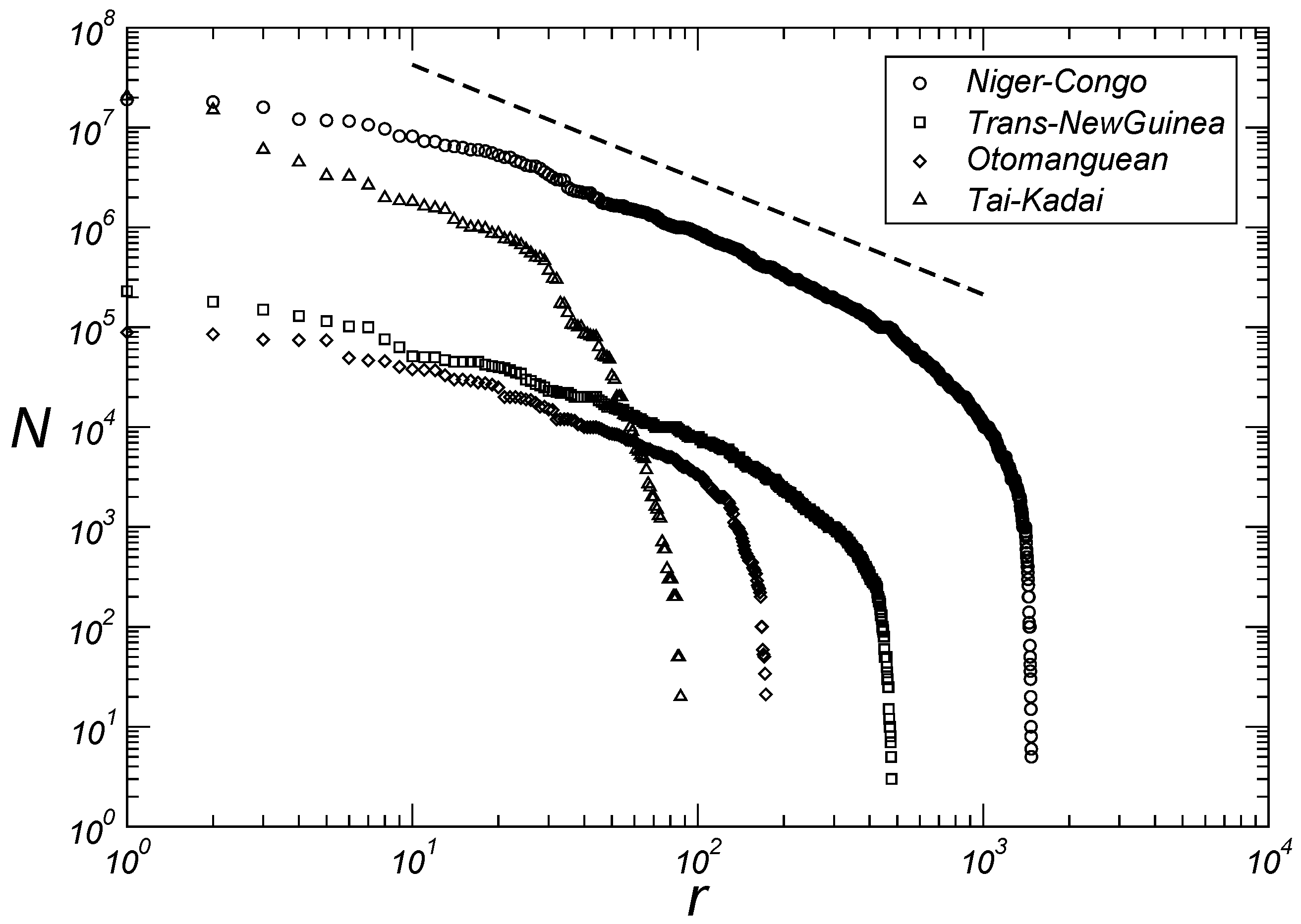
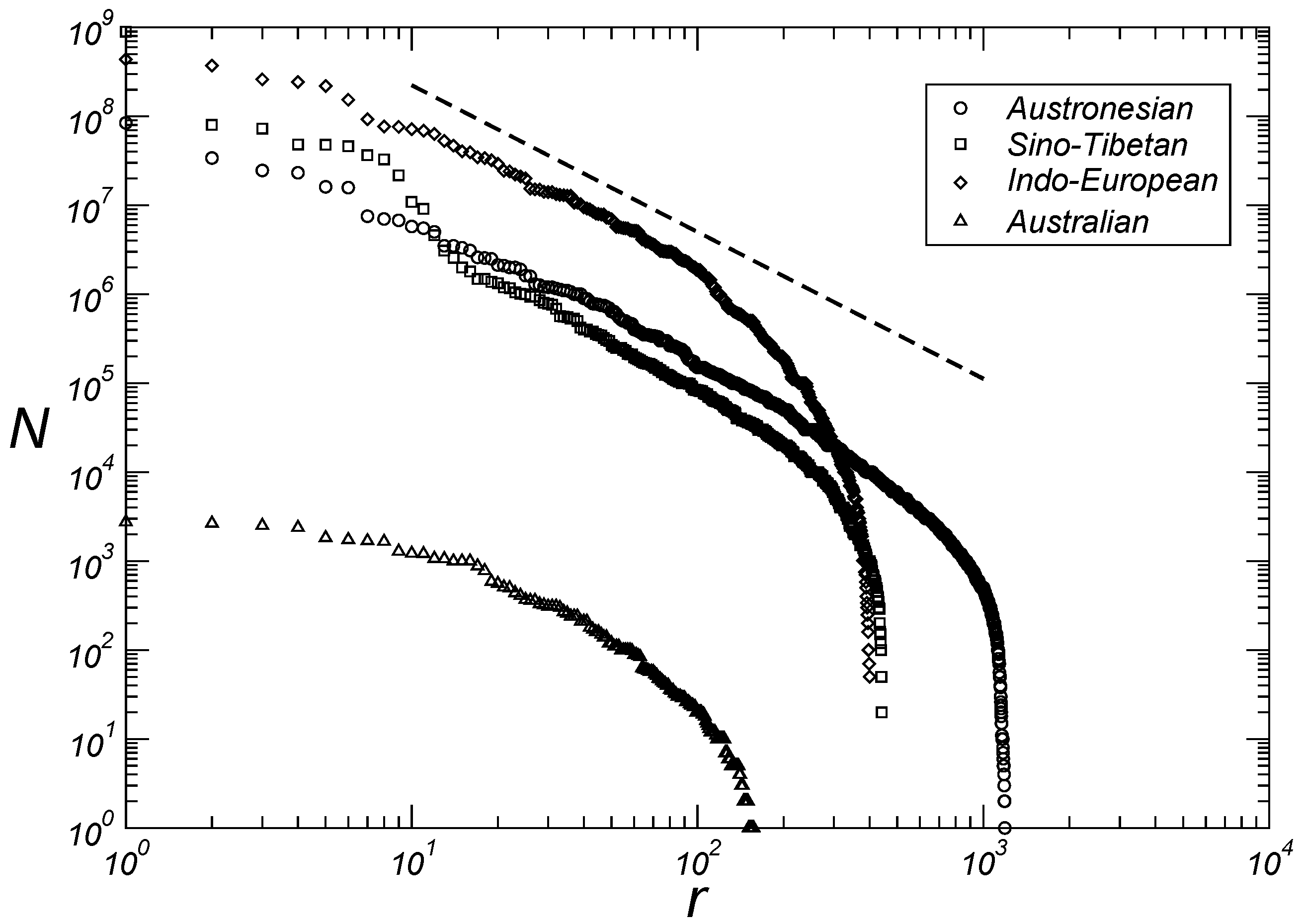
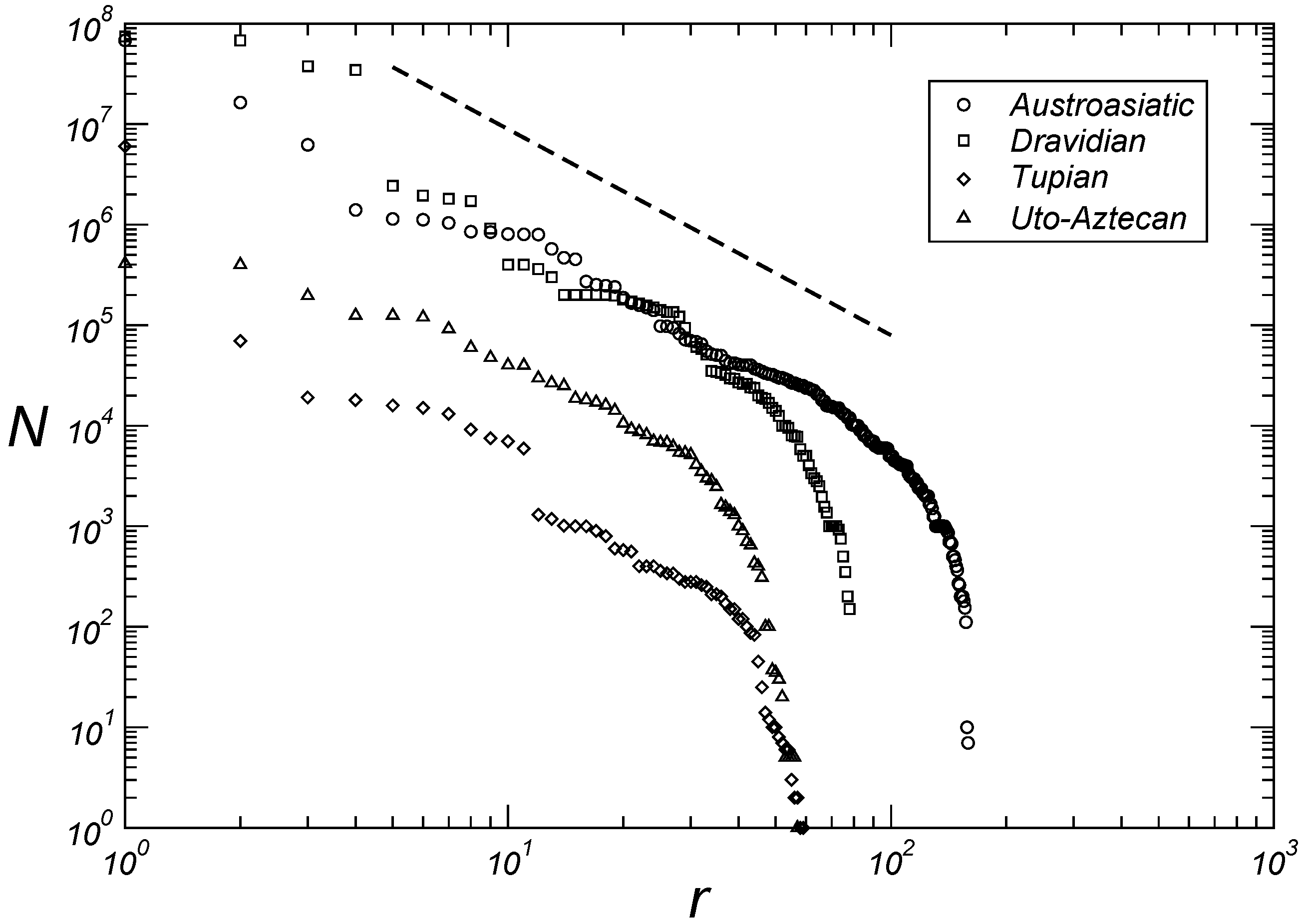
3. Results and Discussion
3.1. Macroscopic Aspects
3.2. Microscopic Aspects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Christensen, K.; Olami, Z. Scaling, phase transitions, and nonuniversality in a self-organized critical cellular-automaton model. Phys. Rev. A 1992, 46, 1829–1838. [Google Scholar] [CrossRef] [PubMed]
- Kello, C.T.; Brown, G.D.A.; Ferrer-i Cancho, R.; Holden, J.G.; Linkenkaer-Hansen, K.; Rhodes, T.; Van Orden, G.C. Scaling laws in cognitive sciences. Trends in Cognitive Sciences 2010, 14, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Balasubrahmanyan, V.K.; Naranan, S. Quantitative linguistics and complex system studies. J. Quant. Linguist. 1996, 3, 177–228. [Google Scholar] [CrossRef]
- Kretzschmar, W.A. Language and Complex Systems; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Stanisz, T.; Drożdż, S.; Kwapień, J. Complex systems approach to natural language. Phys. Rep. 2024, 1053, 1–84. [Google Scholar] [CrossRef]
- Altmann, E.G.; Gerlach, M. Statistical laws in linguistics. In Creativity and Universality in Language. Lecture Notes in Morphogenesis; Degli Esposti, M., Altmann, E., Pachet, F., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Galam, S. Sociophysics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Bentley, R.A.; Hahn, M.W.; Shennan, S.J. Random drift and culture change. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2024, 271, 1443–1450. [Google Scholar] [CrossRef] [PubMed]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Gell-Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; Macmillan: Shipley, UK, 1995. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Zipf, G.K. Human Behavior and the Principle of Least Effort; Addison-Wesley: Cambridge, UK, 1949. [Google Scholar]
- Ferrer i Cancho, R.; Solé, R.V. Zipf’s law and random texts. Adv. Complex Syst. 2002, 5, 1–6. [Google Scholar] [CrossRef]
- Ferrer i Cancho, R. The variation of Zipf’s law in human language. Eur. Phys. J. B 2005, 44, 249–257. [Google Scholar] [CrossRef]
- Jayaram, B.D.; Vidya, M.N. Zipf’s law for indian languages. J. Quant. Linguist. 2008, 15, 293–317. [Google Scholar] [CrossRef]
- Baixeries, J.; Elvevåg, B.; Ferrer-i Cancho, R. The evolution of the exponent of Zipf’s law in language ontogeny. PLoS ONE 2013, 8, e53227. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Sánchez, I.; Font-Clos, F.; Corral, Á. Large-scale analysis of Zipf’s law in english texts. PLoS ONE 2016, 11, e0147073. [Google Scholar] [CrossRef] [PubMed]
- Gomes, M.A.F.; Vasconcelos, G.L.; Tsang, I.J.; Tsang, I.R. Scaling relations for diversity of languages. Phys. A Stat. Mech. Its Appl. 1999, 271, 489–495. [Google Scholar] [CrossRef]
- Santos, M.R.F.; Gomes, M.A.F. Revisiting scaling relations for linguistic diversity. Phys. A Stat. Mech. Its Appl. 2019, 532, 121821. [Google Scholar] [CrossRef]
- Zanette, D.H. Self-similarity in the taxonomic classification of human languages. Adv. Complex Syst. 2001, 4, 281–286. [Google Scholar] [CrossRef]
- Wichmann, S. On the power-law distribution of language family sizes. J. Linguist. 2005, 41, 117–131. [Google Scholar] [CrossRef]
- Hammarström, H. A full-scale test of the language farming dispersal hypothesis. Diachronica 2010, 27, 197–213. [Google Scholar] [CrossRef]
- Simons, G.F.; Fennig, C.D. Ethnologue: Languages of the World, 20th ed.; SIL International: Dallas, TX, USA, 2017. [Google Scholar]
- Hammarströmm, H. Ethnologue 16/17/18th editions: A comprehensive review. Language 2015, 91, 723–737. [Google Scholar] [CrossRef]
- Greenhill, S.J. Demographic correlates of language diversity. In The Routledge Handbook of Historical Linguistics; Bowern, C., Evans, B., Eds.; Routledge: Amsterdam, The Netherlands, 2014; pp. 557–578. [Google Scholar]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Takayasu, H. Fractals in the Physical Sciences; Manchester University Press: Manchester, UK, 1990. [Google Scholar]
- Ruhlen, M. A Guide to the World’s Languages; Classification; Stanford University Press: Redwood City CA, USA, 1987; Volume I. [Google Scholar]
| r | Family | N (in Millions) | |||
|---|---|---|---|---|---|
| 01 | Niger–Congo | 1526 | 458.90 | 03 | |
| 02 | Austronesian | 1224 | 324.88 | 05 | |
| 03 | Trans-New Guinea | 478 | 3.55 | 21 | |
| 04 | Sino-Tibetan | 452 | 1355.71 | 02 | |
| 05 | Indo-European | 440 | 3077.11 | 01 | |
| 06 | Afro-Asiatic | 366 | 444.85 | 04 | |
| 07 | Nilo-Saharan | 201 | 50.33 | 12 | |
| 08 | Australian | 193 | 0.04 | 51 | |
| 09 | Otomanguean | 176 | 1.68 | 24 | |
| 10 | Austro-Asiatic | 166 | 104.99 | 09 | |
| 11 | Tai-Kadai | 90 | 80.1 | 10 | |
| 12 | Dravidian | 85 | 228.1 | 06 | |
| 13 | Tupian | 66 | 6.2 | 19 | |
| 14 | Uto-Astecan | 58 | 1.9 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, M.R.F.d.; Gomes, M.A.d.F. Scaling Laws in Language Families. Entropy 2025, 27, 588. https://doi.org/10.3390/e27060588
Santos MRFd, Gomes MAdF. Scaling Laws in Language Families. Entropy. 2025; 27(6):588. https://doi.org/10.3390/e27060588
Chicago/Turabian StyleSantos, Maelyson Rolim Fonseca dos, and Marcelo Andrade de Filgueiras Gomes. 2025. "Scaling Laws in Language Families" Entropy 27, no. 6: 588. https://doi.org/10.3390/e27060588
APA StyleSantos, M. R. F. d., & Gomes, M. A. d. F. (2025). Scaling Laws in Language Families. Entropy, 27(6), 588. https://doi.org/10.3390/e27060588









