Tail Risk Spillover Between Global Stock Markets Based on Effective Rényi Transfer Entropy and Wavelet Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Effective Rényi Transfer Entropy
2.2. Connectedness Framework
2.3. Network Construction and Analysis
2.4. Maximal Overlap Discrete Wavelet Transform
3. Results
3.1. Data Description
3.2. Empirical Results
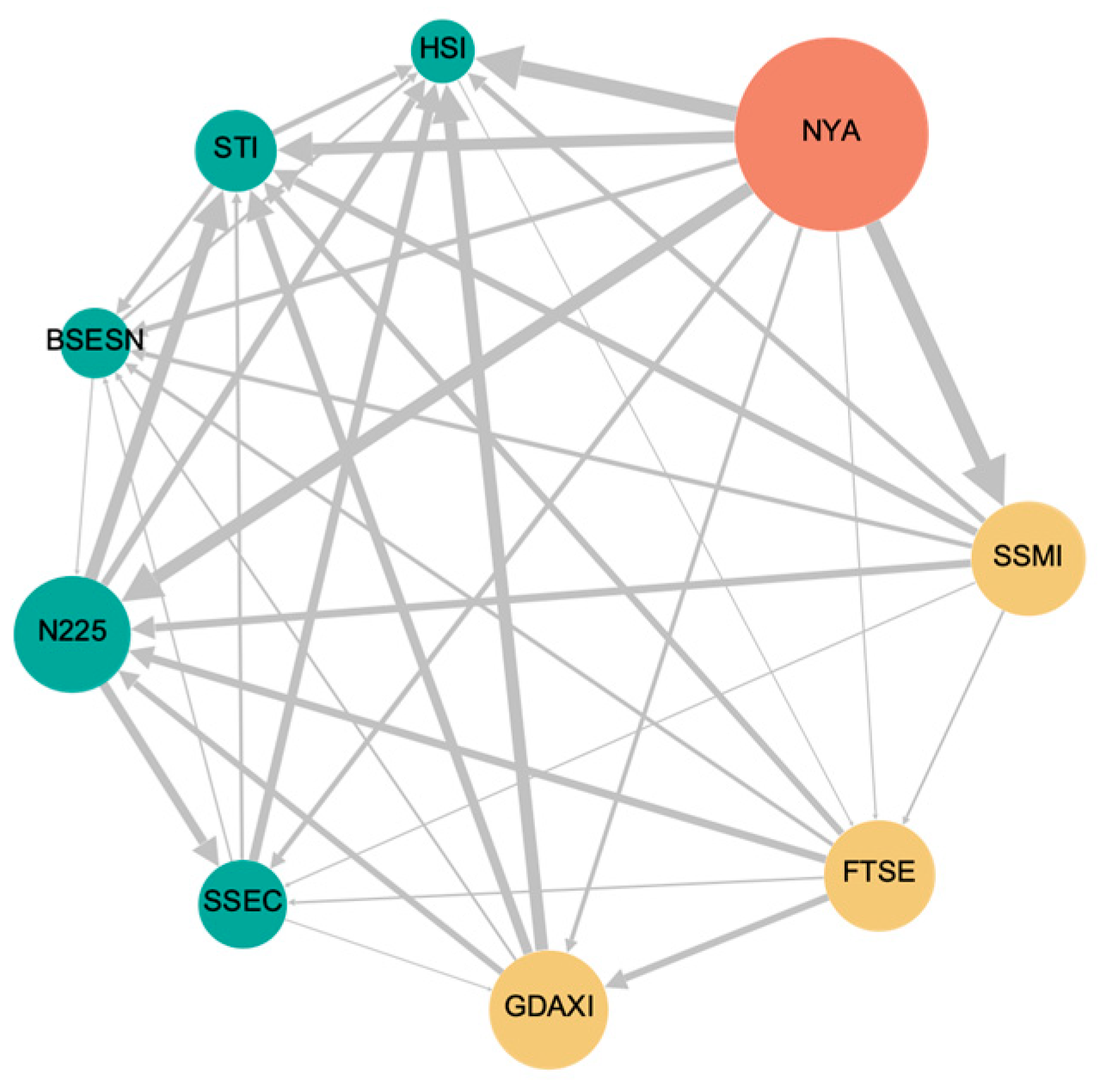
3.2.1. Overall Analysis of Tail-Risk Information Spillover
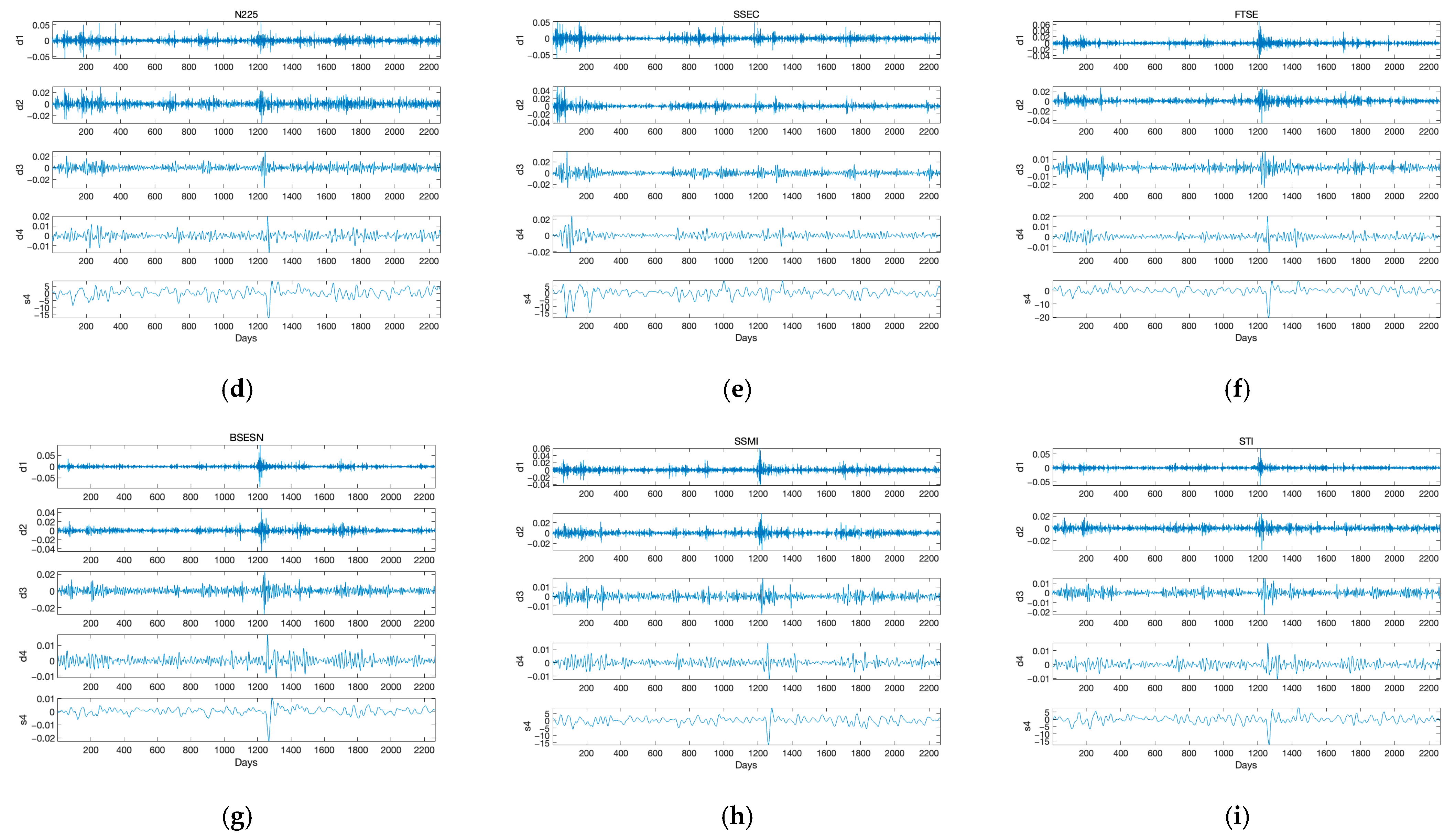
3.2.2. Time-Frequency Analysis of Tail-Risk Information Spillover
3.3. Robustness Test
3.3.1. Robustness Test for Overall Characteristics
3.3.2. Robustness Test for Multi-Scale Characteristics
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Tongurai, J.; Vithessonthi, C. Financial openness and financial market development. J. Multinatl. Financ. Manag. 2023, 67, 100782. [Google Scholar] [CrossRef]
- Qin, W.; Cho, S.; Hyde, S. Time-varying bond market integration and the impact of financial crises. Int. Rev. Financ. Anal. 2023, 90, 102909. [Google Scholar] [CrossRef]
- Chen, B.X.; Jiang, Y.Y.; Zhou, D.H. Risk contagion network and characteristic measurement among international financial markets. Pac.-Basin Financ. J. 2025, 92, 102766. [Google Scholar] [CrossRef]
- Wątorek, M.; Kwapień, J.; Drożdż, S. Cryptocurrencies Are Becoming Part of the World Global Financial Market. Entropy 2023, 25, 377. [Google Scholar] [CrossRef] [PubMed]
- Heil, T.L.A.; Peter, F.J.; Prange, P. Measuring 25 years of global equity market co-movement using a time-varying spatial model. J. Int. Money Financ. 2022, 128, 102708. [Google Scholar] [CrossRef]
- Naeem, M.A.; Yousaf, I.; Karim, S.; Yarovaya, L.; Ali, S. Tail-event driven NETwork dependence in emerging markets. Emerg. Mark. Rev. 2023, 55, 100971. [Google Scholar] [CrossRef]
- Abuzayed, B.; Bouri, E.; Al-Fayoumi, N.; Jalkh, N. Systemic risk spillover across global and country stock markets during the COVID-19 pandemic. Econ. Anal. Policy 2021, 71, 180–197. [Google Scholar] [CrossRef]
- Li, P.; Zhang, P.Y.; Guo, Y.H.; Li, J.H. How has the relationship between major financial markets changed during the Russia-Ukraine conflict? Humanit. Soc. Sci. Commun. 2024, 11, 1731. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, L.; Zhu, Y.; Chen, L.; Wang, G.; Wang, C. Spillovers from the Russia-Ukraine conflict. Res. Int. Bus. Financ. 2023, 66, 102006. [Google Scholar] [CrossRef]
- Yahya, M.; Allahdadi, M.R.; Uddin, G.S.; Park, D.; Wang, G.-J. Multilayer information spillover network between ASEAN-4 and global bond, forex and stock markets. Financ. Res. Lett. 2024, 59, 104748. [Google Scholar] [CrossRef]
- Wang, B.; Xiao, Y. Risk spillovers from China’s and the US stock markets during high-volatility periods: Evidence from East Asianstock markets. Int. Rev. Financ. Anal. 2023, 86, 102538. [Google Scholar] [CrossRef]
- Mamman, S.O.; Wang, Z.; Iliyasu, J. Commonality in BRICS stock markets’ reaction to global economic policy uncertainty: Evidence from a panel GARCH model with cross sectional dependence. Financ. Res. Lett. 2023, 55, 103877. [Google Scholar] [CrossRef]
- Ali, S.; Rehman, M.U.; Shahzad, S.J.H.; Raza, N.; Vo, X.V. Financial integration in emerging economies: An application of threshold cointegration. Stud. Nonlinear Dyn. Econom. 2021, 25, 213–228. [Google Scholar] [CrossRef]
- Horvath, J.; Yang, G.Y. Global Financial Risk, Equity Returns and Economic Activity in Emerging Countries. Oxf. Bull. Econ. Stat. 2024, 86, 672–689. [Google Scholar] [CrossRef]
- Lee, D. Financial integration and international risk spillovers. Econ. Lett. 2023, 225, 111049. [Google Scholar] [CrossRef]
- Joe, H.; Li, H.J. Tail Risk of Multivariate Regular Variation. Methodol. Comput. Appl. Probab. 2011, 13, 671–693. [Google Scholar] [CrossRef]
- Lang, C.; Hu, Y.; Corbet, S.; Hou, Y. Tail risk connectedness in G7 stock markets: Understanding the impact of COVID-19 and related variants. J. Behav. Exp. Financ. 2024, 41, 100889. [Google Scholar] [CrossRef]
- Lu, X.; Zeng, Q.; Zhong, J.; Zhu, B. International stock market volatility: A global tail risk sight. J. Int. Financ. Mark. Inst. Money 2024, 91, 101904. [Google Scholar] [CrossRef]
- Jian, Z.; Lu, H.; Zhu, Z.; Xu, H. Frequency heterogeneity of tail connectedness: Evidence from global stock markets. Econ. Model. 2023, 125, 106354. [Google Scholar] [CrossRef]
- Zhong, J.D.; Long, H.G.; Ma, F.; Wang, J.Q. International commodity-market tail risk and stock volatility. Appl. Econ. 2023, 55, 5790–5799. [Google Scholar] [CrossRef]
- Salisu, A.A.; Pierdzioch, C.; Gupta, R. Geopolitical risk and forecastability of tail risk in the oil market: Evidence from over a century of monthly data. Energy 2021, 235, 121333. [Google Scholar] [CrossRef]
- Salisu, A.A.; Olaniran, A.; Tchankam, J.P. Oil tail risk and the tail risk of the US Dollar exchange rates. Energy Econ. 2022, 109, 105960. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, X.; Huang, S.; Sun, Q.; Chen, Z.; Tang, R.; Di, Z. Measuring systemic risk contribution of global stock markets: A dynamic tail risk network approach. Int. Rev. Financ. Anal. 2022, 84, 102361. [Google Scholar] [CrossRef]
- Yao, C.Z.; Zhang, Z.K.; Li, Y.L. The Analysis of Risk Measurement and Association in China’s Financial Sector Using the Tail Risk Spillover Network. Mathematics 2023, 11, 2574. [Google Scholar] [CrossRef]
- Chen, B.X.; Sun, Y.L. Financial market connectedness between the U.S. and China: A new perspective based on non-linear causality networks. J. Int. Financ. Mark. Inst. Money 2024, 90, 101886. [Google Scholar] [CrossRef]
- Paeng, S.; Senteney, D.; Yang, T. Spillover effects, lead and lag relationships, and stable coins time series. Q. Rev. Econ. Financ. 2024, 95, 45–60. [Google Scholar] [CrossRef]
- Canh, N.P.; Wongchoti, U.; Thanh, S.D.; Thong, N.T. Systematic risk in cryptocurrency market: Evidence from DCC-MGARCH model. Financ. Res. Lett. 2019, 29, 90–100. [Google Scholar] [CrossRef]
- Tian, M.X.; El Khoury, R.; Alshater, M.M. The nonlinear and negative tail dependence and risk spillovers between foreign exchange and stock markets in emerging economies. J. Int. Financ. Mark. Inst. Money 2023, 82, 101712. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.; Yin, S.; Ji, H. The asymmetric contagion effect between stock market and cryptocurrency market. Financ. Res. Lett. 2022, 46, 102345. [Google Scholar] [CrossRef]
- Härdie, W.K.; Wang, W.N.; Yu, L.N. TENET: Tail-Event driven NETwork risk. J. Econom. 2016, 192, 499–513. [Google Scholar] [CrossRef]
- Fan, Y.; Härdle, W.K.; Wang, W.N.; Zhu, L.X. Single-Index-Based CoVaR with Very High-Dimensional Covariates. J. Bus. Econ. Stat. 2018, 36, 212–226. [Google Scholar] [CrossRef]
- Xu, Q.H.; Zhang, Y.X.; Zhang, Z.Y. Tail-risk spillovers in cryptocurrency markets. Financ. Res. Lett. 2021, 38, 101453. [Google Scholar] [CrossRef]
- Hu, C.L.; Guo, R.R. Research on Risk Contagion in ESG Industries: An Information Entropy-Based Network Approach. Entropy 2024, 26, 206. [Google Scholar] [CrossRef] [PubMed]
- Ando, T.; Greenwood-Nimmo, M.; Shin, Y. Quantile Connectedness: Modeling Tail Behavior in the Topology of Financial Networks. Manag. Sci. 2022, 68, 2401–2431. [Google Scholar] [CrossRef]
- Mensi, W.; Shafiullah, M.; Vo, X.V.; Kang, S.H. Spillovers and connectedness between green bond and stock markets in bearish and bullish market scenarios. Financ. Res. Lett. 2022, 49, 103120. [Google Scholar] [CrossRef]
- Ji, Q.; Marfatia, H.; Gupta, R. Information spillover across international real estate investment trusts: Evidence from an entropy-based network analysis. North Am. J. Econ. Financ. 2018, 46, 103–113. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kwon, O.; Yang, J.S. Information flow between stock indices. Europhys. Lett. 2008, 82, 68003. [Google Scholar] [CrossRef]
- Xie, W.J.; Yong, Y.; Wei, N.; Yue, P.; Zhou, W.X. Identifying states of global financial market based on information flow network motifs. North Am. J. Econ. Financ. 2021, 58, 101459. [Google Scholar] [CrossRef]
- Jizba, P.; Kleinert, H.; Shefaat, M. Renyi’s information transfer between financial time series. Phys. A-Stat. Mech. Its Appl. 2012, 391, 2971–2989. [Google Scholar] [CrossRef]
- Korbel, J.; Jiang, X.F.; Zheng, B. Transfer Entropy between Communities in Complex Financial Networks. Entropy 2019, 21, 1124. [Google Scholar] [CrossRef]
- Li, S.; He, J.; Song, K. Network Entropies of the Chinese Financial Market. Entropy 2016, 18, 331. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. The impact of the financial crisis on transatlantic information flows: An intraday analysis. J. Int. Financ. Mark. Inst. Money 2014, 31, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, S.H. The impact of investor sentiment on crude oil market risks: Evidence from the wavelet approach. Quant Financ 2019, 19, 1357–1371. [Google Scholar] [CrossRef]
- Yao, Y.; Li, J.; Chen, W. Multiscale extreme risk spillovers among the Chinese mainland, Hong Kong, and London stock markets: Comparing the impacts of three Stock Connect programs. Int. Rev. Econ. Financ. 2024, 89, 1217–1233. [Google Scholar] [CrossRef]
- Phiri, A.; Anyikwa, I.; Moyo, C. Co-movement between Covid-19 and G20 stock market returns: A time and frequency analysis. Heliyon 2023, 9, e14195. [Google Scholar] [CrossRef]
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale characteristics of the emerging global cryptocurrency market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Yoon, S.M. Dynamic co-movement between oil and stock markets in oil-importing and oil-exporting countries: Two types of wavelet analysis. Energy Econ. 2020, 90, 104835. [Google Scholar] [CrossRef]
- Zhao, L.T.; Liu, H.Y.; Chen, X.H. How does carbon market interact with energy and sectoral stocks? Evidence from risk spillover and wavelet coherence. J. Commod. Mark. 2024, 33, 100386. [Google Scholar] [CrossRef]
- Xi, Z.L.; Yu, J.X.; Sun, Q.R.; Zhao, W.Q.; Wang, H.; Zhang, S. Measuring the multi-scale price transmission effects from crude oil to energy stocks: A cascaded view. Int. Rev. Financ. Anal. 2023, 90, 102891. [Google Scholar] [CrossRef]
- Huang, S.C. Wavelet-based multi-resolution GARCH model for financial spillover effects. Math. Comput. Simul. 2011, 81, 2529–2539. [Google Scholar] [CrossRef]
- Naysary, B.; Shrestha, K. Financial technology and ESG market: A wavelet-DCC GARCH approach. Res. Int. Bus. Financ. 2024, 71, 102466. [Google Scholar] [CrossRef]
- Chiranjivi, G.V.S.; Sensarma, R. The effects of economic and financial shocks on private investment: A wavelet study of return and volatility spillovers. Int. Rev. Financ. Anal. 2023, 90, 102936. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Namdari, A.; Li, Z. A review of entropy measures for uncertainty quantification of stochastic processes. Adv. Mech. Eng. 2019, 11, 1687814019857350. [Google Scholar] [CrossRef]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series: An improved estimator for transfer entropy. Eur. Phys. J. B-Condens. Matter Complex Syst. 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Rényi, A. Probability Theory; North-Holland Publishing Company: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sandoval, L. Structure of a Global Network of Financial Companies Based on Transfer Entropy. Entropy 2014, 16, 4443–4482. [Google Scholar] [CrossRef]
- Shen, Y. International risk transmission of stock market movements. Econ. Model. 2018, 69, 220–236. [Google Scholar] [CrossRef]
- Choi, K.H.; Yoon, S.M. Risk Connectedness among International Stock Markets: Fresh Findings from a Network Approach. Systems 2023, 11, 207. [Google Scholar] [CrossRef]
- Chen, Y.F.; Wang, C.W.; Miao, J.F.; Zhou, T.J. Identifying Risk Transmission in Carbon Market with Energy, Commodity and Financial Markets: Evidence From Time-Frequency and Extreme Risk Spillovers. Front. Energy Res. 2022, 10, 922808. [Google Scholar] [CrossRef]
- Fernandez, V. Time-Scale Decomposition of Price Transmission in International Markets. Emerg. Mark. Financ. Trade 2005, 41, 57–90. [Google Scholar] [CrossRef]
- Shik Lee, H. International transmission of stock market movements: A wavelet analysis. Appl. Econ. Lett. 2004, 11, 197–201. [Google Scholar] [CrossRef]
- Dajčman, S. Interdependence Between Some Major European Stock Markets—A Wavelet Lead/Lag Analysis. Prague Econ. Pap. 2013, 22, 28–49. [Google Scholar] [CrossRef]
- Chow, H.K. Volatility Spillovers and Linkages in Asian Stock Markets. Emerg. Mark. Financ. Trade 2017, 53, 2770–2781. [Google Scholar] [CrossRef]
- Zheng, Q.H.; Song, L.R. Dynamic Contagion of Systemic Risks on Global Main Equity Markets Based on Granger Causality Networks. Discret. Dyn. Nat. Soc. 2018, 2018, 9461870. [Google Scholar] [CrossRef]


| From | |||||
| To |
| Continent | Country/Region | Indices | Abbreviation |
|---|---|---|---|
| America | USA | NYSE Composite Index | NYA |
| Asia | Singapore | Straits Times Index | STI |
| Hong Kong, China | Hang Seng Index | HSI | |
| China | SSE Composite Index | SSEC | |
| Japan | Nikkei 225 | N225 | |
| India | BSE Sensex | BSESN | |
| Europe | Germany | Dax Index | GDAXI |
| UK | FTSE 100 | FTSE | |
| Swiss | Swiss Market Index | SSMI |
| Mean | Maximum | Minimum | Std. Dev. | Skewness | Kurtosis | Jarque-Bera | |
|---|---|---|---|---|---|---|---|
| NYA | 2.10 × 10−4 | 0.096 | −0.126 | 0.011 | −1.115 | 21.991 | 34,506.69 *** |
| HSI | −1.74 × 10−4 | 0.087 | −0.066 | 0.013 | 0.089 | 6.184 | 959.7205 *** |
| GDAXI | 2.13× 10−4 | 0.104 | −0.131 | 0.012 | −0.636 | 14.123 | 11,829.68 *** |
| N225 | 2.78 × 10−4 | 0.077 | −0.083 | 0.012 | −0.092 | 7.799 | 2177.066 *** |
| SSEC | −1.74 × 10−4 | 0.075 | −0.089 | 0.012 | −1.088 | 12.101 | 8264.668 *** |
| FTSE | 6.99 × 10−5 | 0.087 | −0.115 | 0.010 | −0.913 | 16.244 | 16,869.68 *** |
| BSESN | 4.35 × 10−4 | 0.086 | −0.141 | 0.010 | −1.475 | 26.609 | 53,422.92 *** |
| SSMI | 1.08 × 10−4 | 0.068 | −0.101 | 0.009 | −0.742 | 12.584 | 8876.191 *** |
| STI | −9.06 × 10−6 | 0.059 | −0.076 | 0.009 | −0.431 | 11.698 | 7210.419 *** |
| Variables | NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI |
|---|---|---|---|---|---|---|---|---|---|
| NYA | 1.000 | ||||||||
| HSI | 0.259 *** | 1.000 | |||||||
| (0.000) | |||||||||
| GDAXI | 0.639 *** | 0.352 *** | 1.000 | ||||||
| (0.000) | (0.000) | ||||||||
| N225 | 0.236 *** | 0.442 *** | 0.326 *** | 1.000 | |||||
| (0.000) | (0.000) | (0.000) | |||||||
| SSEC | 0.168 *** | 0.540 *** | 0.183 *** | 0.302 *** | 1.000 | ||||
| (0.000) | (0.000) | (0.000) | (0.000) | ||||||
| FTSE | 0.629 *** | 0.378 *** | 0.822 *** | 0.328 *** | 0.200 *** | 1.000 | |||
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |||||
| BSESN | 0.361 *** | 0.419 *** | 0.450 *** | 0.338 *** | 0.236 *** | 0.455 *** | 1.000 | ||
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | ||||
| SSMI | 0.564 *** | 0.307 *** | 0.810 *** | 0.301 *** | 0.178 *** | 0.785 *** | 0.412 *** | 1.000 | |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |||
| STI | 0.311 *** | 0.563 *** | 0.406 *** | 0.483 *** | 0.350 *** | 0.430 *** | 0.511 *** | 0.360 *** | 1.000 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.052 *** | 0.037 *** | 0.031 *** | 0.035 *** | 0.048 *** | 0.051 *** | 0.029 *** | 0.060 *** | 0.342 |
| HSI | 0.102 *** | 0 | 0.052 *** | 0.031 *** | 0.030 *** | 0.049 *** | 0.033 *** | 0.053 *** | 0.017 ** | 0.368 |
| GDAXI | 0.049 *** | 0.011 * | 0 | 0.032 *** | 0.036 *** | 0.022 ** | 0.032 ** | 0 | 0.025 ** | 0.206 |
| N225 | 0.074 *** | 0.007 * | 0.052 *** | 0 | 0 | 0.044 *** | 0.040 *** | 0.054 *** | 0.017 * | 0.288 |
| SSEC | 0.050 *** | 0 | 0.034 ** | 0.029 ** | 0 | 0.032 ** | 0.023 * | 0.049 *** | 0.031 *** | 0.247 |
| FTSE | 0.051 *** | 0.051 *** | 0 | 0.019 ** | 0.027 *** | 0 | 0.023 ** | 0.019 ** | 0.037 *** | 0.227 |
| BSESN | 0.068 *** | 0.024 ** | 0.038 *** | 0.037 *** | 0.027 ** | 0.034 ** | 0 | 0.048 *** | 0.041 *** | 0.317 |
| SSMI | 0.081 *** | 0.035 *** | 0 | 0.030 *** | 0.046 *** | 0.013 * | 0.034 *** | 0 | 0.043 *** | 0.282 |
| STI | 0.097 *** | 0 | 0.056 *** | 0.058 *** | 0.040 *** | 0.058 *** | 0.026 ** | 0.068 *** | 0 | 0.403 |
| To | 0.572 | 0.179 | 0.269 | 0.266 | 0.241 | 0.299 | 0.263 | 0.321 | 0.271 | 0.298 |
| Net | 0.230 | −0.188 | 0.063 | −0.023 | −0.006 | 0.072 | −0.055 | 0.039 | −0.132 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | |
|---|---|---|---|---|---|---|---|---|---|
| d1 | 20.55% | 25.42% | 23.37% | 22.29% | 25.40% | 25.40% | 23.93% | 25.19% | 22.01% |
| d2 | 55.91% | 49.66% | 50.50% | 52.52% | 48.09% | 50.41% | 50.75% | 50.85% | 50.52% |
| d3 | 11.99% | 12.98% | 12.82% | 13.24% | 13.38% | 12.28% | 12.46% | 12.14% | 12.00% |
| d4 | 5.49% | 6.30% | 6.69% | 6.31% | 7.03% | 6.11% | 5.92% | 5.98% | 7.12% |
| s | 6.06% | 5.64% | 6.62% | 5.64% | 6.10% | 5.80% | 6.94% | 5.84% | 8.35% |
| Total | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.044 *** | 0.034 *** | 0.014 *** | 0.003 * | 0.048 *** | 0.043 *** | 0.015 *** | 0.043 *** | 0.244 |
| HSI | 0.043 *** | 0 | 0.013 * | 0.019 ** | 0.014 * | 0.024 *** | 0.013 ** | 0.026 *** | 0.016 * | 0.167 |
| GDAXI | 0.047 *** | 0.016 *** | 0 | 0.026 *** | 0.008 ** | 0.022 *** | 0.028 *** | 0 | 0.024 *** | 0.172 |
| N225 | 0.061 *** | 0.031 *** | 0.029 *** | 0 | 0.018 *** | 0.043 *** | 0.049 *** | 0.036 *** | 0.037 *** | 0.302 |
| SSEC | 0.002 ** | 0.005 ** | 0.007 *** | 0.004 ** | 0 | 0.003 *** | 0.022 *** | 0.038 *** | 0.045 *** | 0.127 |
| FTSE | 0.046 *** | 0.014 *** | 0.017 *** | 0.047 *** | 0.025 *** | 0 | 0.032 *** | 0.019 *** | 0.038 *** | 0.238 |
| BSESN | 0.059 *** | 0.011 * | 0.027 *** | 0.024 *** | 0.017 ** | 0.046 *** | 0 | 0.021 ** | 0.024 *** | 0.228 |
| SSMI | 0.050 *** | 0.021 ** | 0.011 ** | 0.047 *** | 0.057 *** | 0 | 0.037 *** | 0 | 0.032 ** | 0.255 |
| STI | 0.043 *** | 0 | 0.031 *** | 0.026 *** | 0.038 *** | 0.036 *** | 0.015 * | 0.028 ** | 0 | 0.216 |
| To | 0.349 | 0.142 | 0.169 | 0.207 | 0.178 | 0.222 | 0.240 | 0.183 | 0.259 | 0.216 |
| Net | 0.105 | −0.026 | −0.003 | −0.095 | 0.051 | −0.016 | 0.012 | −0.072 | 0.043 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.042 *** | 0.064 *** | 0.047 *** | 0.033 *** | 0.060 *** | 0.063 *** | 0.051 *** | 0.035 *** | 0.396 |
| HSI | 0.055 *** | 0 | 0.041 *** | 0.011 * | 0.029 ** | 0.011 * | 0.016 *** | 0.024 ** | 0 | 0.187 |
| GDAXI | 0.037 *** | 0.042 *** | 0 | 0.061 *** | 0.024 *** | 0.021 *** | 0.049 *** | −0.010 ** | 0.053 *** | 0.277 |
| N225 | 0.103 *** | 0.033 *** | 0.068 *** | 0 | 0.049 *** | 0.056 *** | 0.067 *** | 0.059 *** | 0.040 *** | 0.474 |
| SSEC | 0.029 *** | 0.009 *** | 0.031 *** | 0.032 *** | 0 | 0.010 ** | −0.001 ** | 0.026 *** | 0.022 *** | 0.158 |
| FTSE | 0.040 *** | 0.030 *** | 0.001 ** | 0.030 *** | −0.005 * | 0 | 0.035 *** | 0.007 ** | 0.025 *** | 0.164 |
| BSESN | 0.032 *** | 0.035 *** | 0.046 *** | 0.038 *** | 0.016 ** | 0.048 *** | 0 | 0.053 *** | 0.024 *** | 0.290 |
| SSMI | 0.048 *** | 0.027 ** | 0 | 0.031 *** | 0 | 0.017 ** | 0.020 *** | 0 | 0.027 *** | 0.171 |
| STI | 0.060 *** | 0.020 ** | 0.045 *** | 0.019 ** | 0.018 ** | 0.044 *** | 0.016 ** | 0.017 ** | 0 | 0.238 |
| To | 0.404 | 0.238 | 0.295 | 0.269 | 0.163 | 0.267 | 0.265 | 0.227 | 0.227 | 0.262 |
| Net | 0.009 | 0.050 | 0.019 | −0.205 | 0.005 | 0.103 | −0.025 | 0.056 | −0.011 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | −0.004 ** | 0.010 *** | −0.005 ** | −0.021 * | 0.014 *** | −0.001 *** | −0.018 * | 0 | −0.024 |
| HSI | 0.016 *** | 0 | 0.016 *** | 0 | −0.002 ** | 0.004 ** | −0.003 ** | 0.015 *** | −0.011 * | 0.036 |
| GDAXI | 0.003 *** | 0.008 *** | 0 | 0.010 *** | −0.013 ** | −0.003 ** | 0.024 *** | 0.013 *** | 0.022 *** | 0.066 |
| N225 | 0.003 *** | 0.002 ** | 0.020 *** | 0 | 0.001 *** | −0.003 *** | −0.005 *** | 0.013 *** | −0.005 ** | 0.026 |
| SSEC | 0 | −0.006 *** | −0.007 *** | −0.018 *** | 0 | −0.007 *** | 0 | −0.010 *** | −0.016 ** | −0.064 |
| FTSE | 0.023 *** | 0.007 *** | 0.005 ** | −0.004 ** | 0.004 ** | 0 | 0.005 *** | 0.001 ** | 0.015 *** | 0.055 |
| BSESN | 0.042 *** | −0.011 * | 0.008 *** | 0.022 ** | 0 | 0.007 *** | 0 | 0.019 *** | −0.001 ** | 0.087 |
| SSMI | −0.003 *** | 0 | 0.006 *** | 0.006 ** | −0.015 * | −0.004 ** | 0.007 *** | 0 | −0.001 ** | −0.004 |
| STI | 0.030 *** | −0.007 * | 0.016 *** | −0.004 ** | 0 | 0.002 ** | 0.001 ** | 0.001 ** | 0 | 0.039 |
| To | 0.115 | −0.011 | 0.075 | 0.007 | −0.045 | 0.010 | 0.028 | 0.034 | 0.003 | 0.024 |
| Net | 0.139 | −0.047 | 0.009 | −0.019 | 0.019 | −0.045 | −0.059 | 0.038 | −0.036 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.060 *** | 0.046 *** | 0.029 *** | 0.040 *** | 0.058 *** | 0.054 *** | 0.034 *** | 0.076 *** | 0.396 |
| HSI | 0.111 *** | 0 | 0.058 *** | 0.034 *** | 0.041 *** | 0.055 *** | 0.042 *** | 0.059 *** | 0.024 ** | 0.423 |
| GDAXI | 0.061 *** | 0.016 * | 0 | 0.046 *** | 0.046 *** | 0.031 ** | 0.041 *** | 0 | 0.029 ** | 0.269 |
| N225 | 0.082 *** | 0.014 ** | 0.059 *** | 0 | 0.016 * | 0.048 *** | 0.047 *** | 0.065 *** | 0.022 * | 0.353 |
| SSEC | 0.060 ** | 0 | 0.042 * | 0.034 ** | 0 | 0.038 ** | 0.032 * | 0.059 ** | 0.035 ** | 0.300 |
| FTSE | 0.059 *** | 0.062 ** | 0 | 0.028 *** | 0.033 ** | 0 | 0.032 ** | 0.028 ** | 0.047 *** | 0.288 |
| BSESN | 0.079 *** | 0.032 ** | 0.047 *** | 0.046 *** | 0.030 ** | 0.045 *** | 0 | 0.057 *** | 0.051 *** | 0.386 |
| SSMI | 0.094 *** | 0.043 *** | 0 | 0.034 *** | 0.050 *** | 0.020 ** | 0.036 *** | 0 | 0.054 *** | 0.332 |
| STI | 0.108 *** | 0.016 * | 0.062 *** | 0.067 *** | 0.047 *** | 0.066 *** | 0.034 ** | 0.080 *** | 0 | 0.479 |
| To | 0.654 | 0.242 | 0.313 | 0.318 | 0.302 | 0.359 | 0.317 | 0.381 | 0.338 | 0.358 |
| Net | 0.258 | −0.181 | 0.044 | −0.035 | 0.002 | 0.072 | −0.068 | 0.049 | −0.141 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.188 *** | 0.035 *** | 0.029 *** | 0.032 *** | 0.046 *** | 0.046 *** | 0.028 *** | 0.054 *** | 0.458 |
| HSI | 0.236 *** | 0 | 0.048 *** | 0.026 *** | 0.022 ** | 0.047 *** | 0.025 *** | 0.050 *** | 0.017 ** | 0.472 |
| GDAXI | 0.038 *** | 0 | 0 | 0.024 ** | 0.030 ** | 0.021 ** | 0.025 *** | 0 | 0.017 ** | 0.154 |
| N225 | 0.068 *** | 0 | 0.051 *** | 0 | 0 | 0.044 *** | 0.034 *** | 0.053 *** | 0.015 * | 0.251 |
| SSEC | 0.042 *** | 0 | 0.030 *** | 0.022 ** | 0 | 0.025 ** | 0.020 * | 0.040 *** | 0.030 *** | 0.209 |
| FTSE | 0.043 *** | 0.040 *** | 0 | 0.016 * | 0.022 ** | 0 | 0.018 ** | 0.015 * | 0.029 *** | 0.184 |
| BSESN | 0.061 *** | 0.021 ** | 0.035 ** | 0.031 *** | 0.026 ** | 0.032 *** | 0 | 0.038 *** | 0.034 *** | 0.278 |
| SSMI | 0.070 *** | 0.034 *** | 0 | 0.023 ** | 0.040 *** | 0.015 * | 0.032 *** | 0 | 0.034 *** | 0.248 |
| STI | 0.086 *** | 0 | 0.051 *** | 0.049 *** | 0.032 *** | 0.051 *** | 0.022 ** | 0.061 *** | 0 | 0.353 |
| To | 0.644 | 0.283 | 0.251 | 0.171 | 0.204 | 0.281 | 0.222 | 0.286 | 0.231 | 0.286 |
| Net | 0.187 | −0.189 | 0.097 | −0.079 | −0.005 | 0.097 | −0.056 | 0.038 | −0.122 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BESEN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.057 *** | 0.038 *** | 0.023 *** | 0.009 *** | 0.053 *** | 0.052 *** | 0.015 *** | 0.051 *** | 0.298 |
| HSI | 0.053 *** | 0 | 0.015 ** | 0.024 ** | 0.023 ** | 0.033 ** | 0.018 ** | 0.030 *** | 0.021 ** | 0.216 |
| GDAXI | 0.053 *** | 0.023 *** | 0 | 0.038 *** | 0.014 *** | 0.026 *** | 0.033 *** | −0.017 * | 0.036 *** | 0.206 |
| N225 | 0.074 *** | 0.035 *** | 0.033 *** | 0 | 0.024 *** | 0.048 *** | 0.058 *** | 0.043 *** | 0.046 *** | 0.361 |
| SSEC | 0.004 *** | 0.003 ** | 0.011 *** | 0.013 *** | 0 | 0.015 *** | 0.003 *** | 0.037 *** | 0.027 *** | 0.113 |
| FTSE | 0.057 *** | 0.024 *** | 0.020 *** | 0.063 *** | 0 | 0 | 0.042 *** | 0.007 *** | 0.032 *** | 0.245 |
| BESEN | 0.069 *** | 0.014 ** | 0.032 *** | 0.034 *** | 0.023 *** | 0.054 *** | 0 | 0.058 *** | 0.037 *** | 0.321 |
| SSMI | 0.057 *** | 0.029 *** | 0.008 ** | 0.055 *** | 0.015 ** | 0.024 *** | 0.024 *** | 0 | 0.037 *** | 0.248 |
| STI | 0.054 *** | 0.010 * | 0.041 *** | 0.036 *** | 0.021 ** | 0.053 *** | 0.022 ** | 0.017 ** | 0 | 0.253 |
| To | 0.420 | 0.196 | 0.197 | 0.285 | 0.129 | 0.305 | 0.253 | 0.188 | 0.288 | 0.251 |
| Net | 0.122 | −0.020 | −0.009 | −0.076 | 0.016 | 0.060 | −0.068 | −0.060 | 0.035 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.055 *** | 0.073 *** | 0.066 *** | 0.041 *** | 0.073 *** | 0.084 *** | 0.069 *** | 0.040 *** | 0.501 |
| HSI | 0.064 *** | 0 | 0.043 *** | 0.008 ** | 0.032 ** | 0 | 0.041 *** | 0.028 *** | 0 | 0.216 |
| GDAXI | 0.053 *** | 0.047 *** | 0 | 0.073 *** | 0.030 *** | 0.021 *** | 0.060 *** | −0.012 *** | 0.064 *** | 0.335 |
| N225 | 0.123 *** | 0.044 *** | 0.083 *** | 0 | 0.059 *** | 0.063 *** | 0.080 *** | 0.076 *** | 0.049 *** | 0.577 |
| SSEC | 0.042 *** | 0.018 *** | 0.038 *** | 0.039 *** | 0 | 0.004 *** | 0.032 *** | 0.049 *** | 0.061 *** | 0.284 |
| FTSE | 0.058 *** | 0.039 *** | 0.013 *** | 0.035 *** | 0.027 *** | 0 | 0.042 *** | 0.027 *** | 0.049 *** | 0.289 |
| BSESN | 0.036 *** | 0.043 *** | 0.054 *** | 0.048 *** | 0.022 ** | 0.055 *** | 0 | 0.025 *** | 0.027 *** | 0.310 |
| SSMI | 0.058 *** | 0.033 ** | 0 | 0.042 *** | 0.067 *** | 0 | 0.046 ** | 0 | 0.038 *** | 0.285 |
| STI | 0.072 *** | 0.022 ** | 0.050 *** | 0.019 *** | 0.047 *** | 0.043 *** | 0.019 * | 0.028 *** | 0 | 0.300 |
| To | 0.506 | 0.302 | 0.354 | 0.330 | 0.323 | 0.259 | 0.403 | 0.289 | 0.329 | 0.344 |
| Net | 0.005 | 0.086 | 0.020 | −0.247 | 0.039 | −0.031 | 0.094 | 0.004 | 0.029 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | −0.008 ** | 0.014 *** | −0.003 *** | −0.018 ** | 0.022 *** | −0.003 *** | −0.023 ** | 0 | −0.020 |
| HSI | 0.013 *** | 0 | 0.014 *** | 0 | 0.003 *** | −0.004 *** | −0.002 *** | 0.016 *** | −0.014 * | 0.025 |
| GDAXI | −0.003 *** | 0.014 *** | 0 | 0.014 *** | −0.012 ** | −0.010 *** | 0.034 *** | 0.012 *** | 0.025 *** | 0.073 |
| N225 | −0.004 ** | 0.008 *** | 0.016 *** | 0 | 0.007 *** | −0.002 ** | −0.005 *** | 0.013 *** | −0.001 *** | 0.031 |
| SSEC | −0.038 * | −0.004 *** | −0.006 *** | −0.015 ** | 0 | −0.008 *** | −0.030 ** | −0.012 *** | −0.017 *** | −0.130 |
| FTSE | 0.018 *** | 0.007 *** | 0.002 ** | −0.004 ** | 0.003 *** | 0 | 0.007 *** | −0.005 ** | 0.015 *** | 0.042 |
| BSESN | 0.046 *** | −0.009 ** | 0.005 ** | 0.028 *** | −0.008 ** | 0.013 *** | 0 | 0.021 *** | 0.001 ** | 0.096 |
| SSMI | −0.012 ** | 0.006 *** | 0.004 *** | 0.004 *** | −0.018 ** | −0.010 ** | 0.014 *** | 0 | −0.003 *** | −0.015 |
| STI | 0.028 *** | −0.005 ** | 0.016 *** | −0.002 ** | 0 | −0.002 ** | 0.003 *** | 0.004 ** | 0 | 0.041 |
| To | 0.046 | 0.009 | 0.064 | 0.022 | −0.043 | −0.001 | 0.018 | 0.025 | 0.005 | 0.016 |
| Net | 0.065 | −0.016 | −0.009 | −0.010 | 0.086 | −0.043 | −0.078 | 0.040 | −0.036 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BESEN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.034 *** | 0.035 *** | 0.012 ** | 0 | 0.047 *** | 0.040 *** | 0.022 *** | 0.035 *** | 0.225 |
| HSI | 0.039 *** | 0 | 0.012 * | 0.018 * | 0 | 0.017 ** | 0.013 ** | 0.023 ** | 0.012 * | 0.133 |
| GDAXI | 0.040 *** | 0.010 * | 0 | 0.026 *** | 0.008 * | 0.020 *** | 0.028 *** | 0.004 * | 0.021 ** | 0.157 |
| N225 | 0.050 *** | 0.024 *** | 0.028 *** | 0 | 0.016 ** | 0.042 *** | 0.039 *** | 0.035 *** | 0.027 *** | 0.260 |
| SSEC | 0.001 * | 0 | 0.004 * | 0 | 0 | 0.005 * | 0.003 * | 0.020 ** | 0.017 ** | 0.050 |
| FTSE | 0.035 *** | 0.010 ** | 0.021 *** | 0.035 *** | 0 | 0 | 0.030 *** | 0.012 ** | 0.016 ** | 0.159 |
| BESEN | 0.049 *** | 0 | 0.028 *** | 0.017 ** | 0 | 0.042 *** | 0 | 0.040 *** | 0.021 ** | 0.197 |
| SSMI | 0.046 *** | 0.016 ** | 0.016 ** | 0.038 *** | 0 | 0.017 ** | 0.017 ** | 0 | 0.017 ** | 0.165 |
| STI | 0.033 *** | 0 | 0.027 ** | 0.021 ** | 0.021 ** | 0.039 *** | 0.015 * | 0.024 ** | 0 | 0.180 |
| To | 0.292 | 0.094 | 0.170 | 0.166 | 0.044 | 0.229 | 0.185 | 0.181 | 0.166 | 0.169 |
| Net | 0.067 | −0.039 | 0.013 | −0.094 | −0.006 | 0.070 | −0.012 | 0.015 | −0.014 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.038 *** | 0.064 *** | 0.035 *** | 0.026 *** | 0.056 *** | 0.050 *** | 0.043 *** | 0.027 *** | 0.338 |
| HSI | 0.051 *** | 0 | 0.038 *** | 0.015 * | 0.029 ** | 0.020 *** | 0.028 ** | 0.028 *** | 0 | 0.208 |
| GDAXI | 0.032 *** | 0.038 *** | 0 | 0.049 *** | 0.024 *** | 0.024 *** | 0.042 *** | 0 | 0.045 *** | 0.254 |
| N225 | 0.080 *** | 0.023 *** | 0.054 *** | 0 | 0.044 *** | 0.050 *** | 0.051 *** | 0.049 *** | 0.027 *** | 0.376 |
| SSEC | 0.025 *** | 0.006 ** | 0.025 *** | 0.023 *** | 0 | 0.002 ** | 0.016 * | 0.029 *** | 0.036 *** | 0.161 |
| FTSE | 0.034 *** | 0.023 *** | 0.002 * | 0.025 *** | 0.026 * | 0 | 0.031 *** | 0.013 *** | 0.029 *** | 0.182 |
| BSESN | 0.034 *** | 0.026 *** | 0.042 *** | 0.032 *** | 0.017 *** | 0.040 *** | 0 | 0.022 ** | 0.017 ** | 0.230 |
| SSMI | 0.044 *** | 0.025 ** | 0 | 0.031 *** | 0.047 *** | 0.016 * | 0.034 *** | 0 | 0.027 ** | 0.224 |
| STI | 0.053 *** | 0.017 ** | 0.040 *** | 0.021 ** | 0.034 *** | 0.037 *** | 0.016 * | 0.034 *** | 0 | 0.252 |
| To | 0.352 | 0.196 | 0.264 | 0.230 | 0.247 | 0.244 | 0.267 | 0.217 | 0.209 | 0.247 |
| Net | 0.014 | −0.012 | 0.010 | −0.147 | 0.086 | 0.062 | 0.037 | −0.007 | −0.043 |
| NYA | HSI | GDAXI | N225 | SSEC | FTSE | BSESN | SSMI | STI | From | |
|---|---|---|---|---|---|---|---|---|---|---|
| NYA | 0 | 0.004 ** | 0.011 *** | −0.006 * | 0 | 0.011 *** | 0.003 ** | −0.010 * | 0.002 ** | 0.015 |
| HSI | 0.027 *** | 0 | 0.019 *** | −0.006 * | −0.001 ** | 0.009 *** | 0 | 0.019 *** | 0.002 *** | 0.069 |
| GDAXI | 0.017 *** | 0.009 ** | 0 | 0.010 *** | −0.006 * | 0.009 *** | 0.022 *** | 0.018 *** | 0.017 *** | 0.095 |
| N225 | 0.018 *** | 0.002 ** | 0.025 *** | 0 | 0 | 0.004 ** | −0.005 ** | 0.019 *** | −0.001 *** | 0.063 |
| SSEC | 0 | −0.005 ** | −0.001 ** | 0 | 0 | −0.005 ** | 0 | 0 | 0 | −0.011 |
| FTSE | 0.027 *** | 0.007 ** | 0.007 ** | 0.002 * | 0.008 ** | 0 | 0.009 ** | 0.007 ** | 0.017 *** | 0.083 |
| BSESN | 0.040 *** | 0 | 0.012 *** | 0.015 *** | 0 | 0.011 ** | 0 | 0.023 *** | 0.003 ** | 0.103 |
| SSMI | 0.013 *** | 0.002 ** | 0.012 *** | 0.012 *** | −0.003 ** | 0.005 ** | 0.008 *** | 0 | 0.005 ** | 0.053 |
| STI | 0.032 *** | −0.001 * | 0.018 *** | 0 | 0 | 0.006 ** | 0.001 ** | 0.008 ** | 0 | 0.063 |
| To | 0.173 | 0.016 | 0.102 | 0.026 | −0.002 | 0.048 | 0.037 | 0.085 | 0.046 | 0.059 |
| Net | 0.158 | −0.053 | 0.008 | −0.037 | 0.009 | −0.035 | −0.065 | 0.032 | −0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J. Tail Risk Spillover Between Global Stock Markets Based on Effective Rényi Transfer Entropy and Wavelet Analysis. Entropy 2025, 27, 523. https://doi.org/10.3390/e27050523
Jia J. Tail Risk Spillover Between Global Stock Markets Based on Effective Rényi Transfer Entropy and Wavelet Analysis. Entropy. 2025; 27(5):523. https://doi.org/10.3390/e27050523
Chicago/Turabian StyleJia, Jingjing. 2025. "Tail Risk Spillover Between Global Stock Markets Based on Effective Rényi Transfer Entropy and Wavelet Analysis" Entropy 27, no. 5: 523. https://doi.org/10.3390/e27050523
APA StyleJia, J. (2025). Tail Risk Spillover Between Global Stock Markets Based on Effective Rényi Transfer Entropy and Wavelet Analysis. Entropy, 27(5), 523. https://doi.org/10.3390/e27050523





