Near-Horizon Carnot Engines Beyond Schwarzschild: Exploring Black Brane Thermodynamics

Abstract

Sadi Carnot’s seminal work laid the foundation for exploring the effects of thermodynamics across diverse domains of physics, stretching from quantum to cosmological scales. Here, we build on the principles of the original Carnot heat engine, and apply it in the context of a particular toy model black brane. This theoretical construct of an effectively two-dimensional, stable, and stationary gravitational object in four-dimensional spacetime derives from a hypothetical flat planet collapsed under the influence of gravity. By constructing a thermodynamic cycle involving three such black branes, we explore the possibility of energy extraction or mining, driven by the temperature gradients and gravitational potential differences characteristic of curved spacetime. Analytic solutions obtainable within this toy model illuminate key aspects of black hole thermodynamics in general, particularly for spacetimes that are not asymptotically flat. Central to these findings is the relation between gravitationally induced temperature ratios and entropy changes, which collectively offer a novel perspective on obtainable energy transfer processes around gravitational structures. This analysis highlights potential implications for understanding energy dynamics in gravitational systems in general, including for black hole evaporation and experimentally implemented black hole analogues. The presented findings not only emphasise the universality of the thermodynamic principles first uncovered by Carnot, but also suggest future research directions in gravitational thermodynamics.

1. Introduction

Sadi Carnot’s seminal work “Réflexions sur la puissance motrice du feu”, laid the foundation for applications of thermodynamics across all domains of physics, stretching from microscopic quantum scales all the way to cosmological processes [1]. Here, we focus on a version of Carnot’s heat engine arguments applied to modern black hole thermodynamics. The idea of mining black hole radiation by transferring energy between two infinitely separated Schwarzschild black holes in a thermodynamic or Carnot-engine-type cycle has been well-established [2,3]. This seminal gedanken experiment combining classical thermodynamics and black hole physics revealed a direct connection between energy-transfer processes and spacetime geometry, and gained prominence following the foundational work of Hawking and Bekenstein, who demonstrated that black holes possess thermodynamic properties, including entropy and temperature [4,5,6]. Together, these works embed classical thermodynamics into the framework of general relativity and quantum field theory, underscoring the universality of Carnot’s legacy.

Building on this rich tradition, here we propose a similar thermodynamic cycle in a particular, effectively two-dimensional black hole system, consisting of a theoretical toy model for a black brane. Unlike traditional Schwarzschild or Kerr black hole geometries, this black brane has the distinct advantage that it allows all of the involved calculations to be done analytically, in closed form. Consequently, the toy model serves as a theoretical lens for probing the interplay between entropy, temperature, and energy within curved spacetime geometries. It applies in particular to spacetimes that are not asymptotically flat, but general conclusions will be highlighted.

To obtain a closed Carnot cycle, it turns out we need to employ a system containing three black branes, as opposed to the classic setup containing two Schwarzschild black holes [2]. Focusing on this richer setup offers several advantages. Notably, it is exactly solvable but non-trivial, a rare combination in the study of black hole thermodynamics. Moreover, the interplay of temperature gradients connecting the multiple black branes in this configuration serves as a natural platform to explore fundamental questions about energy extraction, radiation transfer, and the limits of thermodynamics in curved spacetime. The importance of temperature, both as a physical observable and a theoretical construct, remains a hot topic throughout general relativity, underlying, for example, black hole evaporation and the holographic principle. By extending thermodynamic cycles to a system of black branes, these key ideas can be explored in a particularly accessible setting, allowing a fresh view on gravitational thermodynamics.

In this article, we will first provide a detailed overview of the toy model black brane, highlighting the relevance of its properties to thermodynamic analyses. We then analyse a Carnot engine-based thermodynamic cycle in a setup containing three black branes. In this context, we highlight the implications of energy transfer and efficiency within the Carnot cycle in curved spacetime. We conclude by discussing the significance of the obtained results within the broader context of black hole thermodynamics and general relativity.

2. The Toy Model Black Brane

The proposed Carnot cycle will be defined in a system comprising three entities that we term ‘toy model black branes’. They are effectively two-dimensional analogues of the usual point-like black hole singularities in four-dimensional spacetime. To ensure that the toy model black brane contains a massive, sheet-like singularity, we explicitly construct it from the gravitational collapse of a toy model, non-singular planetary body extending infinitely in two spatial dimensions (denoted y and z), while maintaining a finite width along the third (written u). Such a board-like, infinitely large object can be described by a non-singular, static solution to Einstein’s Equations [7]. The metric for such a body, expressed in its proper frame, is given by:

$$\begin{array}{cc}\hfill g_{vv}=-1/g_{uu}& =-\gamma utanh\left({\displaystyle \frac{u}{a}}\right)\hfill \\ \hfill g_{yy}=g_{zz}& =tanh{\left({\displaystyle \frac{\left|u\right|}{a}}\right)}^{-1}.\hfill \end{array}$$

(1)

Here, v represents the temporal coordinate, and a is a measure for the finite width of the planetary object. The centre of mass is located at $u=0$, and the metric is symmetric under reflection in the $u=0$ plane. All details regarding the associated Christoffel symbols, the Riemann tensor, the Ricci tensor, the Ricci scalar, and the pressure and density of this static solution to Einstein’s equations can be found in Appendix A.

When subjected to perturbations, the static planetary configuration becomes dynamically unstable. As long as the perturbation maintains the invariance of the metric in the y and z directions, the gravitational pull in the u-direction induces a uniform collapse, eventually compressing the planetary width a to infinitesimal values (assuming interactions dissipate the involved kinetic energy). The resulting state is characterised by a singularity at $u=0$, where the mass density diverges. This singularity, uniform along the y and z directions, defines the toy model black brane. The metric for this collapsed configuration corresponds to the well-known Rindler metric everywhere except within the infinitesimal region $u\in {lim}_{a\to 0}[-a,a]$, where the singularity resides. Outside this region, the metric has non-zero components [8]:

$$\begin{array}{ccc}\hfill & g_{vv}=-1/g_{uu}=-\gamma \left|u\right|\hfill & \hfill g_{yy}=g_{zz}=1.\end{array}$$

(2)

In this configuration, a horizon emerges at $u\to 0$, thus rendering the sheet-like singularity naked. Its infinite spatial extent, however, causes spacetime to be divided into disconnected regions despite the singularity being naked. Furthermore, as explicitly derived in Appendix A, the black brane features a finite and non-zero surface gravity $\kappa =\gamma /2=2\pi G{\rho }_0$, where we defined ${\rho }_0$ to be the mass density of the singular sheet [9]. Translational symmetry guarantees the surface gravity and mass density to be constant along the horizon.

Unlike conventional Schwarzschild black holes, the toy model black brane permits a global definition of quantum fields across all positions with $u\ne 0$. The resulting mathematical tractability of field-theoretic calculations enables the derivation of analytic solutions for numerous phenomena, providing a general framework for exploring thermodynamic processes in curved spacetime. Moreover, the toy model black brane allows for the construction of potential experimental analogues, offering a platform for empirical validation of any predictions [10,11,12,13].

3. A Black Brane Heat Pump

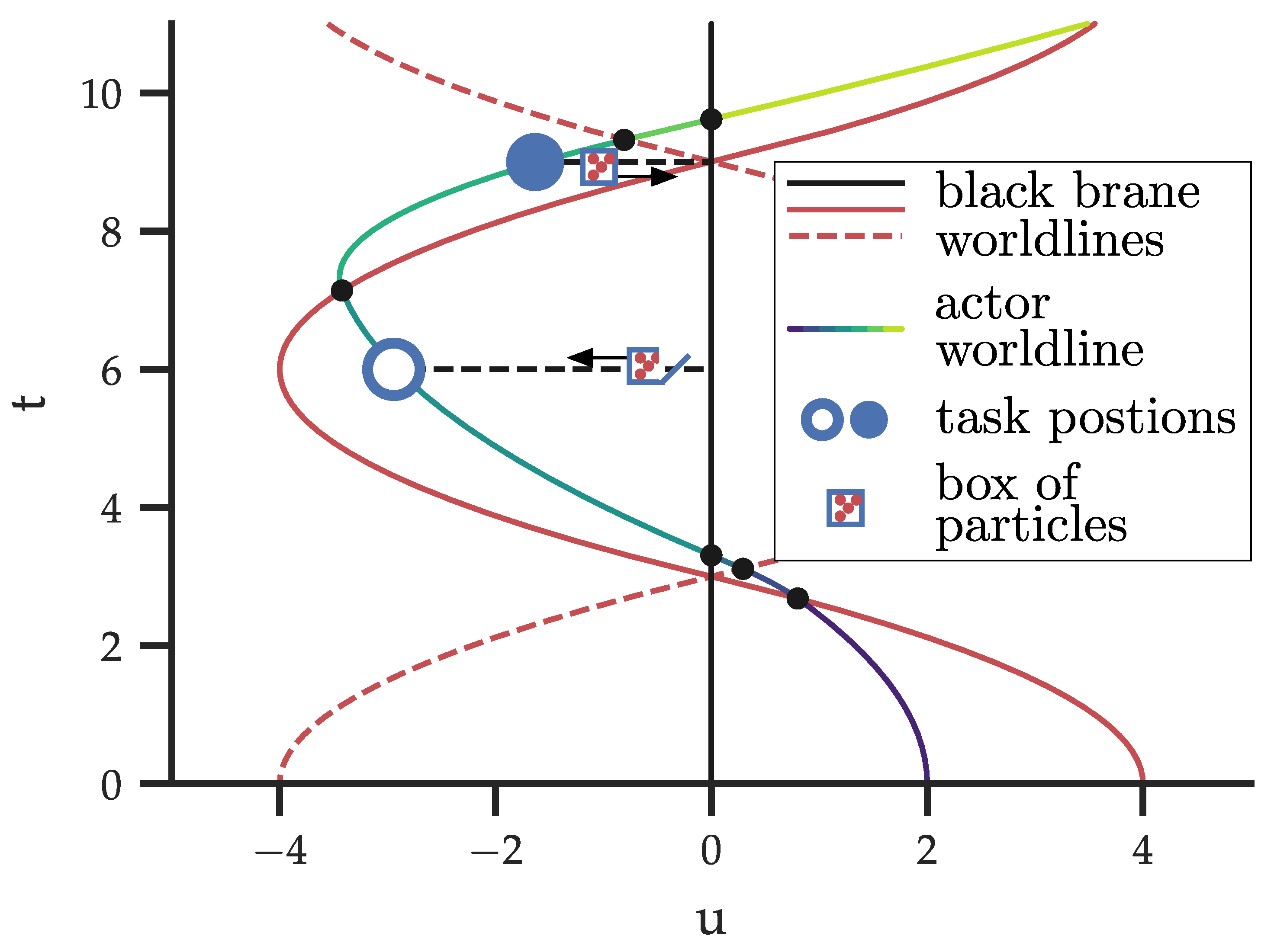
To explore the thermodynamics of black branes, we construct a Carnot cycle involving three distinct black branes, as depicted schematically in Figure 1.

Actors in the thermodynamic cycle—At the initial time $v=0$, the system consists of a central black brane situated at $u=0$ (indicated in Figure 1 by a black worldline), and two outer black branes (shown by red solid and dashed worldlines) positioned symmetrically with respect to the central brane, at $u=\pm b$. The central brane is characterised by mass density ${\rho }_1$, while the outer branes both have mass density ${\rho }_2$. Due to the symmetry of the configuration, the gravitational fields of the outer branes cancel within the region between them, leaving the gravitational potential of the central brane to dominate there.

The two outer branes oscillate around the central brane under its gravitational influence, periodically converging at $u=0$. For the sake of simplicity, we assume that the particles comprising the different branes are entirely non-interacting and can freely traverse the black brane singularity at $u=0$. While non-physical, this assumption does not affect the thermodynamic analysis, while enabling a more intuitive visualization of the cycle. A freely falling observer, acting as an agent, interacts with the system by performing tasks that either consume or generate work. This interaction is facilitated using a massless box of particles, which the agent lowers or raises at specific instances within the temporally varying gravitational potential. In Figure 1, the observer’s worldline is colour-coded to represent the metric changes perceived by the observer. The tasks performed at events indicated by blue circles constitute a Carnot engine similar to that proposed for the mining of spherical black holes [2].

In the classic formulation of black hole mining protocols, extracting particles precisely from the horizon would result in a perpetual motion machine [3]. However, this is unachievable in practice, since adiabatically lowering the box to the horizon requires infinite energy and time. To circumvent this complication, we can consider a second observer, following a reverse cycle compared to the first one. If particles are exchanged between the reservoirs carried by the two observers, a closed thermodynamic cycle can be maintained throughout and traversed in finite time. As shown below, this still allows for a well-defined temperature ratio between horizons associated with different black branes to be established, in direct analogy with the original (perpetual motion) mining protocol.

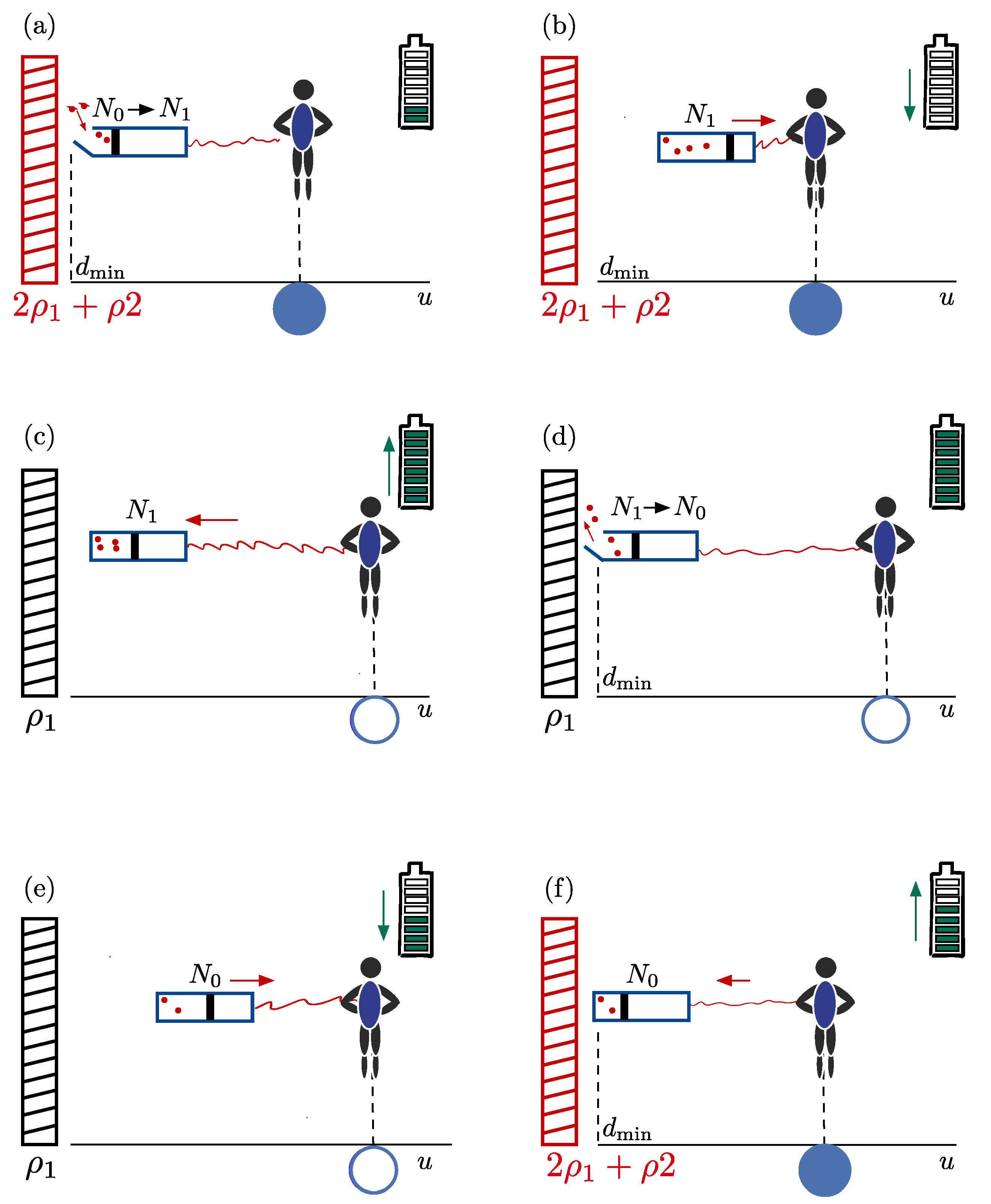
Stages of the thermodynamic cycle—The thermodynamic cycle consists of six distinct steps, each characterised by a task to be performed by the free-falling observer. A cartoon relating the different steps is provided in Figure 2, and a list of the symbols employed in the description can be found in

Table 1. Symbols used to describe the thermodynamic cycle.

$u=0$	Location of central brane
$N_0$	Initial number of particles in box
$U_0$	Initial energy of particles in box
d●	Initial distance of actor to the central brane
	(closed blue dot in Figure 1 and Figure 2)
$d_{○}$	Actor to central brane distance in second position
	(open blue dot in Figure 1 and Figure 2)
$d_{\min }$	Minimal distance between box and central brane
$Q_{\mathrm{H}/\mathrm{C}}$	Heat transferred into/out of box
$W_{\mathrm{in}/\mathrm{out}}$	Work required to raise/lower box

. The stages comprising one full cycle consist of the following:

The initial position—The actor begins at the closed blue dot in Figure 1 and Figure 2, positioned at d_●. At this particular instance of time, the outer branes coincide with the central brane at $u=0$, effectively forming a single brane with high mass-density. The observer carries an energy storage device (a battery), which is partially charged (e.g., it is shown to be $1/4$ full in the cartoon in Figure 2). The observer also holds a closed (massless) box at a distance $d_{\min }$ from the central brane’s horizon, containing $N_0$ particles with total energy $U_0$.

Process (a): Heat Absorption—At the initial position, the observer remotely opens the box, allowing additional particles to flow in. These particles originate either from the black brane horizon (in the perpetual motion formulation) or from the reservoir of a second observer (in the closed-system formulation). Heat $Q_{\mathrm{H}}$ is transferred into the box, increasing the system’s energy to $U=U_0+Q_{\mathrm{H}}$ without performing work.

Process (b): Adiabatic Raising—The observer then adiabatically raises the box to its own position d_●. Adiabatic isolation ensures there is no heat exchange ($\Delta S=0$ and $Q=0$). However, pulling against the gravitational potential requires work $W_{\mathrm{in},1}$, draining the observer’s battery. The system’s energy is $\Delta U=-W_{\mathrm{in},1}$.

Free-fall—In the subsequent stage, the observer free-falls toward the central brane along with their box, traversing an oscillatory trajectory dictated by the gravitational dynamics of the system. Meanwhile, the outer branes separate due to their own oscillatory motion. At some point during their free fall, the observer moves through an outgoing mass sheet, but continues to free-fall unabated. Upon arriving at position $d_{○}$, the observer will perform the next set of tasks. During the entire free fall, the internal energy and particle number in the box remain unchanged.

Process (c): Adiabatic Lowering—At this point, the box will be adiabatically lowered to $d_{\min }$. Gravitational work $W_{\mathrm{out},1}$ increases the battery’s charge during this process. The energy change within the box is $\Delta U=W_{\mathrm{out},1}$, with constant entropy and no heat transfer.

Process (d): Heat Release—Next, particles are allowed to flow out of the box until the initial number of particles, $N_0$, is restored. This reduces the entropy contained in the box, and releases heat $Q_{\mathrm{C}}$. The system’s energy changes by $\Delta U=-Q_{\mathrm{C}}$.

Process (e): Adiabatic Raising—The box is then pulled up to d_●, performing work $W_{\mathrm{in},2}$ against the gravitational potential and partially draining the battery. No heat exchange occurs ($Q=0$ and $\Delta S=0$), thus $\Delta U=W_{\mathrm{in},2}$.

Free-fall—After the box is pulled up, the box and observer free-fall again, and pass through a mass sheet before they return to position d_●. The internal energy does not change during this process.

Process (f): Adiabatic Lowering—Finally, lowering the box to $d_{\min }$ extracts work $W_{\mathrm{out},2}$, and completes the cycle. The battery ends up with a net charge increase, indicating that work has been gained during the cycle. The energy of the box, meanwhile, returns to its initial value $U_0$, satisfying $U_{\mathrm{final}}-U_0=Q_{\mathrm{H}}-W_{\mathrm{in},1}+W_{\mathrm{out},1}-Q_{\mathrm{C}}+W_{\mathrm{in},2}-W_{\mathrm{out},2}=0$.

This sequence can be repeated cyclically, with the observer systematically manipulating the box to extract work. The extracted work is a direct consequence of the gravitational potential differences encountered in the various black brane configurations, and we will discuss the implications of its existence in the next section.

The Carnot cycle—The closed thermodynamic cycle described above can be depicted on an entropy-temperature ($S-T$) diagram, as shown in Figure 3. The labelled arrows indicate the processes encountered during a full cycle, and possible values for the instantaneous charge of the battery at the end of each process (corresponding to those shown in the cartoon depiction of Figure 2) are indicated.

The thermodynamic temperatures indicated in Figure 3 are defined by $T=Q/\Delta S$, applied to the isothermal processes (a) and (d). The changes in entropy associated with the heat transfers $Q_{\mathrm{H}}$ and $Q_{\mathrm{C}}$, encountered close to the black-branes with larger and smaller mass density, respectively, are denoted $\Delta S_{\mathrm{H}}$ and $\Delta S_{\mathrm{C}}$. These changes in entropy are determined entirely by the change in the number of particles in the box, and they are, therefore, equal. The temperature ratio $T_{\mathrm{H}}/T_{\mathrm{C}}$ then becomes:

$$\begin{array}{c}\hfill {\displaystyle \frac{T_{\mathrm{H}}}{T_{\mathrm{C}}}}={\displaystyle \frac{Q_{\mathrm{H}}/\Delta S_{\mathrm{H}}}{Q_{\mathrm{C}}/\Delta S_{\mathrm{C}}}}={\displaystyle \frac{Q_{\mathrm{H}}}{Q_{\mathrm{C}}}}.\end{array}$$

(3)

The presence of this finite ratio defines the thermodynamic process to be a Carnot engine, a cyclic process from which work is extracted. From the definition of temperature as given by Claussius [14], we then know that the heat consumed during each stage of the cycle is proportional to the work gained. In turn, the work that is performed on the actor (or the work the actor performs on the box) is due to the lowering and raising of the box in the gravitational potential. As this is done adiabatically, the work must equal the change in Killing energy $E=N\sqrt{g_{tt}\left(d\right)}{E}_0$, with rest energy $E_0$:

$$\begin{array}{c}\hfill {\displaystyle \frac{T_{\mathrm{H}}}{T_{\mathrm{C}}}}={\displaystyle \frac{(N_1-N_0)E_0\sqrt{{\gamma }_{\mathrm{H}}(d_{●}-d_{\min })}}{(N_1-N_0)E_0\sqrt{{\gamma }_{\mathrm{C}}(d_{○}-d_{\min })}}}\end{array}$$

(4)

Here, ${\gamma }_{\mathrm{C}}=4\pi G{\rho }_1$ and ${\gamma }_{\mathrm{H}}=4\pi G(2{\rho }_2+{\rho }_1)$ are defined by the mass densities of the single or combined black brane systems. At $d_{●}=d_{○}$, we can define a position independent temperature ratio of

$$\begin{array}{c}\hfill {\displaystyle \frac{T_{\mathrm{H}}}{T_{\mathrm{C}}}}=\sqrt{{\displaystyle \frac{{\gamma }_{\mathrm{H}}}{{\gamma }_{\mathrm{C}}}}}.\end{array}$$

(5)

for the temperatures of the boxes during the isothermal processes. Importantly, this ratio is independent of $d_{\min }$ and remains valid in the limit $d_{\min }\to 0$. This is the limit required for the original perpetuum mobile formulation of the mining procedure. In that context, it is often suggested to describe a temperature ratio associated with the horizons for two black holes of different mass. In the present black brane setup, we can likewise recognise the ratio of Equation (5) to be consistent with that of the Unruh temperatures $T_{\mathrm{H},\mathrm{C}}={\alpha }_{\mathrm{H},\mathrm{C}}/\left(2\pi \right)=\sqrt{{\gamma }_{\mathrm{H},\mathrm{C}}}/\left(4\pi \sqrt{\left|u\right|}\right)$ experienced by observers in the metric of Equation (2) undergoing local acceleration $\alpha$ in order to remain static with respect to the black brane singularity.

On thermal equilibrium—The semi-classical description of a heat engine based on black hole mining introduces a well-known interpretational conundrum related to entropy loss [15]. When particles are gradually lowered towards a horizon, their Killing energy approaches zero. Upon crossing the horizon, these particles then contribute to neither the black hole entropy, nor its mass. However, since the particles effectively vanish from the universe, the system appears to lose entropy overall, ostensibly violating the second law of thermodynamics.

The paradox is clarified by two crucial observations. First, the Killing energy reaches zero only at the horizon itself, and it is impossible for any static observer to lower a box of particles to the precise location of the horizon within finite time or energy. As a result, a thermodynamic cycle involving the addition of zero Killing energy particles to the black hole cannot be physically realised, thereby mitigating concerns of entropy loss. Second, even if such a cycle were possible, classical black holes—being perfect absorbers [15]—cannot achieve thermodynamic equilibrium with their surroundings. This renders the concept of temperature for classical black holes undefined and undermines the meaningful assignment of thermodynamic properties in such contexts.

The scenario changes if black holes radiate. Hawking radiation potentially enables black holes to emit energy and establish thermal equilibrium with their environment. In this case, the radiation flux could lend a hypothetical physical basis to the thermodynamic temperature used in black hole mining protocols.

By reframing the discussion to avoid reliance on zero Killing energy particles, an alternative interpretation emerges. Instead of depositing particles into the black brane, one can consider a system where particles are exchanged between two thermodynamic cycles operating in opposite directions. In such a configuration, the Carnot engine’s work originates solely from gravitational potential differences traversed during the cycle. This perspective maintains a classical interpretation: the ratio of temperatures encountered in the Carnot cycle directly reflects the gravitational potential differences or mass ratios of the involved black holes. Thus, the Carnot cycle functions as a precise measurement tool for the properties of the black hole system, rather than as a source of energy extraction.

In the present setup of a thermodynamic cycle based on black branes, the interpretation of the ratio of temperatures reflecting only a ratio of gravitational potentials gains additional credence. The Hawking temperature of the black brane vanishes identically [7], foregoing any possible interpretation in terms of thermodynamic equilibrium or radiation flux.

4. Conclusions

The toy model black brane, with its precise invariance and infinite extent in two spatial directions, does not constitute a realistic description of any actual gravitational object. It instead serves the purpose of making possible a thermodynamic analysis in a mathematically accessible setting constructed out of well-understood gravitational components, consistent with all known laws of nature.

Here, we connected the foundational ideas of Carnot thermodynamics with black brane systems, demonstrating the theoretical feasibility of a thermodynamic cycle involving three symmetrically arranged black branes. We explicitly showed how temperature gradients and gravitational potential differences can drive energy transfer during the thermodynamic cycle. The exact solvability of the black brane system provides theoretical clarity in an area often marred by approximations. It also shows that the idea of gravitational thermodynamic cycles can be applied to spacetimes that are not asymptotically flat, and yield the same type of temperature ratios as in their better-known asymptotically flat cousins.

Black hole thermodynamics is notoriously hard to probe or observe in astronomical settings. Recent progress has been made in simulating and experimentally implementing black hole analogues in a variety of platforms, including electronic systems, gravity waves in fluids, and optical setups [10,11,12,13]. Such gravity analogues are now close to allowing experimental implementation of heat engines and other black hole physics. Because of the invariance of the black brane described here under translations in two spatial directions, its implementation may be especially suitable for setups that naturally favour one-dimensional flows, such as electrons in quantum wires or waves propagating in a flowing fluids [10,13].

The principles encountered in the exact black brane Carnot cycle analysed here, offer insights into energy extraction processes in other gravitational systems, as well as experimental black hole analogues, and the fundamental nature of entropy and temperature in the context of general relativity. As we celebrate 200 years since Carnot’s groundbreaking insights, we reaffirm the timeless relevance of their thermodynamic principles, and their capacity to illuminate physics across all scales.