HECM-Plus: Hyper-Entropy Enhanced Cloud Models for Uncertainty-Aware Design Evaluation in Multi-Expert Decision Systems
Abstract
1. Introduction
2. Cloud Model
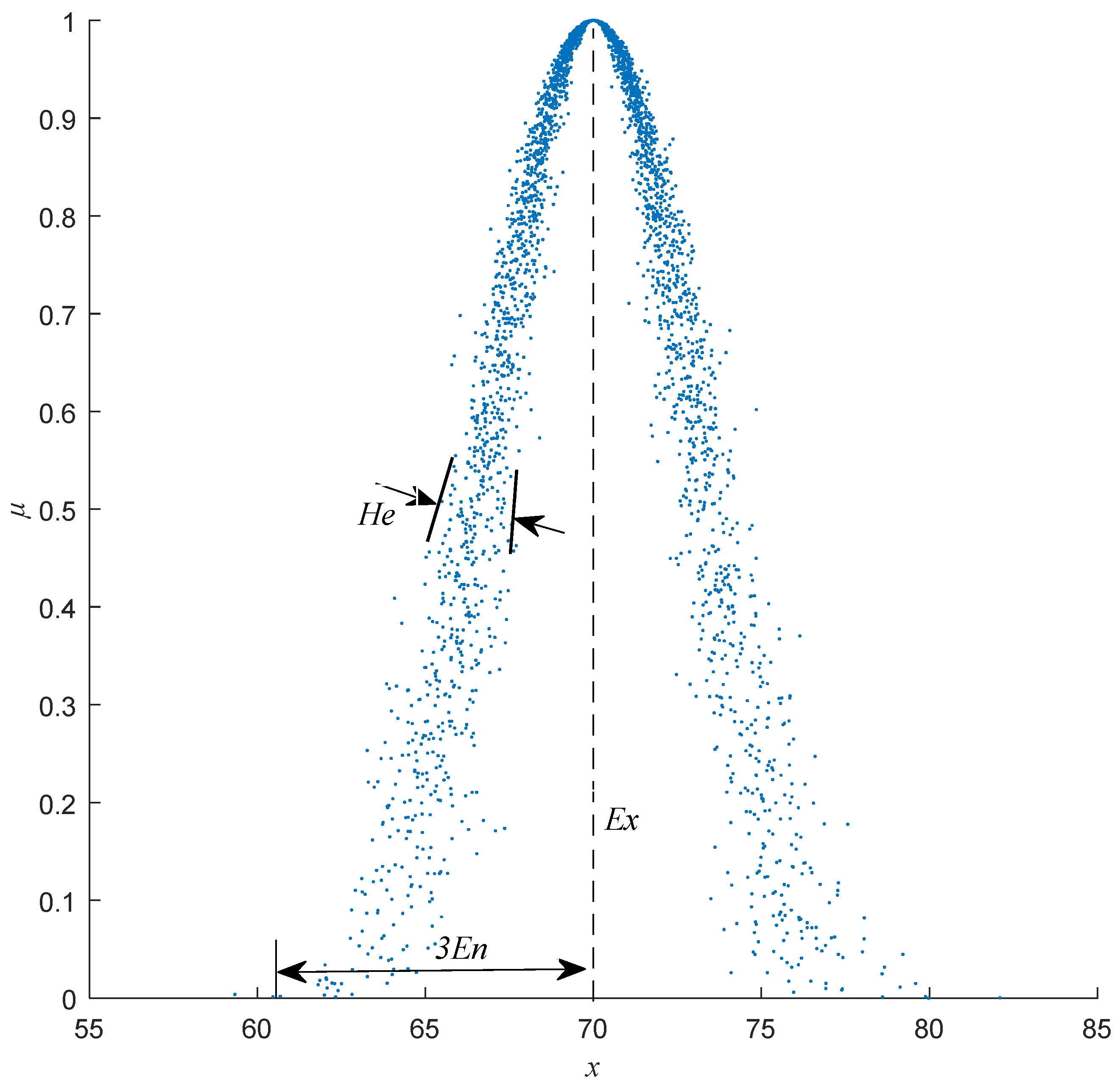
2.1. Cloud and Cloud Drops
2.2. Normal Cloud
2.3. Forward Cloud Algorithm and Reverse Cloud Algorithm
2.3.1. Forward Cloud Algorithm
- Step (1) Generate a normally distributed random number with as the mean and as the standard deviation.
- Step (2) Generate a normally distributed random number with as the mean and (the random number generated in Step 1) as the standard deviation.
- Step (3) Calculate the certainty degree:
- Step (4) Designate the value with certainty degree as a cloud drop in the numerical domain. Repeat Steps (1)~(3) until the required n cloud drops are generated.
2.3.2. Reverse Cloud Algorithm
3. A Normal Cloud Similarity Measurement Method Based on Hellinger Distance
3.1. Normal Cloud Distribution Approximation
3.2. Hellinger Distance Calculation
3.3. Similarity Conversion
3.4. HECM and HECM-Plus Algorithm
3.4.1. HECM Algorithm
3.4.2. HECM-Plus Algorithm
4. Comparative Analysis of Experiments
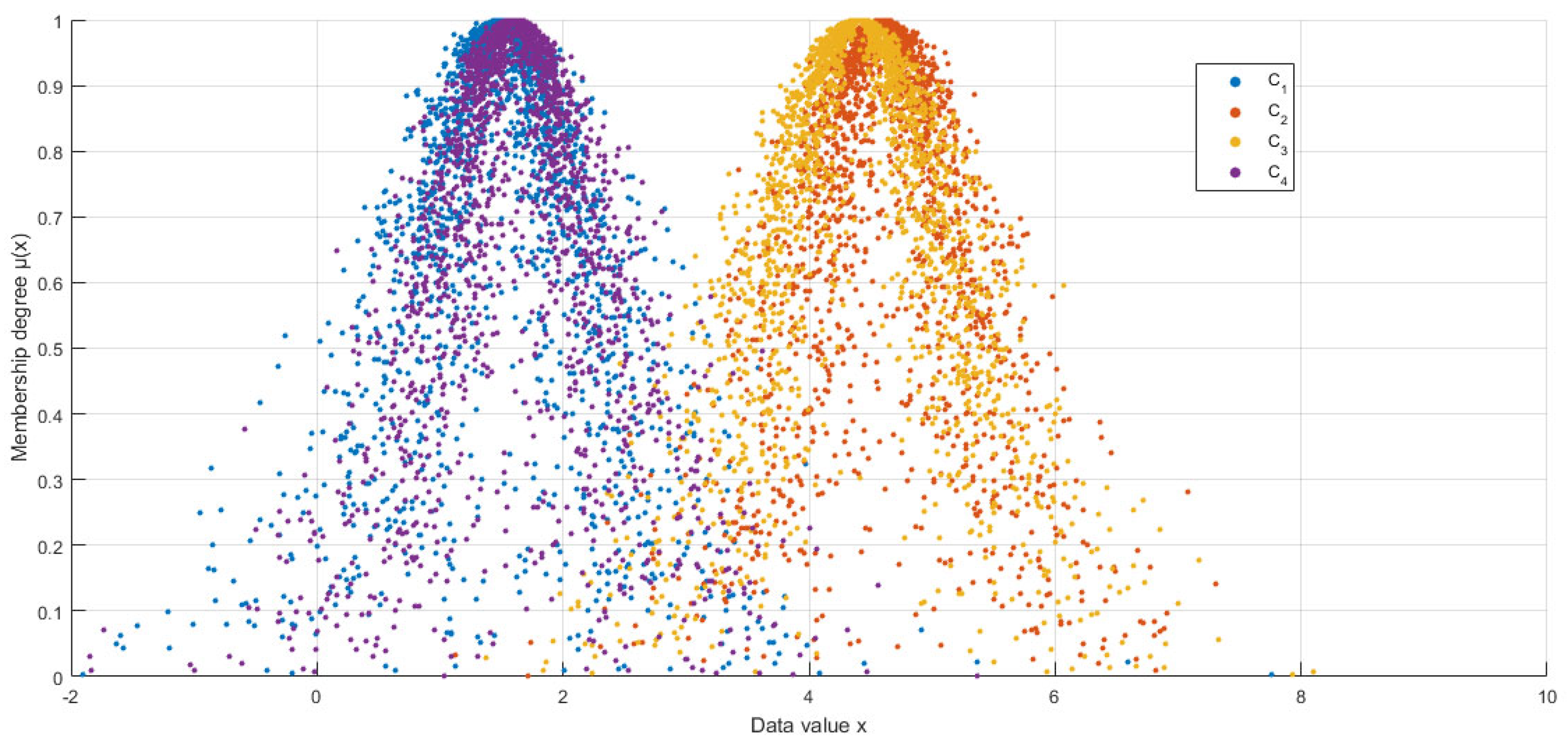
4.1. Numerical Simulation Experiments
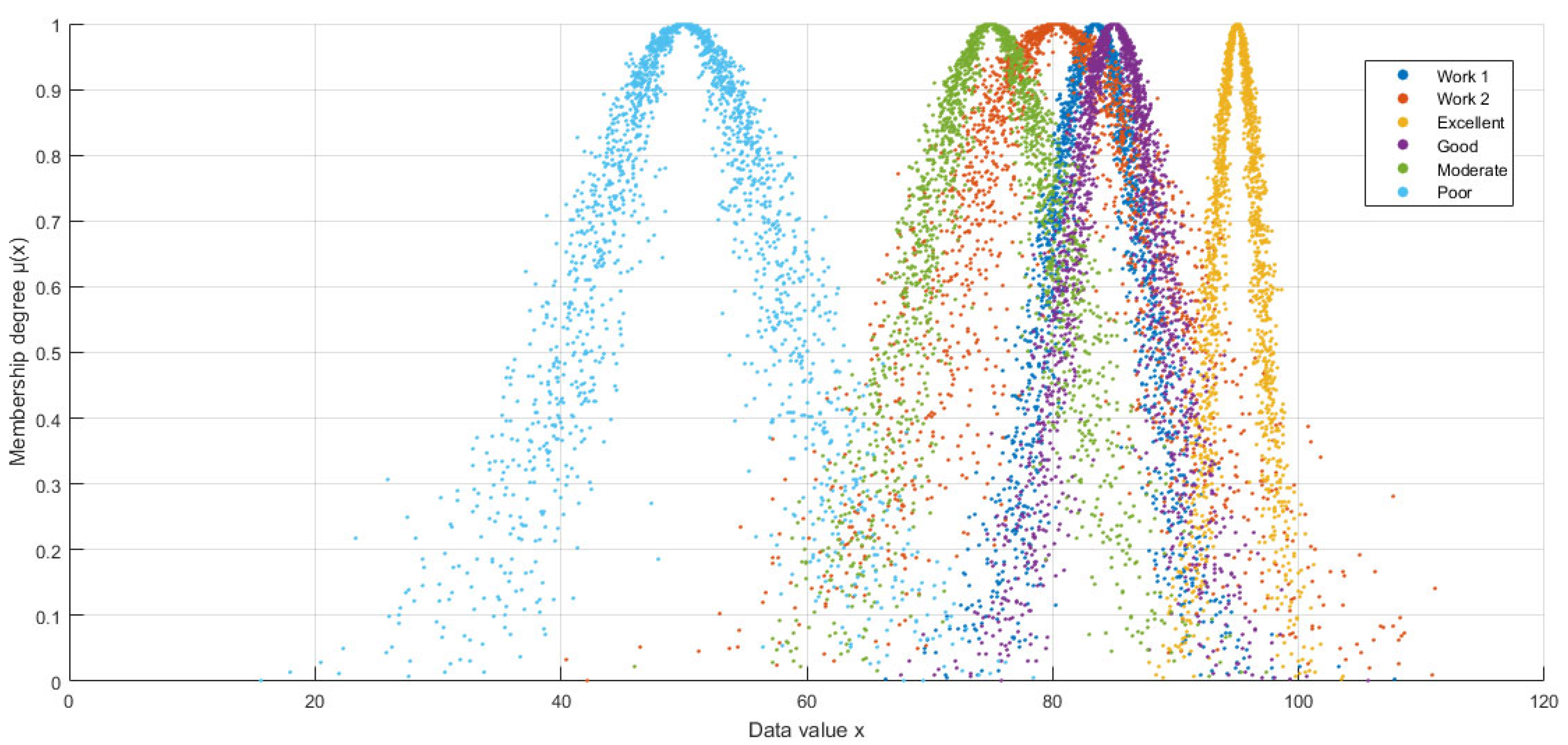
4.2. Time Series Classification Experiments
4.2.1. Classification Calculation Process
- Step (1) Data Preprocessing Stage: The first 90 rows from each category were selected as the training set, and the remaining 10 rows formed the test set, resulting in a training set of 540 time series and a test set of 60 time series.
- Step (2) Segmentation and Dimensionality Reduction: The dimensionality parameter d was adjusted within the range of 2 to 30. Each time series (60 timestamps) was divided into d non-overlapping equal-length segments. If the total length was not perfectly divisible by d, the remainder data points were truncated to ensure equal segment lengths. The mean value of each segment was calculated to achieve dimensionality reduction.
- Step (3) Reverse Cloud Feature Extraction: The reverse cloud algorithm was applied to each dimensional segment to extract digital features of cloud concepts (Ex, En, and He for HECM-Plus; Ex and En for HECM).
- Step (4) Similarity Calculation: Using HECM-Plus and HECM, the similarity between cloud concepts in the training set and the test set was computed, and multi-dimensional similarity matrices were constructed.
- Step (5) Classification Decision: Based on the 1-nearest neighbor principle, the category with the highest similarity in each dimensional similarity matrix was selected as the classification result.
- Step (6) Performance Evaluation: The classification error rate (ratio of misclassified samples to the total samples) was calculated to evaluate the algorithm’s classification performance and accuracy.
4.2.2. Classification Calculation Results
- Comprehensiveness and Accuracy: HECM-Plus effectively captures the geometric characteristics of cloud concepts and quantifies their differences by considering three essential numerical features: Ex, En, and He. This method minimizes information loss and significantly improves the accuracy and reliability of concept differentiation and classification. In particular, Ex indicates the central tendency of cloud concepts, En captures their ambiguity, and He represents the degree of their discreteness. By incorporating these features, HECM-Plus effectively captures the core characteristics of cloud concepts, resulting in more dependable classification results for complex datasets. This method improves classification accuracy and enhances the robustness of the model, ensuring consistent and stable performance across various dataset types and sizes.
- Computational Efficiency: HECM-Plus mainly depends on numerical features to perform direct algebraic operations, eliminating the need for complex integration calculations. Compared with traditional algorithms such as ECM, MCM, and PDCM, HECM-Plus offers a more direct and concise calculation process, leading to a significant reduction in computational complexity. This optimization not only reduces computational resource requirements but also significantly improves computation speed. In particular, when handling large-scale datasets, the algorithm substantially reduces the required time, thereby improving operational efficiency.
- Universality and Extensibility: The Hellinger distance is an f-scattering that meets the criteria of distance axiomatization. Thus, it is suitable for use not only with traditional cloud models but also with higher-order normal clouds and high-dimensional cloud models. The broad applicability of the Hellinger distance is one of its key advantages. The flexibility and adaptability of HECM-Plus allow it to address various real-world challenges, making it a crucial tool in various fields.
5. Application of HECM-Plus to Conflict Resolution in Design
- Excellent: (95, 2, 0.5),
- Good: (85, 4, 1.0),
- Moderate: (75, 6, 1.5),
- Poor: (50, 8, 2.0).
6. Conclusions
- Conceptual discrimination: By reformulating the Hellinger distance with He-adjusted standard deviations (Equations (21)–(24)), HECM-Plus achieved a 12.5% higher discriminative margin than HECM in resolving multi-expert conflicts (Table 6), correcting overestimated similarities (e.g., 0.94 vs. 0.99 for C1–C4 in Table 1) through rigorous uncertainty decomposition.
- Statistical robustness: In time-series classification, HECM-Plus reduced the mean error by 6.8% (0.190 vs. 0.204, p < 0.05) and variance by 26% (Table 4), with a paired t-test confirming significant improvement (t = −3.2856, p = 0.0027), demonstrating superior stability in high-dimensional settings.
- Conflict resolution in multi-criteria design evaluation (MCDM): By reclassifying controversial designs (e.g., overriding an 80.3 average “good” to “moderate” via He-weighted thresholds in Section 5), the algorithm resolved subjective disagreements in expert evaluations, offering a principled framework for design quality assessment.
- Extending HECM-Plus to higher-order normal clouds and high-dimensional scenarios while maintaining its computational efficiency.
- Integrating reliability metrics to dynamically adjust expert contributions during reverse cloud transformations, mitigating bias in He estimation.
- Deploying the algorithm in real-time decision support systems for applications ranging from intelligent design iteration to industrial process monitoring.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.Y.; Liu, C.Y. On the universality of normal cloud model. China Eng. Sci. 2004, 6, 28–34. [Google Scholar] [CrossRef]
- Mandal, S.; Khan, D.A. Cloud-CoCoSo: Cloud Model-Based Combined Compromised Solution Model for Trusted Cloud Service Provider Selection. Arab. J. Sci. Eng. 2022, 47, 10307–10332. [Google Scholar] [CrossRef]
- Li, W.S.; Zhao, J.; Xiao, B. Multimodal medical image fusion by cloud model theory. Signal Image Video Process 2018, 12, 437–444. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.T.; Li, S. Cloud-Cluster: An uncertainty clustering algorithm based on cloud model. Knowl.-Based Syst. 2023, 263, 110261. [Google Scholar] [CrossRef]
- Wu, Y.N.; Chu, H.; Xu, C.B. Risk assessment of wind-photovoltaic-hydrogen storage projects using an improved fuzzy synthetic evaluation approach based on cloud model: A case study in China. J. Energy Storage 2021, 38, 102580. [Google Scholar] [CrossRef]
- Guan, J.; Liu, J.; Chen, H.; Bi, W. A Multi-Criteria Decision-Making Approach for Equipment Evaluation Based on Cloud Model and VIKOR Method. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 1311. [Google Scholar] [CrossRef]
- Chai, S.L.; Wang, Z. Product design evaluation based on FAHP and cloud model. J. Intell. Fuzzy Syst. 2022, 43, 2463–2483. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, Y.; Chai, S.L.; Niu, S.F.; Yang, M.L.; Wu, G.R. Product design evaluation based on improved CRITIC and Comprehensive Cloud-TOPSIS-Applied to automotive styling design evaluation. Adv. Eng. Inform. 2024, 60, 102361. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, R. A review of similarity metrics for cloud model. Data Commun. 2019, 6, 43–49. [Google Scholar]
- Zhang, G.; Li, D.; Li, P.; Kang, J.C.; Chen, G.S. A collaborative filtering recommendation algorithm based on cloud model. J. Softw. 2007, 18, 2403–2411. [Google Scholar] [CrossRef]
- Li, H.-L.; Gong, C.-H.; Qian, W.-R. Similarity measurement between normal cloud models. Acta Electron. Sin. 2011, 39, 2561–2567. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, J.J.; Liu, X.D. An integrated similarity measure method for normal cloud model based on shape and distance. Sys. Eng.—Theory Pract. 2017, 37, 742–751. [Google Scholar] [CrossRef]
- Xu, C.; Xu, H. Similarity measurement method for normal cloud based on Hellinger distance and its application. CAAI Trans. Intell. Syst. 2023, 18, 1312–1321. [Google Scholar] [CrossRef]
- Li, D.Y.; Han, J.W.; Shi, X.M.; Chan, M.C. Knowledge representation and discovery based on linguistic atoms. Knowl.-Based Syst. 1998, 10, 431–440. [Google Scholar] [CrossRef]
- Li, D. Knowledge Representation in KDD Based on Linguistic Atoms. J. Comput. Sci. Technol. 1997, 12, 481–496. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, R.Z.; Qiu, X.W. A survey on cloud model. J. Internet Technol. 2023, 24, 1159–1167. [Google Scholar] [CrossRef]
- Li, Q.; Dong, Q.K.; Zhao, L. Modified forward cloud generator in the cloud model. J. Xidian Univ. 2013, 40, 169–174. [Google Scholar] [CrossRef]
- Chen, H.; Li, B.; Liu, C. An Algorithm of Backward Cloud without Certainty Degree. J. Chin. Comput. Syst. 2015, 36, 544–549. [Google Scholar] [CrossRef]
- Wang, G.Y.; Xu, C.L.; Li, D.Y. Generic normal cloud model. Inf. Sci. 2014, 280, 1–15. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, F.; Duan, J.; Kurths, J. Quantifying model uncertainty for the observed non-Gaussian data by the Hellinger distance. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105720. [Google Scholar] [CrossRef]
- Synthetic Control Chart Time Series. 7 June 1999. Available online: http://archive.ics.uci.edu/ml/datasets/Synthetic+Control+Chart+Time+Series (accessed on 30 May 2024).

| Similarity | LICM | ECM | MCM | PDCM | HECM | HCCM | HECM-Plus |
|---|---|---|---|---|---|---|---|
| S(C1,C2) | 0.96 | 0.01 | 0.33 | 0.01 | 0.04 | 0.22 | 0.04 |
| S(C1,C3) | 0.97 | 0.04 | 0.37 | 0.03 | 0.11 | 0.26 | 0.08 |
| S(C1,C4) | 0.99 | 0.94 | 0.96 | 0.89 | 0.99 | 0.99 | 0.94 |
| S(C2,C3) | 0.99 | 0.86 | 0.95 | 0.80 | 0.97 | 0.86 | 0.87 |
| S(C2,C4) | 0.97 | 0.01 | 0.38 | 0.01 | 0.04 | 0.22 | 0.04 |
| S(C3,C4) | 0.98 | 0.04 | 0.37 | 0.03 | 0.11 | 0.26 | 0.09 |
| Cloud Model | HECM Variance | HECM-Plus Variance | Variance Increase (%) | HECM Standard Deviation Ratio | HECM-Plus Standard Deviation Ratio |
|---|---|---|---|---|---|
| C1 | 0.3927 | 0.5076 | 29.3% | ||
| C4 | 0.3619 | 0.4571 | 26.3% |
| Degree of Variation | LICM | ECM | MCM | PDCM | HECM | HCCM | HECM-Plus |
|---|---|---|---|---|---|---|---|
| δC1 | 0.05 | 1.83 | 1.22 | 1.74 | 1.83 | 1.50 | 1.76 |
| δC2 | 0.05 | 1.70 | 1.19 | 1.58 | 1.86 | 1.28 | 1.66 |
| δC3 | 0.03 | 1.64 | 1.16 | 1.54 | 1.72 | 1.20 | 1.58 |
| δC4 | 0.03 | 1.83 | 1.17 | 1.74 | 1.83 | 1.50 | 1.76 |
| Mean Classification Error Rate | Standard Deviation of Classification Error Rate | |
|---|---|---|
| HECM-Plus | 0.19033905 | 0.034925326 |
| HECM | 0.204222243 | 0.047171944 |
| No. | Expert 1 | Expert 2 | Expert 3 | Expert 4 | Expert 5 | Expert 6 | Expert 7 | Expert 8 | Expert 9 | Expert 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Work 1 | 88 | 85 | 83 | 82 | 89 | 83 | 88 | 83 | 75 | 79 |
| Work 2 | 61 | 90 | 75 | 80 | 85 | 95 | 85 | 82 | 80 | 70 |
| Algorithm | Work | Excellent | Good | Moderate | Poor | Grade |
|---|---|---|---|---|---|---|
| HECM-Plus | 1 | 0.0983 | 0.8716 | 0.4447 | 0.0165 | Good |
| 2 | 0.1989 | 0.5713 | 0.6963 | 0.1199 | Moderate | |
| HECM | 1 | 0.0167 | 0.8144 | 0.2792 | 0.0004 | Good |
| 2 | 0.0936 | 0.5205 | 0.6157 | 0.0204 | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, J.; Liu, Z. HECM-Plus: Hyper-Entropy Enhanced Cloud Models for Uncertainty-Aware Design Evaluation in Multi-Expert Decision Systems. Entropy 2025, 27, 475. https://doi.org/10.3390/e27050475
Pu J, Liu Z. HECM-Plus: Hyper-Entropy Enhanced Cloud Models for Uncertainty-Aware Design Evaluation in Multi-Expert Decision Systems. Entropy. 2025; 27(5):475. https://doi.org/10.3390/e27050475
Chicago/Turabian StylePu, Jiaozi, and Zongxin Liu. 2025. "HECM-Plus: Hyper-Entropy Enhanced Cloud Models for Uncertainty-Aware Design Evaluation in Multi-Expert Decision Systems" Entropy 27, no. 5: 475. https://doi.org/10.3390/e27050475
APA StylePu, J., & Liu, Z. (2025). HECM-Plus: Hyper-Entropy Enhanced Cloud Models for Uncertainty-Aware Design Evaluation in Multi-Expert Decision Systems. Entropy, 27(5), 475. https://doi.org/10.3390/e27050475






