LDPC Codes on Balanced Incomplete Block Designs: Construction, Girth, and Cycle Structure Analysis
Abstract
1. Introduction
- Novel structured construction: We present a systematic framework for constructing LDPC codes using complete BIBDs. The proposed method generates parity-check matrices with guaranteed structural properties that satisfy the row–column (RC) constraints, extending the partial geometry approach established in [18]. The construction method provides a mathematically rigorous yet practically viable coding solution that bridges the gap between theoretical design and communication requirements. This makes it particularly attractive for applications demanding both excellent error correction capability and implementation feasibility.
- Girth guarantees and performance analysis: We provide a rigorous proof that the BIBD-LDPC codes achieve a minimum girth of 6, effectively eliminating detrimental short cycles that impair iterative decoding. The inherent properties of BIBDs, including balanced connectivity and optimized cycle structure, naturally prevent small trapping sets and low-weight code words, thereby enhancing both waterfall-region performance and error-floor characteristics.
- Comprehensive cycle analysis: We develop a systematic methodology for analyzing the cycle structure of the constructed codes. The proposed technique enables precise enumeration of cycles (particularly lengths 6 and 8) in the Tanner graphs, with a generalizable framework that can be extended to count longer cycles (e.g., 10, 12, etc.). This analysis provides valuable insights into the code’s graphical properties and decoding behavior.
2. LDPC Codes Constructed from BIBDs and Their Tanner Graphs
2.1. LDPC Codes and Tanner Graphs
2.2. Balanced Incomplete Block Designs (BIBDs)
- (1)
- Each block in contains exactly points for .
- (2)
- Every pair of distinct points in is contained in exactly blocks.
2.3. LDPC Codes Constructed Based on BIBDs
3. Girth and Cycle Structure Analysis of BIBD-LDPC Codes
3.1. Cycle Structure of BIBD-LDPC Codes
3.2. Girth of BIBD-LDPC Codes
3.3. A Method for Counting Short Cycles of BIBD-LDPC Codes
- Selection of i points from : The number of ways to choose i distinct points from the points in is given by the combination formula expressed asThis quantity is denoted by .
- Exclusion of invalid cases: Among the chosen i points, some cases must be excluded where any t adjacent points (for ) lie in the same block. These cases require a detailed combinatorial analysis, and the number of such invalid cases is denoted by .
- Counting valid cycles of length : For the remaining valid selections of i points, the number of cycles of length that can be formed is denoted by . This involves determining how many distinct cycles of length exist for each valid set of i points. This is analogous to the circle permutation problem but without considering the order of permutation. A simple counting argument shows thatThis formula accounts for the number of distinct cycles that can be formed from i points, treating rotations and reflections as identical.
3.3.1. Number of Cycles of Length 6
3.3.2. Number of Cycles of Length 8
- (1)
- For each block, the number of ways to choose four points is expressed as
- (2)
- The total number of blocks in the BIBD is expressed as
- (3)
- Thus, the total number of cases where four points lie in the same block is expressed as
- (1)
- For each block, the number of ways to choose three points is expressed as
- (2)
- The fourth point must be chosen from the remaining points (since it cannot be in the same block as the first three points).
- (3)
- The total number of blocks in the BIBD is
- (4)
- Thus, the total number of cases where three points lie in the same block and the fourth point lies in a different block is expressed as
4. Short Cycles of Specific BIBD-LDPC Codes
- (1)
- If or , there exists a BIBD.
- (2)
- If or , there exists a BIBD.
- (3)
- If or , there exists a BIBD.
- (4)
- If or for 16, 21, 36, 46, 51, 61, 81, 166, 226, 231, 256, 261, 286, 316, 321, 346, 351, 376, 406, 411, 436, 441, 471, 501, 561, 591, 616, 646, 651, 676, 771, 796, and 801, there exists a BIBD.
- (5)
- If for 1, 2, 3, 5, 6, 12, 14, 17, 19, 22, 27, 33, 37, 39, 42, 47, 59, and 62 or for 3, 19, 34, and 39, there exists a BIBD.
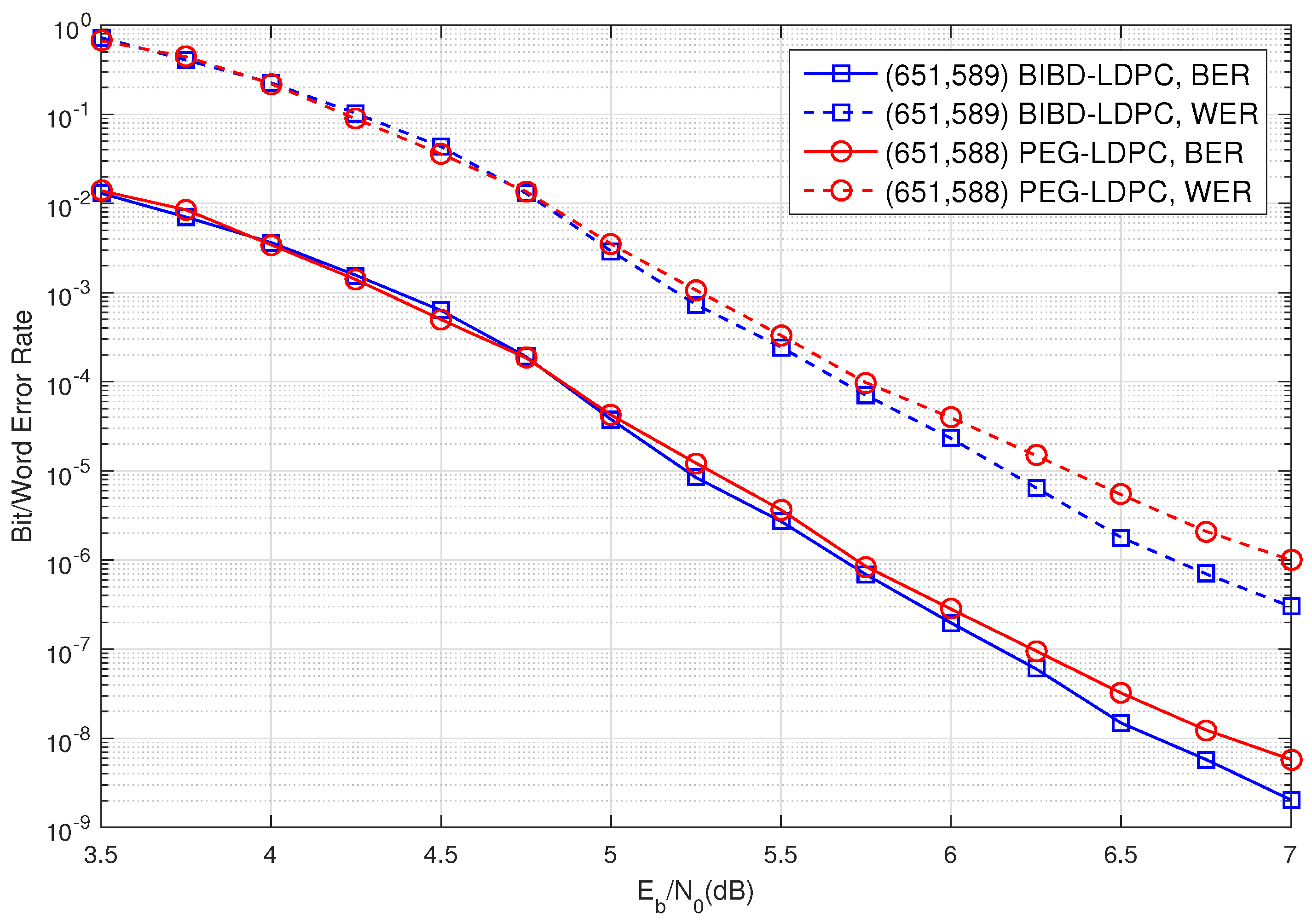
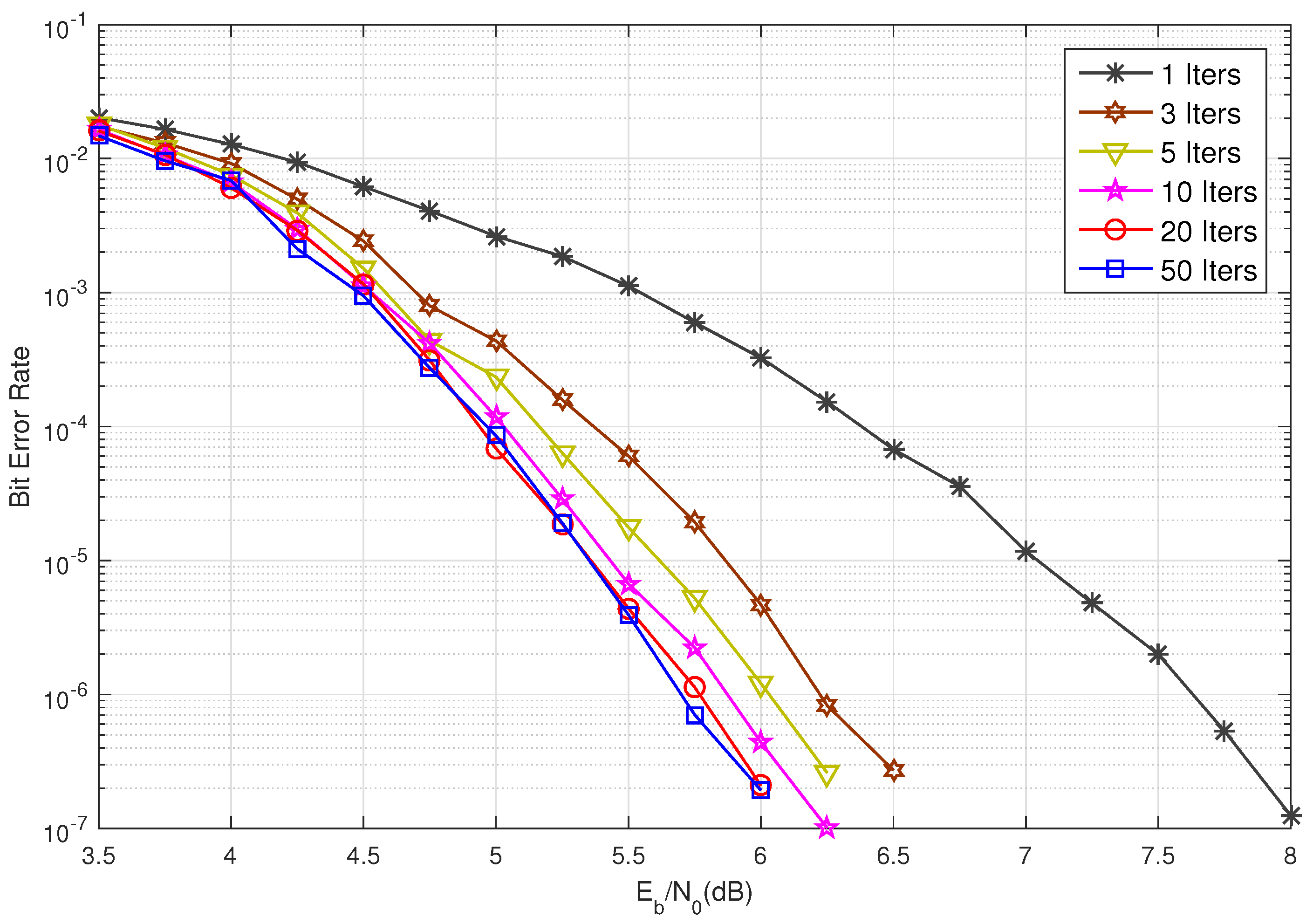
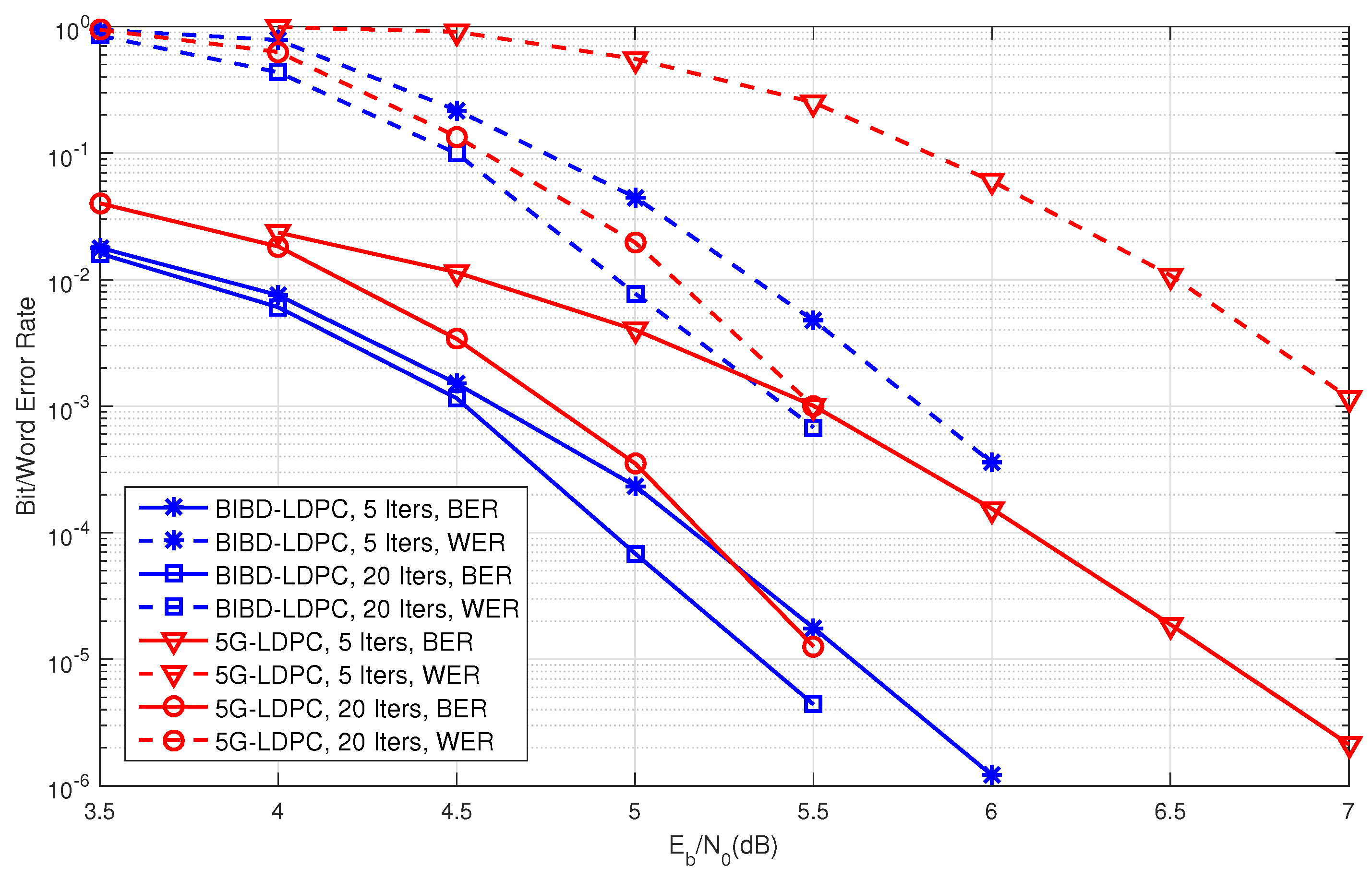
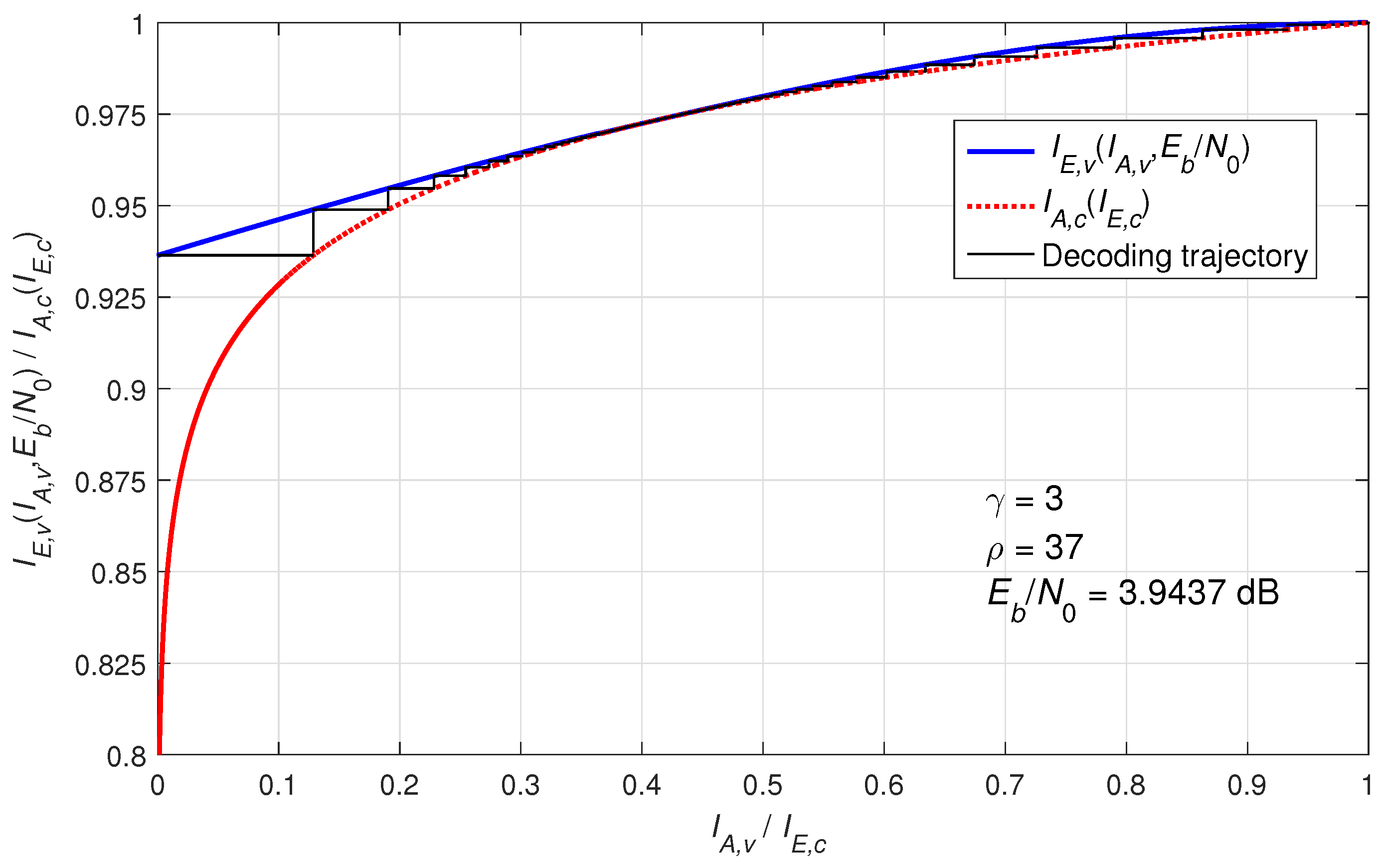
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LDPC | Low-density parity check |
| BIBD | Balanced incomplete block design |
| BIBD-LDPC codes | LDPC codes constructed from BIBDs |
| ML | Maximum likelihood |
| RC | Row–column |
| QC-LDPC | Quasi-cyclic LDPC |
| Number of cycles of length 6 | |
| Number of cycles of length 8 | |
| AWGN | Additive white Gaussian noise |
| BPSK | Binary phase-shift keying |
| SPA | Sum-product algorithm |
| PEG | Progressive edge growth |
| PEG-LDPC | LDPC code based on the progressive edge-growth algorithm |
| BER | Bit-error rate |
| WER | Word-error rate |
References
- Tanner, R.M. A recursive approach to low complexity codes. IEEE Trans. Inf. Theory 1981, 27, 533–547. [Google Scholar] [CrossRef]
- Li, J.; Lin, S.; Abdel-Ghaffar, K.; Ryan, W.E.; Costello, D.J., Jr. LDPC Code Designs, Constructions, and Unification; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Blake, I.F.; Lin, S. On short cycle enumeration in biregular bipartite graphs. IEEE Trans. Inf. Theory 2018, 64, 6526–6535. [Google Scholar] [CrossRef]
- Halford, T.; Chugg, K. An algorithm for counting short cycles in bipartite graphs. IEEE Trans. Inf. Theory 2006, 52, 287–292. [Google Scholar] [CrossRef]
- Karimi, M.; Banihashemi, A.H. Counting Short Cycles of Quasi Cyclic Protograph LDPC Codes. IEEE Commun. Lett. 2012, 16, 400–403. [Google Scholar] [CrossRef]
- Dehghan, A.; Banihashemi, A.H. On Computing the Multiplicity of Cycles in Bipartite Graphs Using the Degree Distribution and the Spectrum of the Graph. IEEE Trans. Inf. Theory 2019, 65, 3778–3789. [Google Scholar] [CrossRef]
- Dehghan, A.; Banihashemi, A.H. Counting Short Cycles in Bipartite Graphs: A Fast Technique/Algorithm and a Hardness Result. IEEE Trans. Commun. 2020, 68, 1378–1390. [Google Scholar] [CrossRef]
- Dehghan, A.; Banihashemi, A.H. On Computing the Number of Short Cycles in Bipartite Graphs Using the Spectrum of the Directed Edge Matrix. IEEE Trans. Inf. Theory 2020, 66, 6037–6047. [Google Scholar] [CrossRef]
- Karimi, M.; Banihashemi, A.H. Message-Passing Algorithms for Counting Short Cycles in a Graph. IEEE Trans. Commun. 2013, 61, 485–495. [Google Scholar] [CrossRef]
- Li, J.; Lin, S.; Abdel-Ghaffar, K. Improved message-passing algorithm for counting short cycles in bipartite graphs. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 416–420. [Google Scholar]
- Fossorier, M. Quasicyclic low-density parity-check codes from circulant permutation matrices. IEEE Trans. Inf. Theory 2004, 50, 1788–1793. [Google Scholar] [CrossRef]
- Wu, X.; You, X.; Zhao, C. A necessary and sufficient condition for determining the girth of quasi-cyclic LDPC codes. IEEE Trans. Commun. 2008, 56, 854–857. [Google Scholar] [CrossRef]
- Gomez-Fonseca, A.; Smarandache, R.; Mitchell, D.G.M. An Efficient Strategy to Count Cycles in the Tanner Graph of Quasi-Cyclic LDPC Codes. IEEE J. Sel. Areas Inf. Theory 2023, 4, 499–513. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.D.; Li, H.; Zhu, H.; Zhang, B.; Liu, H. A cyclic-shift based method for counting cycles of quasi-cyclic LDPC codes. Electron. Lett. 2024, 60, e13085. [Google Scholar] [CrossRef]
- Jiang, X.; Xia, X.G.; Lee, M.H. Efficient Progressive Edge-Growth Algorithm Based on Chinese Remainder Theorem. IEEE Trans. Commun. 2014, 62, 442–451. [Google Scholar] [CrossRef]
- Hu, X.Y.; Eleftheriou, E.; Arnold, D. Regular and irregular progressive edge-growth tanner graphs. IEEE Trans. Inf. Theory 2005, 51, 386–398. [Google Scholar] [CrossRef]
- He, X.; Zhou, L.; Du, J. PEG-Like Design of Binary QC-LDPC Codes Based on Detecting and Avoiding Generating Small Cycles. IEEE Trans. Commun. 2018, 66, 1845–1858. [Google Scholar] [CrossRef]
- Diao, Q.; Tai, Y.Y.; Lin, S.; Abdel-Ghaffar, K. LDPC Codes on Partial Geometries: Construction, Trapping Set Structure, and Puncturing. IEEE Trans. Inf. Theory 2013, 59, 7898–7914. [Google Scholar] [CrossRef]
- Diao, Q.; Li, J.; Lin, S.; Blake, I.F. New Classes of Partial Geometries and Their Associated LDPC Codes. IEEE Trans. Inf. Theory 2016, 62, 2947–2965. [Google Scholar] [CrossRef]
- Li, J.; Gong, Y.; Xiao, X.; Lin, S.; Abdel-Ghaffar, K. Cyclic Partial Geometries and Their Associated LDPC and Constant-Weight Codes. IEEE Trans. Inf. Theory 2023, 69, 5570–5596. [Google Scholar] [CrossRef]
- Xu, H.; Yu, Z.; Feng, D.; Zhu, H. New construction of partial geometries based on group divisible designs and their associated LDPC codes. Phys. Commun. 2020, 39, 100970. [Google Scholar] [CrossRef]
- Li, J.; Liu, K.; Lin, S.; Abdel-Ghaffar, K. Algebraic Quasi-Cyclic LDPC Codes: Construction, Low Error-Floor, Large Girth and a Reduced-Complexity Decoding Scheme. IEEE Trans. Commun. 2014, 62, 2626–2637. [Google Scholar] [CrossRef]
- Tang, H.; Xu, J.; Lin, S.; Abdel-Ghaffar, K. Codes on finite geometries. IEEE Trans. Inf. Theory 2005, 51, 572–596. [Google Scholar] [CrossRef]
- Zhang, G. Type-II quasi-cyclic low-density parity-check codes from Sidon sequences. Electron. Lett. 2016, 52, 367–369. [Google Scholar] [CrossRef]
- Karimi, B.; Banihashemi, A.H. Construction of Irregular Protograph-Based QC-LDPC Codes with Low Error Floor. IEEE Trans. Commun. 2021, 69, 3–18. [Google Scholar] [CrossRef]
- Gruner, A.; Huber, M. Low-Density Parity-Check Codes from Transversal Designs with Improved Stopping Set Distributions. IEEE Trans. Commun. 2013, 61, 2190–2200. [Google Scholar] [CrossRef]
- Li, J.; Liu, K.; Lin, S.; Abdel-Ghaffar, K.; Ryan, W.E. An unnoticed strong connection between algebraic-based and protograph-based LDPC codes, Part I: Binary case and interpretation. In Proceedings of the 2015 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 1–6 February 2015; pp. 36–45. [Google Scholar]
- Johnson, S.; Weller, S. Resolvable 2-designs for regular low-density parity-check codes. IEEE Trans. Commun. 2003, 51, 1413–1419. [Google Scholar] [CrossRef]
- Ammar, B.; Honary, B.; Kou, Y.; Xu, J.; Lin, S. Construction of low-density parity-check codes based on balanced incomplete block designs. IEEE Trans. Inf. Theory 2004, 50, 1257–1269. [Google Scholar] [CrossRef]
- Lan, L.; Tai, Y.Y.; Lin, S.; Memari, B.; Honary, B. New constructions of quasi-cyclic LDPC codes based on special classes of BIBD’s for the AWGN and binary erasure channels. IEEE Trans. Commun. 2008, 56, 39–48. [Google Scholar] [CrossRef]
- Djordjevic, I.B. Quantum LDPC Codes from Balanced Incomplete Block Designs. IEEE Commun. Lett. 2008, 12, 389–391. [Google Scholar] [CrossRef]
- Falsafain, H.; Esmaeili, M. Construction of Structured Regular LDPC Codes: A Design-Theoretic Approach. IEEE Trans. Commun. 2013, 61, 1640–1647. [Google Scholar] [CrossRef]
- Wang, Y.J.; Xiao, Z.Y.; Xiong, X.Y.; Yan, J.Z.; Wang, C.; Shi, S. A Rate Scalable Construction of Non-Homogeneous Quantum LDPC Codes of CSS Type Based on Balanced Incomplete Block Design. IEEE Commun. Lett. 2021, 25, 1408–1411. [Google Scholar] [CrossRef]
- Colbourn, C.J.; Dinitz, J. Handbook of Combinatorial Designs; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Xu, H.; Feng, D.; Luo, R.; Bai, B. Construction of Quasi-Cyclic LDPC Codes via Masking with Successive Cycle Elimination. IEEE Commun. Lett. 2016, 20, 2370–2373. [Google Scholar] [CrossRef]
- 3GPP TS 38.212. 5G NR; Multiplexing and Channel Coding (Release 15) V15.3.0; Sophia Antipolis: Valbonne, France, 2018. [Google Scholar]
- Liva, G.; Chiani, M. Protograph LDPC Codes Design Based on EXIT Analysis. In Proceedings of the IEEE GLOBECOM 2007—IEEE Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007; pp. 3250–3254. [Google Scholar]
| BIBDs | BIBD-LDPC Codes | |||
|---|---|---|---|---|
| Code Length | Row Weight | Column Weight | Code Rate | |
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| BIBDs | Cycle Lengths and Numbers of BIBD-LDPC Codes | ||
|---|---|---|---|
| Length 4 | Length 6 | Length 8 | |
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhang, X.; Xu, M.; Yu, H.; Zhu, H. LDPC Codes on Balanced Incomplete Block Designs: Construction, Girth, and Cycle Structure Analysis. Entropy 2025, 27, 476. https://doi.org/10.3390/e27050476
Xu H, Zhang X, Xu M, Yu H, Zhu H. LDPC Codes on Balanced Incomplete Block Designs: Construction, Girth, and Cycle Structure Analysis. Entropy. 2025; 27(5):476. https://doi.org/10.3390/e27050476
Chicago/Turabian StyleXu, Hengzhou, Xiaodong Zhang, Mengmeng Xu, Haipeng Yu, and Hai Zhu. 2025. "LDPC Codes on Balanced Incomplete Block Designs: Construction, Girth, and Cycle Structure Analysis" Entropy 27, no. 5: 476. https://doi.org/10.3390/e27050476
APA StyleXu, H., Zhang, X., Xu, M., Yu, H., & Zhu, H. (2025). LDPC Codes on Balanced Incomplete Block Designs: Construction, Girth, and Cycle Structure Analysis. Entropy, 27(5), 476. https://doi.org/10.3390/e27050476






