Democratic Thwarting of Majority Rule in Opinion Dynamics: 1. Unavowed Prejudices Versus Contrarians
Abstract
1. Introduction
2. Spontaneous Thwarting of Democratic Global Balance in Homogeneous Populations
3. Heterogeneous Agents: The Contrarian Thwarting
3.1. Size 2
3.2. Size 3
3.3. Size 4
4. Combined Thwarting Effect of Prejudices and Contrarians
4.1. Size 2
4.1.1. Dynamics : Part 1
4.1.2. Dynamics : Part 2
4.2. Size 4
5. A New Unexpected Regime of Stationary Alternating Polarization
6. Conclusions
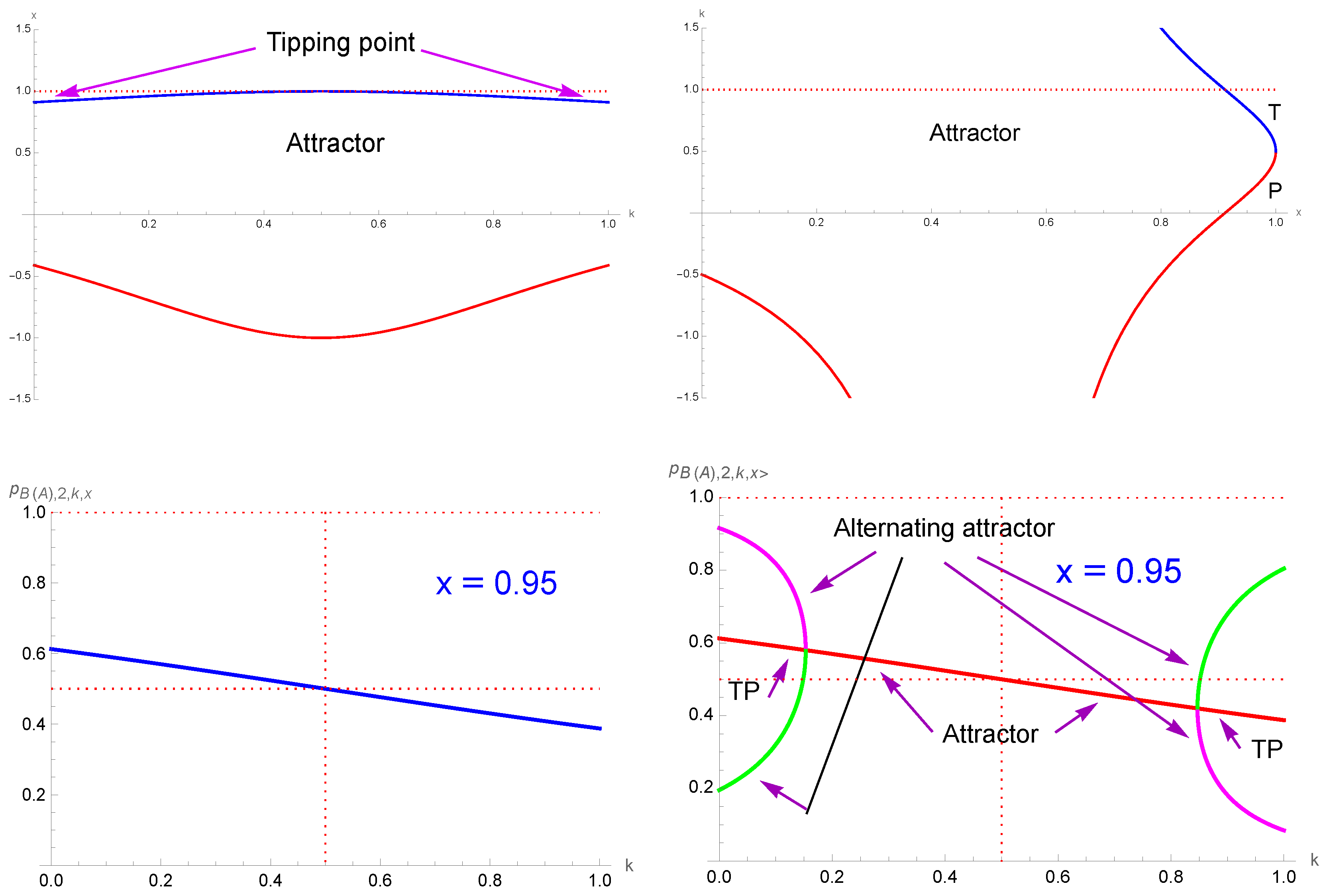
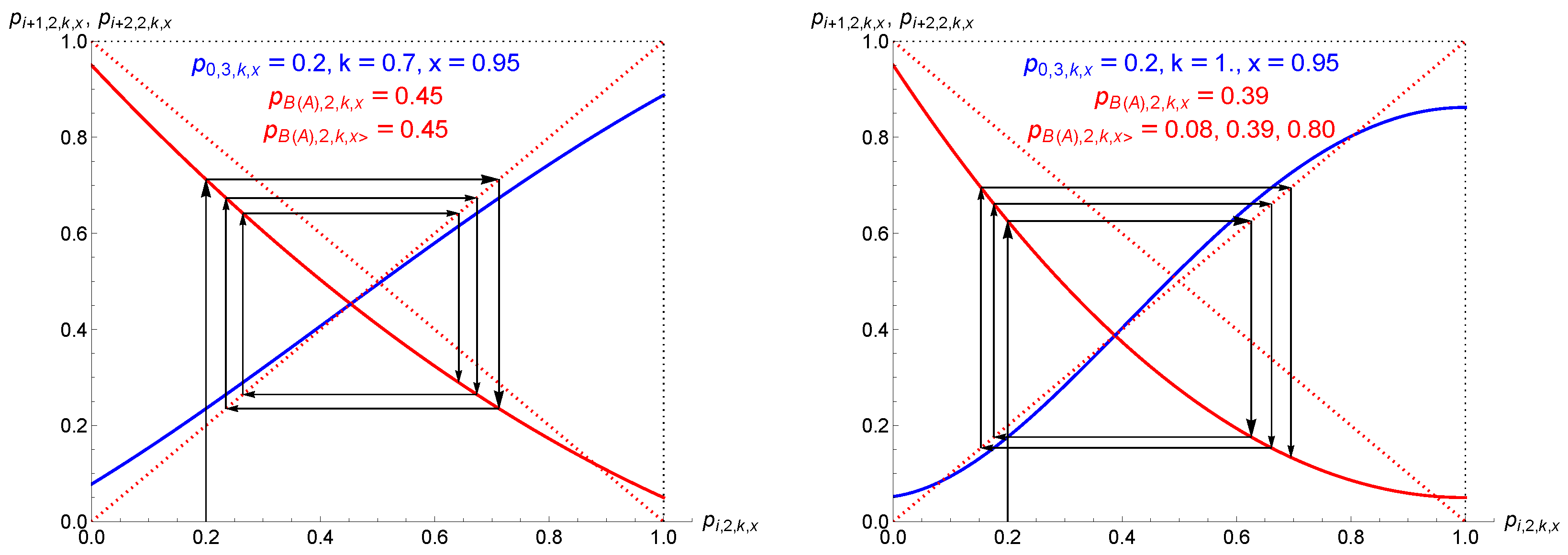
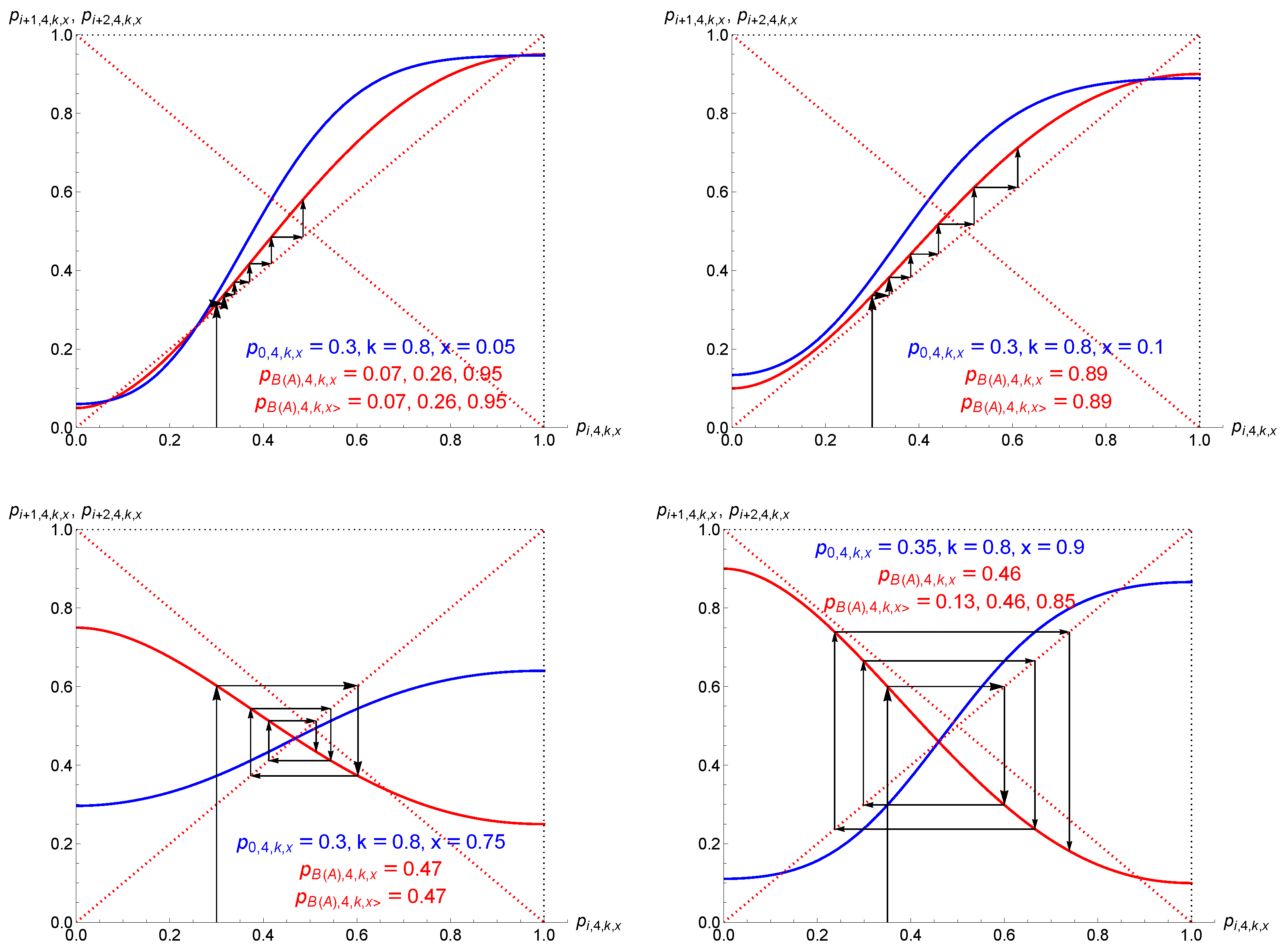
- Tipping point: In the first case, opinion A (B) needs to gather a proportion of initial support larger than the tipping point to ensure a democratic victory over time, with ongoing discussions among the agents. However, the results showed that this regime arises only for extreme proportions of contrarians, either very low or very high values. For , one percent of contrarians suppresses the tipping-point regime.
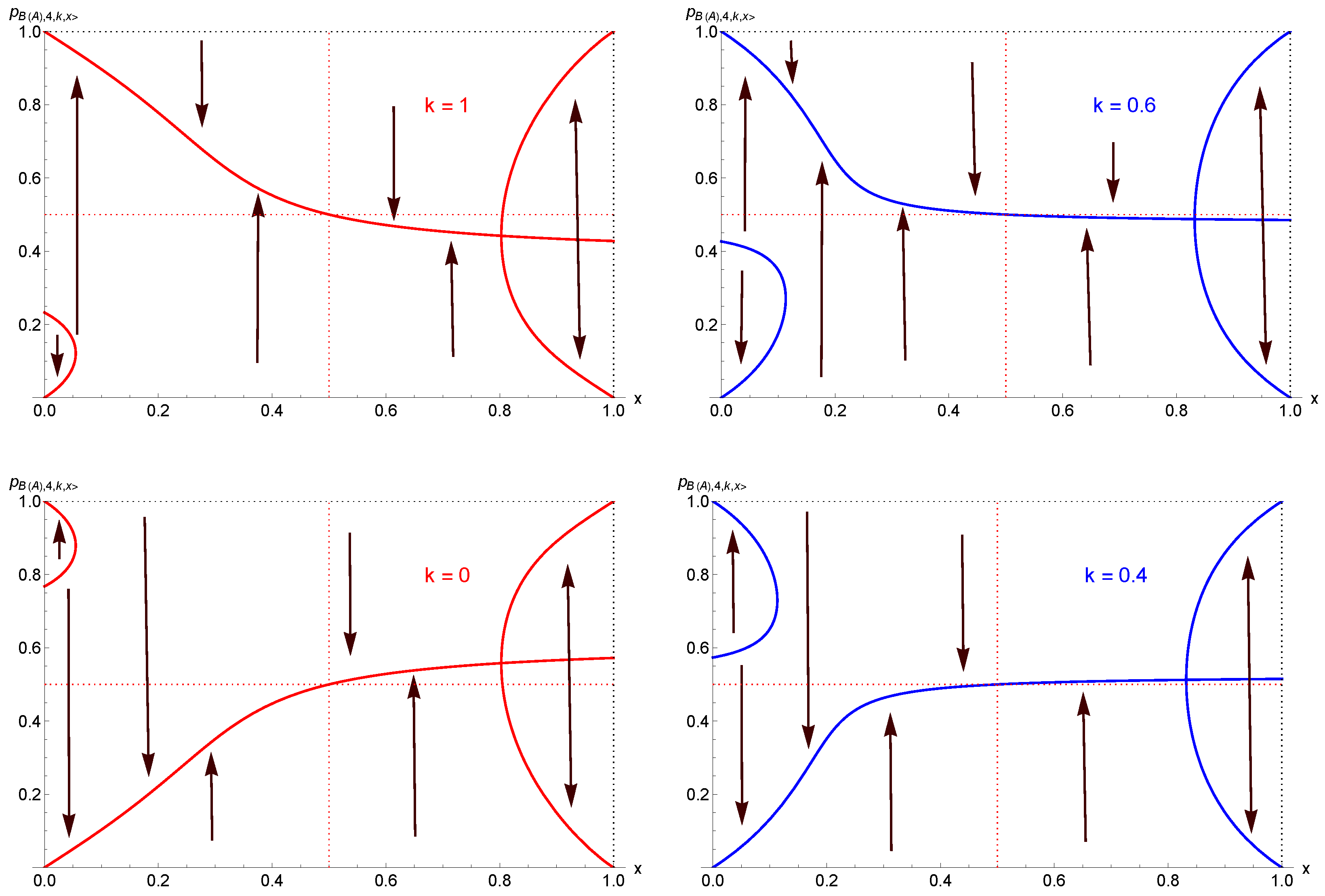
- Alternating polarization: A novel alternating-tipping-point regime was obtained at very high proportions of contrarians (92 percent or more) combined with very low and very high values of tie-breaking prejudices k. This regime is thus very extreme. For , the tipping regime holds only for and at , as seen from Table 1.
- Single attractor: In the second case, which turned out to be the most common, the outcome of the dynamics is predetermined from the start, with a single attractor driving the dynamics of opinion. It is independent of the initial support . Opinion A (B) cannot change the outcome, either victory or defeat depending on the current location of the single attractor with respect to .
A Word of Caution
Funding
Data Availability Statement
Conflicts of Interest
References
- Available online: https://www.ipsos.com/sites/default/files/ct/news/documents/2025-02/ipsos-cesi-la-tribune-les-francais-et-le-referendum-rapport-complet.pdf (accessed on 23 February 2025).
- Galam, S. Contrarian Deterministic Effects on Opinion Dynamics: The Hung Elections Scenario. Phys. A 2004, 333, 453–460. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Condorcet_paradox (accessed on 23 February 2025).
- Brazil, R. The physics of public opinion. Phys. World 2020, 33, 24. [Google Scholar] [CrossRef]
- Schweitzer, F. Sociophysics. Phys. Today 2018, 71, 40–47. [Google Scholar] [CrossRef]
- Galam, S. Sociophysics: A Physicist’s Modeling of Psycho-Political Phenomena; Springer: New York, NY, USA, 2012. [Google Scholar]
- Chakrabarti, B.K.; Chakraborti, A.; Chatterjee, A. (Eds.) Econophysics and Sociophysics: Trends and Perspectives; Wiley-VCH Verlag: Hoboken, NJ, USA, 2006. [Google Scholar]
- Galam, S. Physicists, non physical topics, and interdisciplinarity. Front. Phys. 2022, 10, 986782. [Google Scholar] [CrossRef]
- da Luz, M.G.E.; Anteneodo, C.; Crokidakis, N.; Perc, M. Sociophysics: Social collective behavior from the physics point of view. Chaos Solitons Fractals 2023, 170, 113379. [Google Scholar] [CrossRef]
- Ellero, A.; Fasano, G.; Favaretto, D. Mathematical Programming for the Dynamics of Opinion Diffusion. Physics 2023, 5, 936–951. [Google Scholar] [CrossRef]
- Oestereich, A.L.; Pires, M.A.; Queirós, S.M.D.; Crokidakis, N. Phase Transition in the Galam’s Majority-Rule Model with Information-Mediated Independence. Physics 2023, 5, 911–922. [Google Scholar] [CrossRef]
- Filho, E.A.; Lima, F.W.; Alves, T.F.A.; de Alencar Alves, G.; Plascak, J.A. Opinion Dynamics Systems via Biswas-Chatterjee-Sen Model on Solomon Networks. Physics 2023, 5, 873–882. [Google Scholar] [CrossRef]
- Zheng, S.; Jiang, N.; Li, X.; Xiao, M.; Chen, Q. Faculty Hiring Network Reveals Possible Decision-Making Mechanism. Physics 2023, 5, 851–861. [Google Scholar] [CrossRef]
- Mobilia, M. Polarization and Consensus in a Voter Model under Time-Fluctuating Influences. Physics 2023, 5, 517–536. [Google Scholar] [CrossRef]
- Li, S.; Zehmakan, A.N. Graph-Based Generalization of Galam Model: Convergence Time and Influential Nodes. Physics 2023, 5, 1094–1108. [Google Scholar] [CrossRef]
- Malarz, K.; Masłyk, T. Phase Diagram for Social Impact Theory in Initially Fully Differentiated Society. Physics 2023, 5, 1031–1047. [Google Scholar] [CrossRef]
- Kaufman, M.; Kaufman, S.; Diep, H.T. Social Depolarization: Blume-Capel Model. Physics 2024, 6, 138–147. [Google Scholar] [CrossRef]
- Bittencourt, R.A.; Pereira, H.B.B.; Moret, M.A.; Galam, S.; Lima, I.C.C. Interplay of self, epiphany, and positive actions in shaping individual careers. Phys. Rev. E 2023, 108, 024314. [Google Scholar] [CrossRef]
- Zimmaro, F.; Olsson, H. A meta-model of belief dynamics with Personal, Expressed and Social beliefs. arXiv 2025, arXiv:2502.14362v1. [Google Scholar]
- Zimmaro, F.; Galam, S.; Alberto Javarone, M. Asymmetric games on networks: Mapping to ising models and bounded rationality. Chaos Solitons Fractals 2024, 181, 114666. [Google Scholar] [CrossRef]
- Gimenez, M.C.; Reinaudi, L.; Galam, S.; Vazquez, F. Contrarian majority rule model with external oscillating propaganda and individual inertias. Entropy 2023, 25, 1402. [Google Scholar] [CrossRef] [PubMed]
- Aguilar-Janita, M.; Khalil, N.; Leyva, I.; Sendiǹa-Nadal, I. Cooperation, satisfaction, and rationality in social games on complex networks with aspiration-driven players. arXiv 2025, arXiv:2502.03109. [Google Scholar]
- Kawahata, Y. Theoretical Investigation of Harmful Information Propagation Using Physical Properties of Graphene and TeNPs: Sociophysical Approach. Biomed. J. Sci. Tech. Res. 2024, 60, 52100–52130. [Google Scholar] [CrossRef]
- Bautista, A. Opinion dynamics in bounded confidence models with manipulative agents: Moving the Overton window. arXiv 2025, arXiv:2501.12198v2. [Google Scholar] [CrossRef]
- March-Pons, D.; Ferrero, E.E.; Miguel, M.C. Consensus formation and relative stimulus perception in quality-sensitive, interdependent agent systems. Phys. Rev. Res. 2024, 6, 043205. [Google Scholar] [CrossRef]
- Shirzadi, M.; Zehmakan, A.N. Do Stubborn Users Always Cause More Polarization and Disagreement? A Mathematical Study. arXiv 2024, arXiv:2410.22577v1. [Google Scholar]
- Li, S.; Phan, T.V.; Carlo, L.D.; Wang, G.; Do, V.H.; Mikhail, E.; Austinand, R.H.; Liu, L. Memory and Personality Shape Ideological Polarization. arXiv 2024, arXiv:2409.06660v2. [Google Scholar]
- Demming, A. The Laws of Division: Physicists Probe into the Polarization of Political Opinions. 2023. Available online: https://physicsworld.com/a/the-laws-of-division-physicists-probe-into-the-polarization-of-political-opinions/ (accessed on 10 March 2025).
- Vilone, D.; Polizzi, E. Modeling opinion misperception and the emergence of silence in online social system. PLoS ONE 2024, 19, e0296075. [Google Scholar] [CrossRef]
- Cui, P.-B. Exploring the foundation of social diversity and coherence with a novel attraction-repulsion model framework. Phys. A 2023, 618, 128714. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Wang, F.; Qi, K.; Di, Z. The precursor of the critical transitions in majority vote model with the noise feedback from the vote layer. J. Stat. Mech. 2024, 083402. [Google Scholar] [CrossRef]
- Banisch, S.; Shamon, H. Validating argument-based opinion dynamics with survey experiments. The J. Artif. Soc. Soc. Simul. 2024, 27, 17. [Google Scholar] [CrossRef]
- Pal, R.; Kumar, A.; Santhanam, M.S. Depolarization of opinions on social networks through random nudges. Phys. Rev. E 2023, 108, 034307. [Google Scholar] [CrossRef]
- Bagarello, F. Phase transitions, KMS condition and decision making: An introductory model. Phil. Trans. R. Soc. A 2023, 381, 20220377. [Google Scholar] [CrossRef]
- Crokidakis, N. Radicalization phenomena: Phase transitions, extinction processes and control of violent activities. Int. J. Mod. Phys. C 2023, 34, 2350100. [Google Scholar] [CrossRef]
- Coquidé, C.; Lages, J.; Shepelyansky, D.L. Prospects of BRICS currency dominance in international trade. Appl. Netw. Sci. 2023, 8, 65. [Google Scholar] [CrossRef]
- Mulyaa, D.A.; Muslim, R. Phase transition and universality of the majority-rule model on complex networks. arXiv 2024, arXiv:2402.13434v2. [Google Scholar] [CrossRef]
- Neirotti, J.; Caticha, N. Rebellions and Impeachments in a Neural Network Society. Phys. Rev. E 2024, 110, 054110. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Guo, H.; Hu, S.; Shi, L.; Wang, Z.; Tanimoto, J. How Committed Individuals Shape Social Dynamics: A Survey on Coordination Games and Social Dilemma Games. Eur. Phys. Lett. 2023, 144, 11002. [Google Scholar] [CrossRef]
- Grabisch, M.; Li, F. Anti-conformism in the Threshold Model of Collective Behavior. Dyn. Games Appl. 2020, 10, 444–477. [Google Scholar] [CrossRef]
- Forgerini, F.L.; Crokidakis, N.; Carvalho, M.A.V. Directed propaganda in the majority-rule model. Int. J. Mod. Phys. C 2024, 35, 2450082. [Google Scholar] [CrossRef]
- Crokidakis, N. Recent violent political extremist events in Brazil and epidemic modeling: The role of a SIS-like model on the understanding of spreading and control of radicalism. Int. J. Mod. Phys. C 2024, 35, 2450015. [Google Scholar] [CrossRef]
- Muslim, R.; Mulya, D.A.; Indrayani, H.; Wicaksana, C.A.; Rizki, A. Independence role in the generalized Sznajd model. Phys. A Stat. Mech. Its Appl. 2024, 652, 130042. [Google Scholar]
- Naumisa, G.G.; Samaniego-Steta, F.; del Castillo-Mussot, M.; Vázquez, G.J. Three-body interactions in sociophysics and their role in coalition forming. Phys. A 2007, 379, 226–234. [Google Scholar] [CrossRef]
- Nettasinghe, B.; Percus, A.G.; Lerman, K. How out-group animosity can shape partisan divisions: A model of affective polarization. PNAS Nexus 2025, pgaf082. [Google Scholar] [CrossRef]
- Hamann, H. Opinion Dynamics With Mobile Agents: Contrarian Effects by Spatial Correlations. Front. Robot. AI 2018, 5, 63. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Cheng, Y.; Luo, Z. Opinion Dynamics with the Contrarian Deterministic Effect and Human Mobility on Lattice. Complexity 2015, 20, 43–49. [Google Scholar] [CrossRef]
- Toth, G. Models of opinion dynamics with random parametrisation. J. Math. Phys. 2024, 65, 073301. [Google Scholar] [CrossRef]
- Tiwari, M.; Yang, X.; Sen, S. Modeling the nonlinear effects of opinion kinematics in elections: A simple Ising model with random field based study. Phys. A 2021, 582, 126287. [Google Scholar] [CrossRef]
- Chacoma, A.; Zanette, D.H. Critical phenomena in the spreading of opinion consensus and disagreement. Physics 2014, 6, 060003. [Google Scholar] [CrossRef]
- Cheon, T.; Morimoto, J. Balancer effects in opinion dynamics. Phys. Lett. A 2016, 380, 429–434. [Google Scholar] [CrossRef]
- Landry, N.W.; Restrepo, J.G. Opinion disparity in hypergraphs with community structure. Phys. Rev. E 2023, 108, 034311. [Google Scholar] [CrossRef]
- Ahmad Mulyaa, D.; Muslim, R. Destructive social noise effects on homogeneous and heterogeneous networks: Induced-phases in the majority-rule model. arXiv 2023, arXiv:2310.01731v1. [Google Scholar]
- Mihara, A.; Ferreira, A.A.; Martins, A.C.R.; Ferreira, F.F. Critical exponents of master-node network model. Phys. Rev. E 2023, 108, 054303. [Google Scholar] [CrossRef]
- Gártner, B.; Zehmakan, A.N. Threshold Behavior of Democratic Opinion Dynamics. J. Stat. Phys. 2020, 178, 1442–1466. [Google Scholar] [CrossRef]
- Chen, P.; Redner, S. Majority rule dynamics in finite dimensions. Phys. Rev. E 2005, 71, 026101. [Google Scholar] [CrossRef] [PubMed]
- Kułakowski, K.; Nawojczyk, M. The Galam model of minority opinion spreading and the marriage gap. Int. J. Mod. Phys. C 2008, 19, 611–615. [Google Scholar] [CrossRef]
- Liu, X.; Achterberg, M.A.; Kooij, R. Mean-field dynamics of the non-consensus opinion model. Appl. Netw. Sci. 2024, 9, 47. [Google Scholar] [CrossRef]
- Ellero, A.; Sorato, A.; Fasano, G. A New Model for Estimating the Probability of Information Spreading with Opinion Leaders. 2011. Available online: https://ssrn.com/abstract=2037450 (accessed on 10 March 2025).
- Sendra, N.; Gwizdałła, T.; Czerbniak, J. The application of cellular automata in modeling of opinion formation in society. Ann. Univ. Mariae-Curie-Sklodowska Sect. Ai–Inform. 2015, 3, 213–218. [Google Scholar]
- Crokidakis, N.; Blanco1, V.H.; Anteneodo, C. Impact of contrarians and intransigents in a kinetic model of opinion dynamics. Phys. Rev. E 2014, 89, 013310. [Google Scholar] [CrossRef] [PubMed]
- Tòth, G.; Galam, S. Deviations from the Majority: A Local Flip Model. Chaos Solitons Fractals 2022, 159, 112130. [Google Scholar] [CrossRef]
- Kowalska-Styczeń, A.; Malarz, K. Noise induced unanimity and disorder in opinion formation. PLoS ONE 2020, 15, e0235313. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Pogrebna, G. Quantum-Mechanical Modelling of Asymmetric Opinion Polarisation in Social Networks. arXiv 2024, arXiv:2308.02132v2. [Google Scholar] [CrossRef]
- Redner, S. Reality-inspired voter models: A mini-review. Comptes Rendus Phys. 2019, 20, 275–292. [Google Scholar] [CrossRef]
- Jedrzejewski, A.; Marcjasz, G.; Nail, P.R.; Sznajd-Weron, K. Think then act or act then think? PLoS ONE 2018, 13, e0206166. [Google Scholar] [CrossRef]
- Singh, P.; Sreenivasan, S.; Szymanski, B.K.; Korniss, G. Competing effects of social balance and influence. Phys. Rev. E 2016, 93, 042306. [Google Scholar] [CrossRef] [PubMed]
- Bagnoli, F.; Rechtman, R. Bifurcations in models of a society of reasonable contrarians and conformists. Phys. Rev. E 2015, 92, 042913. [Google Scholar] [CrossRef] [PubMed]
- Carbone, G.; Giannoccaro, I. Model of human collective decision-making in complex environments. Eur. Phys. J. B 2015, 88, 339. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Szwabiński, J.; Weron, R. Is the Person-Situation Debate Important for Agent-Based Modeling and Vice-Versa? PLoS ONE 2014, 9, e112203. [Google Scholar] [CrossRef]
- Javarone, M.A. Networks strategies in election campaigns. J. Stat. Mech. 2014, P08013. [Google Scholar] [CrossRef]
- Javarone, M.A.; Singh, S.P. Strategy revision phase with payoff threshold in the public goods game. J. Stat. Mech. 2024, 023404. [Google Scholar] [CrossRef]
- Goncalves, S.; Laguna, M.F.; Iglesias, J.R. Why, when, and how fast innovations are adopted. Eur. Phys. J. B 2012, 85, 192. [Google Scholar] [CrossRef]
- Ellero, A.; Fasano, G.; Sorato, A. A modified Galam’s model for word-of-mouth information exchange. Phys. A 2009, 388, 3901–3910. [Google Scholar] [CrossRef]
- Gimenez, M.C.; Reinaudi, L.; Vazquez, F. Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance. Entropy 2022, 24, 1140. [Google Scholar] [CrossRef]
- Iacominia, E.; Vellucci, P. Contrarian effect in opinion forming: Insights from Greta Thunberg phenomenon. J. Math. Sociol. 2023, 47, 123–169. [Google Scholar] [CrossRef]
- Brugnoli, E.; Delmastro, M. Dynamics of (mis)information flow and engaging power of narratives. arXiv 2022, arXiv:2207.12264v2. [Google Scholar]
- Sobkowicz, P. Whither Now, Opinion Modelers? Front. Phys. 2020, 8, 587009. [Google Scholar] [CrossRef]
- Weron, T.; Nyczka, P.; Szwabiński, J. Composition of the Influence Group in the q-Voter Model and Its Impact on the Dynamics of Opinions. Entropy 2024, 26, 132. [Google Scholar] [CrossRef] [PubMed]
- Gsänger, M.; Hösel, V.; Mohamad-Klotzbach, C.; Müller, J. Opinion models, data, and politics. arXiv 2024, arXiv:2402.06910v1. [Google Scholar]
- Vilela, A.L.M.; Zubillaga, B.J.; Wang, C.; Wang, M.; Du, R.; Stanley, H.E. Three-State Majority-vote Model on Scale-Free Networks and the Unitary Relation for Critical Exponents. Sci. Rep. 2020, 10, 8255. [Google Scholar] [CrossRef]
- Mobilia, M. Fixation and polarization in a three-species opinion dynamics model. Eur. Phys. Lett. 2011, 95, 50002. [Google Scholar] [CrossRef]
- Calvõ, A.M.; Ramos, M.; Anteneodo, C. Role of the plurality rule in multiple choices. J. Stat. Mech. 2016, 023405. [Google Scholar] [CrossRef]
- Maciel, M.V.; Martins, A.C.R. Ideologically motivated biases in a multiple issues opinion model. Phys. A 2020, 553, 124293. [Google Scholar] [CrossRef]
- Dworak, M.; Malarz, K. Vanishing opinions in Latané model of opinion formation. Entropy 2023, 25, 58. [Google Scholar] [CrossRef]
- Ferri, I.; Gaya-Ávila, A.; Díaz Guilera, A. Three-state opinion model with mobile agents. Chaos 2023, 33, 093121. [Google Scholar] [CrossRef]
- Oliveiraa, I.V.G.; Wang, C.; Dong, G.; Du, R.; Fiore, C.E.; Stanley, H.E.; Vilela, A.L.M. Entropy Production on Cooperative Opinion Dynamics. arXiv 2023, arXiv:2311.05803v1. [Google Scholar] [CrossRef]
- Coquidé, C.; Lages, J.; Shepelyansky, D.L. Opinion Formation in the World Trade Network. Entropy 2024, 26, 141. [Google Scholar] [CrossRef]
- Timpanaro, A.M. Emergence of echo chambers in a noisy adaptive voter model. arXiv 2025, arXiv:2409.12933v2. [Google Scholar]
- Ye, D.; Lin, H.; Jiang, H.; Du, L.; Li, H.; Chen, Q.; Wang, Y.; Yuan, L. Simplex bounded confidence model for opinion fusion and evolution in higher-order interaction. Expert Syst. Appl. 2025, 272, 126551. [Google Scholar] [CrossRef]
- Deffuant, G. Complex Transitions of the Bounded Confidence Model from an Odd Number of Clusters to the Next. Physics 2024, 6, 742–759. [Google Scholar] [CrossRef]
- Malarz, K.; Gronek, P.; Kulakowski, K. Zaller-Deffuant Model of Mass Opinion. J. Artif. Soc. Soc. Simul. 2011, 14, 2. [Google Scholar] [CrossRef]
- Galam, S. Social paradoxes of majority rule voting and renormalization group. J. Stat. Phys. 1990, 61, 943–951. [Google Scholar] [CrossRef]
- Galam, S.; Chopard, B.; Masselot, A.; Droz, M. Competing species dynamics: Qualitative advantage versus geography. Eur. Phys. J. B 1998, 4, 529–531. [Google Scholar] [CrossRef]
- Galam, S. Minority Opinion Spreading in Random Geometry. Eur. Phys. J. B 2002, 25, 403–406. [Google Scholar] [CrossRef]
- Galam, S.; Moscovici, S. Towards a theory of collective phenomena: Consensus and attitude changes in groups. Eur. J. Soc. Psychol. 1991, 21, 49–74. [Google Scholar] [CrossRef]
- Galam, S.; Jacobs, F. The role of inflexible minorities in the breaking of democratic opinion dynamics. Phys. A 2007, 38, 366–376. [Google Scholar] [CrossRef]
- Galam, S. Unanimity, Coexistence, and Rigidity: Three Sides of Polarization. Entropy 2023, 25, 622. [Google Scholar] [CrossRef] [PubMed]
- Galam, S. Fake News: “No Ban, No Spread—With Sequestration”. Physics 2024, 6, 859–876. [Google Scholar] [CrossRef]
- Le Hir, P. Les Mathématiques S’invitent Dans le Débat Européen, Le Monde. Le Monde, 25 February 2005. Available online: https://www.lemonde.fr/planete/article/2005/02/25/les-mathematiques-s-invitent-dans-le-debat-europeen_399570_3244.html (accessed on 10 March 2025).
- Galam, S. The Trump phenomenon: An explanation from sociophysics. Int. J. Mod. Phys. B 2017, 31, 1742015. [Google Scholar] [CrossRef]
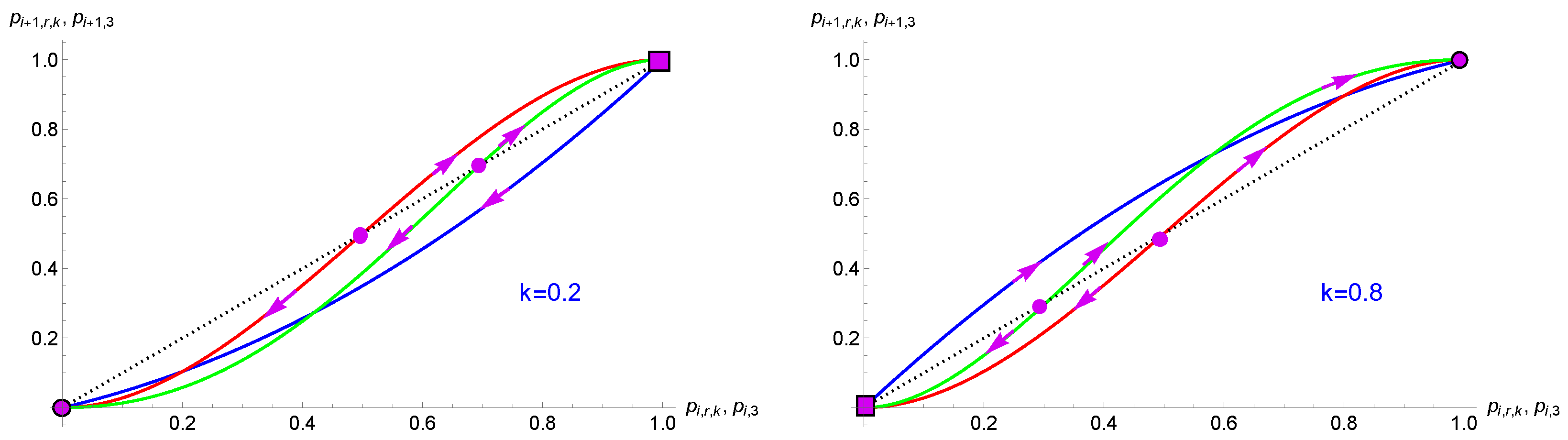
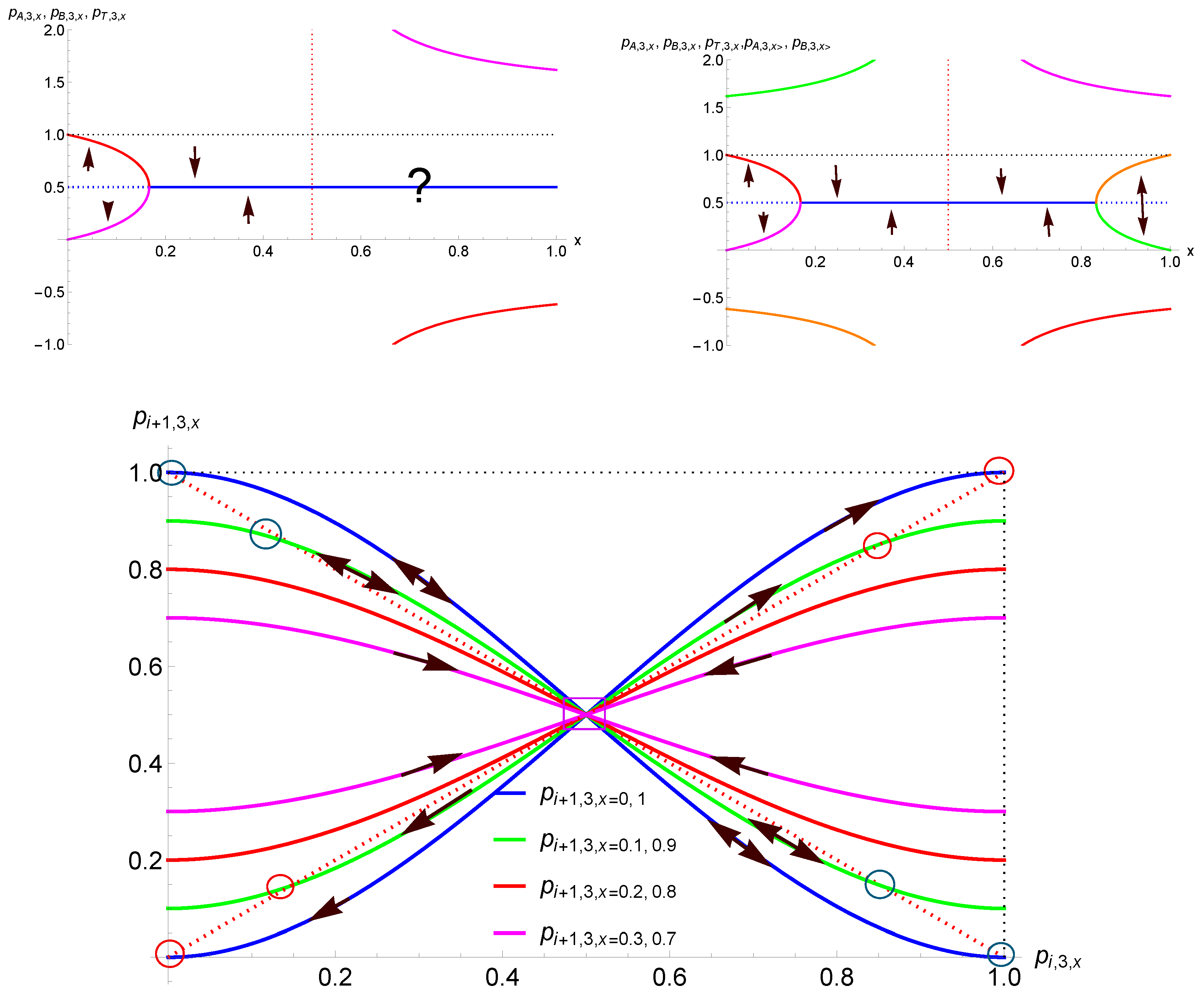
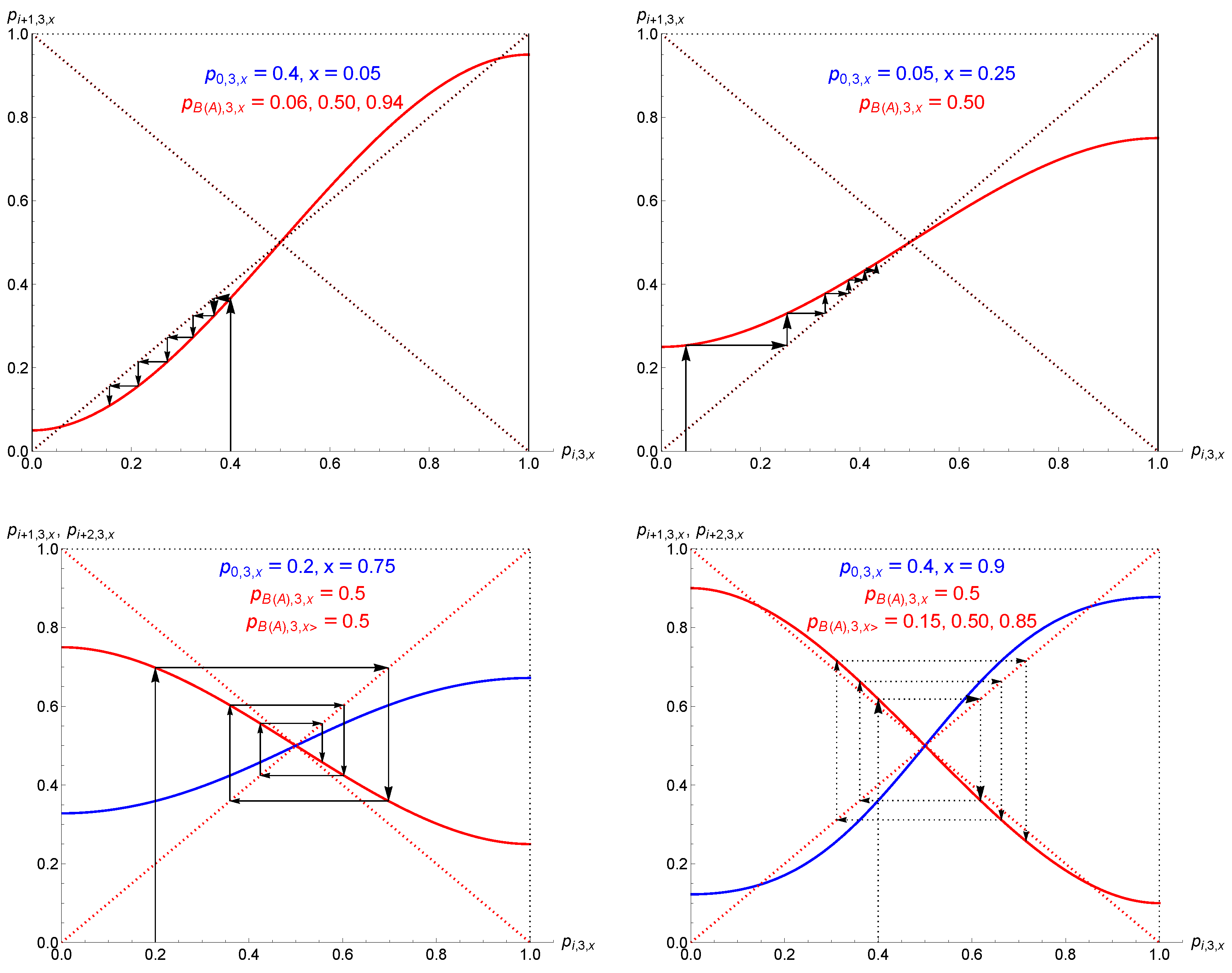
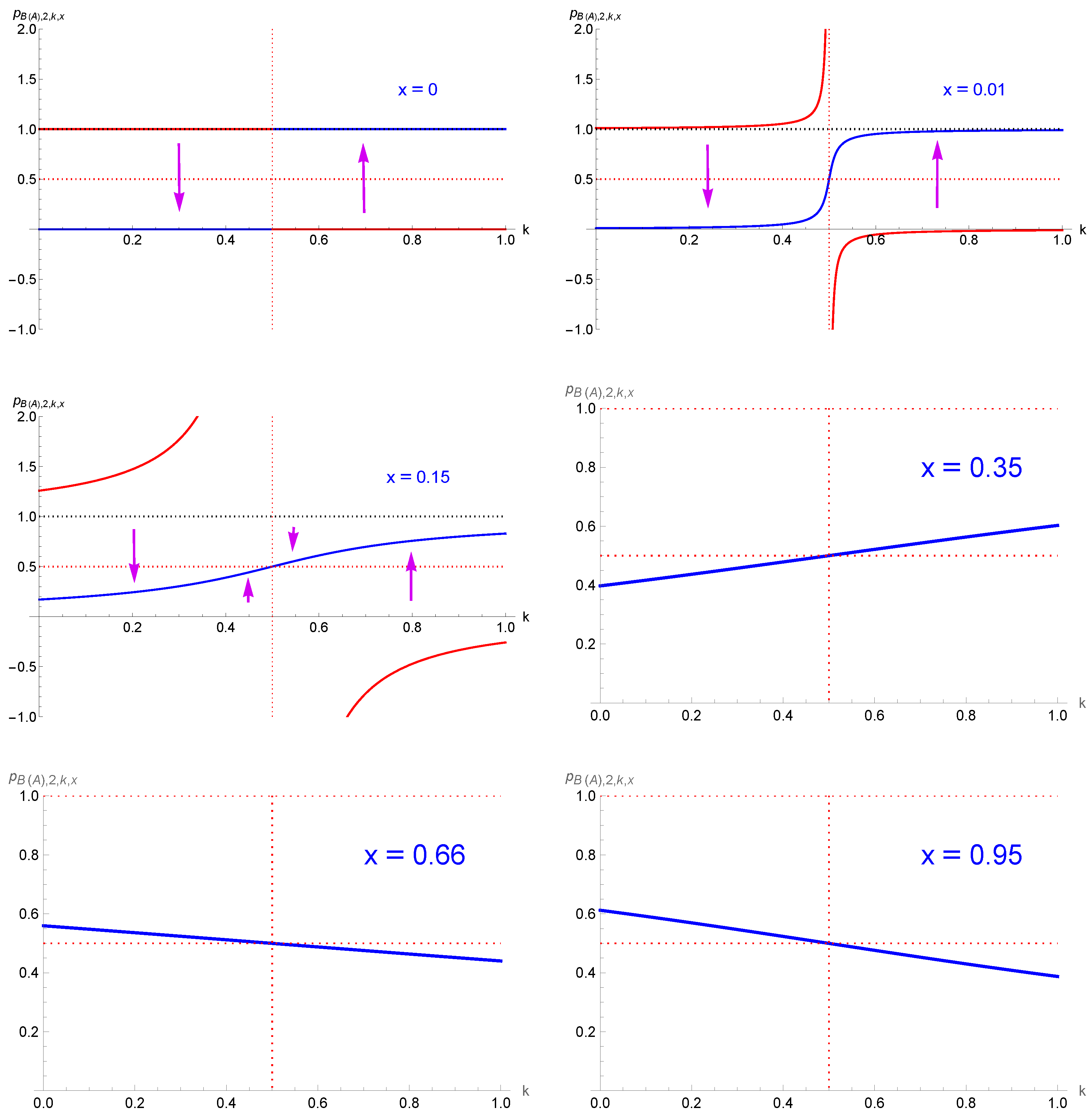
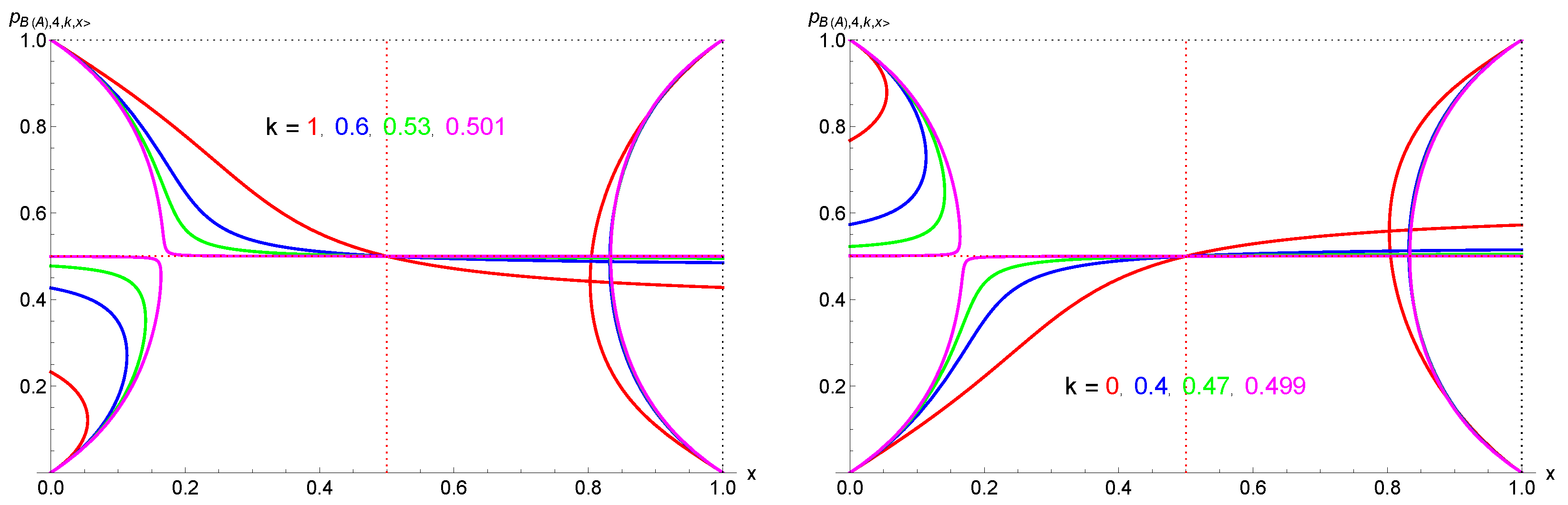
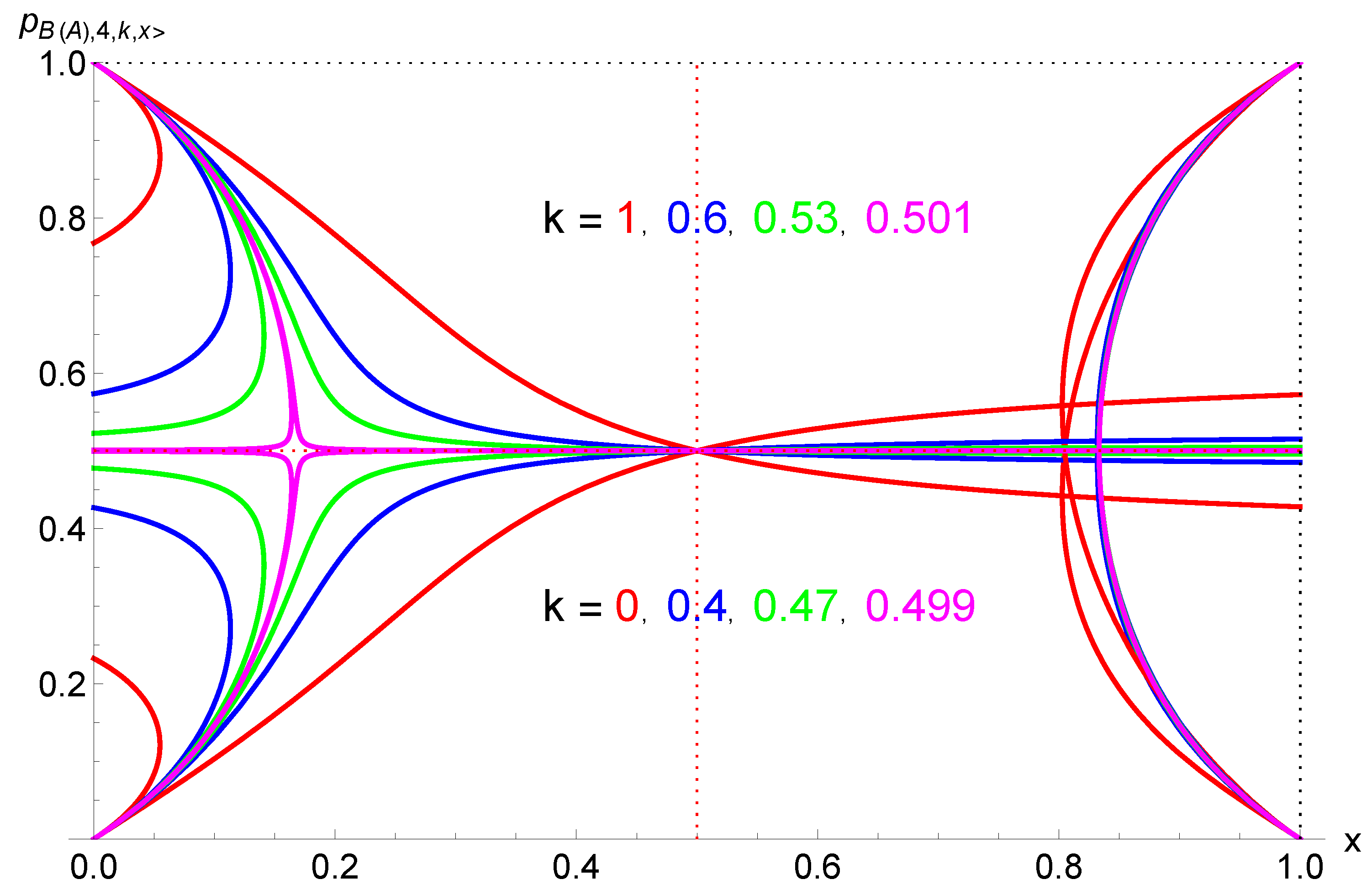
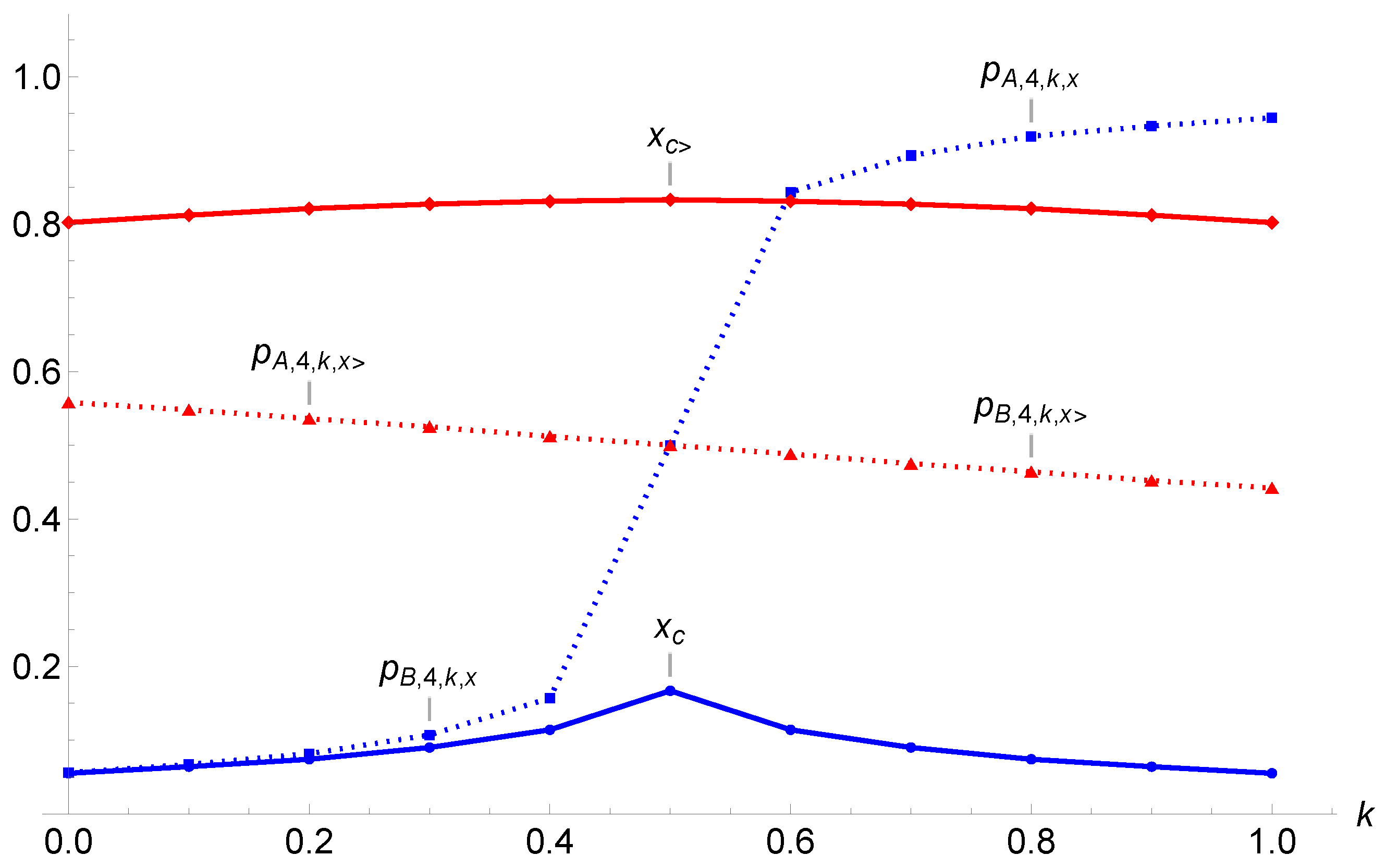
| k | 0, 1 | 0.1, 0.9 | 0.2, 0.8 | 0.3, 0.7 | 0.4, 0.6 | 0.5 |
| 0.055 | 0.064 | 0.074 | 0.09 | 0.114 | 0.167 | |
| 0.056 | 0.067 | 0.0815 | 0.107 | 0.157 | 0.500 | |
| 0.944 | 0.933 | 0.919 | 0.893 | 0.843 | 0.500 | |
| 0.802 | 0.812 | 0.821 | 0.827 | 0.831 | 0.833 | |
| 0.558 | 0.548 | 0.536 | 0.525 | 0.512 | 0.500 | |
| 0.488 | 0.475 | 0.464 | 0.452 | 0.442 | 0.500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galam, S. Democratic Thwarting of Majority Rule in Opinion Dynamics: 1. Unavowed Prejudices Versus Contrarians. Entropy 2025, 27, 306. https://doi.org/10.3390/e27030306
Galam S. Democratic Thwarting of Majority Rule in Opinion Dynamics: 1. Unavowed Prejudices Versus Contrarians. Entropy. 2025; 27(3):306. https://doi.org/10.3390/e27030306
Chicago/Turabian StyleGalam, Serge. 2025. "Democratic Thwarting of Majority Rule in Opinion Dynamics: 1. Unavowed Prejudices Versus Contrarians" Entropy 27, no. 3: 306. https://doi.org/10.3390/e27030306
APA StyleGalam, S. (2025). Democratic Thwarting of Majority Rule in Opinion Dynamics: 1. Unavowed Prejudices Versus Contrarians. Entropy, 27(3), 306. https://doi.org/10.3390/e27030306







