Design Particularities of Quadrature Chaos Shift Keying Communication System with Enhanced Noise Immunity for IoT Applications
Abstract
1. Introduction
2. Chaos Oscillators
2.1. Colpitts Chaos Oscillator
2.2. Vilnius Chaos Oscillator
2.3. Chaotic Synchronization
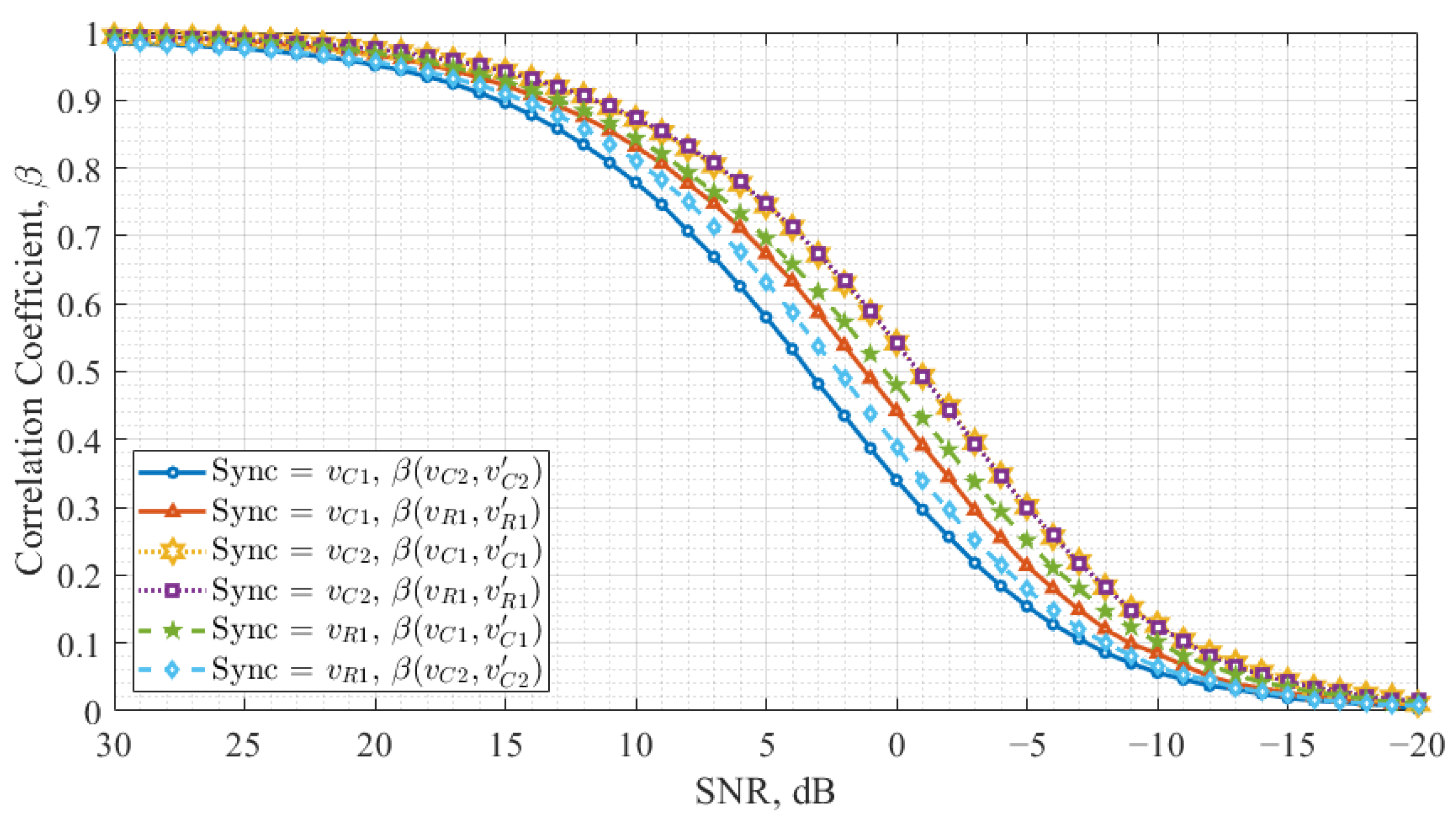
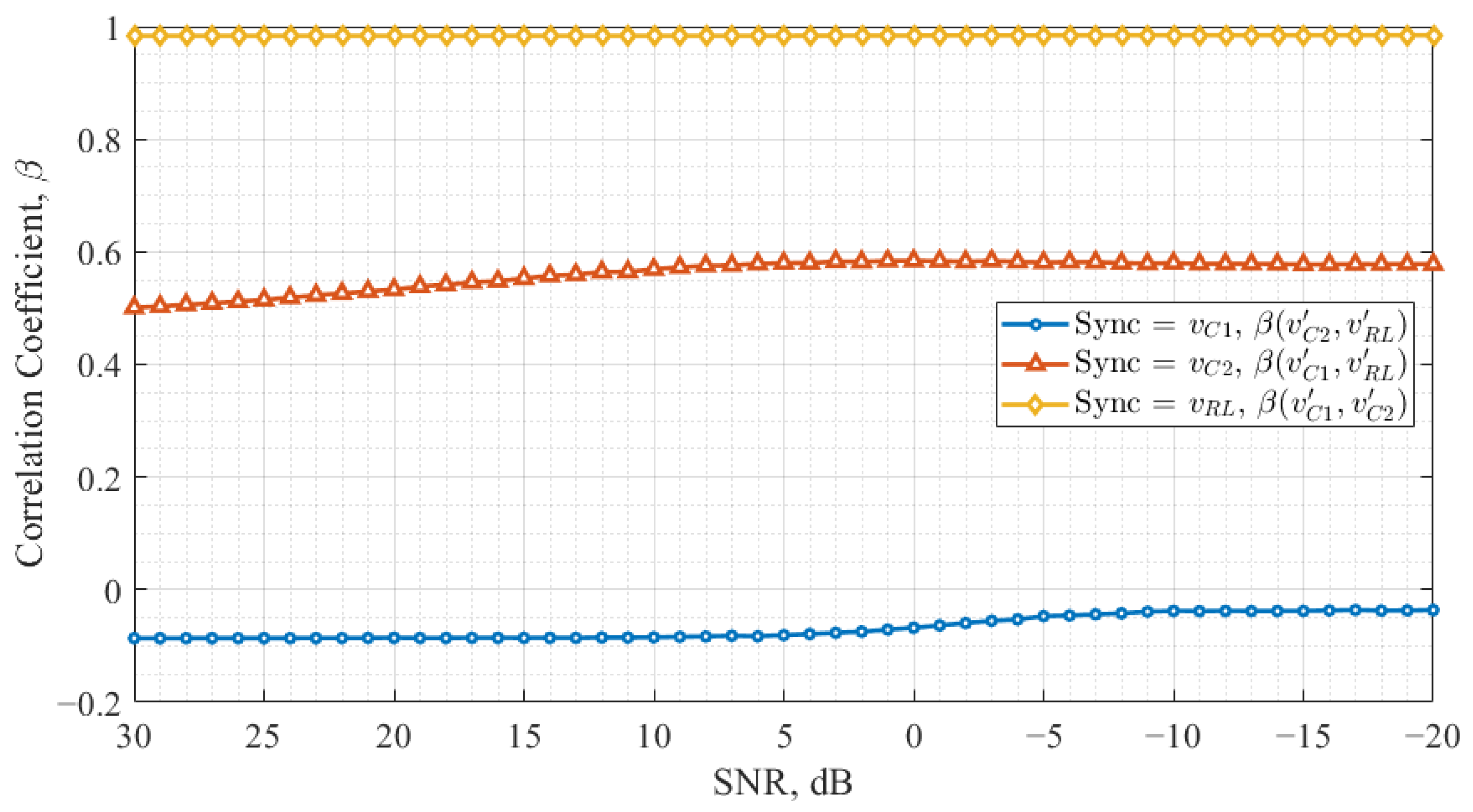
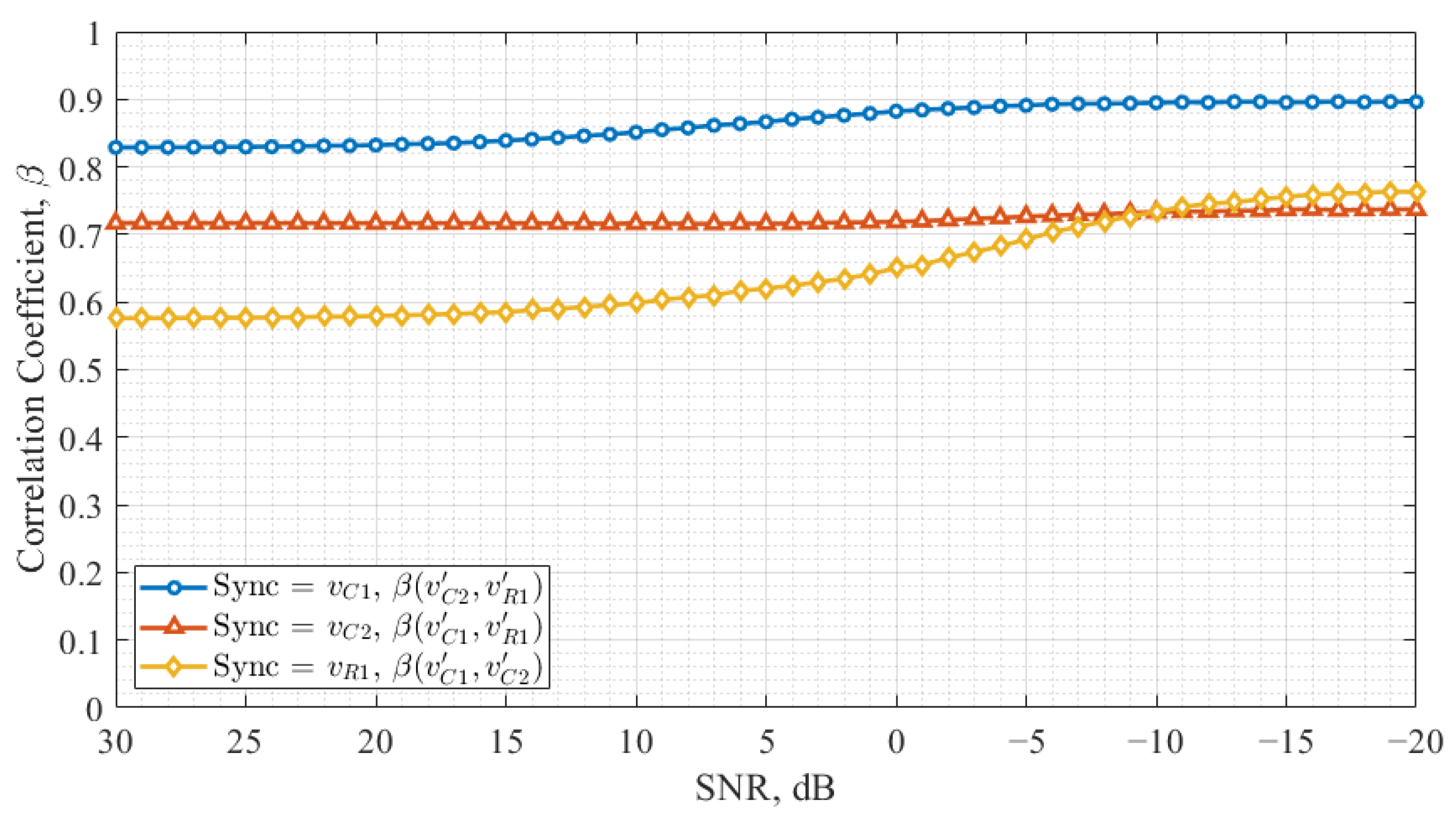
3. Chaos Oscillator Synchronization Noise Immunity
3.1. Study Methodology
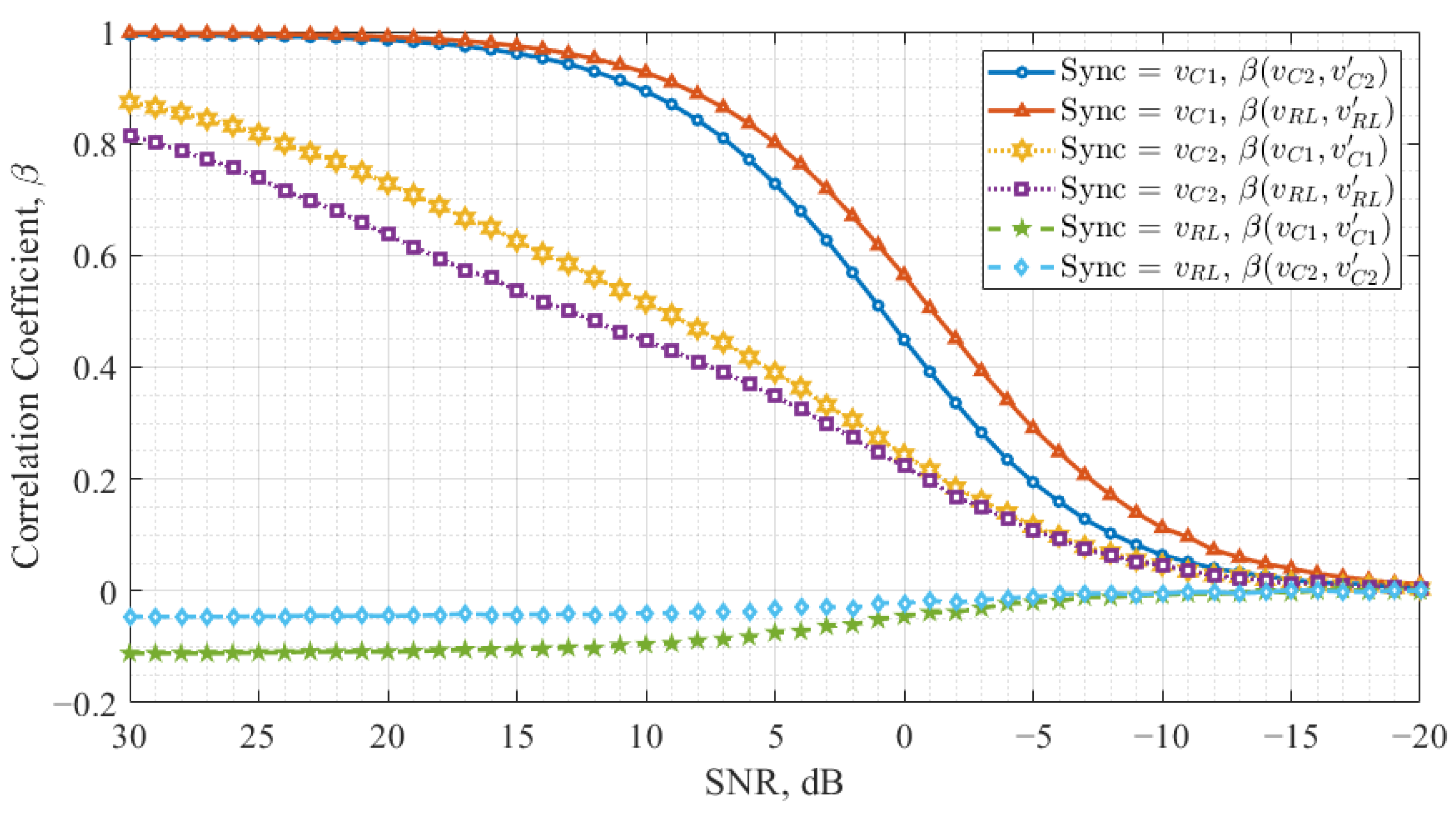
3.2. Result Analyses
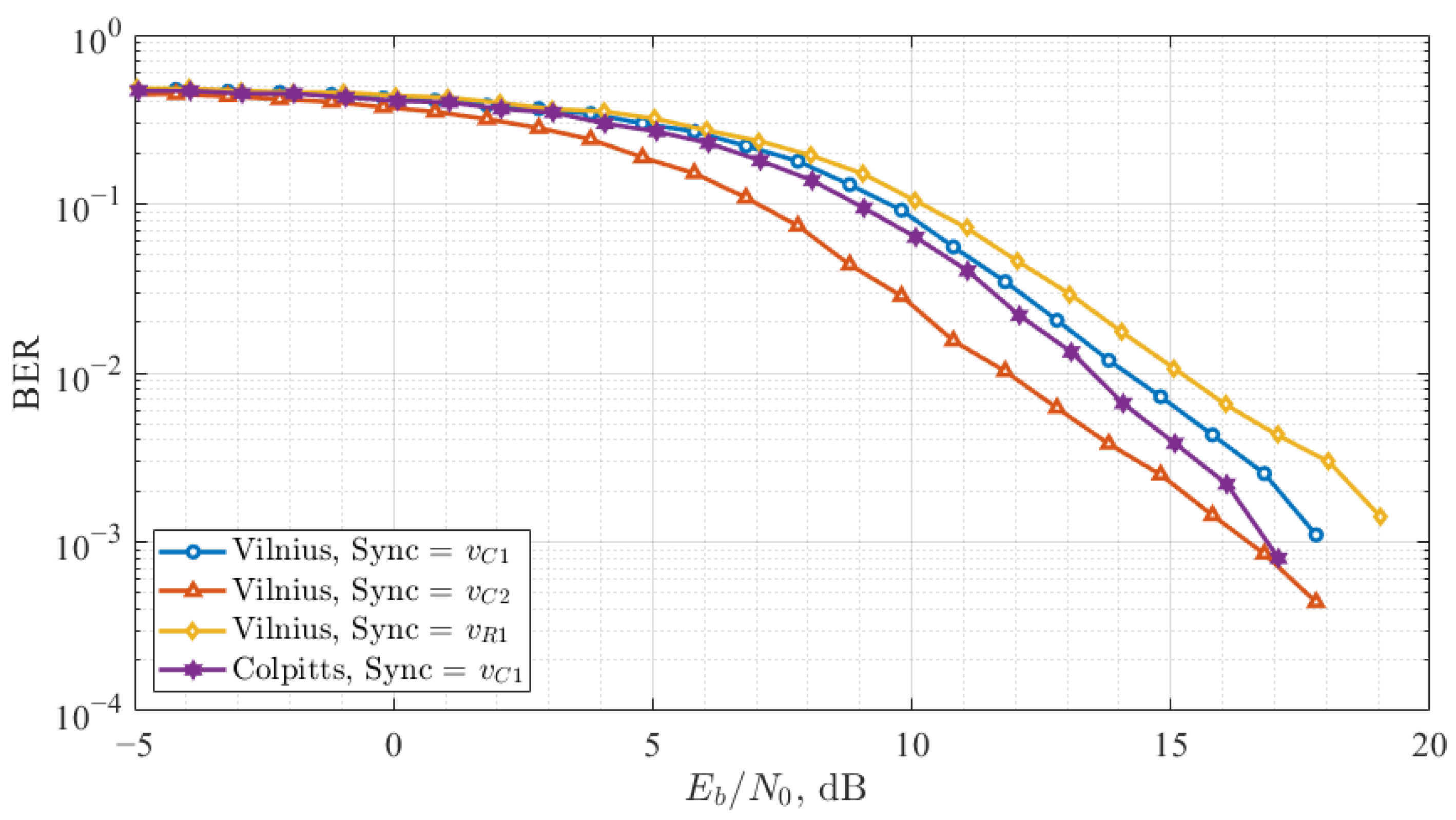
4. Quadrature Chaos Shift Keying Communication System
4.1. System Design Particularities
4.2. Result Analyses
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 5G | Fifth Generation |
| 6G | Sixth Generation |
| AWGN | Additive White Gaussian Noise |
| BER | Bit Error Rate |
| CSK | Chaos Shift Keying |
| DC | Direct Current |
| DCSK | Differential Chaos Shift Keying |
| IoT | Internet of Things |
| LPF | Low-Pass Filter |
| MIMO | Multiple-Input Multiple-Output |
| MSE | Mean Square Error |
| PLS | Physical Layer Security |
| QCSK | Quadrature Chaos Shift Keying |
| RSA | Rivest–Shamir–Adleman |
| SDN | Software-Defined Networking |
| SNR | Signal-to-Noise Ratio |
| WSN | Wireless Sensor Network |
References
- Jonsson, P.; Lundvall, A.; von Koch, D.; Davis, S.; Cerwall, P. Ericsson Mobility Report November 2024; Technical Report; Ericsson: Stockholm, Sweden, 2024; Available online: https://www.ericsson.com/en/reports-and-papers/mobility-report (accessed on 6 January 2025).
- Sun, P.; Shen, S.; Wan, Y.; Wu, Z.; Fang, Z.; Gao, X.Z. A Survey of IoT Privacy Security: Architecture, Technology, Challenges, and Trends. IEEE Internet Things J. 2024, 11, 34567–34591. [Google Scholar] [CrossRef]
- Gautam, K.K.S.; Kumar, R.; Yadav, R.; Sharma, P. Investigation of the Internet of Things (IoT) Security and Privacy Issues. In Proceedings of the 2023 5th International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 3–5 August 2023; pp. 1489–1494. [Google Scholar] [CrossRef]
- Sharbaf, M.S. IoT Driving New Business Model, and IoT Security, Privacy, and Awareness Challenges. In Proceedings of the 2022 IEEE 8th World Forum on Internet of Things (WF-IoT), Yokohama, Japan, 26 October–11 November 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Singh, J.; Singh, G.; Negi, S. Evaluating Security Principals and Technologies to Overcome Security Threats in IoT World. In Proceedings of the 2023 2nd International Conference on Applied Artificial Intelligence and Computing (ICAAIC), Salem, India, 4–6 May 2023; pp. 1405–1410. [Google Scholar] [CrossRef]
- Sauter, T.; Treytl, A. IoT-Enabled Sensors in Automation Systems and Their Security Challenges. IEEE Sensors Lett. 2023, 7, 1–4. [Google Scholar] [CrossRef]
- Omoniwa, B.; Hussain, R.; Javed, M.A.; Bouk, S.H.; Malik, S.A. Fog/Edge Computing-Based IoT (FECIoT): Architecture, Applications, and Research Issues. IEEE Internet Things J. 2019, 6, 4118–4149. [Google Scholar] [CrossRef]
- Hussain, F.; Hussain, R.; Hassan, S.A.; Hossain, E. Machine Learning in IoT Security: Current Solutions and Future Challenges. IEEE Commun. Surv. Tutorials 2020, 22, 1686–1721. [Google Scholar] [CrossRef]
- Karie, N.M.; Sahri, N.M.; Yang, W.; Valli, C.; Kebande, V.R. A Review of Security Standards and Frameworks for IoT-Based Smart Environments. IEEE Access 2021, 9, 121975–121995. [Google Scholar] [CrossRef]
- Hamamreh, J.M.; Furqan, H.M.; Arslan, H. Classifications and Applications of Physical Layer Security Techniques for Confidentiality: A Comprehensive Survey. IEEE Commun. Surv. Tutorials 2019, 21, 1773–1828. [Google Scholar] [CrossRef]
- Rojas, P.; Alahmadi, S.; Bayoumi, M. Physical Layer Security for IoT Communications—A Survey. In Proceedings of the 2021 IEEE 7th World Forum on Internet of Things (WF-IoT), New Orleans, LA, USA, 14 June–31 July 2021; pp. 95–100. [Google Scholar] [CrossRef]
- Illi, E.; Qaraqe, M.; Althunibat, S.; Alhasanat, A.; Alsafasfeh, M.; De Ree, M.; Mantas, G.; Rodriguez, J.; Aman, W.; Al-Kuwari, S. Physical Layer Security for Authentication, Confidentiality, and Malicious Node Detection: A Paradigm Shift in Securing IoT Networks. IEEE Commun. Surv. Tutorials 2024, 26, 347–388. [Google Scholar] [CrossRef]
- Traynor, Z.A.; Curtin, I.M.; Henggeler, C.T.; Sulyman, A.I. Physical-layer security solutions for IoT devices using Radio Frequency Fingerprints. In Proceedings of the 2024 International Conference on Computing, Internet of Things and Microwave Systems (ICCIMS), Gatineau, QC, Canada, 29–31 July 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Mohan, V.; Mathur, A. Secrecy Analysis of DCSK-Based PLC Systems with Multiple Eavesdroppers. IEEE Syst. J. 2023, 17, 3646–3657. [Google Scholar] [CrossRef]
- Capligins, F.; Aboltins, A.; Litvinenko, A.; Kolosovs, D. FPGA Implementation and Study of Synchronization of Modified Chua’s Circuit-Based Chaotic Oscillator for High-Speed Secure Communications. In Proceedings of the 2020 IEEE 8th Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Vilnius, Lithuania, 22–24 April 2021. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Liu, L.; Zhang, Z.; Huang, Y.; He, B.; Cai, S.; Song, Y.; Yin, B.; Du, S.; et al. CCII and FPGA Realization: A Multistable Modified Fourth-Order Autonomous Chua’s Chaotic System with Coexisting Multiple Attractors. Complexity 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Wang, Z.; Wang, Y. A Memristive Fully Connect Neural Network and Application of Medical Image Encryption Based on Central Diffusion Algorithm. IEEE Trans. Ind. Inform. 2024, 20, 3778–3788. [Google Scholar] [CrossRef]
- Sanprang, P.; Amornsusawad, C.; Boonmak, K.; Chimnoy, J.; Karawanich, K.; Prommee, P. Realization of image cryptography using FPAA-based two chaotic systems. In Proceedings of the 2023 20th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Nakhon Phanom, Thailand, 9–12 May 2023; pp. 1–4. [Google Scholar] [CrossRef]
- George, A.E.; Gelóczi, E.; Mexis, N.; Arul, T.; Katzenbeisser, S.; Stavrinides, S.G.; Picos, R.; Anagnostopoulos, N.A. Real-World Secure Communication based on Synchronised Lorenz Chaotic Circuits. In Proceedings of the 2024 13th International Conference on Modern Circuits and Systems Technologies (MOCAST), Sofia, Bulgaria, 26–28 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Michaels, A.J.; Lau, C. Generalized Multi-carrier Chaotic Shift Keying. In Proceedings of the 2014 IEEE Military Communications Conference, Baltimore, MD, USA, 6–8 October 2014; pp. 657–662. [Google Scholar] [CrossRef]
- Hoang, T.M.; Larger, L. Security Improvement for CSK via Breaking Time Correlation among State Variables. In Proceedings of the 2008 Second International Conference on Communications and Electronics, Hoi An, Vietnam, 4–6 June 2008; pp. 200–205. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Exponential Chaotic Model for Generating Robust Chaos. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3713–3724. [Google Scholar] [CrossRef]
- Karimov, T.I.; Druzhina, O.S.; Ostrovskii, V.Y.; Karimov, A.I.; Butusov, D.N. The Study on Multiparametric Sensitivity of Chaotic Oscillators. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 27–30 January 2020; pp. 134–137. [Google Scholar] [CrossRef]
- Arif, J.; Khan, M.A.; Ghaleb, B.; Ahmad, J.; Munir, A.; Rashid, U.; Al-Dubai, A.Y. A Novel Chaotic Permutation-Substitution Image Encryption Scheme Based on Logistic Map and Random Substitution. IEEE Access 2022, 10, 12966–12982. [Google Scholar] [CrossRef]
- Estudillo-Valdez, M.A.; Adeyemi, V.A.; Nuñez-Perez, J.C. FPGA realization of an image encryption system using the DCSK-CDMA technique. Integration 2024, 96, 102157. [Google Scholar] [CrossRef]
- Lu, H.; Alkhazragi, O.; Ng, T.K.; Ooi, B.S. Chip-Scale Random Number Generator Based On Self-Chaotic Dynamics Of Broad-Area VCSELs. In Proceedings of the 2024 IEEE 29th International Semiconductor Laser Conference (ISLC), Orlando, FL, USA, 29 September–2 October 2024; pp. 1–2. [Google Scholar] [CrossRef]
- Hu, X.; Wei, L.; Chen, W.; Chen, Q.; Guo, Y. Color Image Encryption Algorithm Based on Dynamic Chaos and Matrix Convolution. IEEE Access 2020, 8, 12452–12466. [Google Scholar] [CrossRef]
- Moonem, M.A.; Feng, X.; Strank, S.; Hebner, R.E. Secure Data Communication through Power Electronic Converters in a DC Microgrid. In Proceedings of the 2021 IEEE Fourth International Conference on DC Microgrids (ICDCM), Arlington, VA, USA, 18–21 July 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Anagnostopoulos, N.A.; George, A.E.; Mexis, N.; Arul, T.; Katzenbeisser, S.; Picos, R.; Stavrinides, S.G. The Synchronisation is the Message: Real-World Encrypted Communication Based on Synchronised Chaotic Circuits Without Using a Dedicated Synchronisation Line. In Proceedings of the 2024 13th International Conference on Modern Circuits and Systems Technologies (MOCAST), Sofia, Bulgaria, 26–28 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization of chaotic systems. Underst. Complex Syst. 2009, 48, 101–133. [Google Scholar] [CrossRef]
- Kekha Javan, A.A.; Shoeibi, A.; Zare, A.; Hosseini Izadi, N.; Jafari, M.; Alizadehsani, R.; Moridian, P.; Mosavi, A.; Acharya, U.R.; Nahavandi, S. Design of adaptive-robust controller for multi-state synchronization of chaotic systems with unknown and time-varying delays and its application in secure communication. Sensors 2021, 21, 254. [Google Scholar] [CrossRef]
- Karimov, A.; Tutueva, A.; Karimov, T.; Druzhina, O.; Butusov, D. Adaptive Generalized Synchronization between Circuit and Computer Implementations of the Rössler System. Appl. Sci. 2020, 11, 81. [Google Scholar] [CrossRef]
- Cirjulina, D.; Pikulins, D.; Babajans, R.; Anstrangs, D.D.; Chukwuma Victor, I.; Litvinenko, A. Experimental Study of the Impact of Component Nominal Deviations on the Stability of Vilnius Chaotic Oscillator. In Proceedings of the 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 1–2 October 2020; pp. 231–236. [Google Scholar] [CrossRef]
- Cirjulina, D.; Pikulins, D.; Babajans, R.; Zeltins, M.; Kolosovs, D.; Litvinenko, A. Experimental Study on FM-CSK Communication System for WSN. Electronics 2022, 11, 1517. [Google Scholar] [CrossRef]
- Babajans, R.; Cirjulina, D.; Grizans, J.; Aboltins, A.; Pikulins, D.; Zeltins, M.; Litvinenko, A. Impact of the Chaotic Synchronization’s Stability on the Performance of QCPSK Communication System. Electronics 2021, 10, 640. [Google Scholar] [CrossRef]
- Babajans, R.; Cirjulina, D.; Capligins, F.; Kolosovs, D.; Litvinenko, A. Synchronization of Analog-Discrete Chaotic Systems for Wireless Sensor Network Design. Appl. Sci. 2024, 14, 915. [Google Scholar] [CrossRef]
- Babajans, R.; Cirjulina, D.; Capligins, F.; Kolosovs, D.; Grizans, J.; Litvinenko, A. Performance Analysis of Vilnius Chaos Oscillator-Based Digital Data Transmission Systems for IoT. Electronics 2023, 12, 709. [Google Scholar] [CrossRef]
- Suresh, R.; Sathish Kumar, K.; Regan, M.; Niranjan Kumar, K.A.; Narmada Devi, R.; Obaid, A.J. Dynamical properties of a modified chaotic Colpitts oscillator with triangular wave non-linearity. Arch. Control Sci. 2023, 33, 25–53. [Google Scholar] [CrossRef]
- Vasiljevic, I.; Lekic, A.; Stipanovic, D. Lyapunov Analysis of the Chaotic Colpitts Oscillator. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Fattakhov, R.; Loginov, S. Discrete-nonlinear Colpitts oscillator based communication security increasing of the OFDM systems. In Proceedings of the 2021 International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russian, 16–18 November 2021; pp. 253–256. [Google Scholar] [CrossRef]
- Ipatovs, A.; Victor, I.C.; Pikulins, D.; Tjukovs, S.; Litvinenko, A. Complete Bifurcation Analysis of the Vilnius Chaotic Oscillator. Electronics 2023, 12, 2861. [Google Scholar] [CrossRef]
- Rybin, V.; Babkin, I.; Kvitko, D.; Karimov, T.; Nardo, L.; Nepomuceno, E.; Butusov, D. Estimating Optimal Synchronization Parameters for Coherent Chaotic Communication Systems in Noisy Conditions. Chaos Theory Appl. 2023, 5, 141–152. [Google Scholar] [CrossRef]
- Abd, M.H.; Al-Suhail, G.A.; Tahir, F.R.; Ali Ali, A.M.; Abbood, H.A.; Dashtipour, K.; Jamal, S.S.; Ahmad, J. Synchronization of Monostatic Radar Using a Time-Delayed Chaos-Based FM Waveform. Remote Sens. 2022, 14, 1984. [Google Scholar] [CrossRef]
- Chua, L.O.; Wu, C.W.; Huang, A.; Zhong, G.Q. A Universal Circuit for Studying and Generating Chaos—Part II: Strange Attractors. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1993, 40, 745–761. [Google Scholar] [CrossRef]
- Kennedy, M. Chaos in the Colpitts oscillator. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1994, 41, 771–774. [Google Scholar] [CrossRef]
- Tamaševičius, A.; Mykolaitis, G.; Pyragas, V.; Pyragas, K. A simple chaotic oscillator for educational purposes. Eur. J. Phys. 2004, 26, 61. [Google Scholar] [CrossRef]
- Bilgehan, B.; Sabuncu, O. Synchronization and Analysis of Chaotic Circuit with Application to Communication in the internet of things (IoT) Services. In Proceedings of the 2022 International Conference on Artificial Intelligence in Everything (AIE), Lefkosa, Cyprus, 2–4 August 2022; pp. 674–678. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L.; Johnson, G.A.; Mar, D.J.; Heagy, J.F. Fundamentals of synchronization in chaotic systems, concepts, and applications. Chaos 1997, 7, 520–543. [Google Scholar] [CrossRef]
- Yu, Z.; Ling, S.; Liu, P.X.; Wang, H. Compounding and Synchronization of Fractional Order Chaotic Systems with Prescribed Performance for Secure Communication. IEEE Trans. Circuits Syst. Regul. Pap. 2024, 71, 1335–1345. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, N.; Ji, M. Research on an Improved Driver-response Chaotic Synchronization Voice Encryption Technology. In Proceedings of the 2021 International Conference on Electronic Communications, Internet of Things and Big Data (ICEIB), Yilan County, Taiwan, 10–12 December 2021; pp. 330–334. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.; Wang, Z.; Fu, D.; Liu, G.; Guo, R. Stabilization and complete synchronization of a new time-reversed system. In Proceedings of the 2023 IEEE International Conference on Memristive Computing and Applications (ICMCA), Jinan, China, 8–10 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Cirjulina, D.; Babajans, R.; Capligins, F.; Kolosovs, D.; Litvinenko, A. Experimental Study on Colpitts Chaotic Oscillator-Based Communication System Application for the Internet of Things. Appl. Sci. 2024, 14, 1180. [Google Scholar] [CrossRef]
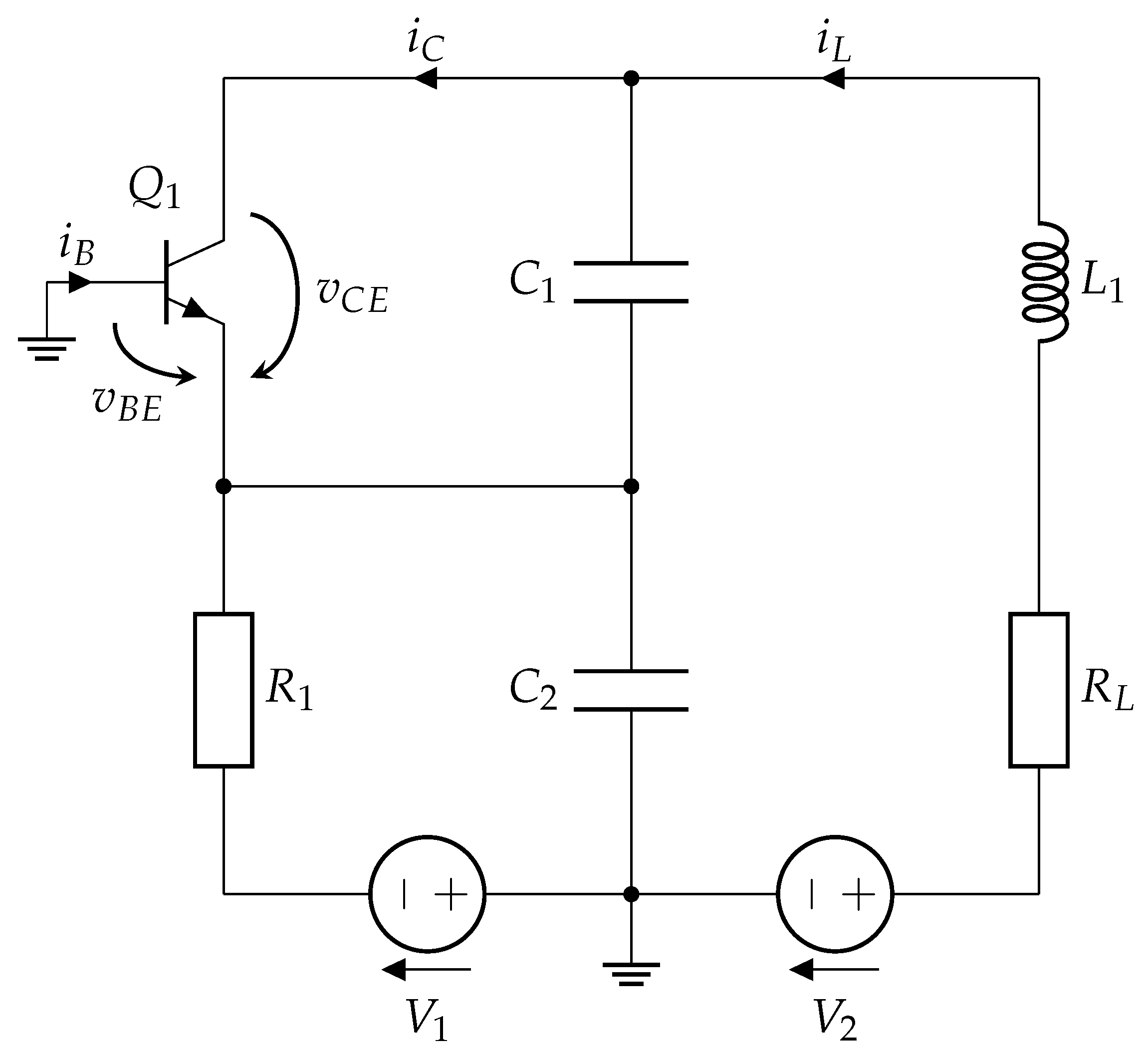
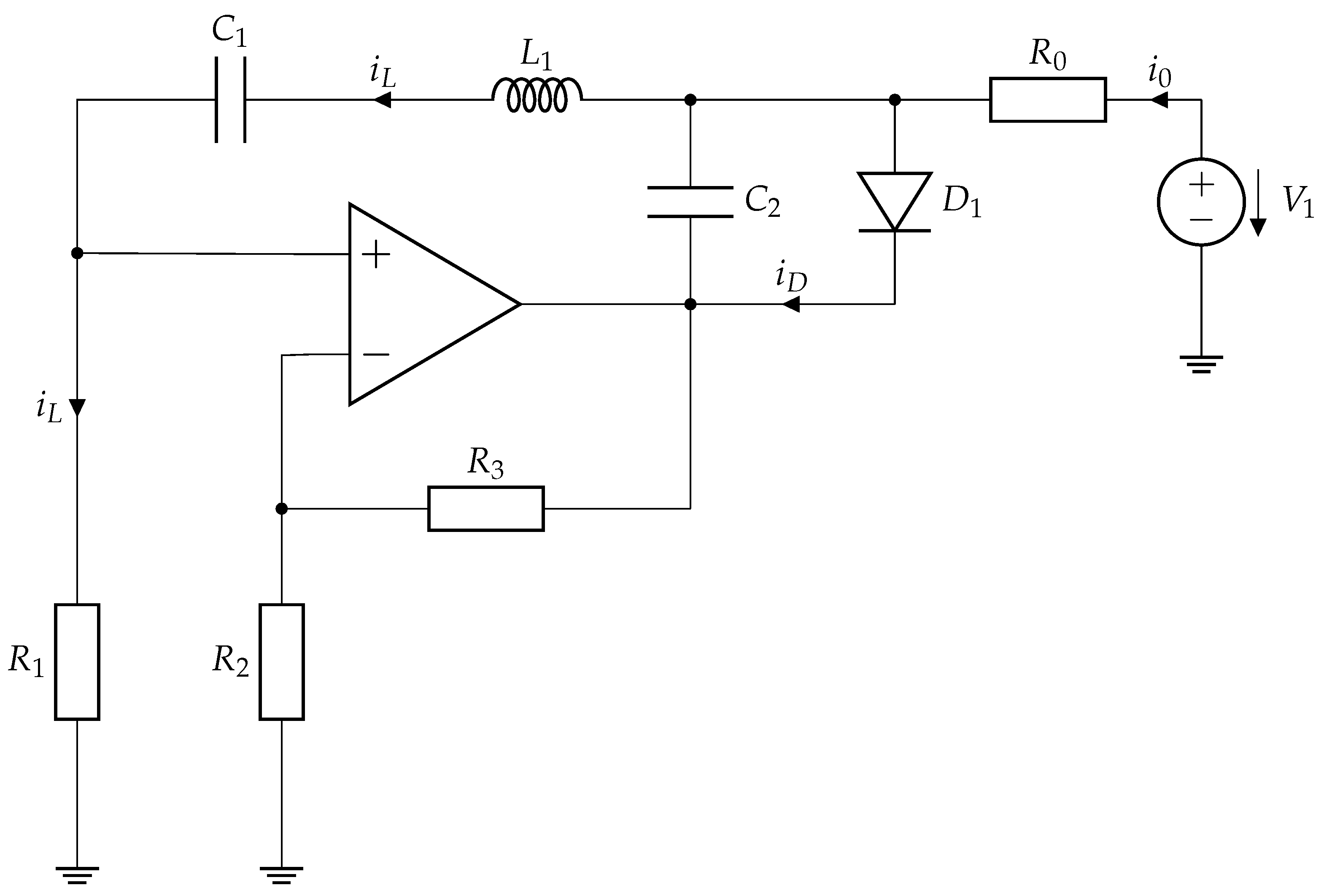

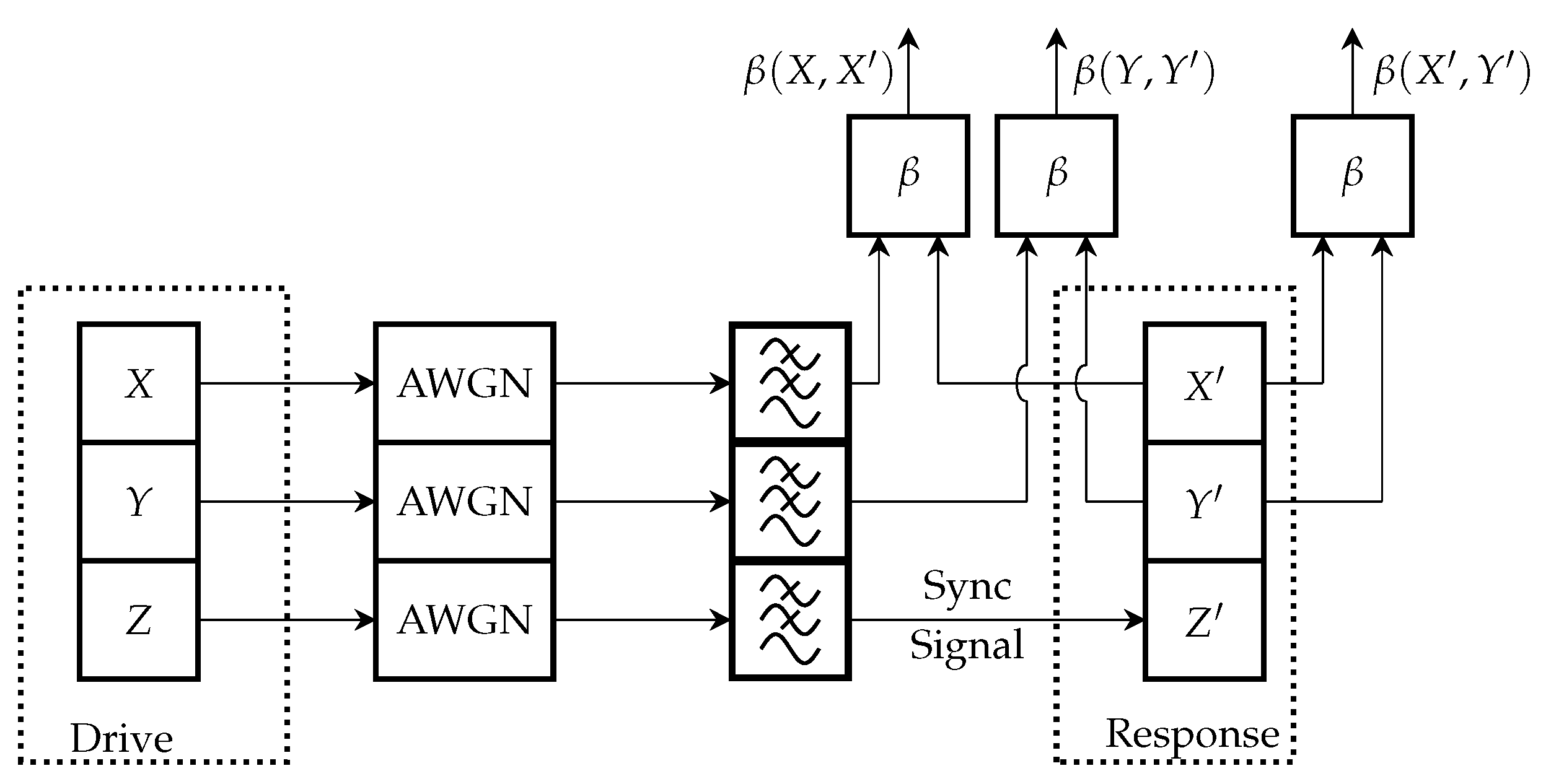

| Colpitts Chaos Oscillator | Vilnius Chaos Oscillator | ||||
|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z |
| SNR, dB | Without Threshold | With Threshold | ||||
|---|---|---|---|---|---|---|
| BER | False ‘0’ Count | False ‘1’ Count | BER | False ‘0’ Count | False ‘1’ Count | |
| 0.4835 | 2414 | 2421 | 0.4810 | 2416 | 2394 | |
| 0.4407 | 2287 | 2120 | 0.4370 | 2168 | 2202 | |
| 0.3249 | 1761 | 1488 | 0.3195 | 1598 | 1597 | |
| 0.1134 | 702 | 432 | 0.1053 | 519 | 534 | |
| 0 | 0.0121 | 79 | 42 | 0.0107 | 57 | 50 |
| 2 | 0.0048 | 34 | 14 | 0.0043 | 21 | 22 |
| 4 | 0.0019 | 12 | 7 | 0.0014 | 7 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cirjulina, D.; Babajans, R.; Kolosovs, D. Design Particularities of Quadrature Chaos Shift Keying Communication System with Enhanced Noise Immunity for IoT Applications. Entropy 2025, 27, 296. https://doi.org/10.3390/e27030296
Cirjulina D, Babajans R, Kolosovs D. Design Particularities of Quadrature Chaos Shift Keying Communication System with Enhanced Noise Immunity for IoT Applications. Entropy. 2025; 27(3):296. https://doi.org/10.3390/e27030296
Chicago/Turabian StyleCirjulina, Darja, Ruslans Babajans, and Deniss Kolosovs. 2025. "Design Particularities of Quadrature Chaos Shift Keying Communication System with Enhanced Noise Immunity for IoT Applications" Entropy 27, no. 3: 296. https://doi.org/10.3390/e27030296
APA StyleCirjulina, D., Babajans, R., & Kolosovs, D. (2025). Design Particularities of Quadrature Chaos Shift Keying Communication System with Enhanced Noise Immunity for IoT Applications. Entropy, 27(3), 296. https://doi.org/10.3390/e27030296









