Research on Active Safety Situation of Road Passenger Transportation Enterprises: Evaluation, Prediction, and Analysis
Abstract
1. Introduction
2. Literature Review
2.1. Assessment of the Safety Situation of Enterprises
2.2. Application of Time Series Forecasting to Traffic Safety
2.3. Driver Operational Characteristics Affecting Traffic Safety
2.4. Research Gap and Contribution
- Most of the above studies have assessed and predicted traffic accident data and the general scope of the study is a country. It is possible for a country to generate traffic accidents on a daily basis, so safety has been studied yearly, monthly, weekly, and daily. However, road passenger transportation enterprises do not have traffic accidents most of the time, so it is difficult to assess and predict their safety dynamically through traffic accident data on a daily basis;
- The impact of driver feedback violation alarms and equipment usage on safety has not yet been studied.
- Considering alarms, driver feedback, and equipment usage, an ASSI is constructed using exploratory factor analysis and validation factor analysis methods to obtain the ASS of each enterprise;
- Relying on the ASSI, we predict the future trend of the enterprises’ ASS based on time series model;
- The WDA-DBN model is proposed, and the deep SHAP method is borrowed to dig deeper into the multifaceted variables that have an impact on ASS.
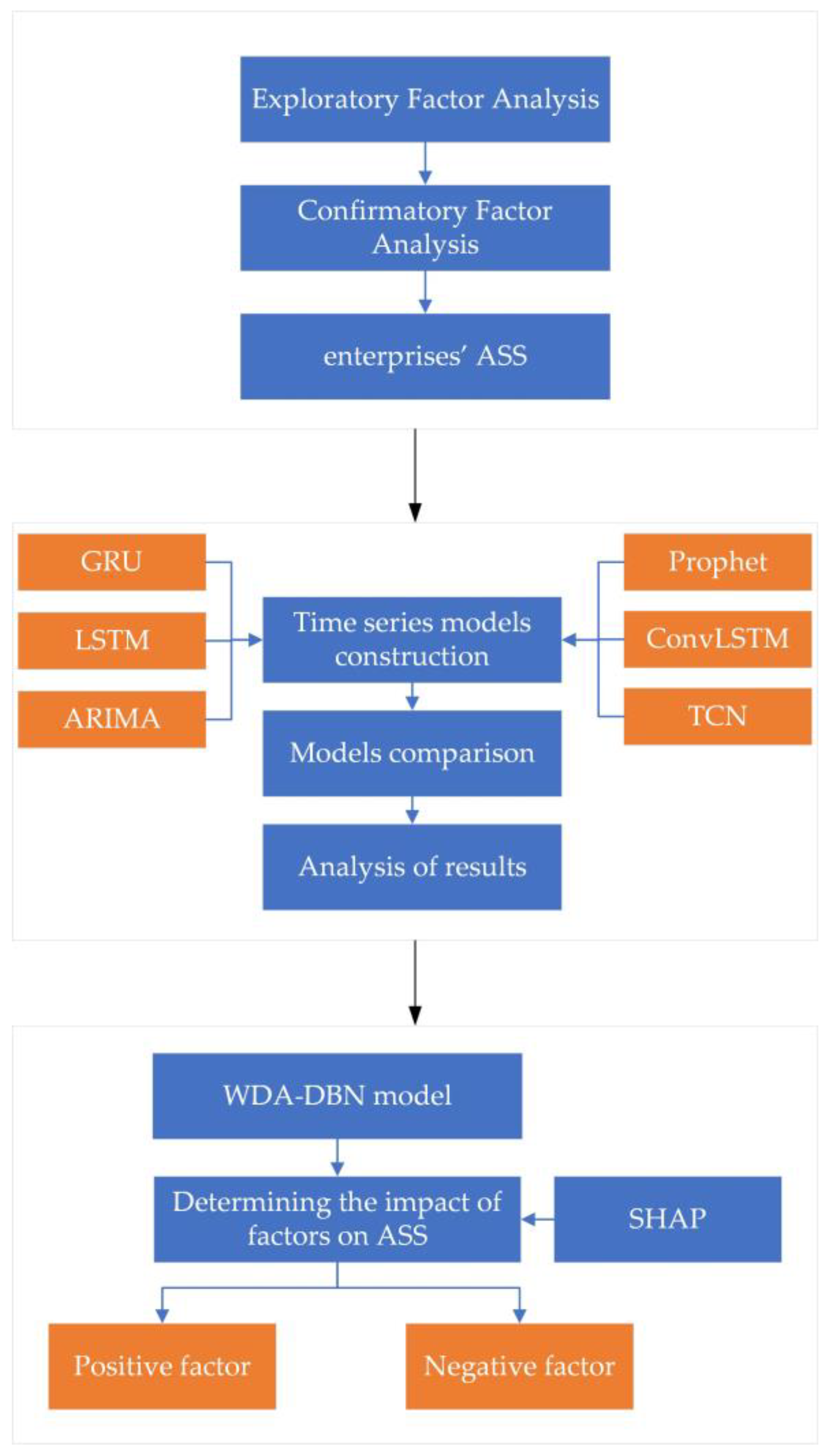
3. Methodology
3.1. Data
3.2. ASS Assessment Methodology Based on Factor Analysis
3.2.1. Exploratory Factor Analysis
3.2.2. Confirmatory Factor Analysis
3.3. A Time Series-Based Method for Predicting ASS
3.3.1. Gated Recurrent Unit (GRU)
3.3.2. Long Short-Term Memory Network (LSTM)
3.3.3. Autoregressive Integrated Moving Average (ARIMA)
3.3.4. Prophet
3.3.5. Convolutional Long Short-Term Memory Networks (Conv_LSTM)
3.3.6. Temporal Convolutional Network (TCN)
3.4. Feature Mining and Visualization Analysis Method Based on WDA-DBN
3.4.1. Deep Belief Network (DBN)
3.4.2. WDA-DBN
3.4.3. SHAP
4. Experimental Setup and Results
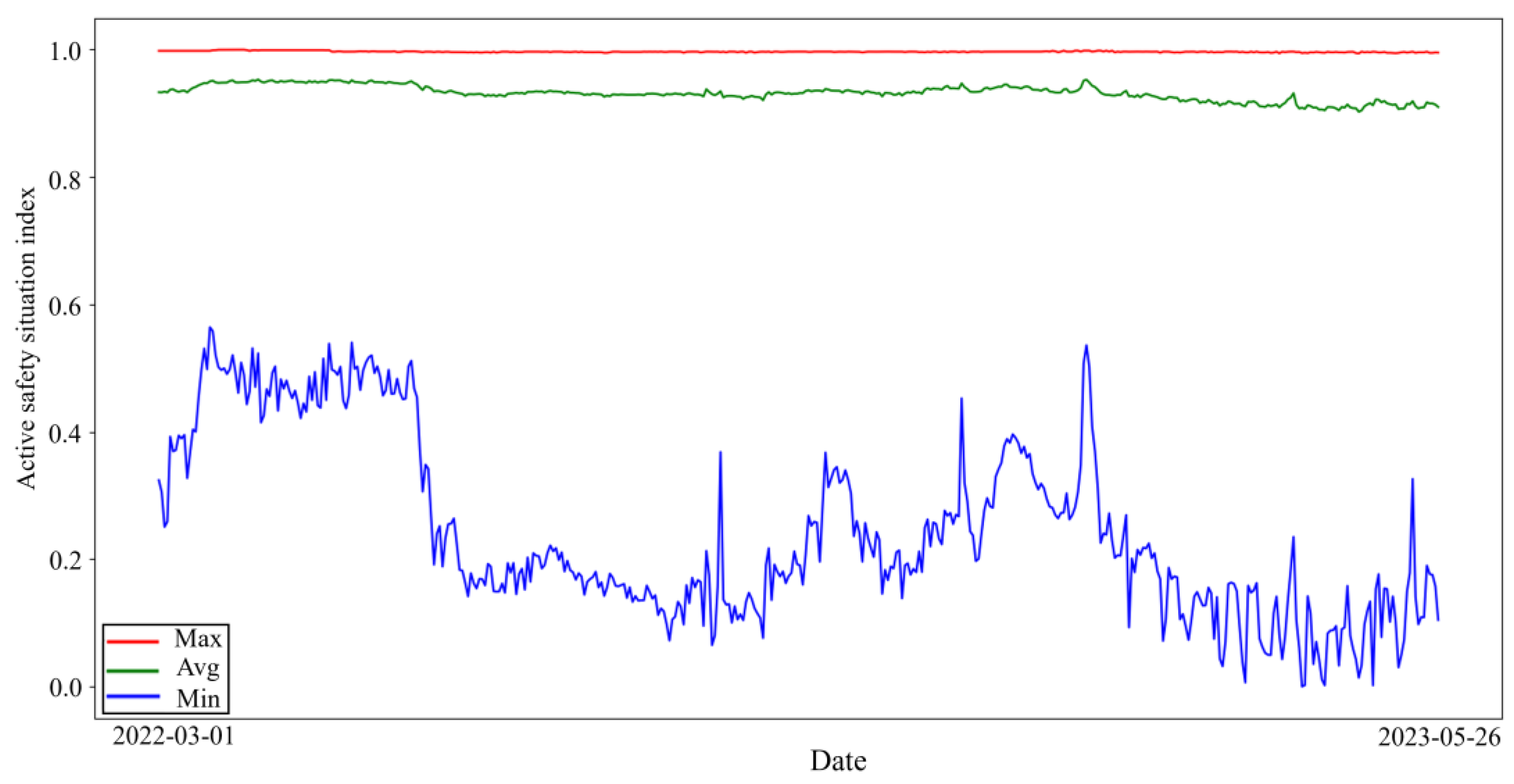
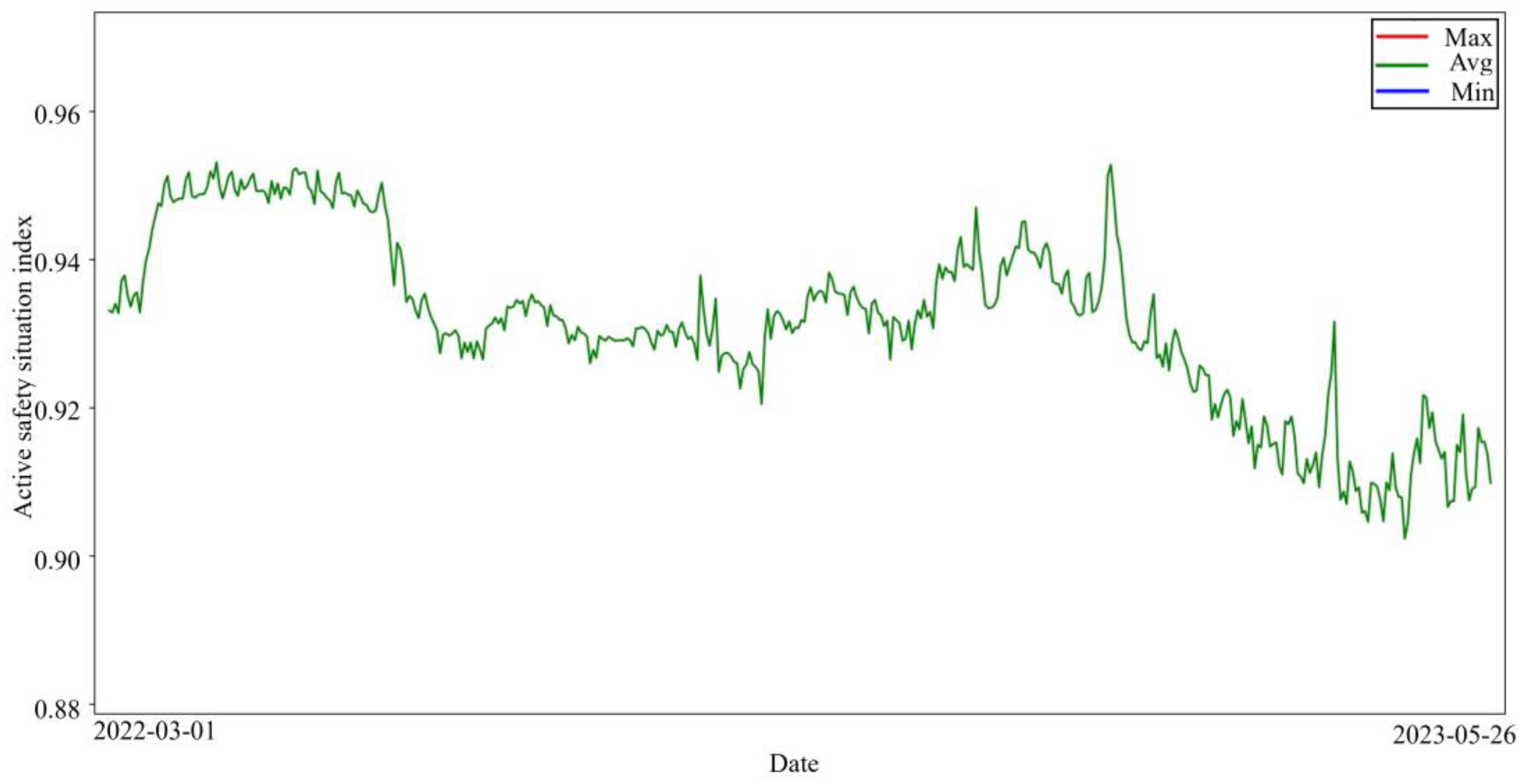
4.1. Assessment of ASS
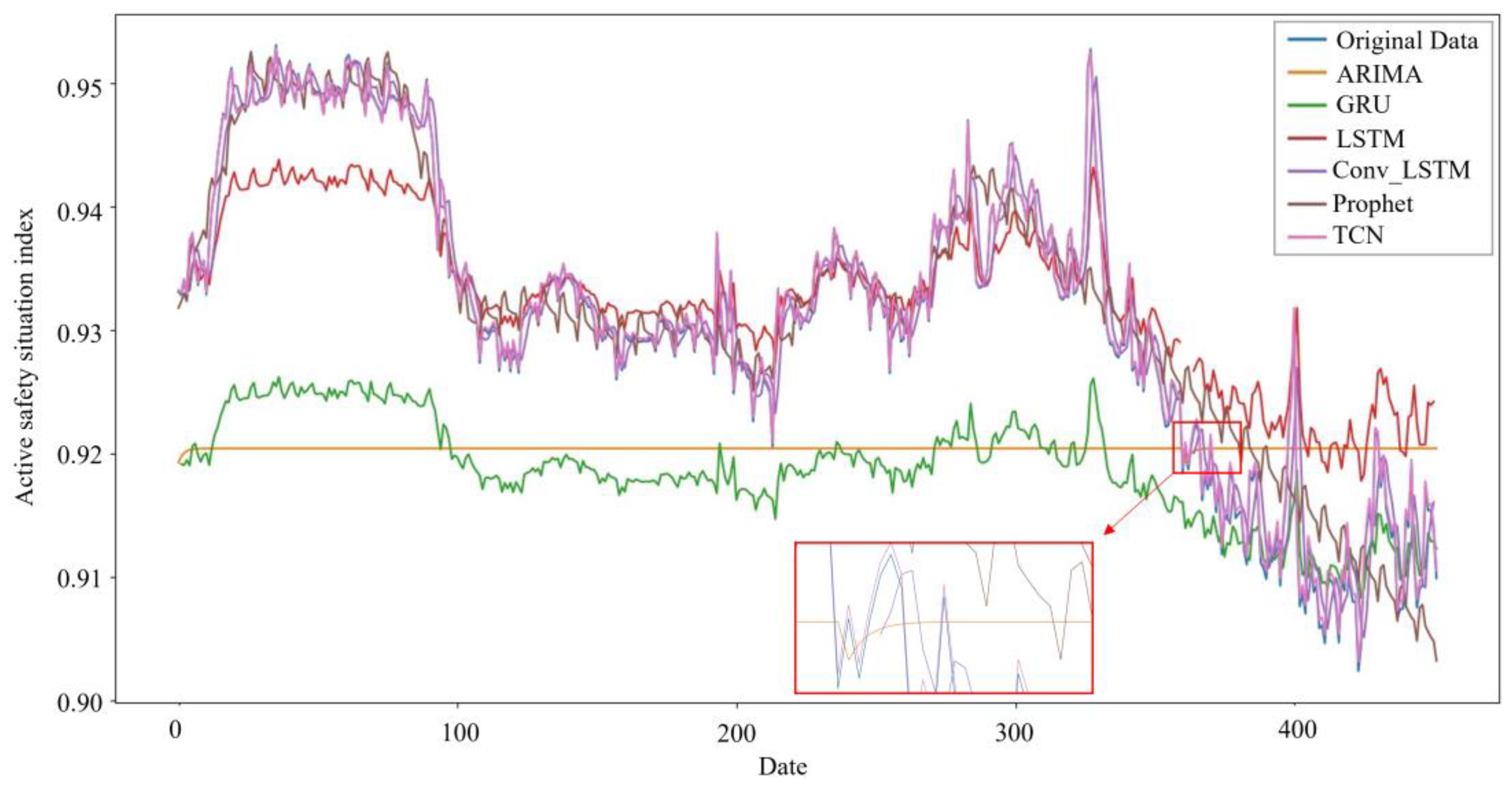
4.2. ASS Prediction
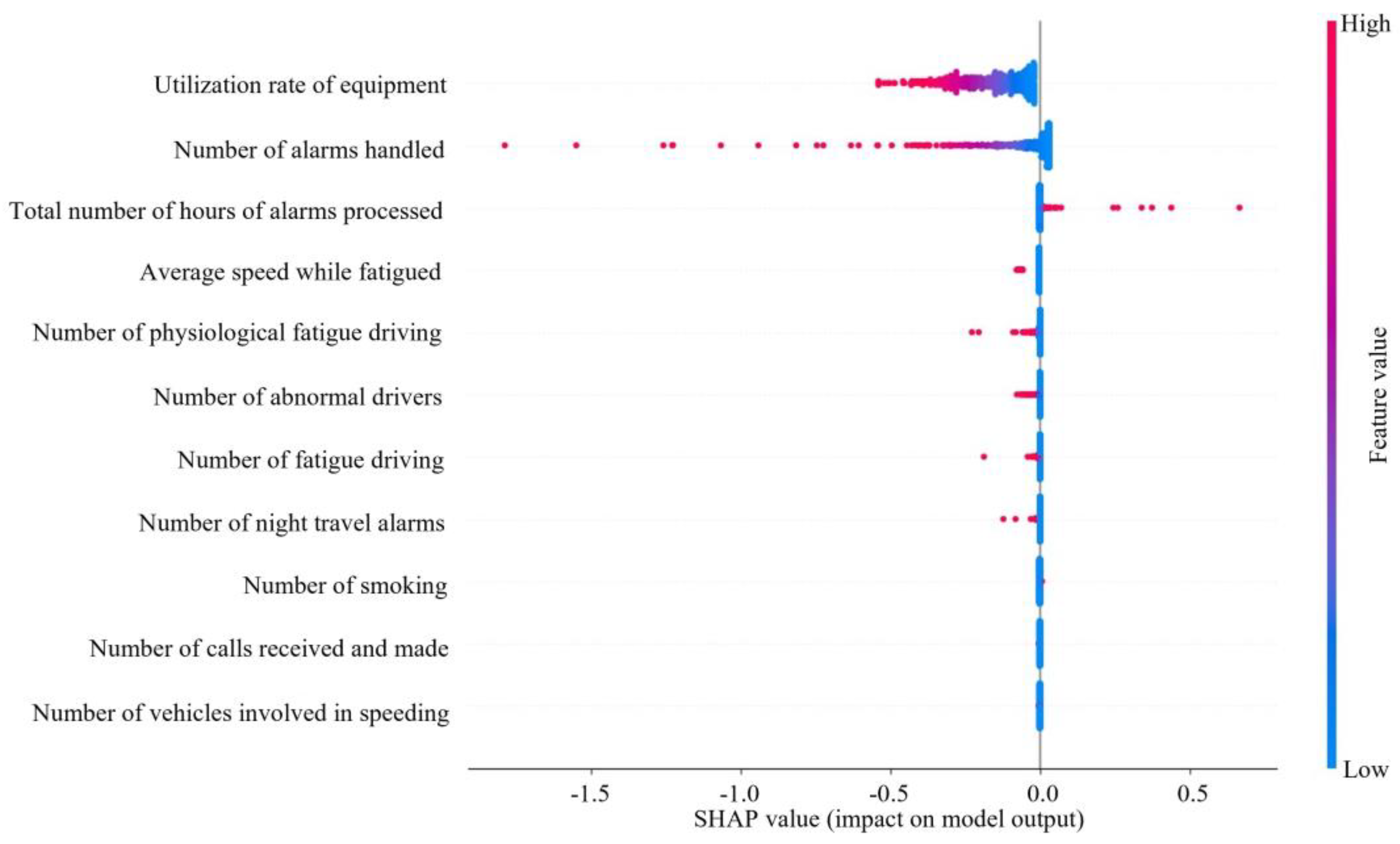
4.3. Analysis of Factors Influencing ASS
4.3.1. Comparison of Methods
4.3.2. Influence Factor Analysis Based on DEEP SHAP
5. Discussion
5.1. Assessment of ASS
5.2. ASS Prediction
5.3. Relationship between ASS and Other Variables
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- EsoNews. Major Accidents Involving Buses Worldwide, 2020–2021. Available online: https://www.163.com/dy/article/GGTF05620552ASSI.html (accessed on 3 October 2023).
- Agency, X.N. Changshen High-Speed Jiangsu Wuxi “9–28” Special Major Road Traffic Accident Investigation Report Published. Available online: https://www.gov.cn/xinwen/2020-09/11/content_5542742.htm (accessed on 4 October 2023).
- U.S. Government Printing Office. Title 49–Transportation. Available online: https://www.ecfr.gov/current/title-49/subtitle-B/chapter-III/subchapter-B (accessed on 4 October 2023).
- Mwale, M.; Mwangilwa, K.; Kakoma, E.; Iaych, K. Estimation of the completeness of road traffic mortality data in Zambia using a three source capture recapture method. Accid. Anal. Prev. 2023, 186, 107048. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhang, J.; Zhang, Y.; Huang, Z. Traffic Accident Data Generation Based on Improved Generative Adversarial Networks. Sensors 2021, 21, 5767. [Google Scholar] [CrossRef] [PubMed]
- Ding, T.; Zhang, L.; Xi, J.; Li, Y.; Zheng, L.; Zhang, K. Bus Fleet Accident Prediction Based on Violation Data: Considering the Binding Nature of Safety Violations and Service Violations. Sustainability 2023, 15, 3520. [Google Scholar] [CrossRef]
- Rahman, M.A.; Das, S.; Sun, X. Understanding the drowsy driving crash patterns from correspondence regression analysis. J. Saf. Res. 2023, 84, 167–181. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Yang, G. Crash Risk Assessment for Heterogeneity Traffic and Different Vehicle-Following Patterns Using Microscopic Traffic Flow Data. Sustainability 2020, 12, 9888. [Google Scholar] [CrossRef]
- Minderhoud, M.M.; Bovy, P.H.L. Extended time-to-collision measures for road traffic safety assessment. Accid. Anal. Prev. 2001, 33, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Yau, K.K.W.; Chen, G. Risk factors associated with traffic violations and accident severity in China. Accid. Anal. Prev. 2013, 59, 18–25. [Google Scholar] [CrossRef] [PubMed]
- de Gelder, E.; Elrofai, H.; Saberi, A.K.; Paardekooper, J.-P.; Opden Camp, O.; de Schutter, B. Risk Quantification for Automated Driving Systems in Real-World Driving Scenarios. IEEE Access 2021, 9, 168953–168970. [Google Scholar] [CrossRef]
- Zhang, G.; Yau, K.K.W.; Zhang, X.; Li, Y. Traffic accidents involving fatigue driving and their extent of casualties. Accid. Anal. Prev. 2016, 87, 34–42. [Google Scholar] [CrossRef]
- Malin, F.; Norros, I.; Innamaa, S. Accident risk of road and weather conditions on different road types. Accid. Anal. Prev. 2019, 122, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef] [PubMed]
- Dong, Q.; Qian, D.L.; Li, C.H.; Fan, H.B. Research on Safety Evaluation Indexes of the Road Transportation Enterprise of Dangerous Goods. In Proceedings of the 2nd International Conference on Civil, Architectural and Hydraulic Engineering (ICCAHE 2013), Zhuhai, China, 27–28 July 2013; pp. 1330–1334. [Google Scholar]
- Wu, J.; Li, C.; Huo, Y. Safety Assessment of Dangerous Goods Transport Enterprise Based on the Relative Entropy Aggregation in Group Decision Making Model. Comput. Intell. Neurosci. 2014, 2014, 571058. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; He, X.; Ding, T.; Li, Y.; Xiao, Z. Analysis of the Accident Propensity of Chinese Bus Drivers: The Influence of Poor Driving Records and Demographic Factors. Mathematics 2022, 10, 4354. [Google Scholar] [CrossRef]
- Gomes, H.; Parasram, V.; Collins, J.; Socias-Morales, C. Time series, seasonality and trend evaluation of 7 years (2015–2021) of OSHA severe injury data. J. Saf. Res. 2023, 86, 30–38. [Google Scholar] [CrossRef]
- Antoniou, C.; Yannis, G. State-space based analysis and forecasting of macroscopic road safety trends in Greece. Accid. Anal. Prev. 2013, 60, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Yousefzadeh-Chabok, S.; Ranjbar-Taklimie, F.; Malekpouri, R.; Razzaghi, A. A Time Series Model for Assessing the Trend and Forecasting the Road Traffic Accident Mortality. Arch. Trauma Res. 2016, 5, e36570. [Google Scholar] [CrossRef] [PubMed]
- Getahun, K.A. Time series modeling of road traffic accidents in Amhara Region. J. Big Data 2021, 8, 102. [Google Scholar] [CrossRef]
- Rabbani, M.B.A.; Musarat, M.A.; Alaloul, W.S.; Rabbani, M.S.; Maqsoom, A.; Ayub, S.; Bukhari, H.; Altaf, M. A Comparison Between Seasonal Autoregressive Integrated Moving Average (SARIMA) and Exponential Smoothing (ES) Based on Time Series Model for Forecasting Road Accidents. Arab. J. Sci. Eng. 2021, 46, 11113–11138. [Google Scholar] [CrossRef]
- Barba, L.; Rodriguez, N.; Montt, C. Smoothing Strategies Combined with ARIMA and Neural Networks to Improve the Forecasting of Traffic Accidents. Sci. World J. 2014, 2014, 152375. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.; Liu, P.; Ukkusuri, S.V. A spatiotemporal deep learning approach for citywide short-term crash risk prediction with multi-source data. Accid. Anal. Prev. 2019, 122, 239–254. [Google Scholar] [CrossRef] [PubMed]
- de Zarza, I.; de Curto, J.; Roig, G.; Calafate, C.T. LLM Multimodal Traffic Accident Forecasting. Sensors 2023, 23, 9225. [Google Scholar] [CrossRef] [PubMed]
- Commandeur, J.J.F.; Bijleveld, F.D.; Bergel-Hayat, R.; Antoniou, C.; Yannis, G.; Papadimitriou, E. On statistical inference in time series analysis of the evolution of road safety. Accid. Anal. Prev. 2013, 60, 424–434. [Google Scholar] [CrossRef] [PubMed]
- Uguz, S.; Buyukgokoglan, E. A Hybrid CNN-LSTM Model for Traffic Accident Frequency Forecasting During the Tourist Season. Teh. Vjesn. Tech. Gaz. 2022, 29, 2083–2089. [Google Scholar]
- Bucsuházy, K.; Matuchová, E.; Zůvala, R.; Moravcová, P.; Kostíková, M.; Mikulec, R. Human factors contributing to the road traffic accident occurrence. Transp. Res. Cent. Brno Czech Repub. 2020, 45, 555–561. [Google Scholar] [CrossRef]
- Yaman, T.T.; Bilgic, E.; Esen, M.F. Analysis of traffic accidents with fuzzy and crisp data mining techniques to identify factors affecting injury severity. J. Intell. Fuzzy Syst. 2022, 42, 575–592. [Google Scholar] [CrossRef]
- Moradi, A.; Nazari, S.S.H.; Rahmani, K. Sleepiness and the risk of road traffic accidents: A systematic review and meta-analysis of previous studies. Transp. Res. Part F-Traffic Psychol. Behav. 2019, 65, 620–629. [Google Scholar] [CrossRef]
- Useche, S.A.; Cendales, B.; Lijarcio, I.; Llamazares, F.J. Validation of the F-DBQ: A short (and accurate) risky driving behavior questionnaire for long-haul professional drivers. Transp. Res. Part F Traffic Psychol. Behav. 2021, 82, 190–201. [Google Scholar] [CrossRef]
- Doecke, S.D.; Kloeden, C.N.; Dutschke, J.K.; Baldock, M.R.J. Safe speed limits for a safe system: The relationship between speed limit and fatal crash rate for different crash types. Traffic Inj. Prev. 2018, 19, 404–408. [Google Scholar] [CrossRef] [PubMed]
- Sayed, T.; Sacchi, E. Evaluating the safety impact of increased speed limits on rural highways in British Columbia. Accid. Anal. Prev. 2016, 95, 172–177. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, P.; Gupta, A.; Velaga, N.R. Perceived risk vs actual driving performance during distracted driving: A comparative analysis of phone use and other secondary distractions. Transp. Res. Part F-Traffic Psychol. Behav. 2022, 86, 296–315. [Google Scholar] [CrossRef]
- Lee, M.L.; Howard, M.E.; Horrey, W.J.; Liang, Y.; Anderson, C.; Shreeve, M.S.; O’Brien, C.S.; Czeisler, C.A. High risk of near-crash driving events following night-shift work. Proc. Natl. Acad. Sci. USA 2016, 113, 176–181. [Google Scholar] [CrossRef] [PubMed]
- Zeller, R.; Williamson, A.; Friswell, R. The effect of sleep-need and time-on-task on driver fatigue. Transp. Res. Part F-Traffic Psychol. Behav. 2020, 74, 15–29. [Google Scholar] [CrossRef]
- Hangoma, P.; Moonga-Mukale, K. Impact of night travel ban on road traffic crashes and fatalities in Zambia: An interrupted time series analysis. BMJ Glob. Health 2021, 6, e005481. [Google Scholar] [CrossRef] [PubMed]
- Ayuso, M.; Guillen, M.; Alcaniz, M. The impact of traffic violations on the estimated cost of traffic accidents with victims. Accid. Anal. Prev. 2010, 42, 709–717. [Google Scholar] [CrossRef] [PubMed]
- Treiblmaier, H.; Filzmoser, P. Exploratory factor analysis revisited: How robust methods support the detection of hidden multivariate data structures in IS research. Inf. Manag. 2010, 47, 197–207. [Google Scholar] [CrossRef]
- Shrestha, N. Factor Analysis as a Tool for Survey Analysis. Am. J. Appl. Math. Stat. 2021, 9, 4–11. [Google Scholar] [CrossRef]
- Nassiri, H.; Mohammadpour, S.I.; Dahaghin, M. Forecasting time trend of road traffic crashes in Iran using the macro-scale traffic flow characteristics. Heliyon 2023, 9, e14481. [Google Scholar] [CrossRef] [PubMed]
- Leoni, L.; Bahootoroody, A.; Abaei, M.M.; Cantini, A.; Bahootoroody, F.; De Carlo, F. Machine learning and deep learning for safety applications: Investigating the intellectual structure and the temporal evolution. Saf. Sci. 2024, 170, 106363. [Google Scholar] [CrossRef]
- Gajamannage, K.; Park, Y.; Jayathilake, D.I. Real-time forecasting of time series in financial markets using sequentially trained dual-LSTMs. Expert Syst. Appl. 2023, 223, 119879. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef]
- Ren, Q.; Li, Y.; Liu, Y. Transformer-enhanced periodic temporal convolution network for long short-term traffic flow forecasting. Expert Syst. Appl. 2023, 227, 120203. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Sheng, Y.; Ma, D. Stock Index Spot–Futures Arbitrage Prediction Using Machine Learning Models. Entropy 2022, 24, 1462. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.; Du, X. A Deep Neural Network Regularization Measure: The Class-Based Decorrelation Method. Entropy 2024, 26, 7. [Google Scholar] [CrossRef] [PubMed]
- Ratnasingam, S.; Muñoz-Lopez, J. Distance Correlation-Based Feature Selection in Random Forest. Entropy 2023, 25, 1250. [Google Scholar] [CrossRef]
- Xia, H.; Chen, X.; Wang, Z.; Chen, X.; Dong, F. A Multi-Modal Deep-Learning Air Quality Prediction Method Based on Multi-Station Time-Series Data and Remote-Sensing Images: Case Study of Beijing and Tianjin. Entropy 2024, 26, 91. [Google Scholar] [CrossRef] [PubMed]
- Katrakazas, C.; Michelaraki, E.; Sekadakis, M.; Ziakopoulos, A.; Kontaxi, A.; Yannis, G. Identifying the impact of the COVID-19 pandemic on driving behavior using naturalistic driving data and time series forecasting. J. Saf. Res. 2021, 78, 189–202. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Lundberg, S.M.; Lee, S.-I. Explaining a series of models by propagating Shapley values. Nat. Commun. 2022, 13, 4512. [Google Scholar] [CrossRef] [PubMed]
- Meister, S.; Wermes, M.; Stueve, J.; Groves, R.M. Investigations on Explainable Artificial Intelligence methods for the deep learning classification of fibre layup defect in the automated composite manufacturing. Compos. Part B-Eng. 2021, 224, 109160. [Google Scholar] [CrossRef]
- Fernando, Z.T.; Singh, J.; Anand, A. A study on the Interpretability of Neural Retrieval Models using DeepSHAP. In Proceedings of the 42nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), Paris, France, 21–25 July 2019; pp. 1005–1008. [Google Scholar]
- Li, J.; Goerlandt, F.; Reniers, G. An overview of scientometric mapping for the safety science community: Methods, tools, and framework. Saf. Sci. 2021, 134, 105093. [Google Scholar] [CrossRef]
- Calabrese, C.G.; Molesworth, B.R.C.; Hatfield, J. The effect of punishment and feedback on correcting erroneous behavior. J. Saf. Res. 2023, 87, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Borghetti, F.; Marchionni, G.; Bianchi, M.D.; Barabino, B.; Bonera, M.; Caballini, C. A new methodology for accidents analysis: The case of the State Road 36 in Italy. Int. J. Transp. Dev. Integr. 2021, 5, 278–290. [Google Scholar] [CrossRef]
- Gnardellis, C.; Tzamalouka, G.; Papadakaki, M.; Chliaoutakis, J.E. An investigation of the effect of sleepiness, drowsy driving, and lifestyle on vehicle crashes. Transp. Research. Part F Traffic Psychol. Behaviour. 2008, 11, 270–281. [Google Scholar] [CrossRef]
- Cendales, B.; Llamazares, F.J.; Useche, S.A. Are subjective outcomes a “missing link” between driving stress and risky driving behaviors of commuters? Assessing the case of a LMIC. Saf. Sci. 2023, 158, 105996. [Google Scholar] [CrossRef]
- Lu, J.; Xie, X.; Zhang, R. Focusing on appraisals: How and why anger and fear influence driving risk perception. J. Safety Res. 2013, 45, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Crizzle, A.M.; Bigelow, P.; Adams, D.; Gooderham, S.; Myers, A.M.; Thiffault, P. Health and wellness of long-haul truck and bus drivers: A systematic literature review and directions for future research. J. Transp. Health 2017, 7, 90–109. [Google Scholar] [CrossRef]
- Farmer, C.; Braitman, K.; Lund, A. Cell Phone Use While Driving and Attributable Crash Risk. Traffic Inj. Prev. 2010, 11, 466–470. [Google Scholar] [CrossRef] [PubMed]
- Sohaee, N.; Bohluli, S. Nonlinear Analysis of the Effects of Socioeconomic, Demographic, and Technological Factors on the Number of Fatal Traffic Accidents. Safety 2024, 10, 11. [Google Scholar] [CrossRef]


| Name | Description |
|---|---|
| Date | yyyy-mm-dd |
| Enterprise ID | The name of the enterprise |
| Area ID | The name of the area where the enterprise is located |
| Number of vehicles | The number of vehicles operated by an enterprise |
| Number of alarms | The total number of alarms for vehicles in the enterprise in one day |
| Satellite positioning mileage | Total miles traveled in one day by vehicles in the enterprise |
| Sum of severe alarm levels | The sum of serious alarm levels for vehicles in the enterprise in one day |
| Number of physiological fatigue driving | The total number of alarms due to physiological fatigue of drivers in the enterprise |
| Number of calls received and made | The total number of alarms caused by drivers in the business due to answering a phone call |
| Number of smoking | The total number of alarms due to smoking by drivers in the enterprise |
| Number of abnormal drivers | The total number of alarms caused by drivers in the enterprise due to abnormal emotions |
| Number of speeding | The total number of alarms due to speeding by drivers in the enterprise |
| Number of fatigue driving | The total number of alarms due to fatigued drivers in the enterprise |
| Number of night travel alarms | The total number of alarms caused by drivers in the enterprise due to driving at night during prohibited driving hours |
| Total number of violations of the night travel ban | The total number of times drivers in the enterprise drove at night during prohibited driving hours |
| Number of vehicles involved in the night travel ban | The number of vehicles in the enterprise that engage in driving behavior during hours when driving is prohibited at night |
| Cumulative hours of prohibited traffic violations | Cumulative total hours driven by drivers in the business during hours when driving is prohibited at night |
| Accumulated mileage violation of prohibited traffic | Total cumulative miles driven by drivers in the business during hours when driving at night is prohibited |
| Number of vehicles involved in speeding | The number of vehicles with speeding behavior in the enterprise |
| Accumulated hours of sustained speeding | The total cumulative hours of speeding by drivers in the business |
| Average speed while fatigued | The average speed at which drivers in the enterprise drive when fatigued |
| Number of vehicles involved in fatigued driving | The number of vehicles with fatigued driving behavior in the enterprise |
| Fatigue duration of driving | The total cumulative hours of driver fatigue driving in the enterprise |
| Utilization rate of equipment | The number of vehicles using onboard monitoring equipment in the enterprise / the total number of vehicles traveling in the enterprise on the same day |
| Number of utilization rate of equipment statistics | The number of times an enterprise counts the use of equipment in a day |
| Number of passes for dynamic data | The number of qualified times enterprise dynamic data is uploaded to the platform |
| Average alarm response time | The average length of time for drivers in the enterprise to respond after an alarm occurs |
| Total number of hours of alarms processed | The total time it takes for the driver in the enterprise to deal with the alarm after it occurs |
| Number of alarms handled | The total number of times drivers in the enterprise responded to alarms after they occurred |
| Factor | Variable | Non-Standard Load Factors | Standardized Load Factor | z | S.E. | P |
|---|---|---|---|---|---|---|
| factor 1 | The total number of violations of the nighttime ban | 1.000 | 0.999 | - | - | - |
| The accumulated mileage violation of prohibited traffic | 0.506 | 0.998 | 4995.594 | 0.000 | 0.000 *** | |
| The number of nighttime trip alarms | 0.934 | 0.999 | 5564.666 | 0.000 | 0.000 *** | |
| The number of vehicles involved in the nighttime ban | 0.933 | 0.999 | 5568.836 | 0.000 | 0.000 *** | |
| The cumulative hours of prohibited traffic violations | 0.507 | 0.998 | 5144.007 | 0.000 | 0.000 *** | |
| factor 2 | The number of the utilization rate of equipment statistics | 1.000 | 0.843 | - | - | - |
| The number of alarms | 0.408 | 0.910 | 448.593 | 0.001 | 0.000 *** | |
| Satellite positioning mileage | 0.411 | 0.905 | 444.678 | 0.001 | 0.000 *** | |
| Number of vehicles | 0.524 | 0.865 | 409.552 | 0.001 | 0.000 *** | |
| The number of passes for dynamic data | 0.411 | 0.898 | 438.003 | 0.001 | 0.000 *** | |
| factor 3 | The accumulated hours of sustained speeding | 1.000 | 1.000 | - | - | - |
| The number of speeding | 0.902 | 1.000 | 10,076.52 | 0.000 | 0.000 *** | |
| The umber of vehicles involved in speeding | 1.039 | 0.999 | 9015.846 | 0.000 | 0.000 *** | |
| factor 4 | The fatigue duration of driving | 1.000 | 0.999 | - | - | - |
| Average speed while fatigued | 1.711 | 0.926 | 891.755 | 0.002 | 0.000 *** | |
| The number of vehicles involved in fatigued driving | 0.823 | 0.999 | 6359.075 | 0.000 | 0.000 *** | |
| The number of fatigue driving | 0.407 | 0.999 | 5569.513 | 0.000 | 0.000 *** | |
| factor 5 | The sum of severe alarm levels | 1.000 | 1.000 | - | - | - |
| Model | Loss Function | MSE | MAE |
|---|---|---|---|
| Adagrad-GRU | MAE | 1.559 × 10−6 | 1.286 × 10−4 |
| Adadelta-LSTM | MAE | 1.092 × 10−4 | 9.753 × 10−3 |
| ARIMA(1,1,1) | - | 7.403 × 10−4 | 7.388 × 10−3 |
| Prophet | - | 4. 457 × 10−5 | 5.898 × 10−3 |
| Adam-Conv_LSTM | MSE | 1.989 × 10−5 | 3.511 × 10−3 |
| Adam-TCN | MSE | 2.944 × 10−7 | 5.333 × 10−4 |
| Model | MSE | MAE |
|---|---|---|
| WDA-DBN | 0.0011975 | 0.0221929 |
| DBN | 0.0012969 | 0.0232784 |
| XGBOOST | 0.0012857 | 0.0221388 |
| BPNN | 0.0016549 | 0.02545431 |
| Factor | AVE | CR |
|---|---|---|
| factor 1 | 0.998 | 0.999 |
| factor 2 | 0.744 | 0.925 |
| factor 3 | 0.999 | 1.000 |
| factor 4 | 0.907 | 0.970 |
| factor 5 | 0.999 | 0.999 |
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | Factor 5 | |
|---|---|---|---|---|---|
| factor 1 | 0.999 | ||||
| factor 2 | 0.092 | 0.863 | |||
| factor 3 | 0.300 | 0.112 | 0.999 | ||
| factor 4 | 0.157 | 0.185 | 0.227 | 0.952 | |
| factor 5 | 0.334 | 0.126 | 0.614 | 0.710 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Cao, S.; Ding, T.; Tian, J.; Sun, J. Research on Active Safety Situation of Road Passenger Transportation Enterprises: Evaluation, Prediction, and Analysis. Entropy 2024, 26, 434. https://doi.org/10.3390/e26060434
Zheng L, Cao S, Ding T, Tian J, Sun J. Research on Active Safety Situation of Road Passenger Transportation Enterprises: Evaluation, Prediction, and Analysis. Entropy. 2024; 26(6):434. https://doi.org/10.3390/e26060434
Chicago/Turabian StyleZheng, Lili, Shiyu Cao, Tongqiang Ding, Jian Tian, and Jinghang Sun. 2024. "Research on Active Safety Situation of Road Passenger Transportation Enterprises: Evaluation, Prediction, and Analysis" Entropy 26, no. 6: 434. https://doi.org/10.3390/e26060434
APA StyleZheng, L., Cao, S., Ding, T., Tian, J., & Sun, J. (2024). Research on Active Safety Situation of Road Passenger Transportation Enterprises: Evaluation, Prediction, and Analysis. Entropy, 26(6), 434. https://doi.org/10.3390/e26060434






