Link Prediction in Complex Networks Using Average Centrality-Based Similarity Score
Abstract
1. Introduction
2. Problem Definition
3. Recent Work
4. Related Work
4.1. Existing Similarity Measures
- Local Similarity Measures: Local similarity measures focus on examining the immediate neighbors of a node in the network. Some well-known measures include the common neighbor (CN) [15], Jaccard coefficient (JC) [3], preferential attachment (PA) [30], Adamic–Adar (AA) [31], resource allocation (RA) [32], etc.Common Neighbor: The likelihood of a link being formed between two nodes, v and u, is higher when they share a significant number of common neighbors.In Equation (1), denotes the size of the nodes’ neighborhoods’ intersection; is the set of neighbors of node v.Jaccard Coefficient: The common neighbor is comparable to this metric, which normalizes the score of the common neighbor, as given below.In Equation (2), is the size of the intersection of two nodes’ neighborhoods, out of the total neighbors of nodes v and u, where is the set of neighbors of node v.Preferential Attachment: It counts the richness of two nodes instead of shared neighbors between non-adjacent node pairs. The degrees of nodes v and u are multiplied collectively.requires the degree of nodes and does not consider common neighbors. In Equation (3), is the degree of node v.Resource Allocation: We assume two non-adjacent node pairs, v and u. The amount of resources provided from node v to node u determines how similar the two nodes are when they are transferring resources through their shared nodes.In Equation (4), is the degree of node r.Adamic–Adar: Adamic–Adar is a variant of resource allocation. In real-world scenarios, for example, individuals with a larger number of friends tend to allocate less time and resources to particular friend compared to those with fewer friends. This is defined as follows:In Equation (5), is the degree of node r.
4.2. Recent Measures
- Common Neighbor and Centrality-based Parameterized Algorithm (CCPA): To recommend the creation of new linkages in complex networks, CCPA uses two essential node characteristics—the number of shared neighbors between node pairs, and their centrality measures. In this case, closeness centrality is taken into account as a parameter for missing link prediction. The term “common neighbor” describes the nodes that are shared by two nodes. The term “centrality” refers to the significance of a node inside the network.In Equation (6), the user-generated parameter regulates the centrality and common neighbor relevance. The set of neighbors of node v is represented by , and is the shortest path length between v and u.
- Keyword Network Link Prediction Algorithm (KNLP): KNLP depends on the nodes’ clustering coefficient, and their centrality measure like eigenvector centrality [33]. The stronger correlation between eigenvector centrality and node degree shows that nodes with the highest eigenvector have more connections. For nodes u and v, KNLP is defined as follows:In Equation (7), and are the centrality scores for nodes v and u, and are clustering coefficient values for nodes v and u, and their values always range between 0 and 1. Here, is used to avoid the division by zero error.
4.3. Centrality Measures
- Local Centrality: Local centrality involves only immediate neighborhood. Degree centrality (D) [5] and clustering coefficient (CC) [35] are two popular local centralities used in this paper.Degree Centrality: The node v’s degree centrality is calculated as the fraction of other nodes adjacent to node v out of the possible total. Nodes characterized by a high degree of centrality are referred to as nodes.Clustering Coefficient: The clustering coefficient of a specific node is determined by the ratio of closed triangles within the node’s neighborhood, to the total number of triangles present in that neighborhood. It is also known as transitivity.
- Global Centrality: Global centrality involves the whole graph. Closeness centrality (C) [34] and betweenness centrality (B) [36] are few popular global centralities used in this paper.Closeness Centrality: One method of identifying nodes that can efficiently distribute information throughout a network is through closeness centrality. The closeness centrality of a node, denoted as v, within a graph, is determined by taking the reciprocal of the average shortest path distance from node v to all reachable nodes in the graph.In Equation (10), the shortest path length from v to u is denoted by . In the network, the node that is nearest to every other node is the one with the highest closeness centrality.Betweenness Centrality: A node’s betweenness centrality is a measure of how many shortest paths there are via a particular node.In Equation (11), represents the total number of shortest paths between nodes v and u, and denotes the total number of shortest paths between nodes v and u that pass through node r.
5. Proposed Work
5.1. Similarity Based on Average Centrality Measures (SAC)
| Algorithm 1: An algorithm for common neighbor-based average centrality |
 |
5.2. Time Complexity of Similarity Based on Average Centrality Measures
6. Implementation
6.1. Datasets
6.2. Evaluation Metrics
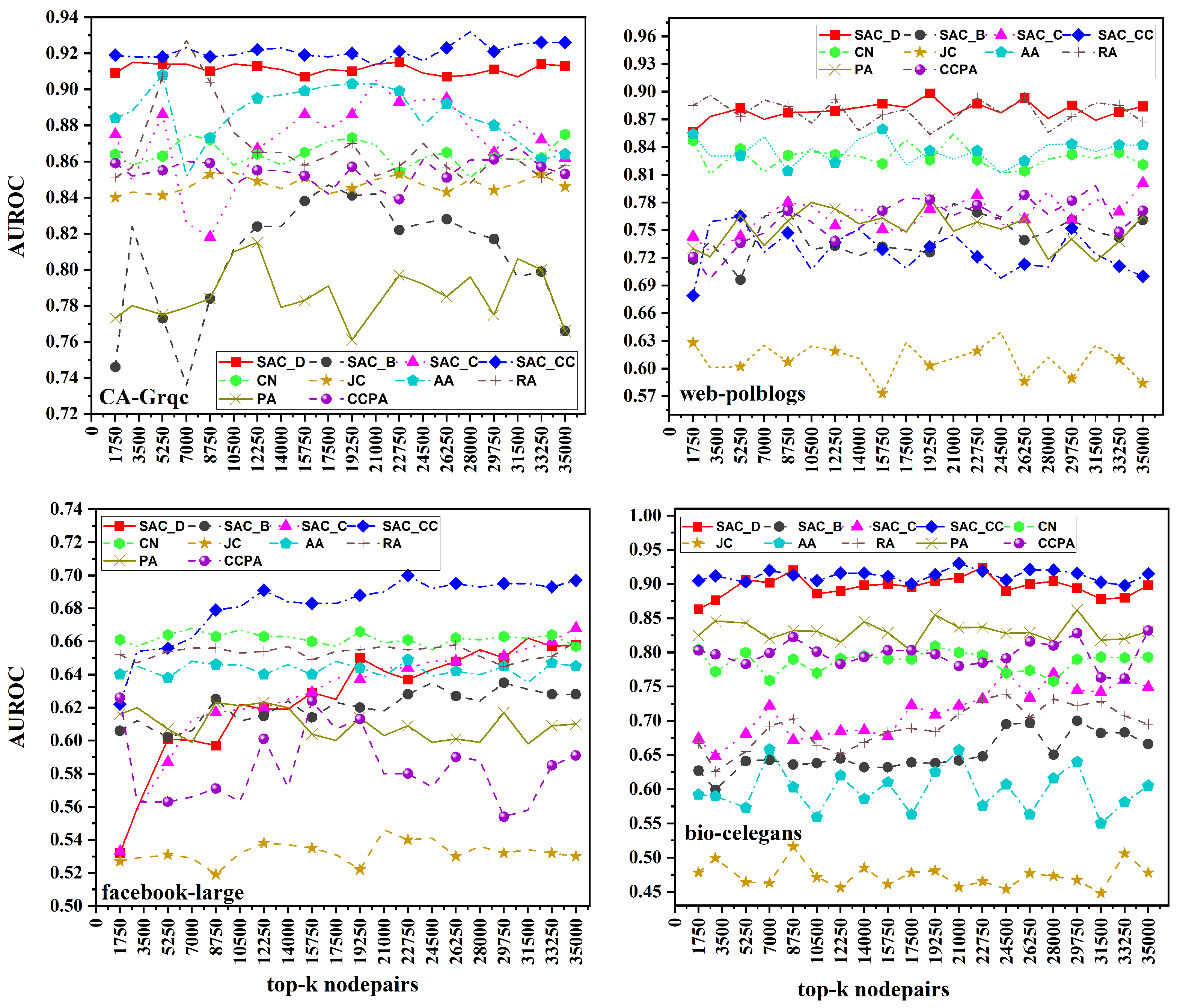
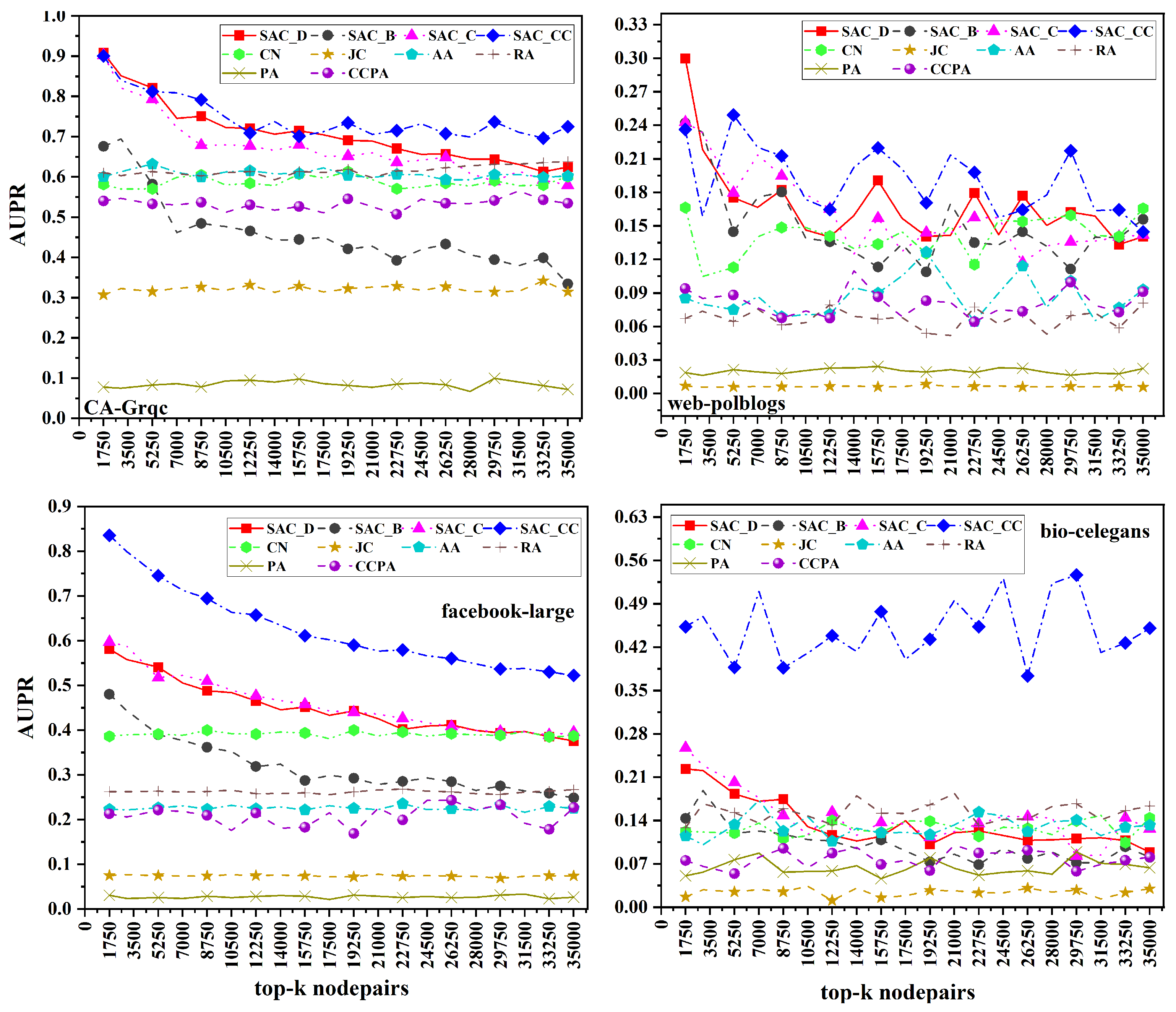
7. Results
7.1. Comparing Proposed Similarity-Based Centralities with Existing Similarity-Based Link Prediction Measures
7.2. Comparing Proposed Measures
7.3. Comparing Proposed Measures with Recent Methods like CCPA and KNLP
7.4. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LP | Link prediction |
| CMs | Centrality measures |
| CNs | Common neighbors |
| JC | Jaccard coefficient |
| AA | Adamic–Adar |
| RA | Resource allocation |
| PA | Preferential attachment |
| D | Degree centrality |
| B | Betweenness centrality |
| C | Closeness centrality |
| CC | Clustering coefficient |
| CCPA | Common Neighbor and Centrality-based Parameterized Algorithm |
| KNLP | Keyword network link prediction algorithm |
| SAC_D | Similarity based on Average Degree |
| SAC_B | Similarity based on Average Betweenness |
| SAC_C | Similarity based on Average Closeness |
| SAC_CC | Similarity based on Average Clustering Coefficient |
| AUROC | Area Under the Receiver Operating Characteristic |
| AUPR | Area Under Precision-Recall |
References
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Musial, K.; Bródka, P.; De Meo, P. Analysis and applications of complex social networks. Complexity 2017, 2017, 3014163. [Google Scholar] [CrossRef]
- Newman, M.E. Clustering and preferential attachment in growing networks. Phys. Rev. E 2001, 64, 025102. [Google Scholar] [CrossRef] [PubMed]
- Liben-Nowell, D.; Kleinberg, J. The link prediction problem for social networks. In Proceedings of the Twelfth International Conference on Information and Knowledge Management, New Orleans, LA, USA, 3–8 November 2003; pp. 556–559. [Google Scholar]
- Freeman, L.C. Centrality in social networks: Conceptual clarification. In Social Network: Critical Concepts in Sociology; Routledg: London, UK, 2002; Volume 1, pp. 238–263. [Google Scholar]
- Kumar, S.; Panda, B.; Aggarwal, D. Community detection in complex networks using network embedding and gravitational search algorithm. J. Intell. Inf. Syst. 2021, 57, 51–72. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Y.; Yang, S. Efficient influence maximization in social networks. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 199–208. [Google Scholar]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Schafer, J.B.; Frankowski, D.; Herlocker, J.; Sen, S. Collaborative filtering recommender systems. In The Adaptive Web: Methods and Strategies of Web Personalization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 291–324. [Google Scholar]
- Leicht, E.A.; Holme, P.; Newman, M.E. Vertex similarity in networks. Phys. Rev. E 2006, 73, 026120. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Huang, J.; Liu, J.; Huang, T.; Chen, H. Relative-path-based algorithm for link prediction on complex networks using a basic similarity factor. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 013104. [Google Scholar] [CrossRef]
- Airoldi, E.M.; Blei, D.; Fienberg, S.; Xing, E. Mixed membership stochastic blockmodels. Adv. Neural Inf. Process. Syst. 2008, 21, 1–8. [Google Scholar]
- Clauset, A.; Moore, C.; Newman, M.E. Hierarchical structure and the prediction of missing links in networks. Nature 2008, 453, 98–101. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. A Stat. Mech. Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Nandini, Y.; Lakshmi, T.J.; Enduri, M.K. Link Prediction in Complex Networks: An Empirical Review. In Proceedings of the International Conference on Frontiers of Intelligent Computing: Theory and Applications, Cardiff, UK, 11–12 April 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 57–67. [Google Scholar]
- Wang, P.; Xu, B.; Wu, Y.; Zhou, X. Link prediction in social networks: The state-of-the-art. Sci. China Inf. Sci. 2015, 1, 1–38. [Google Scholar] [CrossRef]
- Das, K.; Samanta, S.; Pal, M. Study on centrality measures in social networks: A survey. Soc. Netw. Anal. Min. 2018, 8, 13. [Google Scholar] [CrossRef]
- Bloch, F.; Jackson, M.O.; Tebaldi, P. Centrality measures in networks. Soc. Choice Welf. 2023, 61, 413–453. [Google Scholar] [CrossRef]
- Nasiri, E.; Berahmand, K.; Samei, Z.; Li, Y. Impact of centrality measures on the common neighbors in link prediction for multiplex networks. Big Data 2022, 10, 138–150. [Google Scholar] [CrossRef]
- Singh, S.S.; Mishra, S.; Kumar, A.; Biswas, B. Link prediction on social networks based on centrality measures. In Principles of Social Networking: The New Horizon and Emerging Challenges; Springer: Berlin/Heidelberg, Germany, 2022; pp. 71–89. [Google Scholar]
- Ahmad, I.; Akhtar, M.U.; Noor, S.; Shahnaz, A. Missing link prediction using common neighbor and centrality based parameterized algorithm. Sci. Rep. 2020, 10, 364. [Google Scholar] [CrossRef] [PubMed]
- Behrouzi, S.; Sarmoor, Z.S.; Hajsadeghi, K.; Kavousi, K. Predicting scientific research trends based on link prediction in keyword networks. J. Inf. 2020, 14, 101079. [Google Scholar] [CrossRef]
- Kumar, S.; Mallik, A.; Panda, B. Link prediction in complex networks using node centrality and light gradient boosting machine. World Wide Web 2022, 25, 2487–2513. [Google Scholar] [CrossRef]
- Gao, T.; Zhu, X. Link prediction based on the powerful combination of endpoints and neighbors. Int. J. Mod. Phys. B 2020, 34, 2050269. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Level-2 node clustering coefficient-based link prediction. Appl. Intell. 2019, 49, 2762–2779. [Google Scholar] [CrossRef]
- Zhang, P.; Li, J.; Dong, E.; Liu, Q. A method of link prediction based on betweenness. In Proceedings of the Computational Social Networks: 4th International Conference, CSoNet 2015, Beijing, China, 4–6 August 2015; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2015; pp. 228–235. [Google Scholar]
- Wu, Z.; Lin, Y.; Wang, J.; Gregory, S. Link prediction with node clustering coefficient. Phys. A Stat. Mech. Appl. 2016, 452, 1–8. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.D. Predicting missing links in complex networks based on common neighbors and distance. Sci. Rep. 2016, 6, 38208. [Google Scholar] [CrossRef] [PubMed]
- Barabâsi, A.L.; Jeong, H.; Néda, Z.; Ravasz, E.; Schubert, A.; Vicsek, T. Evolution of the social network of scientific collaborations. Phys. A Stat. Mech. Appl. 2002, 311, 590–614. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
- Bonacich, P. Some unique properties of eigenvector centrality. Soc. Netw. 2007, 29, 555–564. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: New York, NY, USA, 2018. [Google Scholar]
- Serrano, M.Á.; Boguna, M. Clustering in complex networks. I. General formalism. Phys. Rev. E 2006, 74, 056114. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Krnc, M.; Škrekovski, R. Group degree centrality and centralization in networks. Mathematics 2020, 8, 1810. [Google Scholar] [CrossRef]
- Rossi, R.; Ahmed, N. The network data repository with interactive graph analytics and visualization. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Boyd, K.; Eng, K.H.; Page, C.D. Area under the precision-recall curve: Point estimates and confidence intervals. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2013, Prague, Czech Republic, 23–27 September 2013; Proceedings, Part III 13. Springer: Berlin/Heidelberg, Germany, 2013; pp. 451–466. [Google Scholar]
- Chawla, N.V. Data mining for imbalanced datasets: An overview. In Data Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2010; pp. 875–886. [Google Scholar]
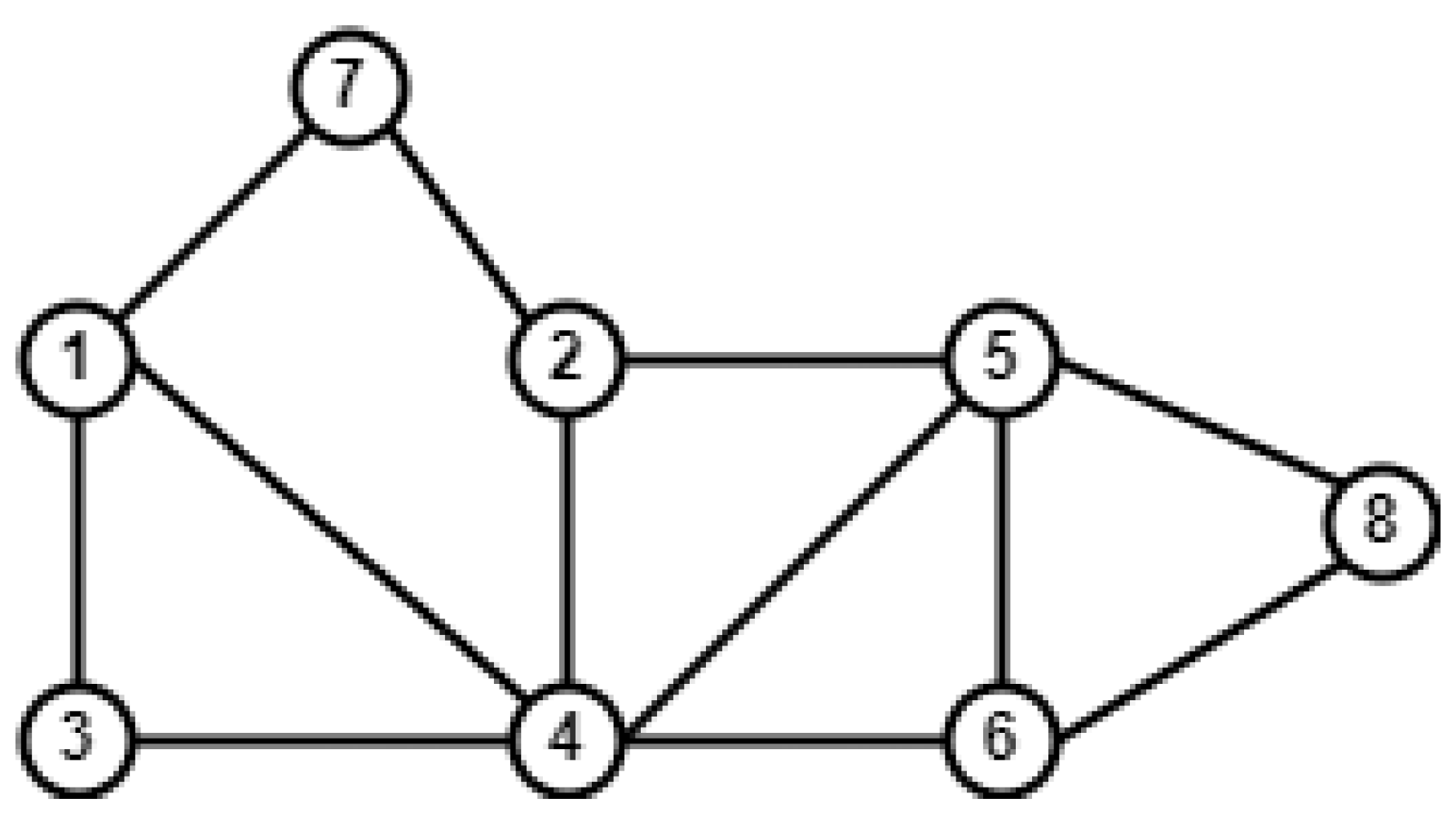


| S.No. | Centrality | Avg | |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
| Various Measures | Node Pair (v,u) | (1,2) | (2,3) | (2,6) | (4,7) | (4,8) | (5,7) |
|---|---|---|---|---|---|---|---|
| Proposed Measures | SACD (v,u) | 1 | 1 | 2 | 2 | 2 | 1 |
| SACB (v,u) | 1 | 1 | 2 | 2 | 1 | 1 | |
| SACC (v,u) | 2 | 1 | 2 | 1 | 1 | 1 | |
| SACCC (v,u) | 0 | 0 | 1 | 0 | 2 | 0 | |
| Basic Measures | 2 | 1 | 2 | 2 | 2 | 2 | |
| 0.5 | 0.2 | 0.5 | 0.4 | 0.4 | 0.2 | ||
| 2 | 0.6 | 1.3 | 1.8 | 1.6 | 0.9 | ||
| 0.7 | 0.2 | 0.4 | 0.6 | 0.5 | 0.3 | ||
| 9 | 6 | 9 | 10 | 10 | 8 | ||
| Recent Measures | 2.4 | 1.5 | 2.4 | 2 | 2.4 | 1.5 | |
| 0.9 | 0.4 | 0.7 | 2.3 | 0.5 | 1.2 |
| Datasets | #Nodes | #Edges | #Max. Degree | #Avg. Degree | #Diameter | #Avg. Clust. Coeff. |
|---|---|---|---|---|---|---|
| bio-celegans | 453 | 2025 | 237 | 8.94 | 7 | 0.646 |
| web-polblogs | 643 | 2280 | 165 | 7.09 | 10 | 0.232 |
| CA-Grqc | 5242 | 14,496 | 81 | 5 | 17 | 0.529 |
| Facebook-large | 22,470 | 171,002 | 709 | 15.22 | 15 | 0.359 |
| Datasets | k | SACD | SACB | SACC | SACCC | CCPA | KNLP |
|---|---|---|---|---|---|---|---|
| CA-Grqc | 1750 | 0.909 | 0.746 | 0.875 | 0.919 | 0.859 | 0.549 |
| 8750 | 0.91 | 0.784 | 0.818 | 0.918 | 0.859 | 0.344 | |
| 17,500 | 0.911 | 0.847 | 0.878 | 0.918 | 0.842 | 0.392 | |
| 26,250 | 0.907 | 0.828 | 0.895 | 0.923 | 0.851 | 0.482 | |
| 35,000 | 0.913 | 0.766 | 0.862 | 0.926 | 0.853 | 0.444 | |
| Facebook-large | 1750 | 0.532 | 0.606 | 0.533 | 0.622 | 0.626 | 0.317 |
| 8750 | 0.597 | 0.625 | 0.617 | 0.679 | 0.571 | 0.304 | |
| 17,500 | 0.625 | 0.623 | 0.638 | 0.683 | 0.607 | 0.251 | |
| 26,250 | 0.648 | 0.627 | 0.648 | 0.695 | 0.59 | 0.257 | |
| 35,000 | 0.658 | 0.628 | 0.668 | 0.697 | 0.591 | 0.392 | |
| web-polblogs | 1750 | 0.856 | 0.718 | 0.743 | 0.679 | 0.721 | 0.456 |
| 8750 | 0.877 | 0.772 | 0.78 | 0.747 | 0.771 | 0.384 | |
| 17,500 | 0.883 | 0.729 | 0.749 | 0.709 | 0.785 | 0.407 | |
| 26,250 | 0.893 | 0.739 | 0.762 | 0.713 | 0.788 | 0.385 | |
| 35,000 | 0.884 | 0.761 | 0.801 | 0.7 | 0.771 | 0.376 | |
| bio-celegans | 1750 | 0.863 | 0.627 | 0.674 | 0.905 | 0.803 | 0.79 |
| 8750 | 0.92 | 0.636 | 0.672 | 0.913 | 0.822 | 0.785 | |
| 17,500 | 0.896 | 0.639 | 0.723 | 0.9 | 0.803 | 0.824 | |
| 26,250 | 0.9 | 0.697 | 0.734 | 0.921 | 0.816 | 0.802 | |
| 35,000 | 0.898 | 0.666 | 0.749 | 0.915 | 0.832 | 0.788 |
| Datasets | k | SACD | SACB | SACC | SACCC | CCPA | KNLP |
|---|---|---|---|---|---|---|---|
| CA-Grqc | 1750 | 0.908 | 0.6756 | 0.9019 | 0.9002 | 0.5403 | 0.0002 |
| 8750 | 0.7507 | 0.4843 | 0.6783 | 0.7915 | 0.5368 | 0.0002 | |
| 17,500 | 0.7043 | 0.4498 | 0.6517 | 0.7123 | 0.5104 | 0.008 | |
| 26,250 | 0.6569 | 0.4327 | 0.6487 | 0.7074 | 0.5341 | 0.0023 | |
| 35,000 | 0.6244 | 0.3336 | 0.5791 | 0.7249 | 0.5345 | 0.0001 | |
| Facebook-large | 1750 | 0.5815 | 0.4803 | 0.5973 | 0.8353 | 0.2132 | 0.0001 |
| 8750 | 0.488 | 0.3619 | 0.5098 | 0.6943 | 0.2092 | 0.0002 | |
| 17,500 | 0.433 | 0.299 | 0.4432 | 0.6023 | 0.2151 | 0.0002 | |
| 26,250 | 0.4115 | 0.285 | 0.4081 | 0.5603 | 0.2431 | 0.0001 | |
| 35,000 | 0.3758 | 0.2482 | 0.3953 | 0.5222 | 0.2268 | 0.0314 | |
| web-polblogs | 1750 | 0.2998 | 0.2419 | 0.2428 | 0.2362 | 0.094 | 0.003 |
| 8750 | 0.1822 | 0.1802 | 0.1948 | 0.2126 | 0.0676 | 0.0015 | |
| 17,500 | 0.1568 | 0.1338 | 0.1273 | 0.2009 | 0.0687 | 0.0024 | |
| 26,250 | 0.1769 | 0.1447 | 0.1171 | 0.1642 | 0.0733 | 0.0021 | |
| 35,000 | 0.1403 | 0.1559 | 0.1418 | 0.1446 | 0.0911 | 0.0016 | |
| bio-celegans | 1750 | 0.2232 | 0.1433 | 0.2572 | 0.453 | 0.0753 | 0.0211 |
| 8750 | 0.1744 | 0.1177 | 0.1483 | 0.3867 | 0.095 | 0.0273 | |
| 17,500 | 0.1396 | 0.091 | 0.1345 | 0.4003 | 0.0755 | 0.0356 | |
| 26,250 | 0.108 | 0.0786 | 0.1461 | 0.3736 | 0.0921 | 0.0297 | |
| 35,000 | 0.0887 | 0.0806 | 0.1265 | 0.4505 | 0.081 | 0.0265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nandini, Y.V.; Lakshmi, T.J.; Enduri, M.K.; Sharma, H. Link Prediction in Complex Networks Using Average Centrality-Based Similarity Score. Entropy 2024, 26, 433. https://doi.org/10.3390/e26060433
Nandini YV, Lakshmi TJ, Enduri MK, Sharma H. Link Prediction in Complex Networks Using Average Centrality-Based Similarity Score. Entropy. 2024; 26(6):433. https://doi.org/10.3390/e26060433
Chicago/Turabian StyleNandini, Y. V., T. Jaya Lakshmi, Murali Krishna Enduri, and Hemlata Sharma. 2024. "Link Prediction in Complex Networks Using Average Centrality-Based Similarity Score" Entropy 26, no. 6: 433. https://doi.org/10.3390/e26060433
APA StyleNandini, Y. V., Lakshmi, T. J., Enduri, M. K., & Sharma, H. (2024). Link Prediction in Complex Networks Using Average Centrality-Based Similarity Score. Entropy, 26(6), 433. https://doi.org/10.3390/e26060433






