Abstract
We investigate both theoretically and numerically the dynamics of out-of-time-ordered correlators (OTOCs) in quantum resonance conditions for a kicked rotor model. We employ various operators to construct OTOCs in order to thoroughly quantify their commutation relation at different times, therefore unveiling the process of quantum scrambling. With the help of quantum resonance condition, we have deduced the exact expressions of quantum states during both forward evolution and time reversal, which enables us to establish the laws governing OTOCs’ time dependence. We find interestingly that the OTOCs of different types increase in a quadratic function of time, breaking the freezing of quantum scrambling induced by the dynamical localization under non-resonance condition. The underlying mechanism is discovered, and the possible applications in quantum entanglement are discussed.
1. Introduction
Quantum scrambling, a fundamental concept elucidating the spread of information across multiple degrees of freedom that is inaccessible via local measurements, has garnered extensive attention in quantum information [1,2,3,4], quantum chaos [5,6,7,8,9], and condensed matter physics [10,11,12,13]. It is well known that the out-of-time ordered correlators (OTOCs) can quantify the process of information scrambling with relevance to the operator growth [14,15]. The exponential growth of OTOCs, facilitated by exponential instability of chaos, produces the boundary of the light cone of information scrambling in many-body systems [16,17], for which the butterfly velocity of scrambling is closely related to the quantum Lyapunov exponent [18,19,20]. The relaxation of OTOCs can detect the character of both the quantum thermalization and quantum entanglement in many-body systems [21,22], providing insights into the underlying connection between quantum chaos and information scrambling [23,24,25]. The dynamics of OTOCs can be used as an order parameter to diagnose phase transitions in both Hermitian [26] and non-Hermitian chaotic systems [27]. Interestingly, genuine quantum chaos, specifically the superexponential instability induced by delta-kicking modulation in nonlinear interactions, can cause the superexponential growth of OTOCs [28], representing a new phenomenon of information scrambling [29,30].
The variants of the quantum kicked rotor (QKR) model under resonance conditions serve as ideal platforms to explore fascinating physics of quantum coherence [31], which has significant implications for the fundamental aspects of quantum transport [32,33] and topological new phases in Floquet systems [34,35,36,37]. The existence of the flat band of quasi-energy spectrum determines the exponential diffusion dynamics in the on-resonance double-kicked rotor model [38]. The resonance condition yields Floquet spectrum [39,40,41] analogous to Hofstadter’s butterfly of an integrable system [42,43,44] and topological phase transitions reminiscent of the integer quantum Hall effect [45,46]. Moreover, a dynamical analog of the integer quantum Hall effect emerges from an intrinsic chaos in spin-1/2 QKR model, enriching our understanding of the quantum topological phenomena induced by chaos [47,48]. Interestingly, the spinor QKR model with quantum resonance condition provides a versatile playground to realize the quantum walk in momentum space [49,50], proposing a new protocol for the manipulation of the quantum transport with Floquet engineering [51]. The state-of-the-art experiments in atom-optics have indeed realized the QKR model and verified the dynamical phase transition and quantum walk therein by precisely tailoring the resonance condition for the driven period [52]. This paves the way for engineering exotic behavior of quantum information [53] and energy diffusion [54] in various generalization of the QKR model.
In this context, we investigate both analytically and numerically the dynamics of different types of OTOCs under the quantum resonance condition. The first type OTOCs involves two angular momentum operators. Furthermore, the second one is constructed by the combination of the translation operator and angular momentum operator. We have derived the exact expression of the quantum state during both forward evolution and time reversal under quantum resonance conditions, which enables us to precisely establish the law governing the time dependence of OTOCs. Our findings reveal that both and exhibit unbounded quadratic growth, indicating a power law scrambling behavior in their long-term evolutions. The observation of similar time dependence laws for different OTOCs suggests a universality in this power law growth for the QKR model. It is known that the exotic physics exhibited by the QKR model under quantum resonance conditions, such as ballistic energy diffusion and topologically protected transport in momentum space, originates from the essential quantum coherence effects, without classical counterparts. Our findings unveil the role of quantum coherence in facilitating quantum scrambling, a connection of potential significance for applications in quantum information.
2. Model and Main Results
The dimensionless Hamiltonian of the QKR model reads
where is the angular momentum operator, is the angle coordinate, with commutation relation . Here, denotes the effective planck’s constant, and K is the kicking strength [55]. One experimental realization of the QKR model involves ultracold atoms exposed to a pulsed laser standing field that mimics a delta-kicking potential [56]. The eigenequation of the angular momentum operator is with an eigenvalue of and eigenstate of . With the complete basis of , an arbitrary state can be expanded as . One period evolution of the quantum state from to is governed by . The Floquet operator U involves two components, i.e., , where the represents the free evolution operator and the kicking term is denoted by .
The OTOCs are defined using the average of the squared commutator, i.e., . Here, both and B are evaluated in the Heisenberg picture. The average refers to the operator’s expectation value concerning the initial state [29,57,58,59,60]. We investigate two distinct OTOCs, one denoted as , and the other as , where represents the translation operator. We focus solely on the quantum resonance condition, i.e., . Without loss of generality, we choose an initial state . Our main findings can be summarized by the following relationships
and
These relations clearly demonstrate the existence of the quadratic growth of different OTOCs.
In order to confirm our above theoretical predictions, we numerically calculate both the and for different Ks. Our results demonstrate that for a specific K (e.g., in Figure 1), both and increase unboundedly with time. Furthermore, the larger the K, the faster they increase, following perfectly with the relations described in Equations (2) and (3). The continuous, unsaturated growth of OTOCs is attributed to the delocalization mechanism under quantum resonance conditions. When the delocalization mechanism is absent, the process of dynamical localization in quantum non-resonance conditions leads to the saturation of OTOCs, which has been reported in our previous investigation in Ref. [27]. It is noteworthy that the dependency of on the parameter offers a means of manipulating quantum scrambling by adjusting the translation operator, shedding light on the quantum control of non-Hermitian Floquet systems.
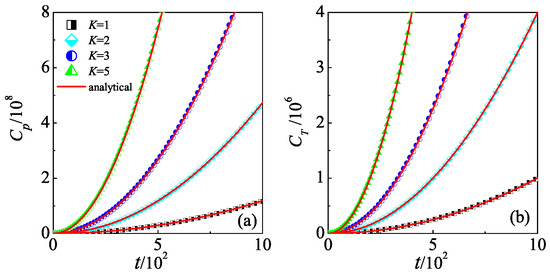
The quadratic growth in OTOCs also emerges when we use the translation operator and a projection operator onto an initial state for OTOCs. In this situation, one can obtain the relation , with being named as fidelity out-of-time-ordered correlators (FOTOCs). Under the condition , straightforward derivation yields the approximation , by neglecting the terms in the Taylor expansion of of orders larger than two. The mean momentum is zero, i.e., due to the symmetry of both the specific initial state and the kicking potential. Therefore, the OTOCs is proportional to the mean energy, i.e., , indicating clearly the quadratic growth. Note that the Fourier spectrum of the FOTOCs can be utilized in constructing the Rényi entropy [61,62,63]. In fact, FOTOCs have been used to characterize the multiple entanglements among different degrees of freedom in the kicked top model, which can be regarded as a collective of many spins [64]. It is known that the QKR model is a limit of the kicked top model with angular momentum being infinity [65]. This provides the theoretical foundation for the significant implications of the quadratic growth of OTOCs in measuring the buildup of quantum entanglement.
In the atom-optics realization of the QKR model, the experimental constraints in practice often introduce very small detuning from the exact quantum resonance condition [66]. We further consider the effects of the slight variation in the value of from quantum resonance condition, i.e., on the quantum scrambling. In this situation, there is a fictitious classical limit in which the parameter plays the role of the effective Planck’s constant [66,67]. We should note that traditional definition of the semiclassical limit with tending to zero does not make sense for the resonance case as . Our numerical results show that for a specific (e.g., in Figure 2a), the follows the quadratic growth of for finite time duration, i.e., , after which it fluctuates around a saturation level. Interestingly, the saturate level decreases with the increase in . For sufficiently large (e.g., ), the remains almost at its initial value and does not increases with time. We further investigate the at a specific time for different . The inset in Figure 2a shows that the decreases with some fluctuations as the absolute value of departs from zero, which demonstrates the suppression of OTOCs by the variation of from quantum resonance condition. The time evolution of also exhibits the reduction from the quadratic growth in with the increase in (see Figure 2b). When the increases from zero, the QKR transitions to the quantum non-resonance regime, where the mechanism of dynamical localization suppresses the growth of OTOCs [27].
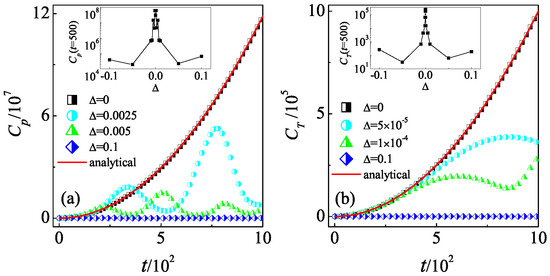
Figure 2.
Time dependence of the (a) and (b) for . In (a), (squares), (circles), 0.005 (triangles), and (diamonds). Inset: The at time versus . In (b), (squares), (circles), (triangles), and (diamonds). Inset: The at time versus . Red lines in (a,b) indicate our theoretical prediction in Equations (2) and (3), respectively. In (b), the value of the translation parameter is .
3. Theoretical Analysis
It is straightforward to derive the relation
where the first two terms on the right side, i.e., two-points correlator, are defined as
and the four-point correlator is given by
with and . Here, denotes the real part of the complex variable [29].
The derivation of at a specific time involves three sequential steps [68]. Firstly, evolving the initial state from to yields . Secondly, applying operator A to produces . Finally, the time reversal from to for results in . Equation (5) indicates that is the expectation value of operator for . The process to derive at time involves four steps. Firstly, applying the operator B to the initial state yields the state . Secondly, the forward evolution for the state results in a state . In the third step, we apply the operator A to the state , which creates a new state . The fourth step involves a time reversal for the state , giving . The norm of defines as shown in Equation (6). With the two states and , we can calculate the based on Equation (7).
Under the quantum resonance condition , each matrix element of the free evolution operator in angular momentum space equals to unity, i.e., . Consequently, the operator has no impact on the time evolution of quantum states. For one period evolution from to , we only need to use the kicking evolution operator to act on the quantum state, i.e., . This leads to an exact expression of a quantum state at arbitrary time in angle coordinate space, i.e., . Based on this, we can derive analytical expressions for both and , which yields the theoretical predictions for the OTOCs .
3.1. Derivation of the
Given the operators and the quantum resonance condition, the three components of the OTOCs are denoted as , , and , with and . At the time , the action the operator p to the state yields a new state , where superscript () denotes the n-th order derivative of the functions. We then perform the time reversal from to starting from and obtain
With this state, one can obtain the analytical expression of
where the function takes the forms .
For the derivation of , we apply the operator p to acting on the initial state, which yields . Then, forward evolution from to creates the state , along with . Conducting the backward evolution from to for the state , we obtain
With the assistance of the two states, we establish the following relations
and
Here, the superscript ∗ indicates the complex conjugate of the variable. The functions and take the forms and . Therefore, we can obtain the expression of the OTOCs
with and indicating the imaginary part of a complex variable. It is obvious that the time dependence of contains a quadratic function, determined by the integral of the functions and , and a linear function related to the integral of the function . The exact dependence of the functions , , and on initial states, as shown above, serves as a crucial knob for controlling the behavior of OTOCs through the preparation of different starting conditions. For example, suppose we choose the initial state , resulting in the equivalence
3.2. Derivation of the
The three components of are represented as , , and . Here, the time-reversed states at time , influenced by the operators and the initial states , take the forms and , respectively. By repeating the same procedure for the derivation of both and of , we can obtain the exact expressions of the two states under quantum resonance condition
and
Consequently, one can derive analytically the three components of the
and
with . Combining these three parts yields
Obviously, the term of quadratic growth in the function is governed by the integral involving the modular square . The term of the linear growth in depends on the integral of the function , which is related to the initial state . The close relationship between and the initial state provides the unique opportunity to engineer the OTOCs’ behavior under various initial states. For a specific form of the initial state , it is straightforward to establish the relation
4. Conclusions and Discussion
In this work, we thoroughly investigate the dynamics of OTOCs, employing and under quantum resonance conditions. The quantifies the commutation relation of two angular momentum operators at different times, while the measures that between the translation operator and angular momentum operator at different times. Our exact deductions of the quantum states during forward evolution and time reversal under quantum resonance allow us to establish the laws governing the time dependence of OTOCs. Our findings demonstrate that both and exhibit quadratic growth with time evolution, revealing an intrinsic power-law scrambling in their late-time behavior. Note that the mechanism of dynamical localization under non-resonant conditions suppresses quantum scrambling [27]. Therefore, the observed quadratic growth of OTOCs finds its origin in essential quantum coherence effects arising from quantum resonance, without classical analogs. We expect that the identification of similar power laws for different types of OTOCs reveals the universality in the power-law growth within the QKR model. It has been found that the delocalization effects with unique quantum coherence leads to the quadratic growth of OTOCs in the QKR model with quantum non-resonance condition [7]. Therefore, our discovery of the crucial role played by quantum coherence in facilitating quantum scrambling has significant implications in the fields of quantum information and quantum chaos [6,8,63].
Author Contributions
Investigation, G.L.; Writing—review & editing, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos. 12065009 and 12365002), the Natural Science Foundation of Jiangxi province (Grant Nos. 20224ACB201006 and 20224BAB201023).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yan, B.; Cincio, L.; Zurek, W.H. Information Scrambling and Loschmidt Echo. Phys. Rev. Lett. 2020, 124, 160603. [Google Scholar] [CrossRef]
- Yan, B.; Sinitsyn, N.A. Recovery of Damaged Information and the Out-of-Time-Ordered Correlators. Phys. Rev. Lett. 2020, 125, 040605. [Google Scholar] [CrossRef]
- Wang, J.H.; Cai, T.Q.; Han, X.Y.; Ma, Y.W.; Wang, Z.L.; Bao, Z.H.; Li, Y.; Wang, H.Y.; Zhang, H.Y.; Sun, L.Y.; et al. Information scrambling dynamics in a fully controllable quantum simulator. Phys. Rev. Res. 2022, 4, 043141. [Google Scholar] [CrossRef]
- Swingle, B. Unscrambling the physics of out-of-time-order correlators. Nat. Phys. 2018, 14, 988. [Google Scholar] [CrossRef]
- Omanakuttan, S.; Chinni, K.; Blocher, P.D.; Poggi, P.M. Scrambling and quantum chaos indicators from long-time properties of operator distributions. Phys. Rev. A 2023, 107, 032418. [Google Scholar] [CrossRef]
- García-Mata, I.; Jalabert, R.A.; Wisniacki, D.A. Out-of-time-order correlators and quantum chaos. Scholarpedia 2023, 18, 55237. [Google Scholar] [CrossRef]
- Hamazaki, R.; Fujimoto, K.; Ueda, M. Operator Noncommutativity and Irreversibility in Quantum Chaos. arXiv 2018, arXiv:1807.02360. [Google Scholar]
- Varikuti, N.D.; Sahu, A.; Lakshminarayan, A.; Madhok, V. Probing dynamical sensitivity of a non-Kolmogorov-Arnold-Moser system through out-of-time-order correlators. Phys. Rev. E 2024, 109, 014209. [Google Scholar] [CrossRef]
- Sreeram, P.G.; Vaibhav, M.; Arul, L. Out-of-time-ordered correlators and the Loschmidt echo in the quantum kicked top: How low can we go? J. Phys. D Appl. Phys. 2021, 54, 274004. [Google Scholar]
- Zhao, S.K.; Ge, Z.Y.; Xiang, Z.C.; Xue, G.M.; Yan, H.S.; Wang, Z.T.; Wang, Z.; Xu, H.K.; Su, F.F.; Yang, Z.H.; et al. Probing Operator Spreading via Floquet Engineering in a Superconducting Circuit. Phys. Rev. Lett. 2022, 129, 160602. [Google Scholar] [CrossRef]
- Dağ, C.B.; Sun, K.; Duan, L.M. Detection of Quantum Phases via Out-of-Time-Order Correlators. Phys. Rev. Lett. 2019, 123, 140602. [Google Scholar] [CrossRef]
- Zamani, S.; Jafari, R.; Langari, A. Out-of-time-order correlations and Floquet dynamical quantum phase transition. Phys. Rev. B 2022, 105, 094304. [Google Scholar] [CrossRef]
- Omanakuttan, S.; Lakshminarayan, A. Out-of-time-ordered correlators and quantum walks. Phys. Rev. E 2019, 99, 062128. [Google Scholar] [CrossRef] [PubMed]
- Yin, C.; Lucas, A. Quantum operator growth bounds for kicked tops and semiclassical spin chains. Phys. Rev. A 2021, 103, 042414. [Google Scholar] [CrossRef]
- Zhang, P.F.; Yu, Z.H. Dynamical Transition of Operator Size Growth in Quantum Systems Embedded in an Environment. Phys. Rev. Lett. 2023, 130, 250401. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.L.; Garrison, J.R.; Deng, D.L.; Gong, Z.X.; Gorshkov, A.V. Asymmetric Particle Transport and Light-Cone Dynamics Induced by Anyonic Statistics. Phys. Rev. Lett. 2018, 121, 250404. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Chakrabarty, S.; Dhar, A.; Kundu, A.; Huse, D.A.; Moessner, R.; Ray, S.S.; Bhattacharjee, S. Light-Cone Spreading of Perturbations and the Butterfly Effect in a Classical Spin Chain. Phys. Rev. Lett. 2018, 121, 024101. [Google Scholar] [CrossRef]
- Keselman, A.; Nie, L.; Berg, E. Scrambling and Lyapunov exponent in spatially extended systems. Phys. Rev. B 2021, 103, L121111. [Google Scholar] [CrossRef]
- Mezei, M.; Sárosi, G. Chaos in the butterfly cone. J. High Energy Phys. 2020, 01, 186. [Google Scholar] [CrossRef]
- Pappalardi, S.; Kurchan, J. Quantum bounds on the generalized lyapunov exponents. Entropy 2023, 25, 246. [Google Scholar] [CrossRef]
- MacCormack, I.; Tan, M.T.; Kudler-Flam, J.; Ryu, S. Operator and entanglement growth in nonthermalizing systems: Many-body localization and the random singlet phase. Phys. Rev. B 2021, 104, 214202. [Google Scholar] [CrossRef]
- Kobrin, B.; Yang, Z.; Kahanamoku-Meyer, G.D.; Olund, C.T.; Moore, J.E.; Stanford, D.; Yao, N.Y. Many body chaos in the Sachdev-Ye-Kitaev model. Phys. Rev. Lett. 2021, 126, 030602. [Google Scholar] [CrossRef] [PubMed]
- Bilitewski, T.; Bhattacharjee, S.; Moessner, R. Classical many-body chaos with and without quasiparticles. Phys. Rev. B 2021, 103, 174302. [Google Scholar] [CrossRef]
- Xu, T.R.; Scaffidi, T.; Cao, X.Y. Does Scrambling Equal Chaos? Phys. Rev. Lett. 2020, 124, 140602. [Google Scholar] [CrossRef]
- Jaiswal, N.; Gautam, M.; Gill, A.; Sarkar, T. Fotoc complexity in the Lipkin-Meshkov-Glick model and its variant. Eur. Phys. J. B 2024, 97, 5. [Google Scholar] [CrossRef]
- Huh, K.-B.; Ikeda, K.; Jahnke, V.; Kim, K.-Y. Diagnosing first- and second-order phase transitions with probes of quantum chaos. Phys. Rev. E 2021, 104, 024136. [Google Scholar] [CrossRef]
- Zhao, W.L.; Wang, R.R.; Ke, H.; Liu, J. Scaling laws of the out-of-time-order correlators at the transition to the spontaneous PT-symmetry breaking in a Floquet system. Phys. Rev. A 2023, 107, 062201. [Google Scholar] [CrossRef]
- Zhao, W.L.; Liu, J. Superexponential behaviors of out-of-time ordered correlators and Loschmidt echo in a non-Hermitian interacting system. arXiv 2023, arXiv:2305.1215. [Google Scholar]
- Zhao, W.L.; Hu, Y.; Li, Z.; Wang, Q. Super-exponential growth of Out-of-time-ordered correlators. Phys. Rev. B 2021, 103, 184311. [Google Scholar] [CrossRef]
- Qi, Z.; Scaffidi, T.; Cao, X. Surprises in the deep Hilbert space of all-to-all systems: From superexponential scrambling to slow entanglement growth. Phys. Rev. B 2023, 108, 054301. [Google Scholar] [CrossRef]
- Santhanam, M.S.; Paul, S.; Kannan, J.B. Quantum kicked rotor and its variants: Chaos, localization and beyond. Phys. Rep. 2022, 956, 1. [Google Scholar] [CrossRef]
- Wang, J.; García-García, A.M. Anderson transition in a three-dimensional kicked rotor. Phys. Rev. E 2009, 79, 036206. [Google Scholar] [CrossRef]
- Scoquart, T.; Wellens, T.; Delande, D.; Cherroret, N. Quench dynamics of a weakly interacting disordered Bose gas in momentum space. Phys. Rev. Res. 2020, 2, 033349. [Google Scholar] [CrossRef]
- Ho, D.Y.H.; Gong, J.B. Quantized Adiabatic Transport In Momentum Space. Phys. Rev. Lett. 2012, 109, 010601. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.Q.; Pan, Y.M.; Wang, H.Q.; Zhang, C.S.; Yu, D.; Gover, A.; Zhang, H.J.; Li, T.; Zhou, L.; Zhu, S.N. Observation of Anomalous π Modes in Photonic Floquet Engineering. Phys. Rev. Lett. 2019, 122, 173901. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.W.; Zhang, D.J. Non-Hermitian Floquet Topological Matter—A Review. Entropy 2023, 25, 1401. [Google Scholar] [CrossRef]
- Zhou, L.W. Entanglement spectrum and entropy in Floquet topological matter. Phys. Rev. Res. 2022, 4, 043164. [Google Scholar] [CrossRef]
- Wang, H.L.; Wang, J.; Guarneri, I.; Casati, G.; Gong, J.B. Exponential quantum spreading in a class of kicked rotor systems near high-order resonances. Phys. Rev. E 2013, 88, 052919. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gong, J.B. Proposal of a cold-atom realization of quantum maps with Hofstadter’s butterfly spectrum. Phys. Rev. A 2008, 77, 031405(R). [Google Scholar] [CrossRef]
- Wang, J.; Gong, J.B. Generating a fractal butterfly Floquet spectrum in a class of driven SU(2) systems. Phys. Rev. E 2010, 81, 026204. [Google Scholar] [CrossRef]
- Wang, H.L.; Ho, D.Y.H.; Lawton, W.; Wang, J.; Gong, J.B. Kicked-Harper model versus on-resonance double-kicked rotor model: From spectral difference to topological equivalence. Phys. Rev. E 2013, 88, 052920. [Google Scholar] [CrossRef]
- Faddeev, L.D.; Kashaev, R.M. Generalized Bethe ansatz equations for Hofstadter problem. Commun. Math. Phys. 1995, 169, 181. [Google Scholar] [CrossRef]
- Ikeda, K. Hofstadter’s butterfly and Langlands duality. J. Math. Phys. 2018, 59, 061704. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sedrakyan, A. Hofstadter problem on the honeycomb and triangular lattices: Bethe ansatz solution. Phys. Rev. B 2006, 73, 235118. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Raghava, G.N.; Zhou, L.W.; Gong, J.B. Floquet topological semimetal phases of an extended kicked Harper model. Phys. Rev. E 2016, 93, 022209. [Google Scholar] [CrossRef]
- Zhou, L.W. Floquet Second-Order Topological Phases in Momentum Space. Nanomaterials 2021, 11, 1170. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, C.S. Planck’s Quantum-Driven Integer Quantum Hall Effect in Chaos. Phys. Rev. Lett. 2014, 113, 216802. [Google Scholar] [CrossRef]
- Tian, C.S.; Chen, Y.; Wang, J. Emergence of integer quantum Hall effect from chaos. Phys. Rev. B 2016, 93, 075403. [Google Scholar] [CrossRef]
- Summy, G.; Wimberger, S. Quantum random walk of a Bose–Einstein condensate in momentum space. Phys. Rev. A 2016, 93, 023638. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Quantum Walk in Momentum Space with a Bose–Einstein Condensate. Phys. Rev. Lett. 2018, 121, 070402. [Google Scholar] [CrossRef] [PubMed]
- Weiß, M.; Groiseau, C.; Lam, W.K.; Burioni, R.; Vezzani, A.; Summy, G.S.; Wimberger, S. Steering random walks with kicked ultracold atoms. Phys. Rev. A 2015, 92, 033606. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Experimental realization of a momentum-space quantum walk. Phys. Rev. A 2019, 99, 043617. [Google Scholar] [CrossRef]
- Delvecchio, M.; Groiseau, C.; Petiziol, F.; Summy, G.S.; Wimberger, S. Quantum search with a continuous-time quantum walk in momentum space. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 065301. [Google Scholar] [CrossRef]
- Vakulchyk, I.; Fistul, M.V.; Flach, S. Wave Packet Spreading with Disordered Nonlinear Discrete-Time Quantum Walks. Phys. Rev. Lett. 2019, 122, 040501. [Google Scholar] [CrossRef]
- Casati, G.; Ford, J. Stochastic Behavior in Classical and Quantum Hamiltonian Systems. Lect. Notes Phys. 1979, 93, 770692. [Google Scholar]
- Moore, F.L.; Robinson, J.C.; Bharucha, C.F.; Sundaram, B.; Raizen, M.G. Atom optics realization of the quantum δ-kicked rotor. Phys. Rev. Lett. 1995, 75, 4598. [Google Scholar] [CrossRef]
- Li, J.; Fan, R.H.; Wang, H.Y.; Ye, B.T.; Zeng, B.; Zhai, H.; Peng, X.H.; Du, J.F. Measuring out-of-time-order correlators on a nuclear magnetic resonance quantum simulator. Phys. Rev. X 2017, 7, 031011. [Google Scholar] [CrossRef]
- Hashimoto, K.; Murata, K.; Yoshii, R. Out-of-time-order correlators in quantum mechanics. J. High Energ. Phys. 2017, 10, 138. [Google Scholar] [CrossRef]
- García-Mata, I.; Saraceno, M.; Jalabert, R.A.; Roncaglia, A.J.; Wisniacki, D.A. Chaos signatures in the short and long time behavior of the out-of-time ordered correlator. Phys. Rev. Lett. 2018, 121, 210601. [Google Scholar] [CrossRef]
- Zonnios, M.; Levinsen, J.; Parish, M.M.; Pollock, F.A.; Modi, K. Signatures of Quantum Chaos in an Out-of-Time-Order Tensor. Phys. Rev. Lett. 2022, 128, 150601. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.H.; Zhang, P.F.; Shen, H.T.; Zhai, H. Out-of-Time Order Correlation for Many-Body Localization. Sci. Bull. 2017, 62, 707. [Google Scholar] [CrossRef]
- Lewis-Swan, R.J.; Safavi-Naini, A.; Bollinger, J.J.; Rey, A.M. Unifying scrambling, thermalization and entanglement through measurement of fidelity out-of-timeorder correlators in the Dicke model. Nat. Commun. 2019, 10, 1581. [Google Scholar] [CrossRef]
- Gärttner, M.; Hauke, P.; Rey, A.M. Relating Out-of-Time-Order Correlations to Entanglement via Multiple-Quantum Coherences. Phys. Rev. Lett. 2018, 120, 040402. [Google Scholar] [CrossRef]
- Li, S.C.; Pezzè, L.; Smerzi, A. Multiparticle entanglement dynamics of quantum chaos in a Bose–Einstein condensate. Phys. Rev. A 2021, 103, 052417. [Google Scholar] [CrossRef]
- Haake, F.; Shepelyansky, D.L. The kicked rotator as a limit of the kicked top. Europhys. Lett. 1988, 5, 671. [Google Scholar] [CrossRef]
- Wimberger, S.; Guarneri, I.; Fishman, S. Quantum resonances and decoherence for delta-kicked atoms. Nonlinearity 2003, 16, 1381. [Google Scholar] [CrossRef]
- Wimberger, S.; Guarneri, I.; Fishman, S. Classical Scaling Theory of Quantum Resonances. Phys. Rev. Lett. 2004, 92, 084102. [Google Scholar] [CrossRef]
- Zhao, W.L.; Liu, J. Quantum criticality at the boundary of the non-Hermitian regime of a Floquet system. arXiv 2023, arXiv:2307.00462. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).