Ensemble and Pre-Training Approach for Echo State Network and Extreme Learning Machine Models
Abstract
1. Introduction
2. Methodology
2.1. Basic Theory of Echo State Network
2.2. Basic Theory of Extreme Learning Machine
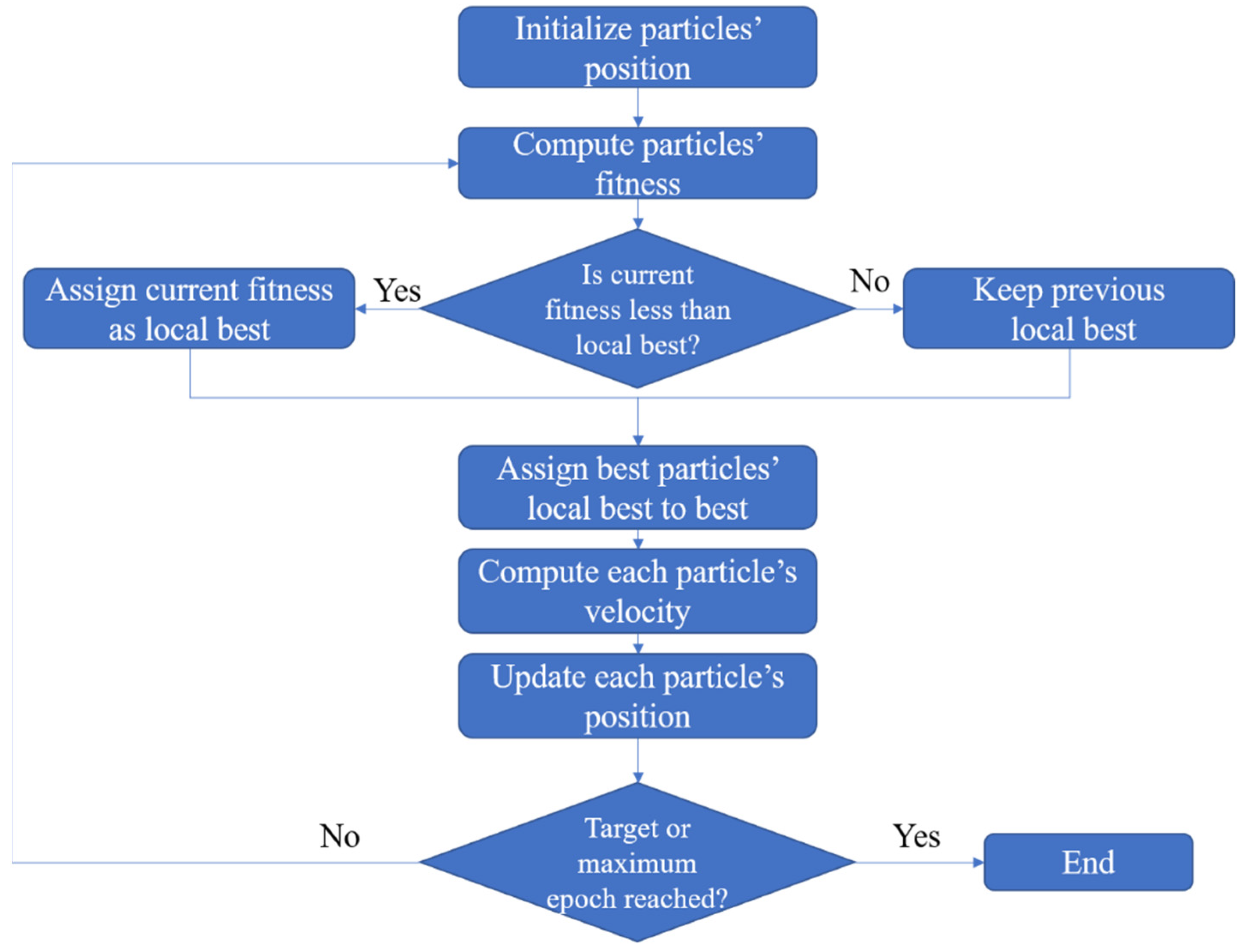
2.3. Basic Particle Swarm Optimization
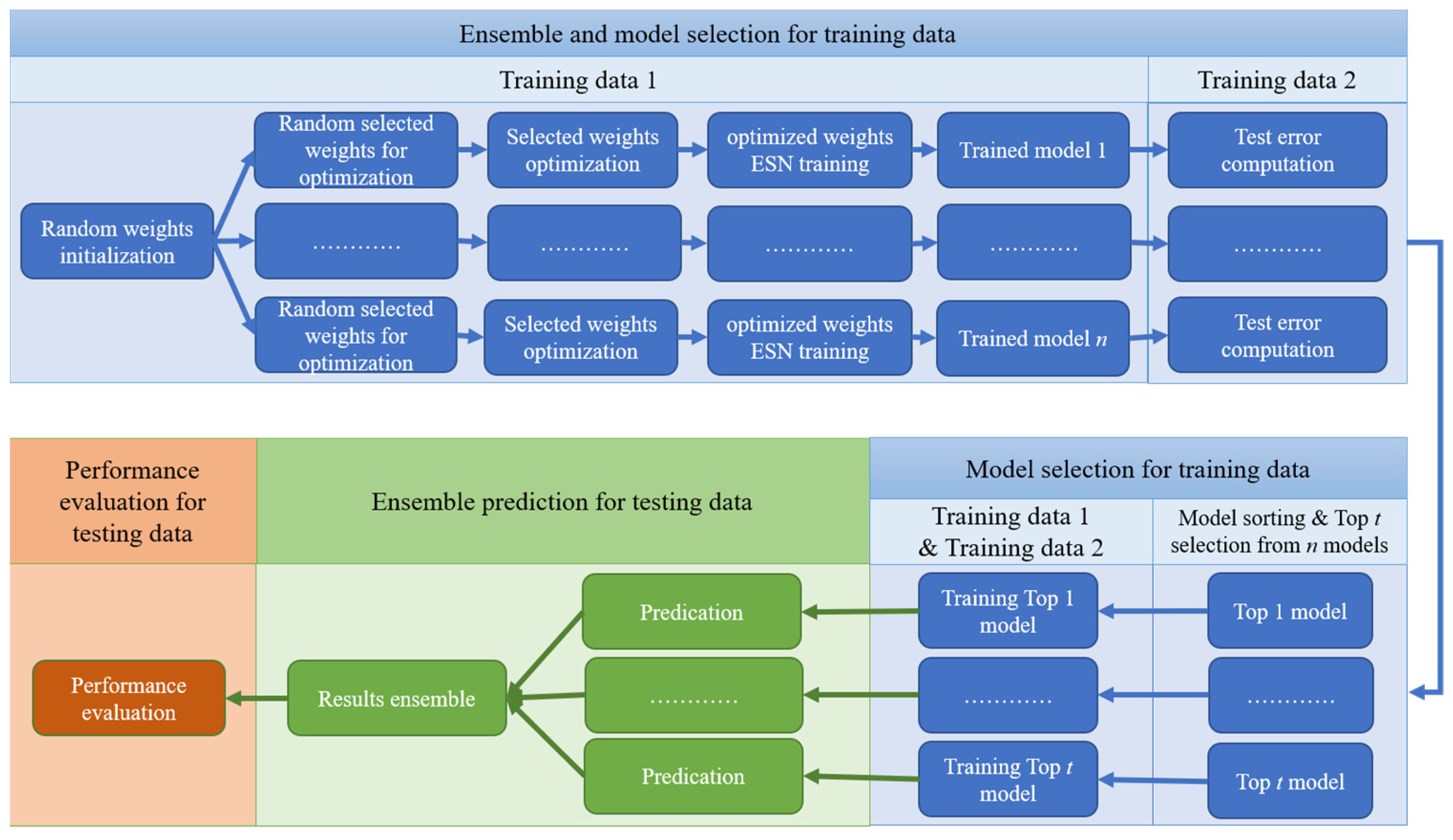
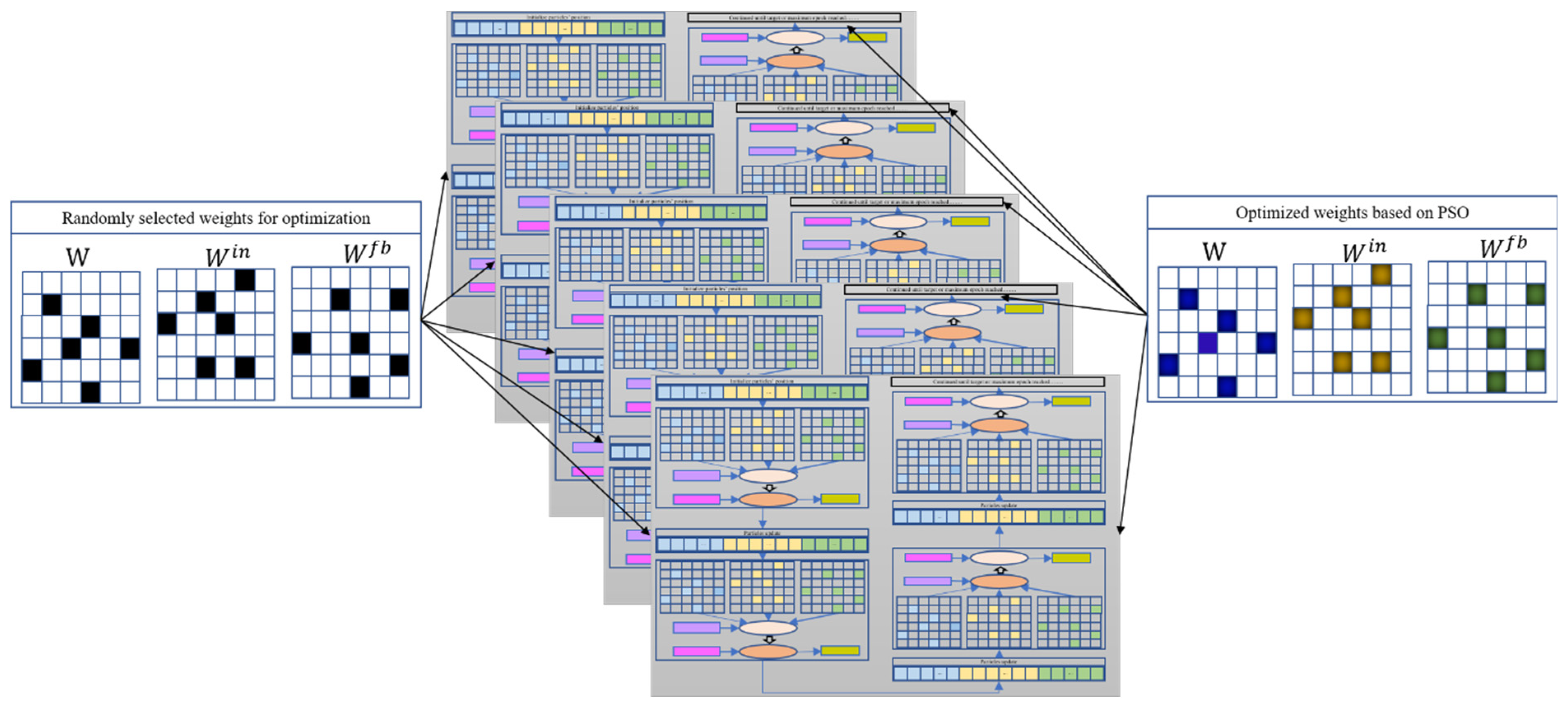
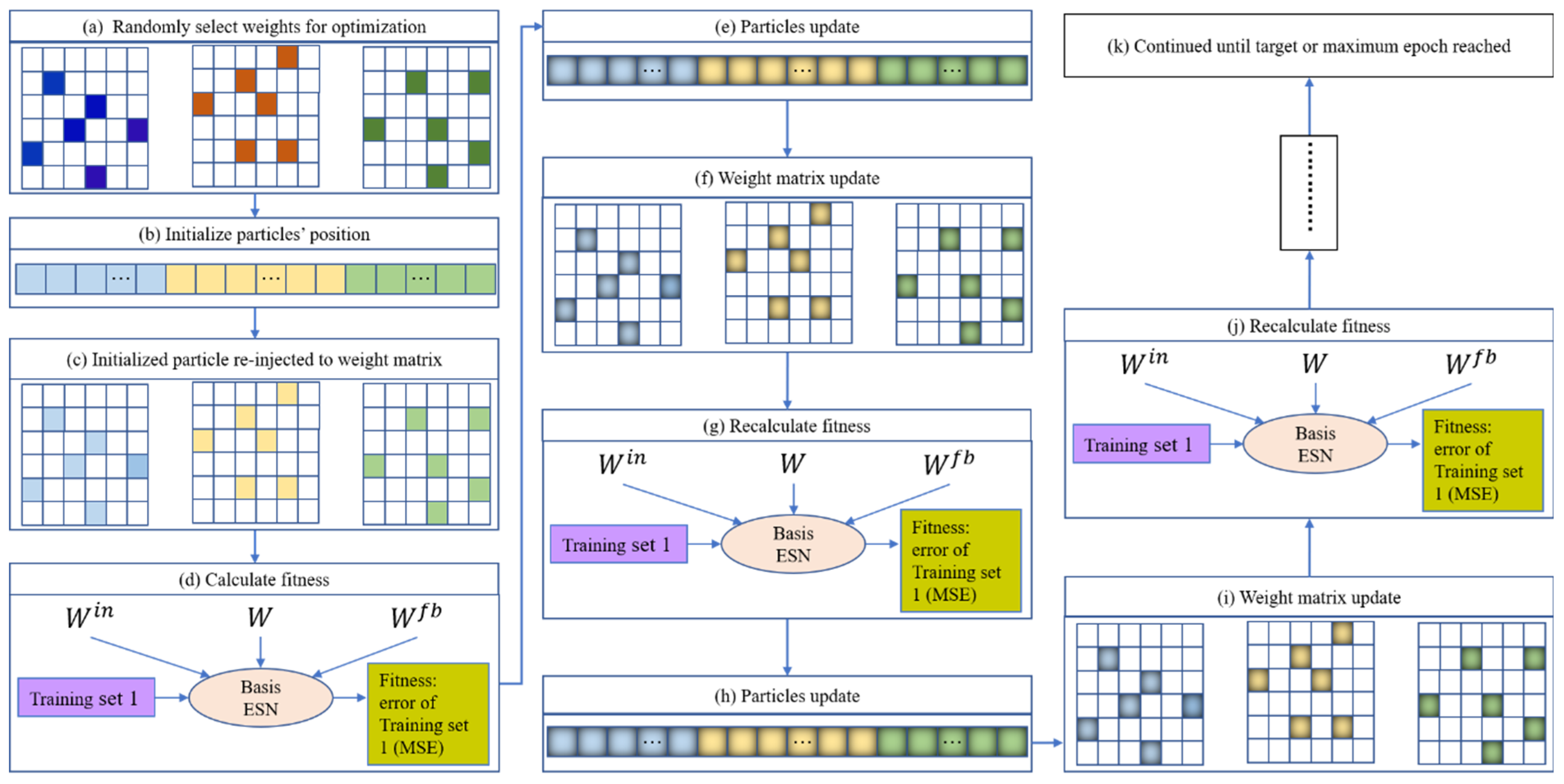
3. Proposed EN-PSO-ESN Model
3.1. Motivation
3.2. Main Steps of EN-PSO-ESN Model
4. Experiments and Results
4.1. Datasets, Performance Evaluation Criteria, and Benchmarks
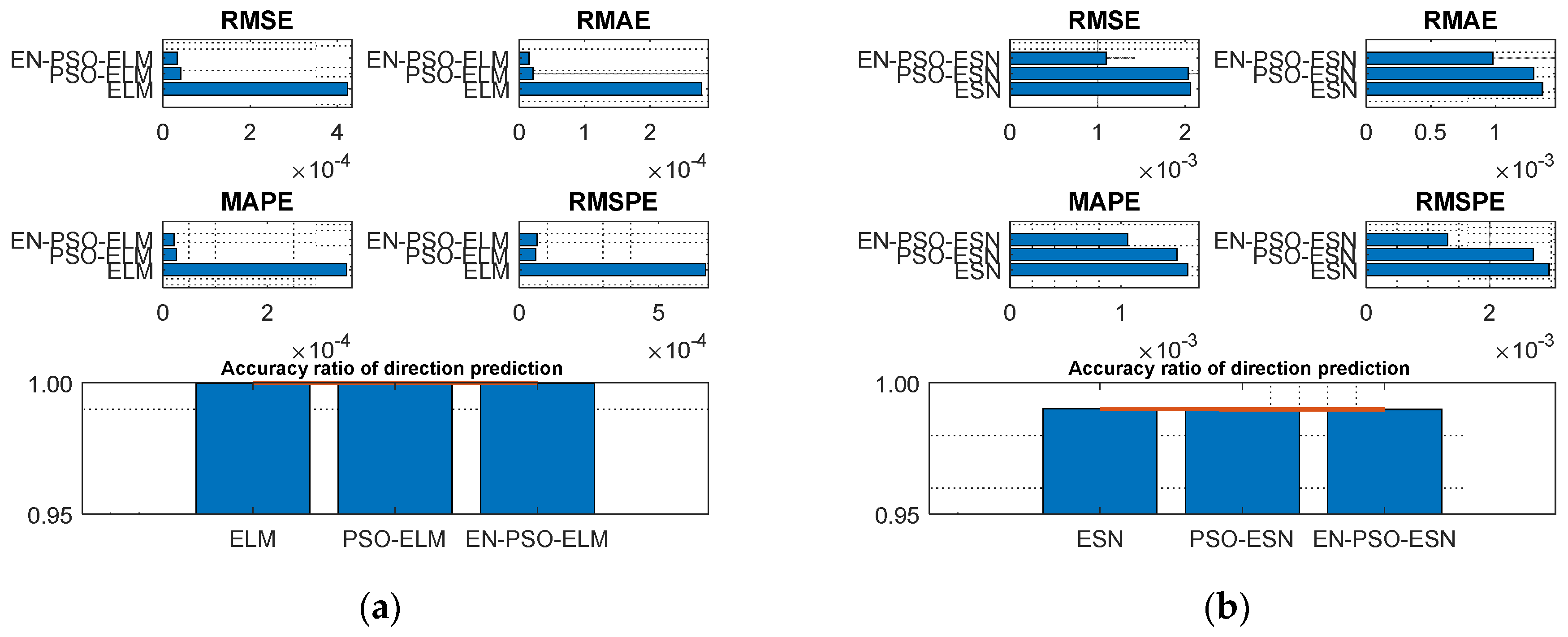
4.2. Experiment for Synthetic Benchmark Time Series Prediction
- (1)
- Mackey and Glass dataset
- (2)
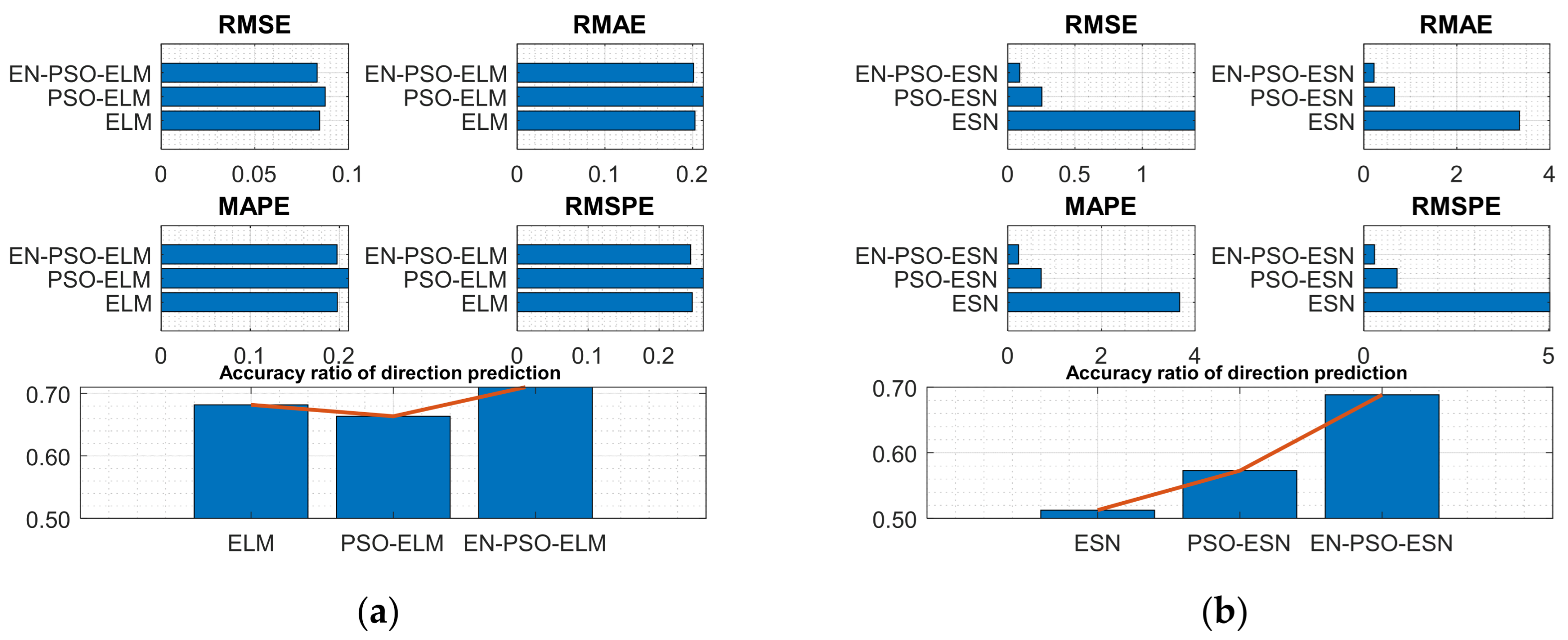
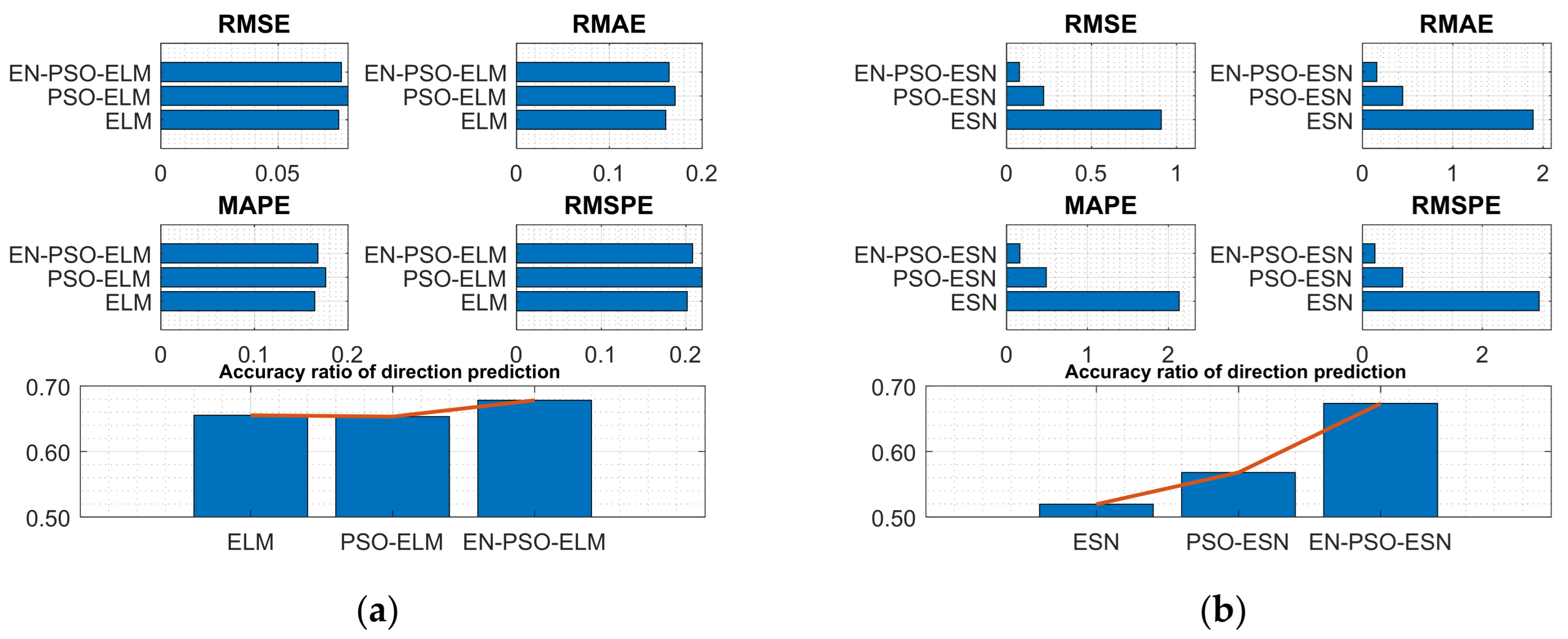
- Nonlinear auto-regressive moving average dataset
- (3)
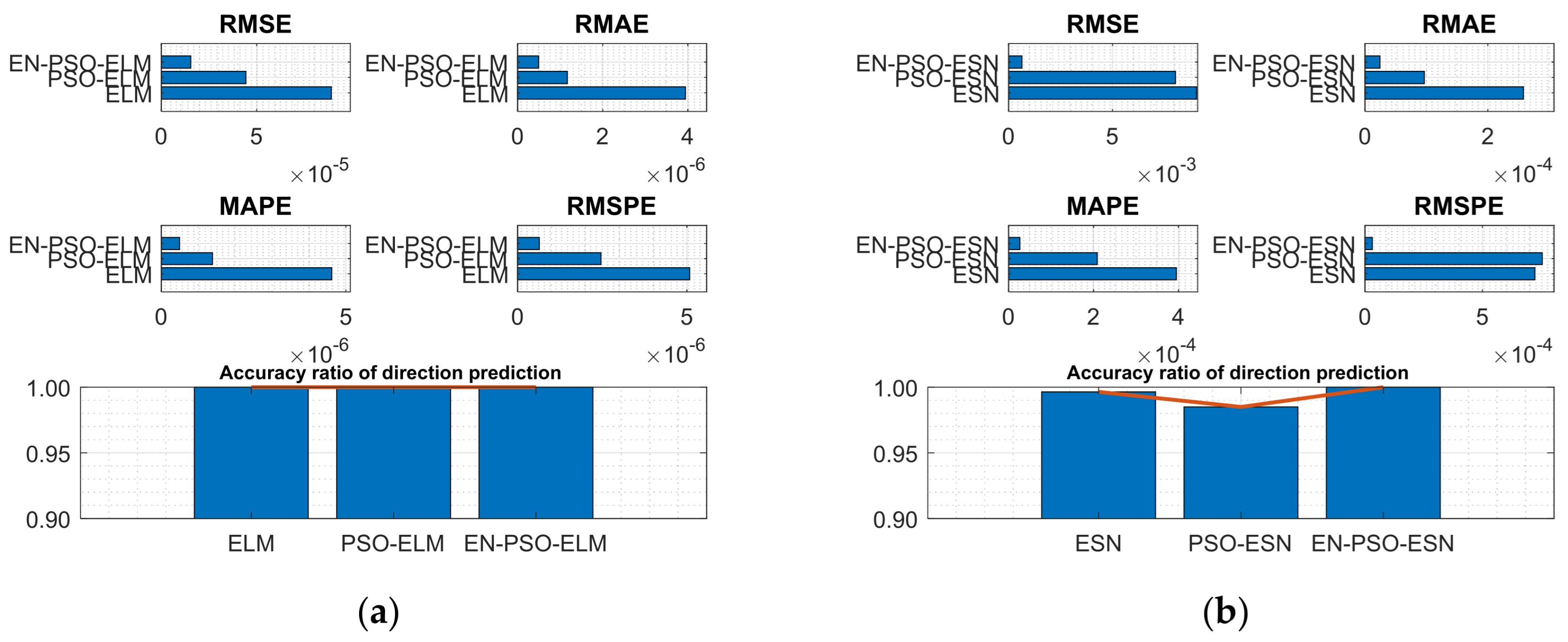
- The Henon attractor and Lorenz attractor data series
4.3. Experiment for Real Benchmark Time Series Prediction
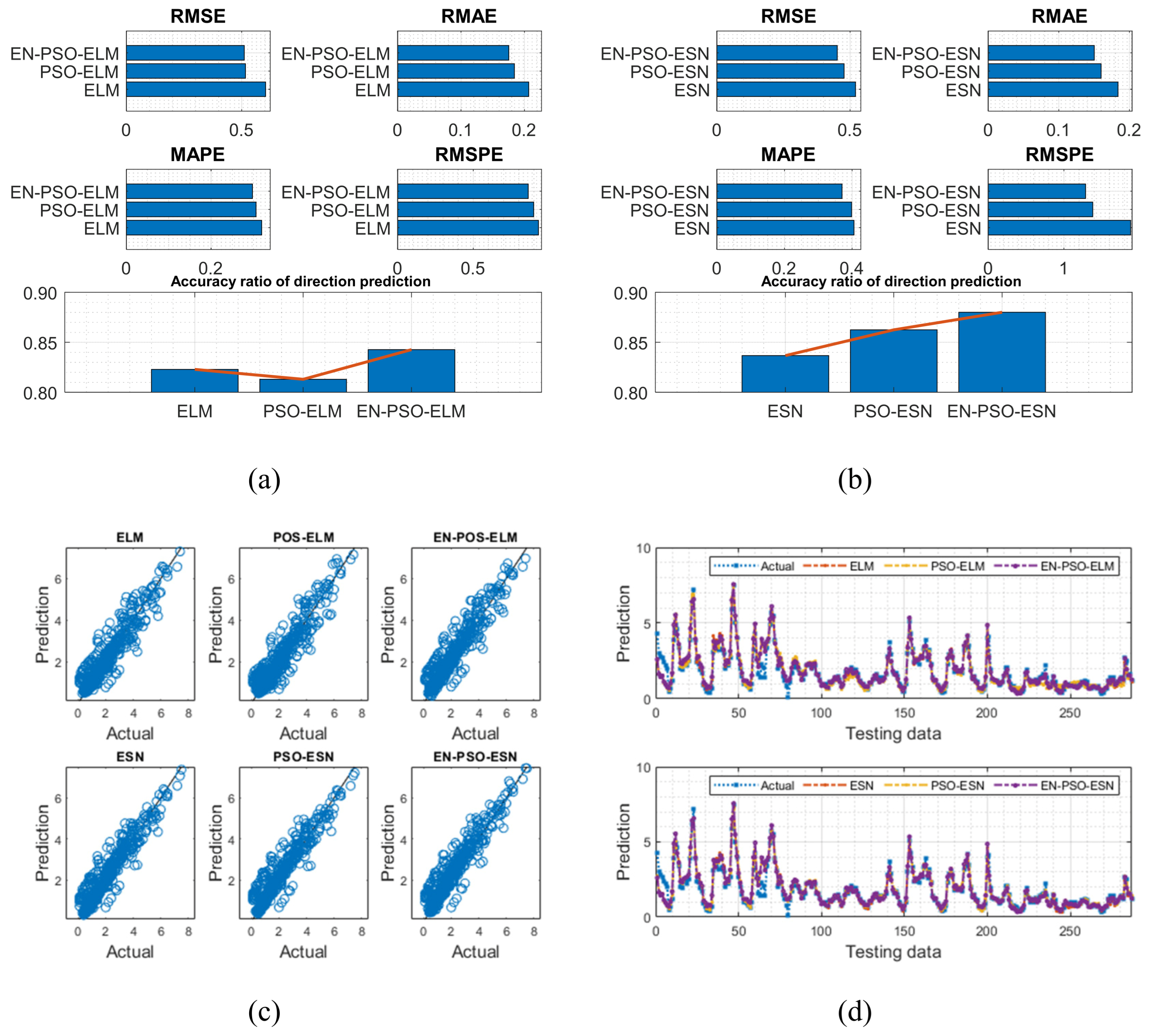
4.3.1. Air Quality (AQ) Dataset
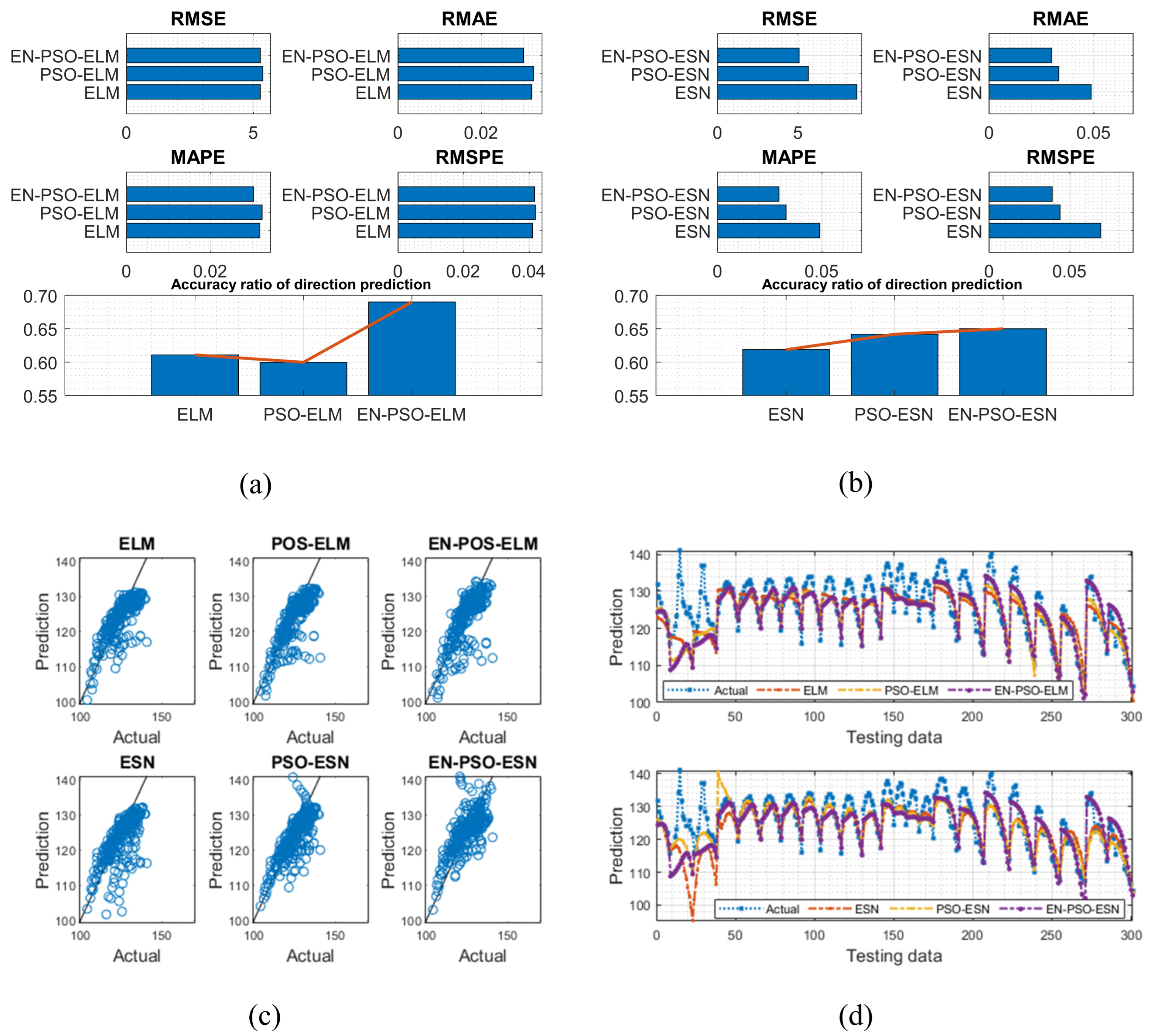
4.3.2. Airfoil Self-Noise (ASN) Dataset
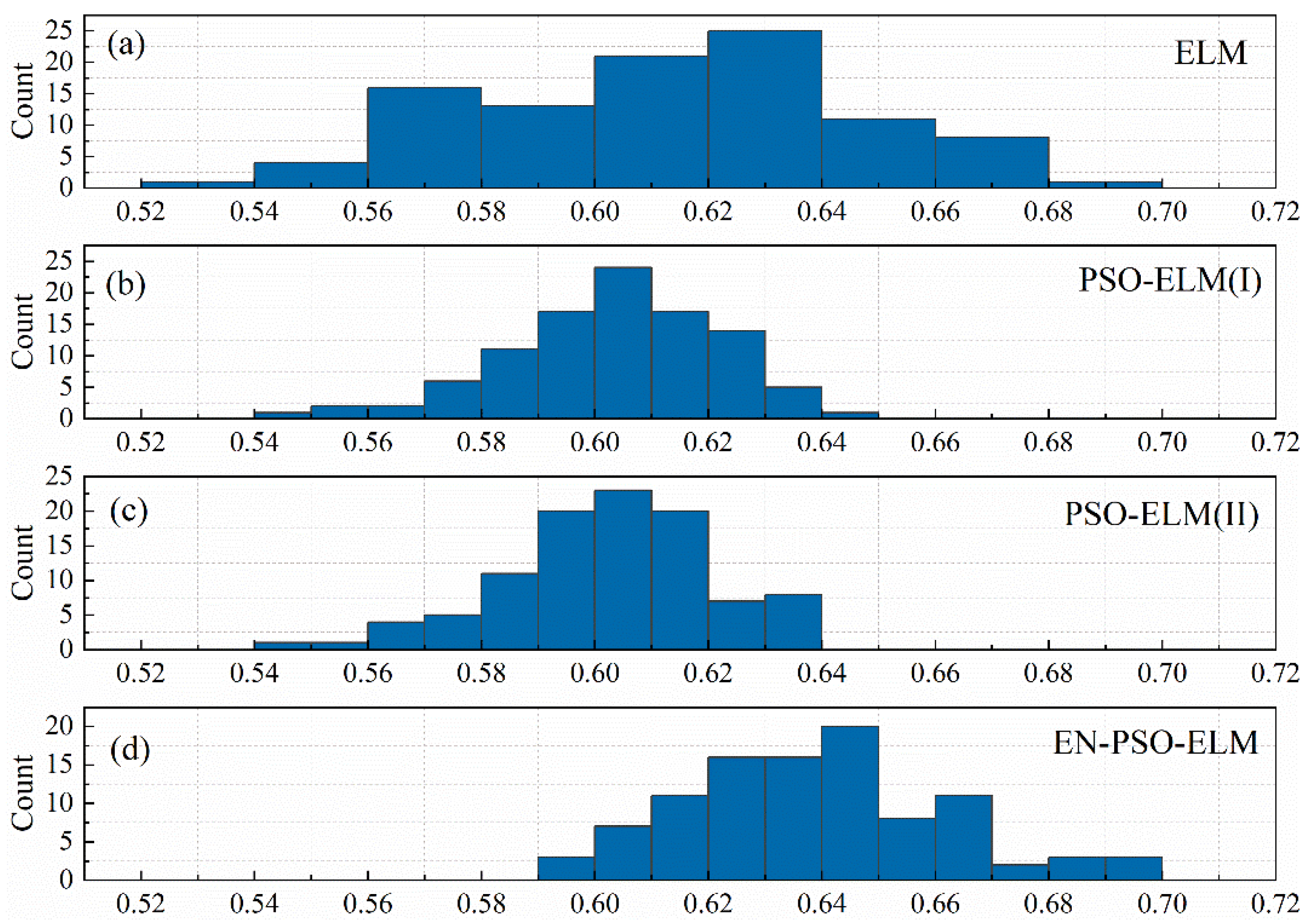
4.4. Additional Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar] [CrossRef]
- Hu, H.; Wang, L.; Peng, L.; Zeng, Y.R. Effective energy consumption forecasting using enhanced bagged echo state network. Energy 2020, 193, 116778. [Google Scholar] [CrossRef]
- Tran, D.H.; Luong, D.L.; Chou, J.S. Nature-inspired metaheuristic ensemble model for forecasting energy consumption in residential buildings. Energy 2020, 191, 116552. [Google Scholar] [CrossRef]
- Sujjaviriyasup, T. A new class of MODWT-SVM-DE hybrid model emphasizing on simplification structure in data pre-processing: A case study of annual electricity consumptions. Appl. Soft Comput. 2017, 54, 150–163. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Liu, C.; Li, C.; Li, L. A hybrid application algorithm based on the support vector machine and artificial intelligence: An example of electric load forecasting. Appl. Math. Model. 2015, 39, 2617–2632. [Google Scholar] [CrossRef]
- Fan, C.; Ding, C.; Zheng, J.; Xiao, L.; Ai, Z. Empirical Mode Decomposition based Multi-objective Deep Belief Network for short-term power load forecasting. Neurocomputing 2020, 388, 110–123. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z. Ultra-short-term wind speed forecasting using an optimized artificial intelligence algorithm. Renew. Energy 2021, 171, 1418–1435. [Google Scholar] [CrossRef]
- Peng, T.; Zhang, C.; Zhou, J.; Nazir, M.S. Negative correlation learning-based RELM ensemble model integrated with OVMD for multi-step ahead wind speed forecasting. Renew. Energy 2020, 156, 804–819. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Niu, X.; Liu, Z. Ensemble wind speed forecasting with multi-objective Archimedes optimization algorithm and sub-model selection. Appl. Energy. 2021, 301, 117449. [Google Scholar] [CrossRef]
- Mishra, D.; Goyal, P.; Upadhyay, A. Artificial intelligence based approach to forecast PM 2.5 during haze episodes: A case study of Delhi, India. Atmos. Environ. 2015, 102, 239–248. [Google Scholar] [CrossRef]
- Li, V.O.K.; Lam, J.C.K.; Han, Y.; Chow, K. A Big Data and Artificial Intelligence Framework for Smart and Personalized Air Pollution Monitoring and Health Management in Hong Kong. Environ. Sci. Policy 2021, 124, 441–450. [Google Scholar] [CrossRef]
- Shams, S.R.; Jahani, A.; Kalantary, S.; Moeinaddini, M.; Khorasani, N. Artificial intelligence accuracy assessment in NO2 concentration forecasting of metropolises air. Sci. Rep. 2021, 11, 1805. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting. Proc. AAAI Conf. Artif. Intell. 2019, 33, 922–929. [Google Scholar] [CrossRef]
- Cai, W.; Yang, J.; Yu, Y.; Song, Y.; Zhou, T.; Qin, J. PSO-ELM: A Hybrid Learning Model for Short-Term Traffic Flow Forecasting. IEEE Access 2020, 8, 6505–6514. [Google Scholar] [CrossRef]
- Du, S.; Li, T.; Gong, X.; Horng, S.-J. A Hybrid Method for Traffic Flow Forecasting Using Multimodal Deep Learning. Int. J. Comput. Intell. Syst. 2020, 13, 85. [Google Scholar] [CrossRef]
- Lalmuanawma, S.; Hussain, J.; Chhakchhuak, L. Applications of machine learning and artificial intelligence for COVID-19 (SARS-CoV-2) pandemic: A review. Chaos Solitons Fractals 2020, 139, 110059. [Google Scholar] [CrossRef]
- da Silva, R.G.; Ribeiro, M.H.D.M.; Mariani, V.C.; Coelho, L.D.S. Forecasting Brazilian and American COVID-19 cases based on artificial intelligence coupled with climatic exogenous variables. Chaos Solitons Fractals 2020, 139, 110027. [Google Scholar] [CrossRef]
- Vaishya, R.; Javaid, M.; Khan, I.H.; Haleem, A. Artificial Intelligence (AI) applications for COVID-19 pandemic. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 337–339. [Google Scholar] [CrossRef]
- Yu, P.; Yan, X. Stock price prediction based on deep neural networks. Neural Comput. Appl. 2020, 32, 1609–1628. [Google Scholar] [CrossRef]
- Ding, G.; Qin, L. Study on the prediction of stock price based on the associated network model of LSTM. Int. J. Mach. Learn. Cybern. 2020, 11, 1307–1317. [Google Scholar] [CrossRef]
- Yun, K.K.; Yoon, S.W.; Won, D. Prediction of stock price direction using a hybrid GA-XGBoost algorithm with a three-stage feature engineering process. Expert Syst. Appl. 2021, 186, 115716. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM. 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Juhn, Y.; Liu, H. Artificial intelligence approaches using natural language processing to advance EHR-based clinical research. J. Allergy Clin. Immunol. 2020, 145, 463–469. [Google Scholar] [CrossRef]
- Trappey, A.J.C.; Trappey, C.V.; Wu, J.L.; Wang, J.W.C. Intelligent compilation of patent summaries using machine learning and natural language processing techniques. Adv. Eng. Inform. 2020, 43, 101027. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Tang, Z.; Xu, Y.; Zhang, H. Evolutionary artificial intelligence model via cooperation search algorithm and extreme learning machine for multiple scales nonstationary hydrological time series prediction. J. Hydrol. 2021, 595, 126062. [Google Scholar] [CrossRef]
- Hussain, D.; Hussain, T.; Khan, A.A.; Naqvi, S.A.A.; Jamil, A. A deep learning approach for hydrological time-series prediction: A case study of Gilgit river basin. Earth Sci. Inform. 2020, 13, 915–927. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Cai, Z.; Tian, X.; Wang, X.; Huang, Y.; Chen, H.; Hu, L. Chaos enhanced grey wolf optimization wrapped ELM for diagnosis of paraquat-poisoned patients. Comput. Biol. Chem. 2019, 78, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Muduli, D.; Dash, R.; Majhi, B. Automated breast cancer detection in digital mammograms: A moth flame optimization based ELM approach. Biomed. Signal Process. Control 2020, 59, 101912. [Google Scholar] [CrossRef]
- Diker, A.; Sönmez, Y.; Özyurt, F.; Avcı, E.; Avcı, D. Examination of the ECG signal classification technique DEA-ELM using deep convolutional neural network features. Multimed. Tools Appl. 2021, 80, 24777–24800. [Google Scholar] [CrossRef]
- Virgeniya, S.C.; Ramaraj, E. A Novel Deep Learning based Gated Recurrent Unit with Extreme Learning Machine for Electrocardiogram (ECG) Signal Recognition. Biomed. Signal Process. Control 2021, 68, 102779. [Google Scholar] [CrossRef]
- Lingyu, T.; Jun, W.; Chunyu, Z. Mode decomposition method integrating mode reconstruction, feature extraction, and ELM for tourist arrival forecasting. Chaos Solitons Fractals 2021, 143, 110423. [Google Scholar] [CrossRef]
- Sun, S.; Wei, Y.; Tsui, K.L.; Wang, S. Forecasting tourist arrivals with machine learning and internet search index. Tour. Manag. 2019, 70, 1–10. [Google Scholar] [CrossRef]
- Maliha, A.; Yusof, R.; Shapiai, M.I. Extreme learning machine for structured output spaces. Neural Comput. Appl. 2018, 30, 1251–1264. [Google Scholar] [CrossRef]
- Patil, A.; Shen, S.; Yao, E.; Basu, A. Hardware architecture for large parallel array of Random Feature Extractors applied to image recognition. Neurocomputing 2017, 261, 193–203. [Google Scholar] [CrossRef]
- Bi, J.W.; Liu, Y.; Li, H. Daily tourism volume forecasting for tourist attractions. Ann. Tour. Res. 2020, 83, 102923. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Shabani, M.; Yousefi, M. An optimized model using LSTM network for demand forecasting. Comput. Ind. Eng. 2020, 143, 106435. [Google Scholar] [CrossRef]
- Bappy, J.H.; Simons, C.; Nataraj, L.; Manjunath, B.S.; Roy-Chowdhury, A.K. Hybrid LSTM and Encoder–Decoder Architecture for Detection of Image Forgeries. IEEE Trans. Image Process. 2019, 28, 3286–3300. [Google Scholar] [CrossRef]
- Ullah, A.; Ahmad, J.; Muhammad, K.; Sajjad, M.; Baik, S.W. Action Recognition in Video Sequences using Deep Bi-Directional LSTM With CNN Features. IEEE Access 2018, 6, 1155–1166. [Google Scholar] [CrossRef]
- Fanta, H.; Shao, Z.; Ma, L. SiTGRU: Single-Tunnelled Gated Recurrent Unit for Abnormality Detection. Inf. Sci. 2020, 524, 15–32. [Google Scholar] [CrossRef]
- Ravanelli, M.; Brakel, P.; Omologo, M.; Bengio, Y. Light Gated Recurrent Units for Speech Recognition. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 92–102. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine Health Monitoring Using Local Feature-Based Gated Recurrent Unit Networks. IEEE Trans. Ind. Electron. 2018, 65, 1539–1548. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, L.; Lin, Z. Multi-attraction, hourly tourism demand forecasting. Ann. Tour. Res. 2021, 90, 103271. [Google Scholar] [CrossRef]
- Mou, L.; Zhou, C.; Zhao, P.; Nakisa, B.; Rastgoo, M.N.; Jain, R.; Gao, W. Driver stress detection via multimodal fusion using attention-based CNN-LSTM. Expert Syst. Appl. 2021, 173, 114693. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Kong, D.; Han, H.; Zhao, Y. EA-LSTM: Evolutionary attention-based LSTM for time series prediction. Knowl. Based Syst. 2019, 181, 104785. [Google Scholar] [CrossRef]
- Song, S.; Lan, C.; Xing, J.; Zeng, W.; Liu, J. Spatio-Temporal Attention-Based LSTM Networks for 3D Action Recognition and Detection. IEEE Trans. Image Process. 2018, 27, 3459–3471. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Wang, X.; Li, Y. Effects of singular value spectrum on the performance of echo state network. Neurocomputing 2019, 358, 414–423. [Google Scholar] [CrossRef]
- Lv, S.-X.; Peng, L.; Wang, L. Stacked autoencoder with echo-state regression for tourism demand forecasting using search query data. Appl. Soft Comput. 2018, 73, 119–133. [Google Scholar] [CrossRef]
- Hu, H.; Wang, L.; Tao, R. Wind speed forecasting based on variational mode decomposition and improved echo state network. Renew. Energy 2021, 164, 729–751. [Google Scholar] [CrossRef]
- Ma, Q.; Shen, L.; Chen, W.; Wang, J.; Wei, J.; Yu, Z. Functional echo state network for time series classification. Inf. Sci. 2016, 373, 1–20. [Google Scholar] [CrossRef]
- Chouikhi, N.; Ammar, B.; Rokbani, N.; Alimi, A.M. PSO-based analysis of Echo State Network parameters for time series forecasting. Appl. Soft Comput. 2017, 55, 211–225. [Google Scholar] [CrossRef]
- Ferreira, A.A.; Ludermir, T.B. Comparing evolutionary methods for reservoir computing pre-training. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 283–290. [Google Scholar] [CrossRef]
- Basterrech, S.; Alba, E.; Snášel, V. An Experimental Analysis of the Echo State Network Initialization Using the Particle Swarm Optimization. arXiv 2015, arXiv:150100436. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2019; Available online: http://archive.ics.uci.edu/ml (accessed on 14 April 2022).



| ESN-Based Models | ELM-Based Models | |
|---|---|---|
| Compared Models |
|
|
|
| |
|
|
| Running Times | Hidden Neuron Number | α | β | Ensemble Number | Leak Rate | The Collection Rate of the Reservoir | |
|---|---|---|---|---|---|---|---|
| ELM | 50 | 100 | \ | \ | \ | \ | \ |
| PSO-ELM | 50 | 100 | 0.1 | \ | \ | \ | \ |
| EN-PSO-ELM | 50 | 100 | 0.1 | \ | 50 | \ | \ |
| Canonical ESN | 50 | 100 | 0.1 | 0.01 | \ | 0.3 | 0.01 |
| PSO-ESN | 50 | 100 | 0.1 | 0.01 | \ | 0.3 | 0.01 |
| EN-PSO-ESN | 50 | 100 | 0.1 | 0.01 | 50 | 0.3 | 0.01 |
| Models | RMSE | RMAE | MAPE | RMSPE | DA | Performance Order | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | |||
| MG(1) | ELM | 4.2333 × 10−4 | 3.6354 × 10−5 | 2.7920 × 10−4 | 1.6822 × 10−5 | 3.5139 × 10−4 | 2.7389 × 10−5 | 6.6799 × 10−4 | 9.5655 × 10−5 | 100.00% | 0 | 3 |
| PSO-ELM | 4.0988 × 10−5 | 1.3745 × 10−5 | 2.1236 × 10−5 | 5.6891 × 10−6 | 2.5438 × 10−5 | 8.2240 × 10−6 | 5.8877 × 10−5 | 3.1339 × 10−5 | 100.00% | 0 | 2 | |
| EN-PSO-ELM | 3.3164 × 10−5 | 1.3182 × 10−5 | 1.5342 × 10−5 | 5.4203 × 10−6 | 2.1275 × 10−5 | 8.1346 × 10−6 | 6.4802 × 10−5 | 3.1238 × 10−5 | 100.00% | 0 | 1 | |
| ESN | 2.0595 × 10−3 | 7.0927 × 10−4 | 1.3627 × 10−3 | 5.0073 × 10−4 | 1.6014 × 10−3 | 5.7275 × 10−4 | 2.9686 × 10−3 | 1.0756 × 10−3 | 99.0201% | 5.1431 × 10−3 | 3 | |
| PSO-ESN | 2.0336 × 10−3 | 4.7435 × 10−4 | 1.2950 × 10−3 | 3.6885 × 10−4 | 1.5015 × 10−3 | 4.4408 × 10−4 | 2.7100 × 10−3 | 8.3517 × 10−4 | 98.9950% | 7.2647 × 10−3 | 2 | |
| EN-PSO-ESN | 1.0973 × 10−3 | 4.6523 × 10−4 | 9.7777 × 10−4 | 3.5712 × 10−4 | 1.0609 × 10−3 | 4.2366 × 10−4 | 1.3206 × 10−3 | 7.8256 × 10−4 | 98.9950% | 5.3627 × 10−3 | 1 | |
| MG(2) | ELM | 3.7327 × 10−4 | 1.8502 × 10−5 | 3.0227 × 10−4 | 1.3882 × 10−5 | 4.0961 × 10−4 | 2.1957 × 10−5 | 6.6574 × 10−4 | 5.1463 × 10−5 | 100.00% | 0 | 3 |
| PSO-ELM | 2.9236 × 10−5 | 6.7239 × 10−6 | 2.3141 × 10−5 | 5.2118 × 10−6 | 2.8240 × 10−5 | 7.4557 × 10−6 | 4.3585 × 10−5 | 2.2779 × 10−5 | 100.00% | 0 | 1 | |
| EN-PSO-ELM | 3.4774 × 10−5 | 6.6342 × 10−6 | 2.7965 × 10−5 | 5.0656 × 10−6 | 3.7718 × 10−5 | 7.3756 × 10−6 | 7.3590 × 10−5 | 2.0232 × 10−5 | 100.00% | 0 | 2 | |
| ESN | 3.7092 × 10−2 | 2.6262 × 10−2 | 2.9828 × 10−2 | 1.9397 × 10−2 | 3.1434 × 10−2 | 1.9213 × 10−2 | 4.3163 × 10−2 | 2.8004 × 10−2 | 76.8342% | 7.7177 × 10−2 | 3 | |
| PSO-ESN | 1.7372 × 10−2 | 7.2545 × 10−3 | 1.5625 × 10−2 | 6.6169 × 10−3 | 1.5896 × 10−2 | 8.3831 × 10−3 | 1.9330 × 10−2 | 1.1820 × 10−3 | 79.8995% | 1.3707 × 10−2 | 2 | |
| EN-PSO-ESN | 2.6844 × 10−3 | 7.2331 × 10−3 | 2.2819 × 10−3 | 6.4356 × 10−3 | 2.7199 × 10−3 | 8.2356 × 10−3 | 4.0754 × 10−3 | 1.0298 × 10−4 | 97.9899% | 1.1635 × 10−2 | 1 | |
| Models | RMSE | RMAE | MAPE | RMSPE | DA | Performance Order | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | |||
| NARMA(1) | ELM | 8.4527 × 10−2 | 1.5725 × 10−3 | 2.0259 × 10−1 | 4.2477 × 10−3 | 1.9763 × 10−1 | 4.2896 × 10−3 | 2.4655 × 10−1 | 5.0867 × 10−3 | 68.1658% | 1.7849 × 10−2 | 2 |
| PSO-ELM | 8.7526 × 10−2 | 3.0443 × 10−3 | 2.1204 × 10−1 | 7.0243 × 10−3 | 2.1022 × 10−1 | 6.5851 × 10−3 | 2.6206 × 10−1 | 8.3883 × 10−3 | 66.3317% | 1.5415 × 10−2 | 3 | |
| EN-PSO-ELM | 8.3184 × 10−2 | 2.6577 × 10−3 | 2.0105 × 10−1 | 6.2344 × 10−3 | 1.9733 × 10−1 | 5.8975 × 10−3 | 2.4445 × 10−1 | 7.5654 × 10−3 | 71.3568% | 1.1103 × 10−2 | 1 | |
| ESN | 1.3926 | 3.6549 × 10−1 | 3.3487 | 7.6720 × 10−1 | 3.6671 | 9.0628 × 10−1 | 5.0313 | 1.4765 | 51.2563% | 2.3409 × 10−2 | 3 | |
| PSO-ESN | 2.5375 × 10−1 | 1.6762 × 10−2 | 6.5980 × 10−1 | 5.2713 × 10−2 | 7.1371 × 10−1 | 7.0387 × 10−2 | 9.0056 × 10−1 | 7.8975 × 10−2 | 57.2864% | 1.3531 × 10−2 | 2 | |
| EN-PSO-ESN | 8.8658 × 10−2 | 1.4525 × 10−2 | 2.2177 × 10−1 | 4.7286 × 10−2 | 2.2927 × 10−1 | 6.6895 × 10−2 | 2.8936 × 10−1 | 6.5657 × 10−2 | 68.8442% | 1.0126 × 10−2 | 1 | |
| NARMA(2) | ELM | 7.5817 × 10−2 | 1.8216 × 10−3 | 1.6056 × 10−1 | 2.9249 × 10−3 | 1.6436 × 10−1 | 2.6978 × 10−3 | 2.0151 × 10−1 | 4.9365 × 10−3 | 65.5276% | 1.9358 × 10−2 | 2 |
| PSO-ELM | 7.9777 × 10−2 | 1.7392 × 10−3 | 1.7079 × 10−1 | 3.6645 × 10−3 | 1.7622 × 10−1 | 4.4762 × 10−3 | 2.1918 × 10−1 | 6.4204 × 10−3 | 65.3266% | 2.0750 × 10−2 | 3 | |
| EN-PSO-ELM | 7.6952 × 10−2 | 1.2366 × 10−3 | 1.6418 × 10−1 | 3.0012 × 10−3 | 1.6772 × 10−1 | 3.8745 × 10−3 | 2.0773 × 10−1 | 4.8673 × 10−3 | 67.8392% | 1.5266 × 10−2 | 1 | |
| ESN | 9.1040 × 10−1 | 2.2495 × 10−1 | 1.8900 | 3.9288 × 10−1 | 2.1331 | 4.7139 × 10−1 | 2.9487 | 7.9041 × 10−1 | 51.9598% | 2.5594 × 10−2 | 3 | |
| PSO-ESN | 2.1788 × 10−1 | 2.5335 × 10−3 | 4.4598 × 10−1 | 6.2503 × 10−3 | 4.9090 × 10−1 | 7.9616 × 10−3 | 6.6947 × 10−1 | 9.9815 × 10−3 | 56.7839% | 2.0675 × 10−2 | 2 | |
| EN-PSO-ESN | 7.5906 × 10−2 | 2.4659 × 10−3 | 1.5905 × 10−1 | 6.0325 × 10−3 | 1.6497 × 10−1 | 7.2377 × 10−3 | 2.1019 × 10−1 | 9.3257 × 10−3 | 67.3367% | 1.6885 × 10−2 | 1 | |
| Models | RMSE | RMAE | MAPE | RMSPE | DA | Performance Order | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | |||
| Henon attractor | ELM | 3.3204 × 10−6 | 1.9751 × 10−6 | 4.4166 × 10−5 | 2.6936 × 10−5 | 3.7655 × 10−5 | 2.3881 × 10−5 | 1.5742 × 10−4 | 1.0435 × 10−4 | 100.00% | 0 | 3 |
| PSO-ELM | 1.4408 × 10−6 | 1.7335 × 10−6 | 1.8179 × 10−5 | 2.4365 × 10−5 | 1.7493 × 10−5 | 1.4665 × 10−5 | 8.0322 × 10−5 | 3.2457 × 10−5 | 100.00% | 0 | 2 | |
| EN-PSO-ELM | 6.8053 × 10−7 | 1.6568 × 10−6 | 8.0781 × 10−6 | 2.4415 × 10−6 | 8.3876 × 10−6 | 1.3622 × 10−5 | 4.3527 × 10−5 | 3.1757 × 10−5 | 100.00% | 0 | 1 | |
| ESN | 1.2784 × 10−5 | 5.6772 × 10−6 | 1.2730 × 10−4 | 5.3143 × 10−5 | 1.3102 × 10−4 | 5.8792 × 10−5 | 8.0622 × 10−4 | 5.8563 × 10−4 | 100.00% | 0 | 3 | |
| PSO-ESN | 4.0724 × 10−6 | 1.9122 × 10−7 | 4.4212 × 10−5 | 1.9947 × 10−6 | 6.4647 × 10−5 | 2.1198 × 10−6 | 5.6427 × 10−4 | 1.3948 × 10−5 | 100.00% | 0 | 2 | |
| EN-PSO-ESN | 9.4210 × 10−8 | 1.8652 × 10−7 | 9.2122 × 10−7 | 1.8257 × 10−6 | 1.1861 × 10−6 | 1.9121 × 10−6 | 9.5494 × 10−6 | 1.2398 × 10−5 | 100.00% | 0 | 1 | |
| Lorenz attractor | ELM | 8.9132 × 10−5 | 6.7269 × 10−5 | 3.9429 × 10−6 | 2.9819 × 10−6 | 4.6187 × 10−6 | 3.4981 × 10−6 | 5.0824 × 10−6 | 3.8467 × 10−6 | 100.00% | 0 | 3 |
| PSO-ELM | 4.4364 × 10−5 | 3.0233 × 10−5 | 1.1664 × 10−6 | 1.0605 × 10−6 | 1.3840 × 10−6 | 1.2885 × 10−6 | 2.4607 × 10−6 | 2.0413 × 10−6 | 100.00% | 0 | 2 | |
| EN-PSO-ELM | 1.5507 × 10−5 | 2.9626 × 10−5 | 4.9162 × 10−7 | 9.2377 × 10−7 | 4.9223 × 10−7 | 1.0132 × 10−6 | 6.4194 × 10−7 | 1.8652 × 10−6 | 100.00% | 0 | 1 | |
| ESN | 9.0528 × 10−3 | 7.2441 × 10−3 | 2.5788 × 10−4 | 2.1277 × 10−4 | 3.9498 × 10−4 | 3.5720 × 10−4 | 7.2311 × 10−4 | 6.5796 × 10−4 | 99.6315% | 4.2861 × 10−3 | 3 | |
| PSO-ESN | 8.0337 × 10−3 | 2.3815 × 10−3 | 9.6566 × 10−5 | 6.0522 × 10−5 | 2.0888 × 10−4 | 6.1014 × 10−4 | 7.5513 × 10−4 | 1.0421 × 10−4 | 98.4925% | 1.1511 × 10−3 | 2 | |
| EN-PSO-ESN | 6.4638 × 10−4 | 2.2356 × 10−3 | 2.4464 × 10−5 | 5.8677 × 10−5 | 2.6527 × 10−5 | 5.8206 × 10−4 | 3.1241 × 10−5 | 8.9885 × 10−5 | 100.00% | 0 | 1 | |
| Models | RMSE | RMAE | MAPE | RMSPE | DA | Performance Order | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | |||
| AQ | ELM | 6.0336 × 10−1 | 3.1730 × 10−2 | 2.0693 × 10−1 | 1.0420 × 10−2 | 3.1946 × 10−1 | 1.5002 × 10−2 | 9.2986 × 10−1 | 7.0943 × 10−2 | 82.3036% | 1.3441 × 10−2 | 3 |
| PSO-ELM | 5.1643 × 10−1 | 2.5506 × 10−2 | 1.8407 × 10−1 | 1.0414 × 10−2 | 3.0602 × 10−1 | 2.3974 × 10−2 | 8.9843 × 10−1 | 9.2220 × 10−2 | 81.3022% | 1.7108 × 10−2 | 2 | |
| EN-PSO-ELM | 5.1077 × 10−1 | 2.2681 × 10−2 | 1.7526 × 10−1 | 1.0287 × 10−2 | 2.9757 × 10−1 | 2.0834 × 10−2 | 8.6287 × 10−1 | 8.9669 × 10−2 | 84.2763% | 1.4262 × 10−2 | 1 | |
| ESN | 5.2005 × 10−1 | 6.1308 × 10−1 | 1.8365 × 10−1 | 8.0975 × 10−2 | 4.0563 × 10−1 | 1.1006 × 10−1 | 1.8808 | 4.5650 × 10−1 | 83.6772% | 2.0616 × 10−2 | 3 | |
| PSO-ESN | 4.7754 × 10−1 | 2.0790 × 10−2 | 1.5994 × 10−1 | 8.6829 × 10−3 | 3.9858 × 10−1 | 2.5555 × 10−2 | 1.3818 | 1.0542 × 10−1 | 86.2597% | 1.1972 × 10−2 | 2 | |
| EN-PSO-ESN | 4.5206 × 10−1 | 1.8512 × 10−2 | 1.5012 × 10−1 | 7.8701 × 10−3 | 3.7002 × 10−1 | 2.3122 × 10−2 | 1.2874 | 8.2653 × 10−2 | 88.0127% | 8.2701 × 10−3 | 1 | |
| Models | RMSE | RMAE | MAPE | RMSPE | DA | Performance Order | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | |||
| ASN | ELM | 5.2713 | 4.7943 × 10−1 | 3.2036 × 10−2 | 2.4332 × 10−3 | 3.1748 × 10−2 | 2.4495 × 10−3 | 4.1038 × 10−2 | 3.7342 × 10−3 | 61.0726% | 3.3335 × 10−2 | 2 |
| PSO-ELM | 5.3758 | 1.0927 | 3.2501 × 10−2 | 6.0878 × 10−3 | 3.2192 × 10−2 | 6.3756 × 10−3 | 4. 1941 × 10−2 | 9.3557 × 10−3 | 59.9668% | 3.4171 × 10−2 | 3 | |
| EN-PSO-ELM | 5.2748 | 9.0837 × 10−1 | 3.0147 × 10−2 | 5.7950 × 10−3 | 3.0231 × 10−2 | 6.2611 × 10−3 | 4.1590 × 10−2 | 8.9755 × 10−3 | 69.0036% | 3.2435 × 10−2 | 1 | |
| ESN | 8.6583 | 4.3130 × 10−1 | 4.8673 × 10−2 | 9.7585 × 10−2 | 4.8916 × 10−2 | 3.8668 × 10−2 | 6.9217 × 10−2 | 3.5095 × 10−2 | 61.8763% | 3.4994 × 10−2 | 3 | |
| PSO-ESN | 5.6447 | 5.5497 × 10−1 | 3.3215 × 10−2 | 3.3487 × 10−3 | 3.2834 × 10−2 | 3.4597 × 10−3 | 4.4033 × 10−2 | 4.5414 × 10−3 | 64.1582% | 4.2528 × 10−2 | 2 | |
| EN-PSO-ESN | 5.0717 | 5.3557 × 10−1 | 2.9766 × 10−2 | 3.1642 × 10−3 | 2.9418 × 10−2 | 3.2883 × 10−3 | 3.9145 × 10−2 | 4.3776 × 10−3 | 65.0027% | 3.0217 × 10−2 | 1 | |
| Description | ||
|---|---|---|
| Models | Canonical ELM model | The traditional ELM model without pre-training |
| PSO-ELM(I) model | Part of the non-zero elements in the Win will be selected as a candidate for pre-training by PSO | |
| PSO-ELM(II) model | Part of the element in the Win, including non-zero and zero elements, will be selected as candidates for pre-training by PSO | |
| EN-PSO-ELM model | Ensemble strategy combined with PSO-ELM(II) model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Wang, J.; Wang, M.; Zhao, C. Ensemble and Pre-Training Approach for Echo State Network and Extreme Learning Machine Models. Entropy 2024, 26, 215. https://doi.org/10.3390/e26030215
Tang L, Wang J, Wang M, Zhao C. Ensemble and Pre-Training Approach for Echo State Network and Extreme Learning Machine Models. Entropy. 2024; 26(3):215. https://doi.org/10.3390/e26030215
Chicago/Turabian StyleTang, Lingyu, Jun Wang, Mengyao Wang, and Chunyu Zhao. 2024. "Ensemble and Pre-Training Approach for Echo State Network and Extreme Learning Machine Models" Entropy 26, no. 3: 215. https://doi.org/10.3390/e26030215
APA StyleTang, L., Wang, J., Wang, M., & Zhao, C. (2024). Ensemble and Pre-Training Approach for Echo State Network and Extreme Learning Machine Models. Entropy, 26(3), 215. https://doi.org/10.3390/e26030215





