Abstract
In this work, we explore information geometry theoretic measures for characterizing neural information processing from EEG signals simulated by stochastic nonlinear coupled oscillator models for both healthy subjects and Alzheimer’s disease (AD) patients with both eyes-closed and eyes-open conditions. In particular, we employ information rates to quantify the time evolution of probability density functions of simulated EEG signals, and employ causal information rates to quantify one signal’s instantaneous influence on another signal’s information rate. These two measures help us find significant and interesting distinctions between healthy subjects and AD patients when they open or close their eyes. These distinctions may be further related to differences in neural information processing activities of the corresponding brain regions, and to differences in connectivities among these brain regions. Our results show that information rate and causal information rate are superior to their more traditional or established information-theoretic counterparts, i.e., differential entropy and transfer entropy, respectively. Since these novel, information geometry theoretic measures can be applied to experimental EEG signals in a model-free manner, and they are capable of quantifying non-stationary time-varying effects, nonlinearity, and non-Gaussian stochasticity presented in real-world EEG signals, we believe that they can form an important and powerful tool-set for both understanding neural information processing in the brain and the diagnosis of neurological disorders, such as Alzheimer’s disease as presented in this work.
1. Introduction
Identifying quantitative features from neurophysiological signals such as electroencephalography (EEG) is critical for understanding neural information processing in the brain and the diagnosis of neurological disorders such as dementia. Many such features have been proposed and employed to analyze neurological signals, which not only resulted in insightful understanding of the brain neurological dynamics of patients with certain neurological disorders versus healthy control (CTL) groups, but also helped build mathematical models that replicate the neurological signal with these quantitative features [1,2,3,4,5].
An important distinction, or non-stationary time-varying effects of the neurological dynamics, is the switching between eyes-open (EO) and eyes-closed (EC) states, where numerous research studies have been conducted on this distinction between EO and EC states to quantify important features of CTL subjects and patients using different techniques on EEG data such as traditional frequency-domain analysis [6,7], transfer entropy [8], energy landscape analysis [9], and nonlinear manifold learning for functional connectivity analysis [10], while also attempting to relate these features to specific clinical conditions and/or physiological variables, including skin conductance levels [11,12], cerebral blood flow [13], brain network connectivity [14,15,16], brain activities in different regions [17], and performance on the unipedal stance test (UPST) [18]. Clinical physiological studies found that there are distinct mental states related to the EO and EC states. Specifically, there is an “exteroceptive” mental activity state characterized by attention and ocular motor activity during EO, and an “interoceptive” mental activity state characterized by imagination and multisensory activity during EC [19,20]. Ref. [21] suggested that the topological organization of human brain networks dynamically switches corresponding to the information processing modes when the brain is visually connected to or disconnected from the external environment. However, patients with Alzheimer’s disease (AD) show loss of brain responsiveness to environmental stimuli [22,23], which might be due to impaired or loss of connectivities in the brain networks. This suggests that dynamical changes between EO and EC might represent an ideal paradigm to investigate the effect of AD pathophysiology and could be developed as biomarkers for diagnosis purposes. However, sensible quantification of robust features of these dynamical changes between EO and EC of both healthy and AD subjects, solely relying on EEG signals, is nontrivial. Despite the success of many statistical and quantitative measures being applied to neurological signal analysis, the main challenges stem from the non-stationary time-varying dynamics of the human brain with nonlinearity and non-Gaussian stochasticity, which makes most, if not all, of these traditional quantitative measures inadequate, and blindly applying these traditional measures to nonlinear and nonstationary time series/signals may produce spurious results, leading to incorrect interpretation.
In this work, by using simulated EEG signals of both CTL groups and AD patients under both EC and EO conditions and based on our previous works on information geometry [24,25,26], we develop novel and powerful quantitative measures in terms of information rate and causal information rate to quantify the important features of neurological dynamics of brains. We are able to find significant and interesting distinctions between CTL subjects and AD patients when they switch between the eyes-open and eyes-closed status. These quantified distinctions may be further related to differences in neural information processing activities of the corresponding brain regions, and to differences in connectivities among these brain regions, and therefore, they can be further developed as important biomarkers to diagnose neurological disorders, including but not limited to Alzheimer’s disease. It should be noted that these novel and powerful quantitative measures in terms of information rate and causal information rate can be applied to experimental EEG signals in a model-free manner, and they are capable of quantifying non-stationary time-varying effects, nonlinearity, and non-Gaussian stochasticity presented in real-world EEG signals, and hence, they are more robust and reliable than other information-theoretic measures applied to neurological signal analysis in the literature [27,28]. Therefore, we believe that these information geometry theoretic measures can form an important and powerful tool set for the neuroscience community.
The EEG signals have been modeled using many different methodologies in the literature. An EEG model in terms of nonlinear stochastic differential equation (SDE) could be sufficiently flexible in that it usually contains many parameters, whose values can be tuned to match the model’s output with actual EEG signals for different neurophysiological conditions, such as EC and EO, of CTL subjects or AD patients. Moreover, an SDE model of EEG can be solved by a number of numerical techniques to generate simulated EEG signals superior to actual EEG signals in terms of much higher temporal resolution and much larger number of sample paths available. These are the two main reasons why we choose to work with SDE models of EEG signals. Specifically, we employed a model of stochastic coupled Duffing–van der Pol oscillators proposed by Ref. [1], which is flexible enough to represent the EC and EO conditions for both CTL and AD subjects and straightforward enough to be simulated by using typical numerical techniques for solving SDE. Moreover, the model parameters reported in Ref. [1] were fine tuned against real-world experimental EEG signals of CTL and AD patients with both EC and EO conditions, and therefore, quantitative investigations on the model’s output of simulated signals are sufficiently representative for a large population of healthy and AD subjects.
2. Methods
2.1. Stochastic Nonlinear Oscillator Models of EEG Signals
A phenomenological model of the EEG based on a coupled system of Duffing–van der Pol oscillators subject to white noise excitation has been introduced [1] with the following form:
where are positions, velocities, and accelerations of the two oscillators, respectively. Parameters are the linear stiffness, cubic stiffness, and van der Pol damping coefficient of the two oscillators, respectively. Parameter represents the intensity of white noise and is a Wiener process representing the additive noise in the stochastic differential system. The physical meanings of these variables and parameters were nicely explained in a schematic figure in Ref. [1].
By using actual EEG signals, Ref. [1] utilized a combination of several different statistical and optimization techniques to fine tune the parameters in the model equations for eyes-closed (EC) and eyes-open (EO) conditions of both healthy control (CTL) subjects and Alzheimer’s disease (AD) patients, and these parameter values for different conditions are summarized in Table 1 and Table 2.

Table 1.
Optimal parameters of the Duffing–van der Pol oscillator for EC and EO of healthy control (CTL) subjects.

Table 2.
Optimal parameters of the Duffing–van der Pol oscillator for EC and EO of Alzheimers disease (AD) patients.
The model Equation (1) can be easily rewritten in a more standard form of stochastic differential equation (SDE) as follows:
which is more readily suitable for stochastic simulations.
2.2. Initial Conditions (ICs) and Specifications of Stochastic Simulations
For simplicity, we employ the Euler–Maruyama scheme [29] to simulate trajectories in total of the model Equation (2); although, other more sophisticated methods for stochastic simulations exist. We simulate such a large number of trajectories, because calculations of information geometry theoretic measures rely on accurate estimation of probability density functions (PDFs) of the model’s variables , which requires a large number of data samples of at any given time t.
Since nonlinear oscillators’ solution is very sensitive to initial conditions, we start the simulation with a certain initial probability distribution (e.g., a Gaussian distribution) for all , which means that the 20 million are randomly drawn from a probability density function (PDF) of the initial distribution. The time-step size is set to to compensate for the very-high values of stiffness parameters and in Table 1 and Table 2. The total number of simulation time steps is , making the total time range of simulation . The is the time interval when the probability density functions (PDFs) and are estimated for calculating information geometry theoretic measures such as information rates and causal information rates, as explained in Section 2.3.
For nonlinear oscillators, different initial conditions can result in dramatically different long-term time evolution. So in order to explore more diverse initial conditions, we simulated the SDE with 6 different initial Gaussian distributions with different means and standard deviations, i.e., , , , , where the parameters are summarized alongside other specifications in Table 3.

Table 3.
Initial conditions (IC): are randomly drawn from Gaussian distributions with different ’s and ’s .
For brevity, in this paper, we use the word “initial conditions” or its abbreviation “IC” to refer to the (set of 4) initial Gaussian distributions from which the 20 million are randomly drawn. For example, the “IC No.6” in Table 3 (and simply “IC6” elsewhere in this paper) refers to the 6th (set of 4) Gaussian distributions with which we start the simulation, and the specifications of this stimulation are listed in the last column of Table 3.
2.3. Information Geometry Theoretic Measures: Information Rate and Causal Information Rate
When a stochastic differential equation (SDE) model exhibits non-stationary time-varying effects, nonlinearity, and/or non-Gaussian stochasticity, while we are interested in large fluctuations and extreme events in the solutions, simple statistics such as mean and variance might not suffice to compare the solutions of different SDE models (or same model with different parameters). In such cases, quantifying and comparing the time evolution of probability density functions (PDFs) of solutions will provide us with more information [30]. The time evolution of PDFs can be studied and compared through the framework of information geometry [31], wherein PDFs are considered as points on a Riemannian manifold (which is called the statistical manifold), and their time evolution can be considered as a motion on this manifold. Several different metrics can be defined on a probability space to equip it with a manifold structure, including a metric related to the Fisher Information [32], known as the Fisher Information metric [33,34], which we use in this work:
Here, denotes a continuous family of PDFs parameterized by parameters . If a time-dependent PDF is considered as a continuous family of PDFs parameterized by a single parameter time t, the metric tensor is then reduced to a scalar metric:
The infinitesimal distance on the manifold is then given by , where is called the Information Length and defined as follows:
The Information Length represents the dimensionless distance, which measures the total distance traveled on the statistical manifold. The time derivative of then represents the speed of motion on this manifold:
which is referred to as the Information Rate. If multiple variables are involved, such as where as in the stochastic nonlinear oscillator model Equation (2), we will use subscript in , e.g., to denote the information rate of signal .
The notion of Causal Information Rate was introduced in Ref. [25] to quantify how one signal instantaneously influences another signal’s information rate. As an example, the causal information rate of signal influencing signal ’s information rate is denoted and defined by , where
and
where the relation between conditional, joint, and marginal PDFs and the fact for are used in the 2nd equal sign above. denotes the (auto) contribution to the information rate from itself, while is given/known and frozen in time. In other words, represents the information rate of when the additional information of (at the same time with ) becomes available or known. Subtracting from following the definition of then gives us the contribution of (knowing the additional information of) to , signifying how instantaneously influences the information rate of . One can easily verify that if signals and are statistically independent such that the equal-time joint PDF can be separated as , then will reduce to , making the causal information rate , which is consistent with the assumption that and are statistically independent at the same time t.
For numerical estimation purposes, one can derive simplified equations = and to ease the numerical calculations and avoid numerical errors in PDFs (due to finite sample-size estimations using a histogram-based approach) being doubled or enlarged when approximating the integrals in the original Equations (7) and (8) by finite summation. On the other hand, the time derivatives of the square root of PDFs are approximated by using temporally adjacent PDFs with each pair of two adjacent PDFs being separated by in time, as mentioned at the end of Section 2.2.
2.4. Shannon Differential Entropy and Transfer Entropy
As a comparison with more traditional and established information-theoretic measures, we also calculate differential entropy and transfer entropy using the numerically estimated PDFs and compare them with information rate and causal information rate, respectively.
The Shannon differential entropy of a signal is defined to extend the idea of Shannon discrete entropy as
where is the Lebesgue measure, and is the probability measure. In other words, differential entropy is the negative relative entropy (Kullback-Leibler divergence) from the Lebesgue measure (considered as an unnormalized probability measure) to a probability measure P (with density p). In contrast, information rate = (see Refs. [24,25,26] for detailed derivations) is related to the rate of change in relative entropy of two infinitesimally close PDFs and . Therefore, although differential entropy can measure the complexity of a signal at time t, it neglects how the signal’s PDF changes instantaneously at that time, which is crucial to quantify how new information can be reflected from the instantaneous entropy production rate of the signal . This is the theoretical reason why the information rate is a much better and more appropriate measure than differential entropy for characterizing the neural information processing from EEG signals of the brain, and the practical reason for this will be illustrated in terms of numerical results and discussed at the end of Section 3.3.2 and Section 3.3.3.
The transfer entropy (TE) measures the directional flow or transfer of information between two (discrete-time) stochastic processes. The transfer entropy from a signal to another signal is the amount of uncertainty reduced in future values of by knowing the past values of given past values of . Specifically, if the amount of information is measured using Shannon’s (discrete) entropy = of a stochastic process and conditional entropy , the transfer entropy from a process to another process (for discrete-time ) can be written as follows:
which quantifies the amount of reduced uncertainty in future value by knowing the past l values of given past k values of , where and are shorthands of past k values and past l values , respectively.
In order to properly compare with causal information rate signifying how one signal instantaneously influences another signal’s information rate (at the same/equal-time t), we set in calculating the transfer entropy between two signals. Also, since the causal information rate involves partial time derivatives, which have to be numerically estimated using temporally adjacent PDFs separated by in time (as mentioned at the end of Section 2.2), the discrete-time in transfer entropy should be changed to with . Therefore, the transfer entropy appropriate for comparing with the causal information rate should be rewritten as follows:
Numerical estimations of the information rate, causal information rate, differential entropy, and transfer entropy are all based on numerical estimation of PDFs using histograms. In particular, in order to sensibly and consistently estimate the causal information rate (e.g., to avoid getting negative values), special caution is required when choosing the binning for histogram estimation of PDFs in calculating and . The finer details for these numerical estimation techniques are elaborated in Appendix A.
3. Results
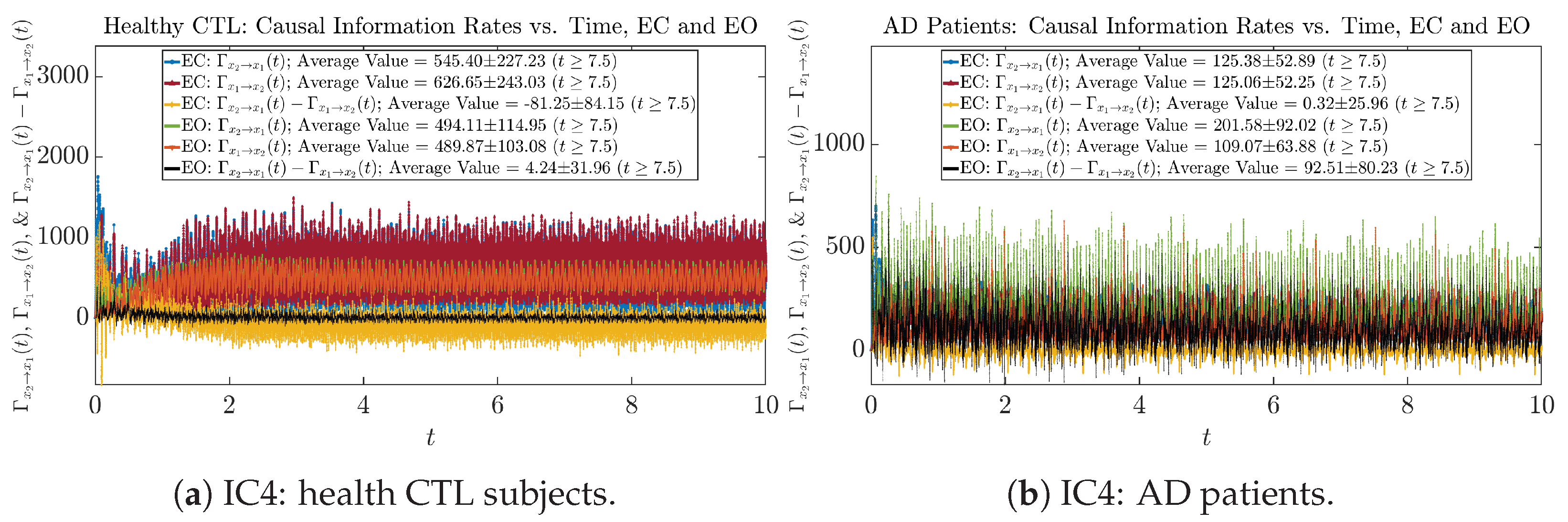
We performed simulations with six different Gaussian initial distributions (with different means and standard deviations summarized in Table 3). Initial Conditions No.1 (IC No.1, or simply IC1) through No.3 (IC3) are Gaussian distributions with a narrow width or smaller standard deviation, whereas IC4 through IC6 have a larger width/standard deviation, and therefore, the simulation results of IC4 through IC6 exhibit more diverse time evolution behaviors (e.g., more complex attractors, as explained next), and hence, the corresponding calculation results are more robust or insensitive to the specific mean values ’s of the initial Gaussian distributions (see Table 3 for more details). Therefore, in the main text here, we focus on these results from initial Gaussian distributions with wider width/larger standard deviation, and we list complete results from all six initial Gaussian distributions in the Appendix B. Specifically, we found that the results from IC4 through IC6 are qualitatively the same or very similar, and therefore, in the main text here, we illustrate and discuss the results from Initial Conditions No.4 (IC4), which is sufficiently representative for IC5 and IC6, and refer to other IC’s (by referencing the relevant sections in Appendix B or explicitly illustrating the results) if needed.
3.1. Sample Trajectories of and
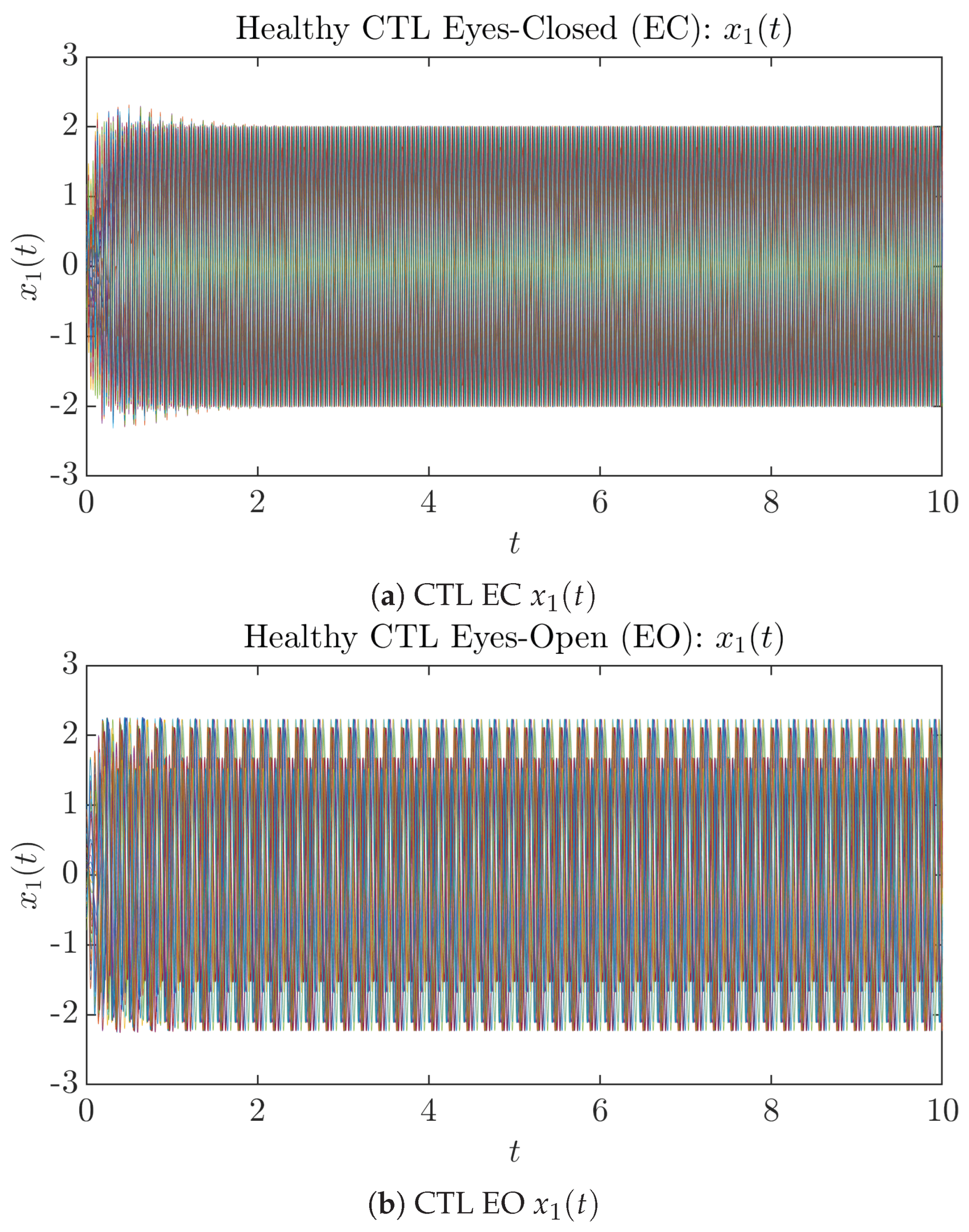
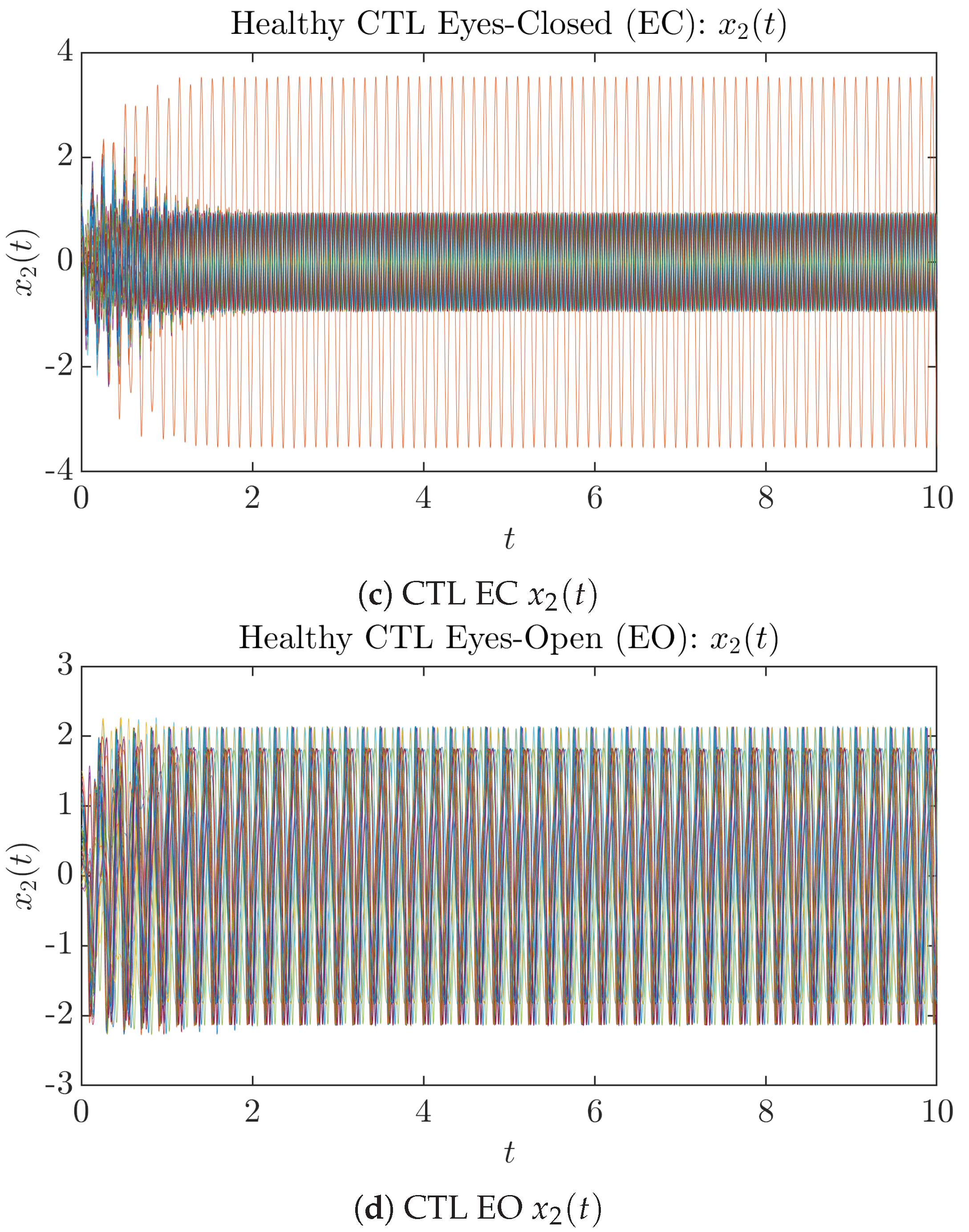
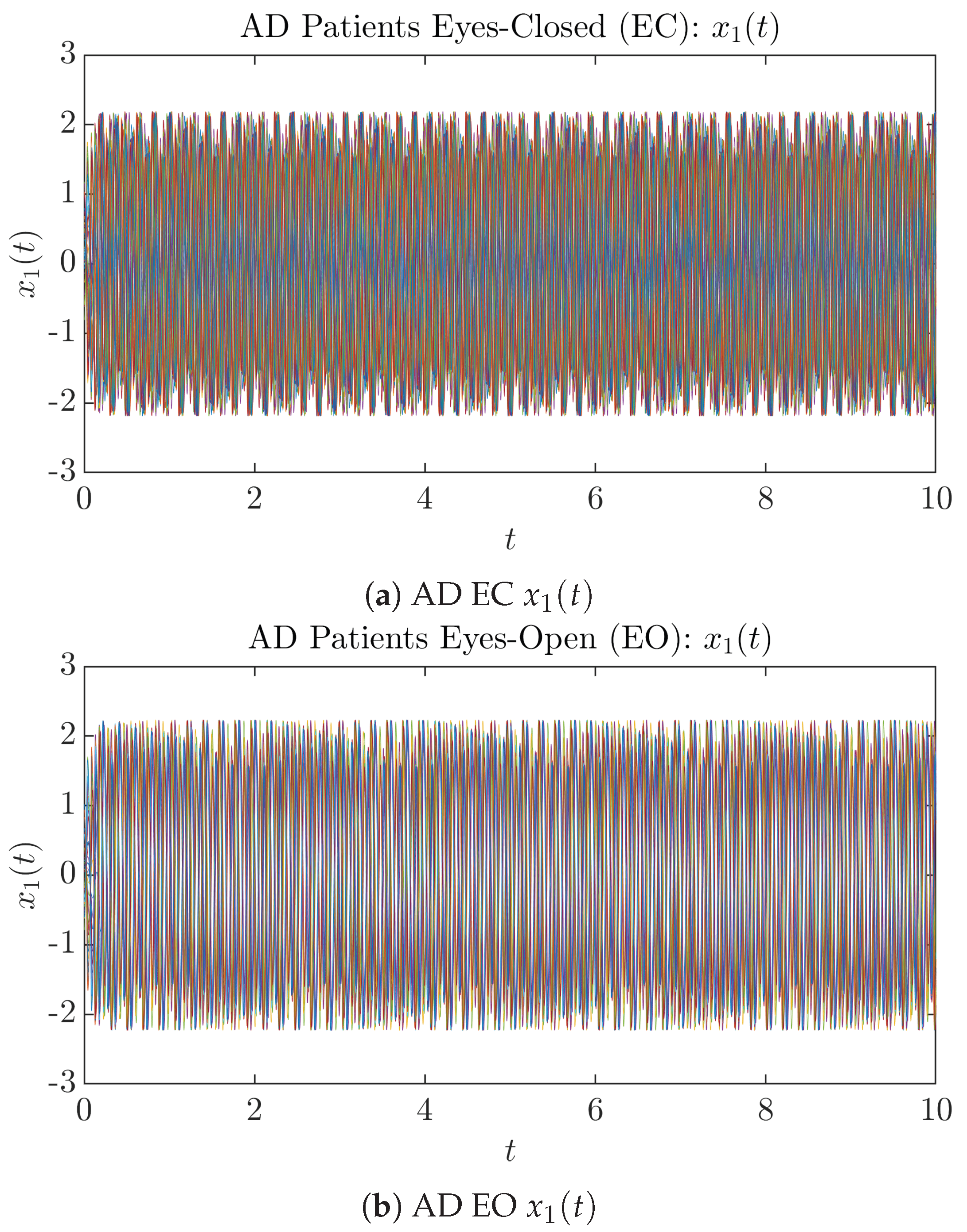
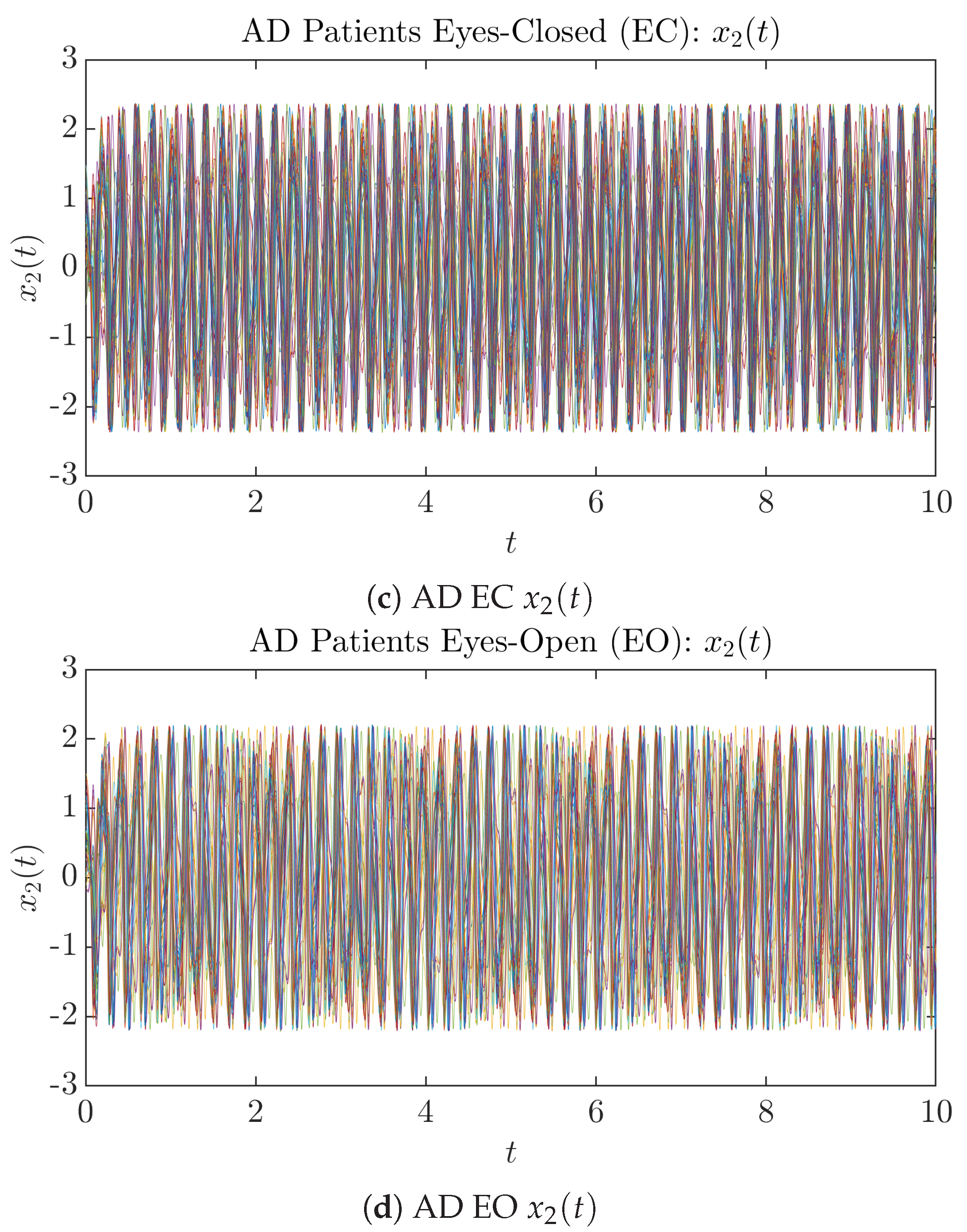
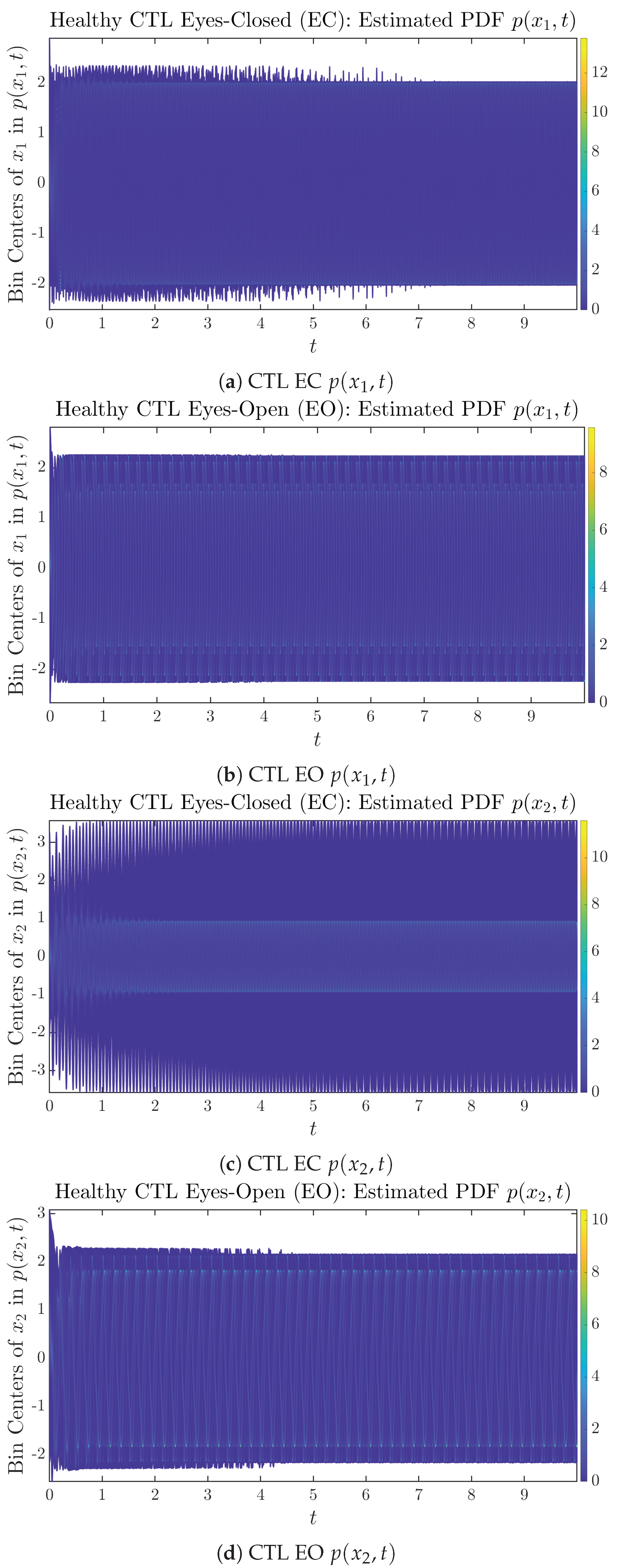
To give a basic idea of how the simulated trajectories evolve in time, we start by illustrating 50 sample trajectories of and from the total simulated trajectories for both CTL subjects and AD patients with both EC and EO conditions, which are visualized in Figure 1 and Figure 2. Notice that from Figure 1c, one can see that it takes some time for the trajectories of to settle down on some complex attractors for EC, which suggests a longer memory associated with EC of CTL. This is more evident as shown in the time evolution of PDF in Figure 3c below.
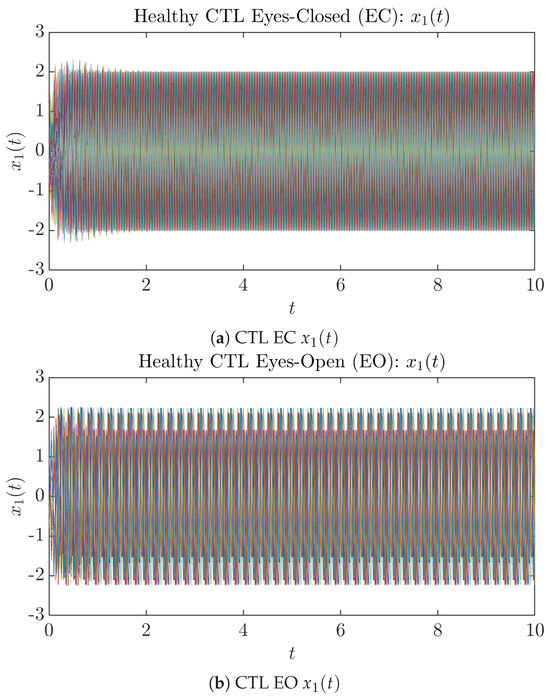
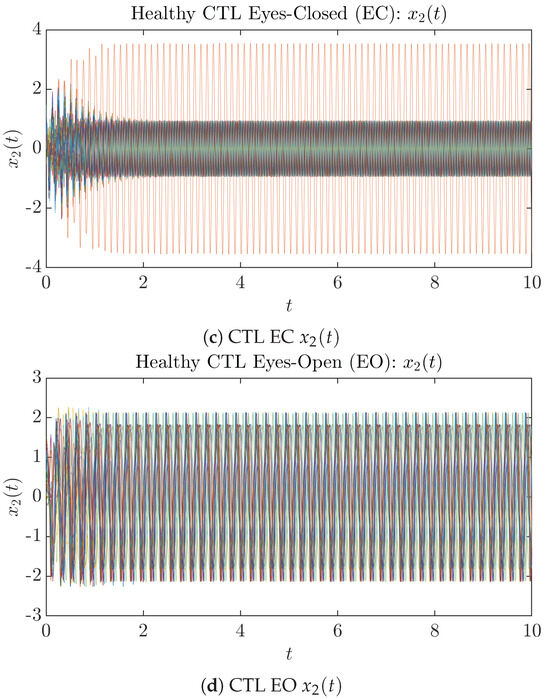
Figure 1.
Fifty Sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure 2.
Fifty Sample trajectories of AD patients. Each single trajectory is labeled by a different color.
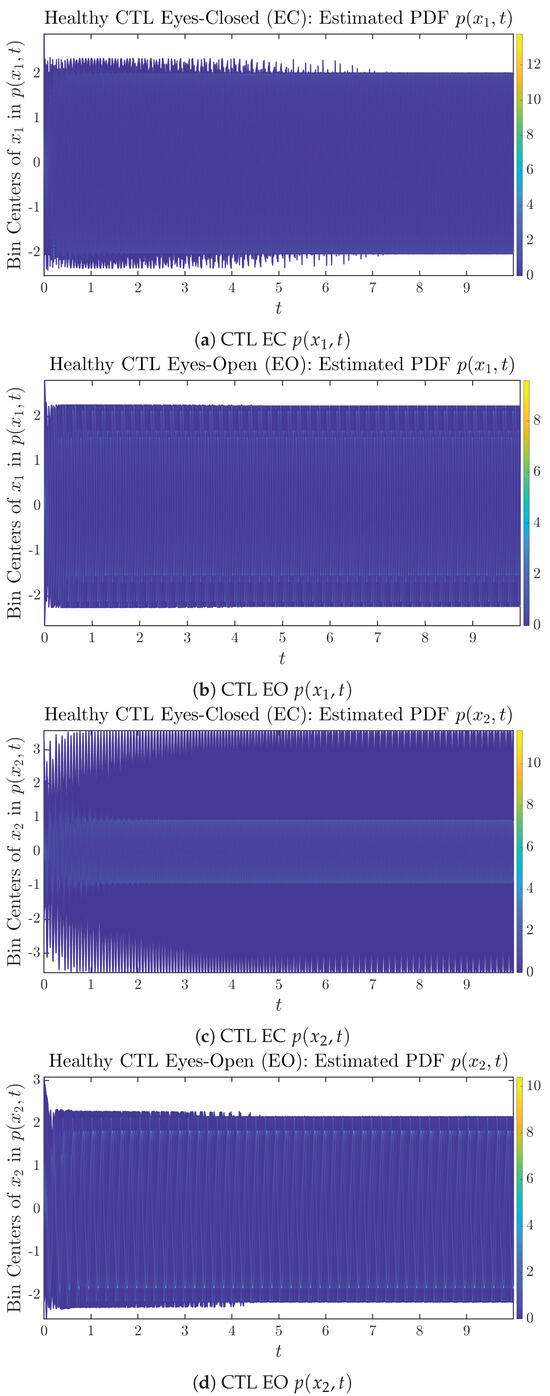
Figure 3.
Time evolution of estimated PDFs of healthy CTL subjects.
3.2. Time Evolution of PDF and
The empirical PDFs and can better illustrate the overall time evolution of a large number of trajectories, and they serve as a basis for calculations of information geometry theoretic measures such as information rates and causal information rates. These empirical PDFs are estimated using a histogram-based approach with Rice’s rule [35,36], where the number of bins is , and since we simulated sample trajectories in total, the is rounded to 542. The centers of bins are plotted on the y-axis in sub-figures of Figure 3 and Figure 4, where the function values of and are color-coded following the color bars.
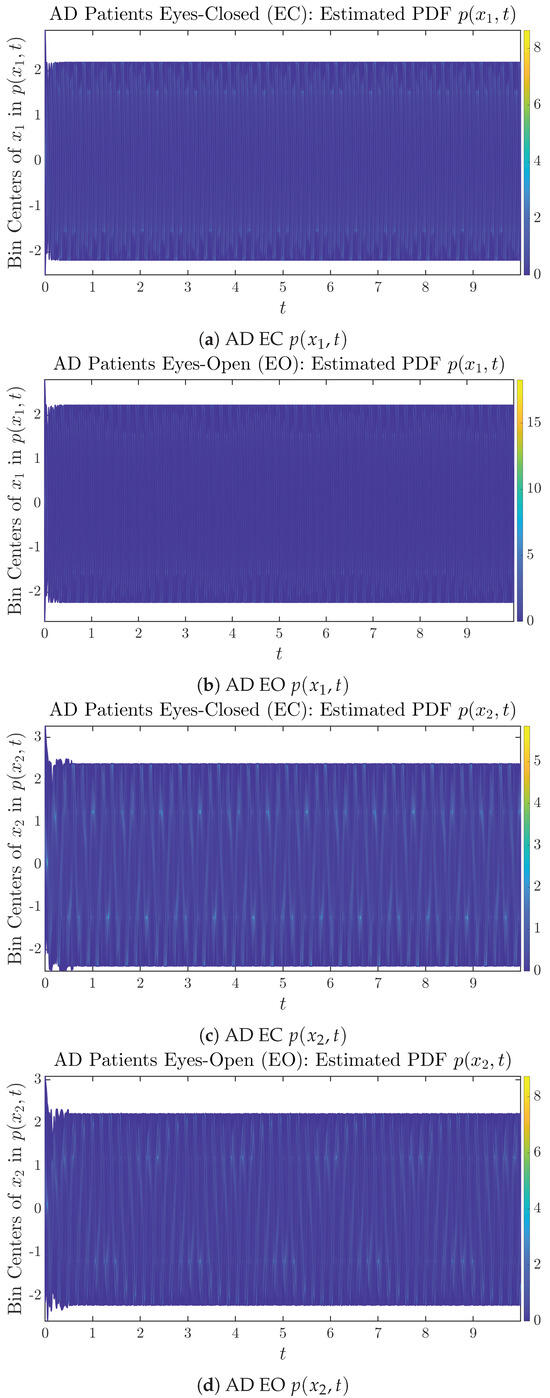
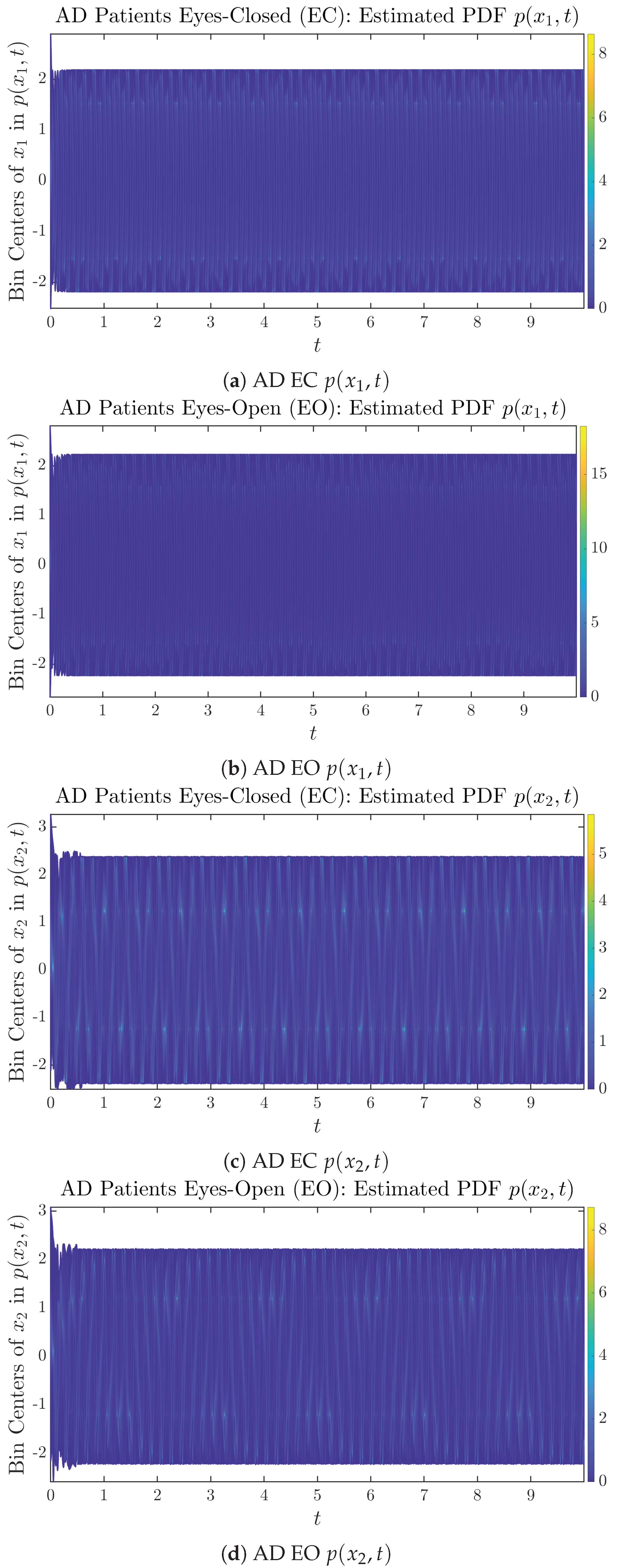
Figure 4.
Time evolution of estimated PDFs of AD patients.
As mentioned in the previous section, from Figure 3c, one can see more clearly that after around , the trajectories settle down on some complex attractors, and the time evolution of undergoes only minor changes. Meanwhile, from Figure 3a, one can observe that a similar settling down of on some complex attractors happens after around . Therefore, we select only PDFs with for statistical analysis of information rates and causal information rates to investigate the stationary properties.
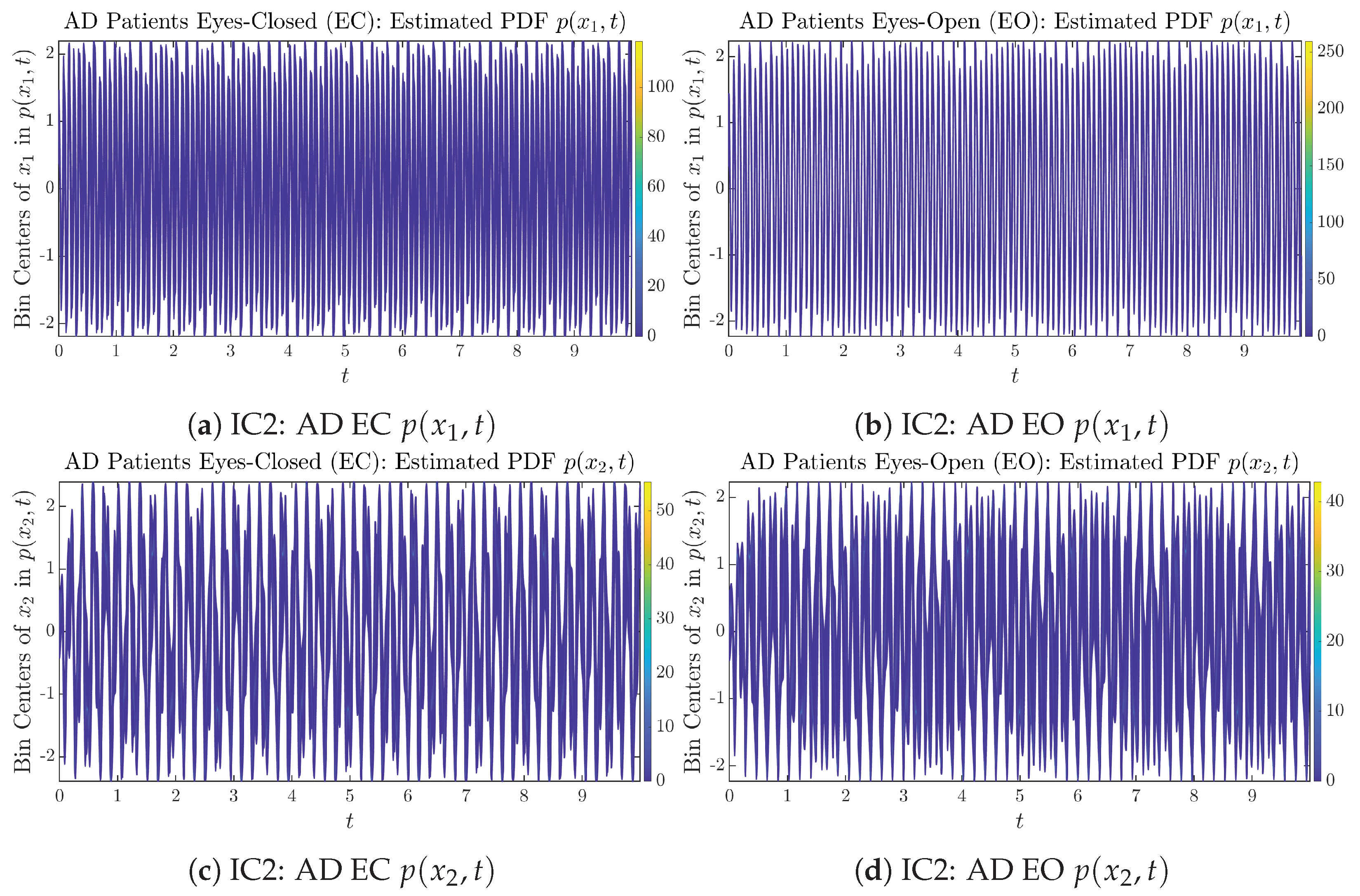
From Figure 3 and Figure 4, one can already observe some qualitative differences between healthy control (CTL) subjects and AD patients. For example, the time evolution patterns of and are significantly different when CTL subjects open their eyes from eyes-closed (EC) state, whereas for AD patients, these differences are relatively minor. One of the best ways to provide quantitative descriptions of these differences (instead of being limited to qualitative descriptions) is using information geometry theoretic measures such as information rates and causal information rates, whose results are listed in Section 3.3 and Section 3.4, respectively.
As can be seen from Appendix B.2, IC1 through IC3 exhibit much simpler attractors than IC4 through IC6. Since the width/standard deviation of the initial Gaussian distributions of IC1 through IC3 is much smaller, they are more sensitive to the specific mean values ’s of the initial Gaussian distribution, and one can see that IC3’s time evolution behaviors of are somewhat qualitatively different from IC1 and IC2, whereas ’s time evolution behaviors of IC4 through IC6 are all qualitatively the same.
3.3. Information Rates and
Intuitively speaking, the information rate is the (instantaneous) speed of PDF’s motion on the statistical manifold, as each given PDF corresponds to a point on that manifold, and when the time changes, a time-dependent PDF will typically move on a curve on the statistical manifold, whereas a stationary or equilibrium state PDF will remain at the same point on the manifold. Therefore, the information rate is a natural tool to investigate the time evolution of PDF.
Moreover, since the information rate is quantifying instantaneous rate of change in the infinitesimal relative entropy between two adjacent PDFs, it is hypothetically a reflection of neural information processing in the brain, and hence, it may provide important insight into the neural activities in different regions of the brain, as long as the regional EEG signals can be sufficiently collected for calculating the information rates.
3.3.1. Time Evolution
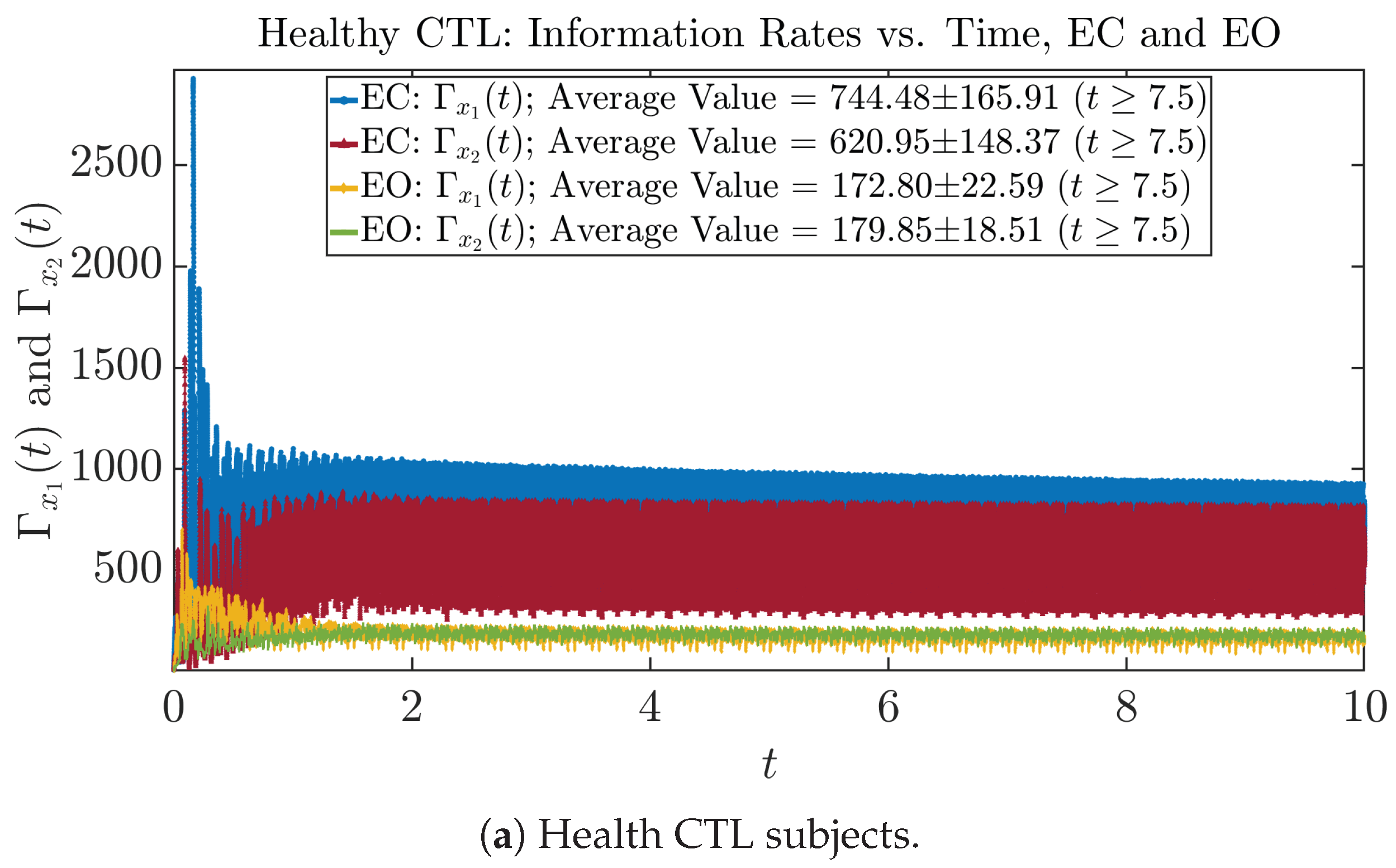
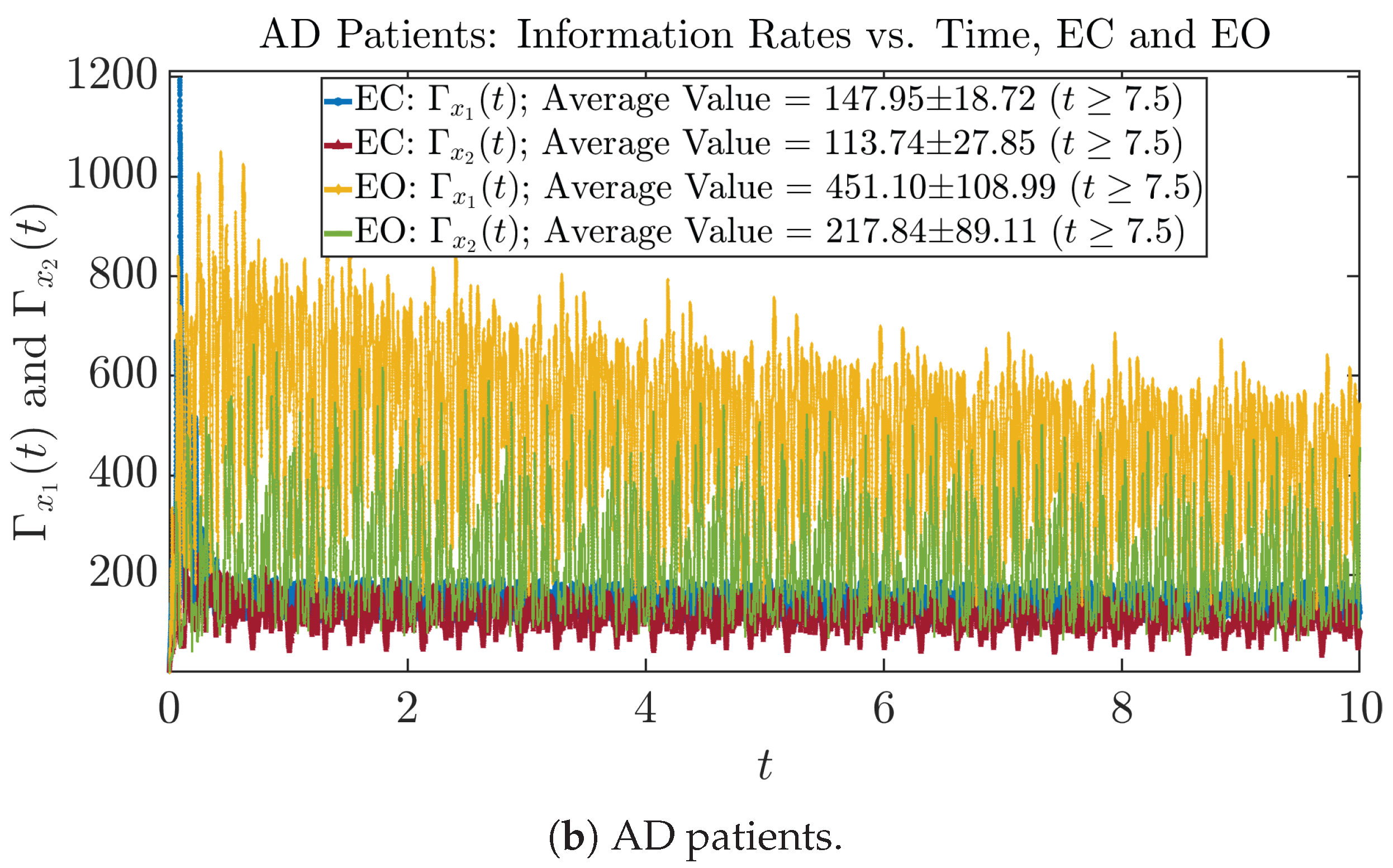
The time evolution of information rates and are shown in Figure 5a,b for CTL subjects and AD patients, respectively. Since and quantify the (infinitesimal) relative entropy production rate instantaneously at time t, they represent the information-theoretic complexities of signals and of the coupled oscillators, respectively, and are hypothetical reflections of neural information processing in the corresponding regions in the brain.
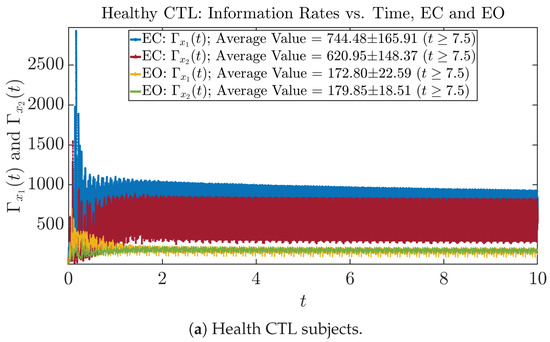
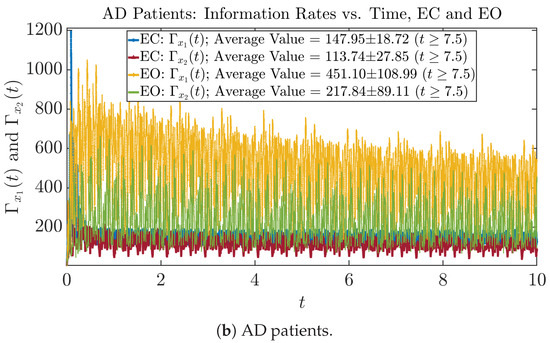
Figure 5.
Information rates along time of CTL and AD subjects.
For example, in Figure 5a, there is a clear distinction between eyes-closed (EC) and eyes-open (EO) for CTL subjects: both and decrease significantly when healthy subjects open their eyes, which may be interpreted as the neural information processing activities of the corresponding brain regions being “suppressed” by the incoming visual information when eyes are opened from being closed.
Interestingly, when AD patients open their eyes, both and are increasing instead of decreasing, as shown in Figure 5b. This might be interpreted as that the incoming visual information received when eyes are opened is in fact “stimulating” the neural information processing activities of the corresponding brain regions, which might be impaired or damaged by the relevant mechanism of Alzheimer’s disease (AD).
In Figure 5a,b, we annotate the mean and standard deviation for and after in the legend, because as mentioned above, the PDFs of this time range reflect longer-term temporal characteristics, and hence, the corresponding and should reflect more reliable and robust features of neural information processing activities of the corresponding brain regions. Therefore, meaningful statistics will require collecting samples of and in this time range, for which the results are shown in the section below.
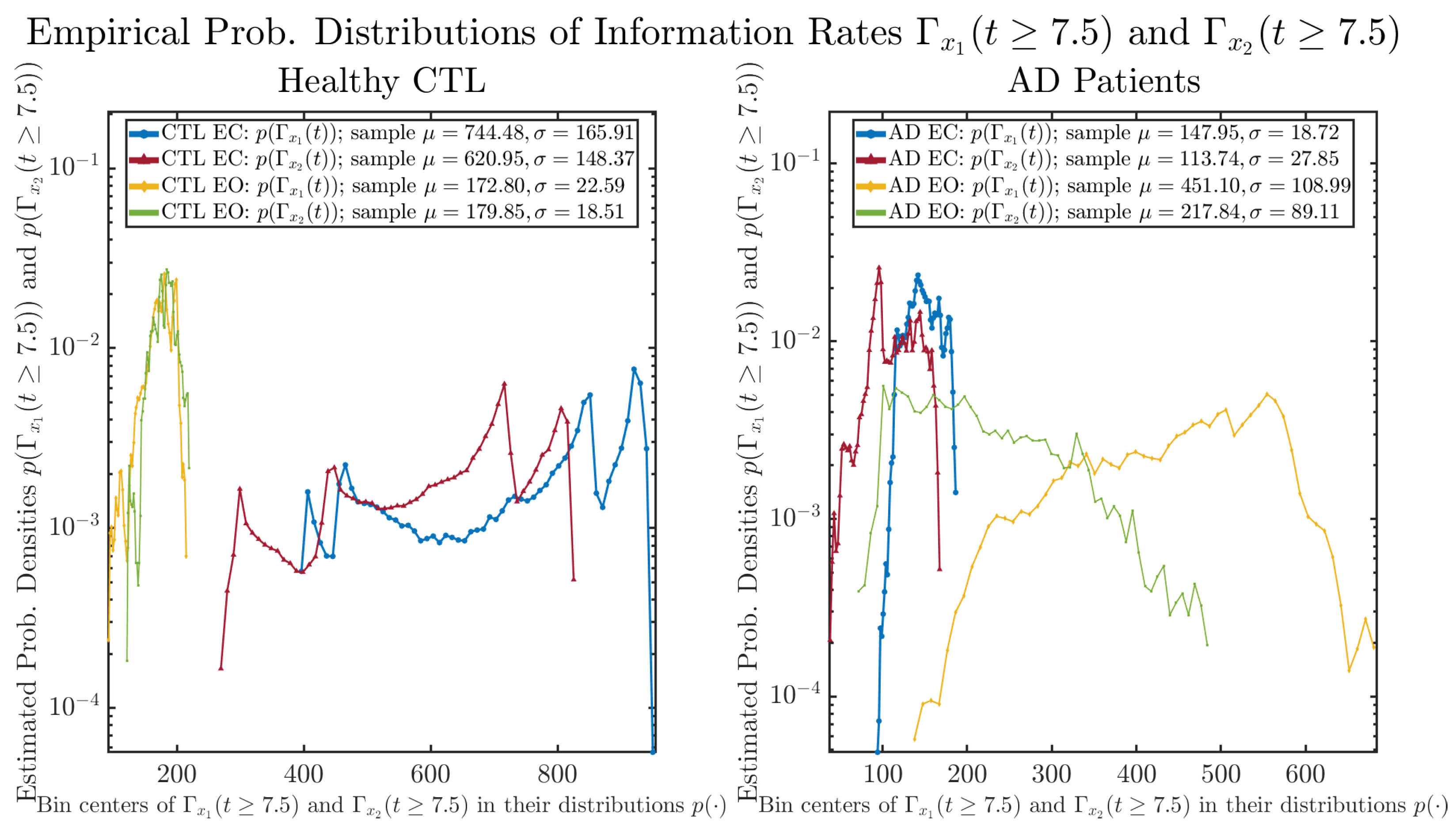
3.3.2. Empirical Probability Distribution (for )
The statistics of and can be further and better visualized using empirical probability distributions of them, as shown in Figure 6. Again, we use histogram-based density estimation with Rice’s rule, and since the time interval for estimating PDFs and computing and is (whereas the time-step size for simulating the SDE model is ), we collected 24,999 samples of both and for , and hence, the number of bins following Rice’s rule is rounded to 58. Figure 6 confirms the observation in the previous section, while it also better visualizes the sample standard deviation in the shapes of the estimated PDFs, indicating that the PDFs of both and are narrowed down when healthy subjects open their eyes but are widened when AD patients do so.
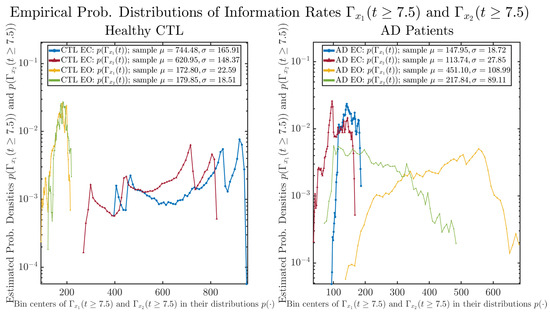
Figure 6.
Empirical probability distributions of information rates and .
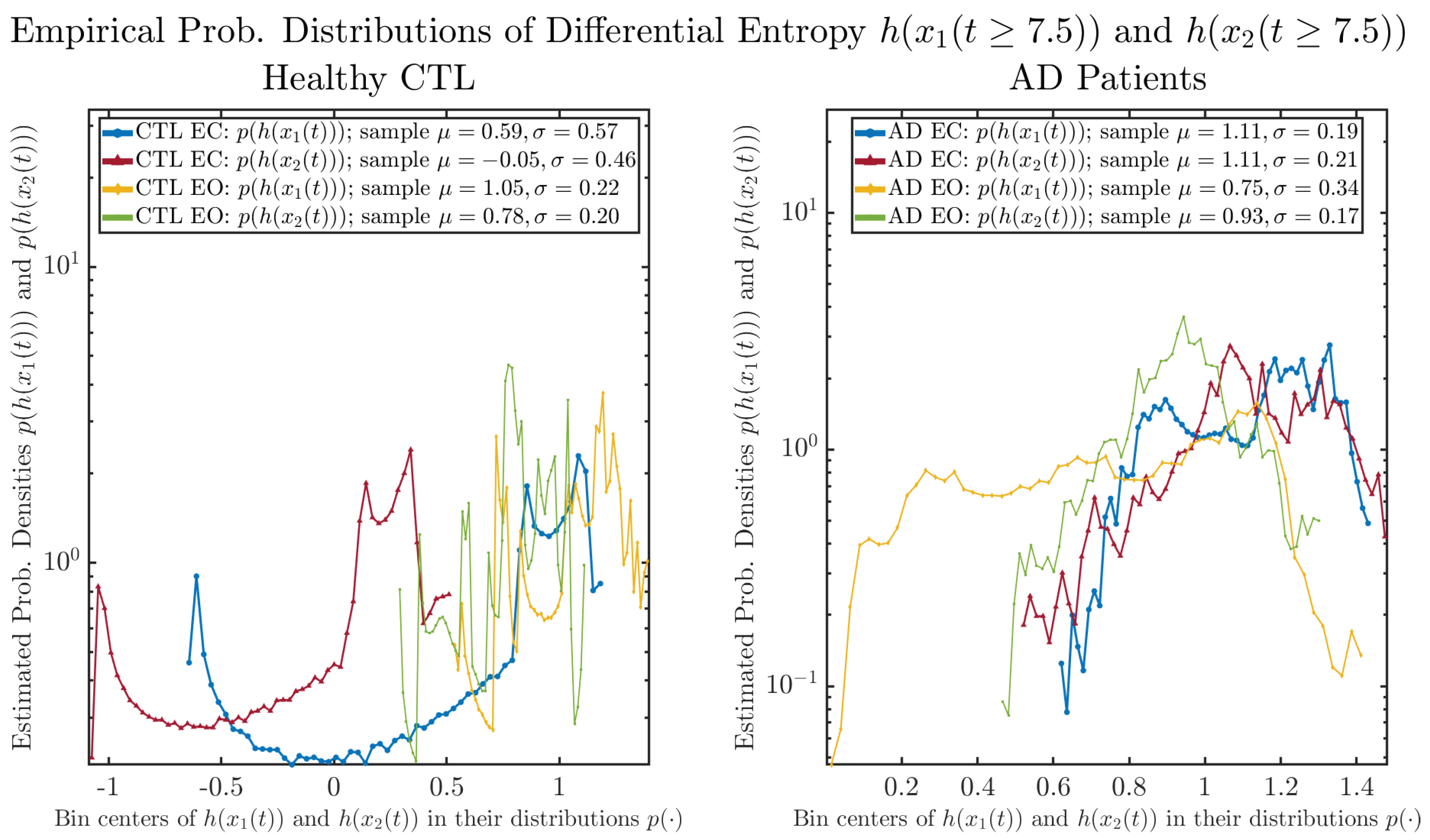
As a comparison, we also calculate more traditional/established information-theoretic measure, namely, the Shannon differential entropy and , and estimate their empirical probability distributions in the same manner as we do for information rates, as shown in Figure 7.
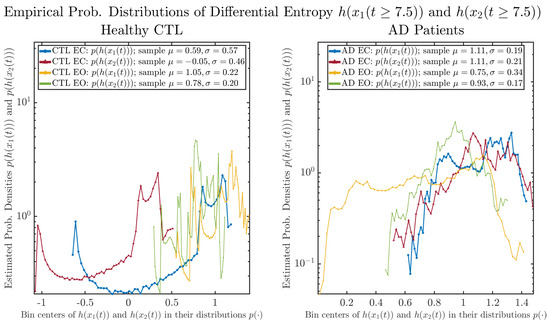
Figure 7.
Empirical probability distributions of differential entropy and .
One can see that the empirical distributions of differential entropy and are not able to make clear distinction between EC and EO conditions, especially for AD patients. This may be better summarized in Table 4, comparing the mean and standard deviation values of information rate vs. differential entropy for the four cases. Therefore, the information rate is a superior measure for quantifying the non-stationary time-varying dynamical changes in EEG signals when switching between EC and EO states and is a better and more reliable reflection of neural information processing in the brain.

Table 4.
Mean and standard deviation values () of information rates & vs. differential entropy & .
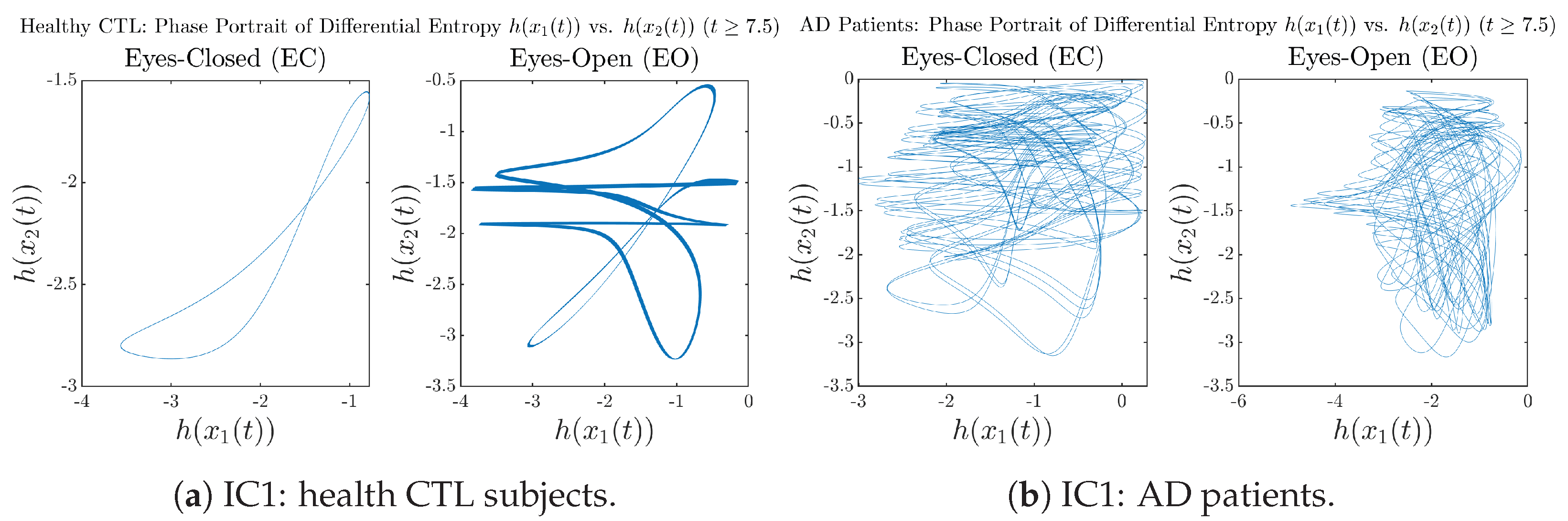
3.3.3. Phase Portraits (for )
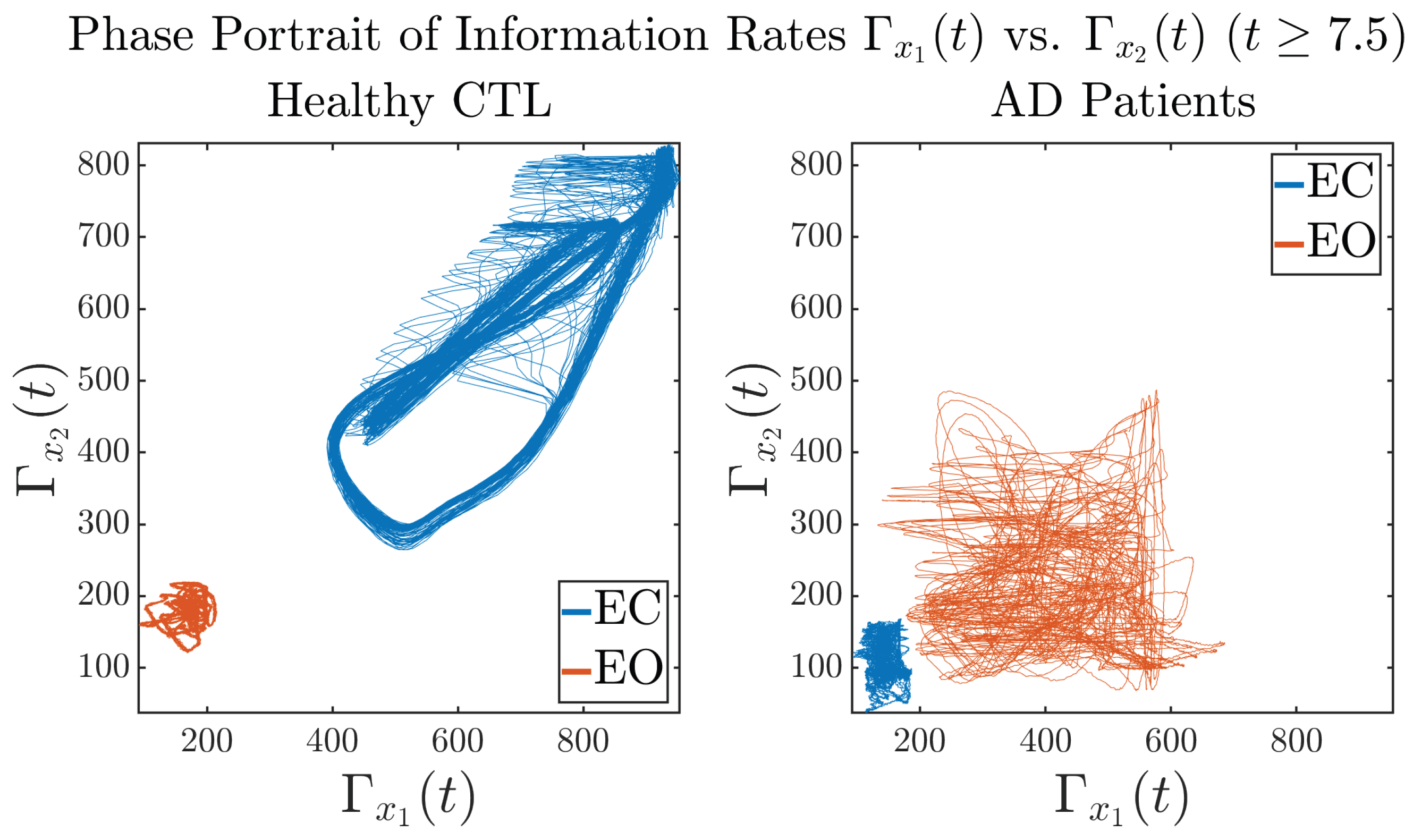
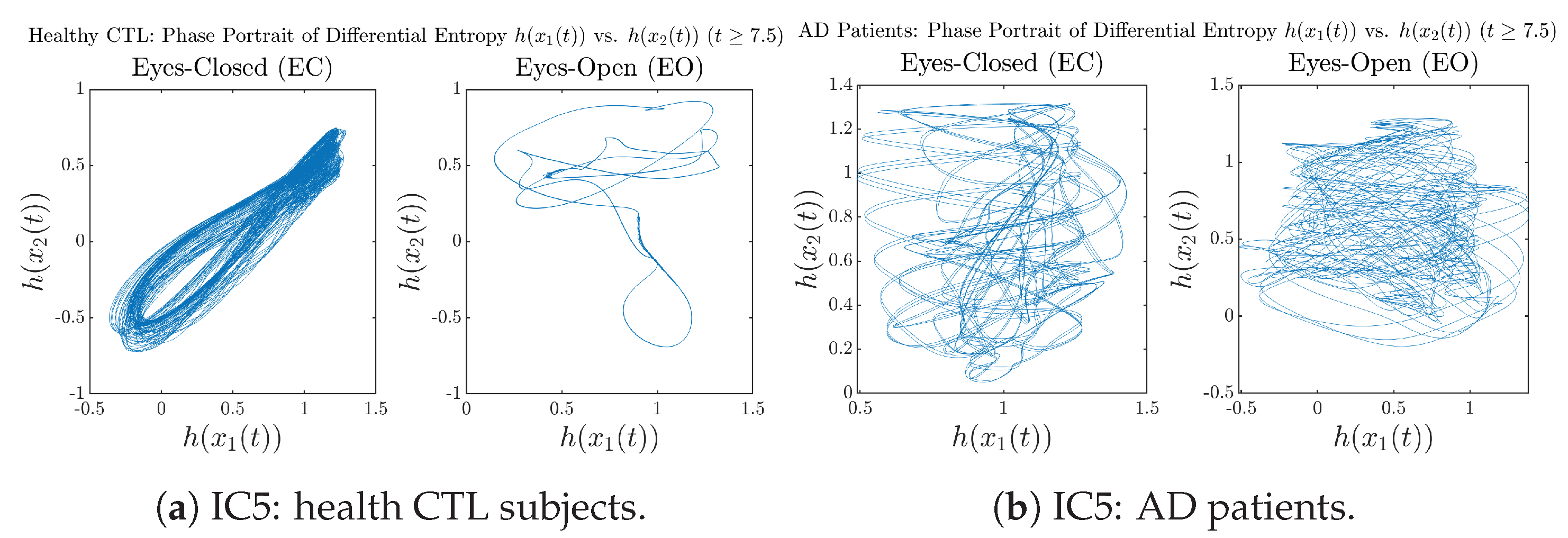
In addition to empirical statistics of information rates for in terms of estimated probability distributions, one can also visualize the temporal dynamical features of and combined using phase portraits, as shown in Figure 8. Notice that when healthy subjects open their eyes, the fluctuation ranges of and shrink by roughly 5-fold, whereas when AD patients open their eyes, the fluctuation ranges are enlarged.
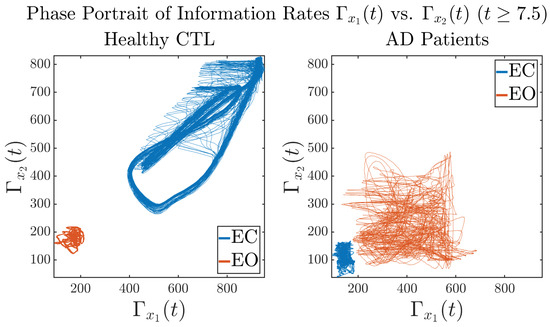
Figure 8.
Phase portraits of information rates vs. .
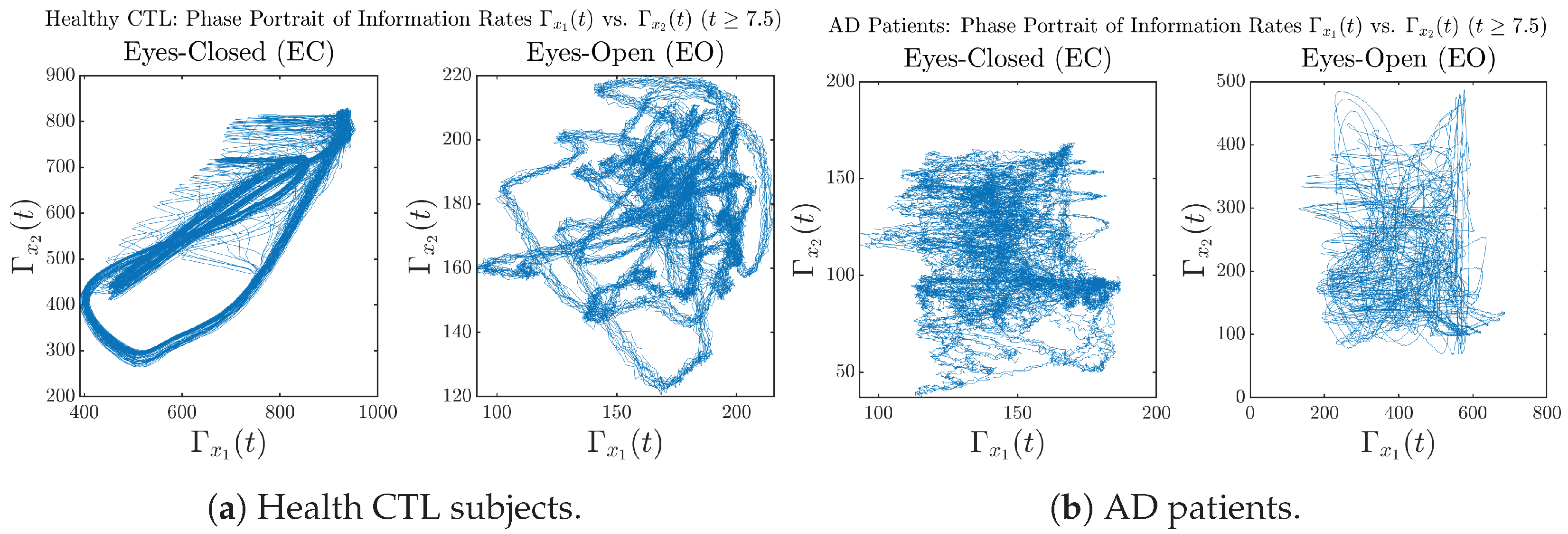
Moreover, when plotting EC and EO of healthy subjects separately in Figure 9a to zoom into the ranges of and for EO, one can also see that the phase portrait of EO exhibits a fractal-like pattern, whereas the phase portrait of EC exhibits more regular dynamical features, including an overall trend of fluctuating between bottom left and top right, indicating that the and are somewhat synchronized, which could be explained by the strong coupling coefficients in Table 1 of healthy subjects. Contrarily, for AD patients, the phase portraits of EC and EO both exhibit fractal-like patterns in Figure 9b.
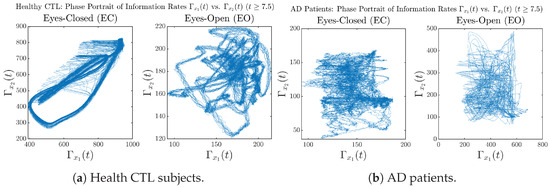
Figure 9.
Phase portraits of information rates vs. of CTL and AD subjects.
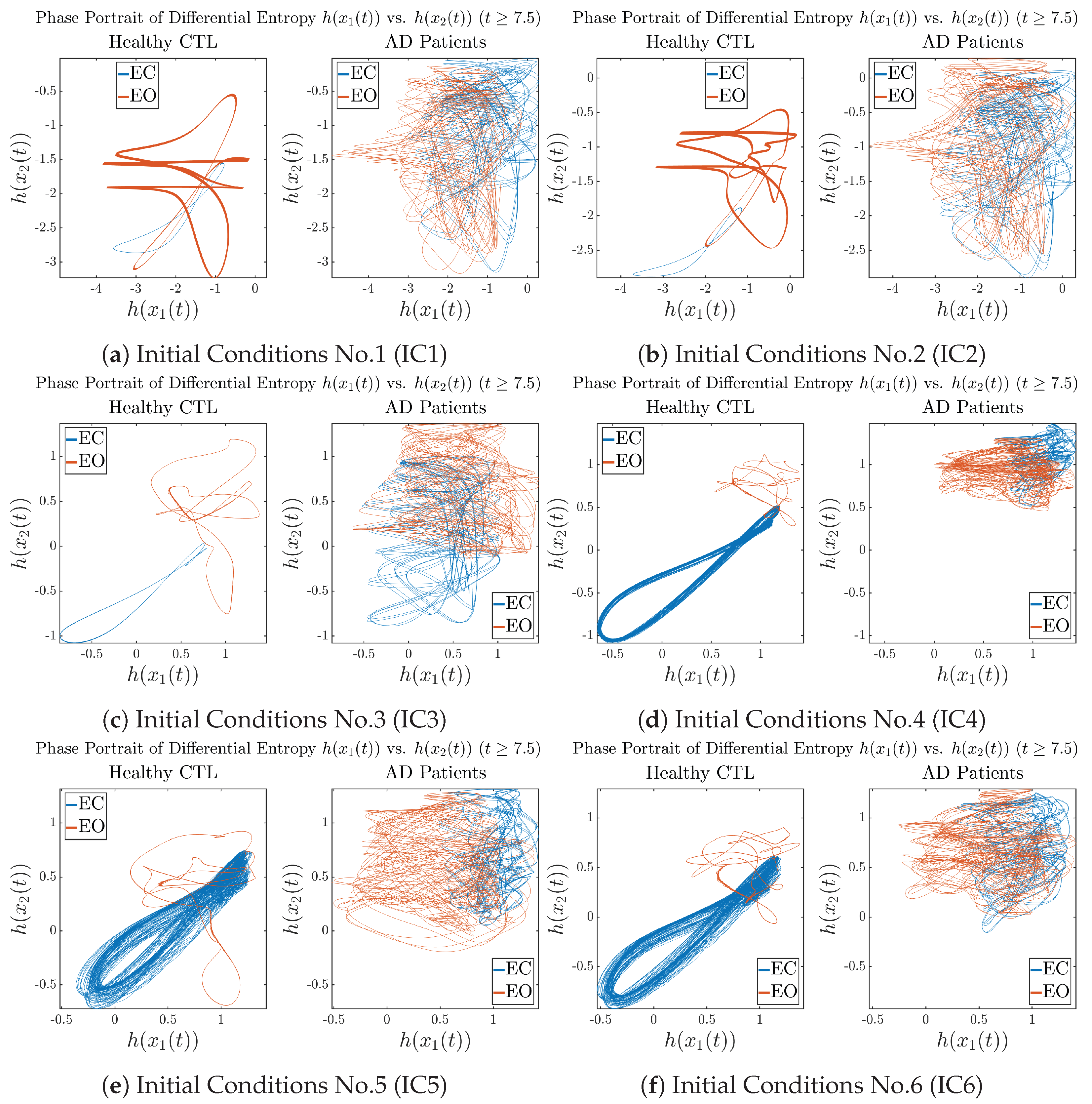
Same as at the end of Section 3.3.2, as a comparison, we also visualize the phase portraits of Shannon differential entropy and in Figure A52d and Figure A56 in Appendix B.4.3, where one can see that it is hard to distinguish the phase portraits of vs. of AD EC from those of AD EO, as they are qualitatively the same or very similar. Contrarily, in Figure 8, the fluctuation ranges of phase portraits of vs. are significantly enlarged when AD patients open their eyes. Therefore, this reconfirms our claim at the end of Section 3.3.2 that the information rate is a superior measure than differential entropy in quantifying the dynamical changes in EEG signals when switching between EO and EO states and is a better and more reliable reflection of neural information processing in the brain.
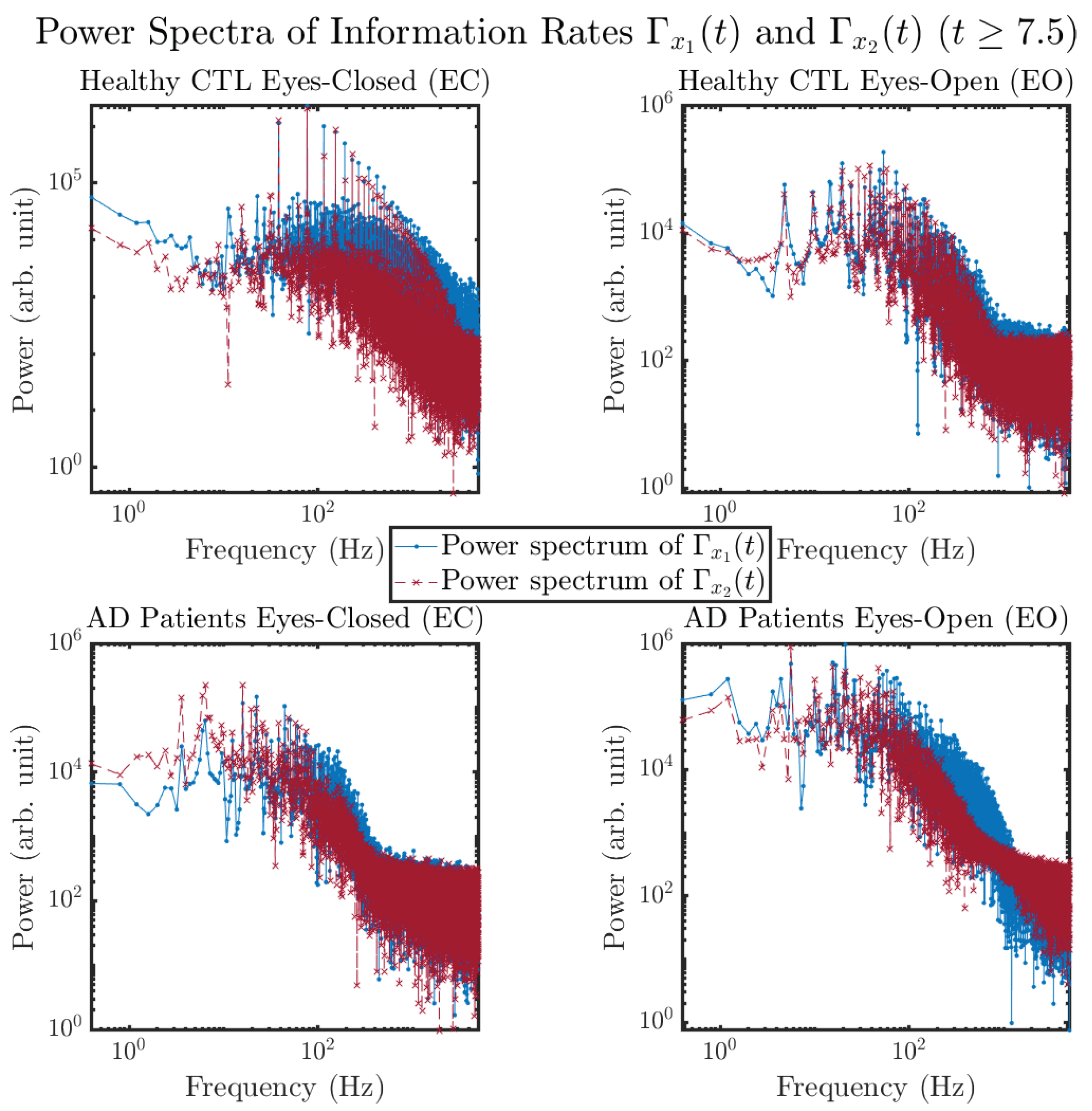
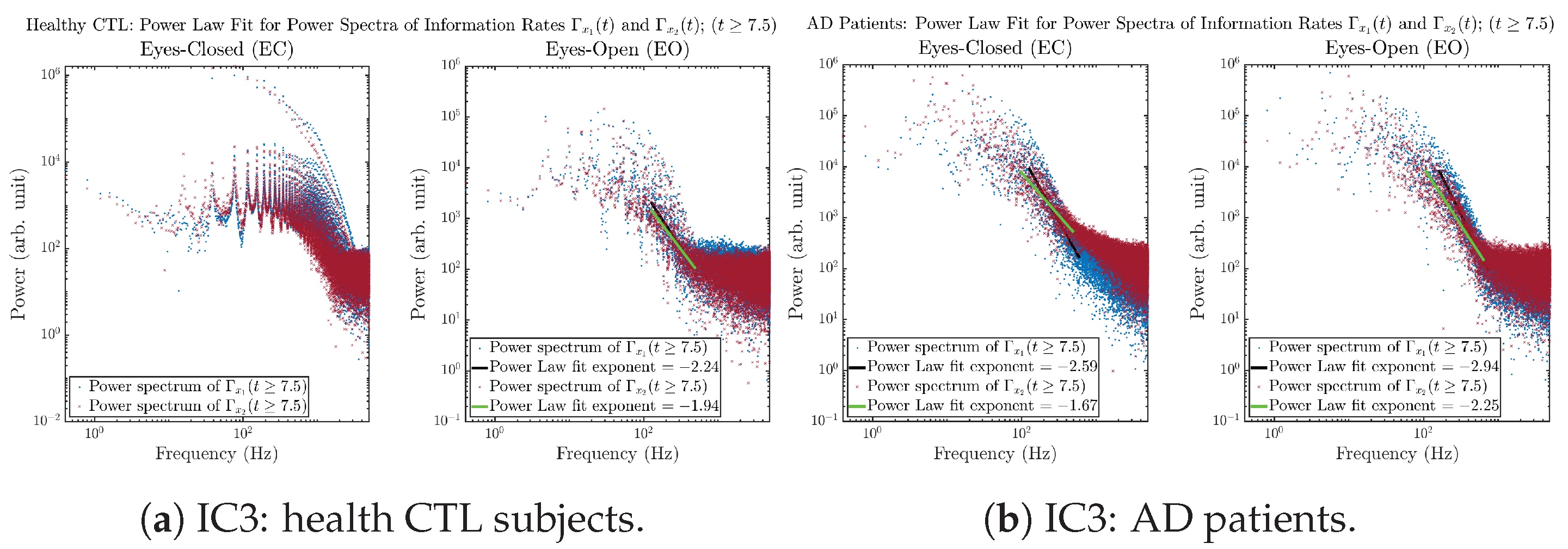
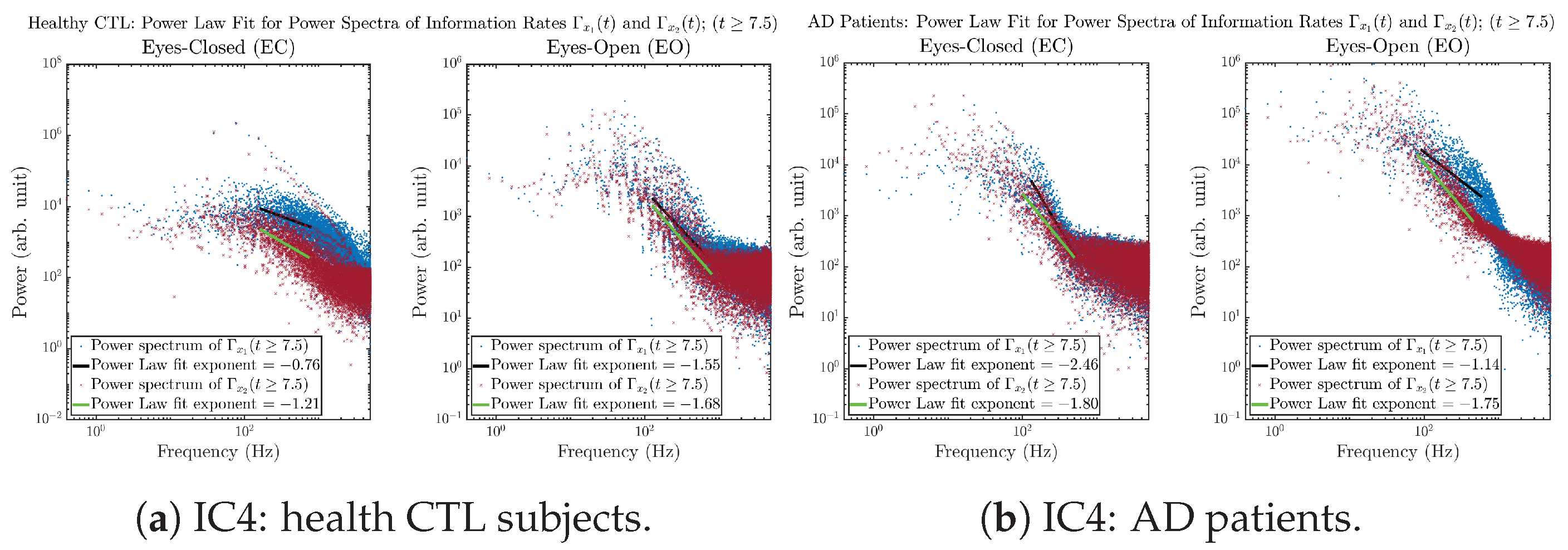
3.3.4. Power Spectra (for )
Another perspective to visualize the dynamical characteristics of and is by using power spectra, i.e., the absolute values of (fast) Fourier transforms of and , as shown in Figure 10. Frequency-based analyses will not make much sense if the signals or time series of and have non-stationary time-varying effects, and this is why we only consider time range for and , when the time evolution patterns of and almost stop changing as shown in Figure 3 (and especially in Figure 3a,c).
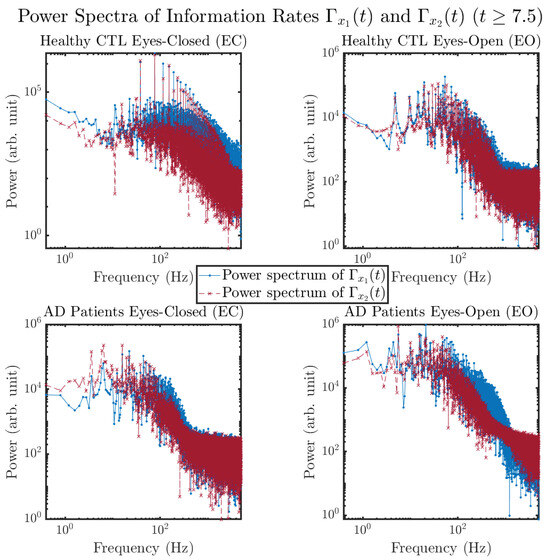
Figure 10.
Power spectra of information rates and .
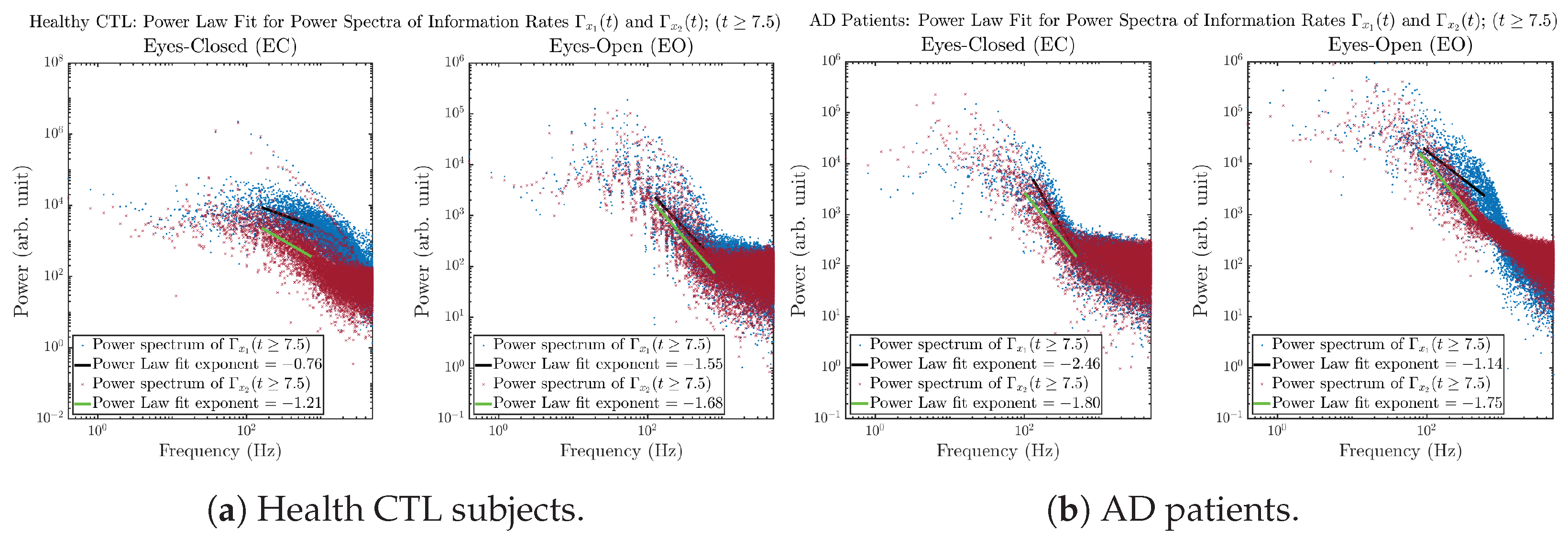
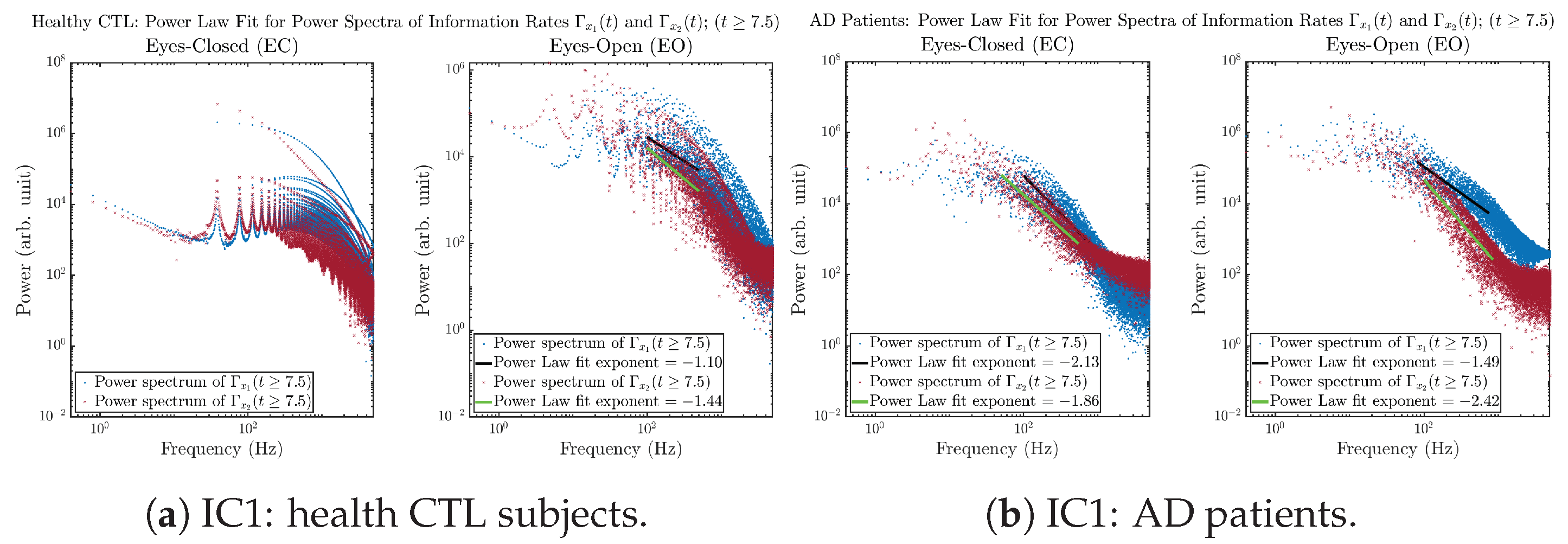
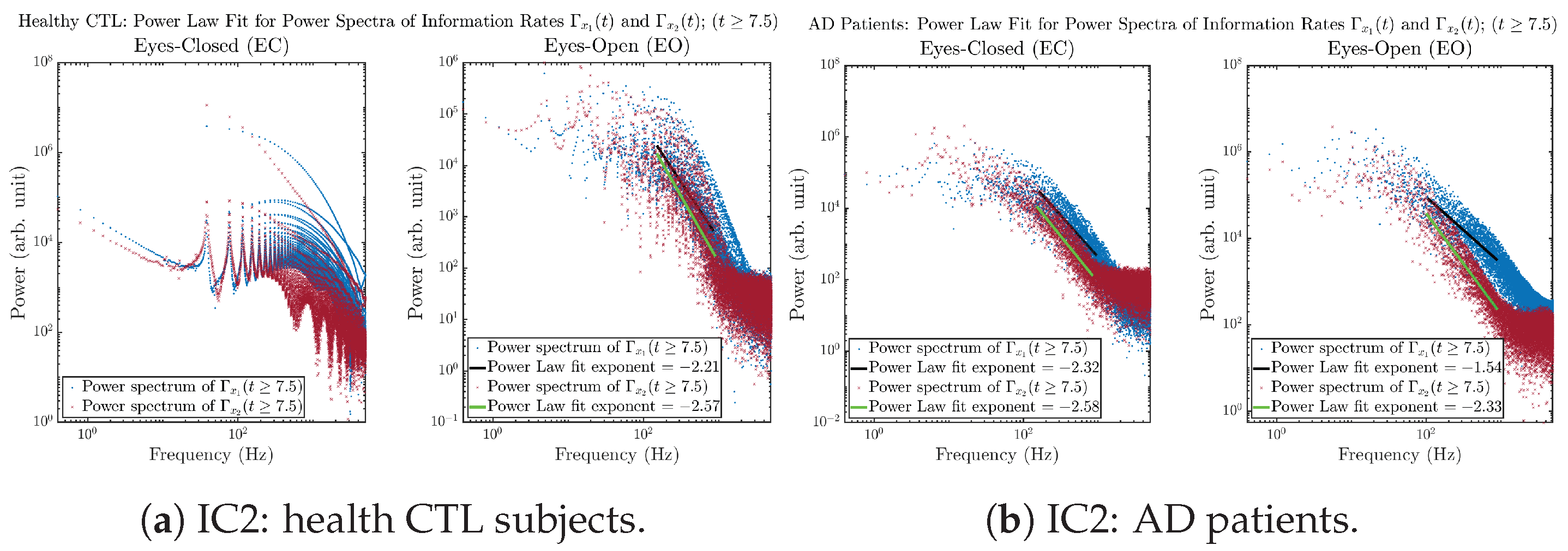
The power spectra of and also exhibit a clear distinction between EC and EO for CTL and AD subjects. Specifically, the power spectra of and can be fit by power law for frequencies between ∼100 Hz to ∼1000 Hz (the typical sampling frequency of experimental EEG signals is 1000 Hz, whereas most of brain wave’s/neural oscillations’ frequencies are below 100 Hz). From Figure 11a, one can see that power law fit exponents (quantifying how fast the power density decreases with increasing frequency) of ’s and ’s power spectra are largely reduced when healthy subjects open their eyes, which indicates that the strength of noise in and decreases significantly when switching from EC to EO. Contrarily, for AD patients as shown in Figure 11b, the power law fit exponents of ’s and ’s power spectra increase significantly and slightly, respectively, indicating that the strength of noise in and increases when switching from EC to EO.
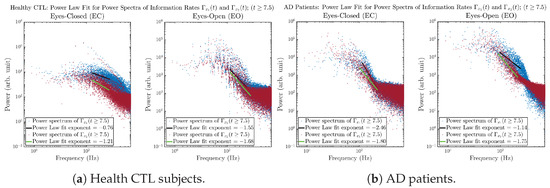
Figure 11.
Power law fit for power spectra of information rates and of CTL and AD subjects.
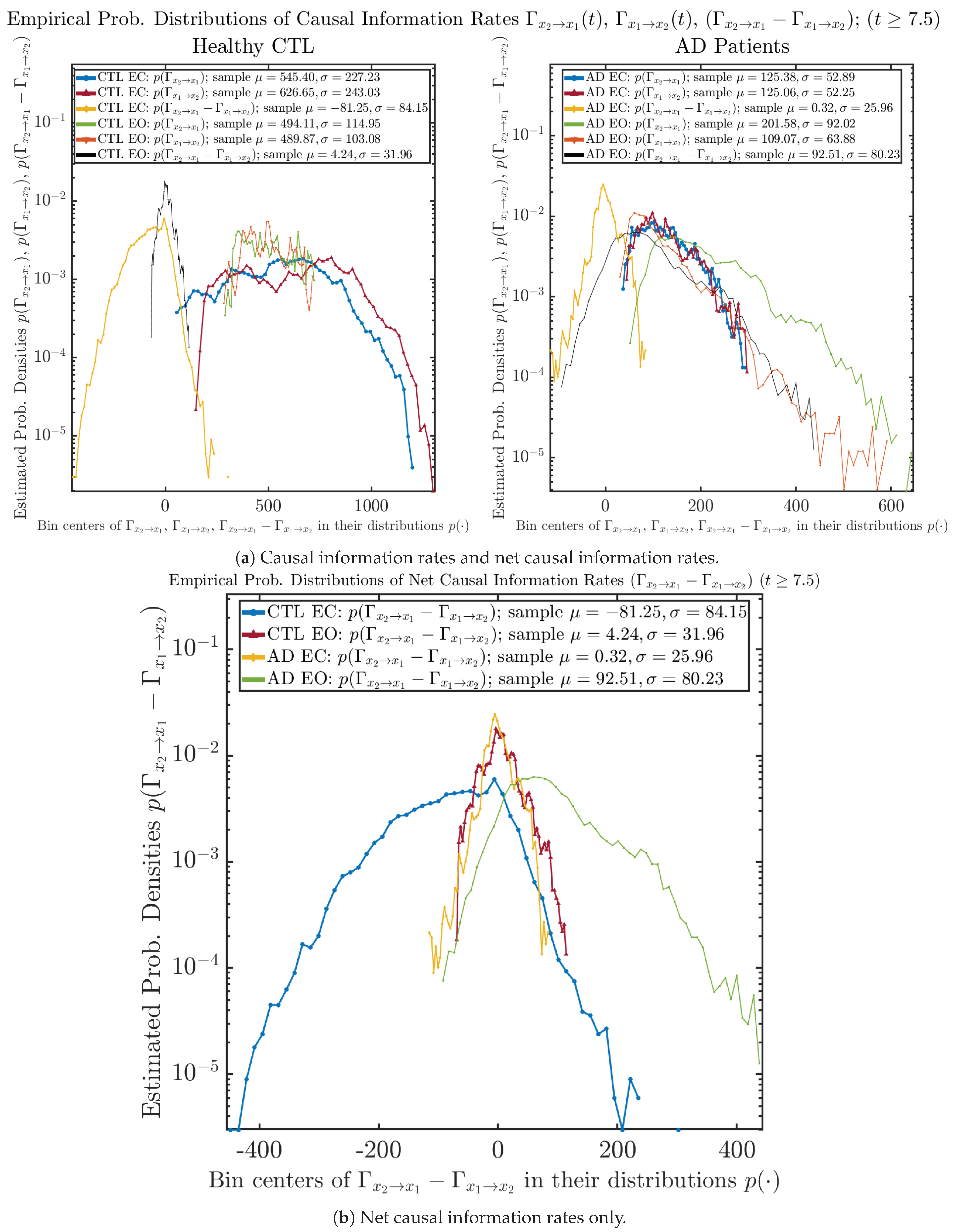
3.4. Causal Information Rates , and Net Causal Information Rates
The notion of causal information rate was introduced in Ref. [25], which quantifies how one signal instantaneously influences another signal’s information rate. A comparable measure of causality is transfer entropy; however, as shown in Appendix B.6, our calculation results of transfer entropy are too spiky/noisy to reliably quantify causality, and hence, the results are only included in Appendix as a comparison, which we will discuss at the end of this section. Nevertheless, similar to net transfer entropy, one can calculate the net causal information rate, e.g., , signifying the net causality measure from signal to . Since is the only variable that is directly affected by random noise in the stochastic oscillator model Equation (2), we calculate for the net causal information rate of the coupled oscillator’s signal influencing .
Notice that for stochastic coupled oscillator model Equation (2), causal information rates and will reflect how strongly the two oscillators are directionally coupled or causally related. Since signals and are the results of neural activities in the corresponding brain regions, the causal information rates can be used to measure connectivities among different regions of the brain.
3.4.1. Time Evolution
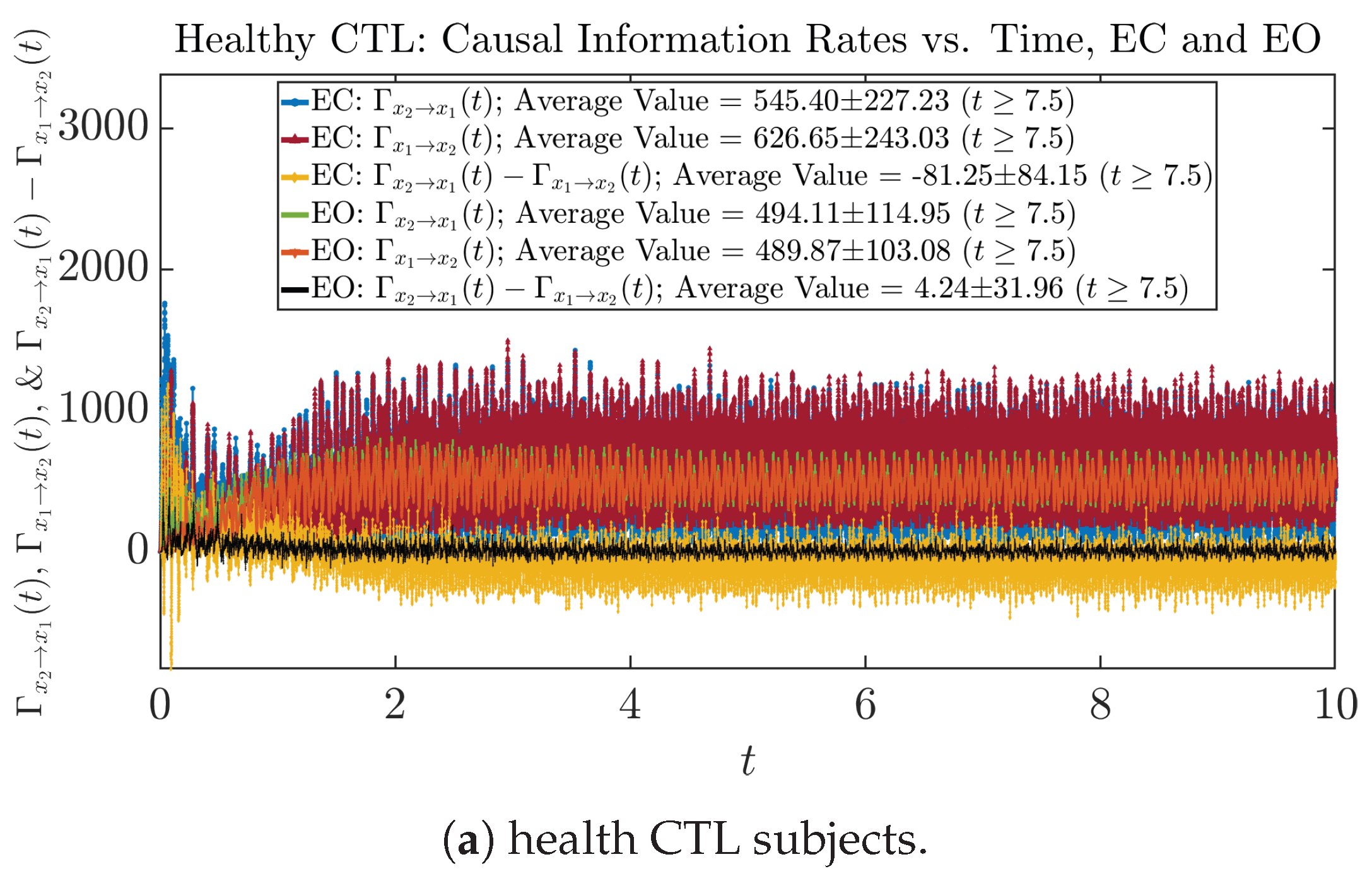
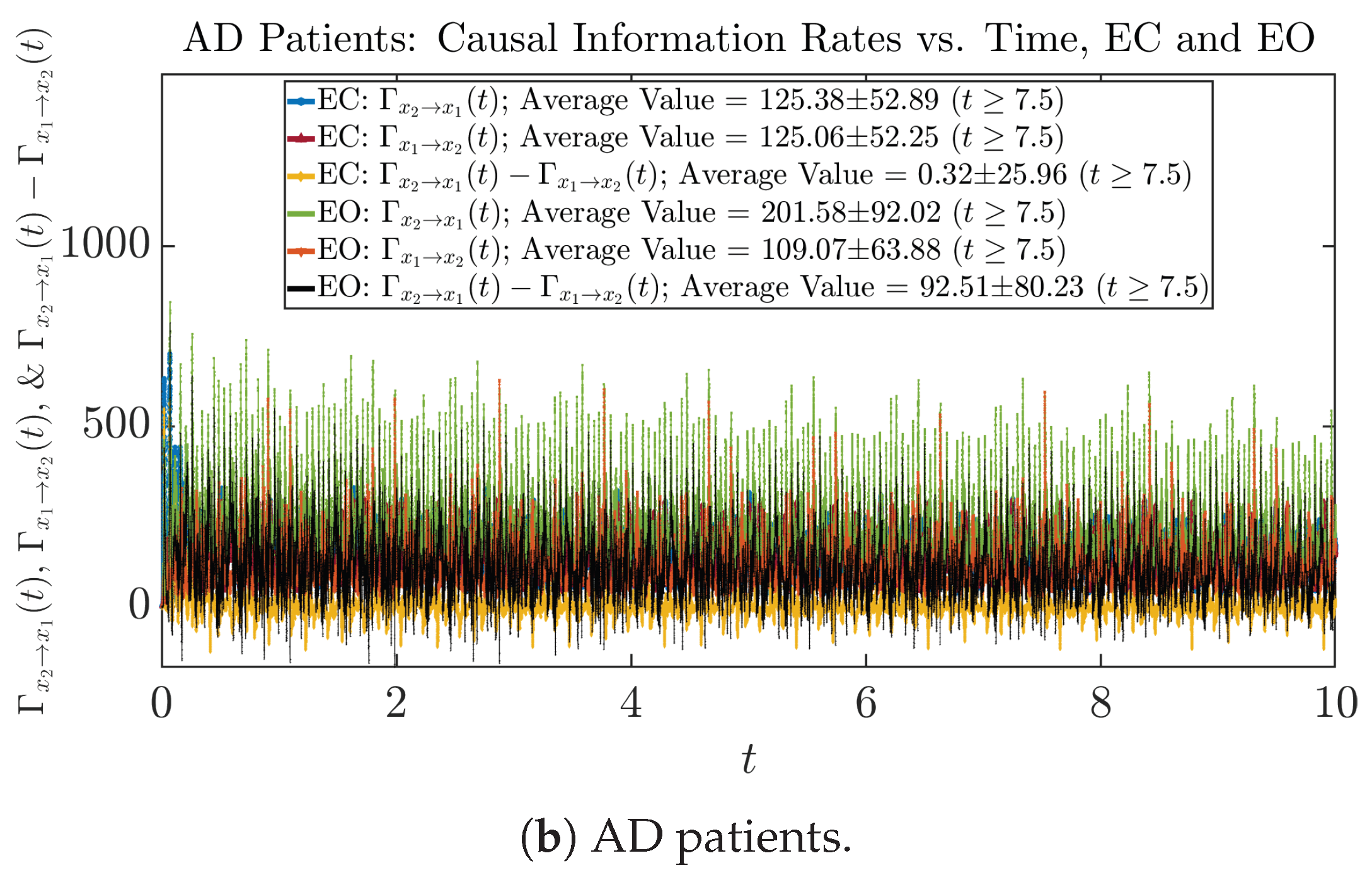
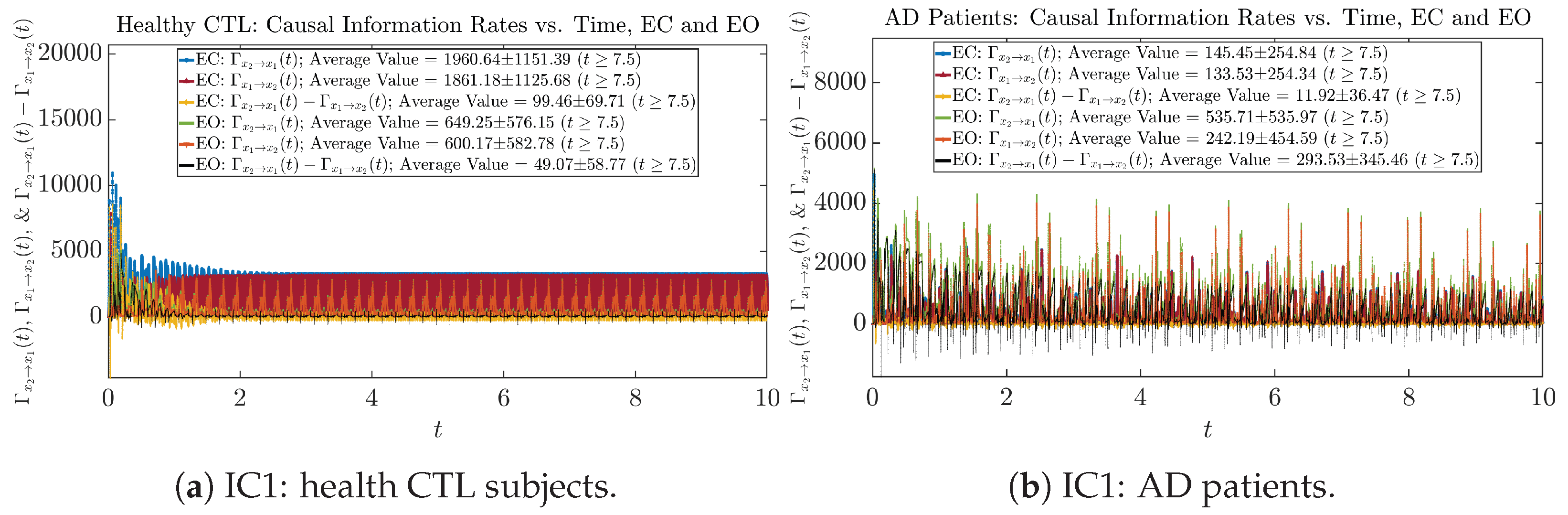
Similar to Section 3.3.1, we also visualize the time evolution of causal information rates and in Figure 12a,b for CTL subjects and AD patients, respectively.
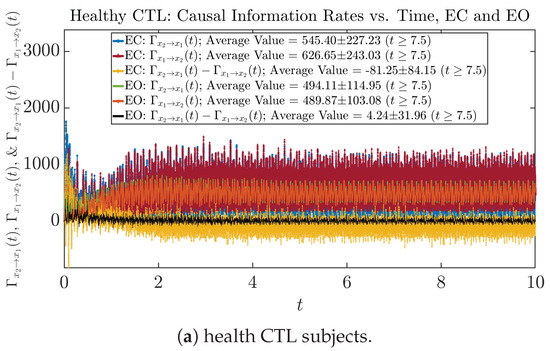
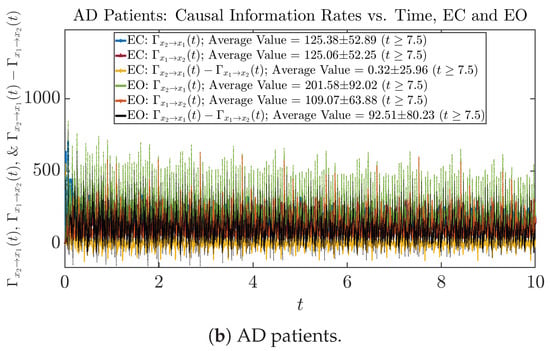
Figure 12.
Causal information rates along time of CTL and AD subjects.
For both CTL and AD subjects, and both decrease when changing from EC to EO, except for AD subjects’ increasing on average. On the other hand, the net causal information rate changes differently: when healthy subjects open their eyes, it increases and changes from significantly negative on average to slightly positive on average, whereas for AD patients, it increases from almost zero on average to significantly positive on average without net directional change. A possible interpretation might be that, when healthy subjects open their eyes, the brain region generating the signal becomes more sensitive to the noise, causing it to influence more compared to the eyes-closed state.
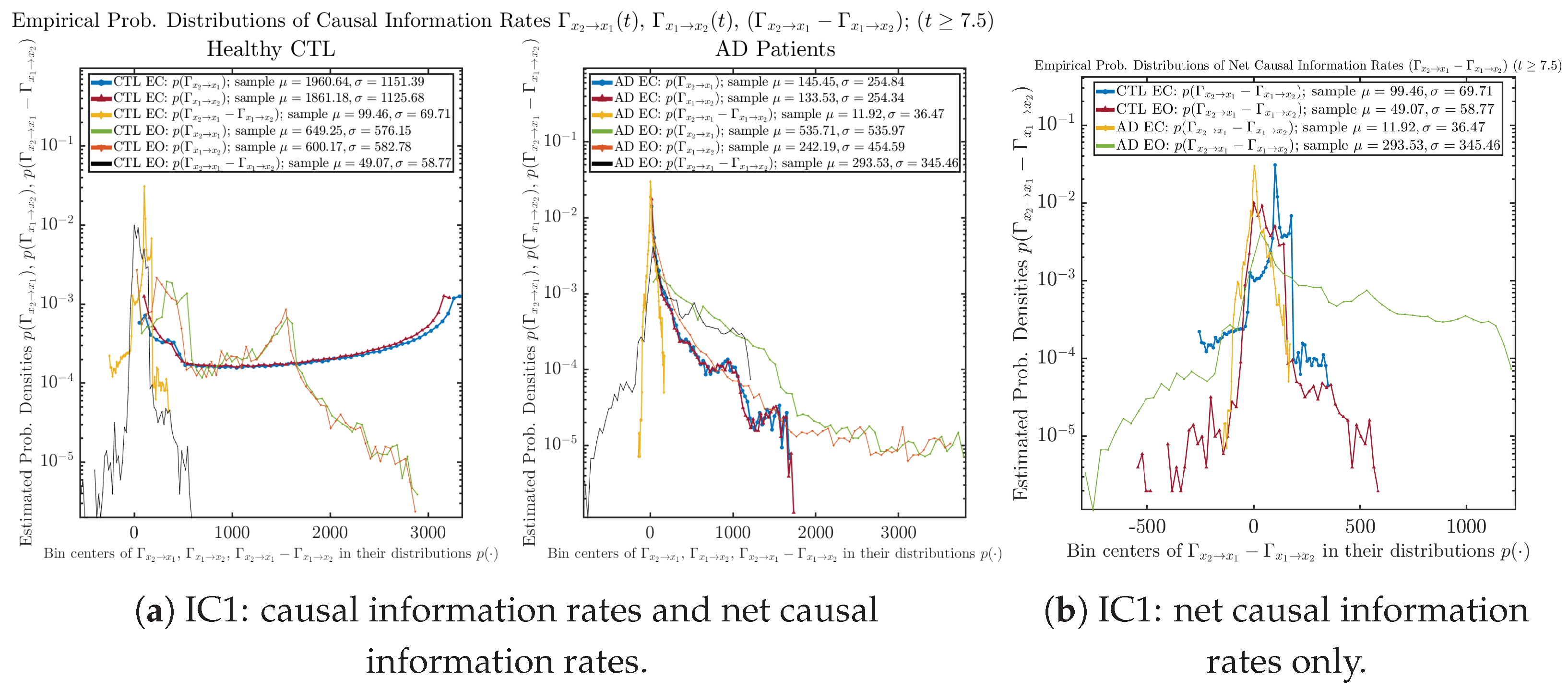
3.4.2. Empirical Probability Distribution (for )
Similar to Section 3.3.2, we also estimate the empirical probability distributions of , and to better visualize their statistics in Figure 13a. In particular, we plot the empirical probability distributions of for both healthy and AD subjects with both EC and EO conditions together in Figure 13b, in order to better visualize and compare net causal information rates’ changes when CTL and AD subjects open their eyes. It can be seen that the estimated PDF of shrinks its width in shape when healthy subjects open their eyes. Combining with the observation that the magnitude of sample mean of is close to 0 for healthy subjects with eyes opened, a possible interpretation might be that the directional connectivity between brain regions generating signals and is reduced to almost zero, either by incoming visual information received by opened eyes or due to the brain region generating signal becoming more sensitive to noise when eyes are opened. Contrarily, the estimated PDF of for AD patients qualitatively change in an inverse direction to become widened in shape.
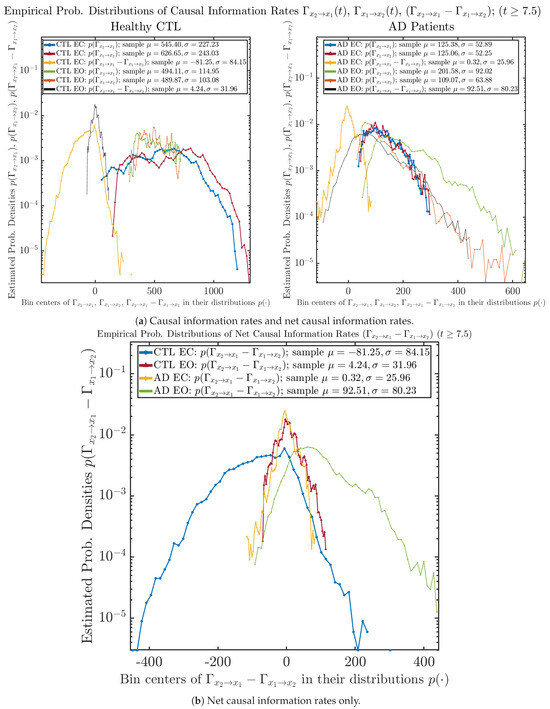
Figure 13.
Empirical probability distributions of causal information rates and net causal information rates .
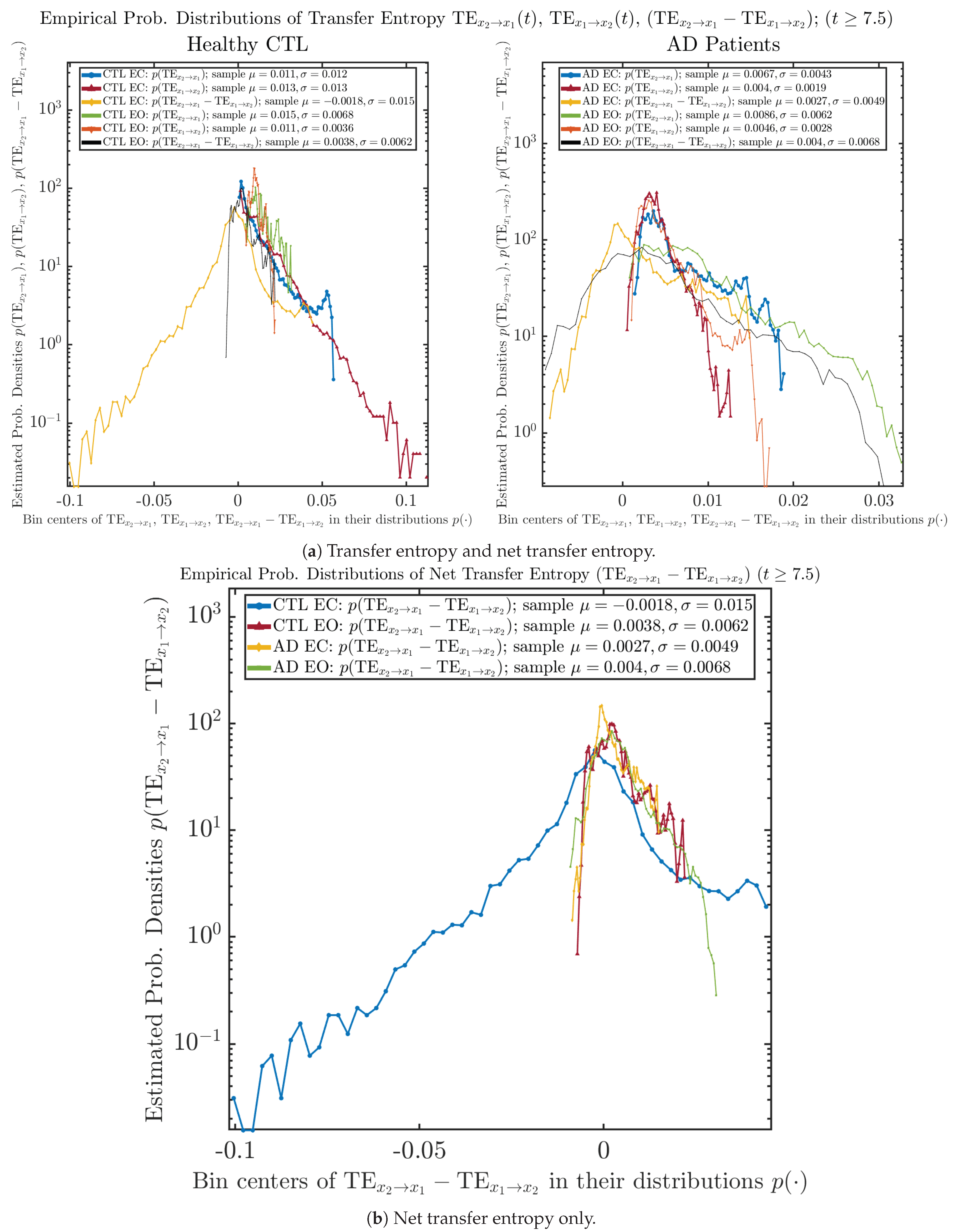
As mentioned earlier, as a comparison, we also calculate more traditional/established information-theoretic measure of causality, i.e., transfer entropy (TE), and estimate their empirical probability distributions in the same manner as we do for causal information rates, as shown in Figure 14.
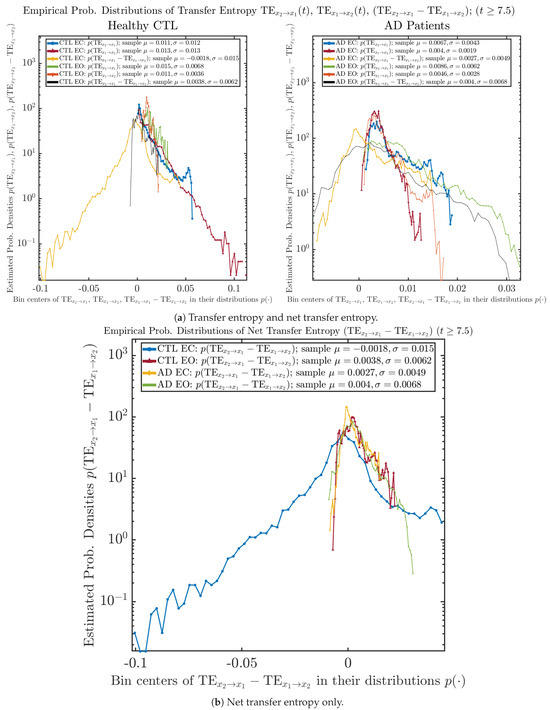
Figure 14.
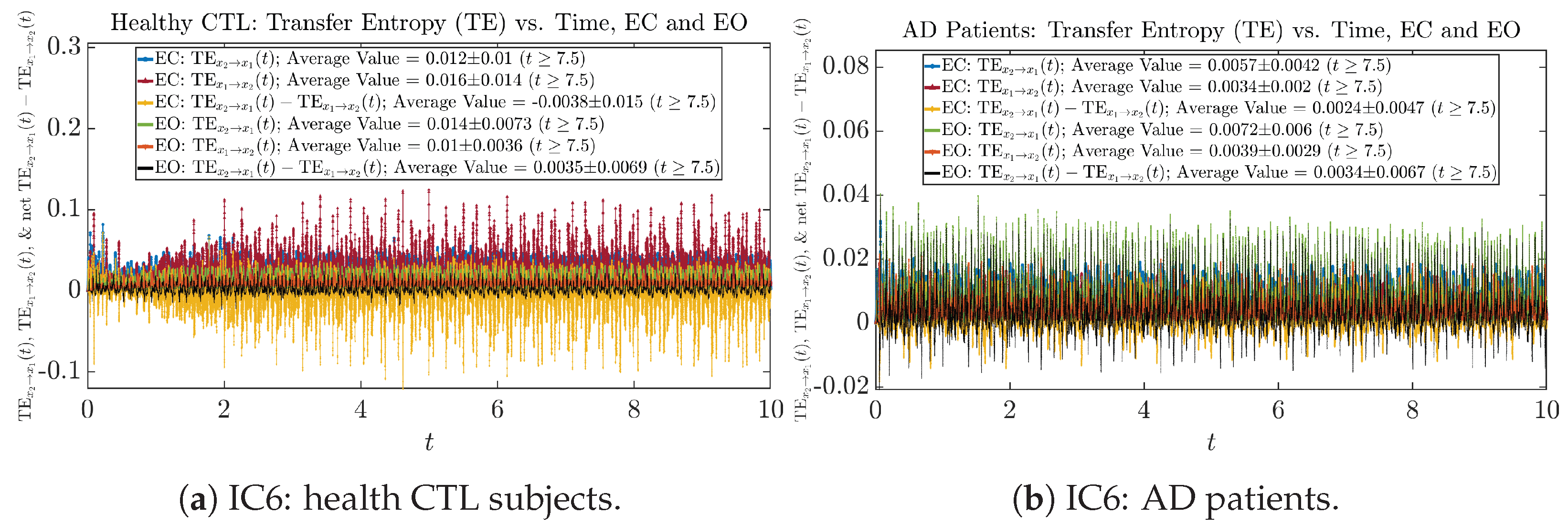
Empirical probability distributions of transfer entropy and net transfer entropy .
One can see that the empirical distributions of transfer entropy and , as well as net transfer entropy are not able to make clear distinction between EC and EO conditions, especially for AD patients in terms of net transfer entropy. This may be better summarized in Table 5, comparing the mean and standard deviation values of causal information rate vs. transfer entropy for the four cases.

Table 5.
Mean and standard deviation values () of causal information rates , and net causal information rates vs. transfer entropy , and net transfer entropy .
Moreover, the magnitude of numeric values of transfer entropy and net transfer entropy is ∼ or ∼, which is too close to zero, making it too noise-like or unreliable to quantify causality. Therefore, the causal information rate is a much superior measure than transfer entropy in quantifying causality, and since causal information rate quantifies how one signal instantaneously influences another signal’s information rate (which is a reflection of neural information processing in corresponding brain region), it can be used to measure directional or causal connectivities among different brain regions.
4. Discussion
A major challenge for practical usage of information geometry theoretic measures on real-world experimental EEG signals is that they require a significant amount of data samples to estimate the probability density functions. For example, in this work, we simulated trajectories or sample paths of the stochastic nonlinear coupled oscillator models, such that at any time instance, we always have a sufficient amount of data samples to accurately estimate the time-dependent probability density functions with a histogram-based approach. This is usually not possible for experimental EEG signals which often contain only one trajectory for each channel, and one has to use a sliding window-based approach to collect data samples for histogram-based density estimation. This approach implicitly assumes that the EEG signals are stationary within each sliding time window, and hence, one has to balance between the sliding time window’s length and number of available data samples, in order to account for non-stationarity while still having enough data samples to accurately and meaningfully estimate the time-dependent probability densities. And therefore, this approach will not work very well if the EEG signals exhibit severely non-stationary time-varying effects, requiring a very short length of sliding windows, which will contain too few data samples.
An alternative approach to overcome this issue is using kernel density estimation to estimate the probability density functions, which usually requires a much smaller number of data samples while still being able to approximate the true probability distribution with acceptable accuracy. However, this approach typically involves a very high computational cost, limiting its practical use for many cases such as computational resource-limited scenarios. A proposed method to avoid this is using the Koopman operator theoretic framework [37,38] and its numerical techniques applicable to experimental data in a model-free manner, since the Koopman operator is the left-adjoint of the Perron–Frobenious operator evolving the probability density functions in time. This exploration will be left for our future investigation.
5. Conclusions
In this work, we explore information geometry theoretic measures to characterize neural information processing from EEG signals simulated by stochastic nonlinear coupled oscillator models. In particular, we utilize information rates to quantify the time evolution of probability density functions of simulated EEG signals and utilize causal information rates to quantify one signal’s instantaneous influence on another signal’s information rate. The parameters of the stochastic nonlinear coupled oscillator models of EEG were fine tuned for both healthy subjects and AD patients, with both eyes-closed and eyes-open conditions. By using information rates and causal information rates, we find significant and interesting distinctions between healthy subjects and AD patients when they change their eyes’ open/closed status. These distinctions may be further related to differences in neural information processing activities of the corresponding brain regions (for information rates) and to differences in connectivities among these brain regions (for causal information rates).
Compared to more traditional or established information-theoretic measures such as differential entropy and transfer entropy, our results show that information geometry theoretic measures such as information rate and causal information rate are superior to their more traditional counterparts, respectively (information rate vs. differential entropy, and causal information rate vs. transfer entropy). Since information rates and causal information rates can be applied to experimental EEG signals in a model-free manner, and they are capable of quantifying non-stationary time-varying effects, nonlinearity, and non-Gaussian stochasticity presented in real-world EEG signals, we believe that these information geometry theoretic measures can become an important and powerful tool-set for both understanding neural information processing in the brain and diagnosis of neurological disorders such as Alzheimer’s disease in this work.
Author Contributions
Conceptualization, J.-C.H., E.-j.K. and F.H.; Methodology, J.-C.H. and E.-j.K.; Software, J.-C.H.; Validation, J.-C.H.; Formal analysis, J.-C.H.; Investigation, J.-C.H., E.-j.K. and F.H.; Resources, E.-j.K. and F.H.; Writing—original draft, J.-C.H.; Writing—review & editing, J.-C.H., E.-j.K. and F.H.; Visualization, J.-C.H.; Supervision, E.-j.K. and F.H.; Project administration, J.-C.H., E.-j.K. and F.H.; Funding acquisition, E.-j.K. and F.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the EPSRC Grant (EP/W036770/1 (https://gow.epsrc.ukri.org/NGBOViewGrant.aspx?GrantRef=EP/W036770/1, accessed on 17 February 2024)).
Data Availability Statement
The stochastic simulation and calculation scripts will be made publicly available in an open repository, which is likely to be updated under https://github.com/jia-chenhua?tab=repositories or https://gitlab.com/jia-chen.hua (both accessed on 17 February 2024).
Acknowledgments
The stochastic simulations and numerical calculations in this work were performed on GPU nodes of Sulis HPC (https://sulis.ac.uk/, accessed on 17 February 2024). The authors would like to thank Alex Pedcenko (https://pureportal.coventry.ac.uk/en/persons/alex-pedcenko, accessed on 17 February 2024) for providing useful help in accessing the HPC resources in order to finish the simulations and calculations in a timely manner.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| probability density function | |
| SDE | stochastic differential equation |
| IC | Initial Conditions (in terms of initial Gaussian distributions) |
| CTL | healthy control (subjects) |
| AD | Alzheimer’s disease |
| EC | eyes-closed |
| EO | eyes-open |
| TE | transfer entropy |
Appendix A. Finer Details of Numerical Estimation Techniques
Recall from Equation (7) that the squared information rate is
where the partial time derivative and integral can be numerically approximated using discretization, i.e., and , respectively, where for brevity and if no ambiguity arises, the summation over index i is often omitted and replaced by x itself as , and the symbol x serves as both the index of summation (e.g., the x-th interval with length ) and the actual value x in .
A common technique to improve the approximation of integral by finite summation is the trapezoidal rule , which will be abbreviated as to indicate that the summation is following the trapezoidal rule imposing a weight/factor on the first and last summation terms (corresponding to the lower and upper bounds of the integral). Similarly, we use to denote a 2D trapezoidal approximation of the double integral , where different weights ( or ) will be applied to the “corner”/boundary terms of the summation. Meanwhile, to distinguish regular summation from trapezoidal approximation, we use the notation to signify a regular summation as a more naive approximation of the integral.
The PDF is numerically estimated using a histogram with Rice’s rule applied, i.e., the number of bins is (with uniform bin width ), which is rounded towards zero to avoid overestimating the number of bins needed. And for joint PDF , since the bins are distributed in a 2D plane of , the number of bins in each dimension is rounded to (and similarly for 3D joint probability as in the transfer entropy calculation, the number of bins in each dimension is rounded to ). Combining all of the above, the information rate’s square will be approximated by
where the bin width can be moved into the square root and multiplied with the PDF to get the probability (mass) of finding a data sample in the x-th bin, which is estimated as , i.e., the number of data samples inside that bin divided by the number of all data samples (using the relevant functions in MATLAB or Python). The trapezoidal rule imposes a factor on the first and last terms of summation, corresponding to the first and last bins.
For the causal information rate , the can be estimated by
where the number of bins in each of the and dimensions is rounded to , and the can be estimated as above as using regular or trapezoidal summation. However, here for , the number of bins for must not be chosen as following the 1D Rice’s rule, which is very critical to avoid insensible or inconsistent estimation of , for which the reason is explained below.
Consider the quantity ; theoretically and by definition, the can be pulled outside the integral over to combine the two integrals into one integral as follows:
and the corresponding numerical approximations of integrals should be combined as
where the sum over is performed on the same bins for both of the two terms inside the large braces above. On the other hand, if one numerically approximates and separately as
then the sum over in the second term should still be performed on the same bins of for the first term involving the joint PDFs estimated by 2D histograms (i.e., using the square root number of bins of Rice’s rule, instead of following the 1D Rice’s rule without the square root), even though this second summation term is written as a separate and “independent” term from the first double-summation term. The definition might result in a misimpression that one can estimate separately by using a Rice’s rule’s binning method containing bins, while estimating using the square root of Rice’s rule’s number of bins . Using different bins for will make it invalid to combine the two summations into one summation over the same ’s (and hence invalid to combine the two integrals into one integral by pulling out the same ).
Using bins for will overestimate the value of , for example, if there are 1 million samples/data points to estimate the PDFs, then for 1D distribution and for 2D joint distribution. Calculating using 200 bins will result in a much larger value than calculating it using 14 bins, which will result in negative values in calculating the causal information rate . When using the same 14 bins of (for estimating the 2D joint PDF of ) to estimate the 1D PDF in , all the unreasonable negative values disappear, except for only some isolated negative values remained, which is related to estimating and using 1D and 2D trapezoidal rules for summations approximating the integrals: if one uses 1D trapezoidal summation for , while on the other hand, one blindly and inconsistently uses 2D trapezoidal summation for , this will also result in some negative values in computing , because the 2D trapezoidal sum will under-estimate the as compared to the 1D trapezoidal-sum-estimated .
To resolve this inconsistent mixing of 1D and 2D trapezoidal rules, there are two possible methods:
- Using 2D trapezoidal rule for both and , that is, , and . In other words, when calculating , instead of estimating marginal PDF and directly by 1D histograms (using the relevant functions in MATLAB or Python), one first estimates the joint PDF and by 2D histograms and integrates over by trapezoidal summation on it. This will reduce the value of estimated , and integrals over both and are both estimated by trapezoidal summation.
- Using the 1D trapezoidal rule for both and , that is, , and . In this approach, the marginal PDF , where the equal sign holds exactly for the regular or naive summation . This is because the histogram estimation in MATLAB and Python is performed by counting the occurrence of data samples inside each bin, and the probability (mass) is estimated as , and the density is estimated as , where is the width of the x-th bin (and for 2D histogram, this is replaced by bin area ), and therefore, summing over is aggregating the 2D bins of and combining or mixing samples with -values/coordinates in the same -bin (but with -values/coordinates in different -bins) together. In other words, it is always true that , where is the number of samples inside the -th bin and is number of samples inside the -th bin in 2D, and hence, for estimated probability (mass), , and for estimated PDFs, , which is why holds exactly for numerically estimated marginal and joint PDFs using histograms, which is consistent with the theoretical relation between marginal and joint PDFs , and this has been numerically verified using the relevant 1D and 2D histogram functions in MATLAB and Python, i.e., by (naively) summing the estimated joint PDF over , and the (naively) summed marginal is exactly the same as the one estimated directly by 1D histogram function. So in this approach, integral over is estimated by naive summation on , but integral over is estimated by trapezoidal summation on .
The 1st approach will violate the relation between joint and marginal , because as explained in the 2nd approach above, when using MATLAB’s and Python’s 1D and 2D histogram functions, one will always get exactly and for naive summation, but not for trapezoidal summation over due to the weights/factors (≠1) imposed on the “corner”/boundary/first/last summation terms, which is used in the 1st approach. However, the 2nd approach puts different importance or weights on the summation over as compared to , which might also be problematic, because the original definition is a double integral over and without different weights/factors imposed by different summation methods.
To resolve this, we use the regular or naive summations on both and , which avoids the issues in both the 1st and 2nd approaches, and we find that the numerical difference between the 1st and 2nd approaches and our adopted simply naive summations are really negligible, and because in this work, we are performing empirical statistics on the estimated causal information rates and illustrating the qualitative features of the empirical probability distributions of them, we use our simple naive summations over both and when estimating and in causal information rate .
Appendix B. Complete Results: All Six Groups of Initial Conditions
For completeness, we list the full results of all figures for all six different initial Gaussian distributions listed in Table 3.
Appendix B.1. Sample Trajectories of and
Appendix B.1.1. Initial Conditions No.1 (IC1)
Figure A1.
Initial Conditions No.1 (IC1): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A1.
Initial Conditions No.1 (IC1): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A2.
Initial Conditions No.1 (IC1): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Figure A2.
Initial Conditions No.1 (IC1): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Appendix B.1.2. Initial Conditions No.2 (IC2)
Figure A3.
Initial Conditions No.2 (IC2): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A3.
Initial Conditions No.2 (IC2): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A4.
Initial Conditions No.2 (IC2): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Figure A4.
Initial Conditions No.2 (IC2): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Appendix B.1.3. Initial Conditions No.3 (IC3)
Figure A5.
Initial Conditions No.3 (IC3): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A5.
Initial Conditions No.3 (IC3): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A6.
Initial Conditions No.3 (IC3): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Figure A6.
Initial Conditions No.3 (IC3): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Appendix B.1.4. Initial Conditions No.4 (IC4)
Figure A7.
Initial Conditions No.4 (IC4): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A7.
Initial Conditions No.4 (IC4): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A8.
Initial Conditions No.4 (IC4): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Figure A8.
Initial Conditions No.4 (IC4): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Appendix B.1.5. Initial Conditions No.5 (IC5)
Figure A9.
Initial Conditions No.5 (IC5): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A9.
Initial Conditions No.5 (IC5): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A10.
Initial Conditions No.5 (IC5): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Figure A10.
Initial Conditions No.5 (IC5): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Appendix B.1.6. Initial Conditions No.6 (IC6)
Figure A11.
Initial Conditions No.6 (IC6): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A11.
Initial Conditions No.6 (IC6): 50 sample trajectories of healthy CTL subjects. Each single trajectory is labeled by a different color.
Figure A12.
Initial Conditions No.6 (IC6): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Figure A12.
Initial Conditions No.6 (IC6): 50 sample trajectories of AD patients. Each single trajectory is labeled by a different color.
Appendix B.2. Time Evolution of PDF and
Appendix B.2.1. Initial Conditions No.1 (IC1)
Figure A13.
Initial Conditions No.1 (IC1): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A13.
Initial Conditions No.1 (IC1): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A14.
Initial Conditions No.1 (IC1): Time evolution of estimated PDFs of AD patients.
Figure A14.
Initial Conditions No.1 (IC1): Time evolution of estimated PDFs of AD patients.
Appendix B.2.2. Initial Conditions No.2 (IC2)
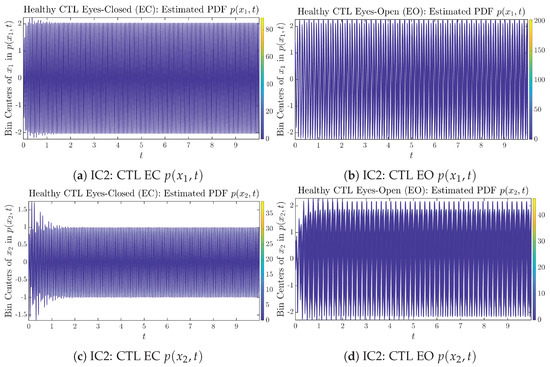
Figure A15.
Initial Conditions No.2 (IC2): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A15.
Initial Conditions No.2 (IC2): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A16.
Initial Conditions No.2 (IC2): Time evolution of estimated PDFs of AD patients.
Figure A16.
Initial Conditions No.2 (IC2): Time evolution of estimated PDFs of AD patients.
Appendix B.2.3. Initial Conditions No.3 (IC3)
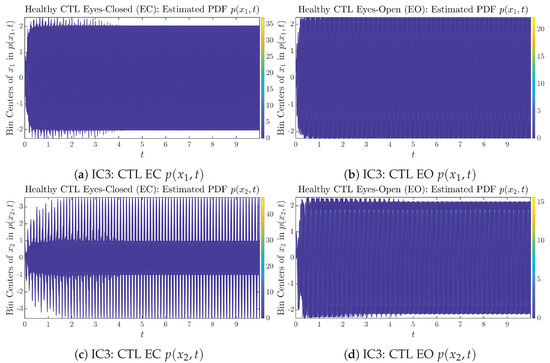
Figure A17.
Initial Conditions No.3 (IC3): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A17.
Initial Conditions No.3 (IC3): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A18.
Initial Conditions No.3 (IC3): Time evolution of estimated PDFs of AD patients.
Figure A18.
Initial Conditions No.3 (IC3): Time evolution of estimated PDFs of AD patients.
Appendix B.2.4. Initial Conditions No.4 (IC4)
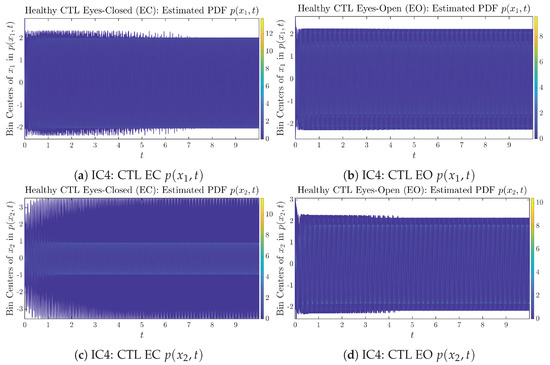
Figure A19.
Initial Conditions No.4 (IC4): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A19.
Initial Conditions No.4 (IC4): Time evolution of estimated PDFs of healthy CTL subjects.
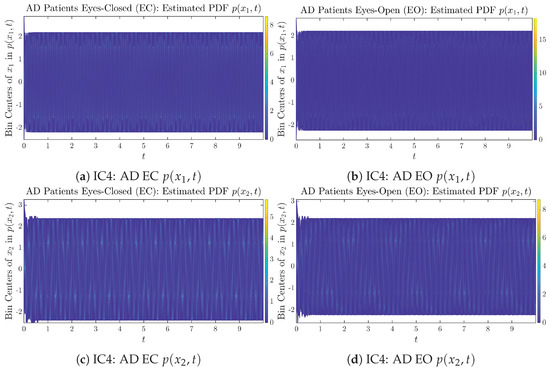
Figure A20.
Initial Conditions No.4 (IC4): Time evolution of estimated PDFs of AD patients.
Figure A20.
Initial Conditions No.4 (IC4): Time evolution of estimated PDFs of AD patients.
Appendix B.2.5. Initial Conditions No.5 (IC5)
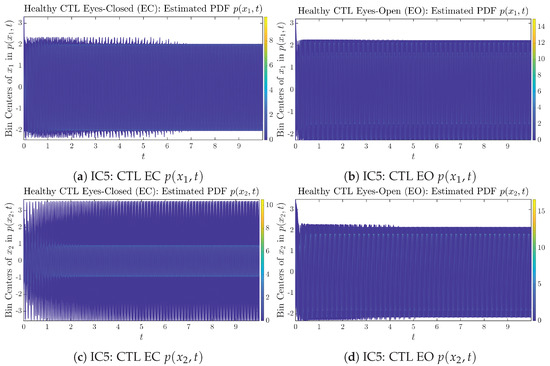
Figure A21.
Initial Conditions No.5 (IC5): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A21.
Initial Conditions No.5 (IC5): Time evolution of estimated PDFs of healthy CTL subjects.
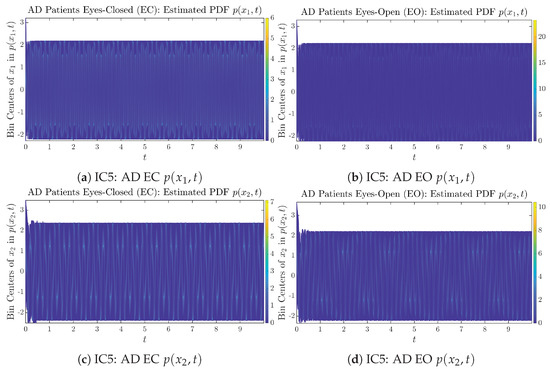
Figure A22.
Initial Conditions No.5 (IC5): Time evolution of estimated PDFs of AD patients.
Figure A22.
Initial Conditions No.5 (IC5): Time evolution of estimated PDFs of AD patients.
Appendix B.2.6. Initial Conditions No.6 (IC6)
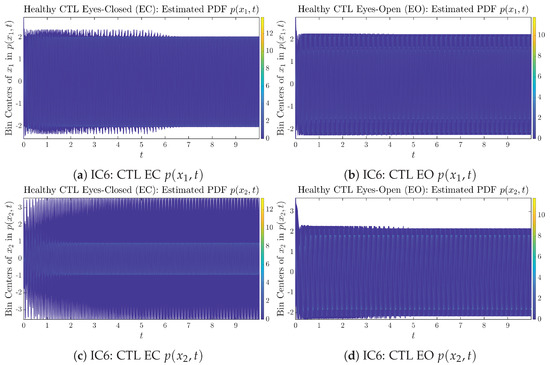
Figure A23.
Initial Conditions No.6 (IC6): Time evolution of estimated PDFs of healthy CTL subjects.
Figure A23.
Initial Conditions No.6 (IC6): Time evolution of estimated PDFs of healthy CTL subjects.
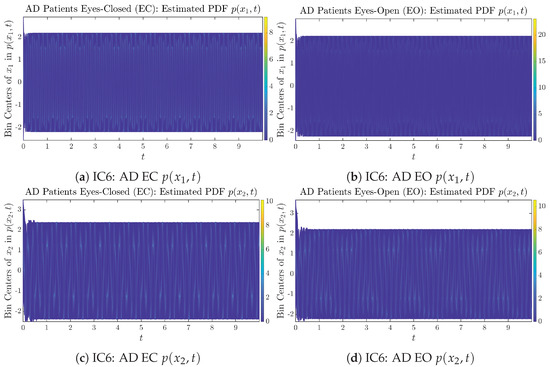
Figure A24.
Initial Conditions No.6 (IC6): Time evolution of estimated PDFs of AD patients.
Figure A24.
Initial Conditions No.6 (IC6): Time evolution of estimated PDFs of AD patients.
Appendix B.3. Information Rates and
Appendix B.3.1. Time Evolution: Information Rates
Initial Conditions No.1 (IC1)
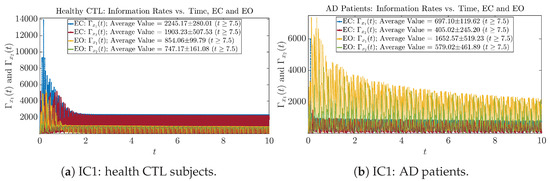
Figure A25.
Initial Conditions No.1 (IC1): Information rates along time of CTL and AD subjects.
Figure A25.
Initial Conditions No.1 (IC1): Information rates along time of CTL and AD subjects.
Initial Conditions No.2 (IC2)
Figure A26.
Initial Conditions No.2 (IC2): Information rates along time of CTL and AD subjects.
Figure A26.
Initial Conditions No.2 (IC2): Information rates along time of CTL and AD subjects.
Initial Conditions No.3 (IC3)
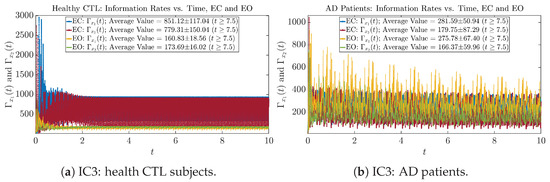
Figure A27.
Initial Conditions No.3 (IC3): Information rates along time of CTL and AD subjects.
Figure A27.
Initial Conditions No.3 (IC3): Information rates along time of CTL and AD subjects.
Initial Conditions No.4 (IC4)
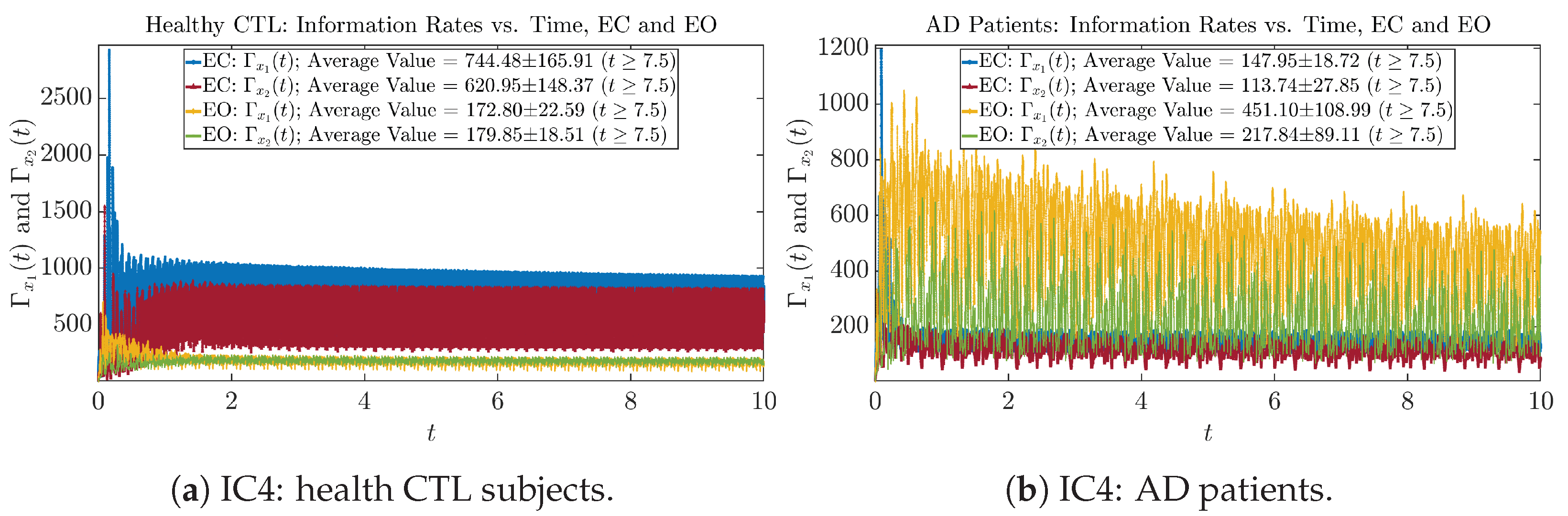
Figure A28.
Initial Conditions No.4 (IC4): Information rates along time of CTL and AD subjects.
Figure A28.
Initial Conditions No.4 (IC4): Information rates along time of CTL and AD subjects.
Initial Conditions No.5 (IC5)
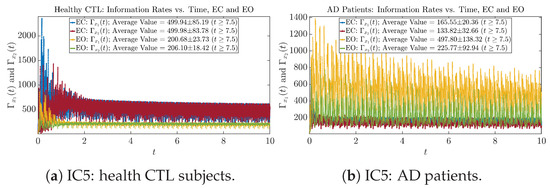
Figure A29.
Initial Conditions No.5 (IC5): Information rates along time of CTL and AD subjects.
Figure A29.
Initial Conditions No.5 (IC5): Information rates along time of CTL and AD subjects.
Initial Conditions No.6 (IC6)
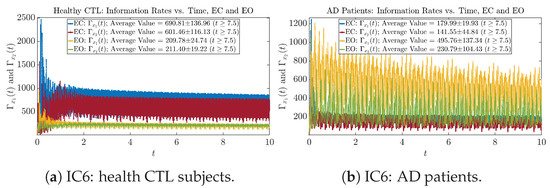
Figure A30.
Initial Conditions No.6 (IC6): Information rates along time of CTL and AD subjects.
Figure A30.
Initial Conditions No.6 (IC6): Information rates along time of CTL and AD subjects.
Appendix B.3.2. Empirical Probability Distribution: Information Rates (for )
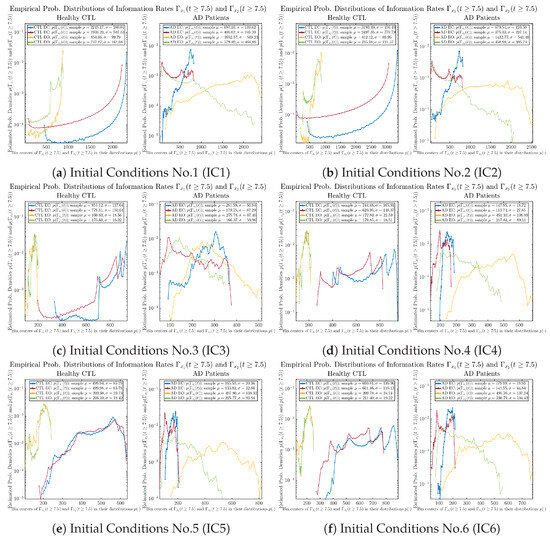
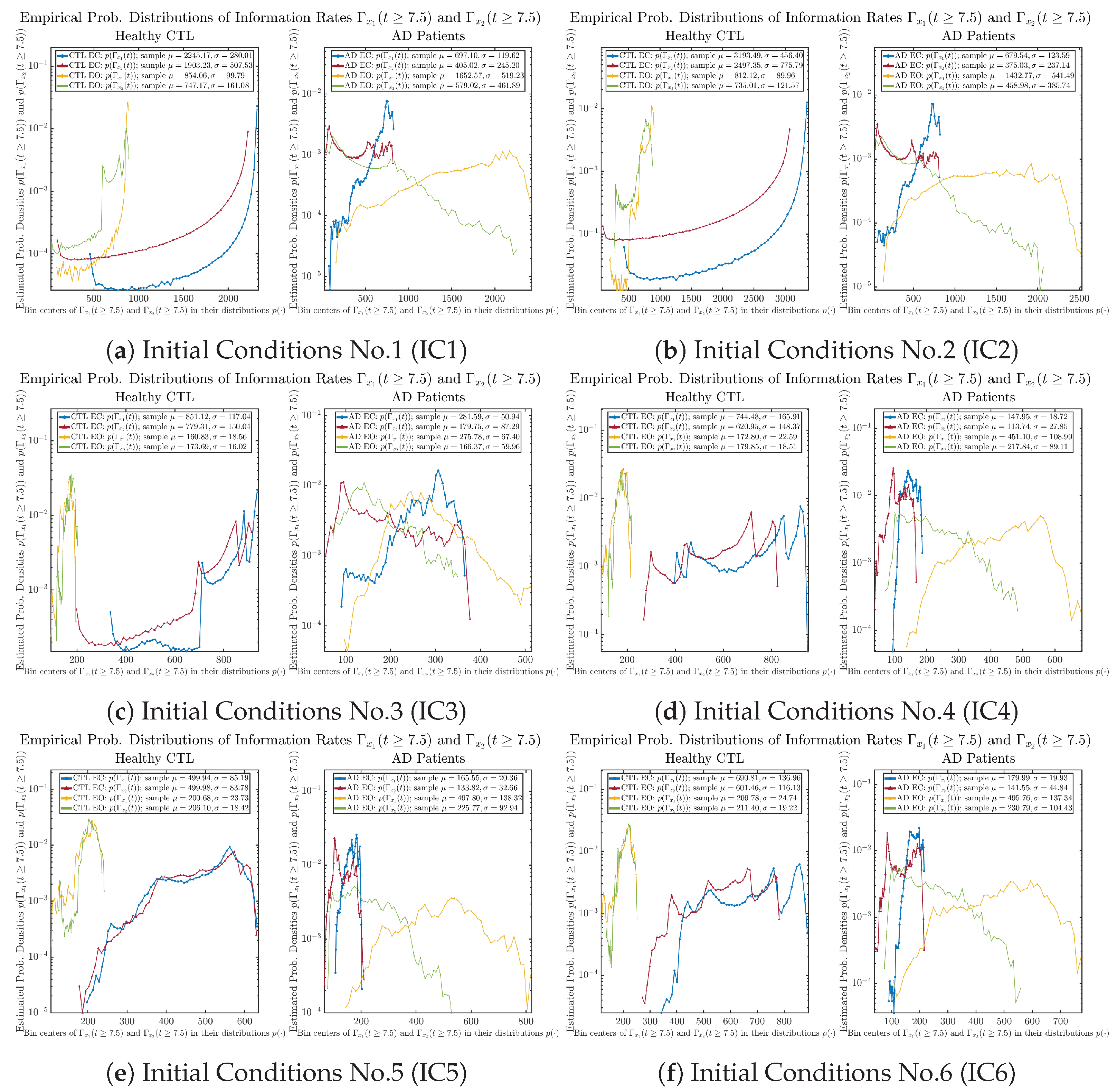
Figure A31.
Empirical probability distributions of information rates and .
Figure A31.
Empirical probability distributions of information rates and .
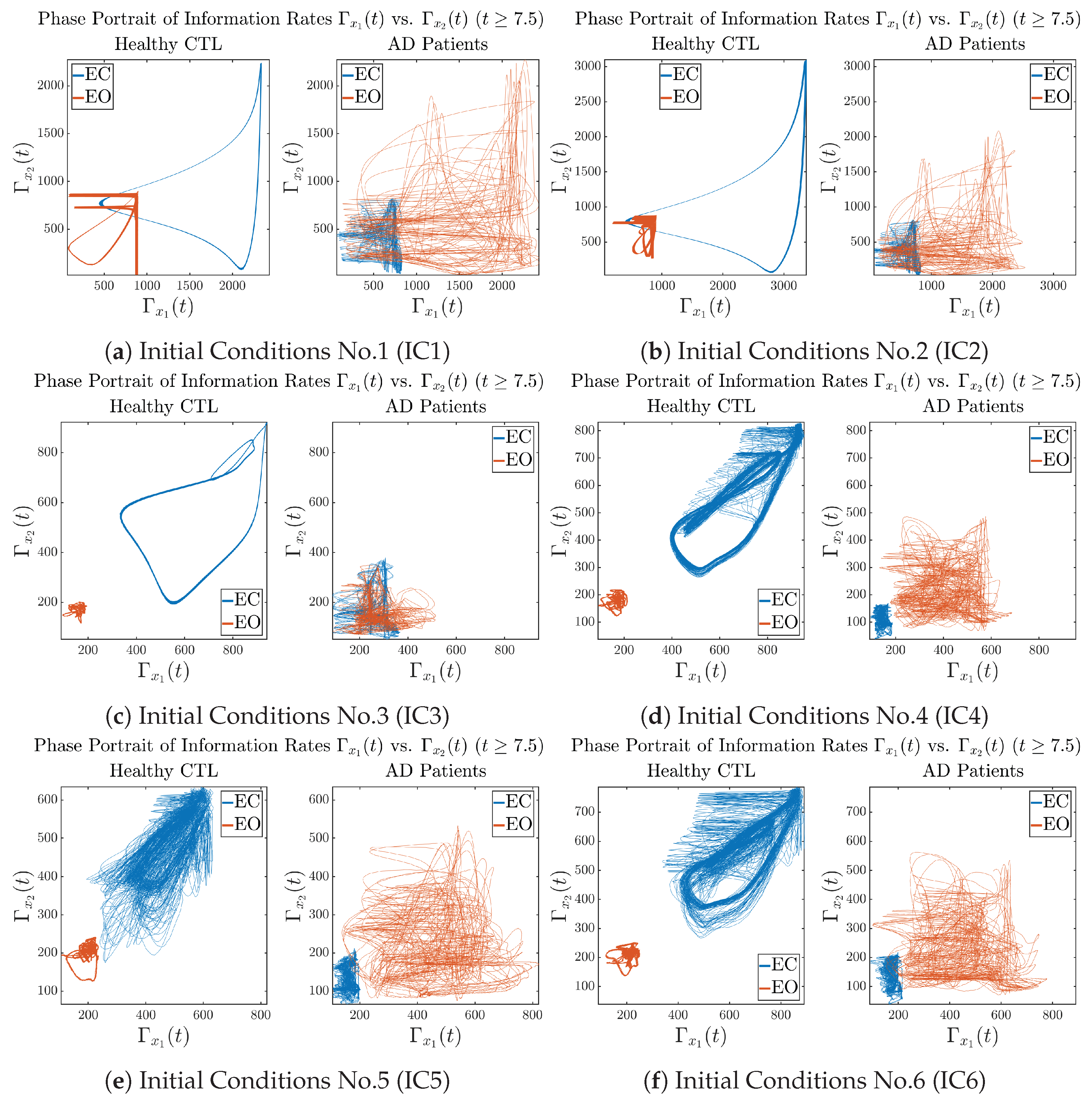
Appendix B.3.3. Phase Portraits: Information Rates (for )
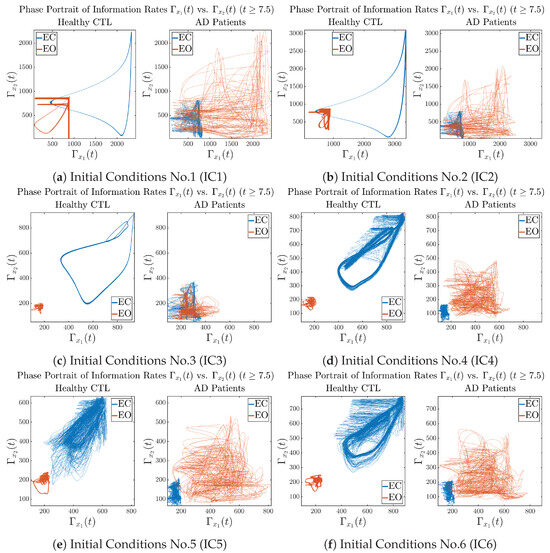
Figure A32.
Phase portraits of information rates vs. .
Figure A32.
Phase portraits of information rates vs. .
Initial Conditions No.1 (IC1):
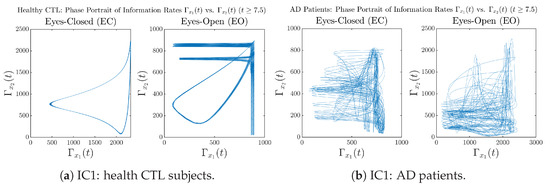
Figure A33.
Initial Conditions No.1 (IC1): Phase portraits of information rates vs. of CTL and AD subjects.
Figure A33.
Initial Conditions No.1 (IC1): Phase portraits of information rates vs. of CTL and AD subjects.
Initial Conditions No.2 (IC2):
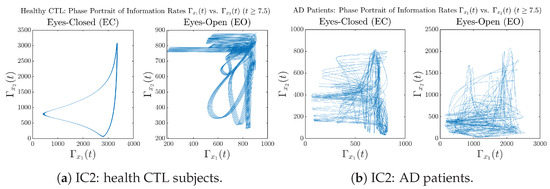
Figure A34.
Initial Conditions No.2 (IC2): Phase portraits of information rates vs. of CTL and AD subjects.
Figure A34.
Initial Conditions No.2 (IC2): Phase portraits of information rates vs. of CTL and AD subjects.
Initial Conditions No.3 (IC3):
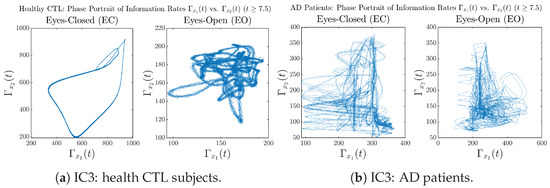
Figure A35.
Initial Conditions No.3 (IC3): Phase portraits of information rates vs. of CTL and AD subjects.
Figure A35.
Initial Conditions No.3 (IC3): Phase portraits of information rates vs. of CTL and AD subjects.
Initial Conditions No.4 (IC4):
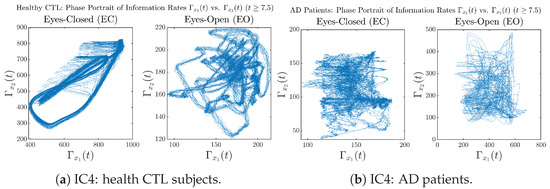
Figure A36.
Initial Conditions No.4 (IC4): Phase portraits of information rates vs. of CTL and AD subjects.
Figure A36.
Initial Conditions No.4 (IC4): Phase portraits of information rates vs. of CTL and AD subjects.
Initial Conditions No.5 (IC5):
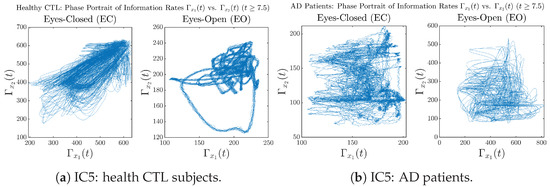
Figure A37.
Initial Conditions No.5 (IC5): Phase portraits of information rates vs. of CTL and AD subjects.
Figure A37.
Initial Conditions No.5 (IC5): Phase portraits of information rates vs. of CTL and AD subjects.
Initial Conditions No.6 (IC6):
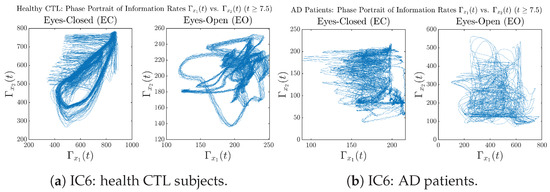
Figure A38.
Initial Conditions No.6 (IC6): Phase portraits of information rates vs. of CTL and AD subjects.
Figure A38.
Initial Conditions No.6 (IC6): Phase portraits of information rates vs. of CTL and AD subjects.
Appendix B.3.4. Power Spectra: Information Rates (for )
Initial Conditions No.1 (IC1):
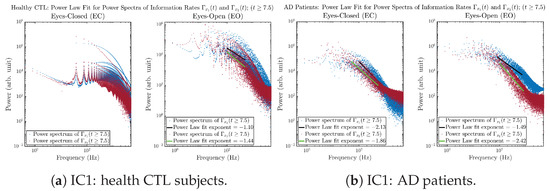
Figure A39.
Initial Conditions No.1 (IC1): Power law fit for power spectra of information rates and of CTL and AD subjects.
Figure A39.
Initial Conditions No.1 (IC1): Power law fit for power spectra of information rates and of CTL and AD subjects.
Initial Conditions No.2 (IC2):
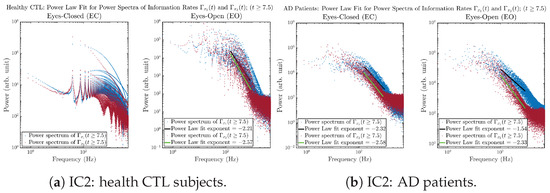
Figure A40.
Initial Conditions No.2 (IC2): Power law fit for power spectra of information rates and of CTL and AD subjects.
Figure A40.
Initial Conditions No.2 (IC2): Power law fit for power spectra of information rates and of CTL and AD subjects.
Initial Conditions No.3 (IC3):
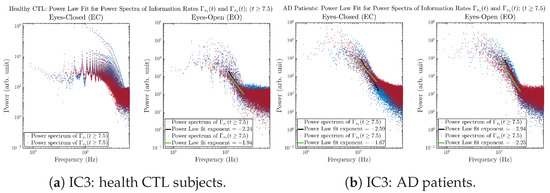
Figure A41.
Initial Conditions No.3 (IC3): Power law fit for power spectra of information rates and of CTL and AD subjects.
Figure A41.
Initial Conditions No.3 (IC3): Power law fit for power spectra of information rates and of CTL and AD subjects.
Initial Conditions No.4 (IC4):
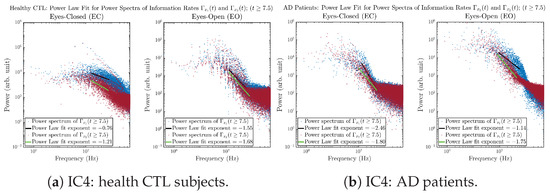
Figure A42.
Initial Conditions No.4 (IC4): Power law fit for power spectra of information rates and of CTL and AD subjects.
Figure A42.
Initial Conditions No.4 (IC4): Power law fit for power spectra of information rates and of CTL and AD subjects.
Initial Conditions No.5 (IC5):
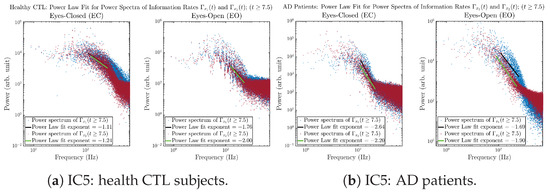
Figure A43.
Initial Conditions No.5 (IC5): Power law fit for power spectra of information rates and of CTL and AD subjects.
Figure A43.
Initial Conditions No.5 (IC5): Power law fit for power spectra of information rates and of CTL and AD subjects.
Initial Conditions No.6 (IC6):
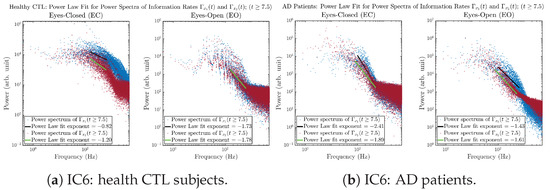
Figure A44.
Initial Conditions No.6 (IC6): Power law fit for power spectra of information rates and of CTL and AD subjects.
Figure A44.
Initial Conditions No.6 (IC6): Power law fit for power spectra of information rates and of CTL and AD subjects.
Appendix B.4. Shannon Differential Entropy of and
Appendix B.4.1. Time Evolution: Shannon Differential Entropy
Initial Conditions No.1 (IC1):
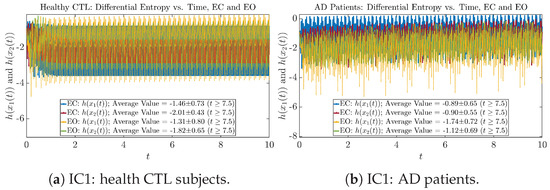
Figure A45.
Initial Conditions No.1 (IC1): Shannon differential entropy along time of CTL and AD subjects.
Figure A45.
Initial Conditions No.1 (IC1): Shannon differential entropy along time of CTL and AD subjects.
Initial Conditions No.2 (IC2):
Figure A46.
Initial Conditions No.2 (IC2): Shannon differential entropy along time of CTL and AD subjects.
Figure A46.
Initial Conditions No.2 (IC2): Shannon differential entropy along time of CTL and AD subjects.
Initial Conditions No.3 (IC3):
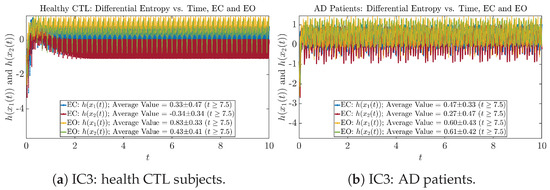
Figure A47.
Initial Conditions No.3 (IC3): Shannon differential entropy along time of CTL and AD subjects.
Figure A47.
Initial Conditions No.3 (IC3): Shannon differential entropy along time of CTL and AD subjects.
Initial Conditions No.4 (IC4):
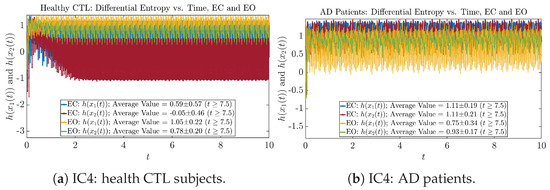
Figure A48.
Initial Conditions No.4 (IC4): Shannon differential entropy along time of CTL and AD subjects.
Figure A48.
Initial Conditions No.4 (IC4): Shannon differential entropy along time of CTL and AD subjects.
Initial Conditions No.5 (IC5):
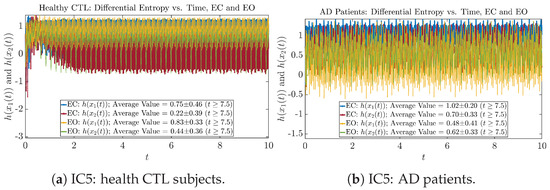
Figure A49.
Initial Conditions No.5 (IC5): Shannon differential entropy along time of CTL and AD subjects.
Figure A49.
Initial Conditions No.5 (IC5): Shannon differential entropy along time of CTL and AD subjects.
Initial Conditions No.6 (IC6):
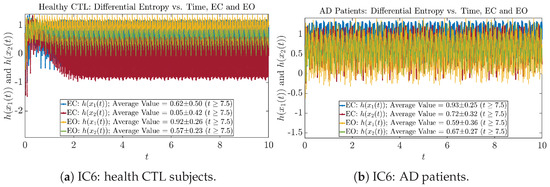
Figure A50.
Initial Conditions No.6 (IC6): Shannon differential entropy along time of CTL and AD subjects.
Figure A50.
Initial Conditions No.6 (IC6): Shannon differential entropy along time of CTL and AD subjects.
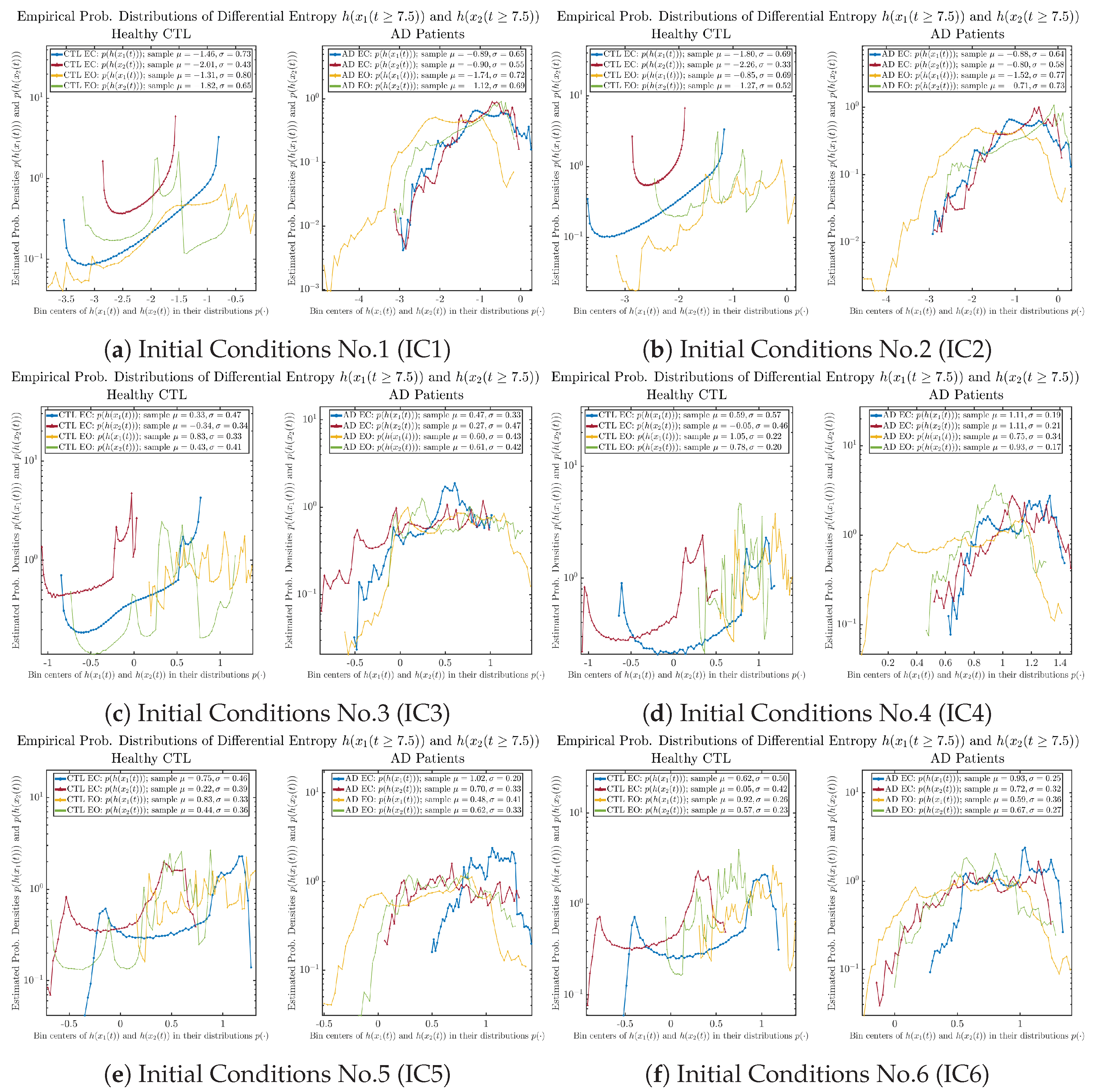
Appendix B.4.2. Empirical Probability Distribution: Shannon Differential Entropy (for )
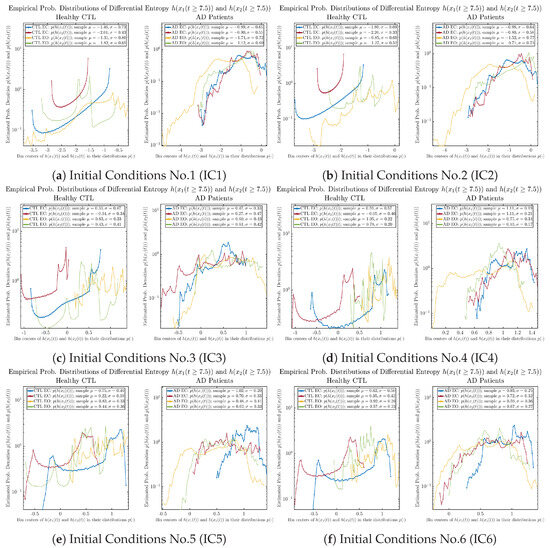
Figure A51.
Empirical probability distributions of Shannon differential entropy and .
Figure A51.
Empirical probability distributions of Shannon differential entropy and .
Appendix B.4.3. Phase Portraits: Shannon Differential Entropy (for )
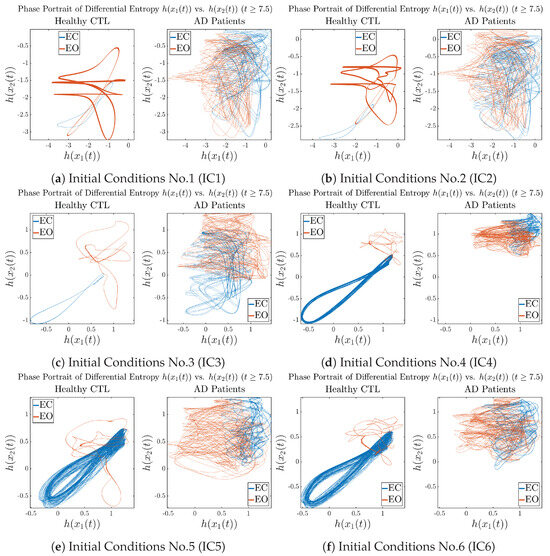
Figure A52.
Phase portraits of Shannon differential entropy and .
Figure A52.
Phase portraits of Shannon differential entropy and .
Initial Conditions No.1 (IC1):
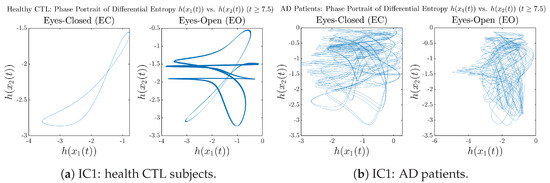
Figure A53.
Initial Conditions No.1 (IC1): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Figure A53.
Initial Conditions No.1 (IC1): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
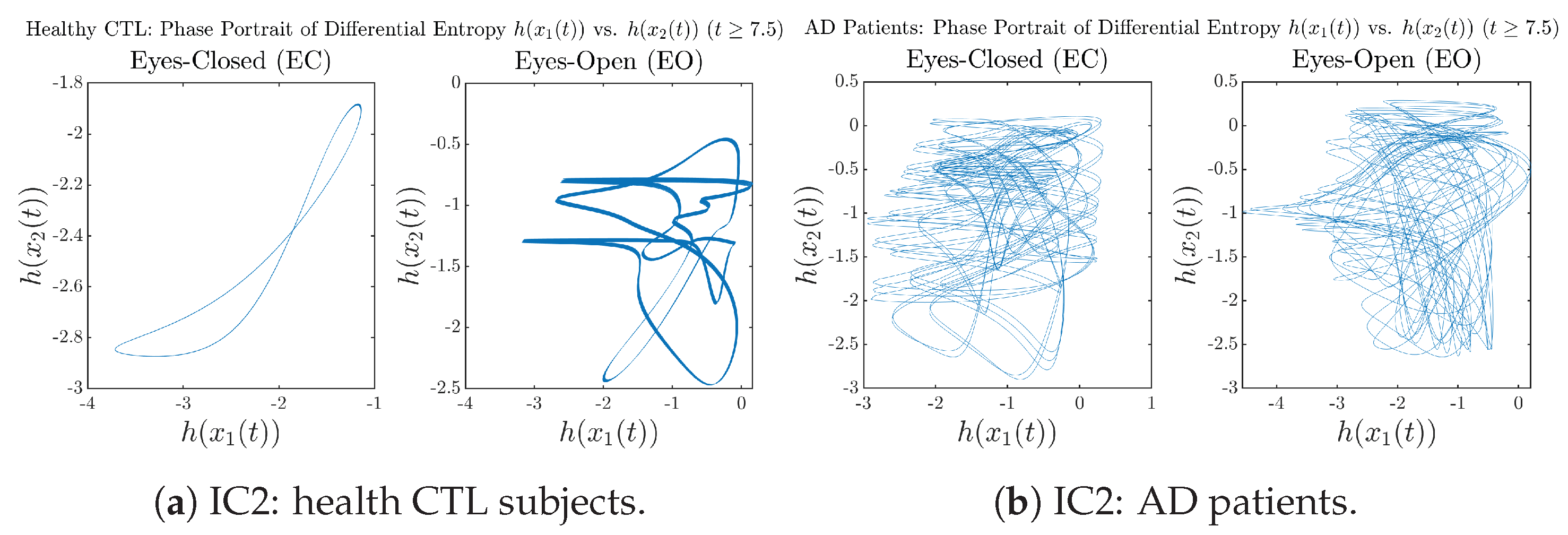
Initial Conditions No.2 (IC2):
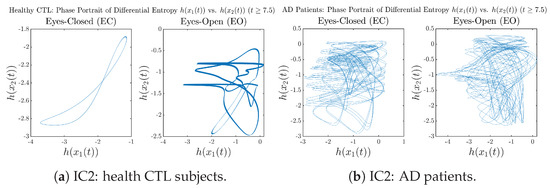
Figure A54.
Initial Conditions No.2 (IC2): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Figure A54.
Initial Conditions No.2 (IC2): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Initial Conditions No.3 (IC3):
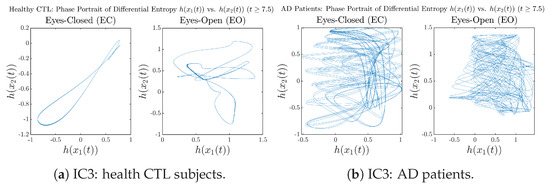
Figure A55.
Initial Conditions No.3 (IC3): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Figure A55.
Initial Conditions No.3 (IC3): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Initial Conditions No.4 (IC4):
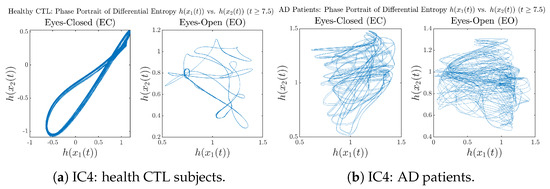
Figure A56.
Initial Conditions No.4 (IC4): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Figure A56.
Initial Conditions No.4 (IC4): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Initial Conditions No.5 (IC5):
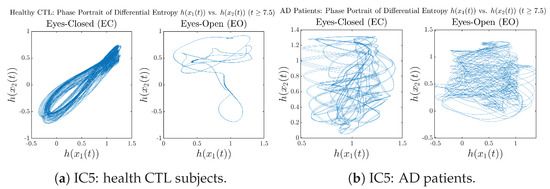
Figure A57.
Initial Conditions No.5 (IC5): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Figure A57.
Initial Conditions No.5 (IC5): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Initial Conditions No.6 (IC6):
Figure A58.
Initial Conditions No.6 (IC6): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Figure A58.
Initial Conditions No.6 (IC6): Phase portraits of Shannon differential entropy and of CTL and AD subjects.
Appendix B.4.4. Power Spectra: Shannon Differential Entropy (for )
Figure A59.
Power spectra of Shannon differential entropy and .
Figure A59.
Power spectra of Shannon differential entropy and .
Appendix B.5. Causal Information Rates , and Net Causal Information Rates
Appendix B.5.1. Time Evolution: Causal Information Rates
Initial Conditions No.1 (IC1):
Figure A60.
Initial Conditions No.1 (IC1): Causal information rates along time of CTL and AD subjects.
Figure A60.
Initial Conditions No.1 (IC1): Causal information rates along time of CTL and AD subjects.
Initial Conditions No.2 (IC2):
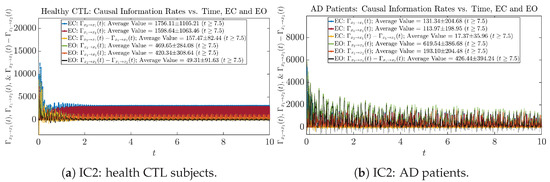
Figure A61.
Initial Conditions No.2 (IC2): Causal information rates along time of CTL and AD subjects.
Figure A61.
Initial Conditions No.2 (IC2): Causal information rates along time of CTL and AD subjects.
Initial Conditions No.3 (IC3):
Figure A62.
Initial Conditions No.3 (IC3): Causal information rates along time of CTL and AD subjects.
Figure A62.
Initial Conditions No.3 (IC3): Causal information rates along time of CTL and AD subjects.
Initial Conditions No.4 (IC4):
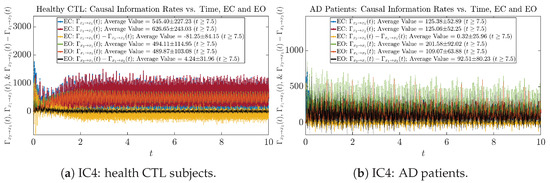
Figure A63.
Initial Conditions No.4 (IC4): Causal information rates along time of CTL and AD subjects.
Figure A63.
Initial Conditions No.4 (IC4): Causal information rates along time of CTL and AD subjects.
Initial Conditions No.5 (IC5):
Figure A64.
Initial Conditions No.5 (IC5): Causal information rates along time of CTL and AD subjects.
Figure A64.
Initial Conditions No.5 (IC5): Causal information rates along time of CTL and AD subjects.
Initial Conditions No.6 (IC6):
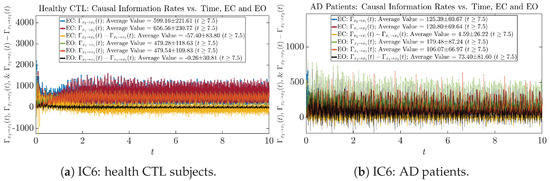
Figure A65.
Initial Conditions No.6 (IC6): Causal information rates along time of CTL and AD subjects.
Figure A65.
Initial Conditions No.6 (IC6): Causal information rates along time of CTL and AD subjects.
Appendix B.5.2. Empirical Probability Distribution: Causal Information Rates (for )
Initial Conditions No.1 (IC1):
Figure A66.
Initial Conditions No.1 (IC1): Empirical probability distributions of causal information rates and net causal information rates .
Figure A66.
Initial Conditions No.1 (IC1): Empirical probability distributions of causal information rates and net causal information rates .
Initial Conditions No.2 (IC2):
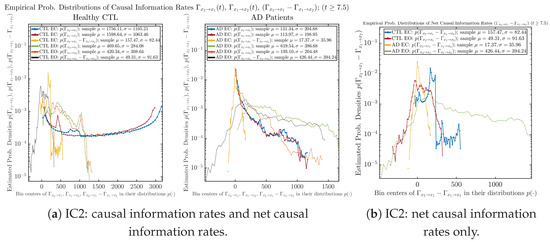
Figure A67.
Initial Conditions No.2 (IC2): Empirical probability distributions of causal information rates and net causal information rates .
Figure A67.
Initial Conditions No.2 (IC2): Empirical probability distributions of causal information rates and net causal information rates .
Initial Conditions No.3 (IC3):
Figure A68.
Initial Conditions No.3 (IC3): Empirical probability distributions of causal information rates and net causal information rates .
Figure A68.
Initial Conditions No.3 (IC3): Empirical probability distributions of causal information rates and net causal information rates .
Initial Conditions No.4 (IC4):
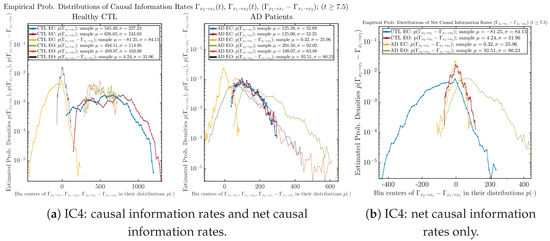
Figure A69.
Initial Conditions No.4 (IC4): Empirical probability distributions of causal information rates and net causal information rates .
Figure A69.
Initial Conditions No.4 (IC4): Empirical probability distributions of causal information rates and net causal information rates .
Initial Conditions No.5 (IC5):
Figure A70.
Initial Conditions No.5 (IC5): Empirical probability distributions of causal information rates and net causal information rates .
Figure A70.
Initial Conditions No.5 (IC5): Empirical probability distributions of causal information rates and net causal information rates .
Initial Conditions No.6 (IC6):
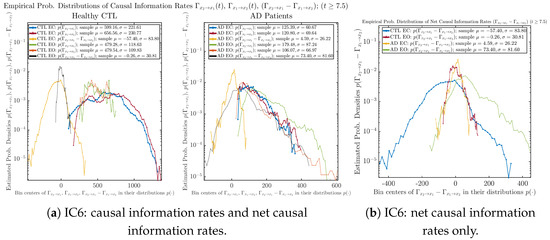
Figure A71.
Initial Conditions No.6 (IC6): Empirical probability distributions of causal information rates and net causal information rates .
Figure A71.
Initial Conditions No.6 (IC6): Empirical probability distributions of causal information rates and net causal information rates .
Appendix B.6. Causality Based on Transfer Entropy (TE)
Appendix B.6.1. Time Evolution: Transfer Entropy (TE)
Initial Conditions No.1 (IC1):
Figure A72.
Initial Conditions No.1 (IC1): Transfer Entropy (TE) along time of CTL and AD subjects.
Figure A72.
Initial Conditions No.1 (IC1): Transfer Entropy (TE) along time of CTL and AD subjects.
Initial Conditions No.2 (IC2):
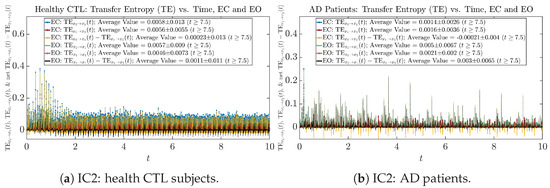
Figure A73.
Initial Conditions No.2 (IC2): Transfer Entropy (TE) along time of CTL and AD subjects.
Figure A73.
Initial Conditions No.2 (IC2): Transfer Entropy (TE) along time of CTL and AD subjects.
Initial Conditions No.3 (IC3):
Figure A74.
Initial Conditions No.3 (IC3): Transfer Entropy (TE) along time of CTL and AD subjects.
Figure A74.
Initial Conditions No.3 (IC3): Transfer Entropy (TE) along time of CTL and AD subjects.
Initial Conditions No.4 (IC4):
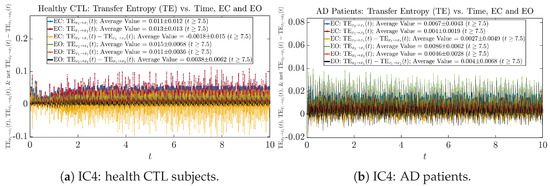
Figure A75.
Initial Conditions No.4 (IC4): Transfer Entropy (TE) along time of CTL and AD subjects.
Figure A75.
Initial Conditions No.4 (IC4): Transfer Entropy (TE) along time of CTL and AD subjects.
Initial Conditions No.5 (IC5):
Figure A76.
Initial Conditions No.5 (IC5): Transfer Entropy (TE) along time of CTL and AD subjects.
Figure A76.
Initial Conditions No.5 (IC5): Transfer Entropy (TE) along time of CTL and AD subjects.
Initial Conditions No.6 (IC6):
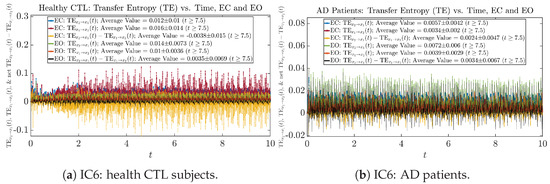
Figure A77.
Initial Conditions No.6 (IC6): Transfer Entropy (TE) along time of CTL and AD subjects.
Figure A77.
Initial Conditions No.6 (IC6): Transfer Entropy (TE) along time of CTL and AD subjects.
Appendix B.6.2. Empirical Probability Distribution: Transfer Entropy (TE) (for )
Initial Conditions No.1 (IC1):
Figure A78.
Initial Conditions No.1 (IC1): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Figure A78.
Initial Conditions No.1 (IC1): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Initial Conditions No.2 (IC2):
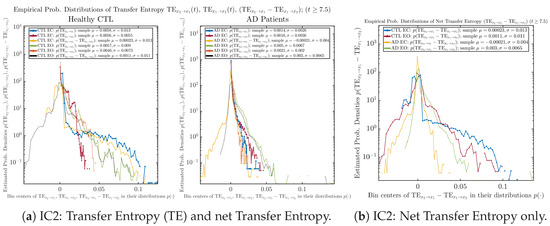
Figure A79.
Initial Conditions No.2 (IC2): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Figure A79.
Initial Conditions No.2 (IC2): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Initial Conditions No.3 (IC3):
Figure A80.
Initial Conditions No.3 (IC3): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Figure A80.
Initial Conditions No.3 (IC3): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Initial Conditions No.4 (IC4):
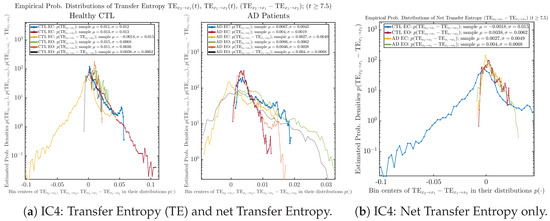
Figure A81.
Initial Conditions No.4 (IC4): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Figure A81.
Initial Conditions No.4 (IC4): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Initial Conditions No.5 (IC5):
Figure A82.
Initial Conditions No.5 (IC5): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Figure A82.
Initial Conditions No.5 (IC5): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Initial Conditions No.6 (IC6):
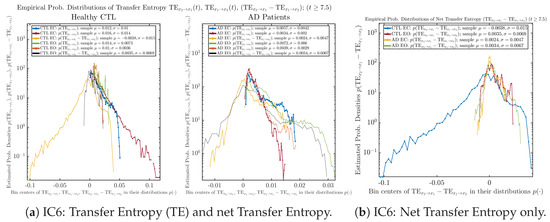
Figure A83.
Initial Conditions No.6 (IC6): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
Figure A83.
Initial Conditions No.6 (IC6): Empirical probability distributions of Transfer Entropy (TE) and net Transfer Entropy .
References
- Ghorbanian, P.; Ramakrishnan, S.; Ashrafiuon, H. Stochastic Non-Linear Oscillator Models of EEG: The Alzheimer’s Disease Case. Front. Comput. Neurosci. 2015, 9, 48. [Google Scholar] [CrossRef]
- Szuflitowska, B.; Orlowski, P. Statistical and Physiologically Analysis of Using a Duffing-van Der Pol Oscillator to Modeled Ictal Signals. In Proceedings of the 2020 16th International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; pp. 1137–1142. [Google Scholar] [CrossRef]
- Nguyen, P.T.M.; Hayashi, Y.; Baptista, M.D.S.; Kondo, T. Collective Almost Synchronization-Based Model to Extract and Predict Features of EEG Signals. Sci. Rep. 2020, 10, 16342. [Google Scholar] [CrossRef] [PubMed]
- Guguloth, S.; Agarwal, V.; Parthasarathy, H.; Upreti, V. Synthesis of EEG Signals Modeled Using Non-Linear Oscillator Based on Speech Data with EKF. Biomed. Signal Process. Control 2022, 77, 103818. [Google Scholar] [CrossRef]
- Szuflitowska, B.; Orlowski, P. Analysis of Parameters Distribution of EEG Signals for Five Epileptic Seizure Phases Modeled by Duffing Van Der Pol Oscillator. In Proceedings of the Computational Science—ICCS 2022, London, UK, 21–23 June 2022; Groen, D., De Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; Volume 13352, pp. 188–201. [Google Scholar] [CrossRef]
- Barry, R.J.; De Blasio, F.M. EEG Differences between Eyes-Closed and Eyes-Open Resting Remain in Healthy Ageing. Biol. Psychol. 2017, 129, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Jennings, J.L.; Peraza, L.R.; Baker, M.; Alter, K.; Taylor, J.P.; Bauer, R. Investigating the Power of Eyes Open Resting State EEG for Assisting in Dementia Diagnosis. Alzheimer’s Res. Ther. 2022, 14, 109. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, J.F.; Mateos, D.M.; López, J.M.D. A Transfer Entropy-Based Methodology to Analyze Information Flow under Eyes-Open and Eyes-Closed Conditions with a Clinical Perspective. Biomed. Signal Process. Control 2023, 86, 105181. [Google Scholar] [CrossRef]
- Klepl, D.; He, F.; Wu, M.; Marco, M.D.; Blackburn, D.J.; Sarrigiannis, P.G. Characterising Alzheimer’s Disease with EEG-Based Energy Landscape Analysis. IEEE J. Biomed. Health Inform. 2022, 26, 992–1000. [Google Scholar] [CrossRef] [PubMed]
- Gunawardena, R.; Sarrigiannis, P.G.; Blackburn, D.J.; He, F. Kernel-Based Nonlinear Manifold Learning for EEG-based Functional Connectivity Analysis and Channel Selection with Application to Alzheimer’s Disease. Neuroscience 2023, 523, 140–156. [Google Scholar] [CrossRef] [PubMed]
- Barry, R.J.; Clarke, A.R.; Johnstone, S.J.; Magee, C.A.; Rushby, J.A. EEG Differences between Eyes-Closed and Eyes-Open Resting Conditions. Clin. Neurophysiol. 2007, 118, 2765–2773. [Google Scholar] [CrossRef]
- Barry, R.J.; Clarke, A.R.; Johnstone, S.J.; Brown, C.R. EEG Differences in Children between Eyes-Closed and Eyes-Open Resting Conditions. Clin. Neurophysiol. 2009, 120, 1806–1811. [Google Scholar] [CrossRef]
- Matsutomo, N.; Fukami, M.; Kobayashi, K.; Endo, Y.; Kuhara, S.; Yamamoto, T. Effects of Eyes-Closed Resting and Eyes-Open Conditions on Cerebral Blood Flow Measurement Using Arterial Spin Labeling Magnetic Resonance Imaging. Neurol. Clin. Neurosci. 2023, 11, 10–16. [Google Scholar] [CrossRef]
- Agcaoglu, O.; Wilson, T.W.; Wang, Y.P.; Stephen, J.; Calhoun, V.D. Resting State Connectivity Differences in Eyes Open versus Eyes Closed Conditions. Hum. Brain Mapp. 2019, 40, 2488–2498. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Zhou, L.; Wu, H.; Huang, Y.; Qiu, M.; Huang, L.; Lee, C.; Lane, T.J.; Qin, P. Eyes-Open and Eyes-Closed Resting State Network Connectivity Differences. Brain Sci. 2023, 13, 122. [Google Scholar] [CrossRef] [PubMed]
- Miraglia, F.; Vecchio, F.; Bramanti, P.; Rossini, P.M. EEG Characteristics in “Eyes-Open” versus “Eyes-Closed” Conditions: Small-world Network Architecture in Healthy Aging and Age-Related Brain Degeneration. Clin. Neurophysiol. 2016, 127, 1261–1268. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Chen, T.; Li, C.; Liu, G.; Qiu, J.; Wei, D. Eyes-Open and Eyes-Closed Resting States with Opposite Brain Activity in Sensorimotor and Occipital Regions: Multidimensional Evidences from Machine Learning Perspective. Front. Hum. Neurosci. 2018, 12, 422. [Google Scholar] [CrossRef] [PubMed]
- Springer, B.A.; Marin, R.; Cyhan, T.; Roberts, H.; Gill, N.W. Normative Values for the Unipedal Stance Test with Eyes Open and Closed. J. Geriatr. Phys. Ther. 2007, 30, 8. [Google Scholar] [CrossRef] [PubMed]
- Marx, E.; Deutschländer, A.; Stephan, T.; Dieterich, M.; Wiesmann, M.; Brandt, T. Eyes Open and Eyes Closed as Rest Conditions: Impact on Brain Activation Patterns. NeuroImage 2004, 21, 1818–1824. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Liang, B.; Wu, X.; Wang, Z.; Xu, P.; Chang, S.; Liu, B.; Liu, M.; Huang, R. Directionality of Large-Scale Resting-State Brain Networks during Eyes Open and Eyes Closed Conditions. Front. Hum. Neurosci. 2015, 9, 81. [Google Scholar] [CrossRef]
- Xu, P.; Huang, R.; Wang, J.; Van Dam, N.T.; Xie, T.; Dong, Z.; Chen, C.; Gu, R.; Zang, Y.F.; He, Y.; et al. Different Topological Organization of Human Brain Functional Networks with Eyes Open versus Eyes Closed. NeuroImage 2014, 90, 246–255. [Google Scholar] [CrossRef]
- Jeong, J. EEG Dynamics in Patients with Alzheimer’s Disease. Clin. Neurophysiol. 2004, 115, 1490–1505. [Google Scholar] [CrossRef]
- Pritchard, W.S.; Duke, D.W.; Coburn, K.L. Altered EEG Dynamical Responsivity Associated with Normal Aging and Probable Alzheimer’s Disease. Dementia 1991, 2, 102–105. [Google Scholar] [CrossRef]
- Thiruthummal, A.A.; Kim, E.j. Monte Carlo Simulation of Stochastic Differential Equation to Study Information Geometry. Entropy 2022, 24, 1113. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.j.; Guel-Cortez, A.J. Causal Information Rate. Entropy 2021, 23, 1087. [Google Scholar] [CrossRef] [PubMed]
- Choong, H.J.; Kim, E.j.; He, F. Causality Analysis with Information Geometry: A Comparison. Entropy 2023, 25, 806. [Google Scholar] [CrossRef] [PubMed]
- Baravalle, R.; Rosso, O.A.; Montani, F. Causal Shannon–Fisher Characterization of Motor/Imagery Movements in EEG. Entropy 2018, 20, 660. [Google Scholar] [CrossRef] [PubMed]
- Montani, F.; Baravalle, R.; Montangie, L.; Rosso, O.A. Causal Information Quantification of Prominent Dynamical Features of Biological Neurons. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20150109. [Google Scholar] [CrossRef] [PubMed]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Guel-Cortez, A.-J.; Kim, E.-j. Information Geometric Theory in the Prediction of Abrupt Changes in System Dynamics. Entropy 2021, 23, 694. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.i.; Nagaoka, H. Methods of Information Geometry; American Mathematical Soc.: Providence, RI, USA, 2000; Volume 191. [Google Scholar]
- Frieden, B.R. Science from Fisher Information; Cambridge University Press: Cambridge, UK, 2004; Volume 974. [Google Scholar]
- Facchi, P.; Kulkarni, R.; Man’ko, V.I.; Marmo, G.; Sudarshan, E.C.G.; Ventriglia, F. Classical and Quantum Fisher Information in the Geometrical Formulation of Quantum Mechanics. Phys. Lett. A 2010, 374, 4801–4803. [Google Scholar] [CrossRef]
- Itoh, M.; Shishido, Y. Fisher Information Metric and Poisson Kernels. Differ. Geom. Its Appl. 2008, 26, 347–356. [Google Scholar] [CrossRef]
- Sahann, R.; Möller, T.; Schmidt, J. Histogram Binning Revisited with a Focus on Human Perception. arXiv 2021, arXiv:cs/2109.06612. [Google Scholar] [CrossRef]
- Terrell, G.R.; Scott, D.W. Oversmoothed Nonparametric Density Estimates. J. Am. Stat. Assoc. 1985, 80, 209–214. [Google Scholar] [CrossRef]
- Budišić, M.; Mohr, R.M.; Mezić, I. Applied Koopmanism. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 047510. [Google Scholar] [CrossRef] [PubMed]
- Koopman, B.O. Hamiltonian Systems and Transformation in Hilbert Space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).