Fast Model Selection and Hyperparameter Tuning for Generative Models
Abstract
1. Introduction
2. Methods
2.1. Non-Stochastic Best-Arm Identification and Successive Halving
| Algorithm 1 Successive Halving |
Input: Budget B, K models
|
2.2. Exponentially Weighed Average of
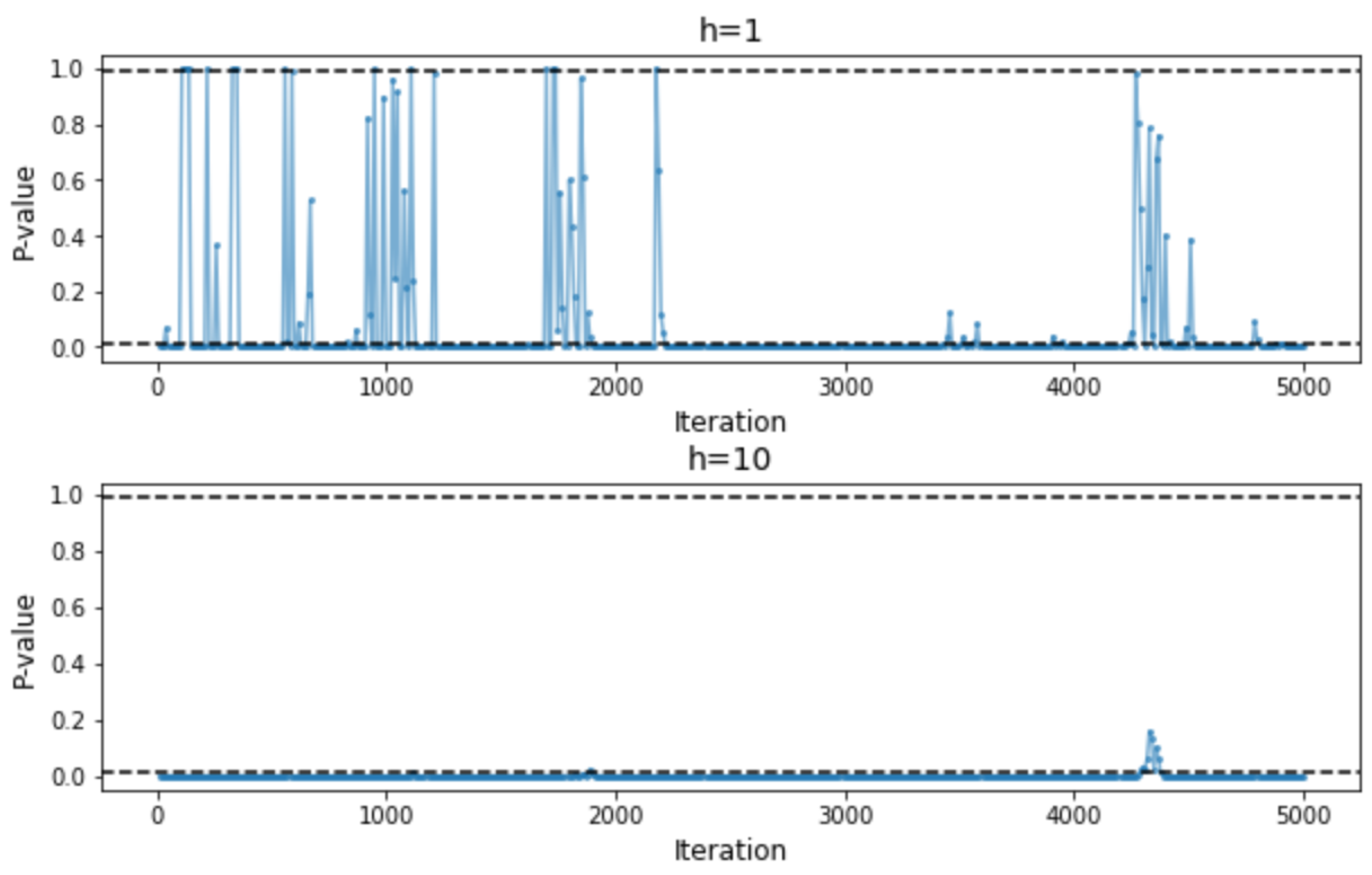
2.3. Adaptive Successive Halving with Hypothesis Testing
| Algorithm 2 Adaptive Successive Halving |
Input: Budget B, K models , decay rate , window size h, significance level
|
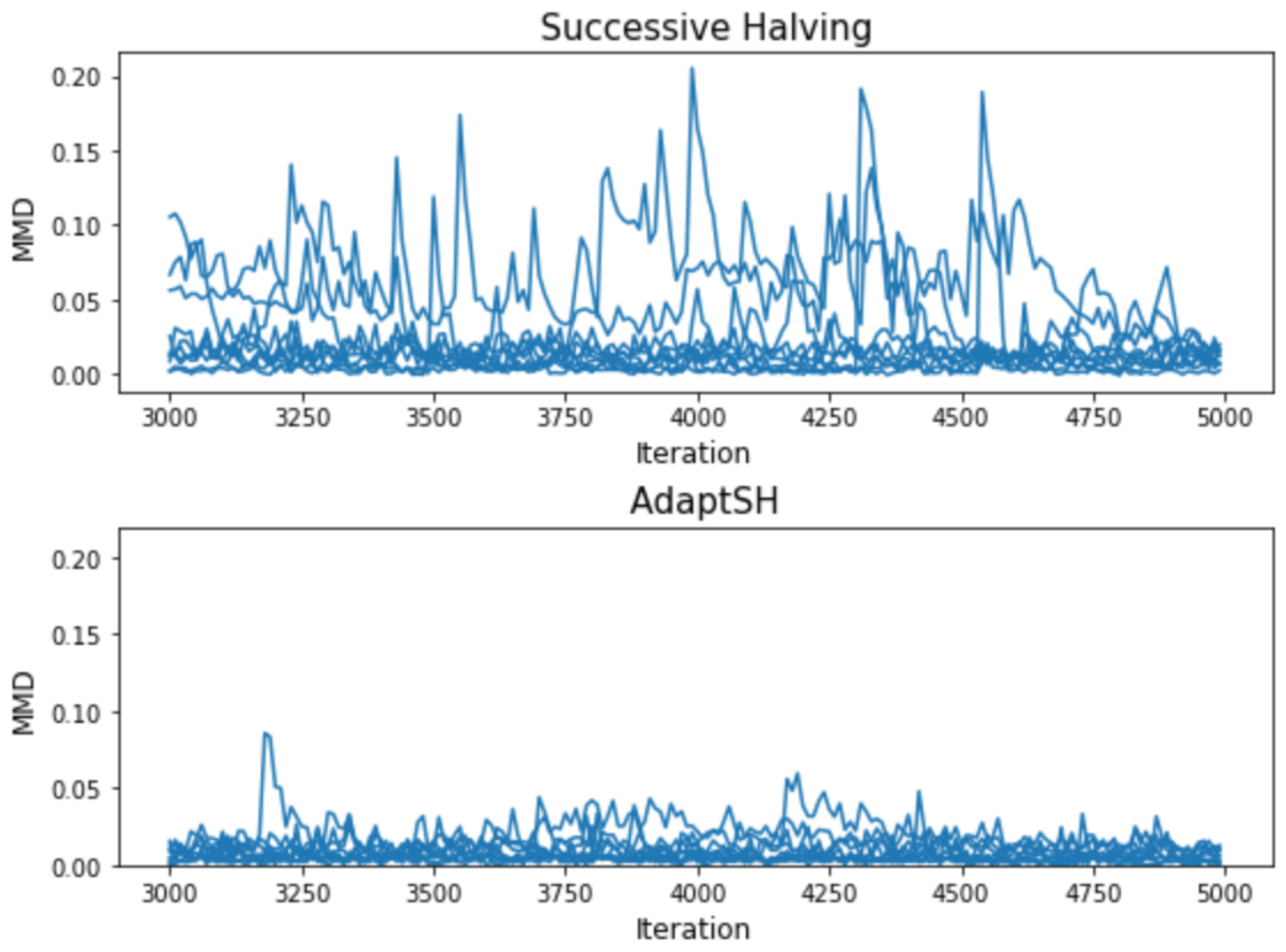
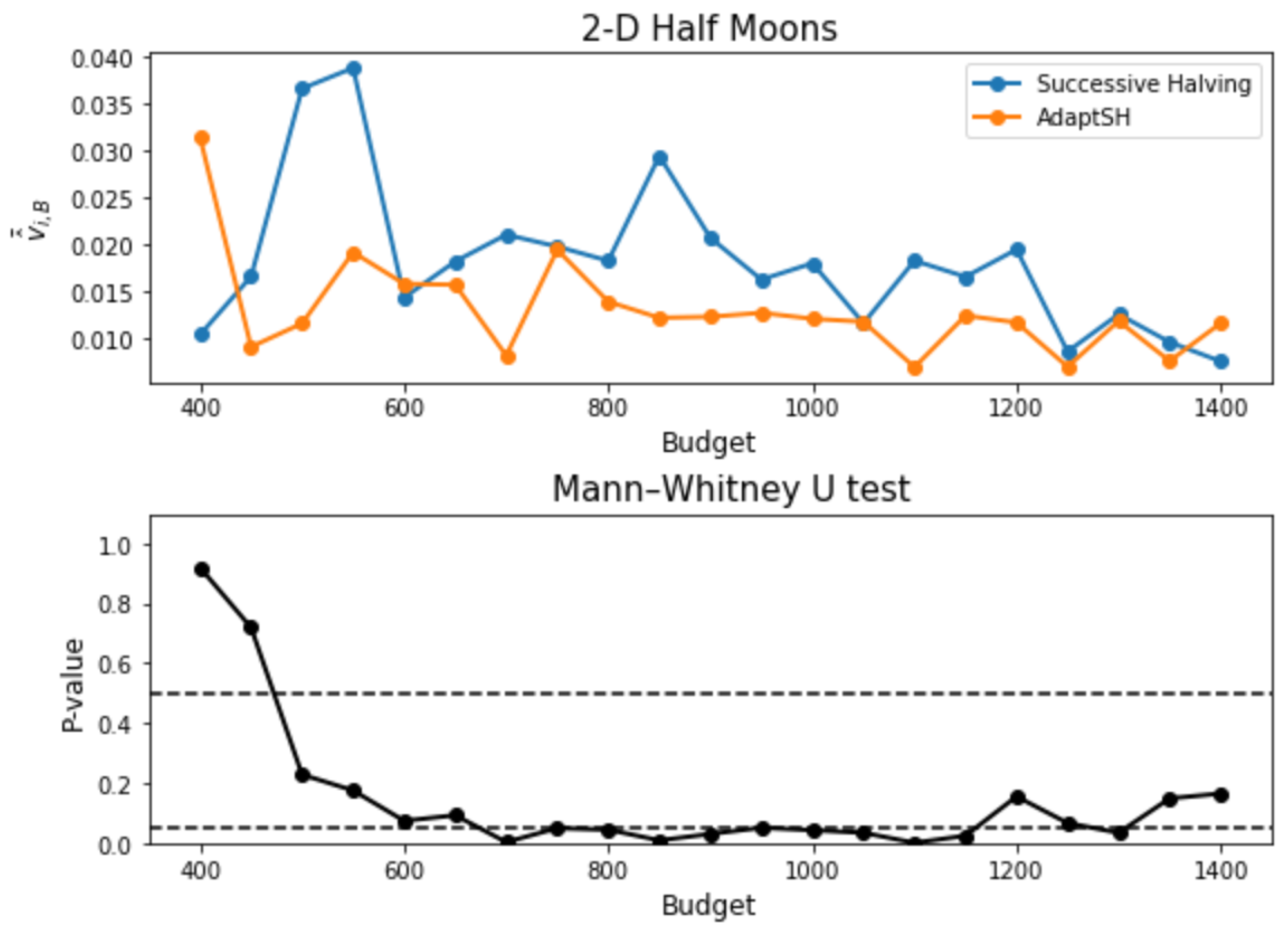
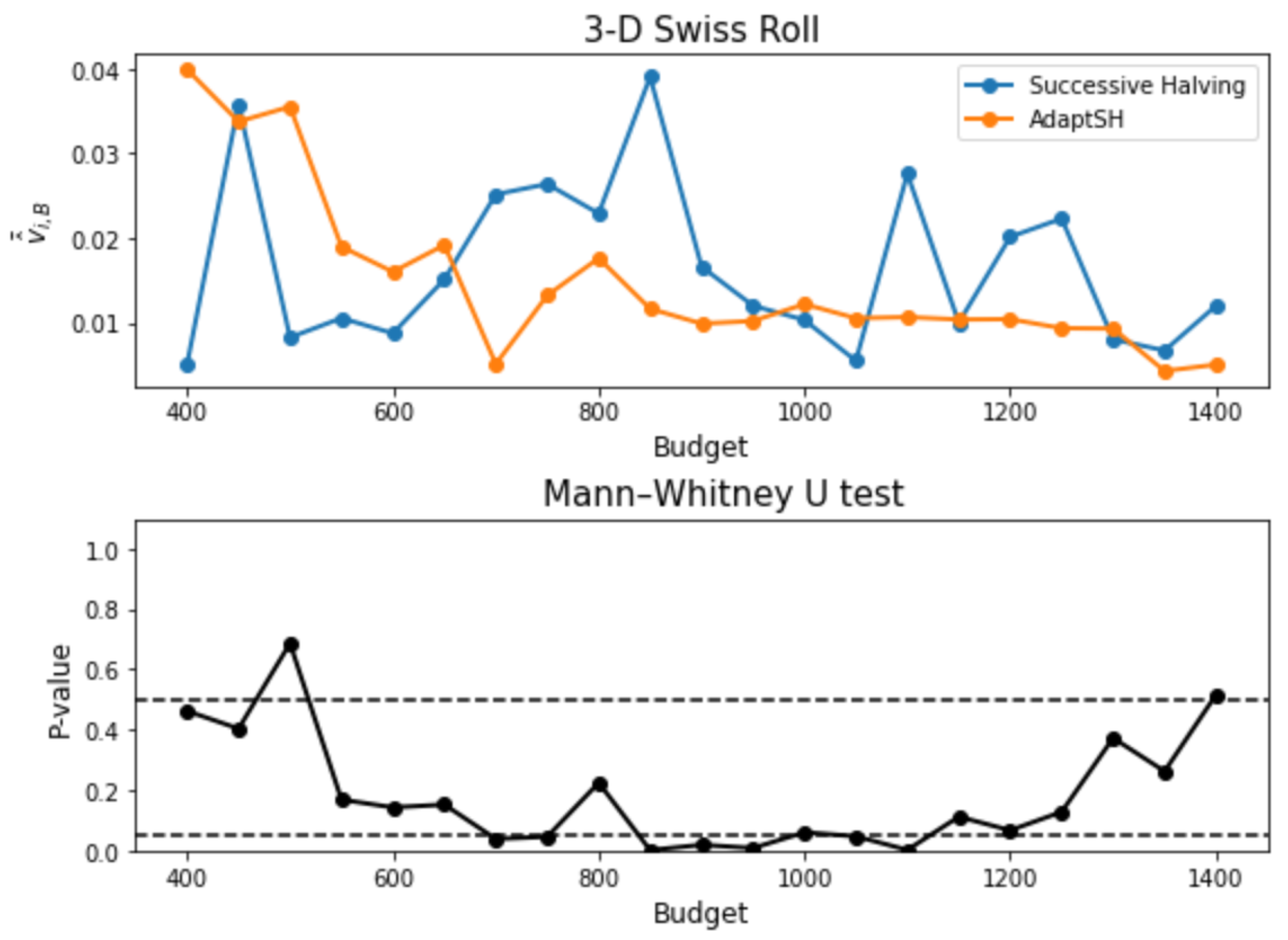
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Covariance Matrix
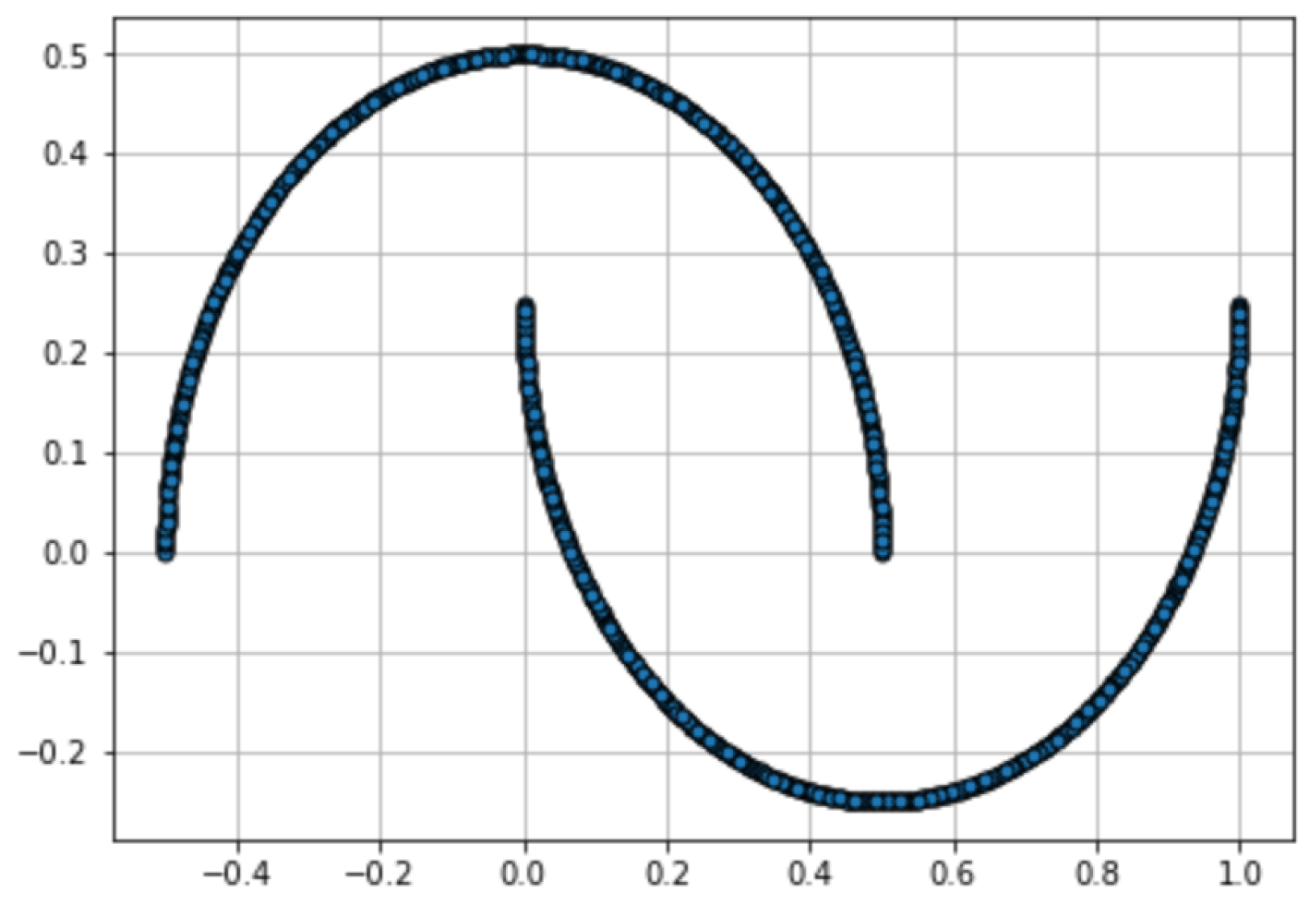
Appendix B. Experiment Settings
| Distance Metric | Hyperparameters |
|---|---|
| ASWD [26] | L: {1000}, : {10, 20}, : {1, 5}, : {0.005, 0.0005} |
| MSWD [27] | : {10, 50} |
| SWD [28] | L: {10, 1000} |
| GSWD [29] | L: {10, 1000}, r: {2, 5} |
| MGSWD [29] | : {10, 50}, r: {2, 5} |
| MGSWNN [29] | : {10, 50} |
| DSWD [30] | L: {1000}, : {10, 20}, : {1, 5}, : {0.005, 0.0005} |
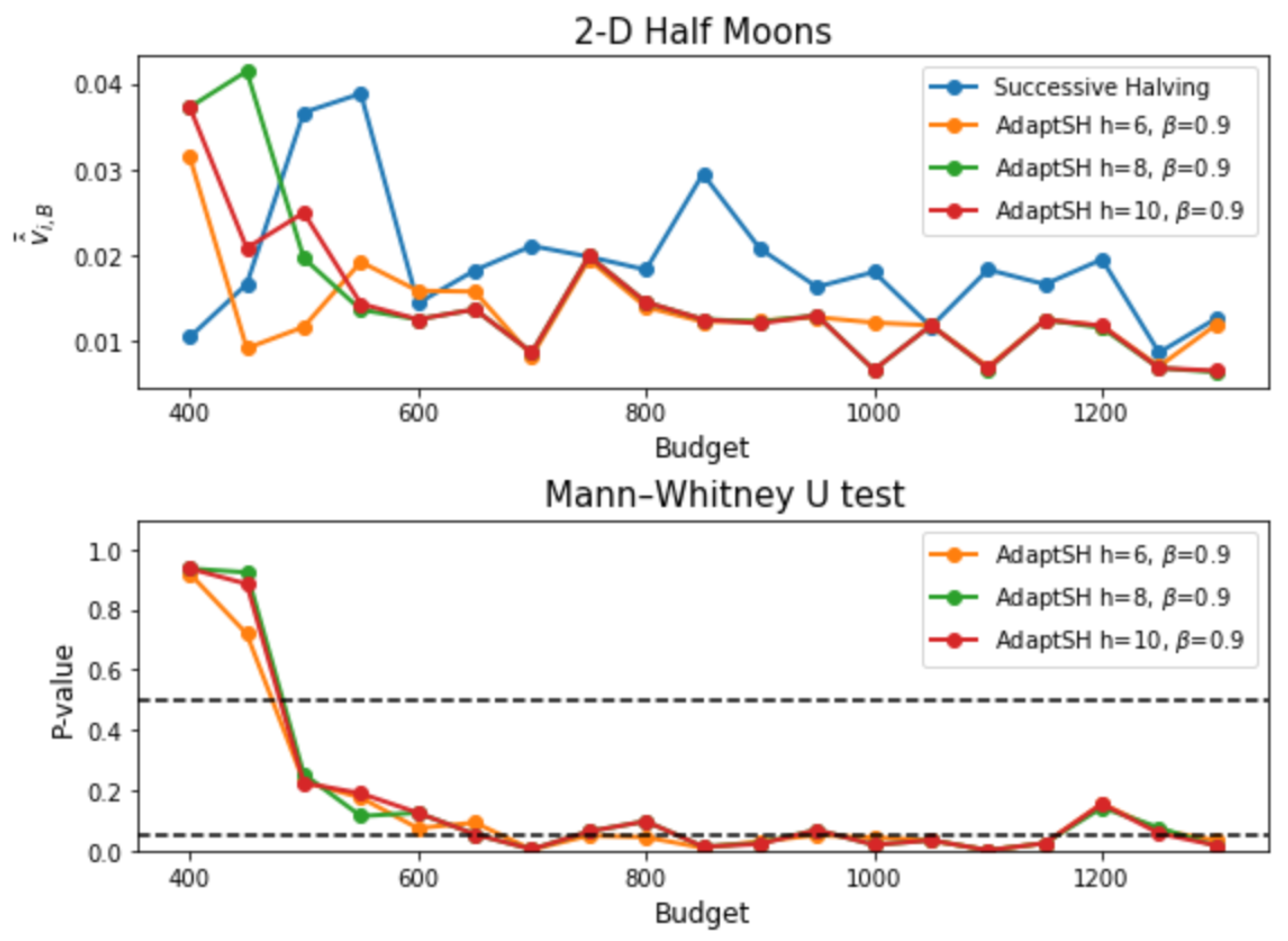
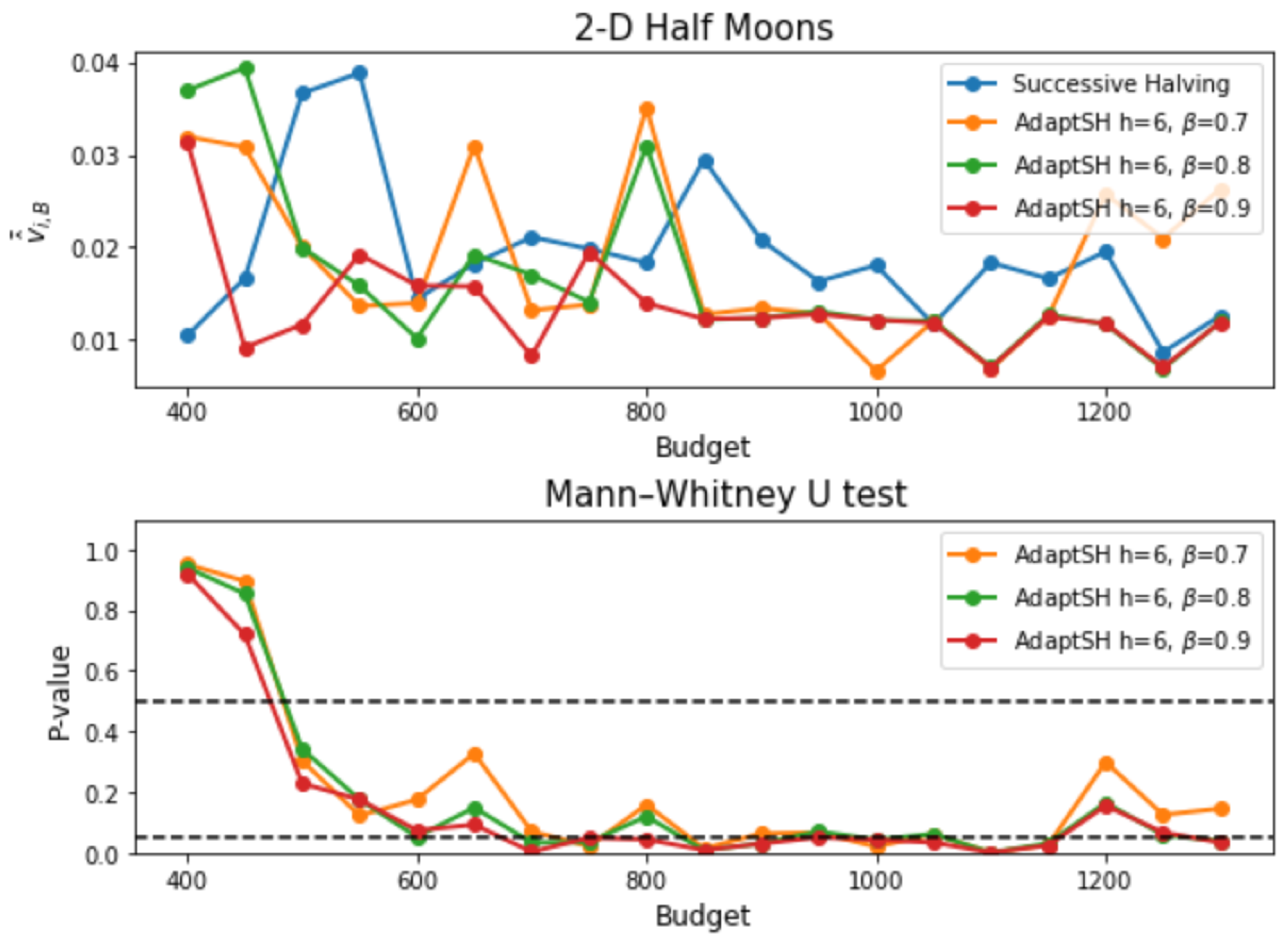
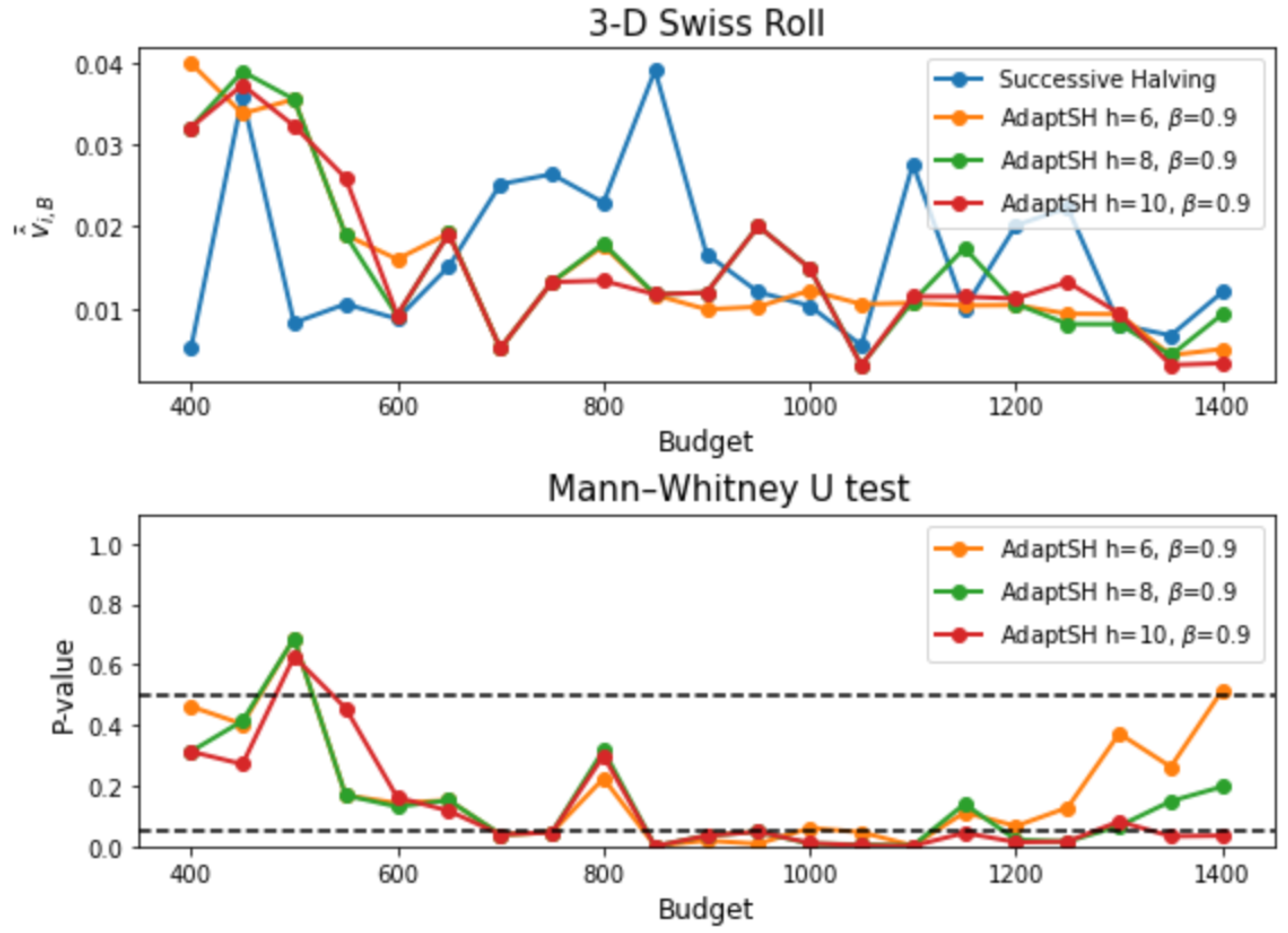
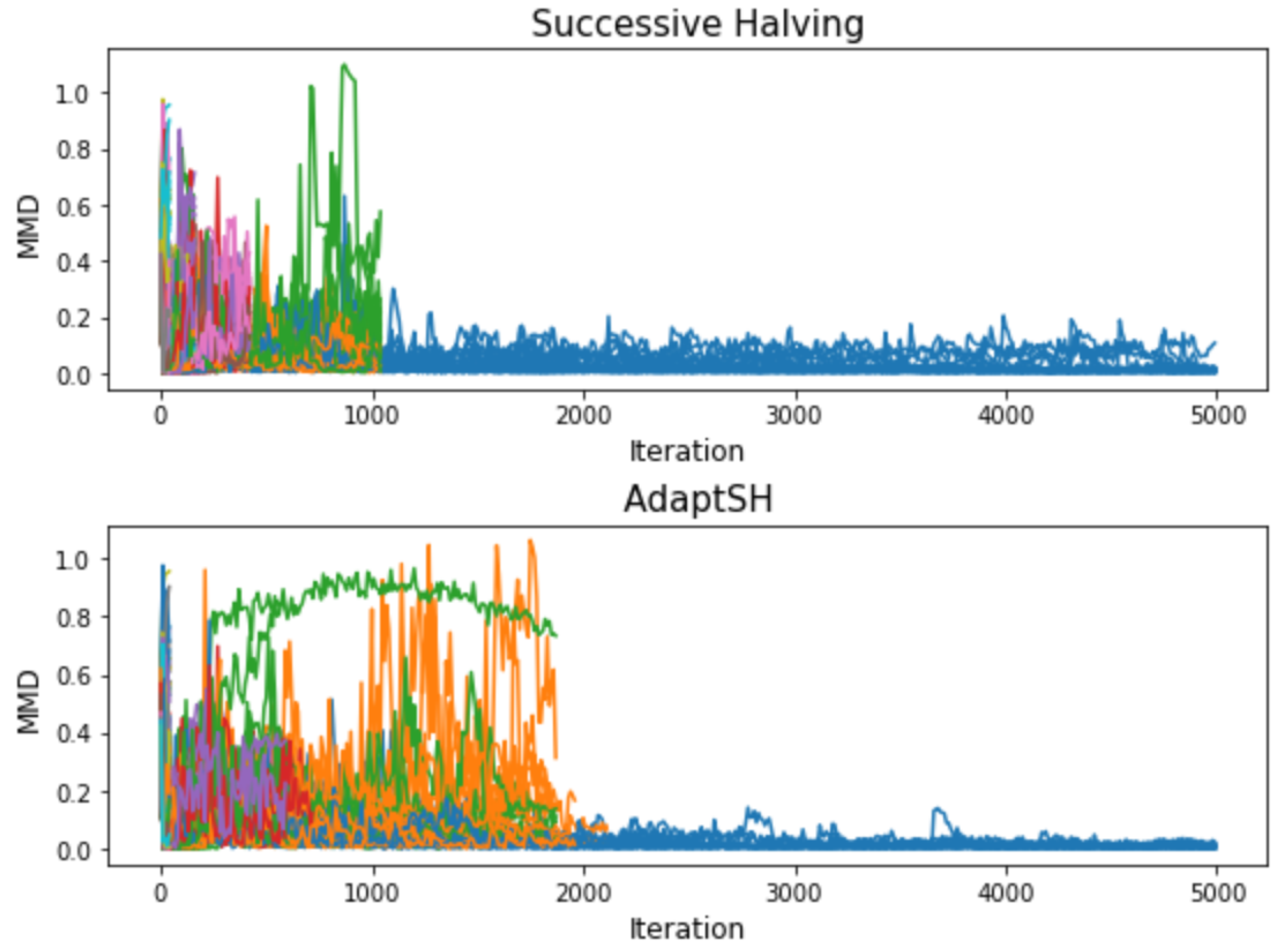
Appendix C. Additional Experimental Results

References
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 25th Annual Conference on Neural Information Processing Systems (NIPS 2011), Granada, Spain, 12–15 December 2011; Neural Information Processing Systems Foundation: La Jolla, CA, USA, 2011; Volume 24. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the International Conference on Learning and Intelligent Optimization, Rome, Italy, 17–21 January 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- Wang, Z.; Zoghi, M.; Hutter, F.; Matheson, D.; De Freitas, N. Bayesian Optimization in High Dimensions via Random Embeddings. In Proceedings of the IJCAI, Beijing, China, 3–9 August 2013; pp. 1778–1784. [Google Scholar]
- Swersky, K.; Snoek, J.; Adams, R.P. Freeze-thaw bayesian optimization. arXiv 2014, arXiv:1406.3896. [Google Scholar]
- Domhan, T.; Springenberg, J.T.; Hutter, F. Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Klein, A.; Falkner, S.; Bartels, S.; Hennig, P.; Hutter, F. Fast bayesian optimization of machine learning hyperparameters on large datasets. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Lauderdale, FL, USA, 20–22 April 2017; pp. 528–536. [Google Scholar]
- Sparks, E.R.; Talwalkar, A.; Haas, D.; Franklin, M.J.; Jordan, M.I.; Kraska, T. Automating model search for large scale machine learning. In Proceedings of the Sixth ACM Symposium on Cloud Computing, Kohala Coast, HI, USA, 27–29 August 2015; pp. 368–380. [Google Scholar]
- Jamieson, K.; Talwalkar, A. Non-stochastic best arm identification and hyperparameter optimization. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 240–248. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Karnin, Z.; Koren, T.; Somekh, O. Almost optimal exploration in multi-armed bandits. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1238–1246. [Google Scholar]
- Wang, Z.; She, Q.; Ward, T.E. Generative adversarial networks in computer vision: A survey and taxonomy. ACM Comput. Surv. (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Villani, C. Optimal Transport: OLD and New; Springer: Berlin/Heidelberg, Germany, 2009; Volume 338. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Theis, L.; Oord, A.v.d.; Bethge, M. A note on the evaluation of generative models. arXiv 2015, arXiv:1511.01844. [Google Scholar]
- Bińkowski, M.; Sutherland, D.J.; Arbel, M.; Gretton, A. Demystifying mmd gans. arXiv 2018, arXiv:1801.01401. [Google Scholar]
- Xu, Q.; Huang, G.; Yuan, Y.; Guo, C.; Sun, Y.; Wu, F.; Weinberger, K. An empirical study on evaluation metrics of generative adversarial networks. arXiv 2018, arXiv:1806.07755. [Google Scholar]
- Müller, A. Integral probability metrics and their generating classes of functions. Adv. Appl. Probab. 1997, 29, 429–443. [Google Scholar] [CrossRef]
- Ramdas, A.; Trillos, N.G.; Cuturi, M. On wasserstein two-sample testing and related families of nonparametric tests. Entropy 2017, 19, 47. [Google Scholar] [CrossRef]
- Genevay, A.; Peyré, G.; Cuturi, M. Learning generative models with sinkhorn divergences. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Playa Blanca, Lanzarote, Spain, 9–11 April 2018; pp. 1608–1617. [Google Scholar]
- Benjamini, Y.; Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001, 29, 1165–1188. [Google Scholar] [CrossRef]
- Bounliphone, W.; Belilovsky, E.; Blaschko, M.B.; Antonoglou, I.; Gretton, A. A test of relative similarity for model selection in generative models. arXiv 2015, arXiv:1511.04581. [Google Scholar]
- Hoeffding, W. A Class of Statistics with Asymptotically Normal Distribution. Ann. Math. Stat. 1948, 293–325. [Google Scholar] [CrossRef]
- Gao, R.; Liu, F.; Zhang, J.; Han, B.; Liu, T.; Niu, G.; Sugiyama, M. Maximum mean discrepancy test is aware of adversarial attacks. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 3564–3575. [Google Scholar]
- Chen, X.; Yang, Y.; Li, Y. Augmented Sliced Wasserstein Distances. arXiv 2020, arXiv:2006.08812. [Google Scholar]
- Deshpande, I.; Hu, Y.T.; Sun, R.; Pyrros, A.; Siddiqui, N.; Koyejo, S.; Zhao, Z.; Forsyth, D.; Schwing, A.G. Max-Sliced Wasserstein distance and its use for GANs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10648–10656. [Google Scholar]
- Deshpande, I.; Zhang, Z.; Schwing, A.G. Generative modeling using the sliced wasserstein distance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3483–3491. [Google Scholar]
- Kolouri, S.; Nadjahi, K.; Simsekli, U.; Badeau, R.; Rohde, G. Generalized sliced wasserstein distances. In Proceedings of the Annual Conference on Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 261–272. [Google Scholar]
- Nguyen, K.; Ho, N.; Pham, T.; Bui, H. Distributional sliced-Wasserstein and applications to generative modeling. arXiv 2020, arXiv:2002.07367. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Ghosh, S.K. Fast Model Selection and Hyperparameter Tuning for Generative Models. Entropy 2024, 26, 150. https://doi.org/10.3390/e26020150
Chen L, Ghosh SK. Fast Model Selection and Hyperparameter Tuning for Generative Models. Entropy. 2024; 26(2):150. https://doi.org/10.3390/e26020150
Chicago/Turabian StyleChen, Luming, and Sujit K. Ghosh. 2024. "Fast Model Selection and Hyperparameter Tuning for Generative Models" Entropy 26, no. 2: 150. https://doi.org/10.3390/e26020150
APA StyleChen, L., & Ghosh, S. K. (2024). Fast Model Selection and Hyperparameter Tuning for Generative Models. Entropy, 26(2), 150. https://doi.org/10.3390/e26020150







