A Time-Varying Mixture Integer-Valued Threshold Autoregressive Process Driven by Explanatory Variables
Abstract
1. Introduction
2. The First-Order Time-Varying Mixture Thinning Integer-Valued Threshold Autoregressive Model
- and That is, indicates that TVMTTINAR(1) represents the process (1).
- For fixed ,where are the regression coefficients, is a sequence of stationary, weakly dependent, and observable explanatory variables with a constant mean vector and covariance matrix. For fixed t, is assumed to be independent of .
- The binomial thinning operator “∘”, proposed by [5], is defined as , where , is a sequence of i.i.d. Bernoulli random variables satisfying and is independent of X.
- The negative binomial thinning operator “∗”, proposed by [20], is defined as , where , is a sequence of i.i.d. Geometric random variables with parameter and is independent of X.
- is a sequence of i.i.d. Poisson distributed random variables with mean λ. For fixed t, is assumed to be independent of , , and for all .
3. Parameters’ Estimation and Testing
3.1. Conditional Least Squares Estimation
3.2. Conditional Maximum Likelihood Estimation
3.3. Inference Methods for Threshold r
- Step 1. Denote and as the 10th and 90th quantile value of the observations , for each , and find such that
- Step 2. The parameter vector is estimated by (6) under the estimator , and all the parameters under r unknown cases are as follows:
- Similarly, the CML estimates for the threshold variable r can also be achieved based on the following steps:
- Step 1. Denote and as the 10th and 90th quantile value of the observations , for each , and find such that
- Step 2. The parameter vector is estimated by (6) under the estimator , and all the parameters under r unknown cases are as follows:
3.4. Testing the Existence of the Piecewise Structure
3.5. Testing the Existence of Explanatory Variables
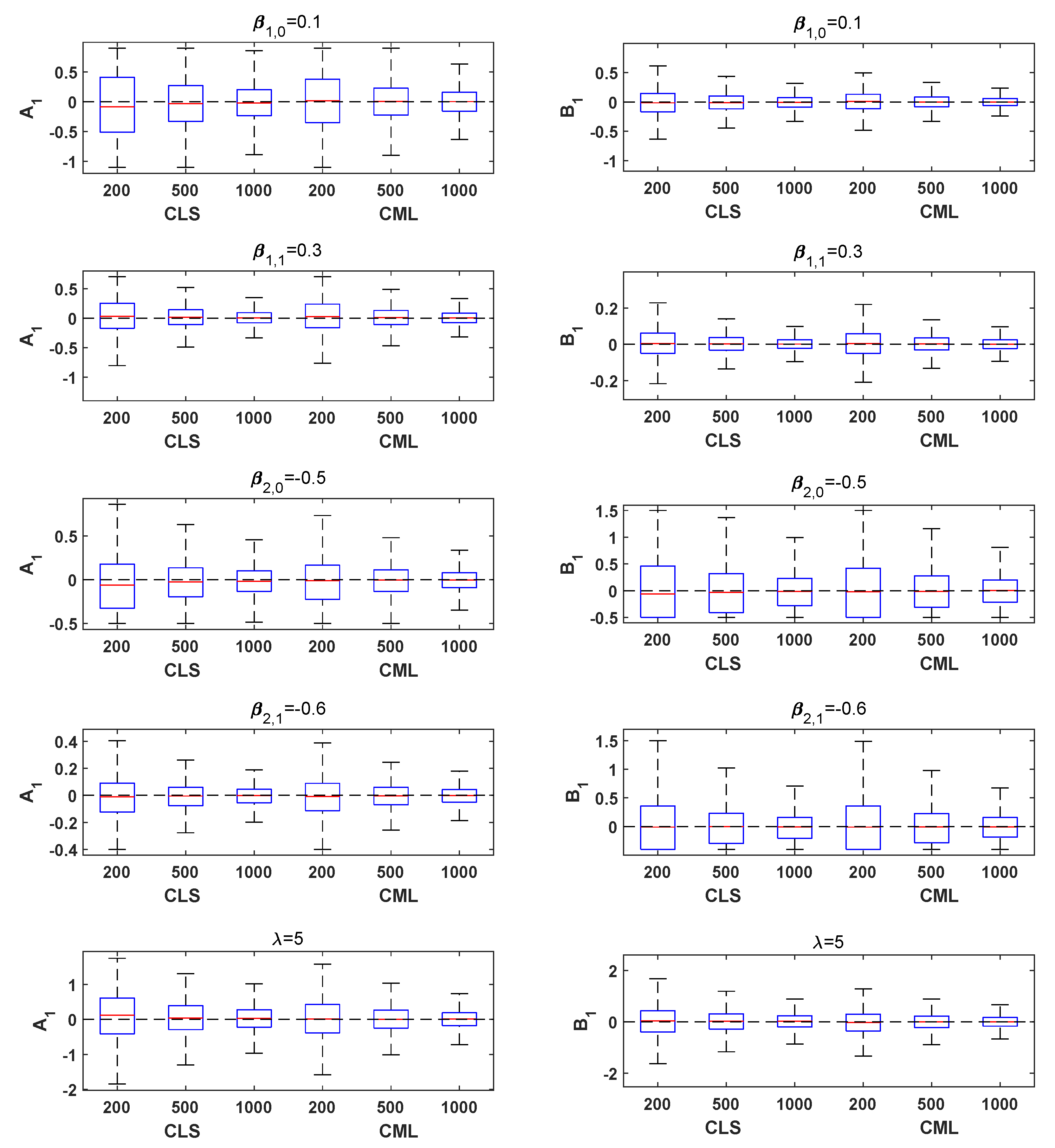
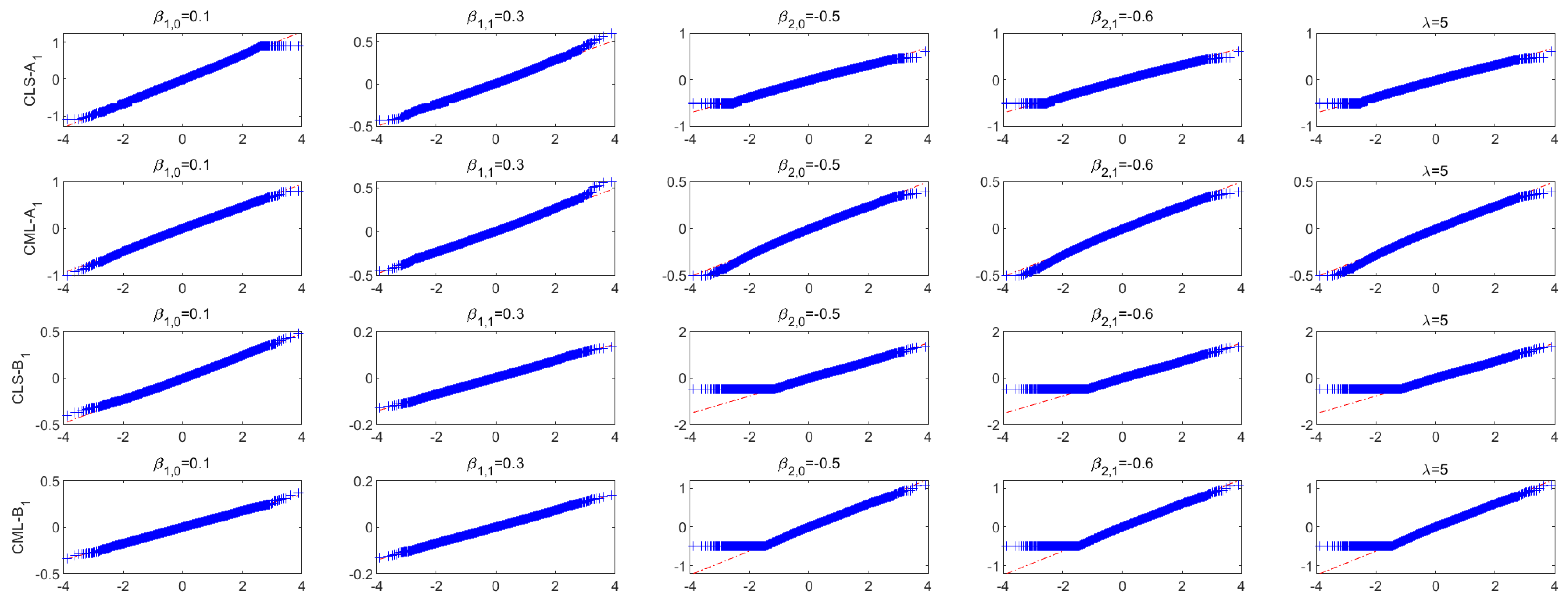
4. Simulation Studies
- Model A1 (B1): Generated from the TVMTTINAR(1) process (3) with (), , , , . The explanatory variables are generalized from the i.i.d. normal distribution .
- Model A2 (B2): Generated from the TVMTTINAR(1) process (3) with (), , , , . The explanatory variables are generalized from an AR(1) process, i.e., with , .
- Model A3 (B3): Generated from the TVMTTINAR(1) process (3) with (), , , , . The explanatory variables are generalized from an AR(1) process, i.e., with , ; is generalized from a seasonal series, i.e., with .
4.1. Simulation Study When r Is Known
4.2. Simulation Study When r Is Unknown
4.3. Empirical Sizes and Powers of the Wald Test
- Model : Generated from the TVINAR(1)-B process (13) with .
- Model : Generated from the TVINAR(1)-B process (13) with .
- Model : Generated from the TVINAR(1)-G process (14) with .
- Model : Generated from the TVINAR(1)-G process (14) with .
- Model : Generated from the TVMTTINAR(1) process (3) with , , , , . The explanatory variables are generalized from an AR(1) process, i.e., with , ; is generalized from a seasonal series, i.e., with .
- Model : Generated from the TVMTTINAR(1) process (3) with , , , , . The explanatory variables are generalized from an AR(1) process, i.e., with , ; is generalized from a seasonal series, i.e., with .
4.4. Empirical Sizes and Powers of the Proposed Test in Section 3.5
- Model : Generated from the MTTINAR(1) process (11) with = .
- Model : Generated from the MTTINAR(1) process (11) with = .
- Model : Generated from the TVMTTINAR(1) process (3) with , , , , . The explanatory variables are generalized from the i.i.d. uniform distribution .
- Model : Generated from the TVMTTINAR(1) process (3) with , , , , . The explanatory variables are generalized from the i.i.d. uniform distribution .
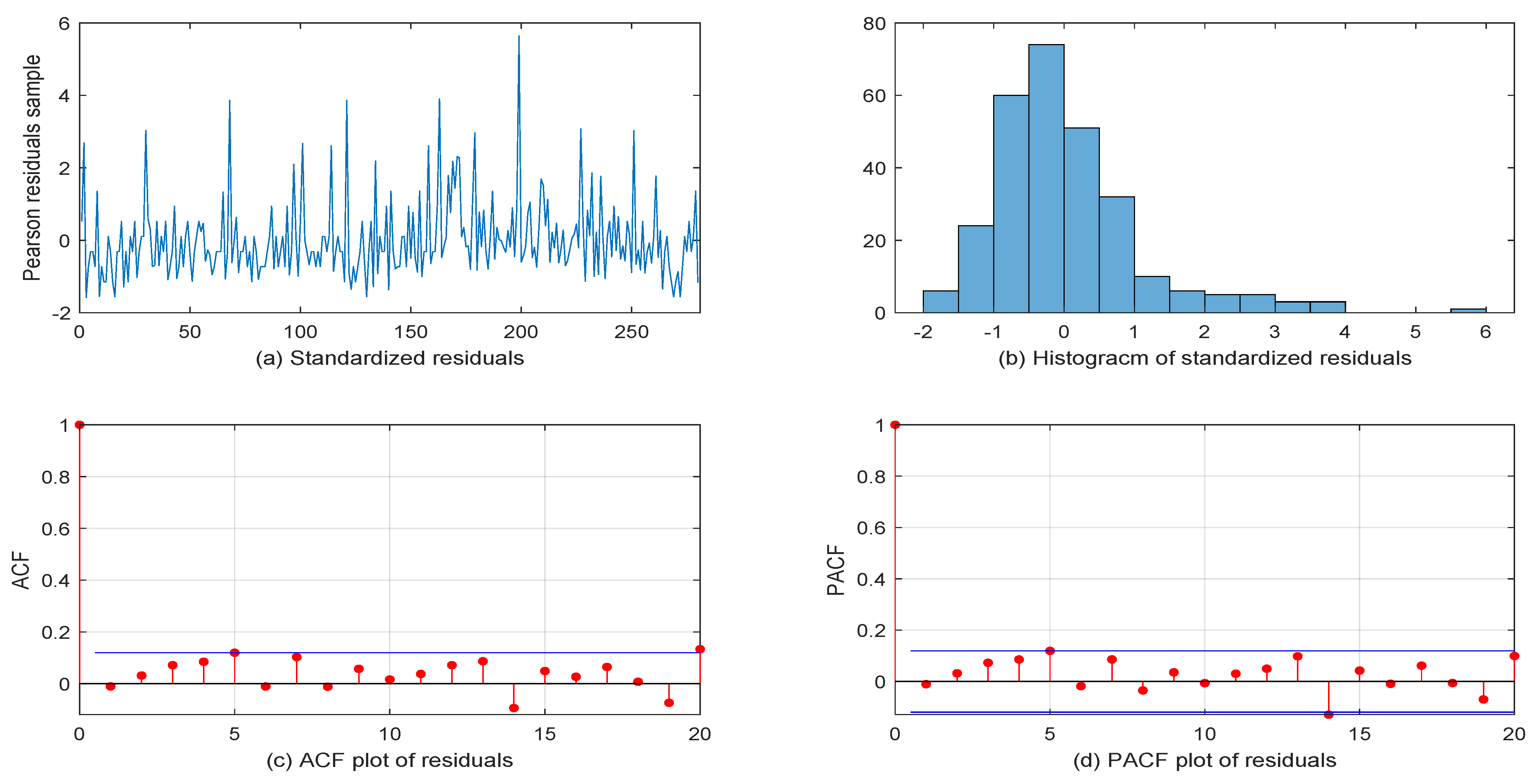
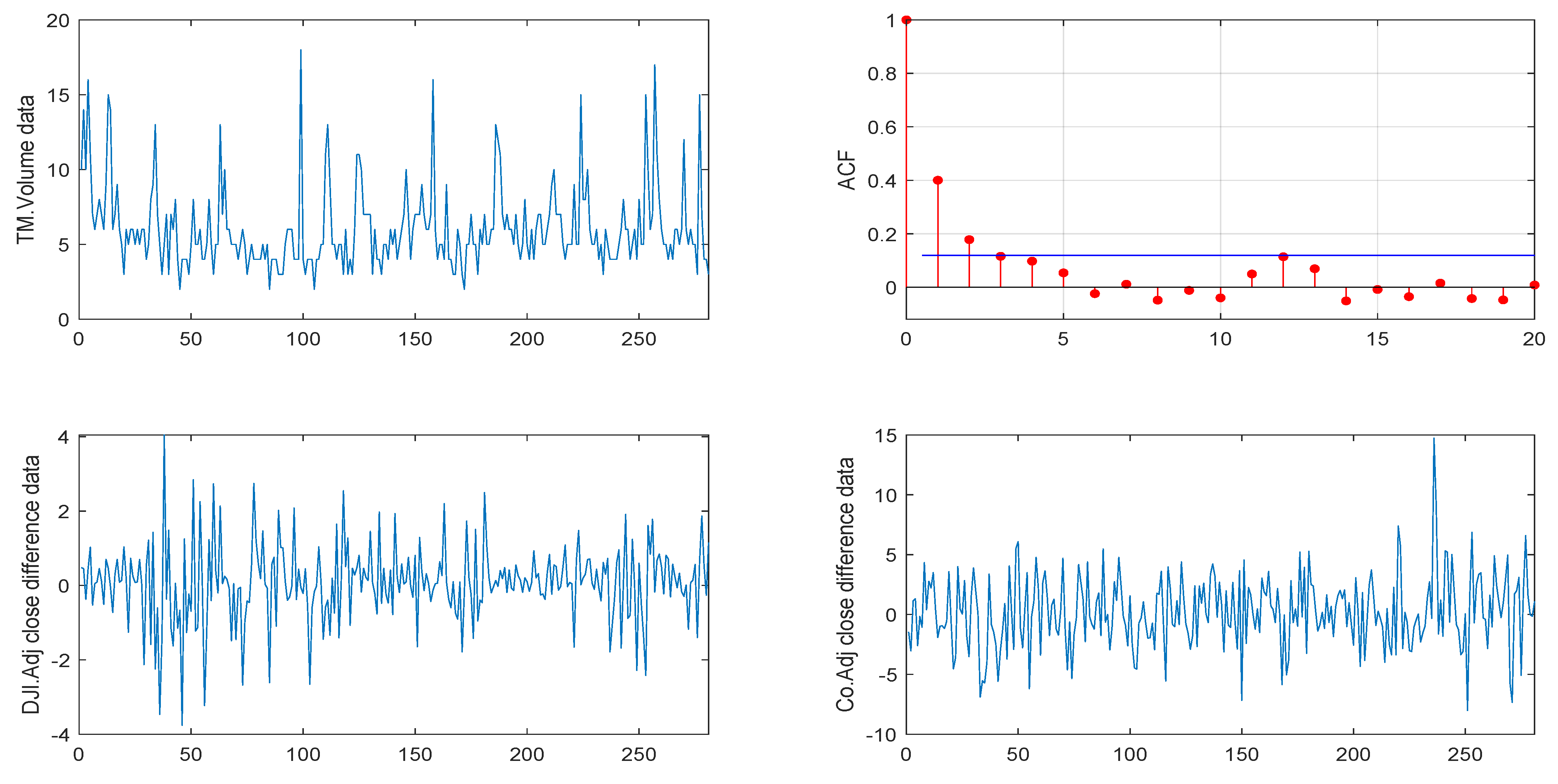
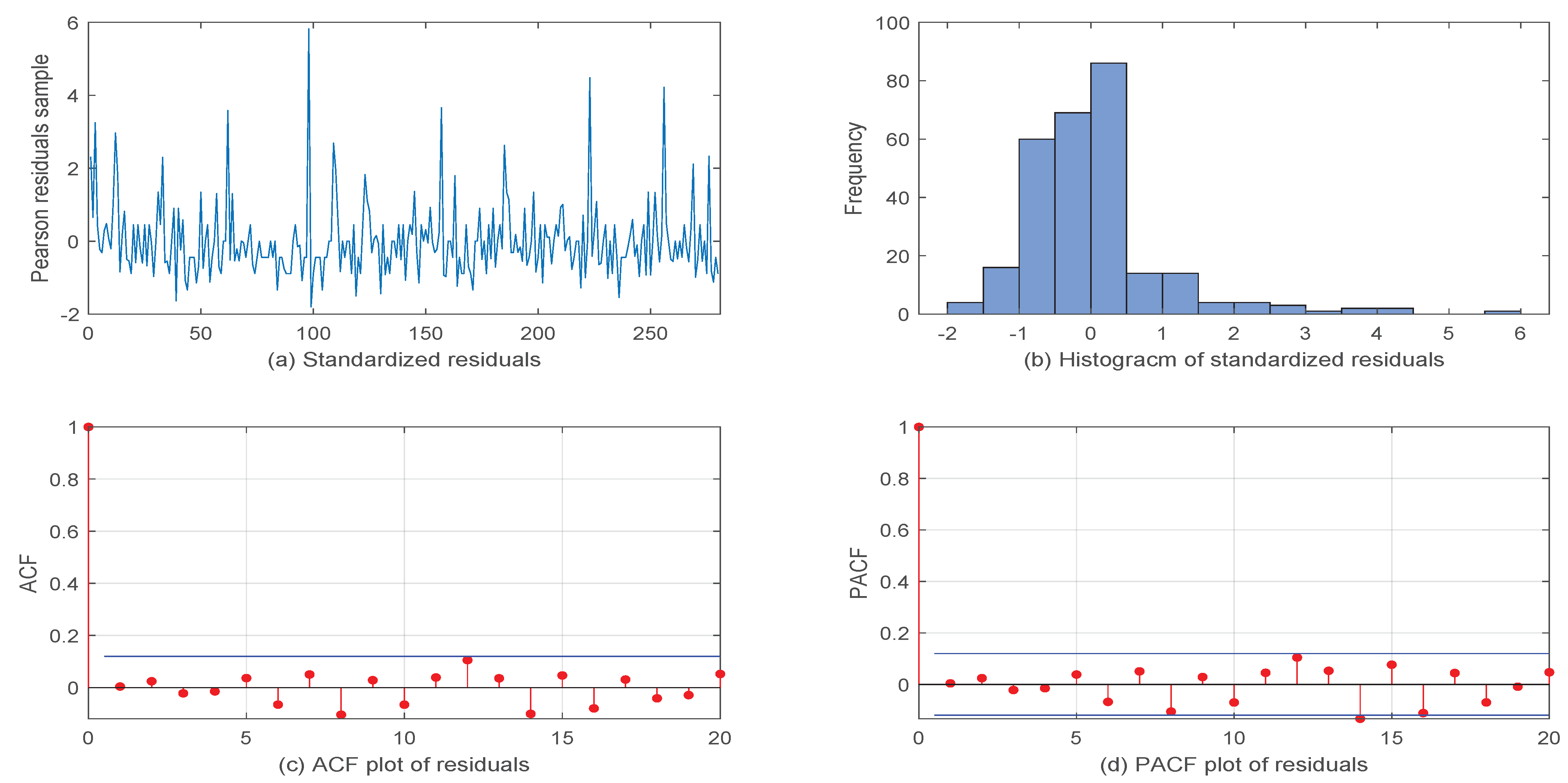
5. Real Data Example
5.1. Volkswagen Corporation Daily Stock Trading Volume Data
5.2. Another VOW Daily Stock Trading Volume Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Brännäs, K.; Shahiduzzaman Quoreshi, A.M.M. Integer-valued moving average modelling of the number of transactions in stocks. Appl. Financ. Econ. 2010, 20, 1429–1440. [Google Scholar] [CrossRef]
- Schweer, S.; Weiß, C.H. Compound Poisson INAR (1) processes: Stochastic properties and testing for overdispersion. Comput. Stat. Data Anal. 2014, 77, 267–284. [Google Scholar] [CrossRef]
- Guan, G.; Hu, X. On the analysis of a discrete-time risk model with INAR (1) processes. Scand. Actuar. J. 2022, 2022, 115–138. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive (INAR(1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Steutel, F.W.; Van Harn, K. Discrete analogues of self-decomposability and stability. Ann. Probab. 1979, 7, 893–899. [Google Scholar] [CrossRef]
- Weiß, C.H. Thinning operations for modeling time series of counts—A survey. Asta Adv. Stat. Anal. 2008, 92, 319. [Google Scholar] [CrossRef]
- Freeland, R.K. True integer value time series. Asta Adv. Stat. Anal. 2010, 94, 217–229. [Google Scholar] [CrossRef]
- Kachour, M.; Truquet, L. A p-order signed integer-valued autoregressive (SINAR(p)) model. J. Time Ser. Anal. 2011, 32, 223–236. [Google Scholar] [CrossRef]
- Nasti, A.S.; Risti, M.M.; Bakouch, H.S. A combined geometric INAR(p) model based on negative binomial thinning. Math. Comput. Model. 2012, 55, 1665–1672. [Google Scholar] [CrossRef]
- Khoo, W.C.; Ong, S.H.; Biswas, A. Modeling time series of counts with a new class of INAR(1) model. Stat. Pap. 2017, 58, 1–24. [Google Scholar] [CrossRef]
- Li, H.; Yang, K.; Zhao, S.; Wang, D. First-order random coefficients integer-valued threshold autoregressive processes. Asta Adv. Stat. Anal. 2018, 102, 305–331. [Google Scholar] [CrossRef]
- Monteiro, M.; Scotto, M.G.; Pereira, I. Integer-valued self-exciting threshold autoregressive processes. Commun.-Stat.-Theory Methods 2012, 41, 2717–2737. [Google Scholar] [CrossRef]
- Wang, C.; Liu, H.; Yao, J.F.; Davis, R.A.; Li, W.K. Self-excited threshold Poisson autoregression. J. Am. Stat. Assoc. 2014, 109, 776–787. [Google Scholar] [CrossRef]
- Möller, T.A.; Silva, M.E.; Weiß, C.H.; Scotto, M.G.; Pereira, I. Self-exciting threshold binomial autoregressive processes. Asta Adv. Stat. Anal. 2016, 100, 369–400. [Google Scholar] [CrossRef]
- Yang, K.; Wang, D.; Jia, B.; Li, H. An integer-valued threshold autoregressive process based on negative binomial thinning. Stat. Pap. 2018, 59, 1131–1160. [Google Scholar] [CrossRef]
- Möller, T.A.; Weiß, C.H. Threshold models for integer-valued time series with infinite or finite range. Stoch. Model. Stat. Their Appl. 2015, 122, 327–334. [Google Scholar]
- Sheng, D.; Wang, D.; Sun, L.Q. A new First-Order mixture integer-valued threshold autoregressive process based on binomial thinning and negative binomial thinning. J. Stat. Plan. Inference 2024, 231, 106143. [Google Scholar] [CrossRef]
- Yang, K.; Li, H.; Wang, D.; Zhang, C. Random coefficients integer-valued threshold autoregressive processes driven by logistic regression. Asta Adv. Stat. Anal. 2021, 105, 533–557. [Google Scholar] [CrossRef]
- Sheng, D.; Wang, D.; Kang, Y. A new RCAR(1) model based on explanatory variables and observations. Commun. Stat.-Theory Methods 2022, 1–22. [Google Scholar] [CrossRef]
- Ristić, M.M.; Bakouch, H.S.; Nastixcx, A.S. A new geometric first-order integer-valued autoregressive (NGINAR(1)) process. J. Stat. Plan. Inference 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- Tweedie, R.L. Sufficient conditions for ergodicity and recurrence of Markov chains on a general state space. Stoch. Processes Appl. 1975, 3, 385–403. [Google Scholar] [CrossRef]
- Yang, K.; Li, H.; Wang, D. Estimation of parameters in the self-exciting threshold autoregressive processes for nonlinear time series of counts. Appl. Math. Model. 2018, 57, 226–247. [Google Scholar] [CrossRef]
- Hall, P.; Heyde, C.C. Martingale Limit Theory and Its Application; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Gorgi, P. Integer-valued autoregressive models with survival probability driven by a stochastic recurrence equation. J. Time Ser. Anal. 2018, 39, 150–171. [Google Scholar] [CrossRef]
- Wald, A. Note on the consistency of the maximum likelihood estimate. Ann. Math. Stat. 1949, 20, 595–601. [Google Scholar] [CrossRef]
- Rao, R.R. Relations between weak and uniform convergence of measures with applications. Ann. Math. Stat. 1962, 33, 659–680. [Google Scholar] [CrossRef]
- Billingsley, P. Convergence of Probability Measures, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Durrett, R. Probability: Theory and Examples; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]

| A1 | A2 | ||||||||
| CLS | CML | CLS | CML | ||||||
| Sample Size | Para. | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| −0.0544 | 0.3579 | 0.0076 | 0.2669 | −0.0856 | 0.3338 | 0.0071 | 0.2476 | ||
| 0.0430 | 0.1017 | 0.0398 | 0.0955 | 0.0261 | 0.0915 | 0.0273 | 0.0882 | ||
| −0.0607 | 0.0991 | −0.0302 | 0.0731 | −0.0837 | 0.0931 | −0.0419 | 0.0671 | ||
| −0.0216 | 0.0255 | −0.0164 | 0.0229 | −0.0186 | 0.0216 | −0.0160 | 0.0189 | ||
| 0.0856 | 0.4181 | 0.0245 | 0.3047 | 0.1343 | 0.3908 | 0.0438 | 0.2752 | ||
| −0.0245 | 0.1947 | 0.0020 | 0.1150 | −0.0472 | 0.1886 | 0.0032 | 0.1149 | ||
| 0.0209 | 0.0374 | 0.0156 | 0.0337 | 0.0158 | 0.0323 | 0.0141 | 0.0297 | ||
| −0.0324 | 0.0547 | −0.0156 | 0.0344 | −0.0464 | 0.0515 | −0.0194 | 0.0313 | ||
| −0.0114 | 0.0105 | −0.0077 | 0.0090 | −0.0098 | 0.0085 | −0.0077 | 0.0068 | ||
| 0.0449 | 0.2357 | 0.0141 | 0.1417 | 0.0778 | 0.2224 | 0.0214 | 0.1307 | ||
| −0.0157 | 0.1056 | −0.0014 | 0.0564 | −0.0190 | 0.1021 | 0.0046 | 0.0534 | ||
| 0.0094 | 0.0169 | 0.0067 | 0.0154 | 0.0084 | 0.0152 | 0.0063 | 0.0135 | ||
| −0.0197 | 0.0300 | −0.0101 | 0.0169 | −0.0226 | 0.0283 | −0.0075 | 0.0154 | ||
| −0.0070 | 0.0053 | −0.0048 | 0.0045 | −0.0058 | 0.0044 | −0.0037 | 0.0035 | ||
| 0.0279 | 0.1324 | 0.0108 | 0.0717 | 0.0369 | 0.1239 | 0.0073 | 0.0645 | ||
| B1 | B2 | ||||||||
| CLS | CML | CLS | CML | ||||||
| Sample Size | Para. | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| −0.0084 | 0.0553 | 0.0089 | 0.0338 | −0.0304 | 0.0466 | 0.0031 | 0.0271 | ||
| 0.0057 | 0.0070 | 0.0045 | 0.0066 | 0.0052 | 0.0039 | 0.0041 | 0.0036 | ||
| 0.0718 | 0.3459 | 0.0684 | 0.2918 | 0.1148 | 0.4075 | 0.1362 | 0.3766 | ||
| 0.0583 | 0.2060 | 0.0587 | 0.2037 | 0.0767 | 0.2385 | 0.0745 | 0.2307 | ||
| 0.0100 | 0.3801 | −0.0315 | 0.2366 | 0.0794 | 0.3770 | −0.0158 | 0.2228 | ||
| −0.0031 | 0.0257 | 0.0013 | 0.0147 | −0.0135 | 0.0225 | −0.0006 | 0.0121 | ||
| 0.0024 | 0.0026 | 0.0018 | 0.0025 | 0.0026 | 0.0018 | 0.0019 | 0.0017 | ||
| 0.0155 | 0.1914 | 0.0101 | 0.1454 | 0.0323 | 0.2214 | 0.0393 | 0.1878 | ||
| −0.0002 | 0.0982 | 0.0005 | 0.0951 | 0.0209 | 0.1220 | 0.0198 | 0.1179 | ||
| 0.0050 | 0.1838 | −0.0043 | 0.1083 | 0.0370 | 0.1855 | 0.0003 | 0.1014 | ||
| −0.0053 | 0.0140 | −0.0007 | 0.0077 | −0.0100 | 0.0110 | −0.0032 | 0.0058 | ||
| 0.0012 | 0.0013 | 0.0007 | 0.0012 | 0.0014 | 0.0008 | 0.0010 | 0.0008 | ||
| −0.0084 | 0.1157 | −0.0018 | 0.0860 | −0.0045 | 0.1376 | 0.0055 | 0.1119 | ||
| −0.0163 | 0.0590 | −0.0135 | 0.0567 | −0.0127 | 0.0662 | −0.0114 | 0.0639 | ||
| 0.0121 | 0.1020 | 0.0007 | 0.0578 | 0.0278 | 0.0934 | 0.0083 | 0.0504 | ||
| A3 | B3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CLS | CML | CLS | CML | ||||||
| Sample Size | Para. | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| −0.0905 | 0.4153 | 0.0203 | 0.3111 | −0.0285 | 0.0593 | 0.0005 | 0.0371 | ||
| 0.0539 | 0.1056 | 0.0588 | 0.1019 | 0.0088 | 0.0070 | 0.0075 | 0.0065 | ||
| −0.0004 | 0.2013 | 0.0026 | 0.1929 | 0.0071 | 0.0126 | 0.0041 | 0.0118 | ||
| −0.0837 | 0.1029 | −0.0360 | 0.0698 | 0.0269 | 0.3911 | 0.0432 | 0.3349 | ||
| −0.0179 | 0.0196 | −0.0150 | 0.0172 | −0.0159 | 0.1750 | −0.0101 | 0.1707 | ||
| −0.0283 | 0.0371 | −0.0203 | 0.0329 | 0.1030 | 0.2927 | 0.1025 | 0.2824 | ||
| 0.1419 | 0.4508 | 0.0369 | 0.3043 | 0.0598 | 0.3590 | −0.0090 | 0.2323 | ||
| −0.0467 | 0.2223 | 0.0027 | 0.1373 | −0.0137 | 0.0258 | −0.0014 | 0.0149 | ||
| 0.0394 | 0.0423 | 0.0351 | 0.0392 | 0.0043 | 0.0025 | 0.0040 | 0.0023 | ||
| 0.0183 | 0.0768 | 0.0148 | 0.0708 | 0.0040 | 0.0052 | 0.0028 | 0.0050 | ||
| −0.0398 | 0.0490 | −0.0166 | 0.0300 | −0.0221 | 0.2194 | −0.0052 | 0.1678 | ||
| −0.0082 | 0.0069 | −0.0066 | 0.0059 | −0.0422 | 0.0848 | −0.0352 | 0.0803 | ||
| −0.0118 | 0.0142 | −0.0068 | 0.0121 | 0.0182 | 0.1339 | 0.0204 | 0.1276 | ||
| 0.0716 | 0.2330 | 0.0216 | 0.1395 | 0.0312 | 0.1635 | 0.0011 | 0.0974 | ||
| −0.0152 | 0.1161 | 0.0076 | 0.0638 | −0.0089 | 0.0140 | −0.0018 | 0.0077 | ||
| 0.0222 | 0.0216 | 0.0172 | 0.0193 | 0.0016 | 0.0013 | 0.0013 | 0.0012 | ||
| 0.0101 | 0.0356 | 0.0070 | 0.0329 | 0.0019 | 0.0025 | 0.0013 | 0.0023 | ||
| −0.0174 | 0.0252 | −0.0053 | 0.0144 | −0.0197 | 0.1215 | −0.0047 | 0.0866 | ||
| −0.0037 | 0.0036 | −0.0028 | 0.0032 | −0.0282 | 0.0507 | −0.0225 | 0.0470 | ||
| −0.0062 | 0.0071 | −0.0028 | 0.0061 | −0.0064 | 0.0781 | −0.0025 | 0.0748 | ||
| 0.0305 | 0.1260 | 0.0049 | 0.0684 | 0.0202 | 0.0922 | 0.0025 | 0.0517 | ||
| A1 | A2 | ||||||||
| CLS | CML | CLS | CML | ||||||
| Sample Size | Para. | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| −0.1673 | 0.4649 | −0.0095 | 0.3159 | −0.2118 | 0.4925 | −0.0109 | 0.2932 | ||
| −0.0600 | 0.2097 | 0.0236 | 0.1342 | −0.0609 | 0.1886 | 0.0198 | 0.1131 | ||
| −0.0811 | 0.0973 | −0.0319 | 0.0738 | −0.1050 | 0.0948 | −0.0450 | 0.0680 | ||
| −0.0372 | 0.0451 | −0.0259 | 0.0283 | −0.0250 | 0.0350 | −0.0222 | 0.0212 | ||
| 0.1526 | 0.4610 | 0.0338 | 0.3177 | 0.2131 | 0.4566 | 0.0547 | 0.2883 | ||
| r | 1.0142 | 5.3096 | 0.2577 | 1.2313 | 0.8968 | 5.2976 | 0.1642 | 0.8174 | |
| −0.0566 | 0.2308 | −0.0009 | 0.1222 | −0.0682 | 0.2172 | 0.0014 | 0.1180 | ||
| 0.0054 | 0.0536 | 0.0157 | 0.0367 | 0.0061 | 0.0416 | 0.0140 | 0.0307 | ||
| −0.0408 | 0.0566 | −0.0166 | 0.0350 | −0.0517 | 0.0534 | −0.0199 | 0.0316 | ||
| −0.0187 | 0.0132 | −0.0093 | 0.0093 | −0.0123 | 0.0096 | −0.0082 | 0.0069 | ||
| 0.0703 | 0.2566 | 0.0166 | 0.1451 | 0.0935 | 0.2394 | 0.0226 | 0.1321 | ||
| r | 0.1719 | 0.8427 | 0.0181 | 0.0705 | 0.1054 | 0.6042 | 0.0067 | 0.0281 | |
| n = 1000 | −0.0188 | 0.1093 | −0.0015 | 0.0565 | −0.0191 | 0.1023 | 0.0046 | 0.0534 | |
| 0.0080 | 0.0181 | 0.0067 | 0.0155 | 0.0083 | 0.0152 | 0.0064 | 0.0135 | ||
| −0.0207 | 0.0304 | −0.0101 | 0.0169 | −0.0226 | 0.0284 | −0.0075 | 0.0154 | ||
| −0.0078 | 0.0055 | −0.0048 | 0.0045 | −0.0058 | 0.0044 | −0.0037 | 0.0035 | ||
| 0.0304 | 0.1350 | 0.0109 | 0.0718 | 0.0370 | 0.1240 | 0.0073 | 0.0645 | ||
| r | 0.0121 | 0.0411 | 0.0009 | 0.0059 | 0.0003 | 0.0003 | −0.0001 | 0.0001 | |
| B1 | B2 | ||||||||
| CLS | CML | CLS | CML | ||||||
| Sample Size | Para. | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| 0.0394 | 0.0738 | 0.0146 | 0.0382 | 0.0001 | 0.0673 | −0.0008 | 0.0333 | ||
| 0.0164 | 0.0232 | 0.0078 | 0.0074 | 0.0200 | 0.0155 | 0.0066 | 0.0040 | ||
| 0.3713 | 0.6543 | 0.1386 | 0.3408 | 0.5624 | 0.8281 | 0.3572 | 0.4869 | ||
| 0.3190 | 0.4057 | 0.1768 | 0.2646 | 0.5179 | 0.5136 | 0.3818 | 0.3591 | ||
| −0.2125 | 0.7856 | −0.0367 | 0.3023 | −0.1115 | 0.8718 | 0.0031 | 0.3169 | ||
| r | 2.5127 | 15.9965 | 0.4938 | 1.2152 | 3.2435 | 25.3375 | 0.1035 | 1.0955 | |
| 0.0188 | 0.0330 | 0.0021 | 0.0152 | 0.0361 | 0.0372 | −0.0037 | 0.0137 | ||
| 0.0077 | 0.0048 | 0.0025 | 0.0025 | 0.0114 | 0.0055 | 0.0025 | 0.0017 | ||
| 0.1333 | 0.3180 | 0.0325 | 0.1566 | 0.5518 | 0.6754 | 0.3191 | 0.2900 | ||
| 0.0926 | 0.1770 | 0.0390 | 0.1133 | 0.4852 | 0.4148 | 0.3708 | 0.2623 | ||
| −0.0858 | 0.3009 | −0.0053 | 0.1144 | −0.1831 | 0.4647 | 0.0112 | 0.1245 | ||
| r | 0.8616 | 5.2522 | 0.1170 | 0.1640 | 2.3496 | 18.1162 | −0.1513 | 0.3999 | |
| −0.0019 | 0.0150 | −0.0007 | 0.0077 | 0.0423 | 0.0197 | −0.0004 | 0.0063 | ||
| 0.0020 | 0.0015 | 0.0008 | 0.0012 | 0.0072 | 0.0018 | 0.0013 | 0.0008 | ||
| 0.0105 | 0.1346 | 0.0023 | 0.0884 | 0.5346 | 0.5129 | 0.3481 | 0.2311 | ||
| 0.0005 | 0.0723 | −0.0054 | 0.0608 | 0.4726 | 0.3270 | 0.3973 | 0.2285 | ||
| −0.0011 | 0.1162 | 0.0008 | 0.0582 | −0.1783 | 0.2391 | −0.0017 | 0.0570 | ||
| r | 0.1303 | 0.7299 | 0.0207 | 0.0231 | 1.2562 | 9.8408 | −0.1482 | 0.2074 | |
| A3 | B3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CLS | CML | CLS | CML | ||||||
| Sample Size | Para. | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| −0.2088 | 0.4902 | 0.0025 | 0.3416 | −0.0076 | 0.0699 | 0.0050 | 0.0394 | ||
| −0.1031 | 0.2460 | 0.0372 | 0.1274 | 0.0179 | 0.0152 | 0.0107 | 0.0069 | ||
| −0.1352 | 0.3164 | −0.0169 | 0.2225 | 0.0144 | 0.0274 | 0.0055 | 0.0123 | ||
| −0.1069 | 0.1053 | −0.0389 | 0.0711 | 0.1478 | 0.4684 | 0.0648 | 0.3516 | ||
| −0.0330 | 0.0369 | −0.0219 | 0.0196 | 0.1450 | 0.3211 | 0.0455 | 0.2047 | ||
| −0.0315 | 0.0598 | −0.0251 | 0.0365 | 0.2349 | 0.3862 | 0.1481 | 0.3138 | ||
| 0.2373 | 0.5380 | 0.0512 | 0.3236 | −0.0311 | 0.5100 | −0.0161 | 0.2623 | ||
| r | 1.2538 | 7.7742 | 0.1827 | 0.8443 | 1.3943 | 9.2127 | 0.2116 | 0.5360 | |
| −0.0612 | 0.2341 | 0.0012 | 0.1395 | −0.0109 | 0.0266 | −0.0009 | 0.0150 | ||
| 0.0284 | 0.0513 | 0.0352 | 0.0402 | 0.0052 | 0.0027 | 0.0042 | 0.0023 | ||
| 0.0084 | 0.0855 | 0.0148 | 0.0721 | 0.0045 | 0.0057 | 0.0029 | 0.0050 | ||
| −0.0433 | 0.0499 | −0.0171 | 0.0302 | −0.0082 | 0.2310 | −0.0029 | 0.1692 | ||
| −0.0106 | 0.0078 | −0.0069 | 0.0059 | −0.0301 | 0.0983 | −0.0304 | 0.0834 | ||
| −0.0137 | 0.0151 | −0.0071 | 0.0122 | 0.0305 | 0.1447 | 0.0251 | 0.1307 | ||
| 0.0837 | 0.2443 | 0.0228 | 0.1406 | 0.0206 | 0.1745 | 0.0001 | 0.0982 | ||
| r | 0.0853 | 0.4439 | 0.0044 | 0.0140 | 0.1002 | 0.5810 | 0.0163 | 0.0277 | |
| −0.0161 | 0.1170 | 0.0075 | 0.0639 | −0.0088 | 0.0141 | −0.0018 | 0.0077 | ||
| 0.0216 | 0.0218 | 0.0172 | 0.0193 | 0.0017 | 0.0013 | 0.0013 | 0.0012 | ||
| 0.0095 | 0.0359 | 0.0070 | 0.0330 | 0.0020 | 0.0025 | 0.0013 | 0.0023 | ||
| −0.0177 | 0.0253 | −0.0053 | 0.0144 | −0.0190 | 0.1224 | −0.0045 | 0.0867 | ||
| −0.0039 | 0.0036 | −0.0028 | 0.0032 | −0.0280 | 0.0513 | −0.0221 | 0.0473 | ||
| −0.0063 | 0.0071 | −0.0028 | 0.0061 | −0.0060 | 0.0785 | −0.0020 | 0.0750 | ||
| 0.0313 | 0.1269 | 0.0049 | 0.0685 | 0.0198 | 0.0927 | 0.0024 | 0.0517 | ||
| r | 0.0031 | 0.0103 | 0.0000 | 0.0006 | 0.0036 | 0.0228 | 0.0014 | 0.0020 | |
| CLS | CML | ||||
| Model | Sample Size | Frequency | Average Time (s) | Frequency | Average Time (s) |
| A1 | 200 | 0.6330 | 0.5269 | 0.7841 | 2.3501 |
| 500 | 0.9159 | 0.6343 | 0.9694 | 4.8531 | |
| 1000 | 0.9913 | 0.7666 | 0.9989 | 9.0141 | |
| A2 | 200 | 0.7164 | 0.4614 | 0.8564 | 2.2148 |
| 500 | 0.9619 | 0.6495 | 0.9885 | 5.2616 | |
| 1000 | 0.9997 | 0.7582 | 0.9999 | 9.3752 | |
| A3 | 200 | 0.6700 | 0.6728 | 0.8479 | 3.8789 |
| 500 | 0.9619 | 0.9298 | 0.9880 | 9.2877 | |
| 1000 | 0.9974 | 1.0712 | 0.9994 | 16.3961 | |
| CLS | CML | ||||
| Model | Sample Size | Frequency | Average Time (s) | Frequency | Average Time (s) |
| B1 | 200 | 0.4341 | 0.3850 | 0.6511 | 2.0574 |
| 500 | 0.7767 | 0.4581 | 0.8909 | 4.6666 | |
| 1000 | 0.9574 | 0.5514 | 0.9793 | 9.2278 | |
| B2 | 200 | 0.1633 | 0.4005 | 0.4463 | 2.4881 |
| 500 | 0.2720 | 0.5062 | 0.6398 | 5.6456 | |
| 1000 | 0.5250 | 0.6105 | 0.7944 | 11.5242 | |
| B3 | 200 | 0.6513 | 0.4865 | 0.8069 | 3.1971 |
| 500 | 0.9540 | 0.6448 | 0.9776 | 7.5834 | |
| 1000 | 0.9965 | 0.8010 | 0.9980 | 14.9456 | |
| Empirical Sizes, Significance Level | |||||||||
| Sample Size | Sample Size | ||||||||
| Model | Method | Model | Method | ||||||
| 0.0497 | 0.0515 | 0.0517 | 0.0255 | 0.0517 | 0.0559 | ||||
| 0.0123 | 0.0448 | 0.0527 | 0.0012 | 0.0127 | 0.0501 | ||||
| Empirical Powers, Significance Level | |||||||||
| Sample Size | Sample Size | ||||||||
| Model | Method | Model | Method | ||||||
| 0.8414 | 0.9507 | 0.9972 | 0.5016 | 0.7979 | 0.967 | ||||
| Empirical Sizes, Significance Level | |||||||||
| Sample Size | Sample Size | ||||||||
| Model | Method | Model | Method | ||||||
| 0.0580 | 0.0466 | 0.0475 | 0.0320 | 0.0413 | 0.0445 | ||||
| 0.0504 | 0.0502 | 0.0495 | 0.0456 | 0.0487 | 0.0509 | ||||
| Empirical Power, Significance Level | |||||||||
| Sample Size | Sample Size | ||||||||
| Model | Method | Model | Method | ||||||
| 0.9987 | 1.0000 | 1.0000 | 0.9987 | 1.0000 | 1.0000 | ||||
| 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||||
| Model | Para. | CML | SE | AIC | BIC | RMS | |
|---|---|---|---|---|---|---|---|
| SETINAR(2,1) | 0.0169 | 0.0221 | 6 | 1395.9685 | 1406.8836 | 3.3266 | |
| 0.3071 | 0.0092 | ||||||
| 5.9064 | 0.0032 | ||||||
| NBTINAR(1) | 0.2689 | 0.0034 | 6 | 1369.2936 | 1380.2087 | 12.3344 | |
| 0.3371 | 0.0041 | ||||||
| v | 17.0000 | 0.0004 | |||||
| RCTINAR(1) | 0.0000 | 4.4123 | 6 | 1405.0371 | 1415.9521 | 3.3656 | |
| 0.2295 | 0.0034 | ||||||
| 6.3869 | 0.0006 | ||||||
| BiNB−MTTINAR(1) | 0.4852 | 0.0076 | 10 | 1358.6573 | 1369.5724 | 3.3655 | |
| (R = 0) | 0.5202 | 0.0027 | |||||
| 3.7781 | 0.0013 | ||||||
| BiNB−MTTINAR(1) | 0.3910 | 0.0038 | 4 | 1430.5887 | 1441.5038 | 3.7434 | |
| (R = 1) | 0.6003 | 0.0012 | |||||
| 4.6621 | 0.0061 | ||||||
| TVMTTINAR(1) | −0.5391 | −0.0006 | 6 | 1352.1336 | 1377.6020 | 3.1897 | |
| (R = 0) | 0.0203 | 0.0001 | |||||
| 0.0215 | 0.0000 | ||||||
| 0.0300 | 0.0001 | ||||||
| −0.2134 | −0.0005 | ||||||
| 0.0573 | 0.0003 | ||||||
| 4.0801 | 0.0030 | ||||||
| TVMTTINAR(1) | −0.1093 | −0.0002 | 12 | 1366.3313 | 1391.7998 | 3.2179 | |
| (R = 1) | −0.1298 | −0.0003 | |||||
| 0.0793 | 0.0002 | ||||||
| −0.0765 | −0.0002 | ||||||
| −0.2039 | −0.0007 | ||||||
| 0.0367 | 0.0002 | ||||||
| 3.8956 | 0.0030 |
| Rate | Mean() | Var() | ||
|---|---|---|---|---|
| 0.5018 | 2.2343 | 35.2307 | 0.0041 | 1.1116 |
| Model | Para. | CML | SE | AIC | BIC | RMS | |
|---|---|---|---|---|---|---|---|
| SETINAR(2,1) | 0.2470 | 0.0028 | 6 | 1257.6000 | 1268.5151 | 2.5162 | |
| 0.3511 | 0.0068 | ||||||
| 4.2692 | 0.0053 | ||||||
| NBTINAR(1) | 0.1245 | 0.0172 | 6 | 1259.0943 | 1270.0094 | 33.9008 | |
| 0.1605 | 0.0104 | ||||||
| v | 39.0000 | 0.0001 | |||||
| RCTINAR(1) | 0.0228 | 0.0079 | 6 | 1268.9508 | 1279.8659 | 2.5308 | |
| 0.2181 | 0.0017 | ||||||
| 5.4232 | 0.0007 | ||||||
| BiNB−MTTINAR(1) | 0.4788 | 0.0073 | 8 | 1259.9032 | 1270.8183 | 2.5413 | |
| (R = 0) | 0.4955 | 0.0022 | |||||
| 3.1526 | 0.0010 | ||||||
| BiNB−MTTINAR(1) | 0.4441 | 0.0022 | 4 | 1295.9314 | 1306.8464 | 2.9048 | |
| (R = 1) | 0.6682 | 0.0018 | |||||
| 3.3134 | 0.0041 | ||||||
| TVMTTINAR(1) | −0.3448 | −0.0003 | 6 | 1258.9090 | 1284.3775 | 2.5260 | |
| (R = 0) | 0.0404 | 0.0000 | |||||
| 0.0176 | 0.0000 | ||||||
| −0.2200 | −0.0002 | ||||||
| 0.0163 | 0.0000 | ||||||
| −0.0080 | 0.0000 | ||||||
| 3.4359 | 0.0063 | ||||||
| TVMTTINAR(1) | −1.1063 | −0.0010 | 5 | 1254.5145 | 1279.9829 | 2.4856 | |
| (R = 1) | 0.1417 | 0.0001 | |||||
| −0.0427 | 0.0000 | ||||||
| −19.9998 | −4.3550 | ||||||
| −0.2643 | −0.0002 | ||||||
| 3.3629 | 0.0030 | ||||||
| 4.9869 | 0.0072 |
| Rate | Mean() | Var() | ||
|---|---|---|---|---|
| 0.5267 | 1.6682 | 63.9769 | 0.0015 | 1.0148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, D.; Wang, D.; Zhang, J.; Wang, X.; Zhai, Y. A Time-Varying Mixture Integer-Valued Threshold Autoregressive Process Driven by Explanatory Variables. Entropy 2024, 26, 140. https://doi.org/10.3390/e26020140
Sheng D, Wang D, Zhang J, Wang X, Zhai Y. A Time-Varying Mixture Integer-Valued Threshold Autoregressive Process Driven by Explanatory Variables. Entropy. 2024; 26(2):140. https://doi.org/10.3390/e26020140
Chicago/Turabian StyleSheng, Danshu, Dehui Wang, Jie Zhang, Xinyang Wang, and Yiran Zhai. 2024. "A Time-Varying Mixture Integer-Valued Threshold Autoregressive Process Driven by Explanatory Variables" Entropy 26, no. 2: 140. https://doi.org/10.3390/e26020140
APA StyleSheng, D., Wang, D., Zhang, J., Wang, X., & Zhai, Y. (2024). A Time-Varying Mixture Integer-Valued Threshold Autoregressive Process Driven by Explanatory Variables. Entropy, 26(2), 140. https://doi.org/10.3390/e26020140







