Discrete and Semi-Discrete Multidimensional Solitons and Vortices: Established Results and Novel Findings
Abstract
1. Introduction
1.1. Discrete Nonlinear Schrödinger Equations
1.1.1. The Basic Equation
1.1.2. Extended Equations
The Gross–Pitaevskii Equations Amended by Effects of Quantum Fluctuations
The Ablowitz–Ladik and Salerno–Model Equations
Self-Trapping in Lattices with the Self-Repulsion Strength Growing from the Center to the Periphery
Discrete Nonlinear Schrödinger Equations with Long-Range Dipole–Dipole and Quadrupole–Quadrupole Intersite Interactions
The 2D Discrete Second-Harmonic-Generating () System
1.2. One-Dimensional DNLS Solitons
1.2.1. Fundamental Solitons
1.2.2. Higher-Order One-Dimensional Modes: Twisted Discrete Solitons and Bound States
1.2.3. One-Dimensional Solitons in the Salerno Model
1.3. The Subject and Structure of the Present Article
2. Two-Dimensional Nonlinear Schrödinger Lattices: Fundamental and Vortex Solitons and Their Bound States
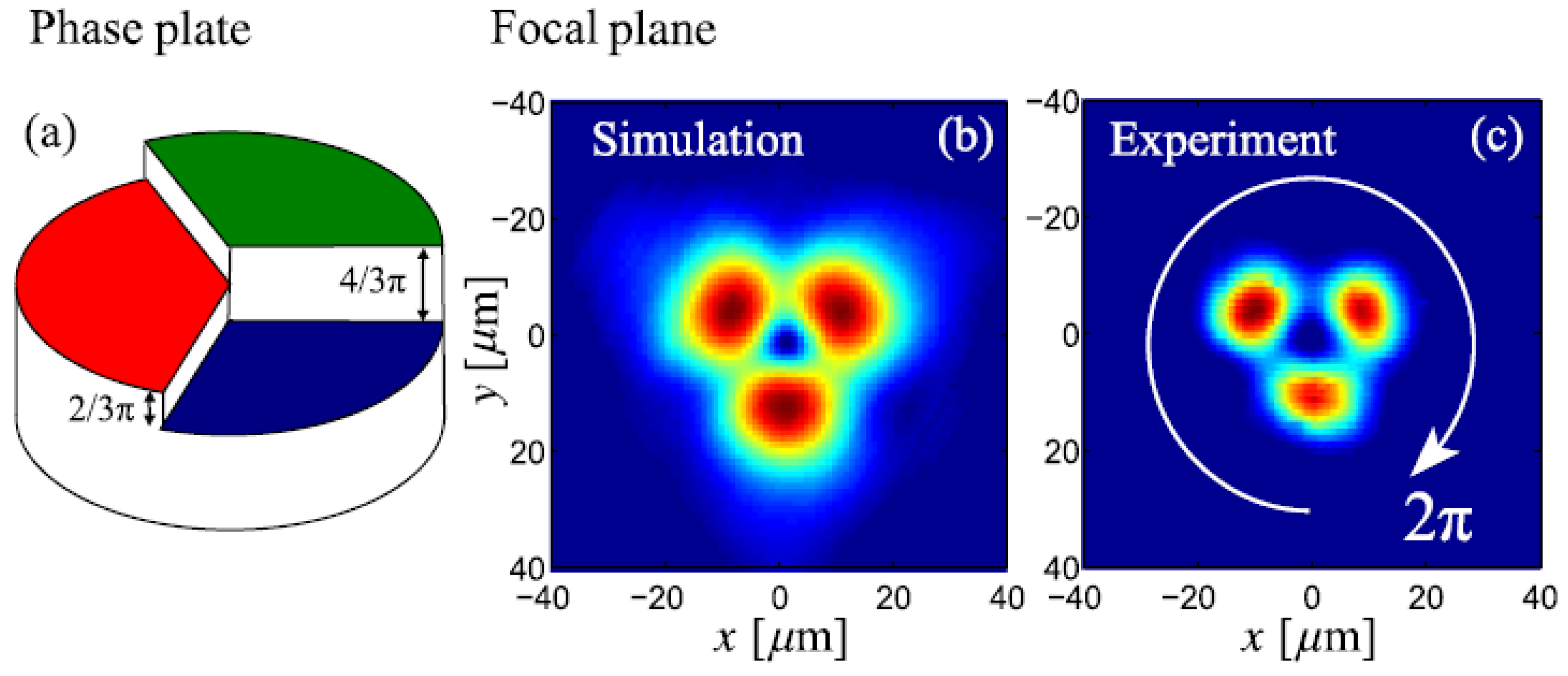
2.1. Vortex Solitons: Theoretical and Experimental Results
2.2. Bound States of 2D Discrete Solitons and Solitary Vortices
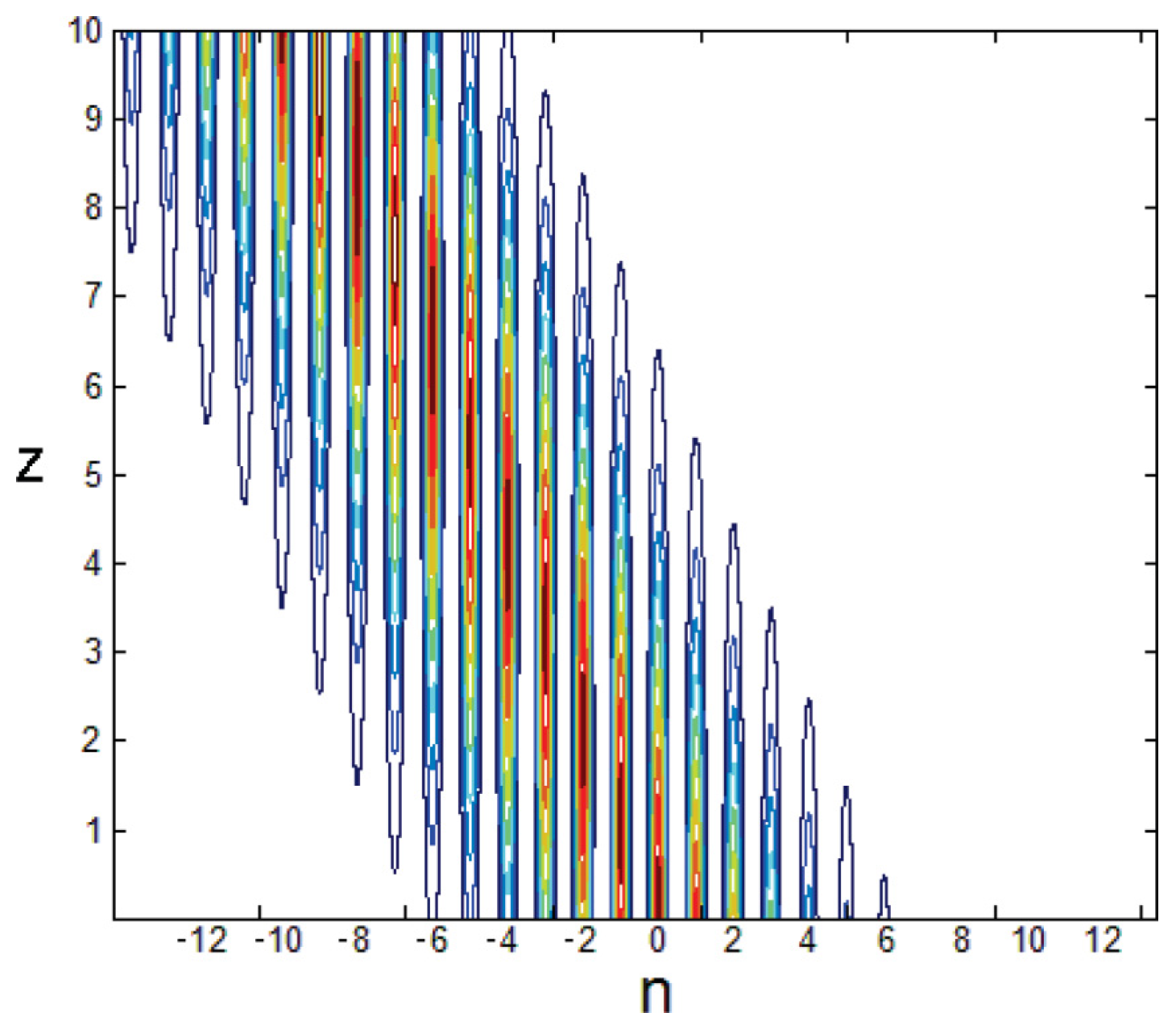
2.3. Two-Dimensional Discrete Solitons in Mini-Gaps of a Spatially Modulated Lattice
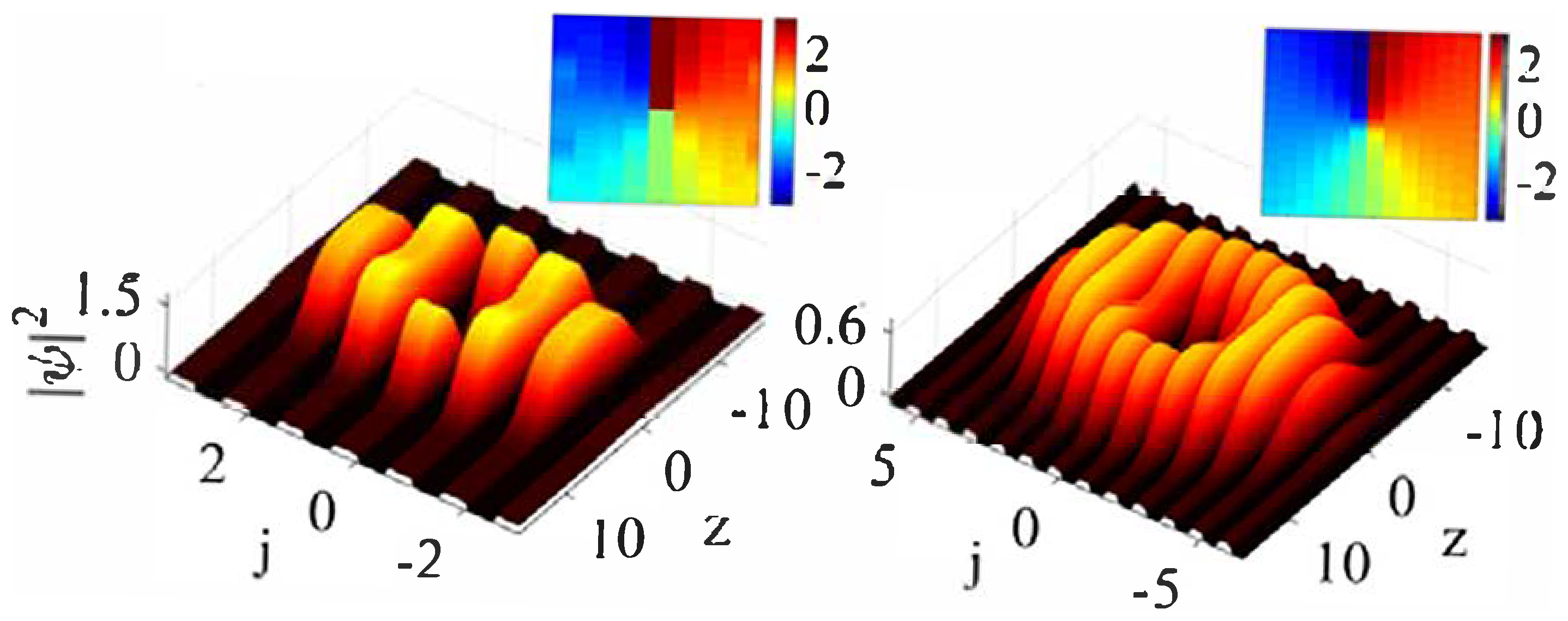
2.4. Two-Dimensional Discrete Solitons in a Rotating Lattice
2.5. Spontaneous Symmetry Breaking of the 2D Discrete Solitons in Linearly Coupled Lattices
3. Two-Dimensional Discrete Solitons in the Salerno Model (SM)
4. Solitons of the Semi-Vortex and Mixed-Mode Types in the Discrete 2D Spin–Orbit-Coupling System
5. Stable Soliton Species in the 3D Discrete Nonlinear Schrödinger Equation
5.1. The 3D Setting
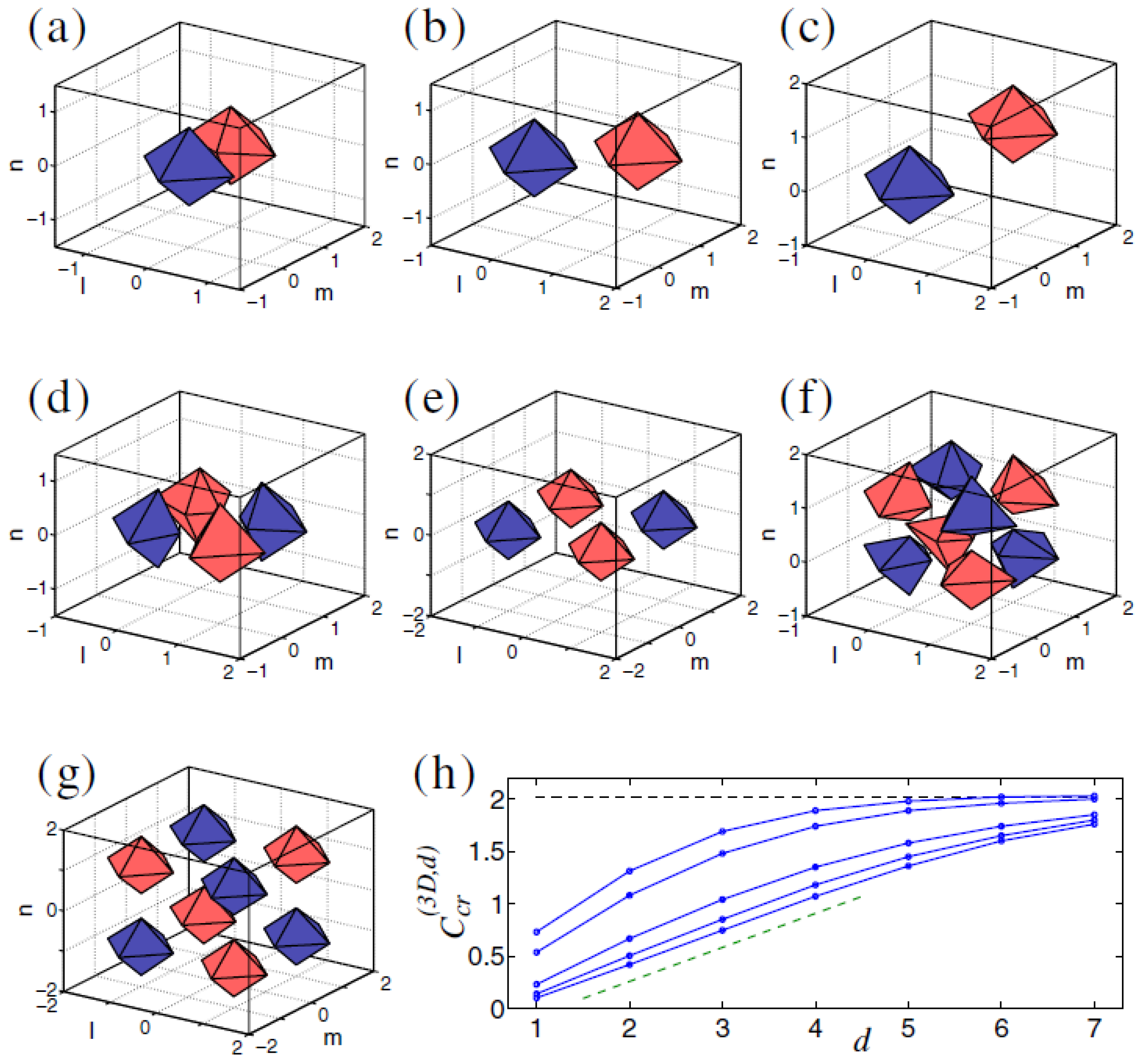
5.2. Results
5.2.1. Single-Component 3D Solitons
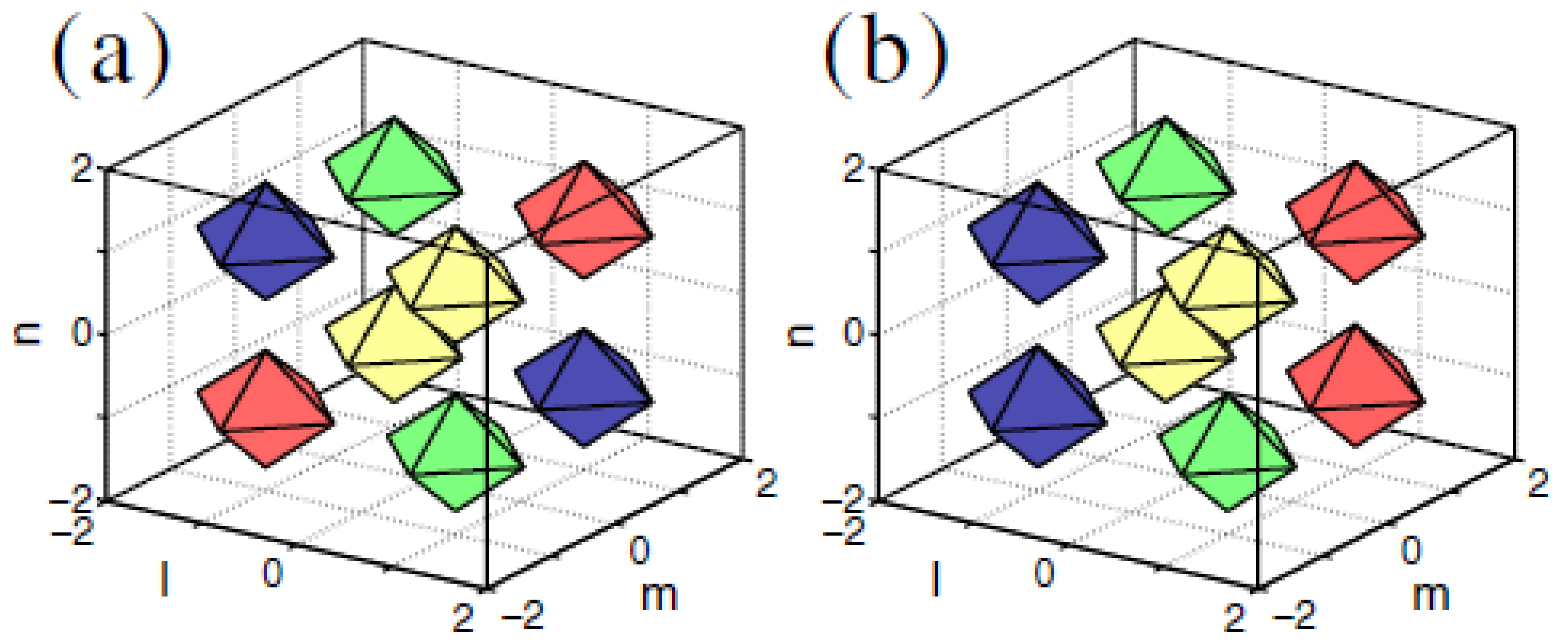
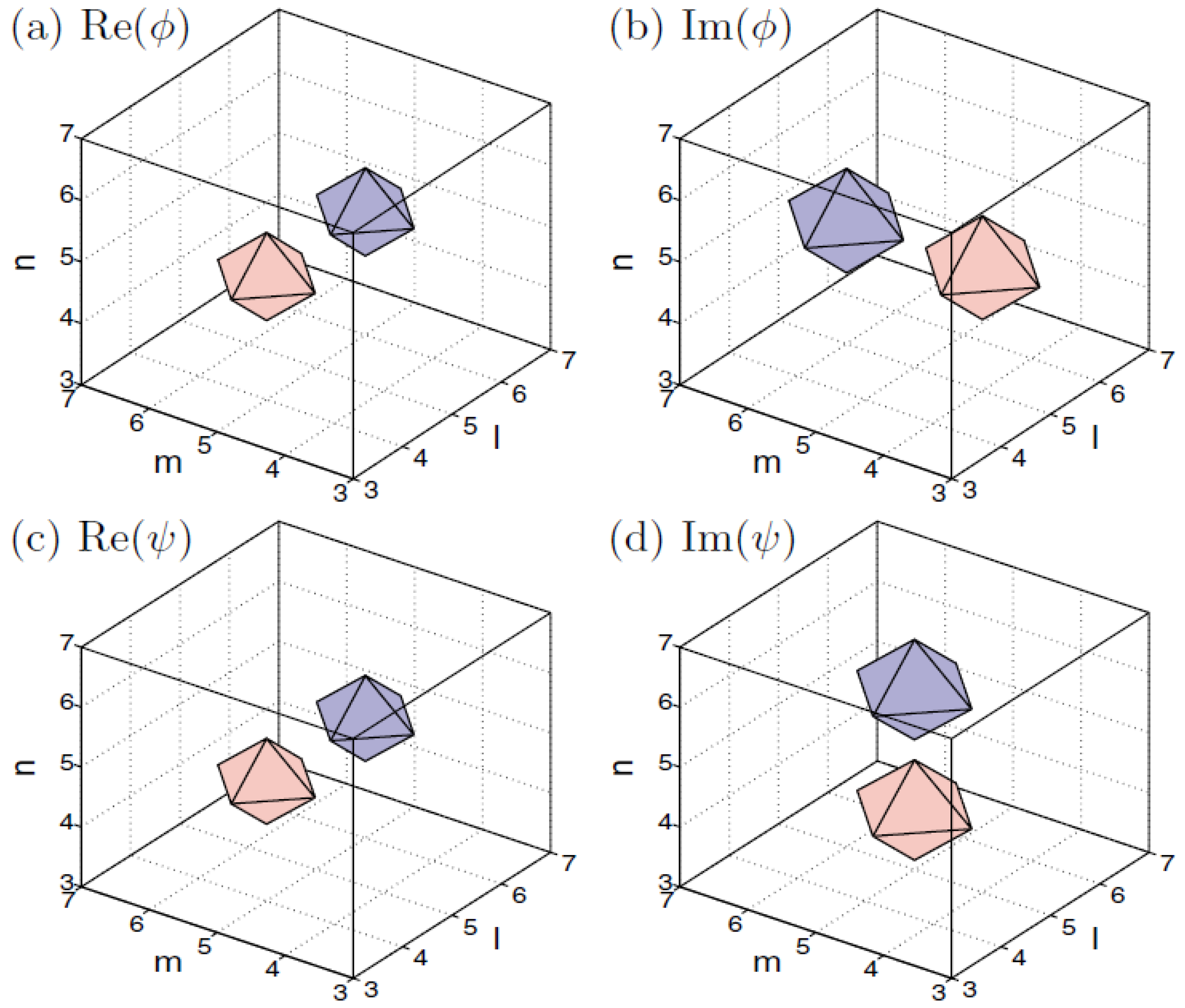
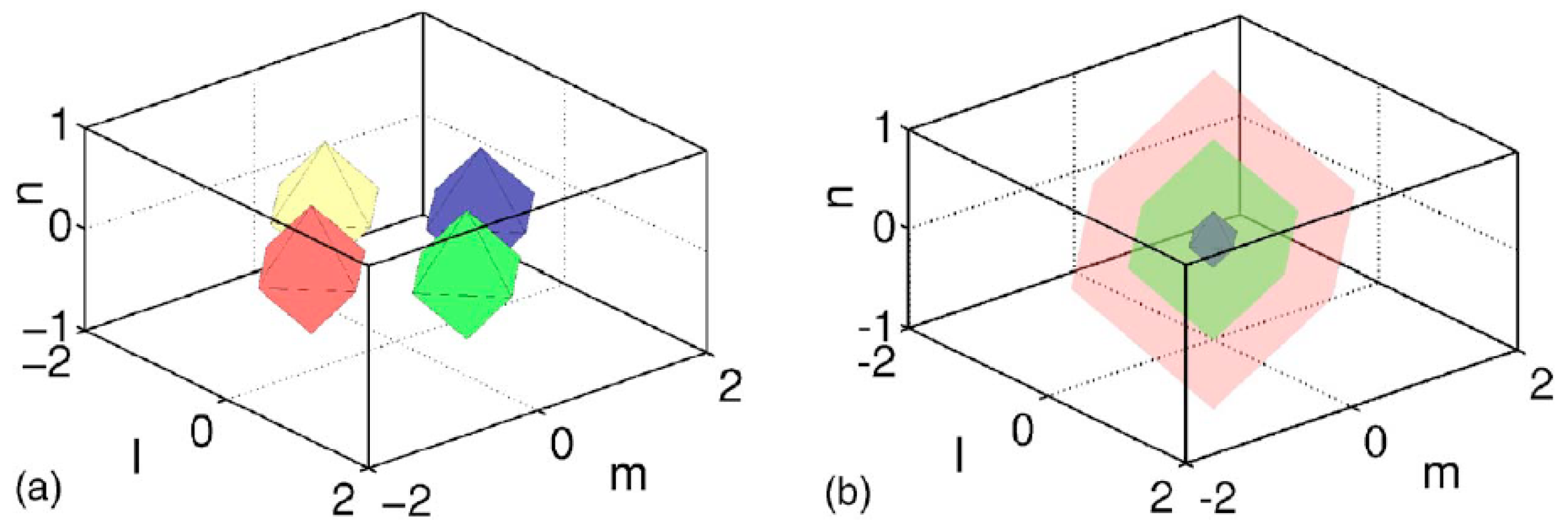
5.2.2. Two-Component 3D Solitons (Including Skyrmions)
6. Two-Dimensional Solitons and Solitary Vortices in Semi-Discrete Systems
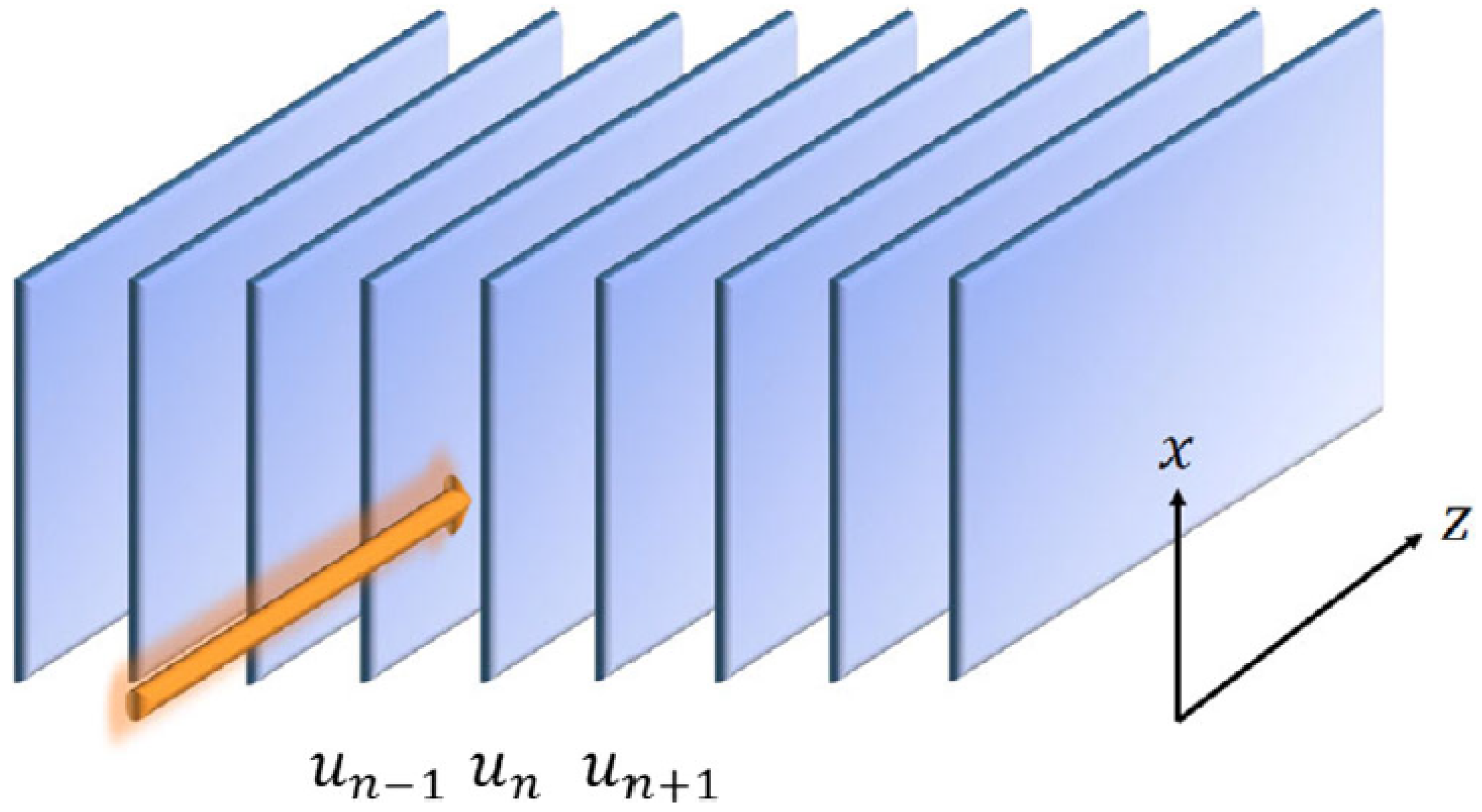
6.1. Spatiotemporal Optical Solitons in Arrayed Waveguides
6.2. Semi-Discrete Quantum and Photonic Droplets
7. Two-Dimensional Fundamental and Vortical Discrete Solitons in a Two-Component (Parity-Time) Symmetric Lattice
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Pitaevskii, L.P.; Stringari, S. Bose–Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Fibich, G. The Nonlinear Schrödinger Equation: Singular Solutions and Optical Collapse; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Morsch, O.; Oberthaler, M. Dynamics of Bose–Einstein condensates in optical lattice. Rev. Mod. Phys. 2006, 78, 179–215. [Google Scholar] [CrossRef]
- Porter, M.A.; Carretero-González, R.; Kevrekidis, P.G.; Malomed, B.A. Nonlinear lattice dynamics of Bose–Einstein condensates. Chaos 2005, 15, 015115. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.V.; Vysloukh, V.A.; Torner, L. Soliton shape and mobility control in optical lattices. Prog. Opt. 2009, 52, 63–148. [Google Scholar]
- Skorobogatiy, M.; Yang, J. Fundamentals of Photonic Crystal Guiding; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Christodoulides, D.N.; Joseph, R.I. Discrete self-focusing in nonlinear arrays of coupled waveguides. Opt. Lett. 1988, 13, 794–796. [Google Scholar] [CrossRef]
- Eisenberg, H.S.; Silberberg, Y.; Morandotti, R.; Boyd, A.R.; Aitchison, J.S. Discrete spatial optical solitons in waveguide arrays. Phys. Rev. Lett. 1998, 81, 3383–3386. [Google Scholar] [CrossRef]
- Christodoulides, D.N.; Lederer, F.; Silberberg, Y. Discretizing light behaviour in linear and nonlinear waveguide lattices. Nature 2003, 424, 817–823. [Google Scholar] [CrossRef] [PubMed]
- Lederer, F.; Stegeman, G.I.; Christodoulides, D.N.; Assanto, G.; Segev, M.; Silberberg, Y. Discrete solitons in optics. Phys. Rep. 2008, 463, 1–126. [Google Scholar] [CrossRef]
- Ye, F.; Mihalache, D.; Hu, B.; Panoiu, N.C. Subwavelength plasmonic lattice solitons in arrays of metallic nanowires. Phys. Rev. Lett. 2010, 104, 106802. [Google Scholar] [CrossRef]
- Smerzi, A.; Trombettoni, A. Nonlinear tight-binding approximation for Bose–Einstein condensates in a lattice. Phys. Rev. A 2003, 68, 023613. [Google Scholar] [CrossRef]
- Alfimov, G.; Kevrekidis, P.; Konotop, V.; Salerno, M. Wannier functions analysis of the nonlinear Schrödinger equation with a periodic potential. Phys. Rev. E 2002, 66, 046608. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419–1475. [Google Scholar] [CrossRef]
- Szameit, A.; Keil, R.; Dreisow, F.; Heinrich, M.; Pertsch, T.; Nolte, S.; Tünnermann, A. Observation of discrete solitons in lattices with second-order interaction. Opt. Lett. 2009, 34, 2838–2840. [Google Scholar] [CrossRef]
- Chong, C.; Carretero-González, R.; Malomed, B.A.; Kevrekidis, P.G. Variational approximations in discrete nonlinear Schrödinger equations with next-nearest-neighbor couplings. Phys. D 2011, 240, 1205–1212. [Google Scholar] [CrossRef]
- Szameit, A.; Pertsch, T.; Nolte, S.; Tünnermann, A.; Lederer, F. Long-range interaction in waveguide lattices. Phys. Rev. A 2008, 77, 043804. [Google Scholar] [CrossRef]
- Locatelli, A.; Modotto, D.; Paloschi, D.; Angelis, C.D. All optical switching in ultrashort photonic crystal couplers. Opt. Commun. 2004, 237, 97–102. [Google Scholar] [CrossRef]
- Herring, G.; Kevrekidis, P.G.; Malomed, B.A.; Carretero-González, R.; Frantzeskakis, D.J. Symmetry breaking in linearly coupled dynamical lattices. Phys. Rev. E 2007, 76, 066606. [Google Scholar] [CrossRef]
- Aubry, S. Breathers in nonlinear lattices: Existence, linear stability and quantization. Phys. D 1997, 103, 201–250. [Google Scholar] [CrossRef]
- Rothos, V.M. Nonlinear wave propagation in discrete and continuous systems. Eur. Phys. J. Spec. Top. 2016, 225, 943–958. [Google Scholar] [CrossRef]
- Tsoy, E.N.; Umarov, B.A. Introduction to nonlinear discrete systems: Theory and modelling. Eur. J. Phys. 2018, 39, 055803. [Google Scholar] [CrossRef]
- Malomed, B.A. Nonlinearity and discreteness: Solitons in lattices. In Emerging Frontiers in Nonlinear Science; Kevrekidis, P.G., Cuevas-Maraver, J., Saxena, A., Eds.; Springer Nature: Cham, Switzerland, 2020; pp. 81–110. [Google Scholar]
- Kevrekidis, P.G. The Discrete Nonlinear Schrödinger Equation: Mathematical Analysis, Numerical Computations, and Physical Perspectives; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Laedke, E.W.; Spatschek, K.H.; Turitsyn, S.K. Stability of discrete solitons and quasicollapse to intrinsically localized modes. Phys. Rev. Lett. 1994, 73, 1055–1059. [Google Scholar] [CrossRef]
- Kartashov, Y.; Astrakharchik, G.; Malomed, B.; Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 2019, 1, 185–197. [Google Scholar] [CrossRef]
- Malomed, B.A. Multidimensional Solitons; AIP Publishing: Melville, NY, USA, 2022. [Google Scholar]
- Malomed, B.A. Multidimensional Soliton Systems. Adv. Phys. X 2024, 9, 2301592. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low temperature properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Cabrera, C.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose–Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose–Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets of atomic mixtures in free space? Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Dynamics of one-dimensional quantum droplets. Phys. Rev. A 2018, 98, 01363. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Manakov, S.V.; Novikov, S.P.; Pitaevskii, L.P. Solitons: The Inverse Scattering Method; Nauka Publishers: Moscow, Russia, 1980; English Translation: Consultants Bureau: New York, NY, USA, 1984. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitons and Inverse Scattering Method; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Calogero, F.; Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations; North-Holland: New York, NY, USA, 1982. [Google Scholar]
- Newell, A.C. Solitons in Mathematics and Physics; SIAM: Philadelphia, PA, USA, 1985. [Google Scholar]
- Ablowitz, M.J.; Herbst, B.M. On homoclinic structure and numerically induced chaos for the nonlinear Schrödinger equation. SIAM J. Appl. Math. 1990, 50, 339–351. [Google Scholar] [CrossRef]
- Levi, D.; Petrera, M.; Scimiterna, C. On the integrability of the discrete nonlinear Schrödinger equation. Europhys. Lett. 2008, 84, 10003. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Ladik, J.F. Nonlinear differential–difference equations and Fourier analysis. J. Math. Phys. 1976, 17, 1011–1018. [Google Scholar] [CrossRef]
- Suris, Y.B. The Problem of Integrable Discretization: Hamiltonian Approach; Birkhauser: Basel, Switzerland, 2003. [Google Scholar]
- Duncan, D.B.; Eilbeck, J.C.; Feddersen, H.; Wattis, A.D. Solitons on lattices. Phys. D 1993, 68, 1–11. [Google Scholar] [CrossRef]
- Toda, M. Vibration of a chain with a non-linear interaction. J. Phys. Soc. Jpn. 1967, 22, 431–436. [Google Scholar] [CrossRef]
- Salerno, M. A new method to solve the quantum Ablowitz–Ladik system. Phys. Lett. A 1992, 162, 381–384. [Google Scholar] [CrossRef]
- Dutta, O.; Gajda, M.; Hauke, P.; Lewenstein, M.; Luhmann, D.-S.; Malomed, B.A.; Sowinski, T.; Zakrzewski, J. Non-standard Hubbard models in optical lattices: A review. Rep. Prog. Phys. 2015, 78, 066001. [Google Scholar] [CrossRef]
- Cai, D.; Bishop, A.R.; Grønbech-Jensen, N. Perturbation theories of a discrete, integrable nonlinear Schrödinger equation. Phys. Rev. E 1996, 53, 4131–4136. [Google Scholar] [CrossRef]
- Gómez-Garde nes, J.; Malomed, B.A.; Floría, L.M.; Bishop, A.R. Solitons in the Salerno model with competing nonlinearities. Phys. Rev. E 2006, 73, 036608. [Google Scholar] [CrossRef]
- Chen, D.; Aubry, S.; Tsironis, G.P. Breather mobility in discrete φ4 nonlinear lattices. Phys. Rev. Lett. 1996, 77, 4776–4779. [Google Scholar] [CrossRef]
- Borovkova, O.V.; Kartashov, Y.V.; Torner, L.; Malomed, B.A. Bright solitons from defocusing nonlinearities. Phys. Rev. E 2011, 84, 035602. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Hadzievski, L.; Malomed, B.A. Discrete localized modes supported by an inhomogeneous defocusing nonlinearity. Phys. Rev. E 2013, 88, 032905. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Malomed, B.A.; Saxena, A.; Bishop, A.R.; Frantzeskakis, D.J. Solitons and vortices in two-dimensional discrete nonlinear Schrödinger systems with spatially modulated nonlinearity. Phys. Rev. E 2015, 91, 043201. [Google Scholar] [CrossRef]
- Pedri, P.; Santos, L. Two-dimensional bright solitons in dipolar Bose–Einstein condensates. Phys. Rev. Lett. 2005, 95, 200404. [Google Scholar] [CrossRef] [PubMed]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 126401. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Stepić, M.; Hadžievski, L.; Malomed, B.A. Discrete vortex solitons in dipolar Bose–Einstein condensates. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 055303. [Google Scholar] [CrossRef]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Anisotropic solitons in dipolar Bose–Einstein condensates. Phys. Rev. Lett. 2008, 100, 090406. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, J.; Pang, W.; Malomed, B.A. Lattice solitons with quadrupolar intersite interactions. Phys. Rev. A 2013, 88, 063635. [Google Scholar] [CrossRef]
- Buryak, V.; Trapani, P.D.; Skryabin, D.V.; Trillo, S. Optical solitons due to quadratic nonlinearities: From basic physics to futuristic applications. Phys. Rep. 2002, 370, 63–235. [Google Scholar] [CrossRef]
- Susanto, H.; Kevrekidis, P.G.; Carretero-González, R.; Malomed, B.A.; Frantzeskakis, D.J. Mobility of discrete solitons in quadratically nonlinear media. Phys. Rev. Lett. 2007, 99, 214103. [Google Scholar] [CrossRef] [PubMed]
- Kivshar, Y.S.; Peyrard, M. Modulational instabilities in discrete lattices. Phys. Rev. A 1992, 46, 3198–3205. [Google Scholar] [CrossRef]
- Malomed, B.A. Variational methods in nonlinear fiber optics and related fields. Prog. Opt. 2002, 43, 71–193. [Google Scholar]
- Malomed, B.A.; Weinstein, M.I. Soliton dynamics in the discrete nonlinear Schrödinger equation. Phys. Lett. A 1996, 220, 91–99. [Google Scholar] [CrossRef]
- Papacharalampous, I.E.; Kevrekidis, P.G.; Malomed, B.A.; Frantzeskakis, D. Soliton collisions in the discrete nonlinear Schrödinger equation. Phys. Rev. E 2003, 68, 046604. [Google Scholar] [CrossRef] [PubMed]
- Kaup, D.J. Variational solutions for the discrete nonlinear Schrödinger equation. Math. Comput. Simulat. 2005, 69, 322–333. [Google Scholar] [CrossRef]
- Malomed, B.A.; Kaup, D.J.; Gorder, R.A.V. Unstaggered-staggered solitons in two-component discrete nonlinear Schrödinger lattices. Phys. Rev. E 2012, 85, 026604. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, J.; James, G.; Kevrekidis, P.G.; Malomed, B.A.; Sánchez-Rey, B.S. Approximation of solitons in the discrete NLS equation. J. Nonlinear Math. Phys. 2008, 15 (Suppl. S3), 124–136. [Google Scholar] [CrossRef]
- Chong, C.; Pelinovsky, D.E.; Schneider, G. On the validity of the variational approximation in discrete nonlinear Schrödinger equations. Phys. D 2012, 241, 115–124. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Krolikowski, W.; Chubykalo, O.A. Dark solitons in discrete lattices. Phys. Rev. E 1994, 50, 5020–5032. [Google Scholar] [CrossRef] [PubMed]
- Alfimov, G.L.; Konotop, V.V.; Salerno, M. Matter solitons in Bose–Einstein condensates with optical lattices. Europhys. Lett. 2002, 58, 7–13. [Google Scholar] [CrossRef]
- Mandelik, D.; Morandotti, R.; Aitchison, J.S.; Silberberg, Y. Gap solitons in waveguide arrays. Phys. Rev. Lett. 2004, 92, 093904. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Lv, Y.; Feng, Z.F.; Li, P.F. Unidirectional flow of the discrete dark solitons and excitation of the discrete X-waves in PT-symmetric optical waveguide arrays. Rom. Rep. Phys. 2022, 74, 110. [Google Scholar]
- Cuevas, J.; James, G.; Kevrekidis, P.G.; Law, K.J.H. Vortex solutions of the discrete Gross–Pitaevskii equation starting from the anti-continuum limit. Phys. D 2009, 238, 1422–1431. [Google Scholar] [CrossRef][Green Version]
- Darmanyan, S.; Kobyakov, A.; Lederer, F. Stability of strongly localized excitations in discrete media with cubic nonlinearity. J. Exp. Theor. Phys. 1998, 86, 682–686. [Google Scholar] [CrossRef]
- Kapitula, T.; Kevrekidis, P.G.; Malomed, B.A. Stability of multiple pulses in discrete systems. Phys. Rev. E 2001, 63, 036604. [Google Scholar] [CrossRef] [PubMed]
- Pelinovsky, D.E.; Kevrekidis, P.G.; Frantzeskakis, D.J. Stability of discrete solitons in nonlinear Schrödinger lattices. Phys. D 2005, 212, 1–19. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Malomed, B.A.; Bishop, A.R. Bound states of two-dimensional solitons in the discrete nonlinear Schrödinger equation. J. Phys. A Math. Gen. 2001, 34, 9615–9629. [Google Scholar] [CrossRef]
- Cai, D.; Bishop, A.R.; Grønbech-Jensen, N. Resonance in the collision of two discrete intrinsic localized excitations. Phys. Rev. E 1997, 56, 7246–7252. [Google Scholar] [CrossRef]
- Dmitriev, S.V.; Kevrekidis, P.G.; Malomed, B.A.; Frantzeskakis, D. Two-soliton collisions in a near-integrable lattice system. Phys. Rev. E 2003, 68, 056603. [Google Scholar] [CrossRef]
- Blit, R.; Malomed, B.A. Propagation and collisions of semi-discrete solitons in arrayed and stacked waveguides. Phys. Rev. A 2012, 86, 043841. [Google Scholar] [CrossRef]
- Driben, R.; Konotop, V.V.; Malomed, B.A.; Meier, T.; Yulin, A. Nonlinearity-induced localization in a periodically driven semidiscrete system. Phys. Rev. E 2018, 97, 062210. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Zheng, Y.; Chen, Z.; Liu, B.; Huang, C.; Malomed, B.; Li, Y. Semidiscrete quantum droplets and vortices. Phys. Rev. Lett. 2019, 123, 133901. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Ou, G.; Chen, Z.; Liu, B.; Malomed, B.A.; Li, Y. Semidiscrete vortex solitons. Adv. Photonics Res. 2021, 2, 2000082. [Google Scholar] [CrossRef]
- Neshev, D.N.; Alexander, T.J.; Ostrovskaya, E.A.; Kivshar, Y.S.; Martin, H.; Makasyuk, I.; Chen, Z.G. Observation of discrete vortex solitons in optically induced photonic lattices. Phys. Rev. Lett. 2004, 92, 123903. [Google Scholar] [CrossRef]
- Fleischer, J.W.; Bartal, G.; Cohen, O.; Manela, O.; Segev, M.; Hudock, J.; Christodoulides, D.N. Observation of vortex-ring “discrete” solitons in 2D photonic lattices. Phys. Rev. Lett. 2004, 92, 123904. [Google Scholar] [CrossRef]
- Ford, J. The Fermi-Pasta-Ulam problem—Paradox turns discovery. Phys. Rep. 1992, 213, 271–310. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S. The Frenkel–Kontorova Model: Concepts, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Chen, Z.; Liu, J.; Fu, S.; Li, Y.; Malomed, B.A. Discrete solitons and vortices on two-dimensional lattices of PT-symmetric couplers. Opt. Exp. 2014, 22, 29679–29692. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, M.I. Excitation thresholds for nonlinear localized modes on lattices. Nonlinearity 1999, 12, 673. [Google Scholar] [CrossRef]
- Chong, C.; Carretero-González, R.; Malomed, B.A.; Kevrekidis, P. Multistable solitons in higher-dimensional cubic–quintic nonlinear Schrödinger lattices. Phys. D 2009, 238, 126–136. [Google Scholar] [CrossRef][Green Version]
- Malomed, B.A.; Kevrekidis, P.G. Discrete vortex solitons. Phys. Rev. E 2001, 64, 026601. [Google Scholar] [CrossRef]
- Pelinovsky, D.E.; Kevrekidis, P.G.; Frantzeskakis, D.J. Persistence and stability of discrete vortices in nonlinear Schrödinger lattices. Phys. D 2005, 212, 20–53. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-Trapping of Optical Beams. Phys. Rev. Lett. 1964, 13, 479–482. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Logvin, Y.A.; Volkov, V.M. The theory of spiral laser beams in nonlinear media. J. Mod. Opt. 1992, 39, 2277–2291. [Google Scholar] [CrossRef]
- Malomed, B.A. (INVITED) Vortex solitons: Old results and new perspectives. Phys. D 2019, 399, 108–137. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Malomed, B.A.; Chen, Z.; Frantzeskakis, D.J. Stable higher-order vortices and quasivortices in the discrete nonlinear Schrödinger equation. Phys. Rev. E 2004, 70, 056612. [Google Scholar] [CrossRef] [PubMed]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R.; Malomed, B.A.; Bishop, A.R. Discrete solitons and vortices on anisotropic lattices. Phys. Rev. E 2005, 72, 046613. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M.; Wilson, D.W.; Muller, R.E.; Maker, P.D. Self-trapping of an optical vortex by use of the bulk photovoltaic effect. Phys. Rev. Lett. 1997, 78, 2948–2951. [Google Scholar] [CrossRef]
- Chen, Z.; Shih, M.-F.; Segev, M.; Wilson, D.W.; Muller, R.E.; Maker, P.D. Steady-state vortex-screening solitons formed in biased photorefractive media. Opt. Lett. 1997, 22, 1751–1753. [Google Scholar] [CrossRef]
- Bezryadina, A.; Eugenieva, E.; Chen, Z. Self-trapping and flipping of double-charged vortices in optically induced photonic lattices. Opt. Lett. 2006, 31, 2456–2458. [Google Scholar] [CrossRef]
- Terhalle, B.; Richter, T.; Law, K.J.H.; Göries, D.; Rose, P.; Alexander, T.J.; Kevrekidis, P.G.; Desyatnikov, A.S.; Krolikowski, W.; Kaiser, F.; et al. Observation of double-charge discrete vortex solitons in hexagonal photonic lattices. Phys. Rev. A 2009, 79, 043821. [Google Scholar] [CrossRef]
- Malomed, B.A. Potential of interaction between two- and three-dimensional solitons. Phys. Rev. E 1998, 58, 7928–7933. [Google Scholar] [CrossRef]
- De Sterke, C.M.; Sipe, J.E. Gap solitons. Prog. Opt. 1994, XXXIII, 203–260. [Google Scholar]
- Brazhnyi, V.A.; Konotop, V.V. Theory of nonlinear matter waves in optical lattices. Mod. Phys. Lett. B 2004, 18, 627–651. [Google Scholar] [CrossRef]
- Eiermann, B.; Anker, T.; Albiez, M.; Taglieber, M.; Treutlein, P.; Marzlin, K.-P.; Oberthaler, M.K. Bright Bose–Einstein gap solitons of atoms with repulsive interaction. Phys. Rev. Lett. 2004, 92, 230401. [Google Scholar] [CrossRef] [PubMed]
- Mok, J.T.; de Sterke, C.M.; Litte, I.C.M.; Eggleton, B.J. Dispersionless slow light using gap solitons. Nat. Phys. 2006, 2, 775–780. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Hadzievski, L.; Malomed, B.A. Localized modes in mini-gaps opened by periodically modulated intersite coupling in two-dimensional nonlinear lattices. Chaos 2014, 24, 023124. [Google Scholar] [CrossRef]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Cuevas, J.; Malomed, B.A.; Kevrekidis, P.G. Two-dimensional discrete solitons in rotating lattices. Phys. Rev. E 2007, 76, 046608. [Google Scholar] [CrossRef]
- Malomed, B.A. Spontaneous symmetry breaking in nonlinear systems: An overview and a simple model. In Nonlinear Dynamics: Materials, Theory and Experiments; Tlidi, M., Clerc, M., Eds.; Springer Proceedings in Physics; Springer: Cham, Switzerland, 2016; Volume 173, p. 97. [Google Scholar]
- Iooss, G.; Joseph, D.D. Elementary Stability Bifurcation Theory; Springer: New York, NY, USA, 1980. [Google Scholar]
- Gómez-Garde nes, J.; Malomed, B.A.; Floría, L.M.; Bishop, A.R. Discrete solitons and vortices in the two-dimensional Salerno model with competing nonlinearities. Phys. Rev. E 2006, 74, 036607. [Google Scholar] [CrossRef]
- Lin, Y.-J.; Jiménez-García, K.; Spielman, I.B. Spin-orbit-coupled Bose–Einstein condensates. Nature 2011, 471, 83–86. [Google Scholar] [CrossRef]
- Galitski, V.; Spielman, I.B. Spin-orbit coupling in quantum gases. Nature 2013, 494, 49–54. [Google Scholar] [CrossRef]
- Goldman, N.; Juzeliunas, G.; Öhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef]
- Zhai, H. Degenerate quantum gases with spin–orbit coupling. Rep. Prog. Phys. 2015, 78, 026001. [Google Scholar] [CrossRef]
- Malomed, B.A. Creating solitons by means of spin–orbit coupling. EPL 2018, 122, 36001. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Li, B.; Malomed, B.A. Creation of two-dimensional composite solitons in spin–orbit-coupled self-attractive Bose–Einstein condensates in free space. Phys. Rev. E 2014, 89, 032920. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Discrete and continuum composite solitons in Bose–Einstein condensates with the Rashba spin–orbit coupling in one and two dimensions. Phys. Rev. E 2014, 90, 062922. [Google Scholar] [CrossRef]
- Pelinovsky, D. Localization in Periodic Potentials: From Schrödinger Operators to the Gross-Pitaevskii Equation; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kevrekidis, P.G.; Malomed, B.A.; Frantzeskakis, D.J.; Carretero-González, R. Three-dimensional solitary waves and vortices in a discrete nonlinear Schrödinger lattice. Phys. Rev. Lett. 2004, 93, 080403. [Google Scholar] [CrossRef]
- Carretero-González, R.; Kevrekidis, P.G.; Malomed, B.A.; Frantzeskakis, D.J. Three-dimensional nonlinear lattices: From oblique vortices and octupoles to discrete diamonds and vortex cubes. Phys. Rev. Lett. 2005, 94, 203901. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Anglin, J.R. Creating vortex rings and three-dimensional skyrmions in Bose–Einstein condensates. Phys. Rev. Lett. 2001, 86, 3934–3937. [Google Scholar] [CrossRef]
- Khawaja, U.A.; Stoof, H. Skyrmions in a ferromagnetic Bose–Einstein condensate. Nature 2001, 411, 918–920. [Google Scholar] [CrossRef]
- Battye, R.A.; Cooper, N.R.; Sutcliffe, P.M. Stable skyrmions in two-component Bose–Einstein condensates. Phys. Rev. Lett. 2002, 88, 080401. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Carretero-González, R.; Frantzeskakis, D.J.; Malomed, B.A.; Diakonos, F.K. Skyrmion-like states in two- and three-dimensional dynamical lattices. Phys. Rev. E 2007, 75, 026603. [Google Scholar] [CrossRef]
- Kudryavtsevy, A.; Piette, B.; Zakrzewski, W.J. Skyrmions and domain walls in (2 + 1) dimensions. Nonlinearity 1998, 11, 783–795. [Google Scholar] [CrossRef]
- Weidig, T. The baby Skyrme models and their multi-skyrmions. Nonlinearity 1999, 12, 1489–1503. [Google Scholar] [CrossRef]
- Aceves, A.B.; Angelis, C.D.; Rubenchik, A.M.; Turitsyn, S.K. Multidimensional solitons in fiber arrays. Opt. Lett. 1994, 19, 329. [Google Scholar] [CrossRef]
- Minardi, S.; Eilenberger, F.; Kartashov, Y.V.; Szameit, A.; Kobelke, U.R.J.; Schuster, K.; Bartelt, H.; Nolte, S.; Torner, L.; Lederer, F.; et al. Three-dimensional light bullets in arrays of waveguides. Phys. Rev. Lett. 2010, 105, 263901. [Google Scholar] [CrossRef]
- Eilenberger, F.; Prater, K.; Minardi, S.; Geiss, R.; Kobelke, U.R.J.; Schuster, K.; Bartelt, H.; Nolte, S.; Tünnermann, A.; Pertsch, T. Observation of discrete, vortex light bullets. Phys. Rev. X 2013, 3, 041031. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.Z.J.; Xiang, H.; Zhang, L.; Chen, Z.; Nie, Z.; Malomed, B.A.; Li, Y. Semidiscrete optical vortex droplets in quasi-phase-matched photonic crystals. Opt. Exp. 2023, 31, 38343–38354. [Google Scholar] [CrossRef]
- Panoiu, N.C.; Osgood, R.M.; Malomed, B.A. Semi-discrete composite solitons in arrays of quadratically nonlinear waveguides. Opt. Lett. 2006, 31, 1097–1099. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Musslimani, Z.H. Beam dynamics in PT symmetric optical lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Konotop, V.V.; Yang, J.; Zezyulin, D. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
- Suchkov, S.V.; Huang, A.A.S.J.; Dmitriev, S.V.; Lee, C.; Kivshar, Y.S. Nonlinear switching and solitons in PT-symmetric photonic systems. Laser Phot. Rev. 2016, 10, 177–213. [Google Scholar] [CrossRef]
- Driben, R.; Malomed, B.A. Stability of solitons in parity-time-symmetric couplers. Opt. Lett. 2011, 36, 4323–4325. [Google Scholar] [CrossRef] [PubMed]
- Alexeeva, N.V.; Barashenkov, I.V.; Sukhorukov, A.A.; Kivshar, Y.S. Optical solitons in PT-symmetric nonlinear couplers with gain and loss. Phys. Rev. A 2012, 85, 063837. [Google Scholar] [CrossRef]
- Burlak, G.; Malomed, B.A. Stability boundary and collisions of two-dimensional solitons in PT-symmetric couplers with the cubic–quintic nonlinearity. Phys. Rev. E 2013, 88, 062904. [Google Scholar] [CrossRef]
- Konotop, V.V.; Pelinovsky, D.E.; Zezyulin, D.A. Discrete solitons in PT-symmetric lattices. Europhys. Lett. 2012, 100, 56006. [Google Scholar] [CrossRef]
- Huang, C.; Li, C.; Dong, L. Stabilization of multipole-mode solitons in mixed linear-nonlinear lattices with a PT-symmetry. Opt. Exp. 2013, 21, 3917–3925. [Google Scholar] [CrossRef]
- Leykam, D.; Konotop, V.V.; Desyatnikov, A.S. Discrete vortex solitons and parity time symmetry. Opt. Lett. 2013, 38, 371–373. [Google Scholar] [CrossRef] [PubMed]
- Pelinovsky, D.E.; Zezyulin, D.A.; Konotop, V.V. Nonlinear modes in a generalized PT-symmetric discrete nonlinear Schrödinger equation. J. Phys. A Math. Gen. 2014, 47, 085204. [Google Scholar] [CrossRef]
- D’Ambroise, J.; Kevrekidis, P.G.; Malomed, B.A. Staggered parity-time-symmetric ladders with cubic nonlinearity. Phys. Rev. E 2015, 91, 033207. [Google Scholar] [CrossRef]
- Wimmer, M.; Regensburger, A.; Miri, M.A.; Bersch, C.; Christodoulides, D.N.; Peschel, U. Observation of optical solitons in PT-symmetric lattices. Nat. Commun. 2015, 6, 7782. [Google Scholar] [CrossRef] [PubMed]
- Belićev, P.; Petrovixcx, G.G.J.; Maluckov, A.; Hadžievski, L.; Malomed, B.A. Composite localized modes in discretized spin–orbit-coupled Bose–Einstein condensates. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 065301. [Google Scholar] [CrossRef]
- Kivshar, Y.S. Nonlinear Tamm states and surface effects in periodic photonic structures. Laser Phys. Lett. 2008, 5, 703–713. [Google Scholar] [CrossRef]
- Gulevich, D.R.; Yudin, D.; Skryabin, D.V.; Iorsh, I.V.; Shelykh, I.A. Edge solitons in kagome lattice. Sci. Rep. 2017, 7, 1780. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.V.; Skryabin, D.V. Modulational instability and solitary waves in polariton topological insulators. Optica 2016, 3, 1228. [Google Scholar] [CrossRef]
- Molina, M.I. The two-dimensional fractional discrete nonlinear Schrödinger equation. Phys. Lett. A 2020, 384, 126835. [Google Scholar] [CrossRef]
- Hakim, V.; Rappel, W.J. Dynamics of the globally coupled complex Ginzburg-Landau equation. Phys. Rev. A 1992, 46, 7347–7350. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Discrete Ginzburg-Landau solitons. Phys. Rev. E 2003, 67, 026606. [Google Scholar] [CrossRef]
- Maruno, K.; Ankiewicz, A.; Akhmediev, N. Exact localized and periodic solutions of the discrete complex Ginzburg-Landau equation. Opt. Commun. 2003, 221, 199–209. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N.; Hizanidis, K. Two-dimensional discrete Ginzburg-Landau solitons. Phys. Rev. A 2007, 76, 043839. [Google Scholar] [CrossRef]
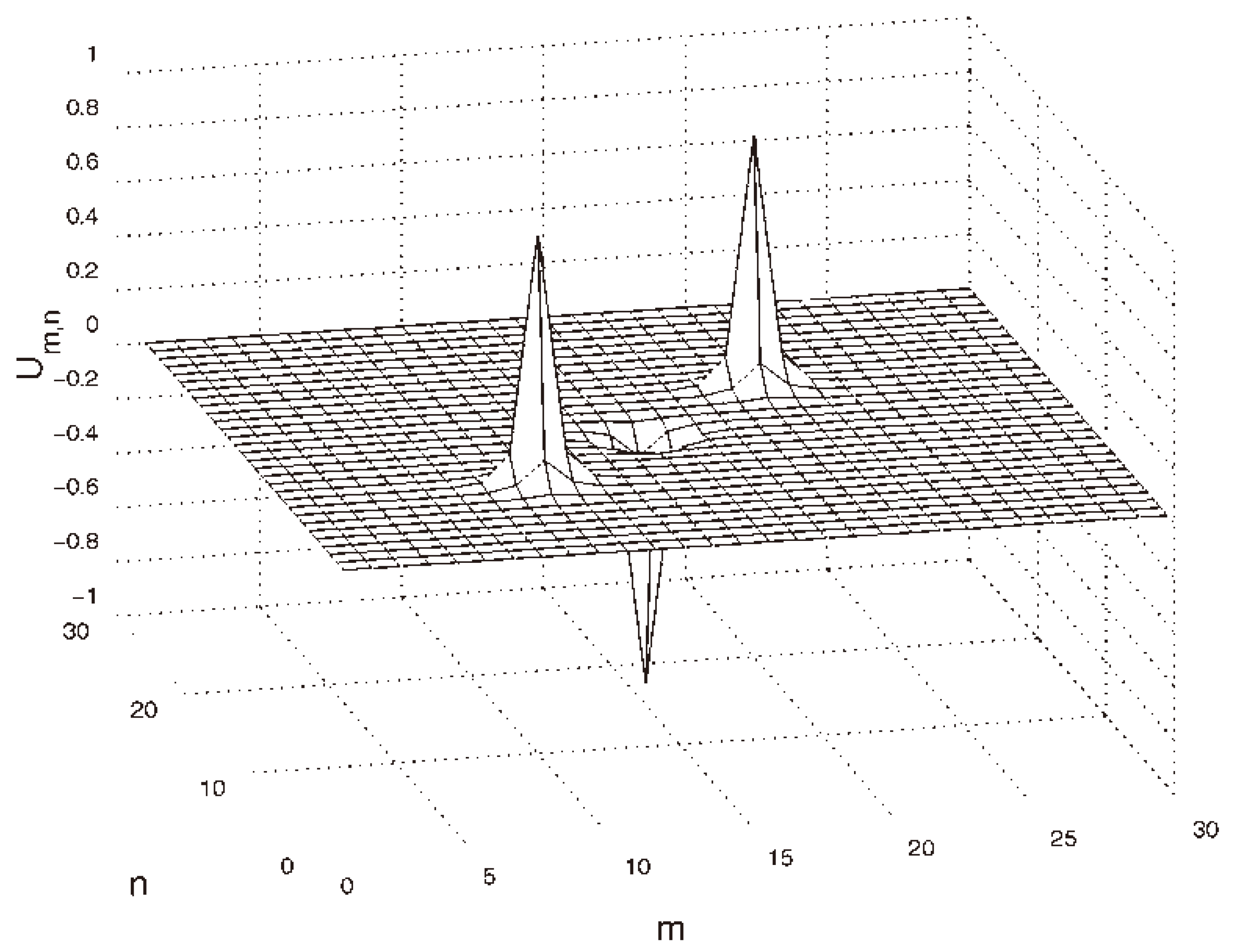
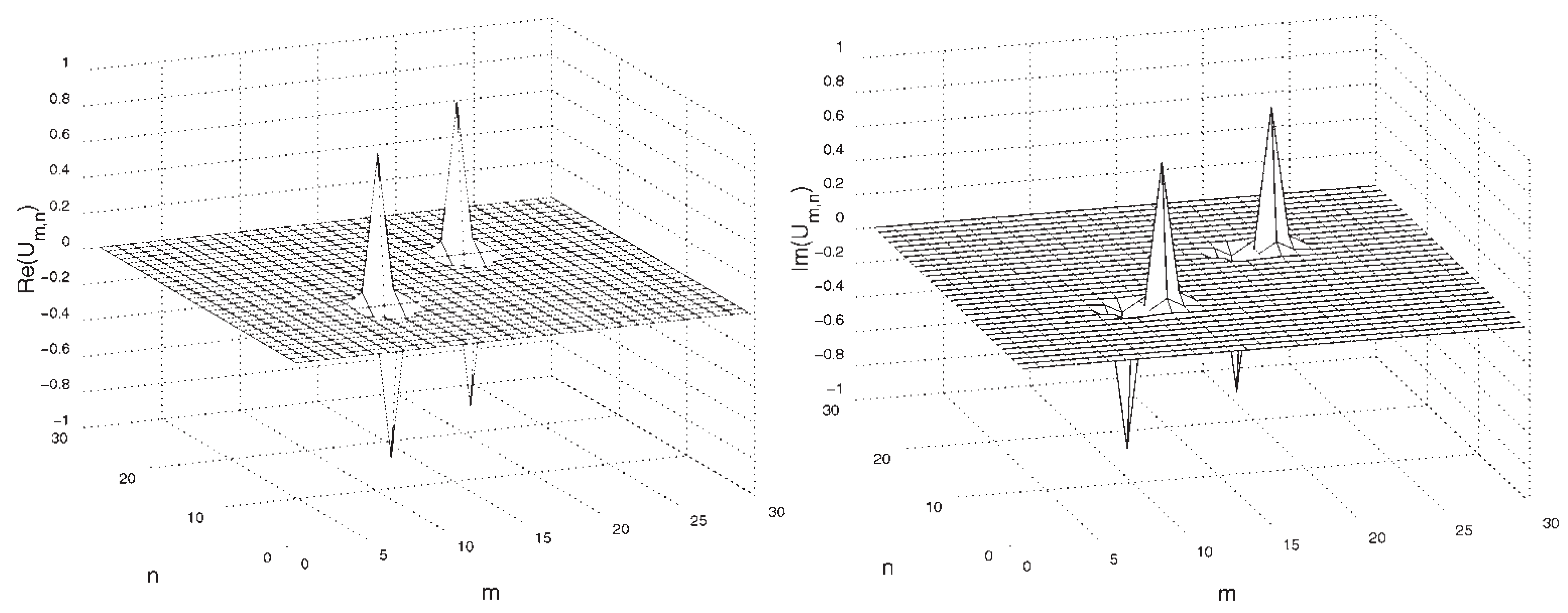
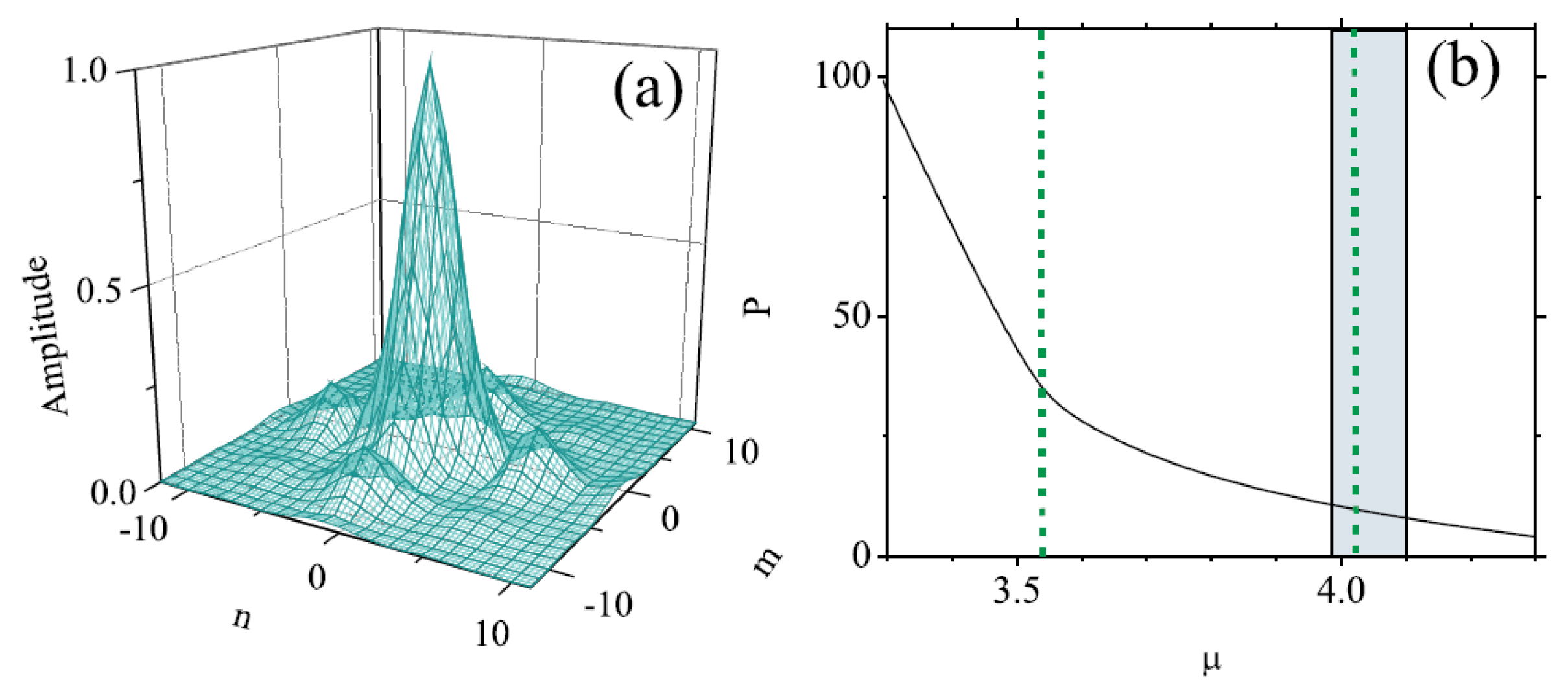

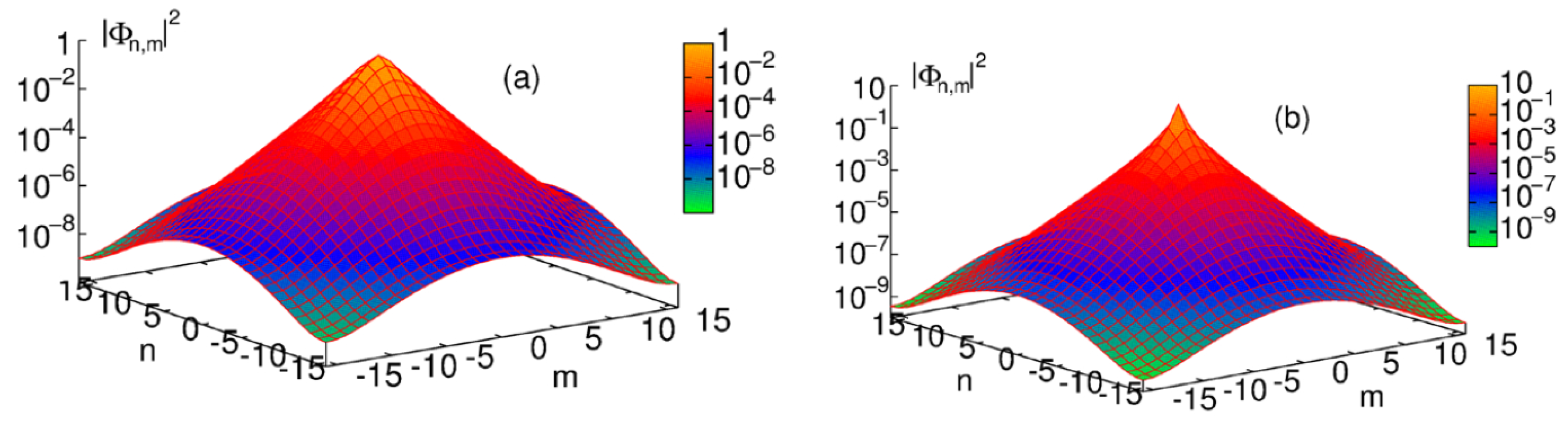
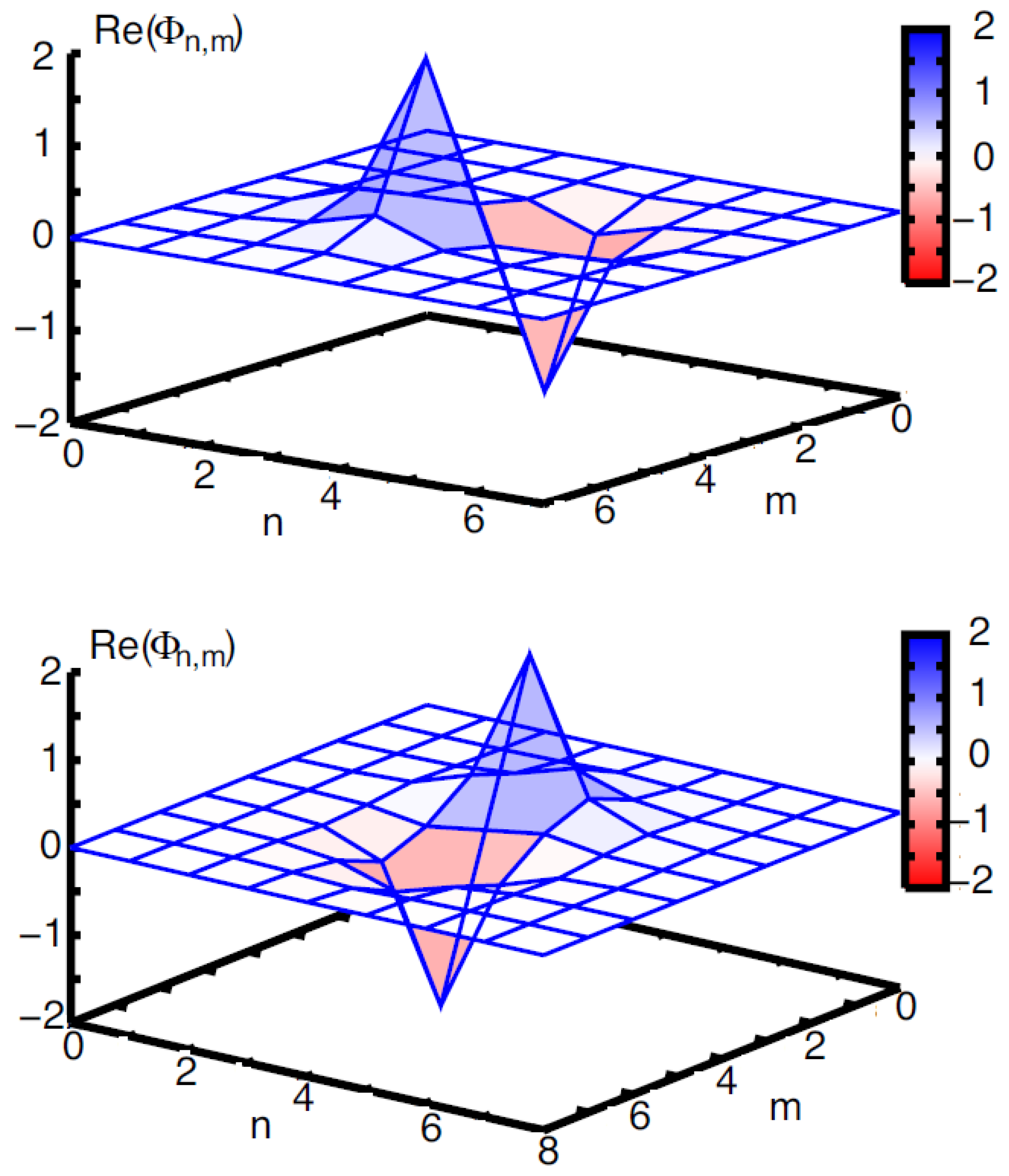
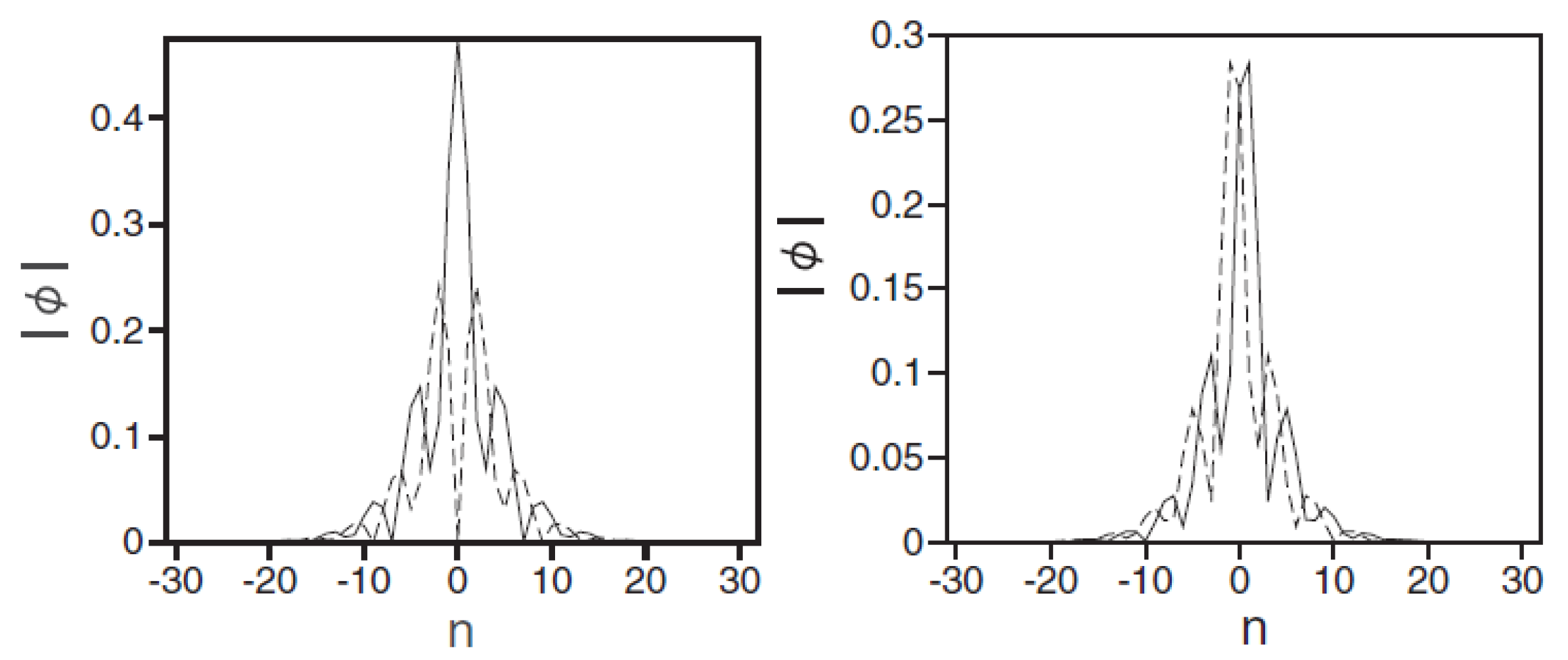
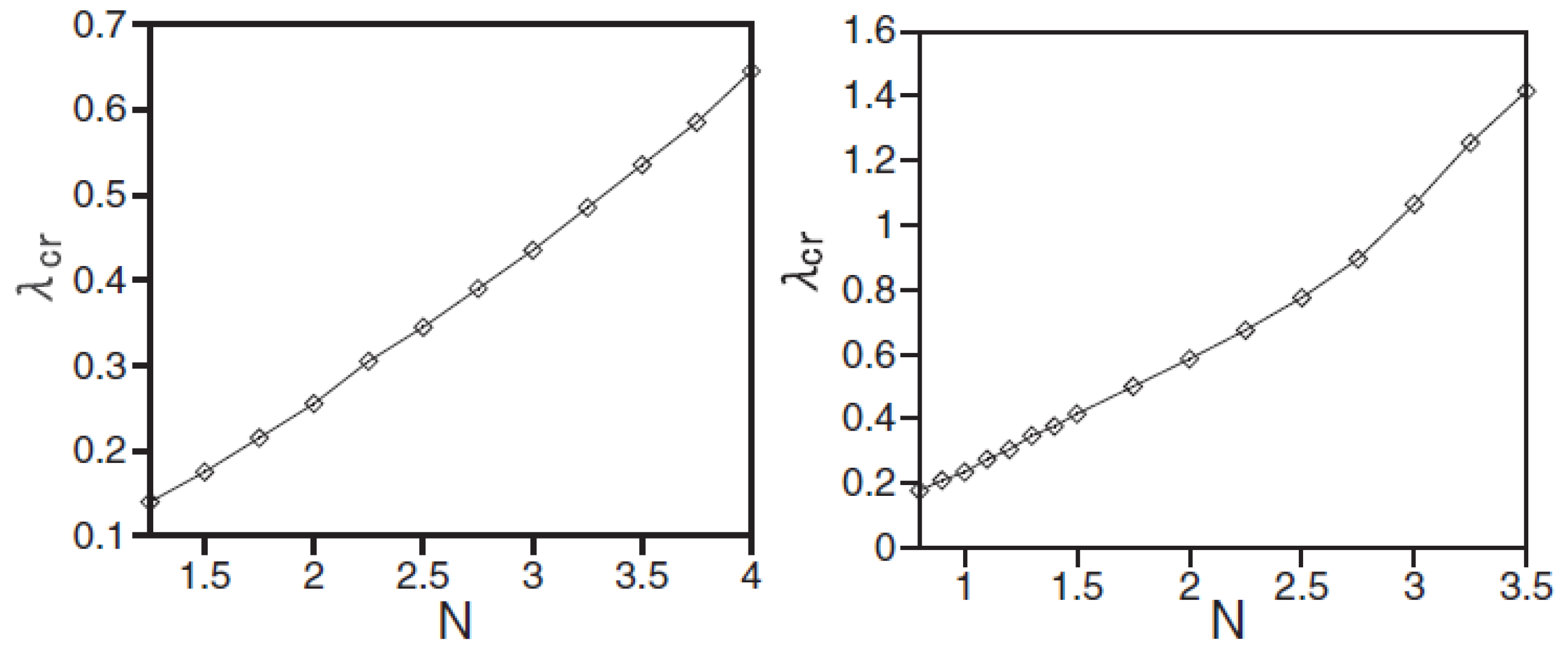
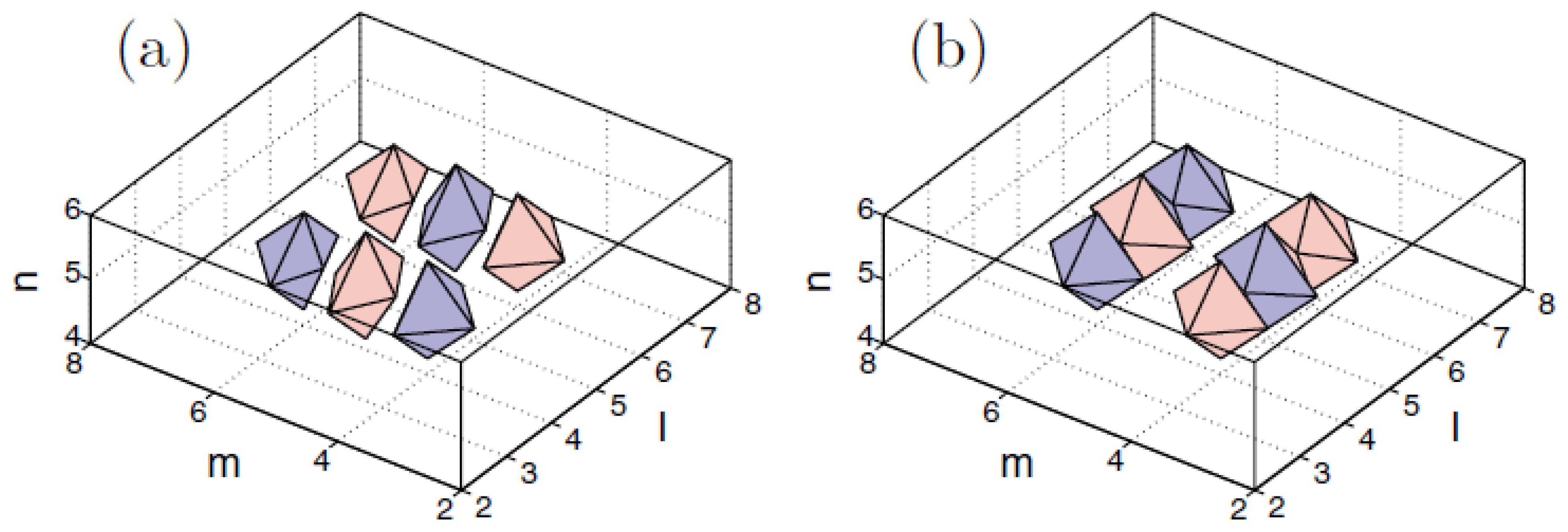
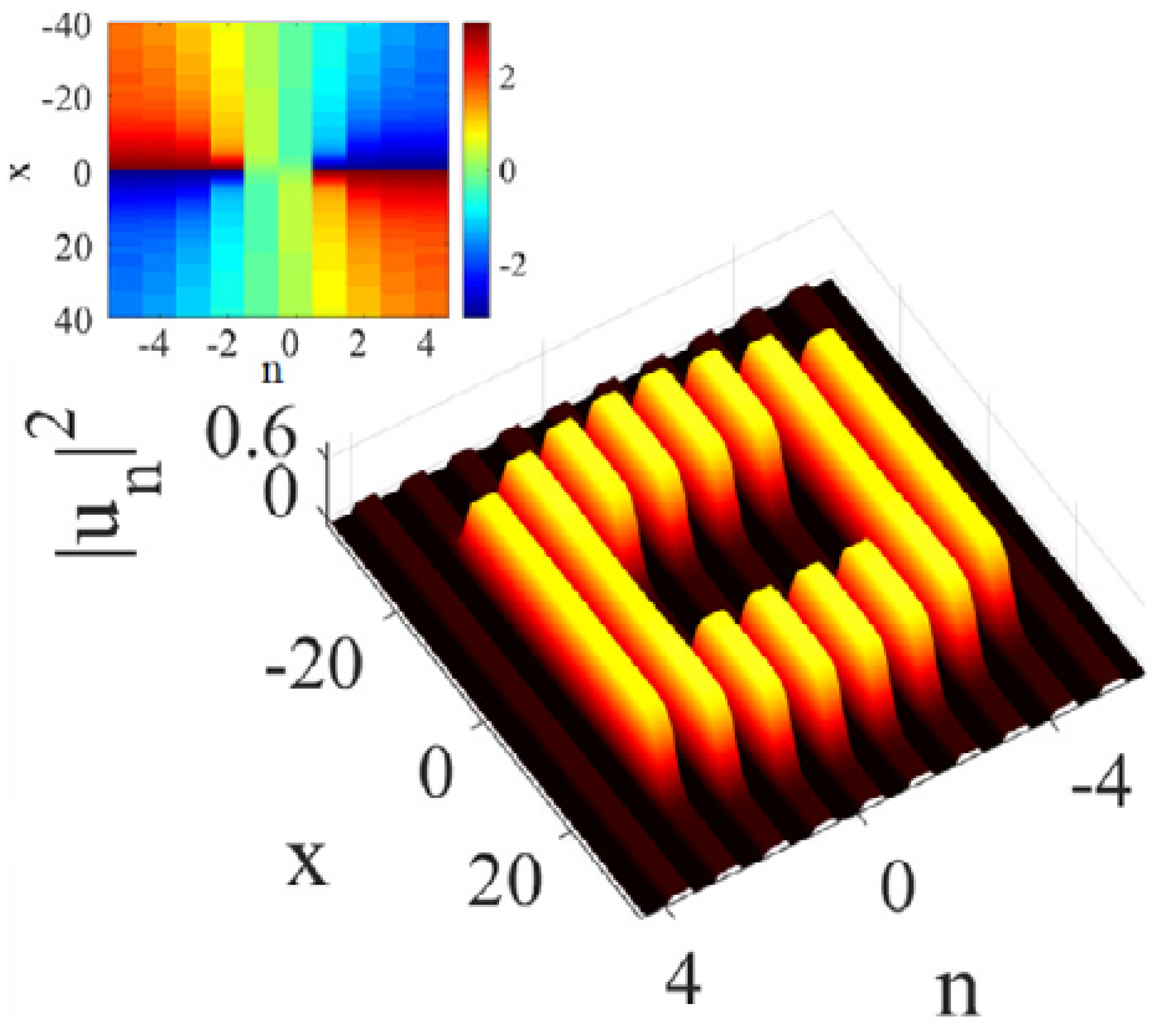
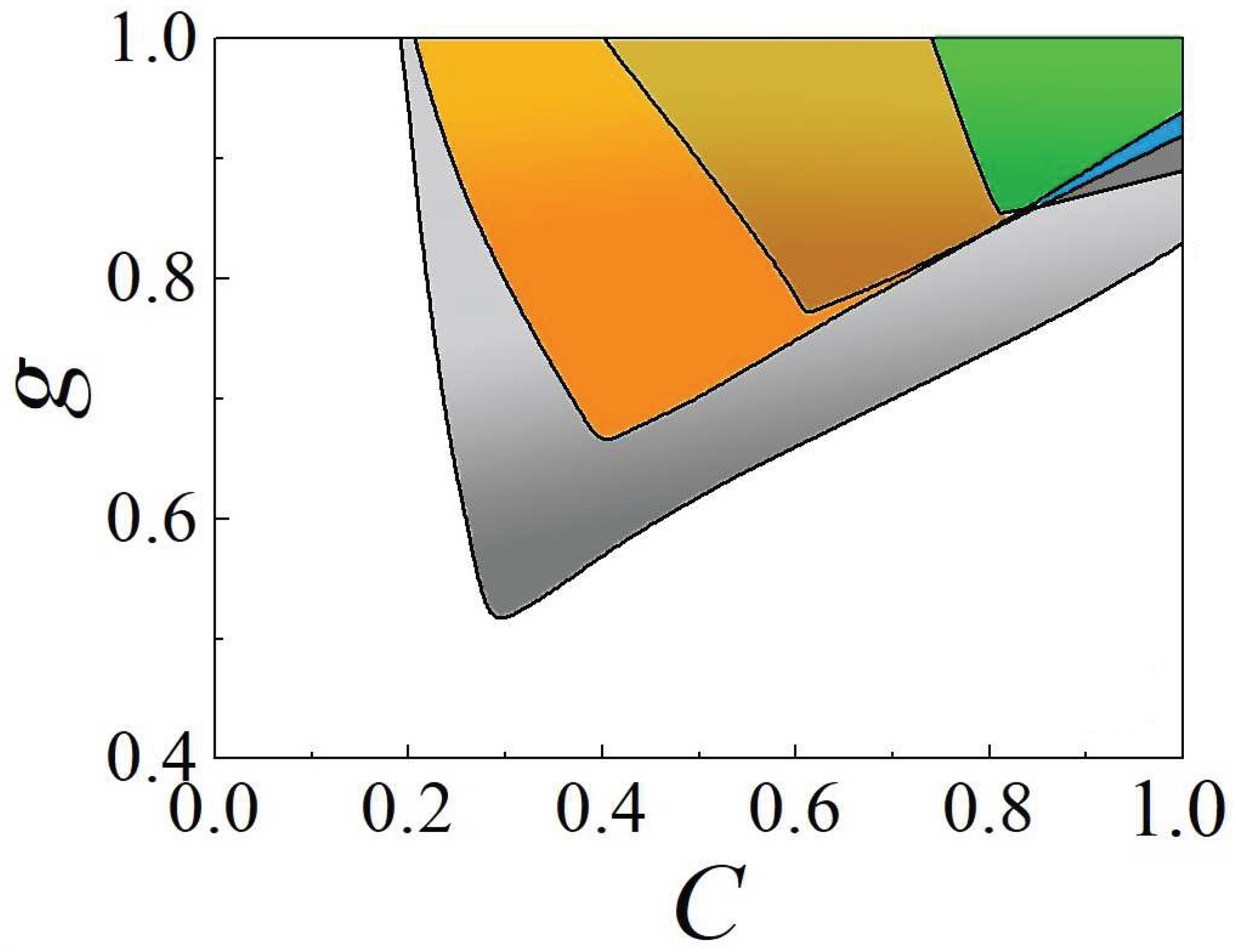
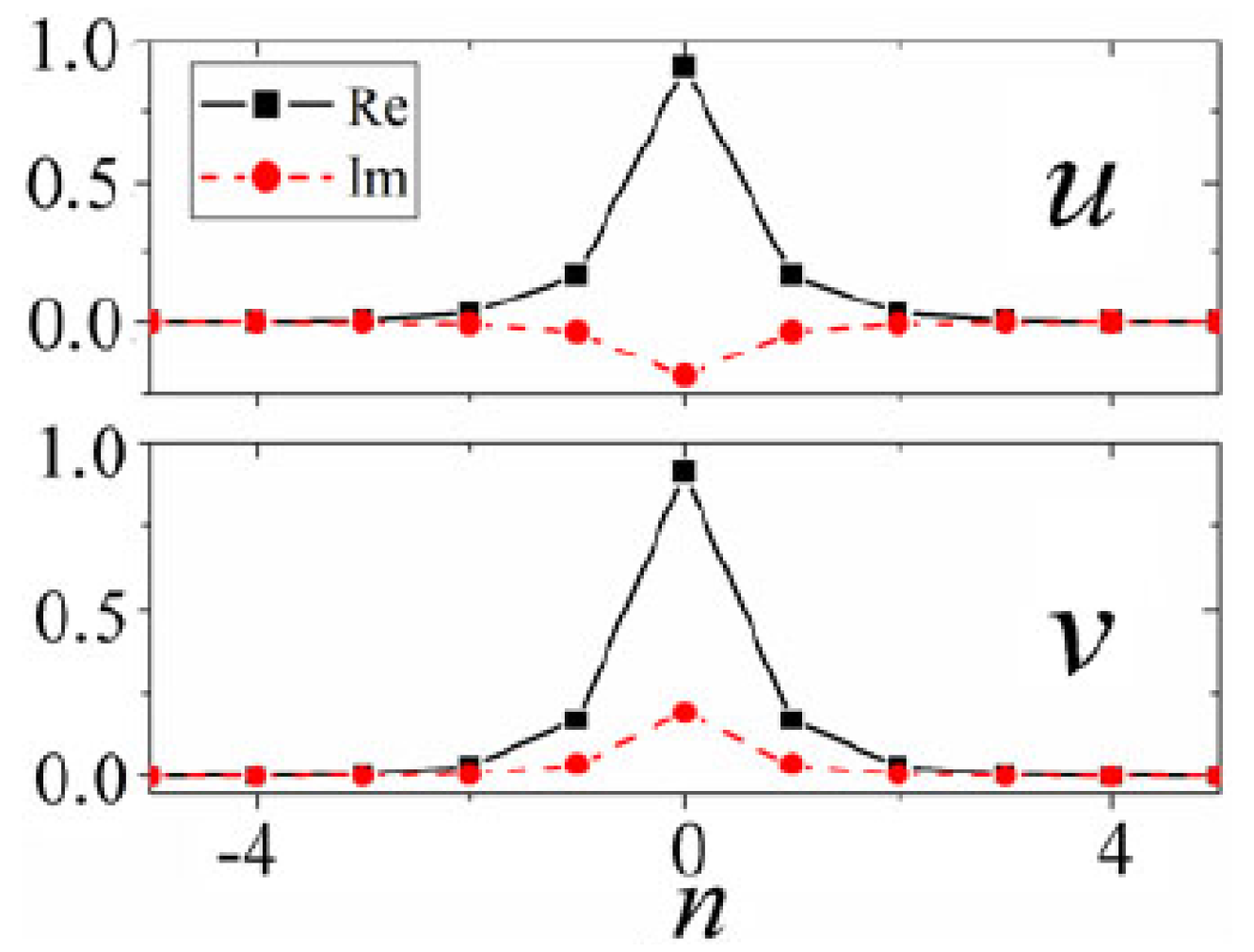
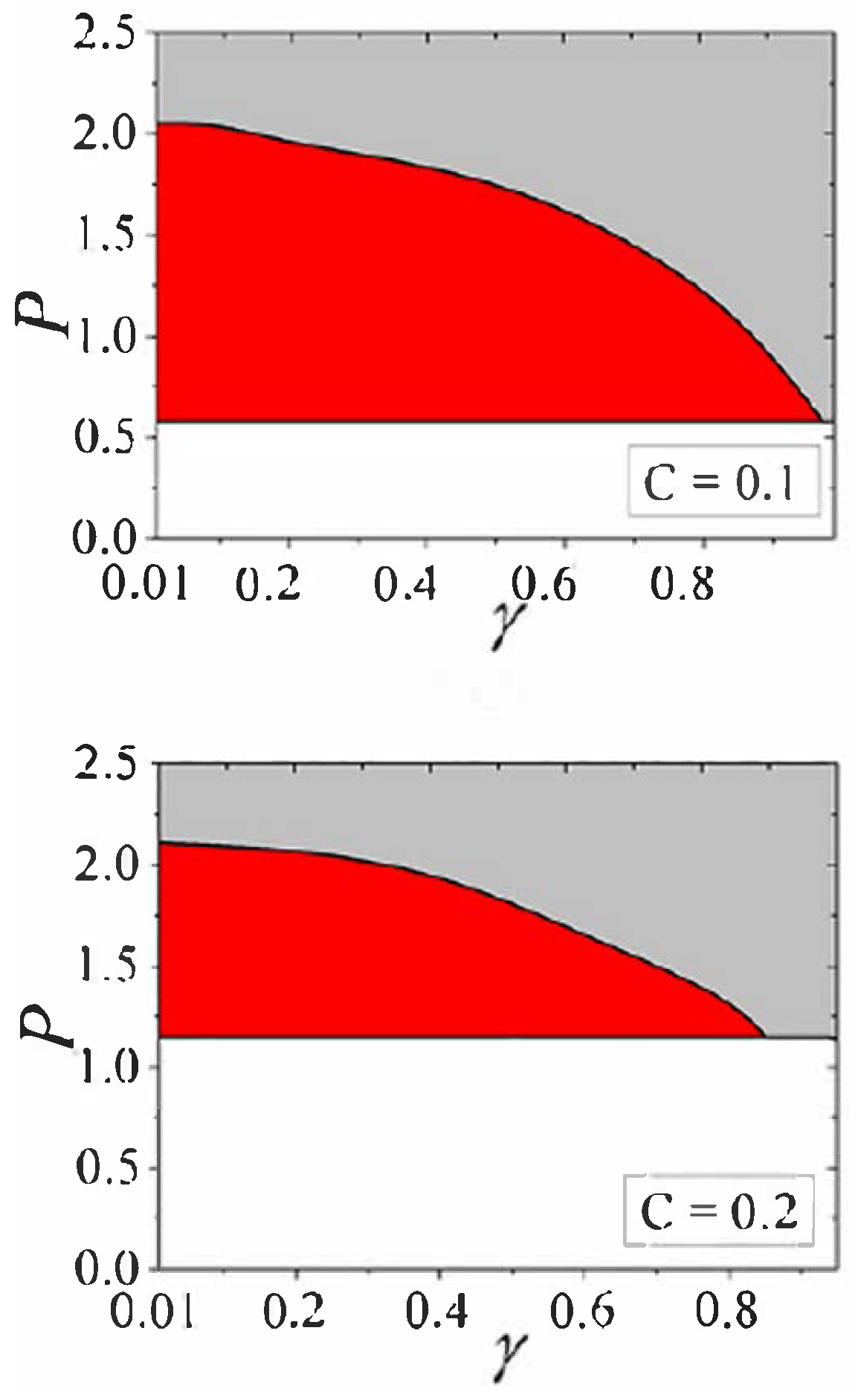
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malomed, B.A. Discrete and Semi-Discrete Multidimensional Solitons and Vortices: Established Results and Novel Findings. Entropy 2024, 26, 137. https://doi.org/10.3390/e26020137
Malomed BA. Discrete and Semi-Discrete Multidimensional Solitons and Vortices: Established Results and Novel Findings. Entropy. 2024; 26(2):137. https://doi.org/10.3390/e26020137
Chicago/Turabian StyleMalomed, Boris A. 2024. "Discrete and Semi-Discrete Multidimensional Solitons and Vortices: Established Results and Novel Findings" Entropy 26, no. 2: 137. https://doi.org/10.3390/e26020137
APA StyleMalomed, B. A. (2024). Discrete and Semi-Discrete Multidimensional Solitons and Vortices: Established Results and Novel Findings. Entropy, 26(2), 137. https://doi.org/10.3390/e26020137