Perturbational Decomposition Analysis for Quantum Ising Model with Weak Transverse Fields
Abstract
1. Introduction
2. Preliminary
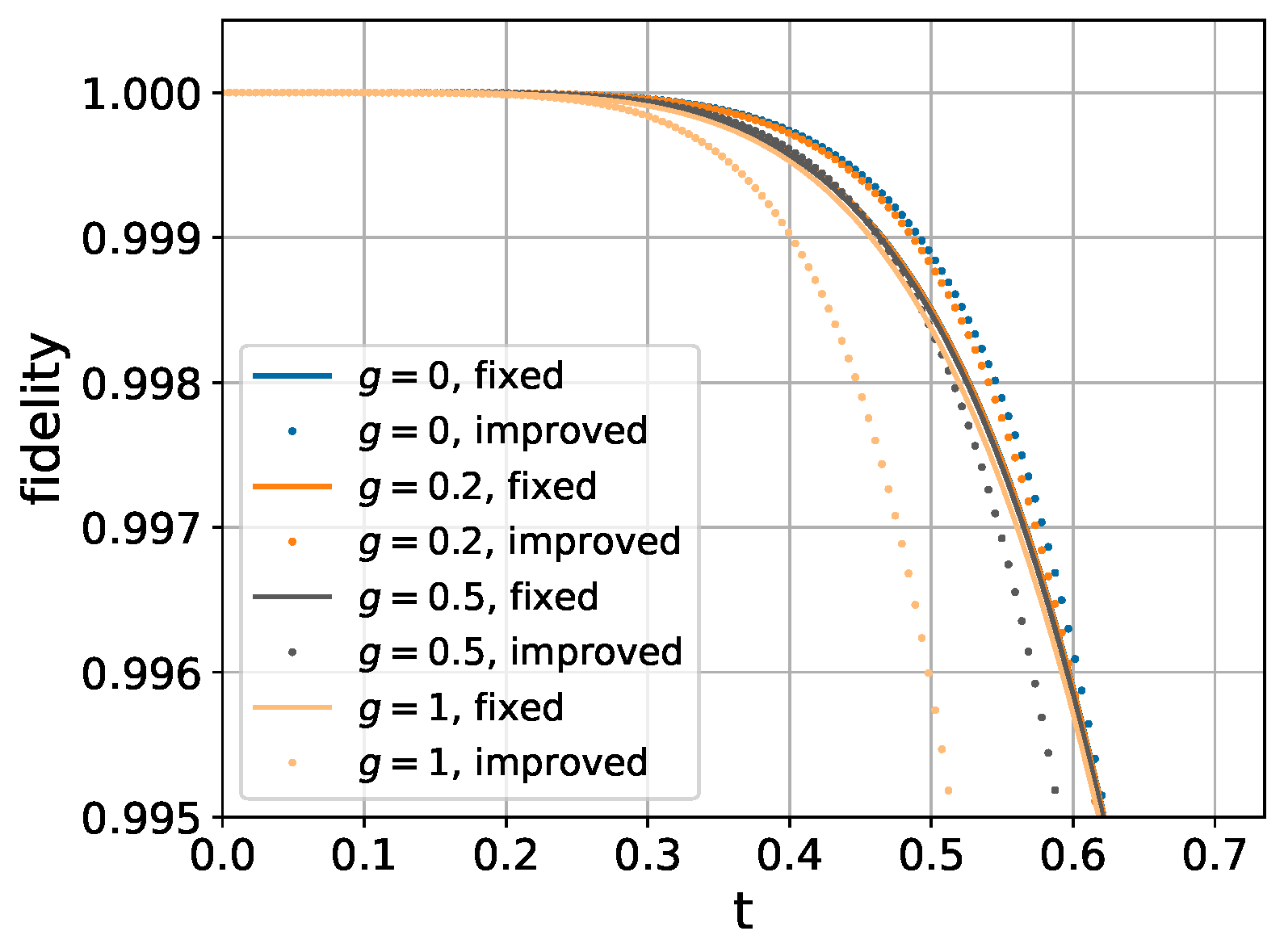
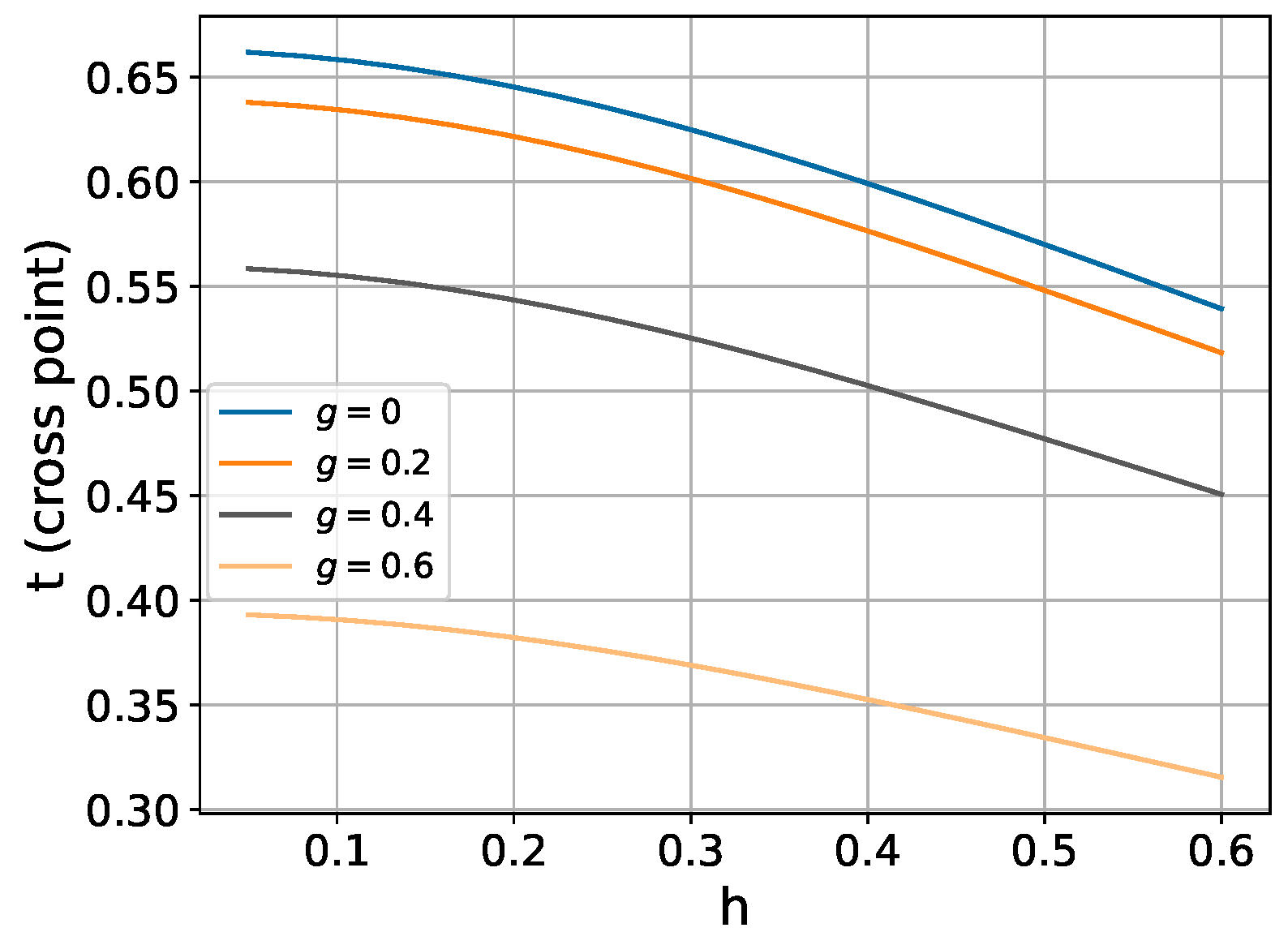
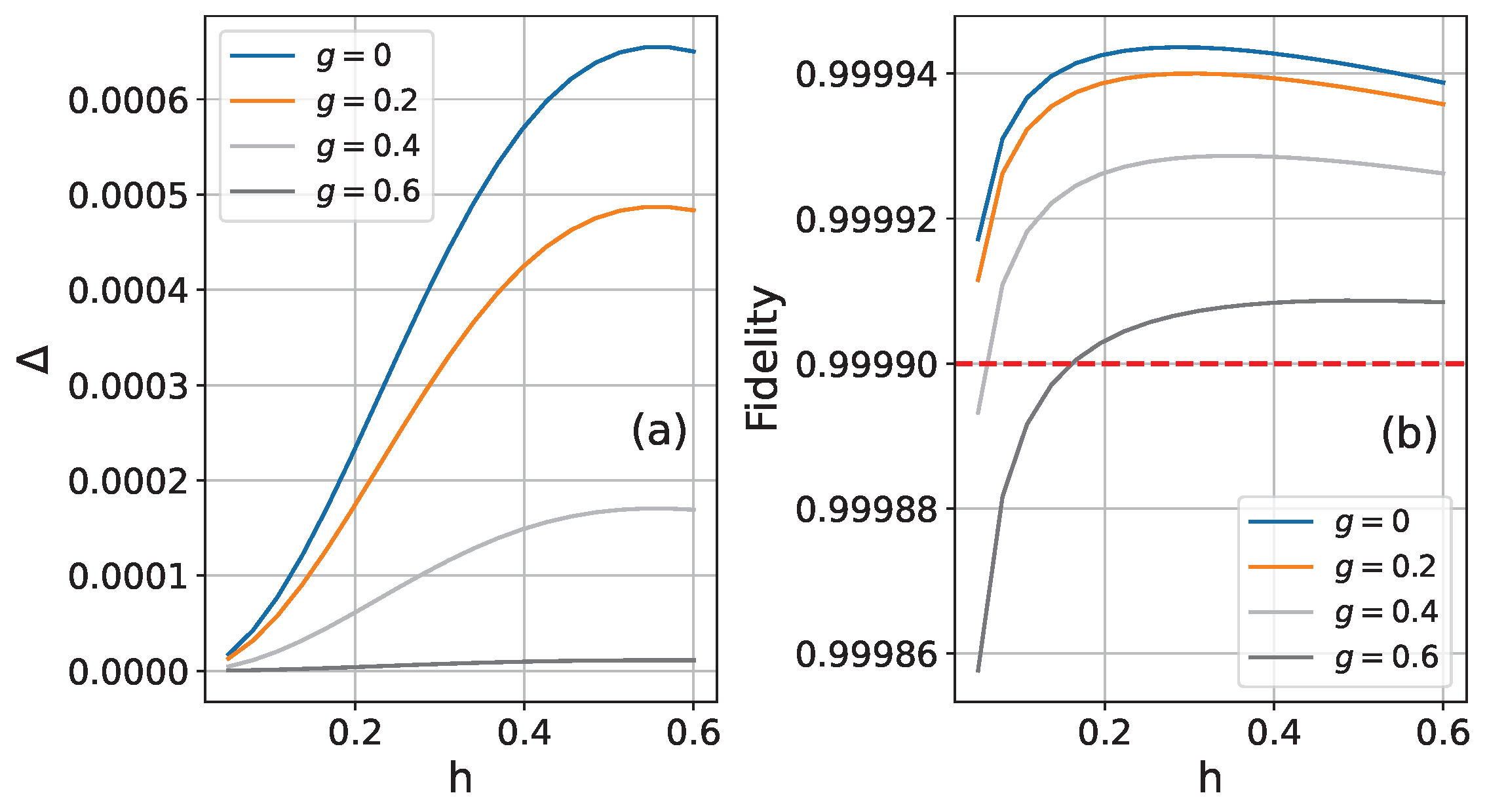
3. Perturbational Composition for Ising Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Childs, A.M.; Su, Y. Nearly Optimal Lattice Simulation by Product Formulas. Phys. Rev. Lett. 2019, 123, 050503. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef] [PubMed]
- Altman, E.; Brown, K.R.; Carleo, G.; Carr, L.D.; Demler, E.; Chin, C.; DeMarco, B.; Economou, S.E.; Eriksson, M.A.; Fu, K.-M.C.; et al. Quantum Simulators: Architectures and Opportunities. PRX Quantum 2021, 2, 017003. [Google Scholar] [CrossRef]
- Childs, A.M.; Su, Y.; Tran, M.C.; Wiebe, N.; Zhu, S. Theory of Trotter Error with Commutator Scaling. Phys. Rev. X 2021, 11, 011020. [Google Scholar] [CrossRef]
- Haah, J.; Hastings, M.B.; Kothari, R.; Low, G.H. Quantum Algorithm for Simulating Real Time Evolution of Lattice Hamiltonians. SIAM J. Comput. 2021, 52, FOCS18. [Google Scholar]
- Tran, M.C.; Su, Y.; Carney, D.; Taylor, J.M. Faster Digital Quantum Simulation by Symmetry Protection. PRX Quantum 2021, 2, 010323. [Google Scholar] [CrossRef]
- Semeghini, G.; Levine, H.; Keesling, A.; Ebadi, S.; Wang, T.T.; Bluvstein, D.; Verresen, R.; Pichler, H.; Kalinowski, M.; Samajdar, R.; et al. Probing topological spin liquids on a programmable quantum simulator. Science 2021, 374, 1242–1247. [Google Scholar] [CrossRef] [PubMed]
- Ebadi, S.; Wang, T.T.; Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Bluvstein, D.; Samajdar, R.; Pichler, H.; Ho, W.W.; et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 2021, 595, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Ippoliti, M.; Quintana, C.; Greene, A.; Chen, Z.; Gross, J.; Arute, F.; Arya, K.; Atalaya, J.; Babbush, R.; et al. Time-crystalline eigenstate order on a quantum processor. Nature 2022, 601, 531–536. [Google Scholar] [CrossRef]
- Suzuki, M. Generalized Trotter’s formula and systematic approximants of exponential operators and inner derivations with applications to many-body problems. Commun. Math. Phys. 1976, 51, 183–190. [Google Scholar] [CrossRef]
- Suzuki, M. Quantum Monte Carlo Methods in Condensed Matter Physics; World Scientific: Singapore, 1997. [Google Scholar]
- Hatano, N.; Suzuki, M. Quantum Annealing and Other Optimization Methods; Springer: Berlin/Heidelberg, Germany, 2005; pp. 37–68. [Google Scholar]
- Lloyd, S. Universal Quantum Simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef] [PubMed]
- Trotter, H.F. On the Product of Semi-Groups of Operators. Proc. Am. Math. Soc. 1959, 10, 545. [Google Scholar] [CrossRef]
- Low, G.H. Hamiltonian simulation with nearly optimal dependence on spectral norm. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, Phoenix, AZ, USA, 23–26 June 2019; pp. 491–502. [Google Scholar]
- Roetteler, M.; Naehrig, M.; Svore, K.M.; Lauter, K. Advances in Cryptology–ASIACRYPT 2017: 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Proceedings, Part II 23; Springer: Berlin/Heidelberg, Germany, 2017; pp. 241–270. [Google Scholar]
- Low, G.H.; Wiebe, N. Hamiltonian Simulation in the Interaction Picture. arXiv 2018, arXiv:1805.00675. [Google Scholar]
- Coldea, R.; Tennant, D.; Wheeler, E.; Wawrzynska, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Kiefer, K. Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry. Science 2010, 327, 177–180. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum phase transitions. Phys. World 1999, 12, 33. [Google Scholar] [CrossRef]
- Dutta, A.; Aeppli, G.; Chakrabarti, B.K.; Divakaran, U.; Rosenbaum, T.F.; Sen, D. Quantum Phase Transitions in Transverse Field Spin Models: From Statistical Physics to Quantum Information; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Bernien, H.; Schwartz, S.; Keesling, A.; Levine, H.; Omran, A.; Pichler, H.; Choi, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 2017, 551, 579–584. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Pagano, G.; Hess, P.W.; Kyprianidis, A.; Becker, P.; Kaplan, H.; Gorshkov, A.V.; Gong, Z.-X.; Monroe, C. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 2017, 551, 601–604. [Google Scholar] [CrossRef] [PubMed]
- King, A.D.; Carrasquilla, J.; Raymond, J.; Ozfidan, I.; Andriyash, E.; Berkley, A.; Reis, M.; Lanting, T.; Harris, R.; Altomare, F.; et al. Observation of topological phenomena in a programmable lattice of 1800 qubits. Nature 2018, 560, 456–460. [Google Scholar] [CrossRef]
- Simon, J.; Bakr, W.S.; Ma, R.; Tai, M.E.; Preiss, P.M.; Greiner, M. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 2011, 472, 307–312. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Hempel, C.; Nigg, D.; Müller, M.; Gerritsma, R.; Zähringer, F.; Schindler, P.; Barreiro, J.T.; Rambach, M.; Kirchmair, G.; et al. Universal Digital Quantum Simulation with Trapped Ions. Science 2011, 334, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Struck, J.; Ölschläger, C.; Targat, R.L.; Soltan-Panahi, P.; Eckardt, A.; Lewenstein, M.; Windpassinger, P.; Sengstock, K. Quantum Simulation of Frustrated Classical Magnetism in Triangular Optical Lattices. Science 2011, 333, 996–999. [Google Scholar] [CrossRef]
- Ferguson, A.L.; Mann, J.K.; Omarjee, S.; Ndung’u, T.; Walker, B.D.; Chakraborty, A.K. Translating HIV sequences into quantitative fitness landscapes predicts viral vulnerabilities for rational immunogen design. Immunity 2013, 38, 606–617. [Google Scholar] [CrossRef] [PubMed]
- Morcos, F.; Pagnani, A.; Lunt, B.; Bertolino, A.; Marks, D.S.; Sander, C.; Zecchina, R.; Onuchic, J.N.; Hwa, T.; Weigt, M. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA 2011, 108, E1293–E1301. [Google Scholar] [CrossRef] [PubMed]
- Weigt, M.; White, R.A.; Szurmant, H.; Hoch, J.A.; Hwa, T. Identification of direct residue contacts in protein–protein interaction by message passing. Proc. Natl. Acad. Sci. USA 2009, 106, 67–72. [Google Scholar] [CrossRef]
- Cavagna, A.; Cimarelli, A.; Giardina, I.; Parisi, G.; Santagati, R.; Stefanini, F.; Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 2010, 107, 11865–11870. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Cavagna, A.; Giardina, I.; Mora, T.; Silvestri, E.; Viale, M.; Walczak, A.M. Statistical mechanics for natural flocks of birds. Proc. Natl. Acad. Sci. USA 2012, 109, 4786–4791. [Google Scholar] [CrossRef] [PubMed]
- Mora, T.; Walczak, A.M.; Castello, L.D.; Ginelli, F.; Melillo, S.; Parisi, L.; Viale, M.; Cavagna, A.; Giardina, I. Local equilibrium in bird flocks. Nat. Phys. 2016, 12, 1153–1157. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef] [PubMed]
- Mehta, P.; Bukov, M.; Wang, C.-H.; Day, A.G.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to Machine Learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef] [PubMed]
- Torlai, G.; Mazzola, G.; Carrasquilla, J.; Troyer, M.; Melko, R.; Carleo, G. Neural-network quantum state tomography. Nat. Phys. 2018, 14, 447–450. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press Cambridge: Cambridge, UK, 2001; Volume 2. [Google Scholar]
- Khaneja, N.; Reiss, T.; Kehlet, C.; Schulte-Herbrüggen, T.; Glaser, S.J. Optimal control of coupled spin dynamics: Design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 2005, 172, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A. A simple formula for the average gate fidelity of a quantum dynamical operation. Phys. Lett. A 2002, 303, 249–252. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Huang, J.; Zhang, C.; Li, J. Perturbational Decomposition Analysis for Quantum Ising Model with Weak Transverse Fields. Entropy 2024, 26, 1094. https://doi.org/10.3390/e26121094
Li Y, Huang J, Zhang C, Li J. Perturbational Decomposition Analysis for Quantum Ising Model with Weak Transverse Fields. Entropy. 2024; 26(12):1094. https://doi.org/10.3390/e26121094
Chicago/Turabian StyleLi, Youning, Junfeng Huang, Chao Zhang, and Jun Li. 2024. "Perturbational Decomposition Analysis for Quantum Ising Model with Weak Transverse Fields" Entropy 26, no. 12: 1094. https://doi.org/10.3390/e26121094
APA StyleLi, Y., Huang, J., Zhang, C., & Li, J. (2024). Perturbational Decomposition Analysis for Quantum Ising Model with Weak Transverse Fields. Entropy, 26(12), 1094. https://doi.org/10.3390/e26121094





