Partition Function Zeros of the Frustrated J1–J2 Ising Model on the Honeycomb Lattice
Abstract
1. Introduction
2. Materials and Methods
2.1. Model
2.2. Partition Function Zeros
2.3. Population Annealing
- Initialize the population by drawing random spin configurations corresponding to the initial inverse temperature .
- Set the iteration counter .
- Determine the next inverse temperature such that the energy histogram overlap between and , given by [63]is approximately equal to the target value of , where refers to the current energy of replica j.
- Increment i by 1.
- Resample the replicas according to their relative Boltzmann weights, that is, make on averagecopies of replica j with energy .
- Carry out Metropolis updates on the replicas until the effective population size (see [62] for definition and discussion) exceeds the threshold value of .
- Calculate estimates for observables as the population averages , where is the value of the observable for the j-th replica. Note that we calculate central moments of the energy directly during the simulation after calculating the average energy, because using raw moments to calculate higher-order central moments and cumulants leads to a complete loss of numeric precision in the latter.
- Unless the lowest temperature of interest is reached, go to step 3.
3. Results
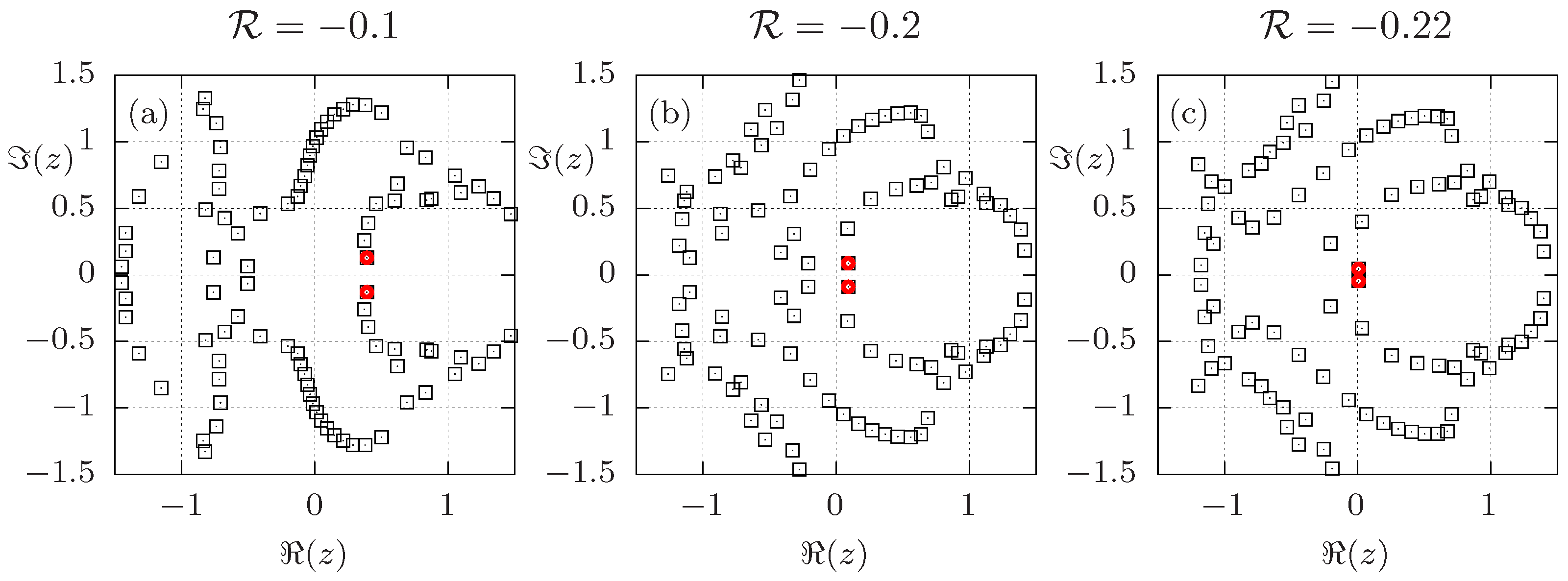
3.1. Solving for all Fisher Zeros in the Complex Temperature Plane
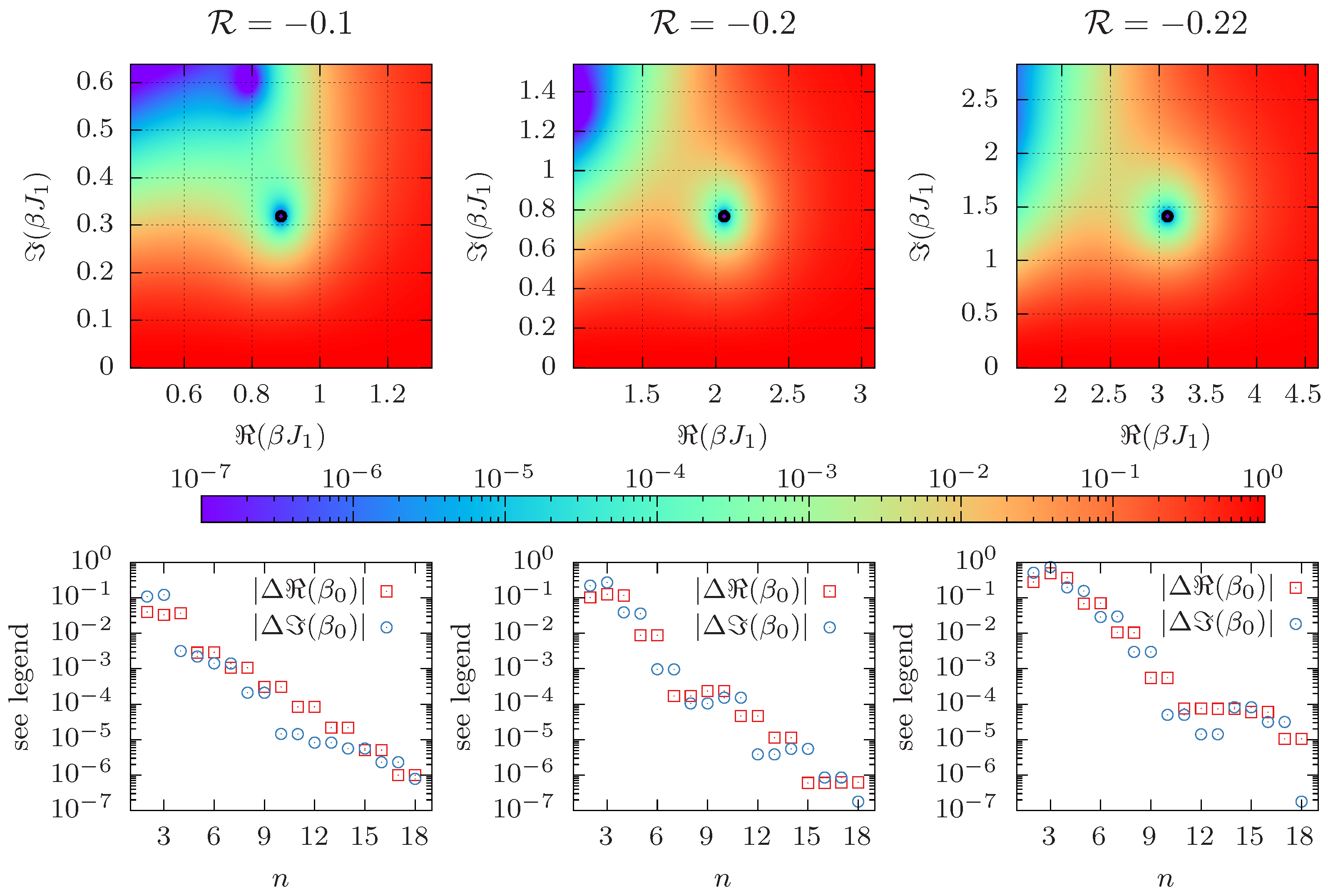
3.2. Determining the Leading Fisher Zero Directly and by the Cumulant Method
3.3. Determining the Leading Lee–Yang Zero Directly and by the Cumulant Method
3.4. Comparison of Standard FSS and Scaling of Partition Function Zeros
3.4.1. Scaling of Fisher Zeros
3.4.2. Scaling of Lee–Yang Zeros
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC | Monte Carlo |
| PA | Population annealing |
| LY | Lee–Yang |
| F | Fisher |
| FSS | Finite-size scaling |
| RG | Renormalization group |
Appendix A. Fisher Zeros for = 0

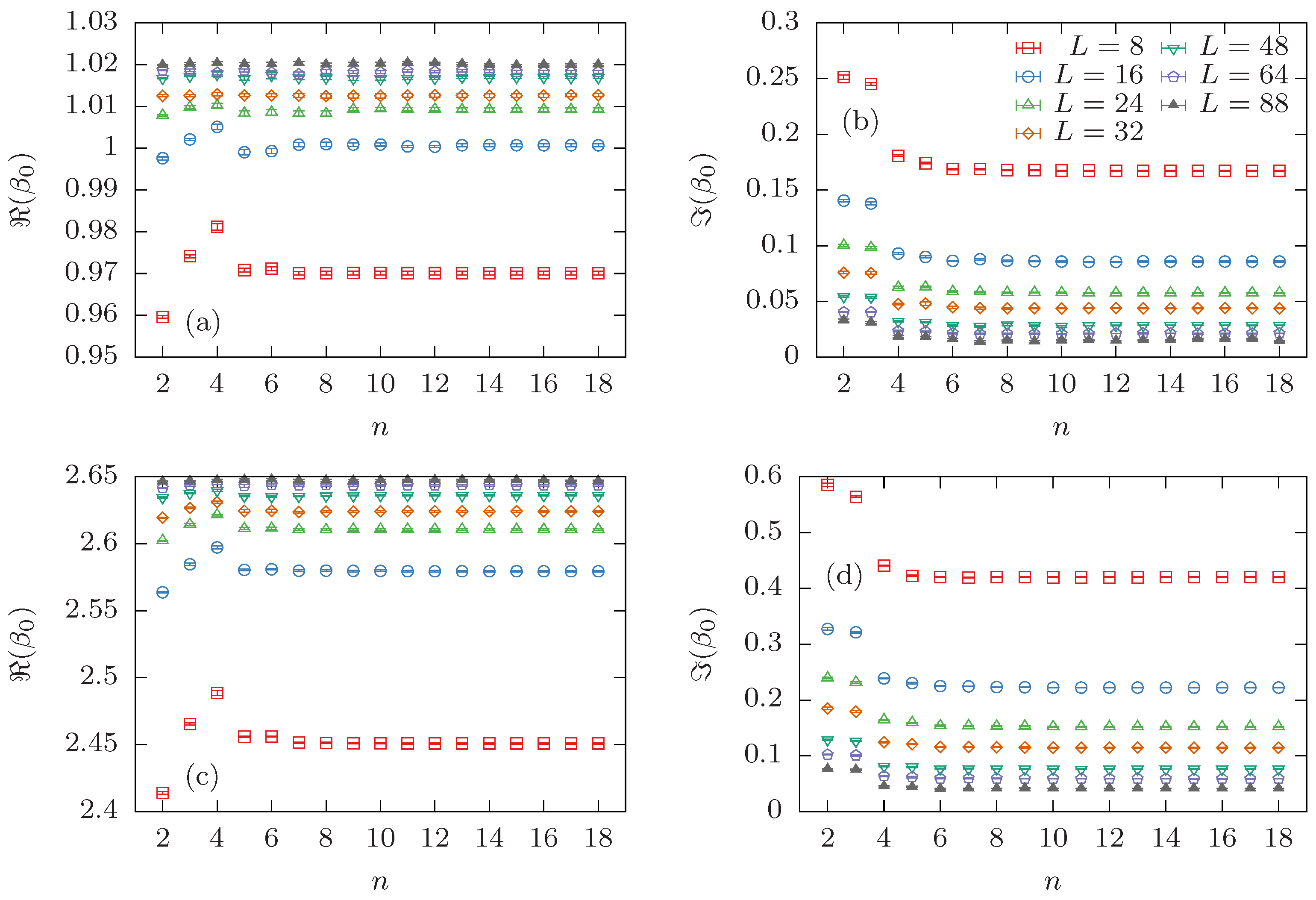
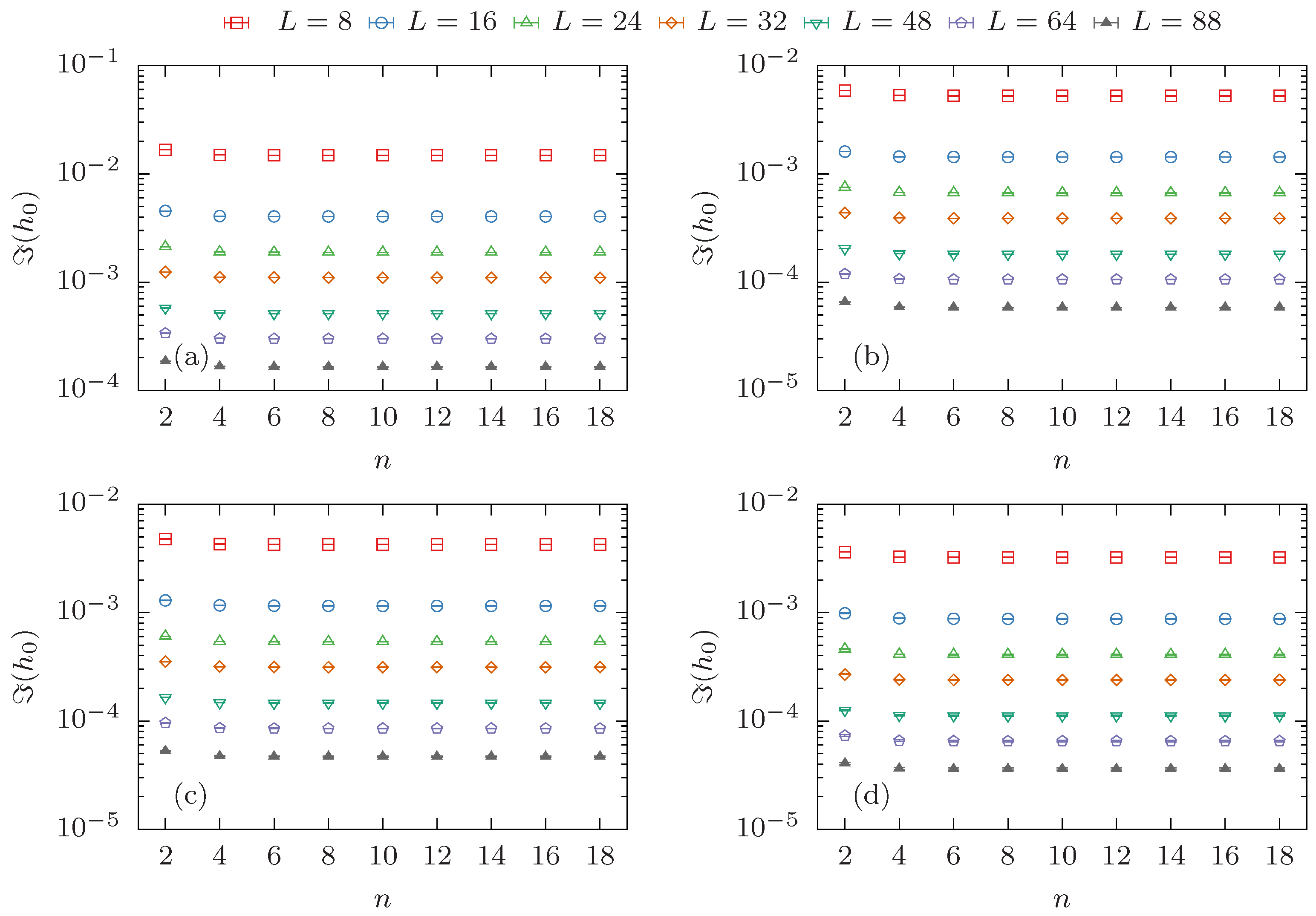
Appendix B. Convergence of the Cumulant Method for Larger System Sizes
References
- Diep, H.T. (Ed.) Frustrated Spin Systems, 2nd ed.; World Scientific: Singapore, 2013. [Google Scholar] [CrossRef]
- Azaria, P.; Diep, H.T.; Giacomini, H. Coexistence of order and disorder and reentrance in an exactly solvable model. Phys. Rev. Lett. 1987, 59, 1629–1632. [Google Scholar] [CrossRef] [PubMed]
- Espriu, D.; Prats, A. Dynamics of the two-dimensional gonihedric spin model. Phys. Rev. E 2004, 70, 046117. [Google Scholar] [CrossRef] [PubMed]
- Mueller, M.; Johnston, D.A.; Janke, W. Multicanonical analysis of the plaquette-only gonihedric Ising model and its dual. Nucl. Phys. B 2014, 888, 214–235. [Google Scholar] [CrossRef]
- Nightingale, M. Non-universality for Ising-like spin systems. Phys. Lett. A 1977, 59, 486–488. [Google Scholar] [CrossRef]
- Jin, S.; Sen, A.; Sandvik, A.W. Ashkin-Teller criticality and pseudo-first-order behavior in a frustrated Ising model on the square lattice. Phys. Rev. Lett. 2012, 108, 045702. [Google Scholar] [CrossRef]
- Kalz, A.; Honecker, A.; Moliner, M. Analysis of the phase transition for the Ising model on the frustrated square lattice. Phys. Rev. B 2011, 84, 174407. [Google Scholar] [CrossRef]
- Kalz, A.; Honecker, A. Location of the Potts-critical end point in the frustrated Ising model on the square lattice. Phys. Rev. B 2012, 86, 134410. [Google Scholar] [CrossRef]
- Yoshiyama, K.; Hukushima, K. Higher-order tensor renormalization group study of the J1-J2 Ising model on a square lattice. Phys. Rev. E 2023, 108, 054124. [Google Scholar] [CrossRef]
- Bobák, A.; Lučivjanský, T.; Žukovič, M.; Borovský, M.; Balcerzak, T. Tricritical behaviour of the frustrated Ising antiferromagnet on the honeycomb lattice. Phys. Lett. A 2016, 380, 2693–2697. [Google Scholar] [CrossRef]
- Acevedo, S.; Arlego, M.; Lamas, C.A. Phase diagram study of a two-dimensional frustrated antiferromagnet via unsupervised machine learning. Phys. Rev. B 2021, 103, 134422. [Google Scholar] [CrossRef]
- Žukovič, M. Critical properties of the frustrated Ising model on a honeycomb lattice: A Monte Carlo study. Phys. Lett. A 2021, 404, 127405. [Google Scholar] [CrossRef]
- Schmidt, M.; Godoy, P. Phase transitions in the Ising antiferromagnet on the frustrated honeycomb lattice. J. Magn. Magn. Mater. 2021, 537, 168151. [Google Scholar] [CrossRef]
- Janke, W. (Ed.) Rugged Free Energy Landscapes—Common Computational Approaches to Spin Glasses, Structural Glasses and Biological Macromolecules; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 736. [Google Scholar] [CrossRef]
- Iba, Y. Population Monte Carlo algorithms. Trans. Jpn. Soc. Artif. Intell. 2001, 16, 279–286. [Google Scholar] [CrossRef]
- Hukushima, K.; Iba, Y. Population annealing and its application to a spin glass. AIP Conf. Proc. 2003, 690, 200–206. [Google Scholar] [CrossRef]
- Machta, J. Population annealing with weighted averages: A Monte Carlo method for rough free-energy landscapes. Phys. Rev. E 2010, 82, 026704. [Google Scholar] [CrossRef]
- Wang, W.; Machta, J.; Katzgraber, H.G. Population annealing: Theory and application in spin glasses. Phys. Rev. E 2015, 92, 063307. [Google Scholar] [CrossRef]
- Christiansen, H.; Weigel, M.; Janke, W. Accelerating molecular dynamics simulations with population annealing. Phys. Rev. Lett. 2019, 122, 060602. [Google Scholar] [CrossRef]
- Rose, N.; Machta, J. Equilibrium microcanonical annealing for first-order phase transitions. Phys. Rev. E 2019, 100, 063304. [Google Scholar] [CrossRef]
- Yang, C.N.; Lee, T.D. Statistical theory of equations of state and phase transitions. I. Theory of condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model. Phys. Rev. 1952, 87, 410–419. [Google Scholar] [CrossRef]
- Fisher, M.E. The nature of critical points. In Lecture Notes in Theoretical Physics; University of Colorado Press: Boulder, CO, USA, 1965; Volume VII C. [Google Scholar]
- Janke, W.; Kenna, R. The strength of first and second order phase transitions from partition function zeroes. J. Stat. Phys. 2001, 102, 1211–1227. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. Analysis of the density of partition function zeroes: A measure for phase transition strength. In Computer Simulation Studies in Condensed-Matter Physics XIV; Landau, D.P., Lewis, S.P., Schüttler, H.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 97–101. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. Density of partition function zeroes and phase transition strength. Comput. Phys. Commun. 2002, 147, 443–446. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. Phase transition strengths from the density of partition function zeroes. Nucl. Phys. B Proc. Suppl. 2002, 106–107, 905–907. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. Finite-size scaling and corrections in the Ising model with Brascamp-Kunz boundary conditions. Phys. Rev. B 2002, 65, 064110. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. Exact finite-size scaling with corrections in the two-dimensional Ising model with special boundary conditions. Nucl. Phys. B Proc. Suppl. 2002, 106–107, 929–931. [Google Scholar] [CrossRef]
- Janke, W.; Johnston, D.A.; Kenna, R. New methods to measure phase transition strength. Nucl. Phys. B Proc. Suppl. 2003, 119, 882–884. [Google Scholar] [CrossRef]
- Janke, W.; Johnston, D.A.; Kenna, R. Phase transition strength through densities of general distributions of zeroes. Nucl. Phys. B 2004, 682, 618–634. [Google Scholar] [CrossRef]
- Janke, W.; Johnston, D.A.; Kenna, R. Critical exponents from general distributions of zeroes. Comput. Phys. Commun. 2005, 169, 457–461. [Google Scholar] [CrossRef][Green Version]
- Janke, W.; Johnston, D.A.; Kenna, R. Properties of phase transitions of higher-order. PoS (LAT2005) 2005, 244. [Google Scholar] [CrossRef]
- Janke, W.; Johnston, D.A.; Kenna, R. Properties of higher-order phase transitions. Nucl. Phys. B 2006, 736, 319–328. [Google Scholar] [CrossRef][Green Version]
- Kenna, R.; Johnston, D.A.; Janke, W. Scaling relations for logarithmic corrections. Phys. Rev. Lett. 2006, 96, 115701. [Google Scholar] [CrossRef]
- Kenna, R.; Johnston, D.A.; Janke, W. Self-consistent scaling theory for logarithmic-correction exponents. Phys. Rev. Lett. 2006, 97, 155702. [Google Scholar] [CrossRef] [PubMed]
- Moueddene, L.; Donoso, A.; Berche, B. Ralph Kenna’s scaling relations in critical phenomena. Entropy 2024, 26, 221. [Google Scholar] [CrossRef] [PubMed]
- Deger, A.; Flindt, C. Determination of universal critical exponents using Lee-Yang theory. Phys. Rev. Res. 2019, 1, 023004. [Google Scholar] [CrossRef]
- Moueddene, L.; G Fytas, N.; Holovatch, Y.; Kenna, R.; Berche, B. Critical and tricritical singularities from small-scale Monte Carlo simulations: The Blume-Capel model in two dimensions. J. Stat. Mech. Theory Exp. 2024, 2024, 023206. [Google Scholar] [CrossRef]
- Monroe, J.L.; Kim, S.Y. Phase diagram and critical exponent ν for the nearest-neighbor and next-nearest-neighbor interaction Ising model. Phys. Rev. E 2007, 76, 021123. [Google Scholar] [CrossRef]
- Kim, S.Y. Ising antiferromagnet on a finite triangular lattice with free boundary conditions. J. Korean Phys. Soc. 2015, 67, 1517–1523. [Google Scholar] [CrossRef]
- Sarkanych, P.; Holovatch, Y.; Kenna, R. On the phase diagram of the 2d Ising model with frustrating dipole interaction. Ukr. J. Phys. 2015, 60, 334–338. [Google Scholar] [CrossRef][Green Version]
- Kim, S.Y. Study of the frustrated Ising model on a square lattice based on the exact density of states. J. Korean Phys. Soc. 2021, 79, 894–902. [Google Scholar] [CrossRef]
- Peng, X.; Zhou, H.; Wei, B.B.; Cui, J.; Du, J.; Liu, R.B. Experimental observation of Lee-Yang zeros. Phys. Rev. Lett. 2015, 114, 010601. [Google Scholar] [CrossRef]
- Ananikian, N.; Kenna, R. Imaginary magnetic fields in the real world. Physics 2015, 8, 2. [Google Scholar] [CrossRef]
- Fläschner, N.; Vogel, D.; Tarnowski, M.; Rem, B.; Lühmann, D.S.; Heyl, M.; Budich, J.; Mathey, L.; Sengstock, K.; Weitenberg, C. Observation of dynamical vortices after quenches in a system with topology. Nat. Phys. 2018, 14, 265–268. [Google Scholar] [CrossRef]
- Macêdo, A.R.S.; Vasilopoulos, A.; Akritidis, M.; Plascak, J.A.; Fytas, N.G.; Weigel, M. Two-dimensional dilute Baxter-Wu model: Transition order and universality. Phys. Rev. E 2023, 108, 024140. [Google Scholar] [CrossRef] [PubMed]
- Flindt, C.; Garrahan, J.P. Trajectory phase transitions, Lee-Yang zeros, and high-order cumulants in full counting statistics. Phys. Rev. Lett. 2013, 110, 050601. [Google Scholar] [CrossRef]
- Itzykson, C.; Pearson, R.B.; Zuber, J.B. Distribution of zeros in Ising and gauge models. Nucl. Phys. B 1983, 220, 415–433. [Google Scholar] [CrossRef]
- Bena, I.; Droz, M.; Lipowski, A. Statistical mechanics of equilibrium and nonequilibrium phase transitions: The Yang–Lee formalism. Int. J. Mod. Phys. B 2005, 19, 4269–4329. [Google Scholar] [CrossRef]
- Fröhlich, J.; Rodriguez, P.F. Some applications of the Lee-Yang theorem. J. Math. Phys. 2012, 53, 095218. [Google Scholar] [CrossRef]
- Krasnytska, M.; Berche, B.; Holovatch, Y.; Kenna, R. Violation of Lee-Yang circle theorem for Ising phase transitions on complex networks. Europhys. Lett. 2015, 111, 60009. [Google Scholar] [CrossRef]
- Katsura, S.; Abe, Y.; Yamamoto, M. Distribution of zeros of the partition function of the Ising model. J. Phys. Soc. Jpn. 1971, 30, 347–357. [Google Scholar] [CrossRef]
- Kenna, R.; Lang, C. Finite size scaling and the zeroes of the partition function in the model. Phys. Lett. B 1991, 264, 396–400. [Google Scholar] [CrossRef]
- Kenna, R.; Lang, C.B. Scaling and density of Lee-Yang zeros in the four-dimensional Ising model. Phys. Rev. E 1994, 49, 5012–5017. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Kim, D.H. Logarithmic finite-size scaling correction to the leading Fisher zeros in the p-state clock model: A higher-order tensor renormalization group study. Phys. Rev. E 2020, 101, 012124. [Google Scholar] [CrossRef] [PubMed]
- Deger, A.; Brandner, K.; Flindt, C. Lee-Yang zeros and large-deviation statistics of a molecular zipper. Phys. Rev. E 2018, 97, 012115. [Google Scholar] [CrossRef] [PubMed]
- Deger, A.; Flindt, C. Lee-Yang theory of the Curie-Weiss model and its rare fluctuations. Phys. Rev. Res. 2020, 2, 033009. [Google Scholar] [CrossRef]
- Deger, A.; Brange, F.; Flindt, C. Lee-Yang theory, high cumulants, and large-deviation statistics of the magnetization in the Ising model. Phys. Rev. B 2020, 102, 174418. [Google Scholar] [CrossRef]
- Janke, W.; Kappler, S. Monte-Carlo study of pure-phase cumulants of 2D q-state Potts models. J. Phys. I 1997, 7, 663–674. [Google Scholar] [CrossRef]
- Gessert, D.; Janke, W.; Weigel, M. Resampling schemes in population annealing—Numerical and theoretical results. Phys. Rev. E 2023, 108, 065309. [Google Scholar] [CrossRef]
- Weigel, M.; Barash, L.; Shchur, L.; Janke, W. Understanding population annealing Monte Carlo simulations. Phys. Rev. E 2021, 103, 053301. [Google Scholar] [CrossRef]
- Barash, L.Y.; Weigel, M.; Borovský, M.; Janke, W.; Shchur, L.N. GPU accelerated population annealing algorithm. Comput. Phys. Commun. 2017, 220, 341–350. [Google Scholar] [CrossRef]
- Gessert, D.; Janke, W.; Weigel, M. (in preparation).
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Landau, D.P. Critical behavior of the three-dimensional Ising model: A high-resolution Monte Carlo study. Phys. Rev. B 1991, 44, 5081–5091. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Efron, B. The Jackknife, the Bootstrap, and Other Resampling Plans; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1982. [Google Scholar] [CrossRef]
- Janke, W. Monte Carlo Simulations in Statistical Physics—From Basic Principles to Advanced Applications. In Order, Disorder and Criticality; Holovatch, Y., Ed.; World Scientific: Singapore, 2012; pp. 93–166. [Google Scholar] [CrossRef]
- Matveev, V.; Shrock, R. Complex-temperature singularities in the d=2 Ising model: Triangular and honeycomb lattices. J. Phys. A 1996, 29, 803–823. [Google Scholar] [CrossRef]
- Kim, S.Y.; Hwang, C.O.; Kim, J.M. Partition function zeros of the antiferromagnetic Ising model on triangular lattice in the complex temperature plane for nonzero magnetic field. Nucl. Phys. B 2008, 805, 441–450. [Google Scholar] [CrossRef]


| 24 | 32 | 48 | 64 | 88 | |
| 8 | |||||
| 16 | – | ||||
| 24 | – | – | |||
| 32 | – | – | – | ||
| 48 | – | – | – | – | |
| 8 | |||||
| 16 | – | ||||
| 24 | – | – | |||
| 32 | – | – | – | ||
| 48 | – | – | – | – | |
| 8 | |||||
| 16 | – | ||||
| 24 | – | – | |||
| 32 | – | – | – | ||
| 48 | – | – | – | – |
| 24 | 32 | 48 | 64 | 88 | |
| 8 | |||||
| 16 | – | ||||
| 24 | – | – | |||
| 32 | – | – | – | ||
| 48 | – | – | – | – | |
| 8 | |||||
| 16 | – | ||||
| 24 | – | – | |||
| 32 | – | – | – | ||
| 48 | – | – | – | – | |
| 8 | |||||
| 16 | – | ||||
| 24 | – | – | |||
| 32 | – | – | – | ||
| 48 | – | – | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gessert, D.; Weigel, M.; Janke, W. Partition Function Zeros of the Frustrated J1–J2 Ising Model on the Honeycomb Lattice. Entropy 2024, 26, 919. https://doi.org/10.3390/e26110919
Gessert D, Weigel M, Janke W. Partition Function Zeros of the Frustrated J1–J2 Ising Model on the Honeycomb Lattice. Entropy. 2024; 26(11):919. https://doi.org/10.3390/e26110919
Chicago/Turabian StyleGessert, Denis, Martin Weigel, and Wolfhard Janke. 2024. "Partition Function Zeros of the Frustrated J1–J2 Ising Model on the Honeycomb Lattice" Entropy 26, no. 11: 919. https://doi.org/10.3390/e26110919
APA StyleGessert, D., Weigel, M., & Janke, W. (2024). Partition Function Zeros of the Frustrated J1–J2 Ising Model on the Honeycomb Lattice. Entropy, 26(11), 919. https://doi.org/10.3390/e26110919






