An Observation-Driven Random Parameter INAR(1) Model Based on the Poisson Thinning Operator
Abstract
1. Introduction
2. Model Construction and Basic Properties
- (i)
- ,
- (ii)
- ,
- (iii)
- .
3. Parameter Estimation and Hypothesis Testing
- (A1)
- is a strictly stationary and ergodic sequence.
- (A2)
- , and are continuous with respect to and dominated by on , where is a positive integrable function.
- (A3)
- are continuous with respect to and dominated by on , where is a positive integrable function.
- (A4)
- , such that , .
- (A5)
- is a full-rank matrix, i.e., of rank .
- (A6)
- The parameters of are identifiable, that is, if , then , where represents the marginal probability measure of .
3.1. Conditional Least Squares Estimation
3.2. Interval Estimation
3.3. Empirical Likelihood Test
3.4. Conditional Maximum Likelihood Estimation
4. Numerical Simulation
4.1. Parameter Estimation
- (i)
- is fixed at , without any randomness. In this case, the log-likelihood function is:
- (ii)
- follows a uniform distribution with mean , minimum value 0, and maximum value . In this case, the log-likelihood function is:where .
- (iii)
- follows an exponential distribution with mean . In this case, the log-likelihood function is:
- (iv)
- follows a chi-square distribution with the mean . Specifically, the density function of is:
4.2. Interval Estimation
4.3. Empirical Likelihood Test
5. Real Data Application
6. Discussion and Conclusions
- (1)
- Combining observation-driven parameters with self-driven parameters, namely self-exciting threshold models: the SETINAR model proposed by Montriro, Scotto, and Pereira [16] is defined as follows:in this model, and represent given positive integers, with for . Additionally, the innovation series and possess probability distributions and on the set of natural numbers , respectively. The constant represents the threshold value responsible for the structural transition in the lagged d-period observation excitation model. Montriro, Scotto, and Pereira [16] demonstrated that model 6.1 possesses a strictly stationary solution when . By effectively combining observation-driven parameter models with self-driven parameter models and flexibly selecting thinning operators, a more diverse range of integer-valued time series models can be characterized.
- (2)
- Expanding upon current observation-driven models to incorporate higher-order models: Du and Li [24] introduced the INAR(p) model:in this model, , and represents a sequence of integer-valued random variables defined on the set of natural numbers . Existing observation-driven models are primarily first-order models. By extending these models to higher-order versions, the capability to describe more intricate and complex parameter dynamics can be achieved. It is important to note that when progressing to higher-order models, the technique utilized in the proof of Property 2. is no longer applicable for establishing the model’s ergodicity. As a result, new proof methods need to be sought from related Markov chain theories.
- (3)
- Extending the observation-driven parameter setting to Integer-valued Autoregressive Conditional Heteroskedasticity (INARCH) models: Fokianos, Rahbek, and Tjøstheim [25] proposed the INARCH model (which they referred to as Poisson Autoregressive) as follows:where , , and . This model is a natural extension of the generalized linear model and helps to capture the fluctuating changes of observed variables over time. Another advantage of this model is its simplicity, which makes it easy to establish the likelihood function of the INARCH model. Extending the observation-driven parameter setting to integer-valued autoregressive conditional heteroskedasticity models allows the model to describe the driving effect of the fluctuations of observed variables on the parameters. However, the challenge in doing so lies in the fact that, compared to the INAR model used in this paper, the ergodicity of the INARCH model is more difficult to establish.
- (4)
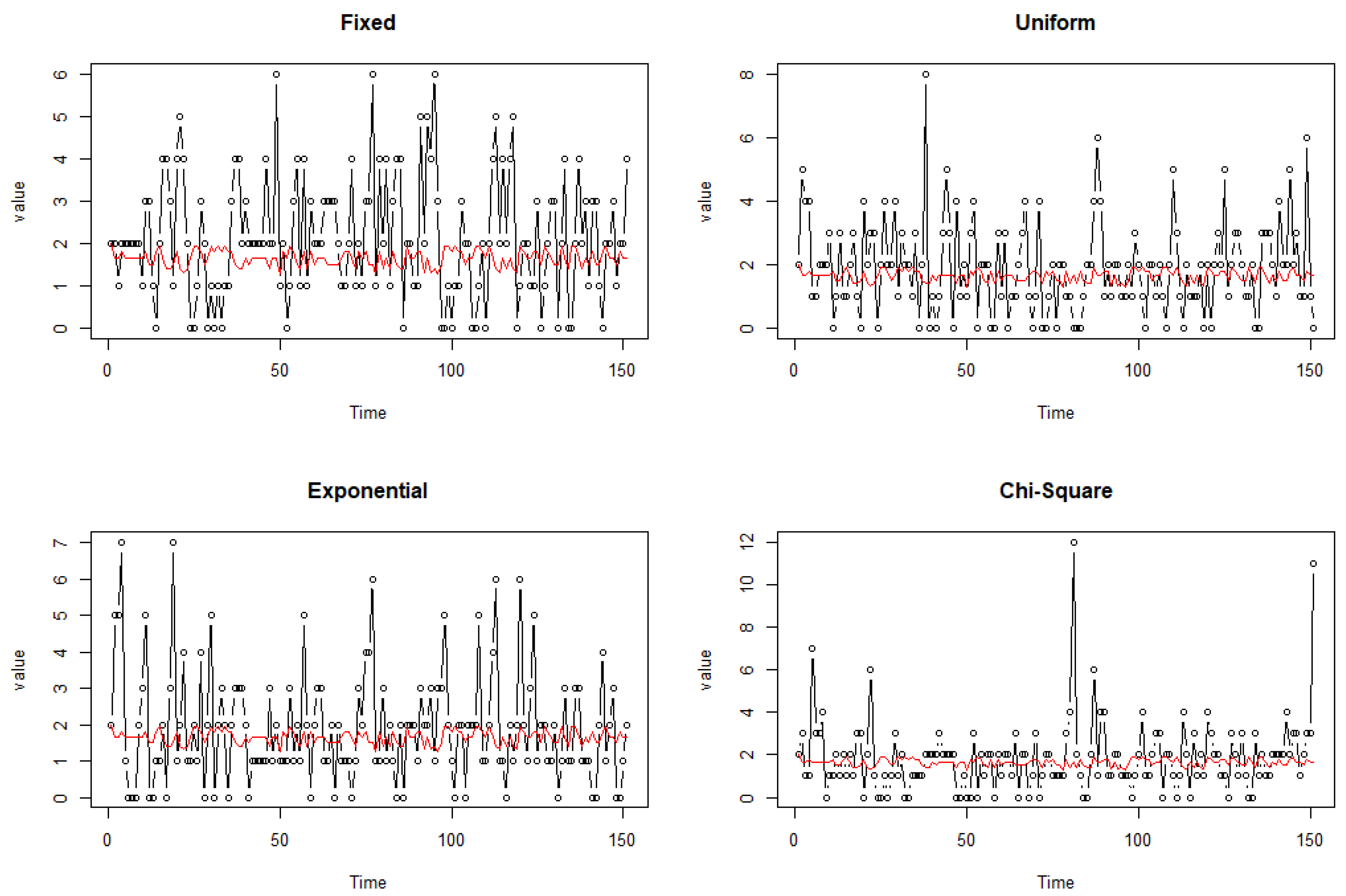
- Forecasting Integer-Valued Time Series: In time series research, it is common to employ h-step forward conditional expectations for forecasting:Nonetheless, this approach does not guarantee that the predicted values will be integers, and such predictions primarily describe the expected characteristics of the model, without capturing potentially time-varying coefficients or other features, as illustrated in Figure A1. Furthermore, Freeland and McCabe [26] highlighted that utilizing conditional medians or conditional modes for forecasting could be misleading. Consequently, it is essential to adopt innovative forecasting methods for integer-valued time series analysis. The rapid advancement of machine learning and deep learning in recent years has offered numerous new perspectives, such as the deep autoregressive model based on autoregressive recurrent neural network proposed by Salinas, Flunkert, Gasthaus, and Januschowski [10], which may hold significant potential for widespread application in the domain of integer-valued time series.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proofs
- (i)
- Given the data generation process (4), the following can be proved using the law of iterated expectation:Using the formula , the result can be proved
- (ii)
- By the law of iterated expectation, we know:From this, it follows that:
- (i)
- , , , , exists and are continuous with respect to .
- (ii)
- For , , , .
- (iii)
- For , there exist functions:such that
- (iv)
- , ,where .
Appendix A.2. Complementary Numerical Simulations
| Sample Size | ||||||
|---|---|---|---|---|---|---|
| , is fixed. | ||||||
| T = 300 | ||||||
| BIAS | 0.4431 | 0.3667 | −0.1879 | −0.1624 | −0.0282 | −0.0306 |
| RMSE | 2.5257 | 2.7556 | 1.4189 | 1.1704 | 0.2811 | 0.2811 |
| MAPE | 0.4738 | 0.4791 | 0.3841 | 0.3682 | 0.0637 | 0.0637 |
| T = 500 | ||||||
| BIAS | 0.2098 | 0.2051 | −0.0759 | −0.0741 | −0.0074 | −0.0085 |
| RMSE | 0.8623 | 0.8619 | 0.4246 | 0.4371 | 0.2066 | 0.2062 |
| MAPE | 0.3049 | 0.3041 | 0.2148 | 0.2141 | 0.0475 | 0.0474 |
| T = 800 | ||||||
| BIAS | 0.1109 | 0.1071 | −0.0346 | −0.0329 | −0.0119 | −0.0126 |
| RMSE | 0.5673 | 0.5609 | 0.1646 | 0.1619 | 0.1783 | 0.1775 |
| MAPE | 0.2229 | 0.2208 | 0.1509 | 0.1496 | 0.0404 | 0.0403 |
| T = 1200 | ||||||
| BIAS | 0.0862 | 0.0848 | −0.0232 | −0.0224 | −0.0093 | −0.0101 |
| RMSE | 0.4491 | 0.4477 | 0.1201 | 0.1193 | 0.1375 | 0.1371 |
| MAPE | 0.1773 | 0.1771 | 0.1169 | 0.1163 | 0.0313 | 0.0311 |
| T = 2000 | ||||||
| BIAS | 0.0278 | 0.0269 | −0.0119 | −0.0115 | 0.0007 | 0.0003 |
| RMSE | 0.3369 | 0.3359 | 0.0889 | 0.0889 | 0.1076 | 0.1074 |
| MAPE | 0.1339 | 0.1333 | 0.0864 | 0.0864 | 0.0246 | 0.0244 |
| , , follows a uniform distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.5624 | 0.3983 | −0.2331 | −0.1424 | −0.0404 | −0.0203 |
| RMSE | 2.0828 | 1.1916 | 1.2894 | 0.4719 | 0.2807 | 0.2534 |
| MAPE | 0.4877 | 0.4146 | 0.4355 | 0.3232 | 0.0641 | 0.0581 |
| T = 500 | ||||||
| BIAS | 0.1717 | 0.1399 | −0.0712 | −0.0593 | −0.0028 | 0.0079 |
| RMSE | 0.8577 | 0.7919 | 0.3289 | 0.2552 | 0.2153 | 0.1982 |
| MAPE | 0.3028 | 0.2852 | 0.2125 | 0.2012 | 0.0496 | 0.0543 |
| T = 800 | ||||||
| BIAS | 0.1036 | 0.0809 | −0.0317 | −0.0285 | −0.0124 | −0.0039 |
| RMSE | 0.5735 | 0.5538 | 0.1547 | 0.1499 | 0.1725 | 0.1563 |
| MAPE | 0.2212 | 0.2158 | 0.1458 | 0.1427 | 0.0405 | 0.0036 |
| T = 1200 | ||||||
| BIAS | 0.0531 | 0.0367 | −0.0152 | −0.0131 | −0.0114 | −0.0067 |
| RMSE | 0.4479 | 0.4334 | 0.1217 | 0.1196 | 0.1445 | 0.1303 |
| MAPE | 0.1785 | 0.1723 | 0.1177 | 0.1167 | 0.0331 | 0.0301 |
| T = 2000 | ||||||
| BIAS | 0.0453 | 0.0385 | −0.0143 | −0.0129 | −0.0048 | −0.0029 |
| RMSE | 0.3493 | 0.3429 | 0.0912 | 0.0898 | 0.1091 | 0.0903 |
| MAPE | 0.1389 | 0.1354 | 0.0885 | 0.0871 | 0.0248 | 0.0231 |
| , , follows an exponential distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.5805 | 0.4213 | −0.2463 | −0.1944 | −0.0092 | 0.0232 |
| RMSE | 2.2029 | 2.0433 | 1.0969 | 1.0533 | 0.2702 | 0.2058 |
| MAPE | 0.5443 | 0.4843 | 0.4557 | 0.3986 | 0.0614 | 0.0466 |
| T = 500 | ||||||
| BIAS | 0.1923 | 0.0879 | −0.0723 | −0.0451 | −0.0131 | −0.0071 |
| RMSE | 1.0283 | 0.8006 | 0.2859 | 0.2364 | 0.2127 | 0.1601 |
| MAPE | 0.3299 | 0.2888 | 0.2236 | 0.1963 | 0.0483 | 0.0359 |
| T = 800 | ||||||
| BIAS | 0.1439 | 0.0929 | −0.0464 | −0.0336 | −0.0061 | 0.0047 |
| RMSE | 0.6386 | 0.5709 | 0.1855 | 0.1605 | 0.1724 | 0.1293 |
| MAPE | 0.2456 | 0.2238 | 0.1653 | 0.1497 | 0.0389 | 0.0291 |
| T = 1200 | ||||||
| BIAS | 0.0699 | 0.0416 | −0.0201 | −0.0167 | −0.0095 | 0.0025 |
| RMSE | 0.4731 | 0.4405 | 0.1242 | 0.1169 | 0.1404 | 0.1049 |
| MAPE | 0.1869 | 0.1744 | 0.1172 | 0.1123 | 0.0322 | 0.0239 |
| T=2000 | ||||||
| BIAS | 0.0519 | 0.0319 | −0.0151 | −0.0111 | −0.0049 | 0.0007 |
| RMSE | 0.3669 | 0.3435 | 0.0976 | 0.9161 | 0.1106 | 0.0818 |
| MAPE | 0.1442 | 0.1369 | 0.0955 | 0.0908 | 0.0251 | 0.0185 |
| , , follows a chi−square distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.9824 | 0.4063 | −0.5663 | −0.1282 | −0.0098 | 0.0078 |
| RMSE | 3.3564 | 2.2437 | 1.6833 | 0.6341 | 0.3081 | 0.1569 |
| MAPE | 0.8569 | 0.5793 | 0.7361 | 0.3699 | 0.0696 | 0.0361 |
| T = 500 | ||||||
| BIAS | 0.4831 | 0.2249 | −0.1805 | −0.0621 | −0.0202 | −0.0068 |
| RMSE | 1.4549 | 0.9875 | 0.8114 | 0.2533 | 0.2293 | 0.1187 |
| MAPE | 0.4856 | 0.3749 | 0.3716 | 0.2354 | 0.0514 | 0.0269 |
| T = 800 | ||||||
| BIAS | 0.2344 | 0.0869 | −0.092 | −0.0305 | −0.008 | 0.0036 |
| RMSE | 1.0181 | 0.7138 | 0.4998 | 0.1758 | 0.1916 | 0.0962 |
| MAPE | 0.3477 | 0.2792 | 0.2501 | 0.1712 | 0.0433 | 0.0221 |
| T = 1200 | ||||||
| BIAS | 0.1382 | 0.0428 | −0.041 | −0.015 | −0.014 | −0.0021 |
| RMSE | 0.6592 | 0.5481 | 0.1766 | 0.1351 | 0.1557 | 0.0782 |
| MAPE | 0.2531 | 0.2164 | 0.1649 | 0.1325 | 0.0353 | 0.0181 |
| T = 2000 | ||||||
| BIAS | 0.0751 | 0.0438 | −0.0269 | −0.0161 | −0.0011 | 0.0019 |
| RMSE | 0.5081 | 0.4318 | 0.1322 | 0.1079 | 0.1211 | 0.0611 |
| MAPE | 0.2017 | 0.1713 | 0.1279 | 0.1061 | 0.0277 | 0.0141 |
| Sample Size | ||||||
|---|---|---|---|---|---|---|
| , , follows a uniform distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.0865 | −1.8661 | −0.0456 | −1.5741 | 0.0046 | 0.4508 |
| RMSE | 0.8065 | 4.647 | 0.2301 | 5.3142 | 0.1454 | 0.4777 |
| MAPE | 0.6267 | 2.7518 | 0.2865 | 3.1747 | 0.0964 | 0.3757 |
| T = 500 | ||||||
| BIAS | 0.0312 | −2.0474 | −0.0228 | −0.788 | 0.0043 | 0.4587 |
| RMSE | 0.5636 | 5.0468 | 0.1567 | 5.2847 | 0.1052 | 0.4753 |
| MAPE | 0.4493 | 2.5831 | 0.2046 | 1.9182 | 0.0703 | 0.3823 |
| T = 800 | ||||||
| BIAS | 0.0292 | −2.1058 | −0.0165 | −0.3596 | 0.0038 | 0.4548 |
| RMSE | 0.4503 | 3.2688 | 0.1244 | 3.0257 | 0.0852 | 0.4657 |
| MAPE | 0.3587 | 2.3491 | 0.1651 | 1.2312 | 0.0563 | 0.3789 |
| T = 1200 | ||||||
| BIAS | 0.0249 | −2.1077 | −0.0127 | −0.0739 | 0.0003 | 0.4558 |
| RMSE | 0.3513 | 2.6833 | 0.0971 | 1.7031 | 0.0689 | 0.4641 |
| MAPE | 0.2815 | 2.1461 | 0.1289 | 0.7674 | 0.0464 | 0.3799 |
| T = 2000 | ||||||
| BIAS | 0.0062 | −2.0216 | −0.0041 | 0.0766 | 0.0016 | 0.4546 |
| RMSE | 0.2735 | 2.2846 | 0.0749 | 1.0373 | 0.0529 | 0.4591 |
| MAPE | 0.2165 | 2.0256 | 0.0983 | 0.5483 | 0.0353 | 0.3788 |
| Parameter: , , is fixed. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.537 | 0.705 | 0.865 | 0.995 | 1 | |
| 0.235 | 0.263 | 0.375 | 0.542 | 0.757 | |
| (true) | 0.038 | 0.045 | 0.043 | 0.052 | 0.055 |
| 0.176 | 0.33 | 0.415 | 0.593 | 0.823 | |
| 0.554 | 0.806 | 0.96 | 1 | 1 | |
| Parameter: , , follows a uniform distribution. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.461 | 0.754 | 0.905 | 0.984 | 1 | |
| 0.212 | 0.304 | 0.417 | 0.54 | 0.786 | |
| (true) | 0.059 | 0.06 | 0.062 | 0.059 | 0.05 |
| 0.167 | 0.321 | 0.407 | 0.588 | 0.845 | |
| 0.645 | 0.845 | 0.975 | 1 | 1 | |
| Parameter: , , follows an exponential distribution. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.495 | 0.722 | 0.943 | 0.991 | 1 | |
| 0.171 | 0.31 | 0.505 | 0.593 | 0.844 | |
| (true) | 0.049 | 0.046 | 0.055 | 0.058 | 0.047 |
| 0.235 | 0.286 | 0.442 | 0.605 | 0.884 | |
| 0.57 | 0.815 | 0.972 | 1 | 1 | |
| Parameter: , , follows a chi−square distribution. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.478 | 0.648 | 0.852 | 0.951 | 1 | |
| 0.195 | 0.334 | 0.491 | 0.612 | 0.807 | |
| (true) | 0.086 | 0.088 | 0.079 | 0.054 | 0.051 |
| 0.115 | 0.225 | 0.318 | 0.515 | 0.795 | |
| 0.417 | 0.635 | 0.859 | 0.946 | 1 | |
| , , follows an exponential distribution, significance level 0.05. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| (true) | 0.437 | 0.446 | 0.416 | 0.51 | 0.427 |
| 0.71 | 0.787 | 0.863 | 0.954 | 0.982 | |
| 0.813 | 0.933 | 0.989 | 0.997 | 1 | |
| 0.912 | 0.983 | 1 | 1 | 1 | |
| 0.945 | 0.982 | 1 | 1 | 1 | |
| , , follows an exponential distribution, significance level 0.10. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| (true) | 0.543 | 0.544 | 0.517 | 0.613 | 0.55 |
| 0.797 | 0.846 | 0.93 | 0.982 | 0.993 | |
| 0.872 | 0.957 | 0.988 | 1 | 1 | |
| 0.945 | 1 | 1 | 1 | 1 | |
| 0.971 | 0.985 | 1 | 1 | 1 | |
Appendix A.3. Complementary Figure
References
- Steutel, F.W.; van Harn, K. Discrete analogues of self-decomposability and stability. Ann. Probab. 1979, 7, 893–899. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive (INAR(1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Latour, A. Existence and stochastic structure of a non-negative integer-valued autoregressive proces. J. Time Ser. Anal. 1998, 719, 439–455. [Google Scholar] [CrossRef]
- Joe, H. Time series models with univariate margins in the convolution-closed infinitely divisible class. J. Appl. Probab. 1996, 33, 664–677. [Google Scholar] [CrossRef]
- Zheng, H.T.; Basawa, I.V.; Datta, S. First-order random coefficient integer-valued autoregressive processes. J. Stat. Plan. Inference 2007, 137, 212–229. [Google Scholar] [CrossRef]
- Gomes, D.; Castro, L.C. Generalized integer-valued random coefficient for a first order structure autoregressive (RCINAR) process. J. Stat. Plan. Inference 2009, 139, 4088–4097. [Google Scholar] [CrossRef]
- Weiß, C.H.; Jentsch, C. Bootstrap-based bias corrections for INAR count time series. J. Stat. Comput. Simul. 2019, 89, 1248–1264. [Google Scholar] [CrossRef]
- Kang, Y.; Wang, D.H.; Yang, K. A new INAR(1) process with bounded support for counts showing equidispersion, under-dispersion and overdispersion. Stat. Pap. 2021, 62, 745–767. [Google Scholar] [CrossRef]
- Pegram, G.G.S. An autoregressive model for multilag Markov chains. J. Appl. Probab. 1980, 17, 350–362. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Huang, J.; Zhu, F.K.; Deng, D.L. A mixed generalized Poisson INAR model with applications. J. Stat. Comput. Simul. 2023, 1–28. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Sajjadnia, Z.; Bakouch, H.S.; Sharafi, M. Zero-and-one inflated Poisson–Lindley INAR(1) process for mod-elling count time series with extra zeros and ones. J. Stat. Comput. Simul. 2022, 92, 2018–2040. [Google Scholar] [CrossRef]
- Scotto, M.G.; Weiß, C.H.; Gouveia, S. Thinning-based models in the analysis of integer-valued time series: A review. Stat. Model. 2015, 15, 590–618. [Google Scholar] [CrossRef]
- Zheng, H.T.; Basawa, I.V. First-order observation-driven integer-valued autoregressive processes. Stat. Probab. Lett. 2008, 78, 1–9. [Google Scholar] [CrossRef]
- Triebsch, L.K. New Integer-Valued Autoregressive and Regression Models with State-Dependent Parameters; TU Kaiserslautern: Munich, Germany, 2008. [Google Scholar]
- Monteiro, M.; Scotto, M.G.; Pereira, I. Integer-valued self-exciting threshold autoregressive processes. Commun. Stat. Theory Methods 2012, 41, 2717–2737. [Google Scholar] [CrossRef]
- Ristić, M.M.; Bakouch, H.S.; Nastić, A.S. A new geometric first-order integer-valued autoregressive (NGINAR(1)) process. J. Stat. Plan. Inference 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- Yu, M.J.; Wang, D.H.; Yang, K. A class of observation-driven random coefficient INAR(1) processes based on negative bi-nomial thinning. J. Korean Stat. Soc. 2018, 48, 248–264. [Google Scholar] [CrossRef]
- Owen, A.B. Empirical likelihood ratio confidence intervals for a single functional. Biometrika 1988, 75, 237–249. [Google Scholar] [CrossRef]
- Qin, J.; Lawless, J. Empirical likelihood and general estimating equations. Ann. Stat. 1994, 22, 300–325. [Google Scholar] [CrossRef]
- Chen, S.X.; Keilegom, I.V. A review on empirical likelihood methods for regression. Test 2003, 18, 415–447. [Google Scholar] [CrossRef]
- Billingsley, P. Statistical Inference for Markov Processes; The University of Chicago Press: Chicago, IL, USA, 1961. [Google Scholar]
- Weiß, C.H. An Introduction to Discrete-Valued Time Series; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Du, J.G.; Li, Y. The Integer-Valued Autoregresive (INAR(p)) Model. J. Time Ser. Anal. 1989, 12, 129–142. [Google Scholar]
- Fokianos, K.; Rahbek, R.; Tjøstheim, D. Poisson Autoregression. J. Am. Stat. Assoc. 2009, 104, 1430–1439. [Google Scholar] [CrossRef]
- Freeland, R.K.; McCabe, B.P.M. Forecasting discrete valued low count time series. Int. J. Forecast. 2004, 20, 427–434. [Google Scholar] [CrossRef]
- Tweedie, R.L. Sufficient conditions for ergodicity and recurrence of Markov chains on a general state space. Stoch. Process. Appl. 1975, 3, 385–403. [Google Scholar] [CrossRef]
- Meyn, S.P.; Tweedie, R.L. Markov Chains and Stochastic Stability, 2nd ed.; Cambridge University Press: London, UK, 2009. [Google Scholar]
- Klimko, L.A.; Nelson, P.I.; Datta, S. On conditional least squares estimation for stochastic processes. Ann. Stat. 1978, 6, 629–642. [Google Scholar] [CrossRef]
- Davidson, J. Stochastic Limit Theory—An Introduction for Econometricians, 2nd ed.; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Stout, W.F. The Hartman-Wintner law of the iterated logarithm for martingaless. Ann. Math. Stat. 1970, 41, 2158–2160. [Google Scholar] [CrossRef]
- Rao, C. Linear Statistical Inference and Its Applications; Wiley: New York, NY, USA, 1973. [Google Scholar]
| Sample Size | ||||||
|---|---|---|---|---|---|---|
is fixed. | ||||||
| T = 300 | ||||||
| BIAS | 0.0571 | 0.0471 | −0.0321 | −0.0287 | 0.0051 | 0.0059 |
| RMSE | 0.7399 | 0.6983 | 0.2096 | 0.2008 | 0.1368 | 0.1337 |
| MAPE | 0.5636 | 0.5486 | 0.2691 | 0.2619 | 0.0909 | 0.0886 |
| T = 500 | ||||||
| BIAS | 0.0506 | 0.0407 | −0.0251 | −0.0221 | 0.0033 | 0.0042 |
| RMSE | 0.5678 | 0.5562 | 0.1556 | 0.1523 | 0.1113 | 0.1091 |
| MAPE | 0.4443 | 0.4346 | 0.1978 | 0.1946 | 0.0738 | 0.0721 |
| T = 800 | ||||||
| BIAS | 0.0349 | 0.0246 | −0.0152 | −0.0127 | −0.0011 | 0.0004 |
| RMSE | 0.4165 | 0.4076 | 0.1188 | 0.1163 | 0.0828 | 0.0817 |
| MAPE | 0.3327 | 0.3254 | 0.1587 | 0.1554 | 0.0546 | 0.0535 |
| T = 1200 | ||||||
| BIAS | 0.0139 | 0.0071 | −0.0074 | −0.0055 | 0.0009 | 0.0017 |
| RMSE | 0.3471 | 0.3393 | 0.0951 | 0.0931 | 0.0697 | 0.0688 |
| MAPE | 0.2726 | 0.2686 | 0.1252 | 0.1234 | 0.0465 | 0.0459 |
| T = 2000 | ||||||
| BIAS | 0.0112 | 0.0085 | −0.0058 | −0.0053 | 0.0017 | 0.0023 |
| RMSE | 0.2719 | 0.2711 | 0.0732 | 0.0728 | 0.0533 | 0.0525 |
| MAPE | 0.2195 | 0.2176 | 0.0981 | 0.0978 | 0.0352 | 0.0347 |
follows a uniform distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.0865 | 0.0428 | −0.0456 | −0.0354 | 0.0046 | 0.0121 |
| RMSE | 0.8065 | 0.7395 | 0.2301 | 0.2163 | 0.1454 | 0.1361 |
| MAPE | 0.6267 | 0.5773 | 0.2865 | 0.2696 | 0.0964 | 0.0903 |
| T = 500 | ||||||
| BIAS | 0.0312 | 0.0076 | −0.0228 | −0.0169 | 0.0043 | 0.0082 |
| RMSE | 0.5636 | 0.5288 | 0.1567 | 0.1488 | 0.1052 | 0.0997 |
| MAPE | 0.4493 | 0.4239 | 0.2046 | 0.1968 | 0.0703 | 0.0657 |
| T = 800 | ||||||
| BIAS | 0.0292 | 0.0062 | −0.0165 | −0.0113 | 0.0038 | 0.0079 |
| RMSE | 0.4503 | 0.4233 | 0.1244 | 0.1191 | 0.0852 | 0.0793 |
| MAPE | 0.3587 | 0.3373 | 0.1651 | 0.1575 | 0.0563 | 0.0525 |
| T = 1200 | ||||||
| BIAS | 0.0249 | 0.0133 | −0.0127 | −0.0108 | 0.0003 | 0.0031 |
| RMSE | 0.3513 | 0.3295 | 0.0971 | 0.0923 | 0.0689 | 0.0639 |
| MAPE | 0.2815 | 0.2627 | 0.1289 | 0.1249 | 0.0464 | 0.0428 |
| T = 2000 | ||||||
| BIAS | 0.0062 | −0.0019 | −0.0041 | −0.0023 | 0.0016 | 0.0032 |
| RMSE | 0.2735 | 0.2529 | 0.0749 | 0.0719 | 0.0529 | 0.0483 |
| MAPE | 0.2165 | 0.1997 | 0.0983 | 0.0942 | 0.0353 | 0.0323 |
follows an exponential distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.1165 | 0.0594 | −0.0594 | −0.0491 | 0.0048 | 0.0135 |
| RMSE | 0.8356 | 0.7986 | 0.2648 | 0.2541 | 0.1407 | 0.1138 |
| MAPE | 0.6249 | 0.5392 | 0.3071 | 0.2785 | 0.0931 | 0.0752 |
| T = 500 | ||||||
| BIAS | 0.0174 | −0.0175 | −0.0195 | −0.0116 | 0.0019 | 0.0088 |
| RMSE | 0.5929 | 0.5009 | 0.1649 | 0.1507 | 0.1059 | 0.0871 |
| MAPE | 0.4677 | 0.3955 | 0.2133 | 0.1932 | 0.0701 | 0.0582 |
| T = 800 | ||||||
| BIAS | 0.0389 | 0.0125 | −0.0177 | −0.0119 | −0.0008 | 0.0042 |
| RMSE | 0.4646 | 0.3871 | 0.1267 | 0.1149 | 0.0839 | 0.0657 |
| MAPE | 0.3673 | 0.3052 | 0.1644 | 0.1486 | 0.0563 | 0.0438 |
| T = 1200 | ||||||
| BIAS | 0.0236 | 0.0014 | −0.0103 | −0.0057 | 0.0016 | 0.0057 |
| RMSE | 0.3709 | 0.3109 | 0.0997 | 0.0903 | 0.0687 | 0.0542 |
| MAPE | 0.2879 | 0.2472 | 0.1299 | 0.1201 | 0.0451 | 0.0362 |
| T = 2000 | ||||||
| BIAS | 0.0196 | 0.0074 | −0.0091 | −0.0072 | −0.0021 | 0.0009 |
| RMSE | 0.2837 | 0.2493 | 0.0795 | 0.0746 | 0.0527 | 0.0427 |
| MAPE | 0.2261 | 0.1991 | 0.1047 | 0.0983 | 0.0356 | 0.0286 |
follows a chi−square distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.9382 | 0.2286 | −0.3652 | −0.1152 | −0.0292 | 0.0041 |
| RMSE | 3.7397 | 1.2307 | 1.7201 | 0.5974 | 0.1471 | 0.0955 |
| MAPE | 1.3992 | 0.7657 | 0.8326 | 0.4475 | 0.0945 | 0.0636 |
| T = 500 | ||||||
| BIAS | 0.3437 | 0.1486 | −0.1325 | −0.0738 | −0.0213 | 0.0007 |
| RMSE | 1.0769 | 0.7791 | 0.3808 | 0.2767 | 0.1129 | 0.0737 |
| MAPE | 0.7455 | 0.5794 | 0.4262 | 0.3345 | 0.0738 | 0.0493 |
| T = 800 | ||||||
| BIAS | 0.1769 | 0.0771 | −0.0628 | −0.0339 | −0.0139 | −0.0006 |
| RMSE | 0.7215 | 0.5257 | 0.2459 | 0.1844 | 0.0889 | 0.0556 |
| MAPE | 0.5301 | 0.4118 | 0.2954 | 0.2363 | 0.0586 | 0.0374 |
| T = 1200 | ||||||
| BIAS | 0.0883 | 0.0452 | −0.0322 | −0.0216 | −0.0054 | 0.0012 |
| RMSE | 0.5649 | 0.4368 | 0.1849 | 0.1498 | 0.0703 | 0.0455 |
| MAPE | 0.4353 | 0.3445 | 0.2367 | 0.1949 | 0.0469 | 0.0299 |
| T = 2000 | ||||||
| BIAS | 0.0766 | 0.0269 | −0.0292 | −0.0128 | −0.0057 | 0.0005 |
| RMSE | 0.4163 | 0.3267 | 0.1345 | 0.1103 | 0.0542 | 0.0371 |
| MAPE | 0.3256 | 0.2585 | 0.1706 | 0.1441 | 0.0361 | 0.0246 |
| Sample Size | ||||||
|---|---|---|---|---|---|---|
follows a uniform distribution, follows a geometric distribution. | ||||||
| T = 300 | ||||||
| BIAS | 0.1823 | 0.8261 | −0.1275 | −0.1563 | −0.0057 | −0.1187 |
| RMSE | 1.2279 | 1.5387 | 0.7587 | 0.4665 | 0.1577 | 0.1798 |
| MAPE | 0.8237 | 1.0551 | 0.4661 | 0.4531 | 0.1027 | 0.1257 |
| T = 500 | ||||||
| BIAS | 0.0931 | 0.7121 | −0.0632 | −0.1079 | −0.0009 | −0.1198 |
| RMSE | 0.7686 | 1.0457 | 0.4375 | 0.2613 | 0.1198 | 0.1574 |
| MAPE | 0.5752 | 0.8394 | 0.3016 | 0.3169 | 0.0786 | 0.1118 |
| T = 800 | ||||||
| BIAS | 0.0858 | 0.6913 | −0.0346 | −0.0914 | 0.0001 | −0.1199 |
| RMSE | 0.5812 | 0.9088 | 0.1651 | 0.1954 | 0.1006 | 0.1468 |
| MAPE | 0.4509 | 0.7538 | 0.2049 | 0.2451 | 0.0657 | 0.1069 |
| T = 1200 | ||||||
| BIAS | 0.0193 | 0.6389 | −0.0132 | −0.0732 | 0.0043 | −0.01191 |
| RMSE | 0.4427 | 0.7848 | 0.1234 | 0.1503 | 0.0829 | 0.1385 |
| MAPE | 0.3495 | 0.6687 | 0.1607 | 0.1913 | 0.0545 | 0.1027 |
| T = 2000 | ||||||
| BIAS | 0.0224 | 0.6386 | −0.0116 | −0.0711 | 0.0021 | −0.1213 |
| RMSE | 0.3576 | 0.7362 | 0.0951 | 0.1243 | 0.0625 | 0.1321 |
| MAPE | 0.2796 | 0.6517 | 0.1234 | 0.1612 | 0.0416 | 0.1016 |
| , , is fixed. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.95 | 0.941 | 0.957 | 0.957 | 0.953 | 0.956 |
| 0.9 | 0.897 | 0.908 | 0.912 | 0.908 | 0.905 |
| , , follows a uniform distribution. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.95 | 0.949 | 0.959 | 0.961 | 0.949 | 0.954 |
| 0.9 | 0.89 | 0.913 | 0.899 | 0.904 | 0.903 |
| , , follows an exponential distribution. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.95 | 0.942 | 0.938 | 0.951 | 0.955 | 0.953 |
| 0.9 | 0.891 | 0.894 | 0.906 | 0.910 | 0.909 |
| , , follows a chi−square distribution. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| 0.95 | 0.905 | 0.917 | 0.918 | 0.92 | 0.939 |
| 0.9 | 0.854 | 0.853 | 0.856 | 0.864 | 0.881 |
| , , is fixed, significance level 0.05. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| (true) | 0.096 | 0.073 | 0.065 | 0.057 | 0.046 |
| 0.296 | 0.386 | 0.658 | 0.823 | 0.935 | |
| 0.707 | 0.802 | 0.941 | 0.984 | 1 | |
| 0.778 | 0.837 | 0.988 | 1 | 1 | |
| 0.822 | 0.861 | 0.997 | 1 | 1 | |
| , , is fixed, significance level 0.10. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| (true) | 0.146 | 0.126 | 0.110 | 0.103 | 0.107 |
| 0.399 | 0.447 | 0.716 | 0.874 | 0.976 | |
| 0.784 | 0.883 | 0.969 | 1 | 1 | |
| 0.823 | 0.904 | 0.993 | 1 | 1 | |
| 0.875 | 0.921 | 1 | 1 | 1 | |
is fixed, significance level 0.05. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| (true) | 0.363 | 0.536 | 0.608 | 0.751 | 0.907 |
| (true) | 0.647 | 0.806 | 0.936 | 0.988 | 1 |
| (true) | 0.768 | 0.935 | 1 | 1 | 1 |
| (true) | 0.875 | 0.945 | 1 | 1 | 1 |
is fixed, significance level 0.10. | |||||
| T | 300 | 500 | 800 | 1200 | 2000 |
| (true) | 0.439 | 0.705 | 0.767 | 0.859 | 0.966 |
| (true) | 0.751 | 0.877 | 0.96 | 1 | 1 |
| (true) | 0.835 | 0.99 | 1 | 1 | 1 |
| (true) | 0.941 | 0.997 | 1 | 1 | 1 |
| 0.302 | 0.209 | 1.379 | 1.305 | 0.658 | 1.244 | |
| −0.151 | −0.143 | −0.227 | −0.244 | −0.097 | −0.231 | |
| 1.463 | 1.493 | 1.201 | 1.196 | 1.359 | 1.166 | |
| - | 1243.986 | 1189.377 | 1151.465 | 1143.669 | 1184.96 | |
| - | 1254.748 | 1200.138 | 1162.227 | 1154.431 | 1195.322 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Tao, T. An Observation-Driven Random Parameter INAR(1) Model Based on the Poisson Thinning Operator. Entropy 2023, 25, 859. https://doi.org/10.3390/e25060859
Yu K, Tao T. An Observation-Driven Random Parameter INAR(1) Model Based on the Poisson Thinning Operator. Entropy. 2023; 25(6):859. https://doi.org/10.3390/e25060859
Chicago/Turabian StyleYu, Kaizhi, and Tielai Tao. 2023. "An Observation-Driven Random Parameter INAR(1) Model Based on the Poisson Thinning Operator" Entropy 25, no. 6: 859. https://doi.org/10.3390/e25060859
APA StyleYu, K., & Tao, T. (2023). An Observation-Driven Random Parameter INAR(1) Model Based on the Poisson Thinning Operator. Entropy, 25(6), 859. https://doi.org/10.3390/e25060859





