Network Synchronization of MACM Circuits and Its Application to Secure Communications
Abstract
1. Introduction
2. Brief Review on Synchronization of Complex Networks
2.1. Synchronization of Complex Network
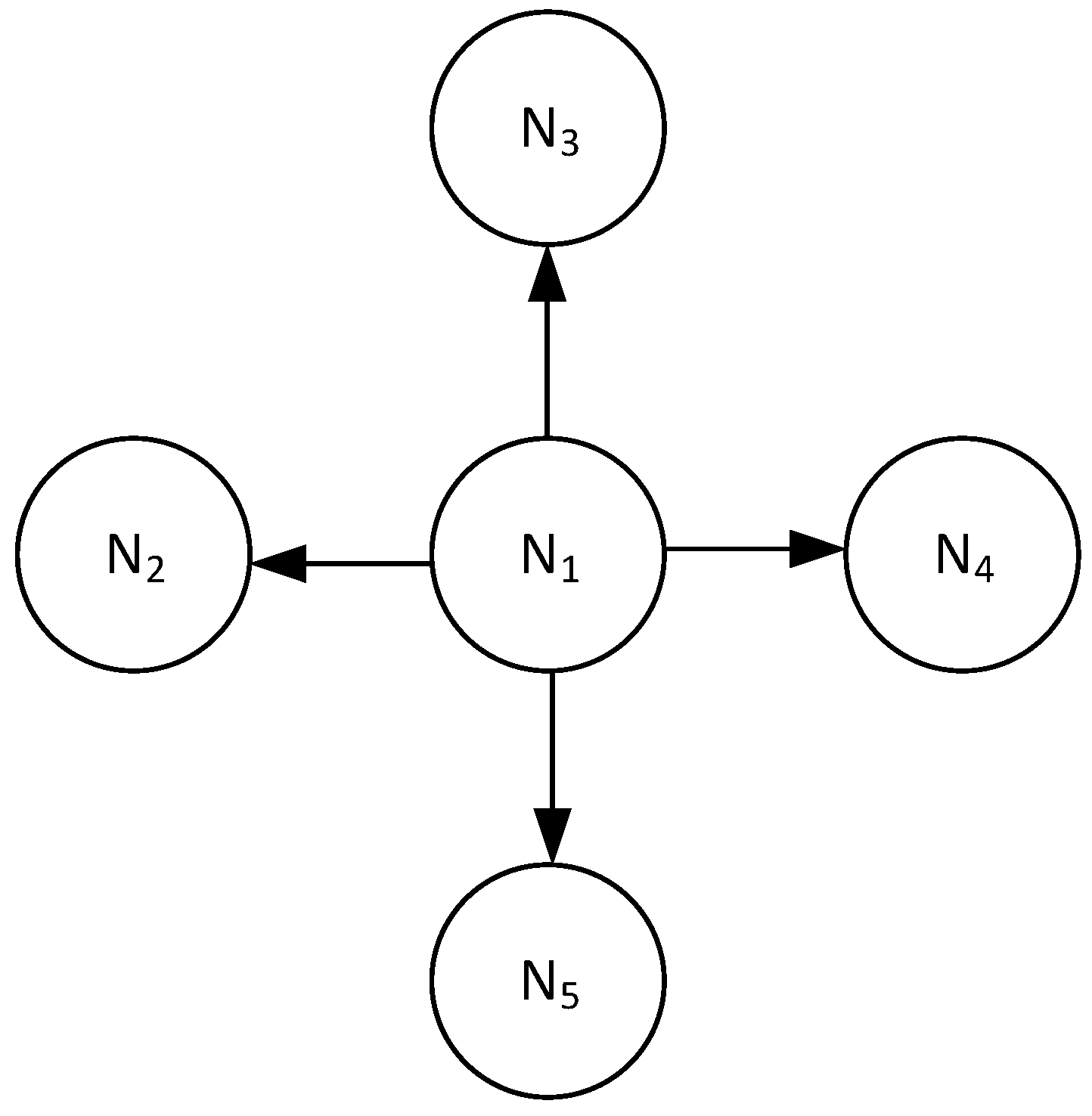
2.2. Star Coupled Networks
2.3. Synchronization Analysis Based on Master Stability Function Approach
3. MACM Circuit like Node
4. Star Network Synchronization of MACM’s Circuits
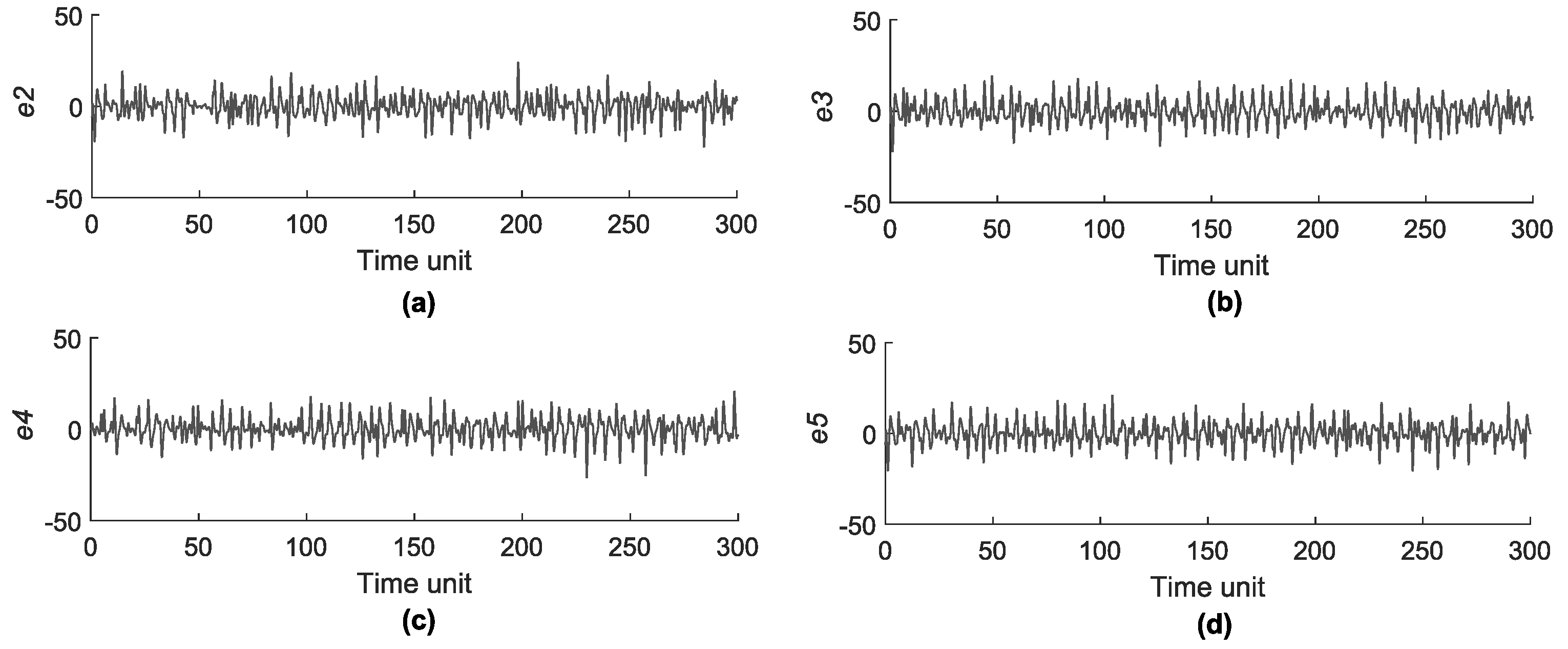
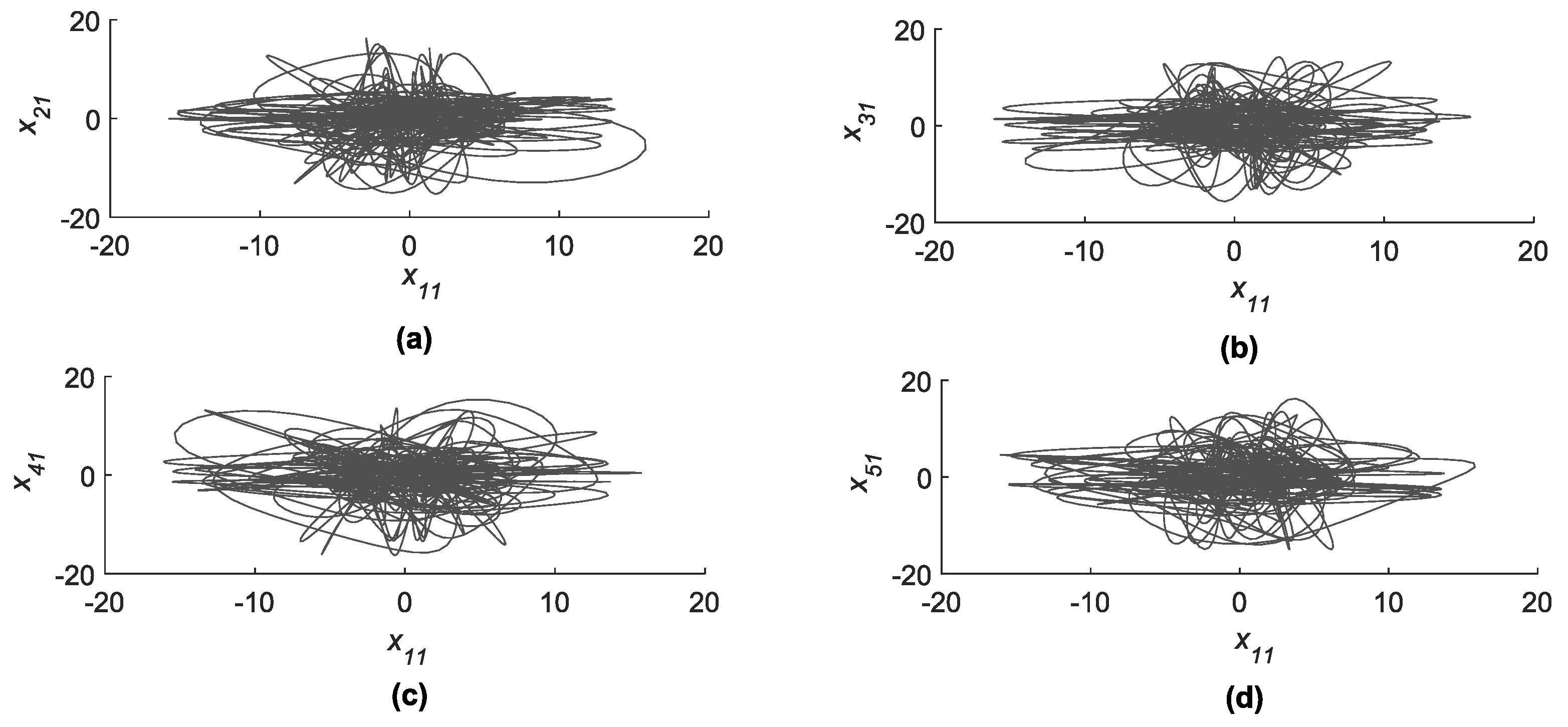
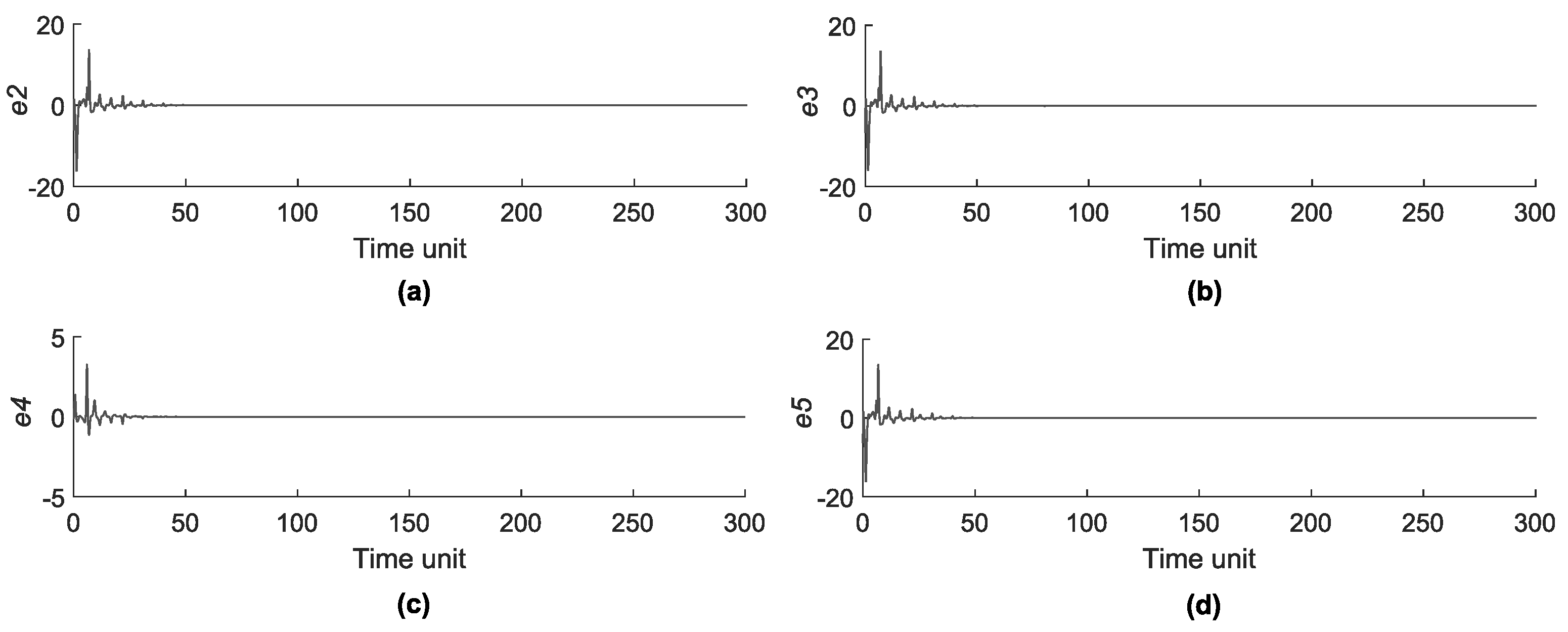
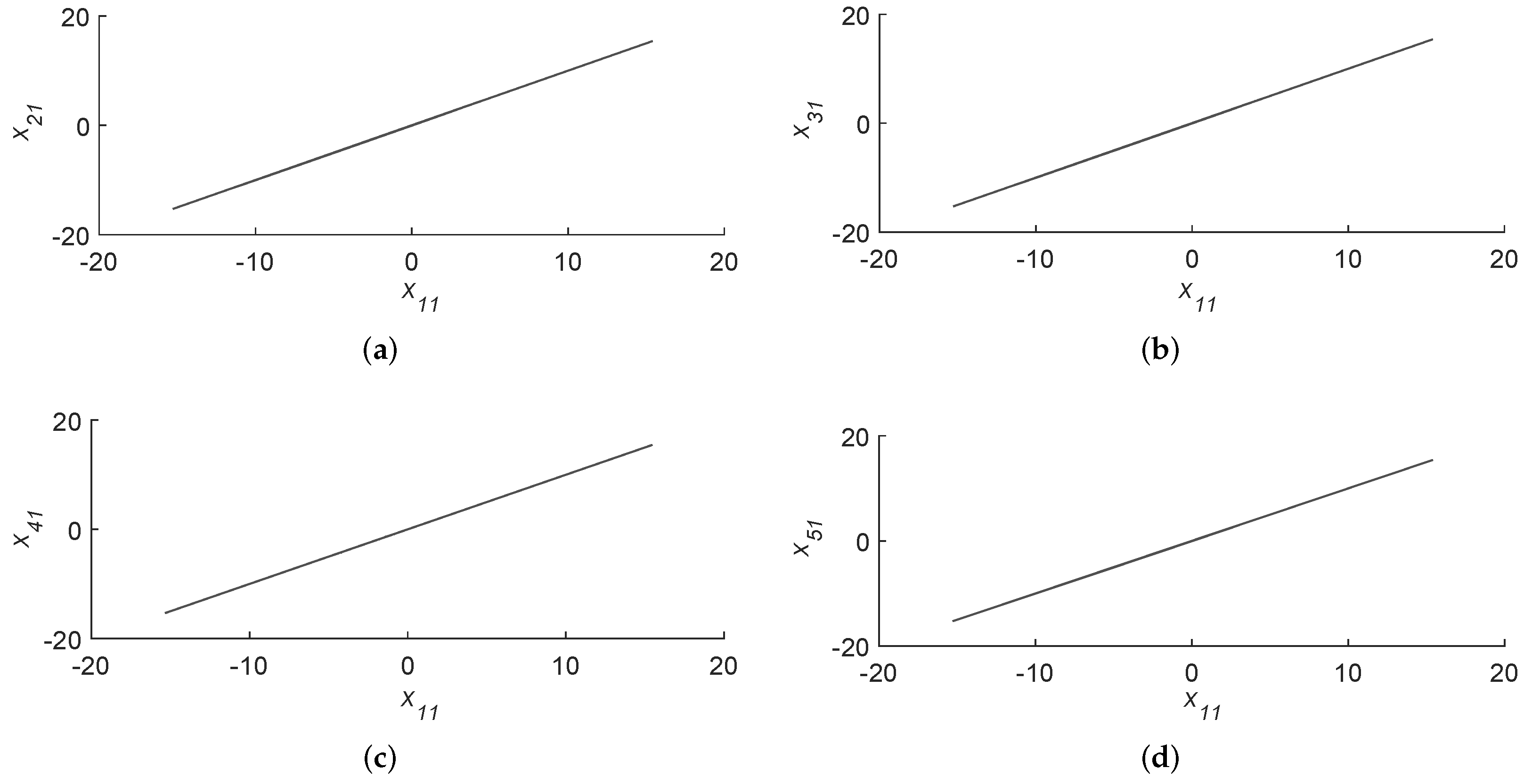
4.1. Synchronization Analysis Based on Master Stability Function Approach and Its Simulation
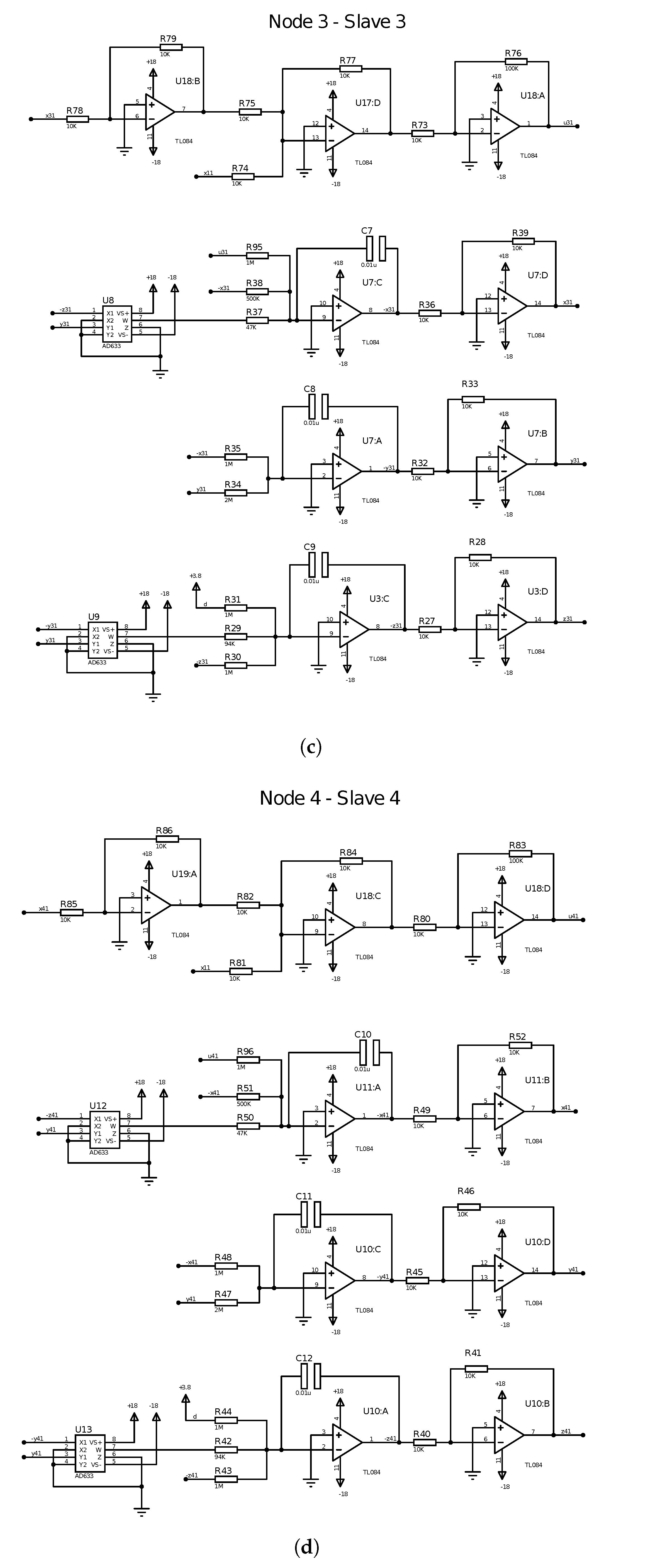
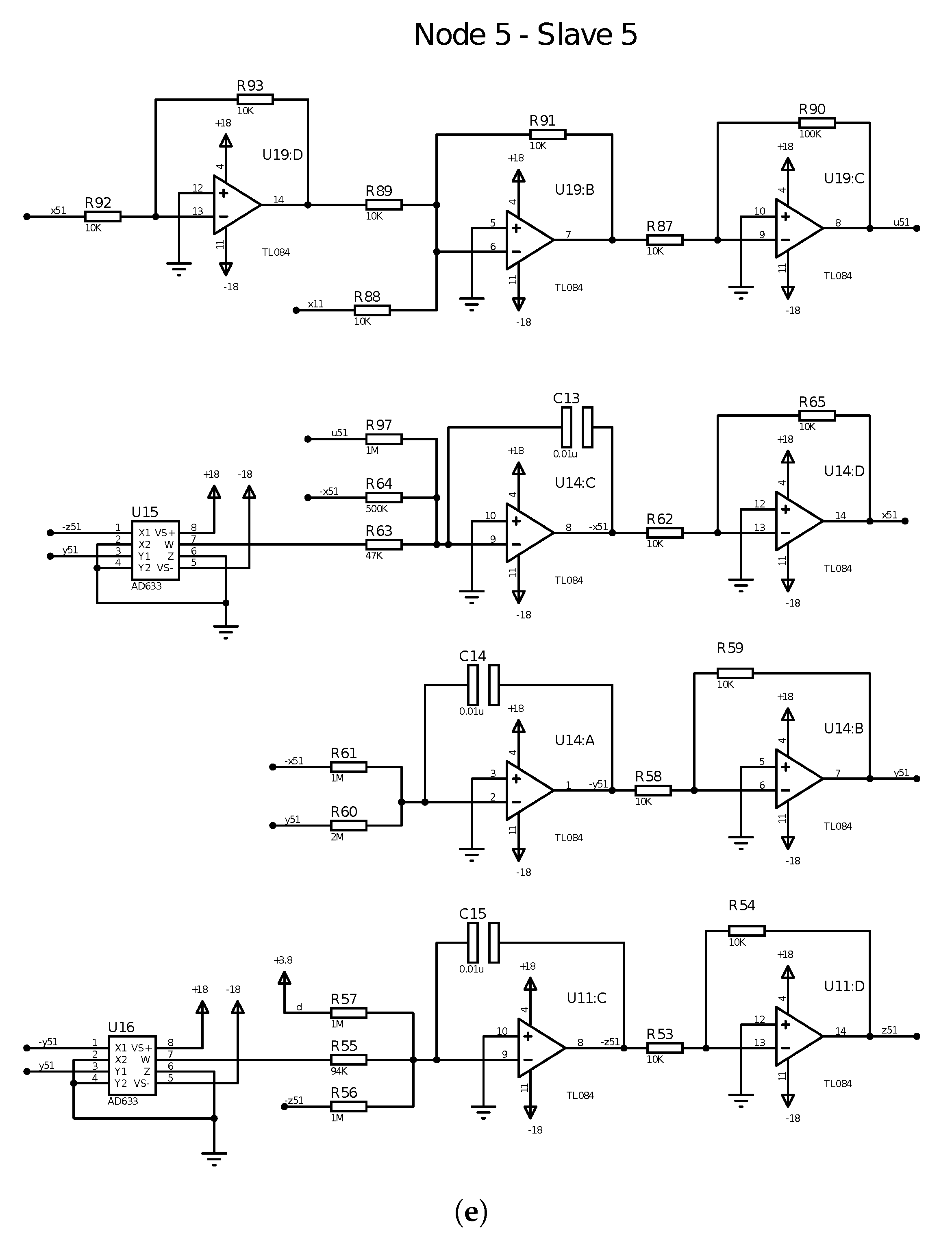
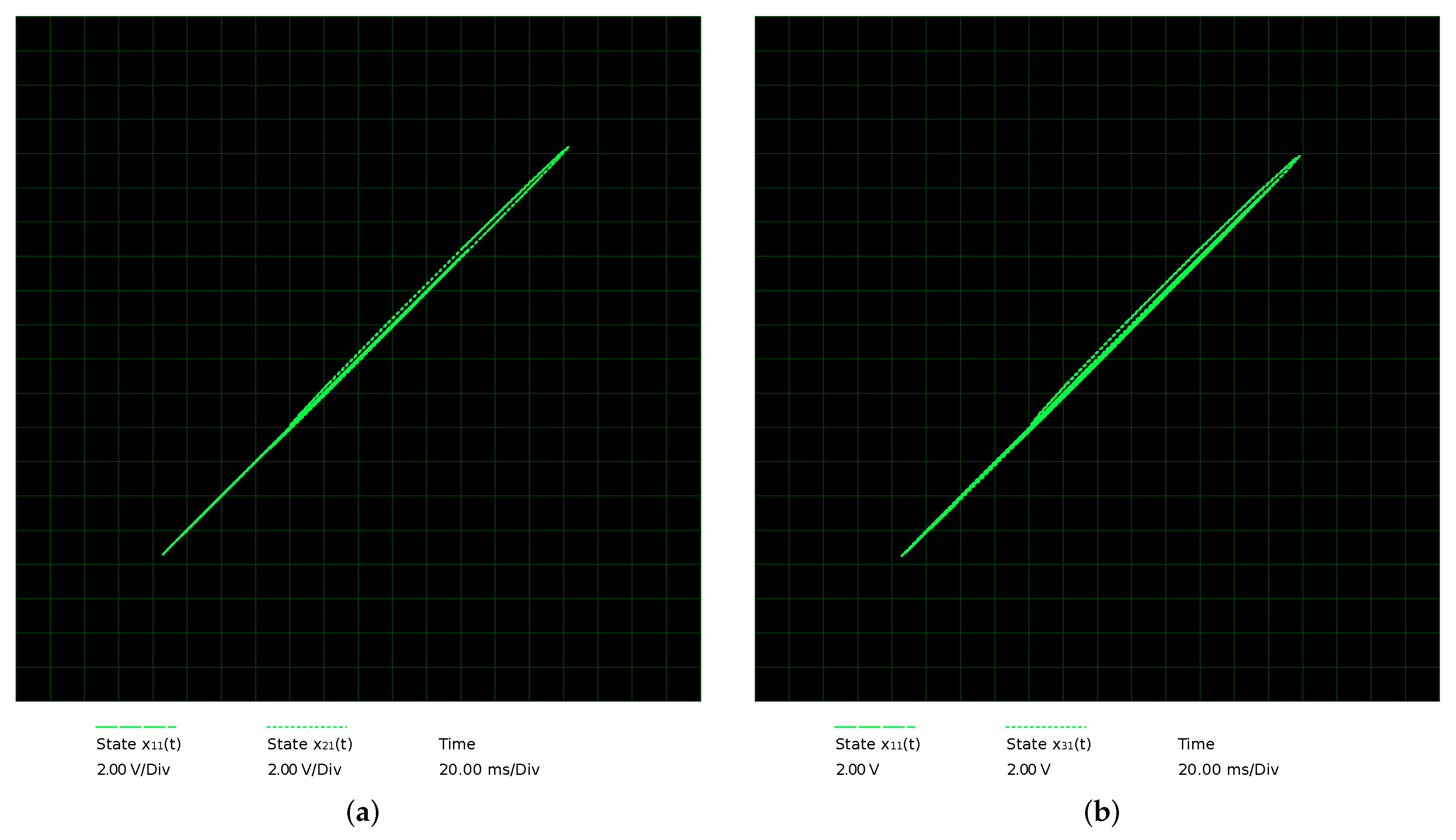
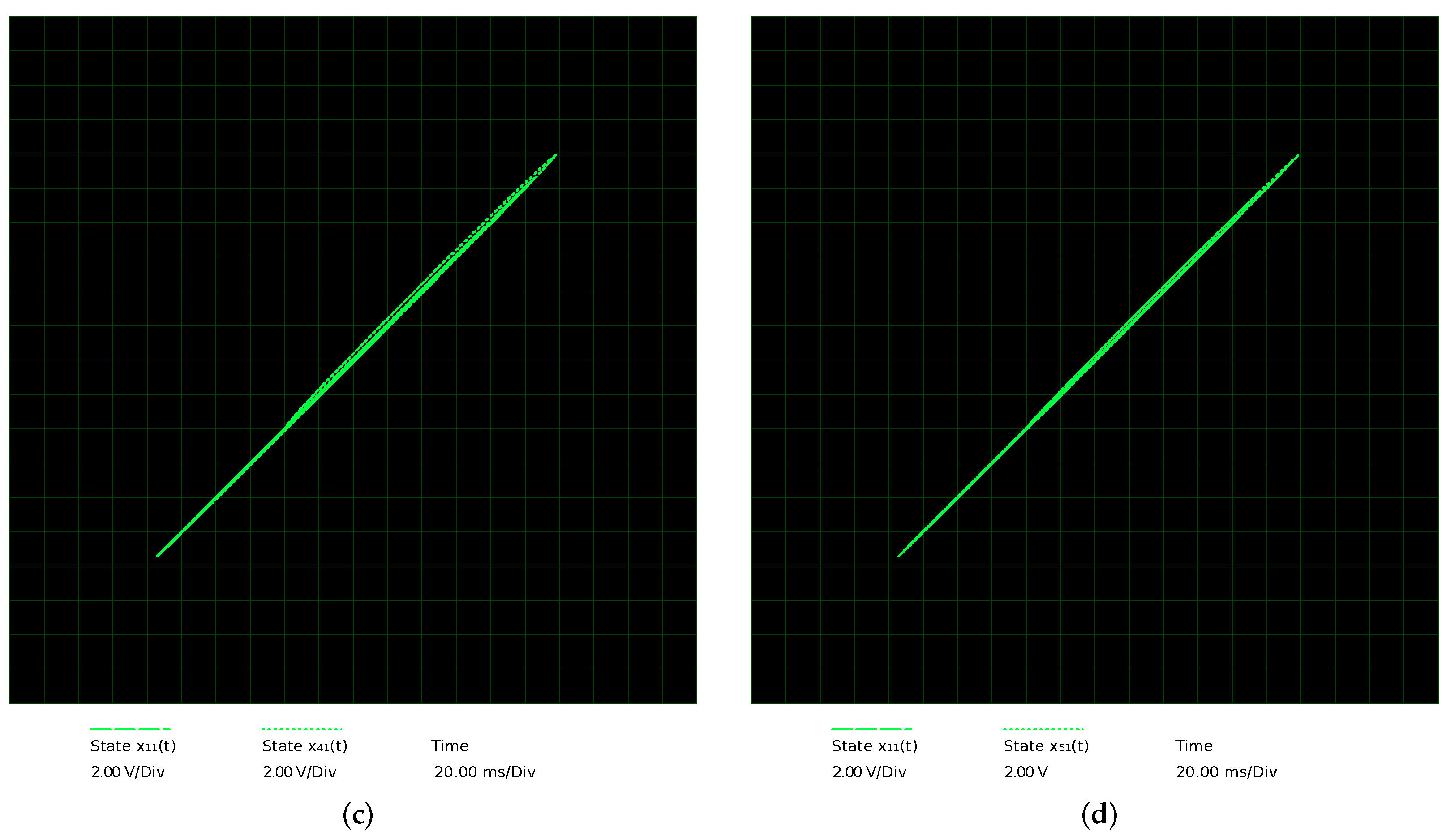
4.2. Star Network Electronic Circuit Synchronization
5. Application to Image Encryption
- 1.
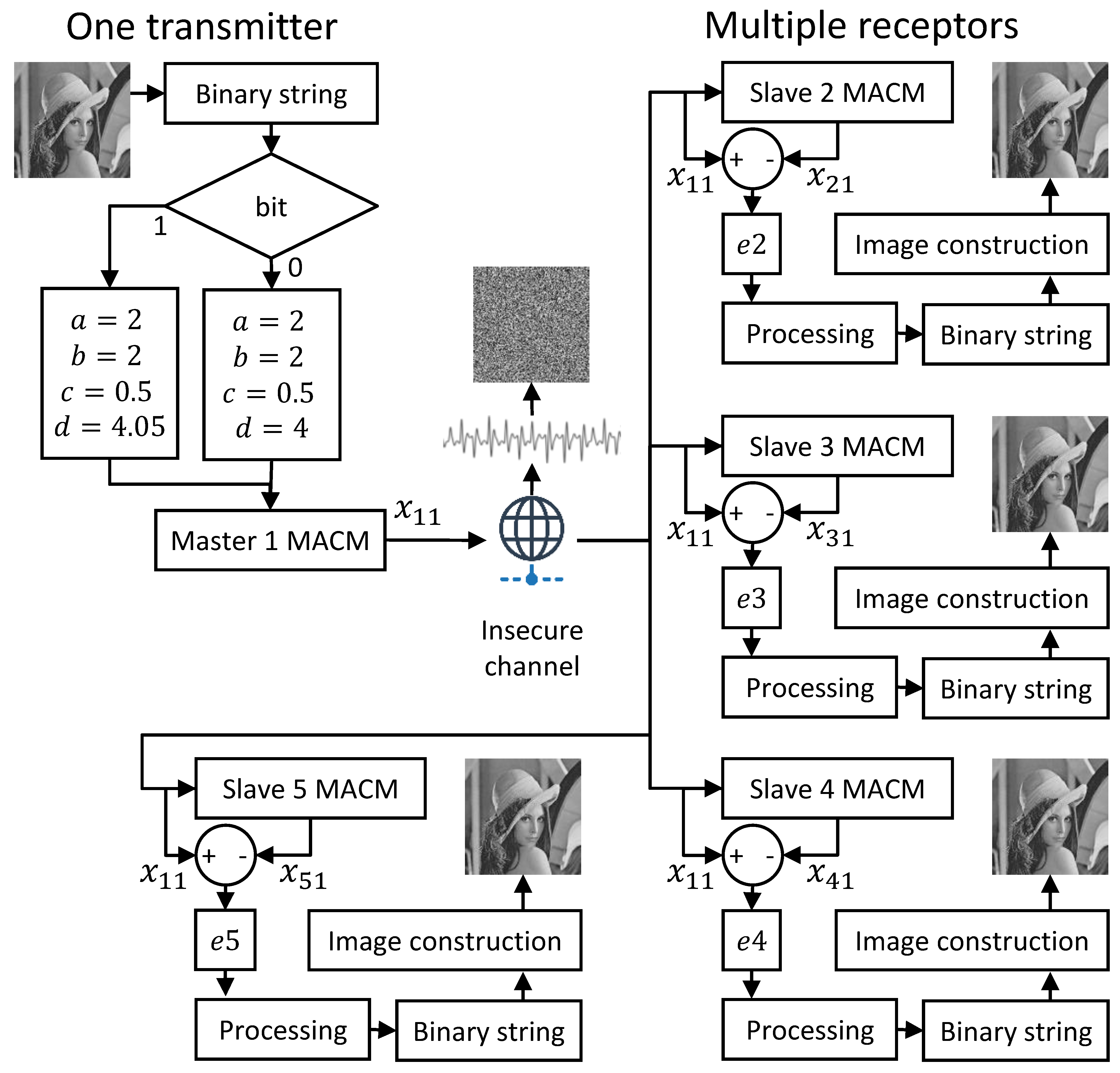
- Binary string. The 8-bit gray-scale digital image with pixels are placed row-by-row in a binary string with bits.
- 2.
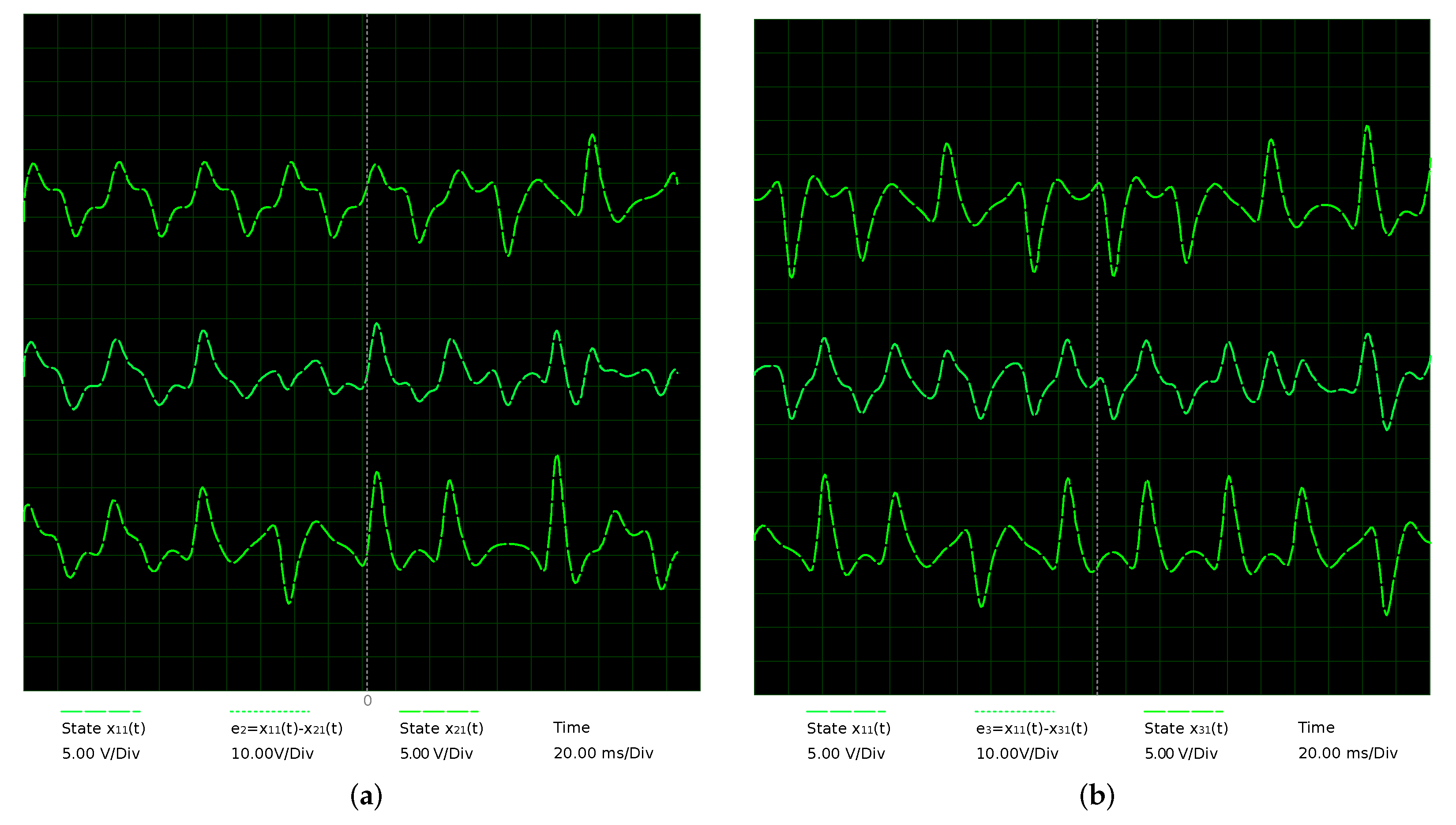
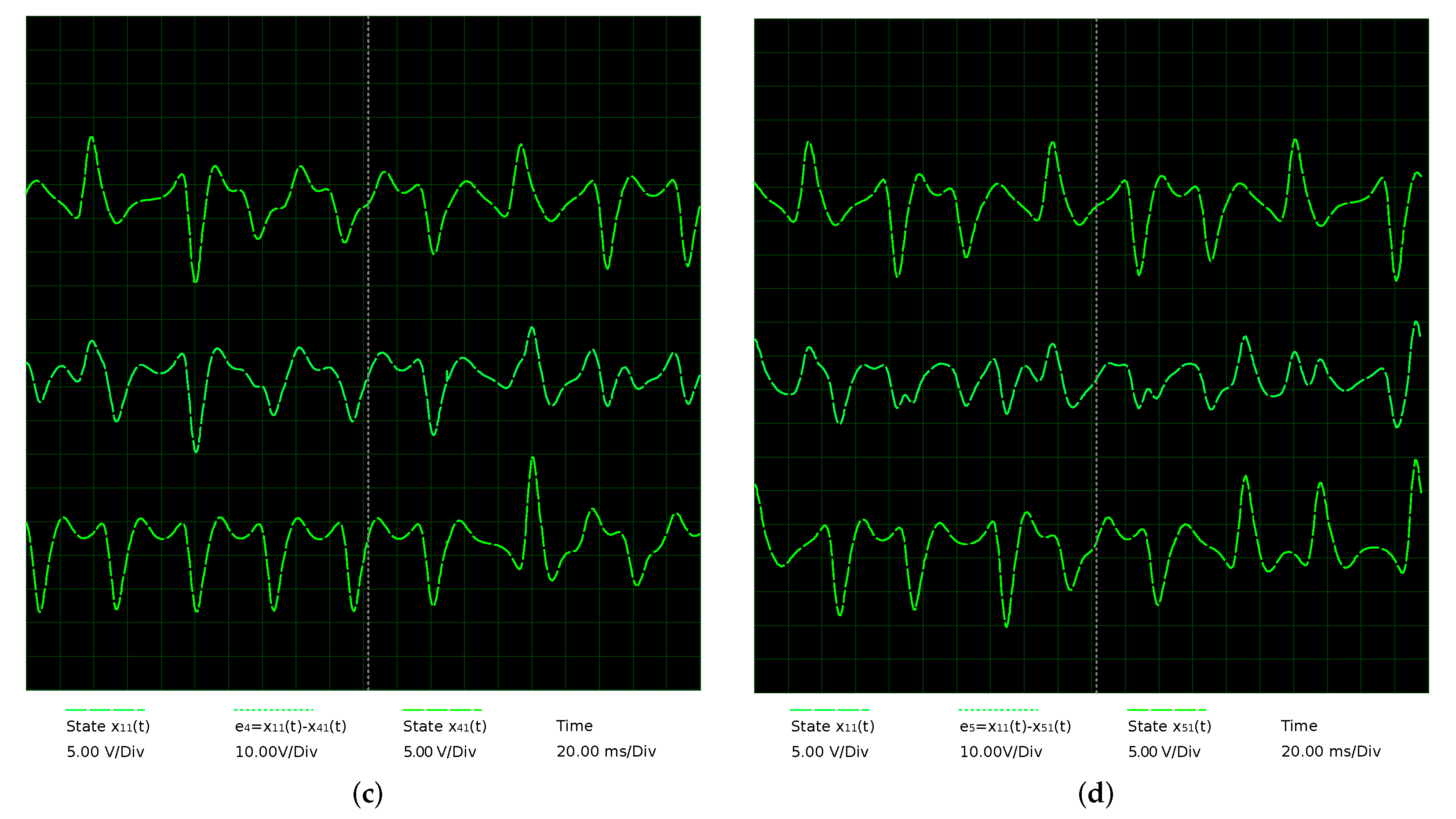
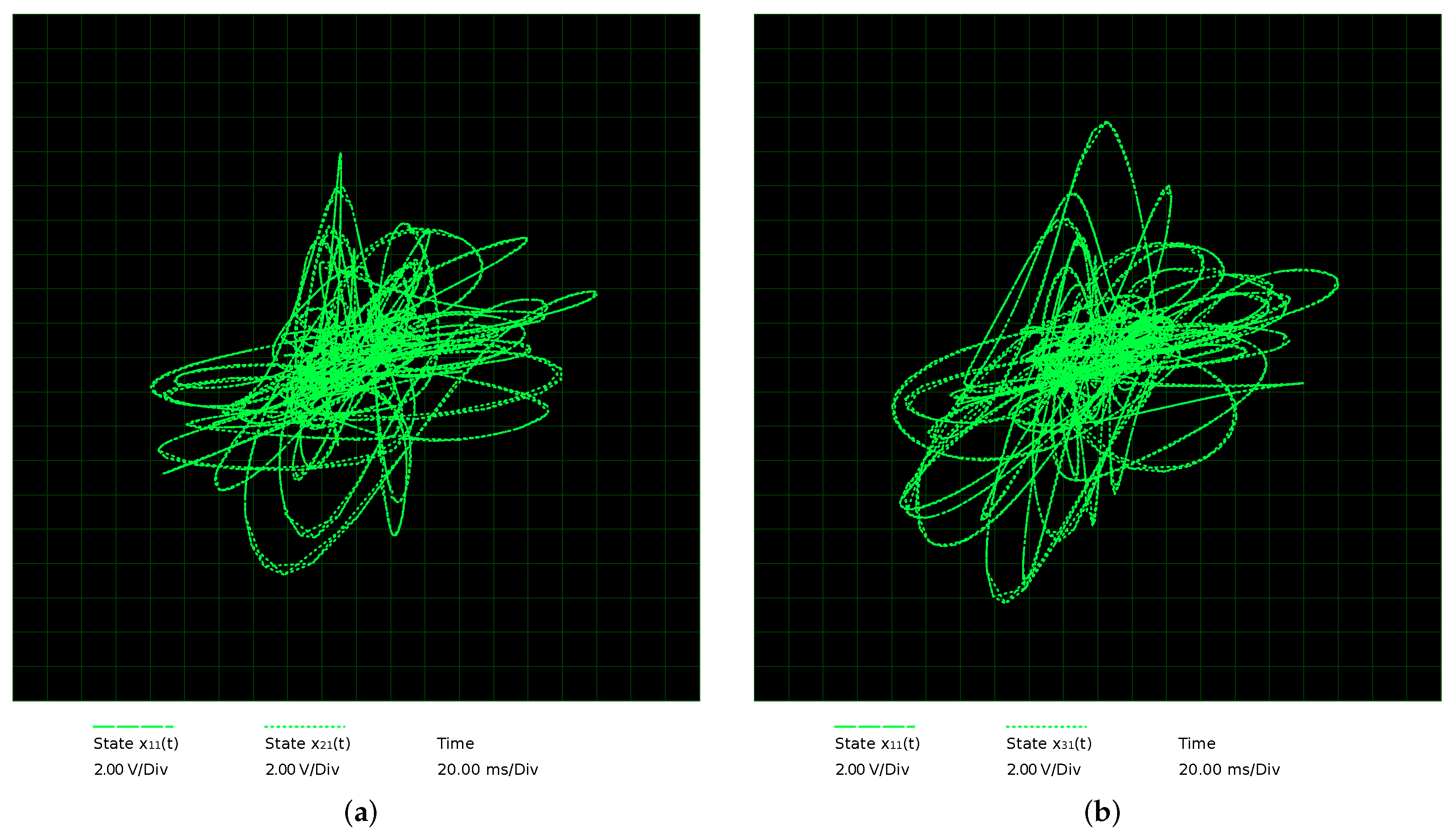
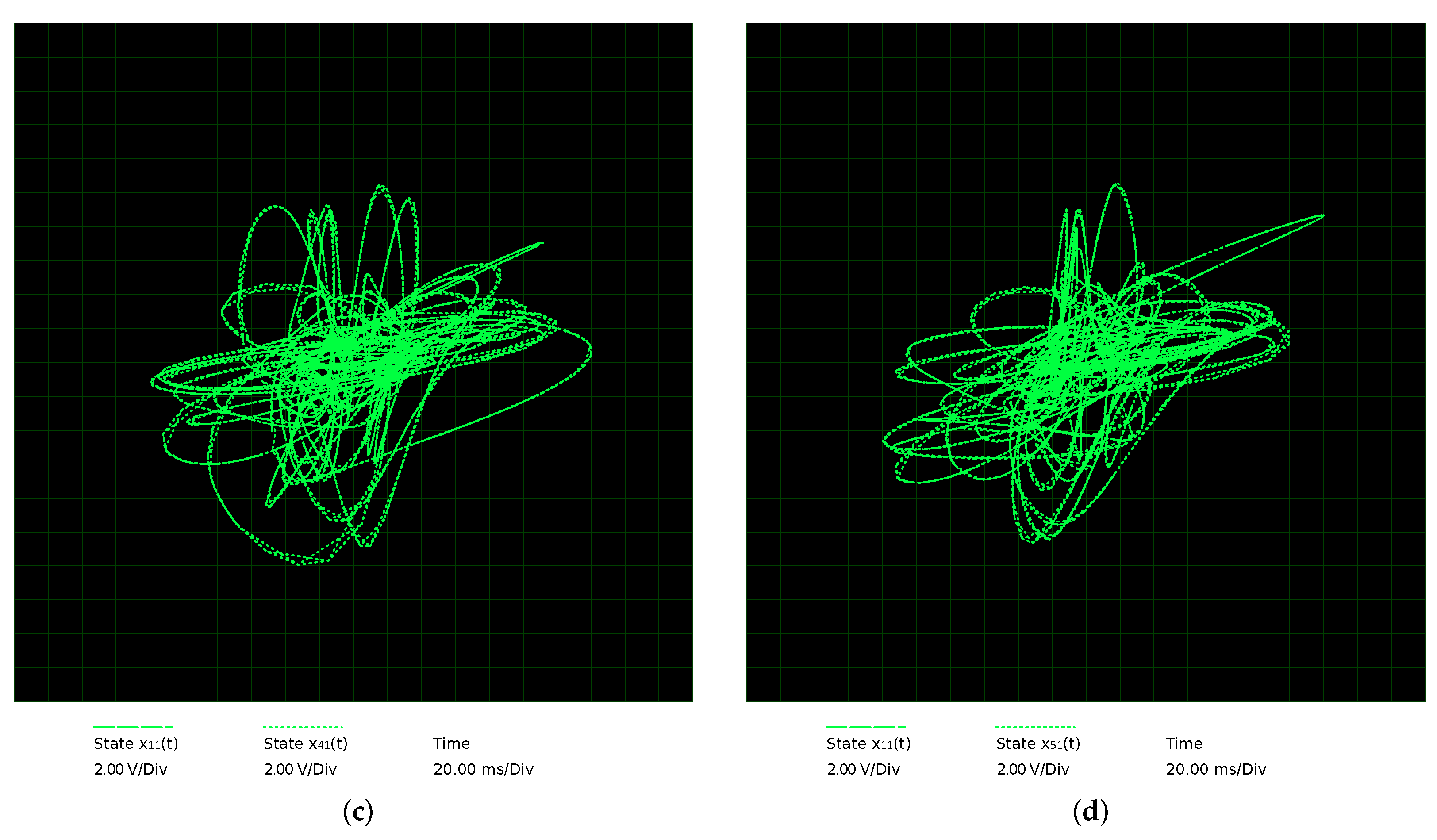
- Synchronization of star network. We used a coupling constant of between the master and slave MACM systems; different initial conditions are used for each MACM system (see Table 1); the control parameters are the same in all MACM systems, i.e., , and . After 50 time units (transient time), the star network is synchronized as shown in Figure 16.
- 3.
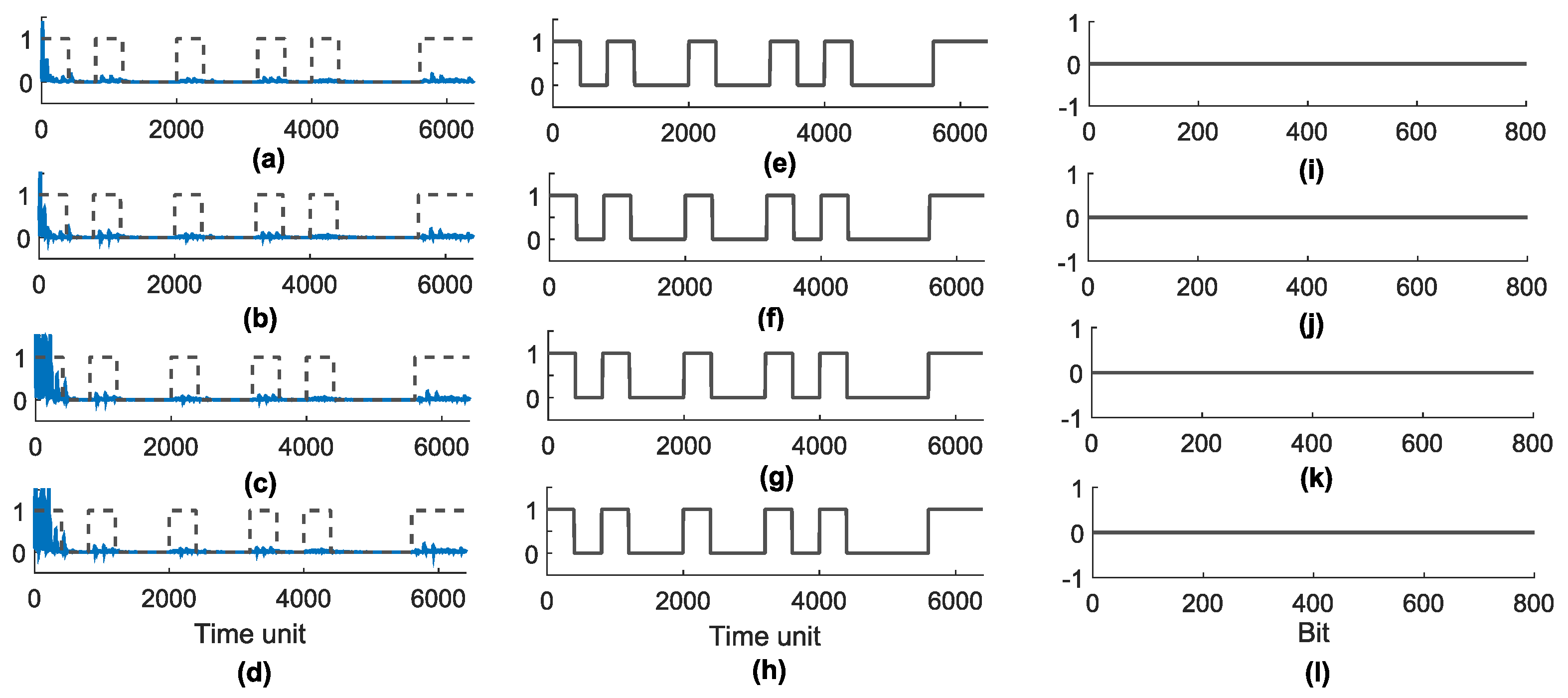
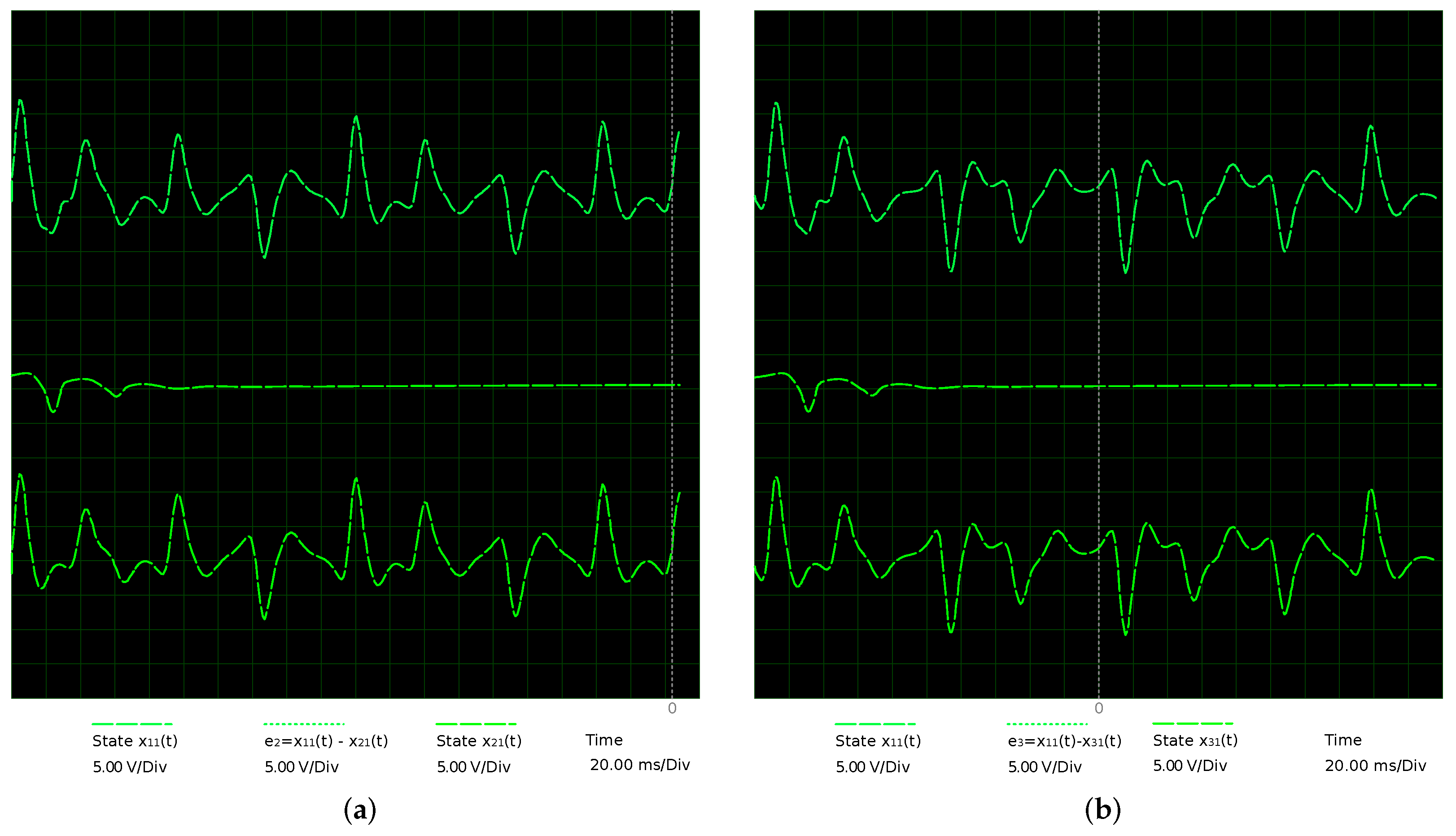
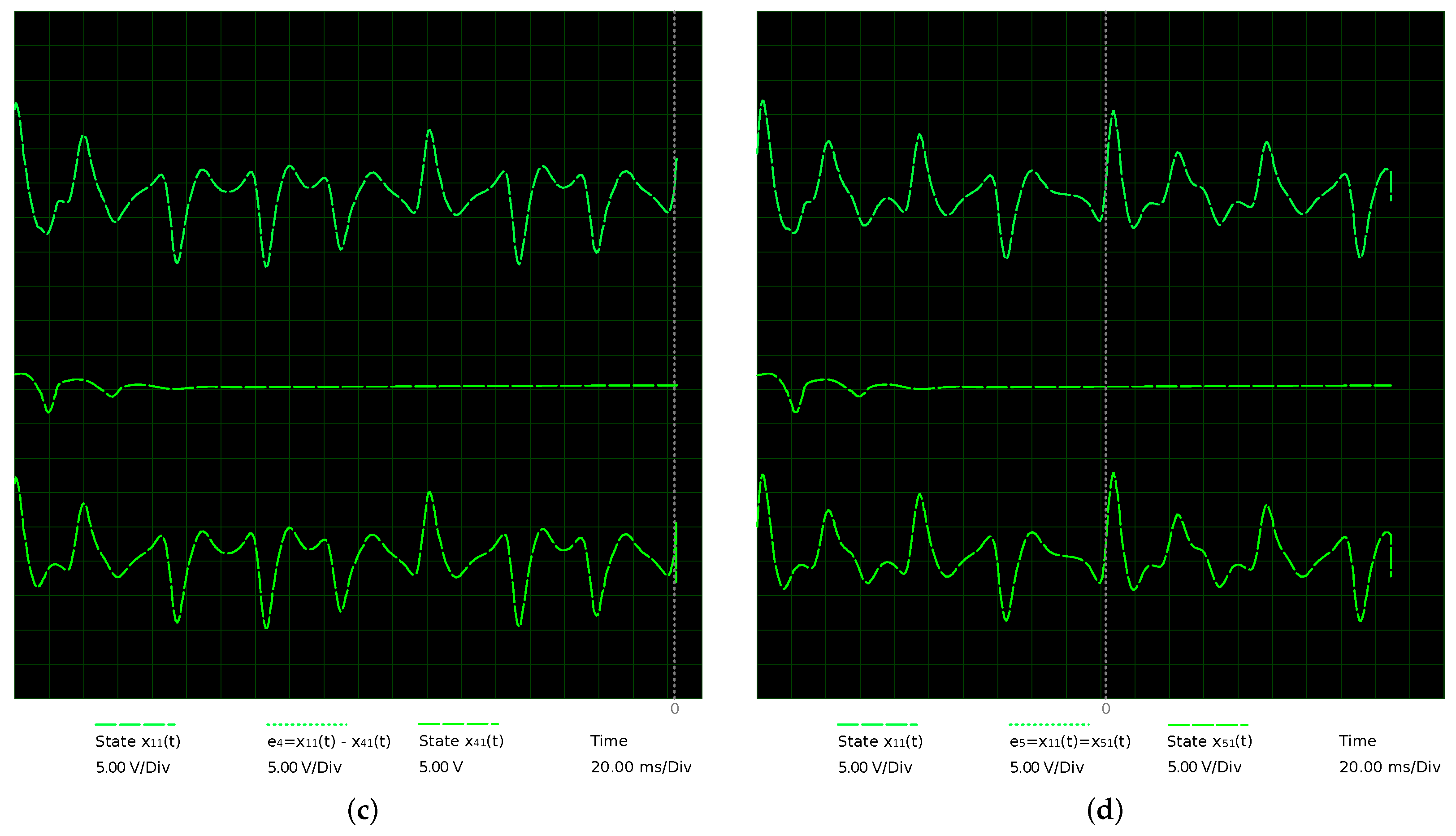
- Extended plain binary data. Since synchronization is achieved after a transient time and to avoid data loss in the receptors, the plain binary string is mounted over 400 time units for each bit producing an extended plain binary data of . As an example, Figure 16a–d show the first two bytes of the plain image transmitted, which are defined as 1010010010100011 with a length of 6400 time units (dashed line).
- 4.
- Switching parameter d of master MACM. The parameter d of the master node is switched between and , for 0 and 1 in the extended plain binary data, respectively. During this time, the absolute synchronization error is determined in , , , and , which are shown in Figure 16a–d with a blue line. Since initial conditions are considerably different at the start communication, the error is bigger in the first time units.
- 5.
- Processing the error. The recovered binary string in the receptor is calculated with the sum of the last 100 data in each error signal considering windows of 400 data; if the sum is greater than 0.7, a bit of 1 is defined for such window or bit of 0 in other case. Figure 16e–h presents the first recovered binary string in each slave MACM system (receptor).
- 6.
- Image construction. The digital image is constructed using the recovered binary string and the inverse process of step 1; the string is separated into 8-bit segments and assigned to rows and columns to form the corresponding digital image. Figure 16i–l present the difference between the plain image and recovered image at the bit level (first 8000 bits) for slaves 2–5, respectively.
5.1. Security Analysis
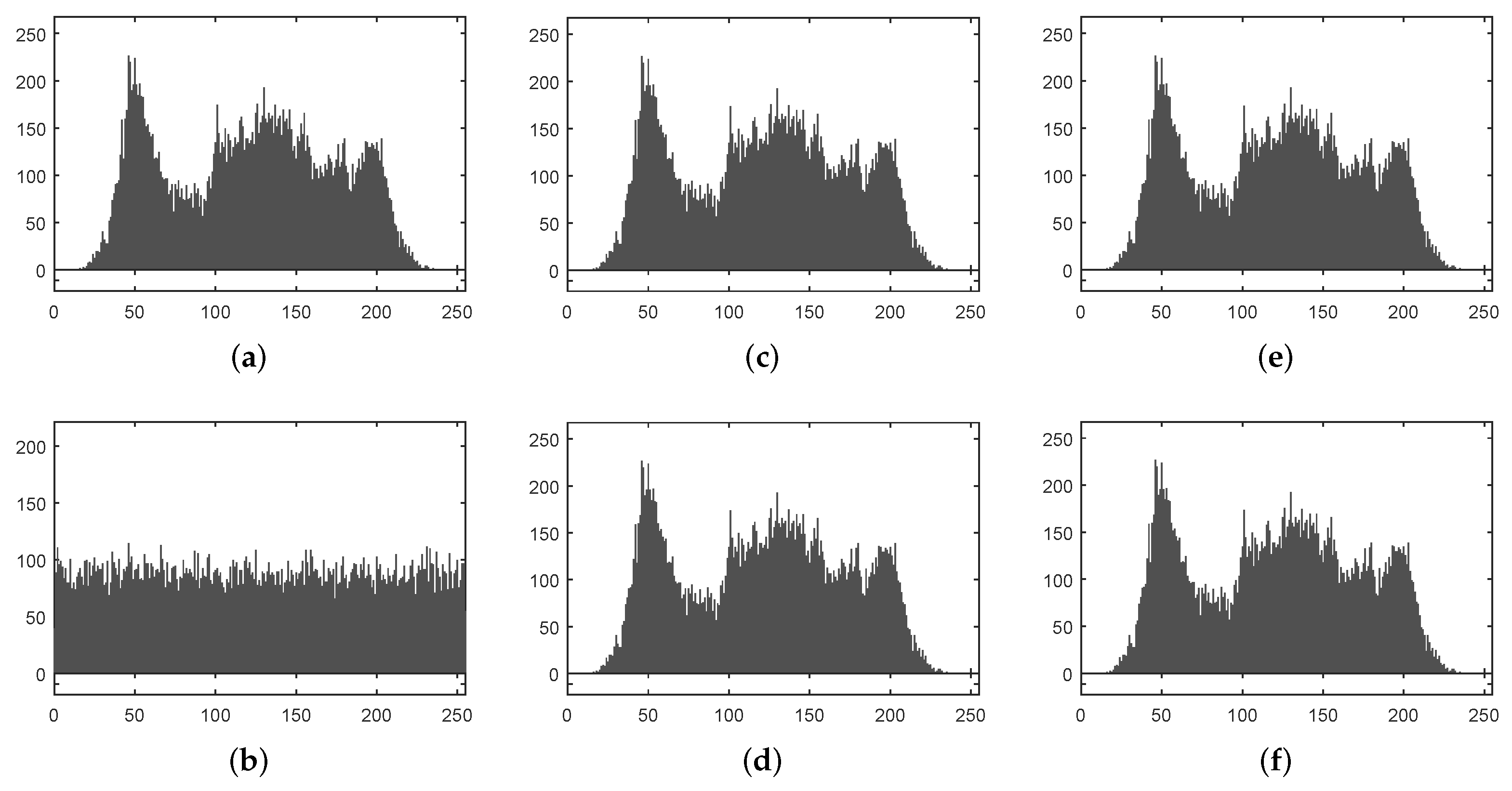
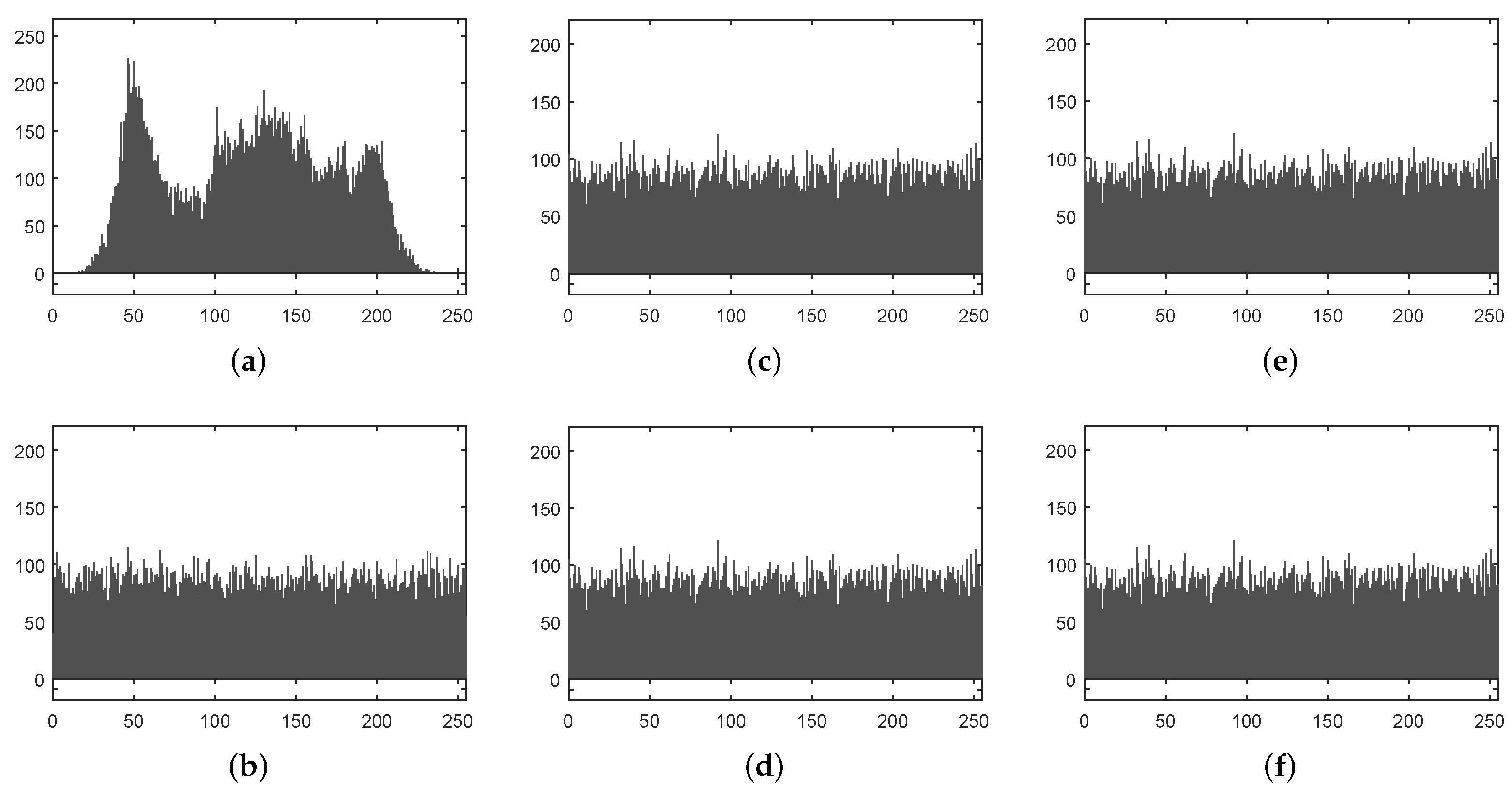
5.1.1. Histograms
5.1.2. Statistics of Histogram
5.1.3. Structural Similarity Index
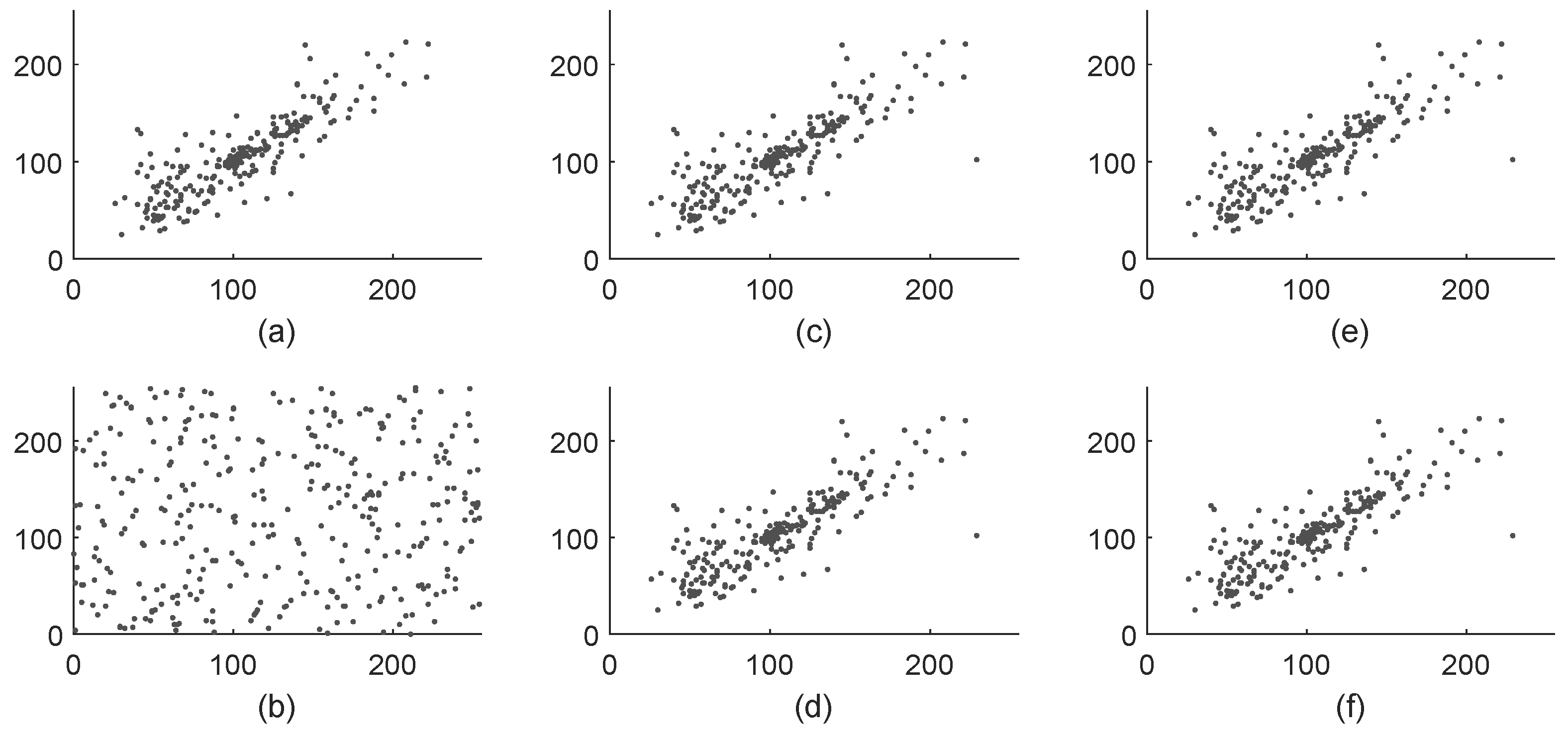
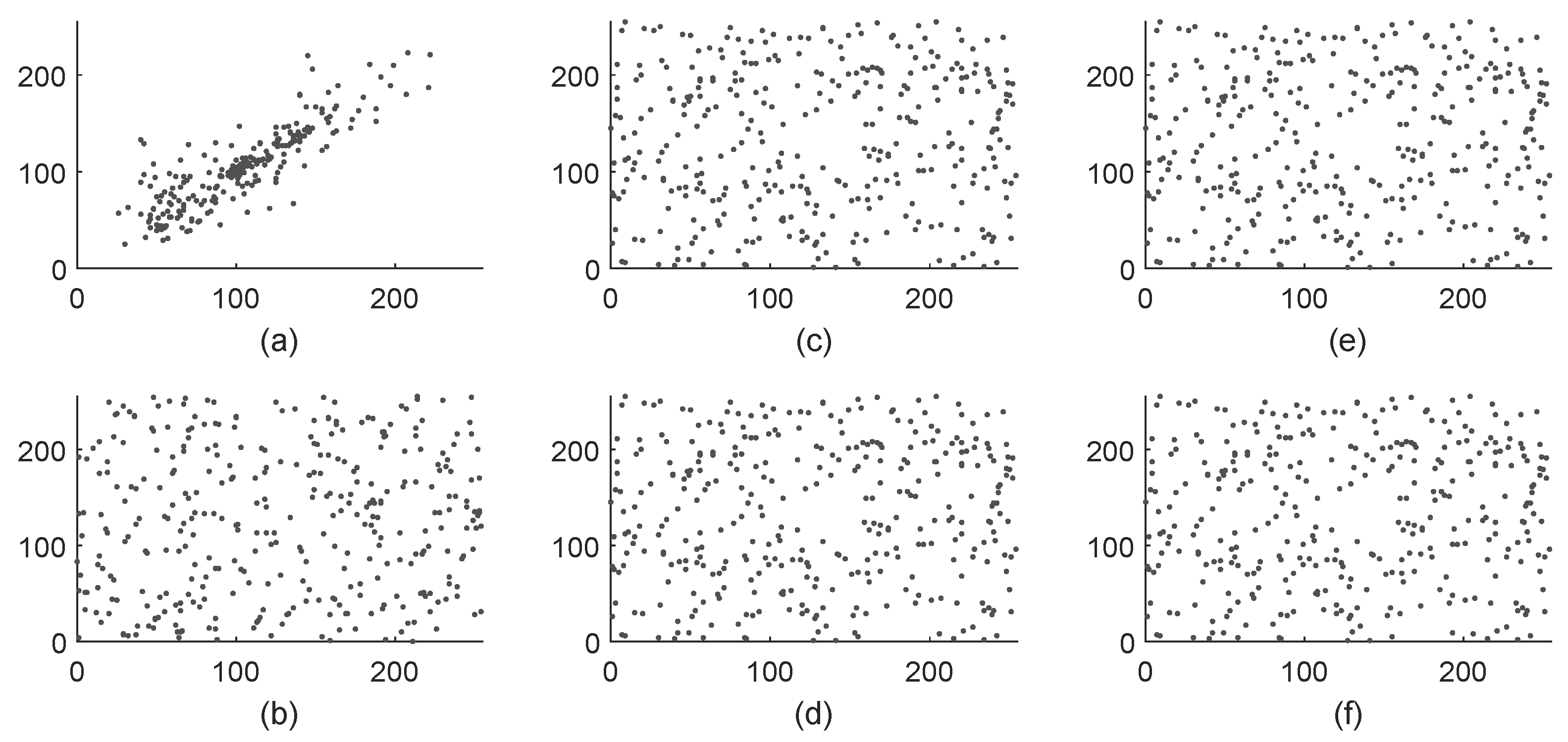
5.1.4. Correlation Analysis
5.1.5. Information Entropy
5.1.6. Decryption Error Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| MACM | Méndez–Arellano–Cruz–Martínez |
| IC | Integrated circuit |
| OA | Operational amplifier |
References
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 812–824. [Google Scholar] [CrossRef] [PubMed]
- Pecora, L.M.; Caroll, T.L. Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 1997, 80, 2109–2112. [Google Scholar] [CrossRef]
- Nijmeijer, H.; Mareels, I.M.Y. An observer looks at synchronization. IEEE Trans. Circuits Syst. I 1997, 44, 882–890. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; Nijmeijer, H. Synchronization through filtering. Int. J. Bifurc. Chaos 2000, 10, 763–775. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Cruz-Hernández, C. Synchronization of chaotic systems: A Generalized Hamiltonian systems approach. Int. Bifurct. Chaos 2001, 11, 1381–1395. [Google Scholar] [CrossRef]
- López-Mancilla, D.; Cruz-Hernández, C. Output synchronization of chaotic systems: Model-matching approach with application to secure communication. Nonlinear Dyn. Syst. Theory 2005, 5, 141–156. [Google Scholar]
- Feldmann, U.; Hasler, M.; Schwarz, W. Communication by chaotic signals: The inverse system approach. Int. J. Circ. Theory Appl. 1996, 24, 551–579. [Google Scholar] [CrossRef]
- Boukabou, A. On nonlinear control and synchronization design for autonomous chaotic systems. Nonlinear Dyn. Syst. Theory 2008, 8, 151–167. [Google Scholar]
- Cruz-Hernández, C.; Martynyuk, A.A. Advances in Chaotic Dynamics with Applications; Cambridge Scientific Publishers: London, UK, 2010; Volume 4. [Google Scholar]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett. 1993, 71, 65–68. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; López-Mancilla, D.; García, V.; Serrano, H.; Núñez, R. Experimental realization of binary signal transmission using chaos. J. Circ. Syst. Comput. 2005, 14, 453–468. [Google Scholar] [CrossRef]
- Cruz-Hernández, C. Synchronization of time-delay Chua’s oscillator with application to secure communication. Nonlinear Dyn. Syst. Theory 2004, 4, 1–13. [Google Scholar]
- Posadas-Castillo, C.; López-Gutiérrez, R.M.; Cruz-Hernández, C. Synchronization of chaotic solid-state Nd:YAG lasers: Application to secure communication. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1655–1667. [Google Scholar] [CrossRef]
- Hou, Y.-Y. Synchronization of Chaotic Systems and Its Application in Security Terminal Sensing Node of Internet of Things. Micromachines 2022, 13, 1993. [Google Scholar] [CrossRef]
- Madan, R.N. (Ed.) Chua’s Circuit: A Paradigm for Chaos; World Scientific: River Edge, NJ, USA, 1993. [Google Scholar]
- Kennedy, M.P. Robust Op-Amp realization of Chua’s circuit. Frequenz 1992, 46, 66–80. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Chua, L.O. Simplest chaotic circuit. Int. J. Bifurc. Chaos 2010, 20, 1567–1580. [Google Scholar] [CrossRef]
- Gámez-Guzmxaxn, L.; Cruz-Hernxaxndez, C.; López-Gutiérrez, R.M.; García-Guerrero, E.E. Synchronization of Chua’s circuits with multi-scroll attractors: Application to communication. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2765–2775. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; Romero-Haros, N. Communicating via synchronized time-delay Chua’s circuits. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 645–659. [Google Scholar] [CrossRef]
- Kusumot, K.; Ohtsubo, J. 1.5-GHz message transmission based on synchronization of chaos in semiconductor lasers. Opt. Lett. 2002, 27, 989–991. [Google Scholar] [CrossRef]
- Lee, M.W.; Paul, J.; Sivaprakasam, S.; Shore, K.A. Comparison of closed-loop and open-loop feedback schemes of message decoding using chaotic laser diodes. Opt. Lett. 2003, 28, 2168–2170. [Google Scholar] [CrossRef]
- Paul, J.; Sivaprakasam, S.; Shore, K.A. Dual-channel chaotic optical communications using external-cavity semiconductor lasers. J. Opt. Soc. Am. B 2004, 21, 514–521. [Google Scholar] [CrossRef]
- Lu, J.; Chen, R. Generating multiscroll chaotic attractors: Theories, methods and applications. Int. J. Bifurc. Chaos 2006, 16, 775–858. [Google Scholar] [CrossRef]
- Cardoza-Avendaño, L.; Spirin, V.; López-Gutiérrez, R.M.; Lxoxpez-Mercado, C.A.; Cruz-Hernández, C. Experimental characterization of DFB and FP chaotic lasers with strong incoherent optical feedback. Opt. Laser Technol. 2011, 43, 949–955. [Google Scholar] [CrossRef]
- Spirin, V.; López-Mercado, C.A.; Miridonov, S.V.; Cardoza-Avendaño, L.; Lxoxpez-Gutiérrez, R.M.; Cruz-Hernández, C. Elimination of low-frequency fluctuations of backscattered Rayleigh radiation from optical fiber with chaotic lasers. Opt. Fiber Technol. 2011, 17, 258–261. [Google Scholar] [CrossRef]
- Tang, S.; Liu, J.M. Chaotic pulsing and quasi-periodic route to chaos in a semiconductor laser with delayed opto-electronic feedback. IEEE J. Quantum Electron. 2001, 37, 329–336. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Y.; He, H. Enhancing the bandwidth of the optical chaotic signal generated by a semiconductor laser with optical feedback. IEEE Photonics Technol. Lett. 2008, 20, 1633–1635. [Google Scholar] [CrossRef]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; García-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Synchronization in small-world dynamical networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar] [CrossRef]
- Wang, X.F. Complex networks: Topology, dynamics and synchronization. Int. J. Bifurc. Chaos 2002, 12, 885–916. [Google Scholar] [CrossRef]
- Posadas-Castillo, C.; Cruz-Hernández, C.; López-Gutiérrez, R.M. Experimental realization of synchronization in complex networks with Chua’s circuits like nodes. Chaos Solitons Fractals 2009, 40, 1963–1975. [Google Scholar] [CrossRef]
- López-Gutiérrez, R.M.; Posadas-Castillo, C.; Lxoxpez-Mancilla, D.; Cruz-Hernández, C. Communicating via robust synchronization of chaotic lasers. Chaos Solitons Fractals 2009, 42, 277–285. [Google Scholar] [CrossRef]
- Posadas-Castillo, C.; Cruz-Hernández, C.; López-Gutiérrez, R.M. Synchronization of chaotic neural networks with delay in irregular networks. Appl. Math. Comput. 2008, 205, 487–496. [Google Scholar] [CrossRef]
- Serrano-Guerrero, H.; Cruz-Hernández, C.; López-Gutiérrez, R.M.; Posadas-Castillo, C.; Inzunza-Gonzxaxlez, E. Chaotic synchronization in star coupled networks of three-dimensional cellular neural networks and its application in communications. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 571–580. [Google Scholar] [CrossRef]
- Acosta-Del Campo, O.R.; Cruz-Hernández, C.; López-Gutiérrez, R.M.; Arellano-Delgado, A.; Cardoza-Avendaño, L.; Chxaxvez-Pxexrez, R. Complex network synchronization of coupled time-delay Chua’s oscillators in different topologies. Nonlinear Dyn. Syst. Theory 2011, 11, 341–372. [Google Scholar]
- Acilina Caneco, J.; Rocha, L.; Grácio, C. Topological Entropy in the Synchronization of Piecewise Linear and Monotone Maps. Coupled Duffing Oscillators. Int. J. Bifurc. Chaos 2009, 11, 3855–3868. [Google Scholar] [CrossRef]
- Acilina Caneco, J. Leonel Rocha and Clara Grácio. Kneading Theory Analysis of the Duffing Equation. Chaos Solitons Fractals 2011, 42, 1529–1538. [Google Scholar] [CrossRef]
- Rocha, J.L.; Carvalho, S. Information Theory, Synchronization and Topological Order in Complete Dynamical Networks of Discontinuous Maps. Math. Comput. Simul. 2021, 182, 340–352. [Google Scholar] [CrossRef]
- Rocha, J.L.; Carvalho, S. Complete Dynamical Networks: Synchronization, Information Transmission and Topological Order, Discontinuity. Nonlinearity Complex. 2023, 1, 99–109. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López-Gutiérrez, R.; Cruz-Hernández, C.; Posadas-Castillo, C.; Cardoza-Avendaño, L.; Serrano-Guerrero, H. Experimental network synchronization via plastic optical fiber. Opt. Fiber Technol. 2013, 19, 93–98. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Cruz-Hernández, C.; Arellano-Delgado, A.; Martínez-Clark, R. A new simple chaotic Lorenz-type system and its digital realization using a TFT touch-screen display embedded system. Complexity 2017, 2017, 6820492. [Google Scholar] [CrossRef]
- Proteus 8 Professional from Labcenter Electronics. Available online: https://www.labcenter.com/ (accessed on 2 February 2023).
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurcat. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M.; Del Campo, O.A. A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015, 109, 119–131. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; López-Gutiérrez, R.M.; Aguilar-Bustos, A.Y.; Posadas-Castillo, C. Communicating encrypted information based on synchronized hyperchaotic maps. Int. J. Nonlin. Sci. Num. 2010, 11, 337–349. [Google Scholar] [CrossRef]
- Abundiz-Pérez, F.; Cruz-Hernández, C.; Murillo-Escobar, M.A.; López-Gutiérrez, R.M.; Arellano-Delgado, A. A fingerprint image encryption scheme based on hyperchaotic Rössler Map. Math. Prob. Eng. 2016, 2016, 2670494. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Li, L.; Zhu, X. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dyn. 2018, 94, 1319–1333. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Meranza-Castillón, M.O.; López-Gutiérrez, R.M.; Cruz-Hernández, C. Suggested integral analysis for chaos-based image cryptosystems. Entropy 2019, 21, 815. [Google Scholar] [CrossRef]





| Initial | Master 1 | Slave 2 | Slave 3 | Slave 4 | Slave 5 |
|---|---|---|---|---|---|
| Condition | MACM | MACM | MACM | MACM | MACM |
| −4.0 | 2.0 | 2.5 | −4.5 | 2.2 | |
| −4.0 | 2.0 | 2.5 | −4.5 | 2.2 | |
| −3.0 | 4.0 | 4.5 | −3.5 | 4.2 |
| Component or IC | Value or Description |
|---|---|
| C1, C2, C3, C4, C5, C6, C7, C8, C9, C10, C11, C12, C13, C14, C15 | 10 nF |
| R1, R25, R38, R51, R64 | 500 k |
| R2, R37, R63 | 47 k |
| R3, R4, R7, R8, R12, R13, R14, R15, R19, R20, R23, R26, R27, R28, R32, R33, R36, R39, R40, R41, R45, R46, R49, R52, R53, R54, R58, R59, R62, R66, R66, R67, R68, R69, R70, R71, R72, R73, R74, R75, R76, R77, R78, R79, R80, R81, R82, R83, R84, R85, R86, R87 R88, R89, R90, R91, R92, R93 | 10 k |
| R5, R9, R11, R17, R18, R22, R31, R30, R35, R43, R44, R48, R56, R57, R61, R94, R95, R96, R97 | 1 M |
| R6, R21, R34, R47, R60 | 2 M |
| R10, R16, R42 | 94 k |
| R24 | 47.5 k |
| R50 | 48 k |
| R29 | 94.5 k |
| R55 | 95 k |
| U1, U4, U5, U6, U8, U9, U12, U13, U15, U16 | Analog-multiplier AD633 |
| U2, U3, U7, U10, U11, U14, U17, U18, U19 | OA TL084 |
| Plain | Encrypted | Image in | Image in | Image in | Image in | |
|---|---|---|---|---|---|---|
| Image | Image | Slave 2 | Slave 3 | Slave 4 | Slave 5 | |
| with | 3713.12 | 101.04 | 3711.78 | 3711.78 | 3711.78 | 3.71178 |
| with | 60.93 | 10.05 | 60.92 | 60.92 | 60.92 | 60.92 |
| Plain | Encrypted | Image in | Image in | Image in | Image in | |
| Image | Image | Slave 2 | Slave 3 | Slave 4 | Slave 5 | |
| with | 3713.12 | 101.04 | 96.91 | 96.87 | 96.91 | 96.93 |
| with | 60.93 | 10.05 | 9.84 | 9.84 | 9.84 | 9.84 |
| P | E | with | with |
|---|---|---|---|
| Plain image | Plain image | 1 | 1 |
| Plain image | Encrypted image | 0.0030 | 0.0030 |
| Plain image | Image in slave 2 | 0.9998 | 0.0135 |
| Plain image | Image in slave 3 | 0.9998 | 0.0134 |
| Plain image | Image in slave 4 | 0.9998 | 0.0135 |
| Plain image | Image in slave 5 | 0.9998 | 0.0134 |
| Coupling | Plain | Encrypted | Image in | Image in | Image in | Image in |
|---|---|---|---|---|---|---|
| Constant | Image | Image | Slave 2 | Slave 3 | Slave 4 | Slave 5 |
| 0.8757 | 0.1255 | 0.8520 | 0.8520 | 0.8520 | 0.8520 | |
| 0.8758 | 0.1256 | 0.1060 | 0.0957 | 0.1060 | 0.0957 |
| Coupling | Plain | Encrypted | Image in | Image in | Image in | Image in |
|---|---|---|---|---|---|---|
| Constant | Image | Image | Slave 2 | Slave 3 | Slave 4 | Slave 5 |
| 7.5250 | 7.9903 | 7.5253 | 7.5253 | 7.5253 | 7.5253 | |
| 7.5250 | 7.9903 | 7.9910 | 7.9910 | 7.9910 | 7.9910 |
| P | D | (%) with | (%) with |
|---|---|---|---|
| Plain image | Encrypted image | 99.5688 | 99.5688 |
| Plain image | Image in slave 2 | 0.0044 | 99.6488 |
| Plain image | Image in slave 3 | 0.0044 | 99.6488 |
| Plain image | Image in slave 4 | 0.0044 | 99.6488 |
| Plain image | Image in slave 5 | 0.0044 | 99.6488 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Méndez-Ramírez, R.; Arellano-Delgado, A.; Murillo-Escobar, M.Á. Network Synchronization of MACM Circuits and Its Application to Secure Communications. Entropy 2023, 25, 688. https://doi.org/10.3390/e25040688
Méndez-Ramírez R, Arellano-Delgado A, Murillo-Escobar MÁ. Network Synchronization of MACM Circuits and Its Application to Secure Communications. Entropy. 2023; 25(4):688. https://doi.org/10.3390/e25040688
Chicago/Turabian StyleMéndez-Ramírez, Rodrigo, Adrian Arellano-Delgado, and Miguel Ángel Murillo-Escobar. 2023. "Network Synchronization of MACM Circuits and Its Application to Secure Communications" Entropy 25, no. 4: 688. https://doi.org/10.3390/e25040688
APA StyleMéndez-Ramírez, R., Arellano-Delgado, A., & Murillo-Escobar, M. Á. (2023). Network Synchronization of MACM Circuits and Its Application to Secure Communications. Entropy, 25(4), 688. https://doi.org/10.3390/e25040688







