Master–Slave Outer Synchronization in Different Inner–Outer Coupling Network Topologies
Abstract
1. Introduction
2. Preliminaries in Complex Dynamical Networks
3. Master Stability Function
4. MACM Chaotic System
5. Analysis of Master–Slave Inner–Outer Coupling Network Topologies
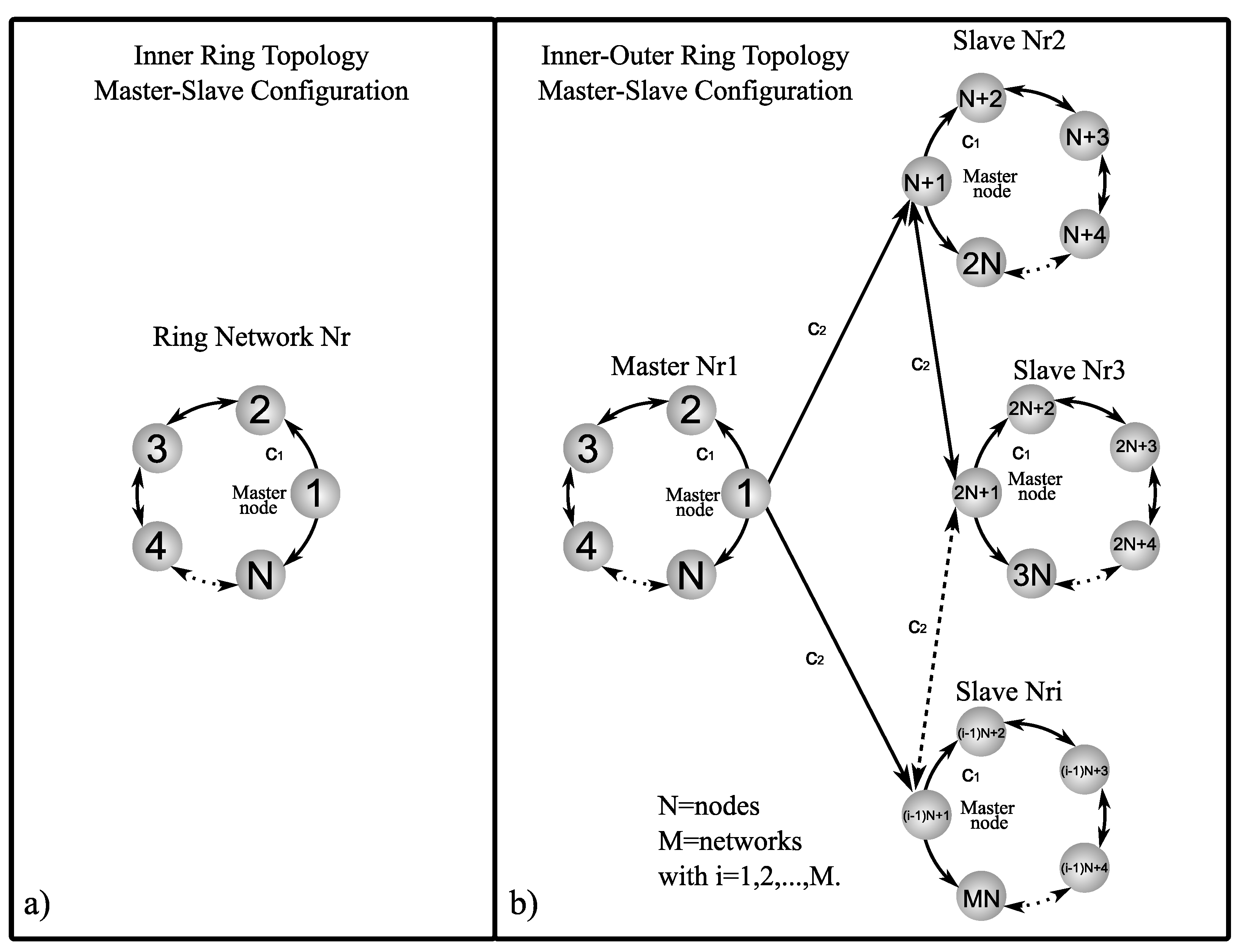
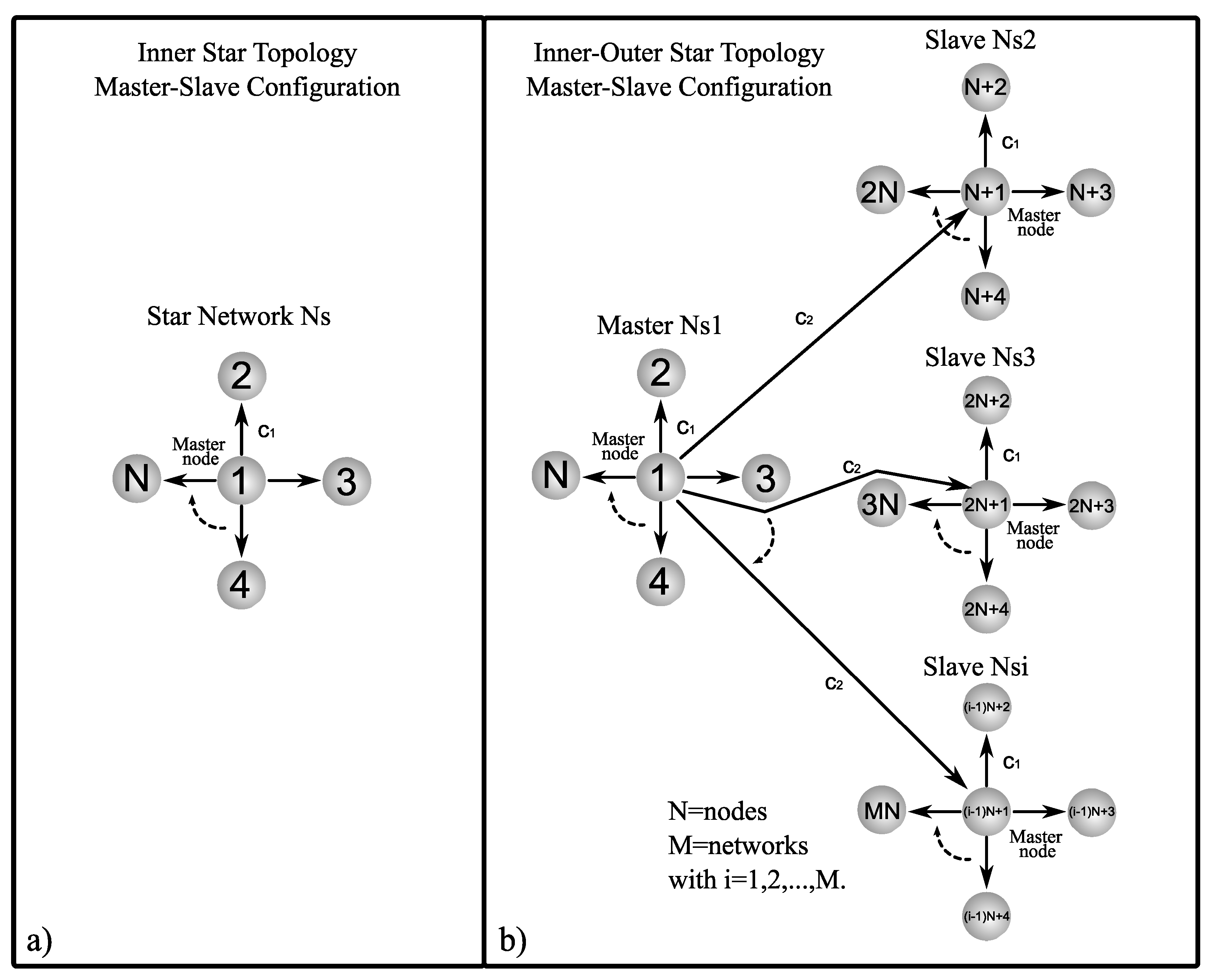
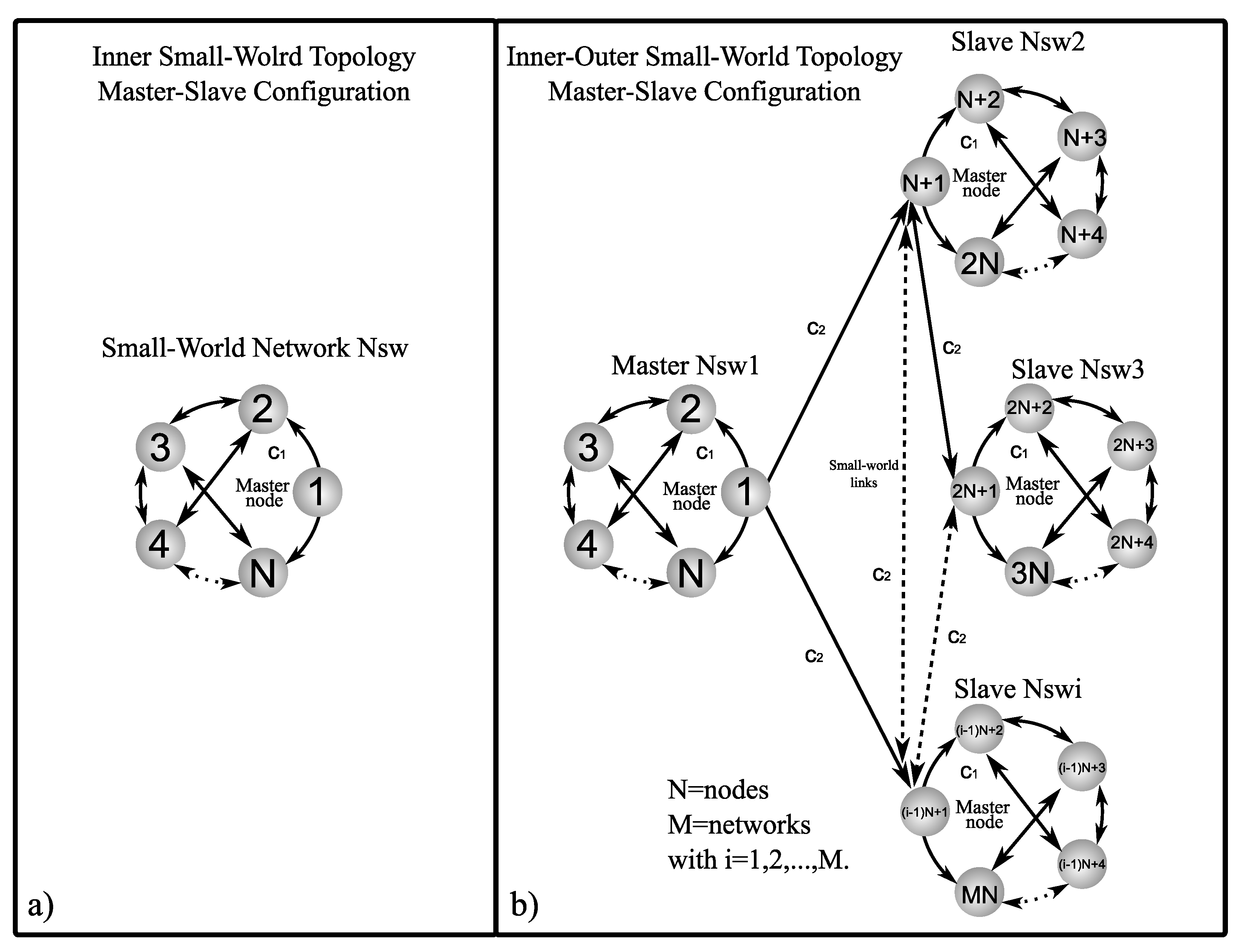
5.1. Inner Topology of Ring, Star, and Small-World Networks in Master–Slave Configuration
5.2. Outer Topology of Ring, Star, and Small-World Networks in Master–Slave Configuration
5.3. A Big Network in Inner–Outer Network Coupling Topology in Master–Slave Configuration
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pikovsky, A.; Rosenblum, M.; Kurths, J. A Universal Concept in Nonlinear Sciences, 1st ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Blasius, B.; Huppert, A.; Stone, L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 1999, 399, 354–359. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1999, 393, 440–442. [Google Scholar] [CrossRef]
- Sun, J.; Bollt, E.M.; Porter, M.A.; Dawkins, M.S. A mathematical model for the dynamics and synchronization of cows. Physica D 2011, 240, 1497–1509. [Google Scholar] [CrossRef]
- Bowen, T.A.; Zhivun, E.; Wickenbrock, A.; Dumont, V.; Bale, S.D.; Pankow, C.; Dobler, G.; Wurtele, J.S.; Budker, D. A network of magnetometers for multi-scale urban science and informatics. Geosci. Instrum. Methods Data Syst. 2019, 8, 129–138. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Zou, C.; Wei, X.; Zhang, Q.; Liu, Y. Synchronization of chemical reaction networks based on DNA strand displacement circuits. IEEE Access 2018, 6, 20584–20595. [Google Scholar] [CrossRef]
- Lü, L.; Zhang, F.; Zou, C. Finite-time synchronization in the laser network based on sliding mode control technology. Optik 2021, 225, 165605. [Google Scholar] [CrossRef]
- Lü, L.; Zhao, L. Finite-time synchronisation transmission of quantum signals between Jaynes-Cummings models based on coupling technology. Opt. Quant. Electron. 2023, 55, 145. [Google Scholar] [CrossRef]
- Bollobas, B. Modern Graph Theory, 1st ed.; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Strogatz, S.H. Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life, 1st ed.; Hyperion Press: Great Britain, UK, 2003. [Google Scholar]
- Lü, L.; Zhang, F.; Han, C. Synchronization transmission of the target signal in the circuit network based on coupling technique. Physica A 2019, 535, 122412. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López-Gutiérrez, R.M.; Cruz-Hernández, C.; Posadas- Castillo, C.; Cardoza-Avendaño, L.; Serrano-Guerrero, H. Experimental network synchronization via plastic optical Fiber. Opt. Fiber Technol. 2013, 19, 93–108. [Google Scholar] [CrossRef]
- Posadas-Castillo, C.; Cruz-Hernández, C.; López-Gutiérrez, R.M. Experimental realization of synchronization in complex networks with Chua’s circuits like nodes. Chaos Solitons Fractals 2009, 40, 1963–1975. [Google Scholar] [CrossRef]
- Goldbeter, A. Biochemical Oscillations and Cellular Rhythms: The Molecular Bases of Periodic and Chaotic Behaviour; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Posadas-Castillo, C.; Cruz-Hernández, C.; López-Gutiérrez, R.M. Synchronization of chaotic neural networks with delay in irregular networks. Appl. Math. Comput. 2008, 205, 487–496. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López Gutiérrez, R.M.; Cruz-Hernández, C.; Martinez-Clark, R. Small-World Outer Synchronization of Small-World Chaotic Networks. J. Comput. Nonlinear Dyn. 2018, 13, 101008. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; Cruz-Hernández, C.; López Gutiérrez, R.M.; Posadas-Castillo, C. Outer Synchronization of Simple Firefly Discrete Models in Coupled Networks. Math. Probl. Eng. 2015, 2015, 895379. [Google Scholar] [CrossRef]
- Zhuchun, L.; Xiaoping, X. Outer synchronization of coupled networks using arbitrary coupling strength. Chaos 2010, 20, 023106. [Google Scholar]
- Li, C.; Xu, C.; Sun, W.; Xu, J.; Kurths, J. Outer synchronization of coupled discrete-time networks. Chaos 2009, 19, 013106. [Google Scholar] [CrossRef]
- Ray, A.; Roychowdhury, A. Outer synchronization of networks with different node dynamics. Eur. Phys. J. Spec. Top. 2014, 223, 1509–1518. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L. Exponential Outer Synchronization between Two Uncertain Time-Varying Complex Networks with Nonlinear Coupling. Entropy 2015, 17, 3097–3109. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, J. Outer Synchronization between Fractional-Order Complex Networks: A Non-Fragile Observer-based Control Scheme. Entropy 2013, 15, 1357–1374. [Google Scholar] [CrossRef]
- Sun, Y.; Li, W.; Zhao, D. Outer synchronization between two complex dynamical networks with discontinuous coupling. Chaos 2012, 22, 043125. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. Outer synchronization between delayed coupling networks with different dynamics and uncertain parameters. Physica A 2018, 2015, 890–901. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Synchronization in small-world dynamical networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar] [CrossRef]
- Wang, X.F. Complex networks: Topology, dynamics and synchronization. Int. J. Bifurc. Chaos 2002, 12, 885–916. [Google Scholar] [CrossRef]
- Pecora, L.M.; Caroll, T.L. Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 1997, 80, 2109–2112. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Cruz-Hernández, C.; Martínez-Clark, R. A New Simple Chaotic Lorenz-Type System and Its Digital Realization Using a TFT Touch-Screen Display Embedded System. Complexity 2017, 2017, 6820492. [Google Scholar] [CrossRef]
- Newman, M.E.; Barabási, A.L.E.; Watts, D.J. The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Dorogovtsev, S.N.; Mendes, J.F.; Dorogovtsev, S.N. Evolution of Networks: From Biological Nets to the Internet and WWW; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
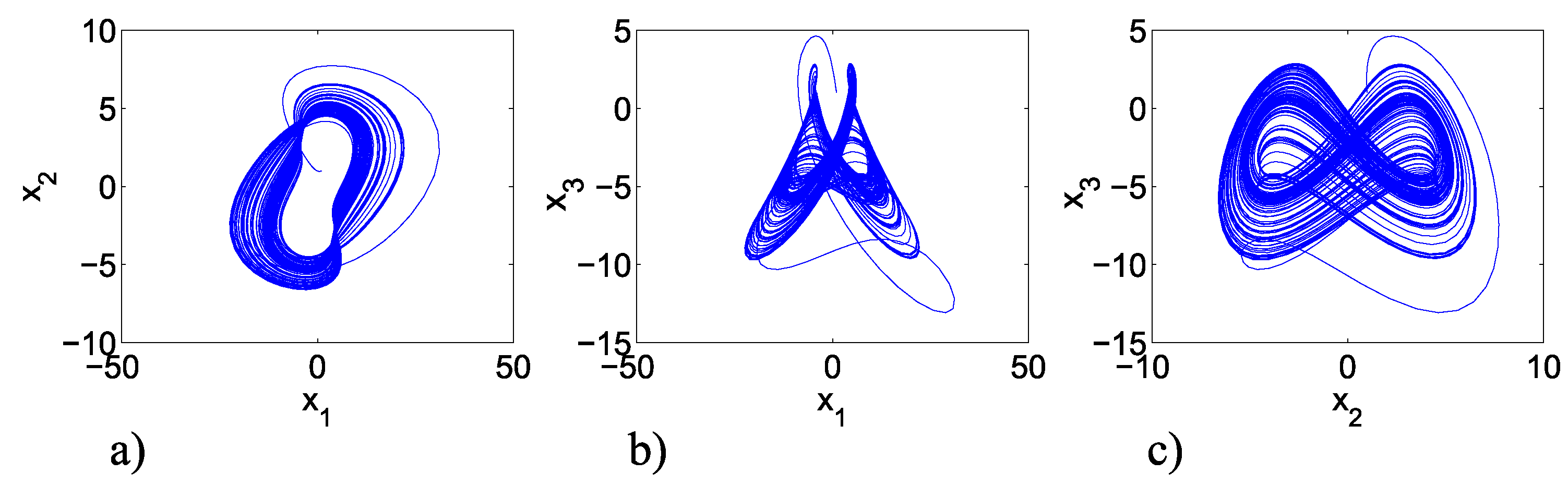

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arellano-Delgado, A.; López-Gutiérrez, R.M.; Murillo-Escobar, M.Á.; Posadas-Castillo, C. Master–Slave Outer Synchronization in Different Inner–Outer Coupling Network Topologies. Entropy 2023, 25, 707. https://doi.org/10.3390/e25050707
Arellano-Delgado A, López-Gutiérrez RM, Murillo-Escobar MÁ, Posadas-Castillo C. Master–Slave Outer Synchronization in Different Inner–Outer Coupling Network Topologies. Entropy. 2023; 25(5):707. https://doi.org/10.3390/e25050707
Chicago/Turabian StyleArellano-Delgado, Adrian, Rosa Martha López-Gutiérrez, Miguel Ángel Murillo-Escobar, and Cornelio Posadas-Castillo. 2023. "Master–Slave Outer Synchronization in Different Inner–Outer Coupling Network Topologies" Entropy 25, no. 5: 707. https://doi.org/10.3390/e25050707
APA StyleArellano-Delgado, A., López-Gutiérrez, R. M., Murillo-Escobar, M. Á., & Posadas-Castillo, C. (2023). Master–Slave Outer Synchronization in Different Inner–Outer Coupling Network Topologies. Entropy, 25(5), 707. https://doi.org/10.3390/e25050707







