Quantum Secure Multi-Party Summation Using Single Photons
Abstract
:1. Introduction
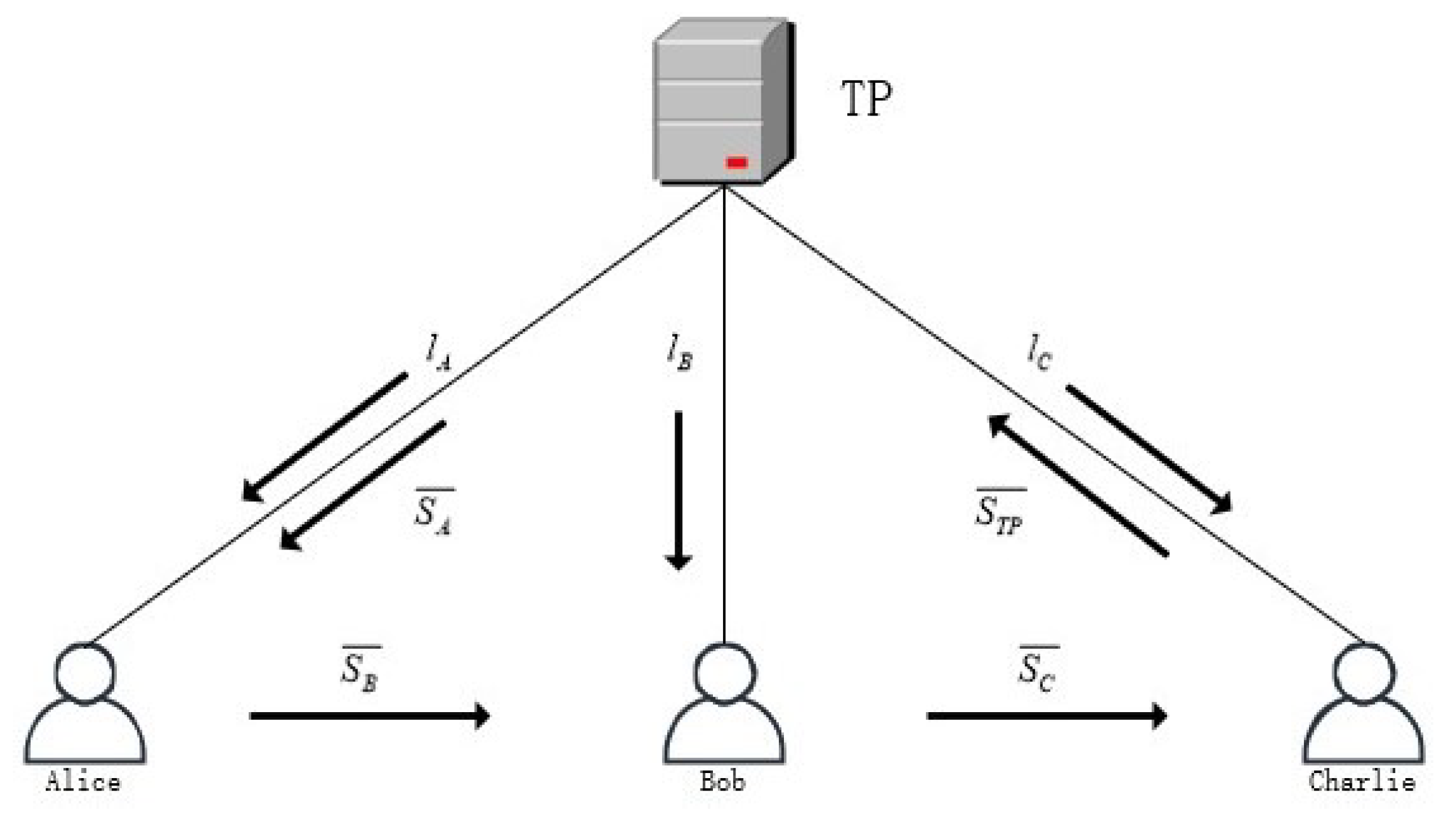
2. The Three-Party Quantum Summation Protocol
2.1. Proposed Protocol
2.2. Correctness
2.3. Security Analysis
2.3.1. Outside Attack
2.3.2. Participant Attack
3. The Multi-Party Quantum Summation Protocol
3.1. Proposed Protocol
3.2. Correctness
3.3. Security Analyse
3.3.1. Outside Attack
3.3.2. Participant Attack
- Case 1:
- The participant attack from one or more dishonest parties
- Case 2:
- The participant attack from TP
4. Comparisons
| Ref. [32] | Ref. [35] | Ref. [34] | Ref. [27] | Ref. [44] | Ref. [28] | Ref. [30] | Ref. [31] | Our Protocol | |
|---|---|---|---|---|---|---|---|---|---|
| Quantum resource | single photons in both polarization and spatial-mode degree of freedom | d-level single-photon state | d-level single-photon state | three-particle entangled state | d-level N-particle entangled state | N-particle entangled state | Bell state | phase GHZ state | single-photon state |
| Quantum operations | Single-photon operators | Unitary operations | Two unitary operations ( and ) | CNOT and Hadamard operators | Quantum Fourier transformand and Pauli operators | Pauli and Hadamard operators | NOT and identity operators | No | Pauli and Hadamard operators |
| Particle transmission mode | circle-type | circle-type | circle-type | tree-type | tree-type | tree-type | circle-type | star-type | circle-type |
| Quantum measurements for TP | Single-photon projective measurements | single qudit measurements | Single qudit measurement | No | No | Single-photon projective measurements | Single-photon projective measurements | No | Single-photon projective measurements |
| Quantum measurement for participants | No | No | No | Single-photon projective measurements | Single qudit measurements | No | Single-photon projective measurements | Computational basis measurements | No |
| Qubit efficiency |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, 3–5 November 1982; IEEE: Piscataway, NJ, USA, 1982; pp. 160–164. [Google Scholar]
- Dery, L.; Tassa, T.; Yanai, A. Fear not, vote truthfully: Secure multiparty computation of score based rules. Expert Syst. Appl. 2021, 168, 114434. [Google Scholar] [CrossRef]
- Cachin, C. Efficient private bidding and auctions with an oblivious third party. In Proceedings of the 6th ACM Conference on Computer and Communications Security, Singapore, 1–4 November 1999; pp. 120–127. [Google Scholar]
- Montenegro, J.A.; Fischer, M.J.; Lopez, J.; Peralta, R. Secure sealed-bid online auctions using discreet cryptographic proofs. Math. Comput. Model. 2013, 57, 2583–2595. [Google Scholar] [CrossRef]
- Boyle, E.; Gilboa, N.; Ishai, Y. Function secret sharing. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 337–367. [Google Scholar]
- Bogdanov, D.; Niitsoo, M.; Toft, T.; Willemson, J. High-performance secure multi-party computation for data mining applications. Int. J. Inf. Secur. 2012, 11, 403–418. [Google Scholar] [CrossRef]
- Shor, P.W. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; IEEE Computer Society Press: Santa Fe, NM, USA, 1994.
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, J.; Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 2018, 98, 042332. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.; Cao, X.-Y.; Fu, Y.; He, Z.-W.; Yin, Z.-J.; Yin, H.-L.; Chen, Z.-B. Experimental measurement-device-independent type quantum key distribution with flawed and correlated sources. Sci. Bull. 2022, 67, 2167–2175. [Google Scholar] [CrossRef]
- Xie, Y.-M.; Lu, Y.-S.; Weng, C.-X.; Cao, X.-Y.; Jia, Z.-Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.-L.; Chen, Z.-B. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Yang, J.; Man, Z.X.; Li, Y. Multiparty secret sharing of quantum information using and identifying bell states. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2005, 33, 133–136. [Google Scholar] [CrossRef]
- Hwang, T.; Hwang, C.-C.; Li, C.-M. Multiparty quantum secret sharing based on ghz states. Phys. Scr. 2011, 83, 045004. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, G. Quantum anonymous voting systems based on entangled state. Opt. Rev. 2008, 15, 219–223. [Google Scholar] [CrossRef]
- Xue, P.; Zhang, X. A simple quantum voting scheme with multi-qubit entanglement. Sci. Rep. 2017, 7, 7586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bao, N.; Halpern, N.Y. Quantum voting and violation of arrow’s impossibility theorem. Phys. Rev. A 2017, 95, 062306. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-R.; Jiang, D.-H.; Zhang, Y.-H.; Liang, X.-Q. A quantum voting protocol using single-particle states. Quantum Inf. Process. 2021, 20, 110. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Y.; Yu, C.; He, H.; Zhang, K. Quantum anonymous ranking and selection with verifiability. Quantum Inf. Process. 2020, 19, 166. [Google Scholar] [CrossRef]
- Shi, W.-M.; Liu, S.-S.; Zhou, Y.-H.; Yang, Y.-G. A secure quantum multi-party ranking protocol based on continuous variables. Optik 2021, 241, 166159. [Google Scholar] [CrossRef]
- He, G.P. Quantum private comparison protocol without a third party. Int. J. Quantum Inf. 2017, 15, 1750014. [Google Scholar] [CrossRef] [Green Version]
- Lang, Y.-F. Quantum gate-based quantum private comparison. Int. J. Theor. Phys. 2020, 59, 833–840. [Google Scholar] [CrossRef]
- Lang, Y.-F. Quantum private comparison using single bell state. Int. J. Theor. Phys. 2021, 60, 4030–4036. [Google Scholar] [CrossRef]
- Hillery, M.; Ziman, M.; Bužek, V.; Bieliková, M. Towards quantum-based privacy and voting. Phys. Lett. A 2006, 349, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.-B.; Xu, G.; Yang, Y.-X.; Wen, Q.-Y. An efficient protocol for the secure multi-party quantum summation. Int. J. Theor. Phys. 2010, 49, 2793–2804. [Google Scholar] [CrossRef]
- Shi, R.-H.; Mu, Y.; Zhong, H.; Cui, J.; Zhang, S. Secure multiparty quantum computation for summation and multiplication. Sci. Rep. 2016, 6, 19655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Situ, H.; Huang, Q.; Yang, P. Multi-party quantum summation without a trusted third party based on single particles. Int. J. Quantum Inf. 2017, 15, 1750010. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.-B.; Fan, W.-Q. An novel protocol for the quantum secure multi-party summation based on two-particle bell states. Int. J. Theor. Phys. 2017, 56, 2783–2791. [Google Scholar] [CrossRef]
- Ji, Z.; Zhang, H.; Wang, H.; Wu, F.; Jia, J.; Wu, W. Quantum protocols for secure multi-party summation. Quantum Inf. Process. 2019, 18, 168. [Google Scholar] [CrossRef]
- Wu, W.; Ma, X. Multi-party quantum summation without a third party based on d-dimensional bell states. Quantum Inf. Process. 2021, 20, 200. [Google Scholar] [CrossRef]
- Hayashi, M.; Koshiba, T. Quantum verifiable protocol for secure modulo zero-sum randomness. Quantum Inf. Process. 2022, 21, 291. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, Z.; Huang, Y.; Long, D. High-capacity quantum summation with single photons in both polarization and spatial-mode degrees of freedom. Int. J. Theor. Phys. 2014, 53, 933–941. [Google Scholar] [CrossRef]
- Gu, J.; Hwang, T.; Tsai, C.-W. Improving the security of ‘high-capacity quantum summation with single photons in both polarization and spatial-mode degrees of freedom’. Int. J. Theor. Phys. 2019, 58, 2213–2217. [Google Scholar] [CrossRef]
- Zhang, C.; Situ, H.; Huang, Q.; Sun, Z.; Huang, Z. Multi-party quantum summation with a single d-level quantum system. Int. J. Quantum Inf. 2019, 17, 1950027. [Google Scholar] [CrossRef]
- Duan, M.-Y. Multi-party quantum summation within a d-level quantum system. Int. J. Theor. Phys. 2020, 59, 1638–1643. [Google Scholar]
- Zhang, C.; Long, Y.; Li, Q. Quantum summation using d-level entanglement swapping. Quantum Inf. Process. 2021, 20, 137. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Shi, R.-H.; Liu, B.; Zhang, M. Measurement-device-independent quantum secure multiparty summation. Quantum Inf. Process. 2022, 21, 122. [Google Scholar] [CrossRef]
- Gisin, N.; Fasel, S.; Kraus, B.; Zbinden, H.; Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 2006, 73, 022320. [Google Scholar] [CrossRef] [Green Version]
- Cai, Q.-Y. Eavesdropping on the two-way quantum communication protocols with invisible photons. Phys. Lett. A 2006, 351, 23–25. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Bangalore, India, 9–12 December 1984. [Google Scholar]
- Shor, P.W.; Preskill, J. Simple proof of security of the bb84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cabello, A. Quantum key distribution in the holevo limit. Phys. Rev. Lett. 2000, 85, 5635. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Ti, Y. Secure multi-party quantum summation based on quantum fourier transform. Quantum Inf. Process. 2018, 17, 129. [Google Scholar]
- Kou, T.-Y.; Che, B.-C.; Dou, Z.; Chen, X.-B.; Lai, Y.-P.; Li, J. Efficient quantum private comparison protocol utilizing single photons and rotational encryption. Chin. Phys. B 2022, 31, 060307. [Google Scholar] [CrossRef]
| = (0, 1, 0) | = (0, 1, 0) | = (0, 1, 1) |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.-Q.; Xie, M.-Z. Quantum Secure Multi-Party Summation Using Single Photons. Entropy 2023, 25, 590. https://doi.org/10.3390/e25040590
Wu W-Q, Xie M-Z. Quantum Secure Multi-Party Summation Using Single Photons. Entropy. 2023; 25(4):590. https://doi.org/10.3390/e25040590
Chicago/Turabian StyleWu, Wan-Qing, and Ming-Zhe Xie. 2023. "Quantum Secure Multi-Party Summation Using Single Photons" Entropy 25, no. 4: 590. https://doi.org/10.3390/e25040590
APA StyleWu, W.-Q., & Xie, M.-Z. (2023). Quantum Secure Multi-Party Summation Using Single Photons. Entropy, 25(4), 590. https://doi.org/10.3390/e25040590





