Closed Formula for Transport across Constrictions
Abstract
1. Introduction
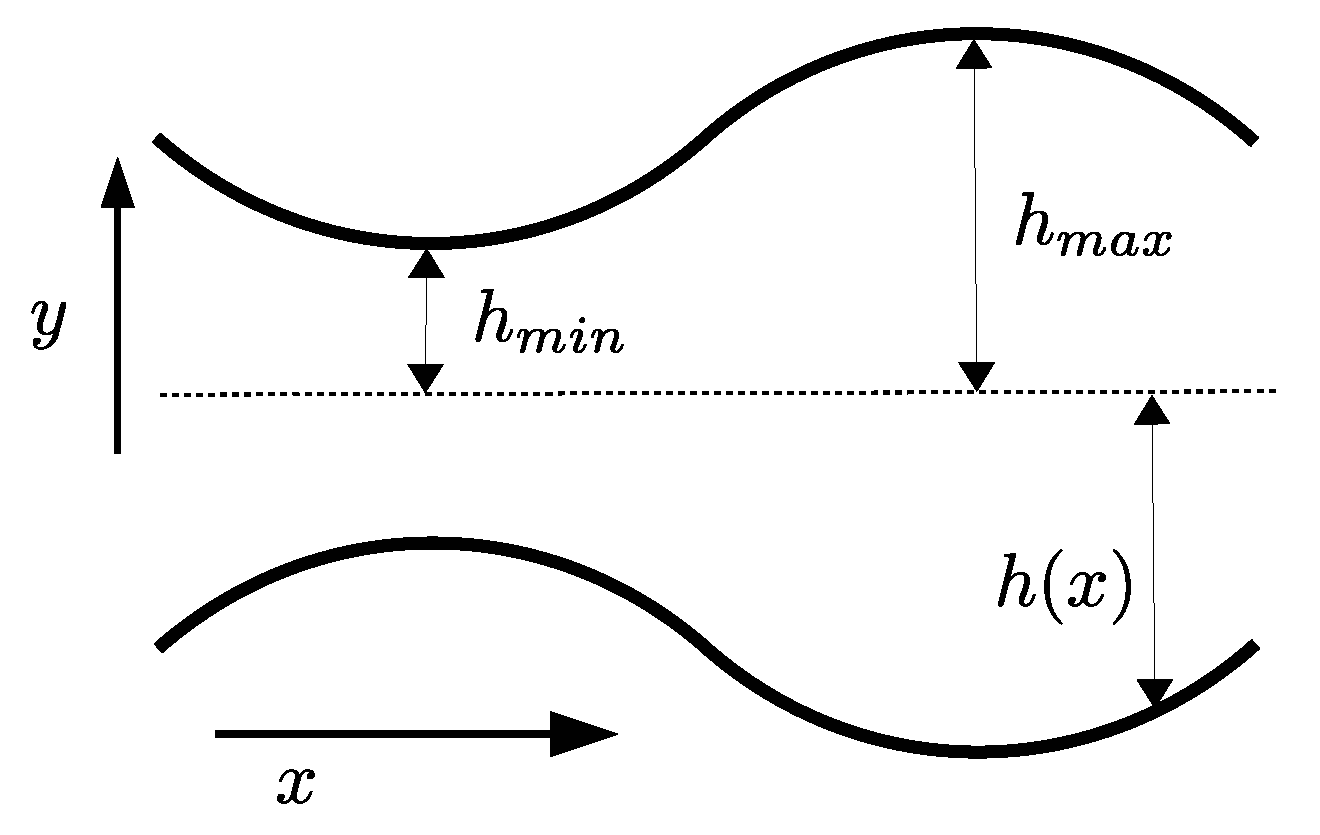
2. Model
2.1. Transport across Free Energy Barriers
2.2. Piecewise Linear Potential and Homogeneous Diffusion Coefficient
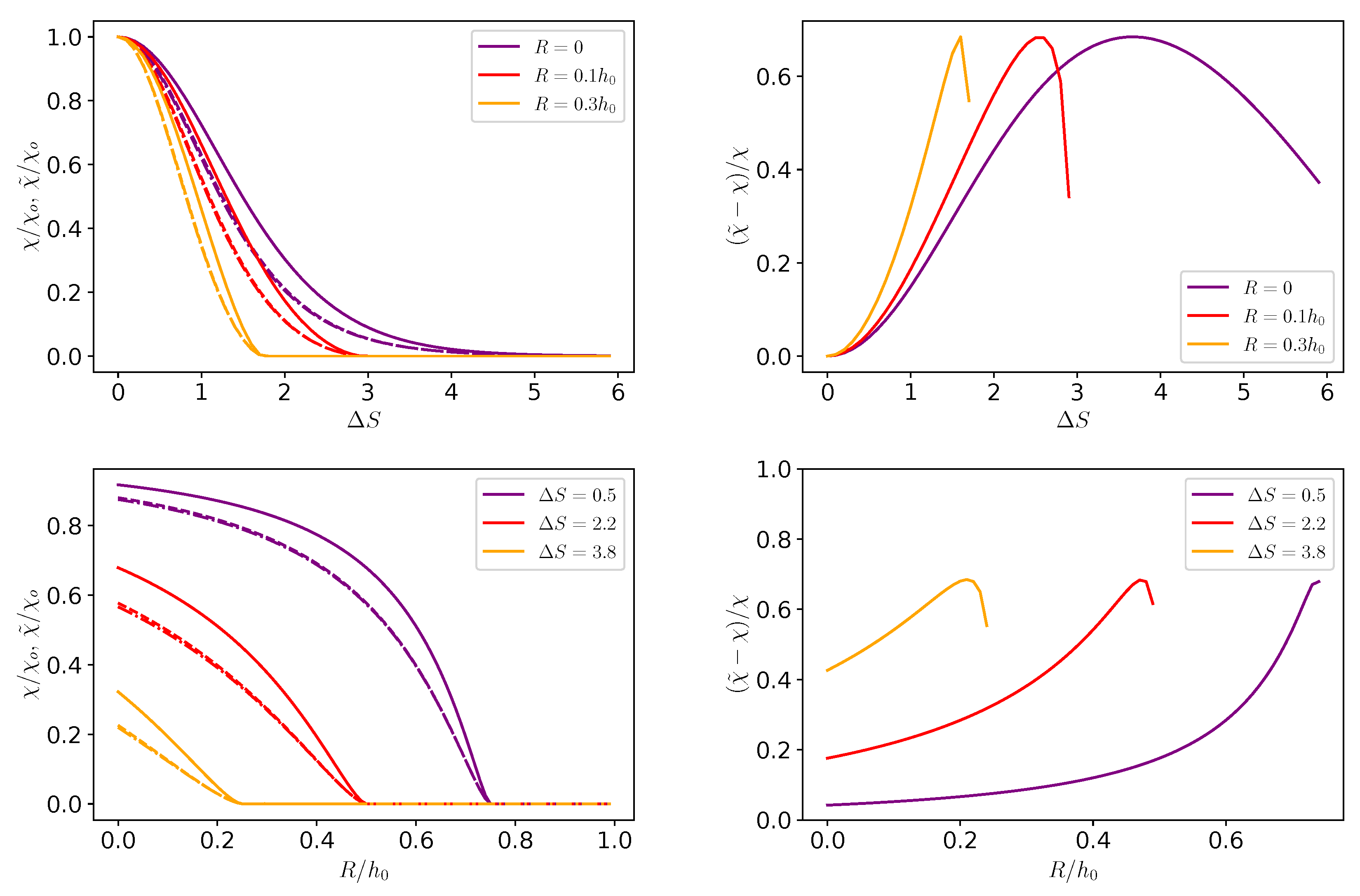
3. Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar] [CrossRef]
- Wang, C.; Quddus, M.A.; Ison, S.G. The effect of traffic and road characteristics on road safety: A review and future research direction. Saf. Sci. 2013, 57, 264–275. [Google Scholar] [CrossRef]
- Vermuyten, H.; Belian, J.; De Boeck, L.; Reniers, G.; Wauters, T. A review of optimisation models for pedestrian evacuation and design problems. Saf. Sci. 2016, 87, 167–178. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Jun, S.C.; Cheon, J.Y.; Park, M. A review on clogging mechanisms and managements in aquifer storage and recovery (ASR) applications. Geosci. J. 2018, 22, 667–679. [Google Scholar] [CrossRef]
- Jäger, R.; Mendoza, M.; Herrmann, H.J. Clogging at pore scale and pressure-induced erosion. Phys. Rev. Fluids 2018, 3, 074302. [Google Scholar] [CrossRef]
- Marin, A.; Lhuissier, H.; Rossi, M.; Kähler, C.J. Clogging in constricted suspension flows. Phys. Rev. E 2018, 97, 021102. [Google Scholar] [CrossRef]
- Kusters, R.; van der Heijden, T.; Kaoui, B.; Harting, J.; Storm, C. Forced transport of deformable containers through narrow constrictions. Phys. Rev. E 2014, 90, 033006. [Google Scholar] [CrossRef]
- Bielinski, C.; Aouane, O.; Harting, J.; Kaoui, B. Squeezing multiple soft particles into a constriction: Transition to clogging. Phys. Rev. E 2021, 104, 065101. [Google Scholar] [CrossRef]
- Garcimartín, A.; Pastor, J.M.; Ferrer, L.M.; Ramos, J.J.; Martín-Gómez, C.; Zuriguel, I. Flow and clogging of a sheep herd passing through a bottleneck. Phys. Rev. E 2015, 91, 022808. [Google Scholar] [CrossRef]
- Altshuler, E.; Ramos, O.; Nuñez, Y.; Fernandez, J.; Batista-Leyva, A.; Noda, C. Symmetry Breaking in Escaping Ants. Am. Nat. 2005, 166, 643–649. [Google Scholar] [CrossRef]
- Zuriguel, I.; Echevería, I.; Maza, D.; anésar Martín-Gómez, R.C.H.; Garcimarín, A. Contact forces and dynamics of pedestrians evacuating a room: The column effect. Saf. Sci. 2020, 121, 394–402. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef]
- Dressaire, E.; Sauret, A. Clogging of microfluidic systems. Soft Matter 2017, 13, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Douféne, K.; Tourné-Péteilh, C.; Etienne, P.; Aubert-Pouëssel, A. Microfluidic Systems for Droplet Generation in Aqueous Continuous Phases: A Focus Review. Langmuir 2019, 35, 12597–12612. [Google Scholar] [CrossRef]
- Convery, N.; Gadegaard, N. 30 years of microfluidics. Micro Nano Eng. 2019, 2, 76–91. [Google Scholar] [CrossRef]
- Weatherall, E.; Willmott, G.R. Applications of tunable resistive pulse sensing. Analyst 2015, 140, 3318–3334. [Google Scholar] [CrossRef]
- Saleh, O.A.; Sohn, L.L. Direct detection of antibody–antigen binding using an on-chip artificial pore. Proc. Natl. Acad. Sci. USA 2003, 100, 820–824. [Google Scholar] [CrossRef]
- Ito, T.; Sun, L.; Bevan, M.A.; Crooks, R.M. Comparison of Nanoparticle Size and Electrophoretic Mobility Measurements Using a Carbon-Nanotube-Based Coulter Counter, Dynamic Light Scattering, Transmission Electron Microscopy, and Phase Analysis Light Scattering. Langmuir 2004, 20, 6940–6945. [Google Scholar] [CrossRef]
- Heins, E.A.; Siwy, Z.S.; Baker, L.A.; Martin, R.C. Detecting Single Porphyrin Molecules in a Conically Shaped Synthetic Nanopore. Nano Lett. 2005, 5, 1824–1829. [Google Scholar] [CrossRef]
- Arjm, I.N.; Van Roy, W.; Lagae, L.; Borghs, G. Measuring the Electric Charge and Zeta Potential of Nanometer-Sized Objects Using Pyramidal-Shaped Nanopores. Anal. Chem. 2012, 84, 8490–8496. [Google Scholar] [CrossRef]
- Robards, K.; Ryan, D. Principles and Practice of Modern Chromatographic Methods; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Reithinger, M.; Arlt, W. Prediction of the Partitioning Coefficient in Liquid-Solid Chromatography using COSMO-RS. Chem. Ing. Tech. 2011, 83, 83–89. [Google Scholar] [CrossRef]
- Michaud, V.; Pracht, J.; Schilfarth, F.; Damm, C.; Platzer, B.; Haines, P.; Harreiß, C.; Guldi, D.M.; Spiecker, E.; Peukert, W. Well-separated water-soluble carbon dots via gradient chromatography. Nanoscale 2021, 13, 13116–13128. [Google Scholar] [CrossRef]
- Seidel-Morgenstern, A.; Keßler, L.C.; Kaspereit, M. New Developments in Simulated Moving Bed Chromatography. Chem. Eng. Technol. 2008, 31, 826–837. [Google Scholar] [CrossRef]
- Soni, G.V.; Singer, A.; Yu, Z.; Sun, Y.; McNally, B.; Meller, A. Synchronous optical and electrical detection of biomolecules traversing through solid-state nanopores. Rev. Sci. Instrum. 2010, 81, 014301. [Google Scholar] [CrossRef]
- Carvalho, M.S. Flow of Complex Fluids through Porous Media: Application in Oil Recovery. In Proceedings of the Offshore Technology Conference, Rio de Janeiro, Brazil, 27–29 October 2015; p. 6. [Google Scholar] [CrossRef]
- Foroozesh, J.; Kumar, S. Nanoparticles behaviors in porous media: Application to enhanced oil recovery. J. Mol. Liq. 2020, 316, 113876. [Google Scholar] [CrossRef]
- Farhadian, H.; Nikvar-Hassani, A. Water flow into tunnels in discontinuous rock: A short critical review of the analytical solution of the art. Bull. Eng. Geol. Environ. 2019, 78, 3833–3849. [Google Scholar] [CrossRef]
- Boon, N.; Roij, R.V. Blue energy: From ion adsorption and electrode charging in sea and river water. Mol. Phys. 2011, 109, 1229–1241. [Google Scholar] [CrossRef]
- Preuster, P.; Papp, C.; Wasserscheid, P. Liquid organic hydrogen carriers (LOHCs): Toward a hydrogen-free hydrogen economy. Acc. Chem. Res. 2017, 50, 74–85. [Google Scholar] [CrossRef] [PubMed]
- Solymosi, T.; Geißelbrecht, M.; Mayer, S.; Auer, M.; Leicht, P.; Terlinden, M.; Malgaretti, P.; Bösmann, A.; Preuster, P.; Harting, J.; et al. Nucleation as a rate-determining step in catalytic gas generation reactions from liquid phase systems. Sci. Adv. 2022, 8, eade3262. [Google Scholar] [CrossRef]
- Suter, T.A.M.; Smith, K.; Hack, J.; Rasha, L.; Rana, Z.; Angel, G.M.A.; Shearing, P.R.; Miller, T.S.; Brett, D.J.L. Engineering Catalyst Layers for Next-Generation Polymer Electrolyte Fuel Cells: A Review of Design, Materials, and Methods. Adv. Energy Mater. 2021, 11, 2101025. [Google Scholar] [CrossRef]
- Du, N.; Roy, C.; Peach, R.; Turnbull, M.; Thiele, S.; Bock, C. Anion-Exchange Membrane Water Electrolyzers. Chem. Rev. 2022, 122, 11830–11895. [Google Scholar] [CrossRef] [PubMed]
- Hepburn, C.; Adlen, E.; Beddington, J.; Carter, E.A.; Fuss, S.; Mac Dowell, N.; Minx, J.C.; Smith, P.; Williams, C.K. The technological and economic prospects for CO2 utilization and removal. Nature 2019, 575, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell; Garland Science: Oxford, UK, 2007. [Google Scholar]
- Pethig, R. Ion, Electron, and Proton Transport in Membranes: A Review of the Physical Processes Involved. In Modern Bioelectrochemistry; Gutmann, F., Keyzer, H., Eds.; Springer: Boston, MA, USA, 1986; pp. 199–239. [Google Scholar] [CrossRef]
- Dubyak, G.R. Ion homeostasis, channels, and transporters: An update on cellular mechanisms. Adv. Physiol. Educ. 2004, 28, 143–154. [Google Scholar] [CrossRef] [PubMed]
- Calero, C.; Faraudo, J.; Aguilella-Arzo, M. First-passage-time analysis of atomic-resolution simulations of the ionic transport in a bacterial porin. Phys. Rev. E 2011, 83, 021908. [Google Scholar] [CrossRef]
- Peyser, A.; Gillespie, D.; Roth, R.; Nonner, W. Domain and Interdomain Energetics Underlying Gating in Shaker-Type KV Channels. Biophys. J. 2014, 107, 1841–1852. [Google Scholar] [CrossRef]
- Lee, H.; Segets, D.; Süß, S.; Peukert, W.; Chen, S.C.; Pui, D.Y. Liquid filtration of nanoparticles through track-etched membrane filters under unfavorable and different ionic strength conditions: Experiments and modeling. J. Membr. Sci. 2017, 524, 682–690. [Google Scholar] [CrossRef]
- Melnikov, D.V.; Hulings, Z.K.; Gracheva, M.E. Electro-osmotic flow through nanopores in thin and ultrathin membranes. Phys. Rev. E 2017, 95, 063105. [Google Scholar] [CrossRef]
- Bacchin, P. Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities. Membranes 2018, 8, 10. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Dagdug, L.; Bezrukov, S.M. Two-site versus continuum diffusion model of blocker dynamics in a membrane channel: Comparative analysis of escape kinetics. J. Chem. Phys. 2019, 151, 054113. [Google Scholar] [CrossRef]
- Nipper, M.; Dixon, J. Engineering the Lymphatic System. Cardiovasc. Eng. Technol. 2011, 2, 296–308. [Google Scholar] [CrossRef]
- Wiig, H.; Swartz, M. Interstitial fluid and lymph formation and transport: Physiological regulation and roles in inflammation and cancer. Physiol. Rev. 2012, 92, 1005–1060. [Google Scholar] [CrossRef]
- Yoganathan, A.P.; Cape, E.G.; Sung, H.W.; Williams, F.P.; Jimoh, A. Review of hydrodynamic principles for the cardiologist: Applications to the study of blood flow and jets by imaging techniques. J. Am. Coll. Cardiol. 1988, 12, 1344–1353. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.H.; Berg-Sørensen, K.; Bruus, H.; Holbrook, N.M.; Liesche, J.; Schulz, A.; Zwieniecki, M.A.; Bohr, T. Sap flow and sugar transport in plants. Rev. Mod. Phys. 2016, 88, 035007. [Google Scholar] [CrossRef]
- Shimmen, T.; Yokota, E. Cytoplasmic streaming in plants. Curr. Opin. Cell Biol. 2004, 16, 68–72. [Google Scholar] [CrossRef]
- Zwanzig, R. Diffusion past an entropy barrier. J. Phys. Chem. 1992, 96, 3926–3930. [Google Scholar] [CrossRef]
- Reguera, D.; Rubi, J.M. Kinetic equations for diffusion in the presence of entropic barriers. Phys. Rev. E 2001, 64, 061106. [Google Scholar] [CrossRef]
- Kalinay, P.; Percus, J.K.P. Projection of two-dimensional diffusion in a narrow channel onto the longitudinal dimension. J. Chem. Phys. 2005, 122, 204701. [Google Scholar] [CrossRef]
- Kalinay, P.; Percus, J.K. Extended Fick-Jacobs equation: Variational approach. Phys. Rev. E 2005, 72, 061203. [Google Scholar] [CrossRef] [PubMed]
- Kalinay, P.; Percus, J.K. Approximations of the generalized Fick-Jacobs equation. Phys. Rev. E 2008, 78, 021103. [Google Scholar] [CrossRef]
- Martens, S.; Schmid, G.; Schimansky-Geier, L.; Hänggi, P. Entropic particle transport: Higher-order corrections to the Fick-Jacobs diffusion equation. Phys. Rev. E 2011, 83, 051135. [Google Scholar] [CrossRef]
- Chacón-Acosta, G.; Pineda, I.; Dagdug, L. Diffusion in narrow channels on curved manifolds. J. Chem. Phys. 2013, 139, 214115. [Google Scholar] [CrossRef] [PubMed]
- Malgaretti, P.; Pagonabarraga, I.; Rubi, J. Entropic transport in confined media: A challenge for computational studies in biological and soft-matter systems. Front. Phys. 2013, 1, 21. [Google Scholar] [CrossRef]
- Malgaretti, P.; Pagonabarraga, I.; Rubi, J.M. Entropic electrokinetics. Phys. Rev. Lett. 2014, 113, 128301. [Google Scholar] [CrossRef] [PubMed]
- Malgaretti, P.; Pagonabarraga, I.; Rubi, J.M. Geometrically Tuned Channel Permeability. Macromol. Symp. 2015, 357, 178–188. [Google Scholar] [CrossRef]
- Malgaretti, P.; Pagonabarraga, I.; Miguel Rubi, J. Entropically induced asymmetric passage times of charged tracers across corrugated channels. J. Chem. Phys. 2016, 144, 034901. [Google Scholar] [CrossRef]
- Chinappi, M.; Malgaretti, P. Charge polarization, local electroneutrality breakdown and eddy formation due to electroosmosis in varying-section channels. Soft Matter 2018, 14, 9083–9087. [Google Scholar] [CrossRef] [PubMed]
- Malgaretti, P.; Janssen, M.; Pagonabarraga, I.; Rubi, J.M. Driving an electrolyte through a corrugated nanopore. J. Chem. Phys. 2019, 151, 084902. [Google Scholar] [CrossRef] [PubMed]
- Reguera, D.; Schmid, G.; Burada, P.S.; Rubi, J.M.; Reimann, P.; Hänggi, P. Entropic Transport: Kinetics, Scaling, and Control Mechanisms. Phys. Rev. Lett. 2006, 96, 130603. [Google Scholar] [CrossRef]
- Reguera, D.; Luque, A.; Burada, P.S.; Schmid, G.; Rubi, J.M.; Hänggi, P. Entropic Splitter for Particle Separation. Phys. Rev. Lett. 2012, 108, 020604. [Google Scholar] [CrossRef] [PubMed]
- Marini Bettolo Marconi, U.; Malgaretti, P.; Pagonabarraga, I. Tracer diffusion of hard-sphere binary mixtures under nano-confinement. J. Chem. Phys. 2015, 143, 184501. [Google Scholar] [CrossRef] [PubMed]
- Malgaretti, P.; Pagonabarraga, I.; Rubi, J. Rectification and non-Gaussian diffusion in heterogeneous media. Entropy 2016, 18, 394. [Google Scholar] [CrossRef]
- Puertas, A.; Malgaretti, P.; Pagonabarraga, I. Active microrheology in corrugated channels. J. Chem. Phys. 2018, 149, 174908. [Google Scholar] [CrossRef]
- Malgaretti, P.; Harting, J. Transport of neutral and charged nanorods across varying-section channels. Soft Matter 2021, 17, 2062–2070. [Google Scholar] [CrossRef]
- Bianco, V.; Malgaretti, P. Non-monotonous polymer translocation time across corrugated channels: Comparison between Fick-Jacobs approximation and numerical simulations. J. Chem. Phys. 2016, 145, 114904. [Google Scholar] [CrossRef]
- Malgaretti, P.; Oshanin, G. Polymer Translocation Across a Corrugated Channel: Ficks-Jacobs Approximation Extended Beyond the Mean First-Passage Time. Polymers 2019, 11, 251. [Google Scholar] [CrossRef] [PubMed]
- Bodrenko, I.V.; Salis, S.; Acosta-Gutierrez, S.; Ceccarelli, M. Diffusion of large particles through small pores: From entropic to enthalpic transport. J. Chem. Phys. 2019, 150, 211102. [Google Scholar] [CrossRef] [PubMed]
- Ledesma-Durán, A.; Hernández-Hernández, S.I.; Santamaría-Holek, I. Generalized Fick–Jacobs Approach for Describing Adsorption–Desorption Kinetics in Irregular Pores under Nonequilibrium Conditions. J. Phys. Chem. C 2016, 120, 7810–7821. [Google Scholar] [CrossRef]
- Chacón-Acosta, G.; Núñez-López, M.; Pineda, I. Turing instability conditions in confined systems with an effective position-dependent diffusion coefficient. J. Chem. Phys. 2020, 152, 024101. [Google Scholar] [CrossRef]
- Burada, P.S.; Schmid, G.; Reguera, D.; Rubi, J.M.; Hänggi, P. Biased diffusion in confined media: Test of the Fick-Jacobs approximation and validity criteria. Phys. Rev. E 2007, 75, 051111. [Google Scholar] [CrossRef]
- Malgaretti, P.; Puertas, A.M.; Pagonabarraga, I. Active microrheology in corrugated channels: Comparison of thermal and colloidal baths. J. Colloid Interface Sci. 2022, 608, 2694–2702. [Google Scholar] [CrossRef]
- Yang, X.; Liu, C.; Li, Y.; Marchesoni, F.; Hänggi, P.; Zhang, H.P. Hydrodynamic and entropic effects on colloidal diffusion in corrugated channels. Proc. Natl. Acad. Sci. USA 2017, 114, 9564–9569. [Google Scholar] [CrossRef] [PubMed]
- Malgaretti, P.; Stark, H. Model microswimmers in channels with varying cross section. J. Chem. Phys. 2017, 146, 174901. [Google Scholar] [CrossRef] [PubMed]
- Sandoval, M.; Dagdug, L. Effective diffusion of confined active Brownian swimmers. Phys. Rev. E 2014, 90, 062711. [Google Scholar] [CrossRef]
- Kalinay, P. Transverse dichotomic ratchet in a two-dimensional corrugated channel. Phys. Rev. E 2022, 106, 044126. [Google Scholar] [CrossRef]
- Antunes, G.C.; Malgaretti, P.; Harting, J.; Dietrich, S. Pumping and Mixing in Active Pores. Phys. Rev. Lett. 2022, 129, 188003. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Pustovoit, M.A.; Bezrukov, S.M. Diffusion in a tube of varying cross section: Numerical study of reduction to effective one-dimensional description. J. Chem. Phys. 2007, 126, 134706. [Google Scholar] [CrossRef] [PubMed]
- Berezhkovskii, A.M.; Dagdug, L.; Bezrukov, S.M. Range of applicability of modified Fick-Jacobs equation in two dimensions. J. Chem. Phys. 2015, 143, 164102. [Google Scholar] [CrossRef]
- Kalinay, P.; Percus, J.K. Corrections to the Fick-Jacobs equation. Phys. Rev. E 2006, 74, 041203. [Google Scholar] [CrossRef] [PubMed]
- Pineda, I.; Alvarez-Ramirez, J.; Dagdug, L. Diffusion in two-dimensional conical varying width channels: Comparison of analytical and numerical results. J. Chem. Phys. 2012, 137, 174103. [Google Scholar] [CrossRef]
- García-Chung, A.A.; Chacón-Acosta, G.; Dagdug, L. On the covariant description of diffusion in two-dimensional confined environments. J. Chem. Phys. 2015, 142, 064105. [Google Scholar] [CrossRef]
- Lifson, S.; Jackson, J.L. On the Self-Diffusion of Ions in a Polyelectrolyte Solution. J. Chem. Phys. 1962, 36, 2410–2414. [Google Scholar] [CrossRef]
- Reimann, P.; Van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.M.; Pérez-Madrid, A. Giant Acceleration of Free Diffusion by Use of Tilted Periodic Potentials. Phys. Rev. Lett. 2001, 87, 010602. [Google Scholar] [CrossRef] [PubMed]
- Berezhkovskii, A.M.; Bezrukov, S.M. Intrinsic diffusion resistance of a membrane channel, mean first-passage times between its ends, and equilibrium unidirectional fluxes. J. Chem. Phys. 2022, 156, 071103. [Google Scholar] [CrossRef] [PubMed]
- Carusela, M.F.; Malgaretti, P.; Rubi, J.M. Antiresonant driven systems for particle manipulation. Phys. Rev. E 2021, 103, 062102. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malgaretti, P.; Harting, J. Closed Formula for Transport across Constrictions. Entropy 2023, 25, 470. https://doi.org/10.3390/e25030470
Malgaretti P, Harting J. Closed Formula for Transport across Constrictions. Entropy. 2023; 25(3):470. https://doi.org/10.3390/e25030470
Chicago/Turabian StyleMalgaretti, Paolo, and Jens Harting. 2023. "Closed Formula for Transport across Constrictions" Entropy 25, no. 3: 470. https://doi.org/10.3390/e25030470
APA StyleMalgaretti, P., & Harting, J. (2023). Closed Formula for Transport across Constrictions. Entropy, 25(3), 470. https://doi.org/10.3390/e25030470






