A Robust Hierarchical Estimation Scheme for Vehicle State Based on Maximum Correntropy Square-Root Cubature Kalman Filter
Abstract
1. Introduction
- (1)
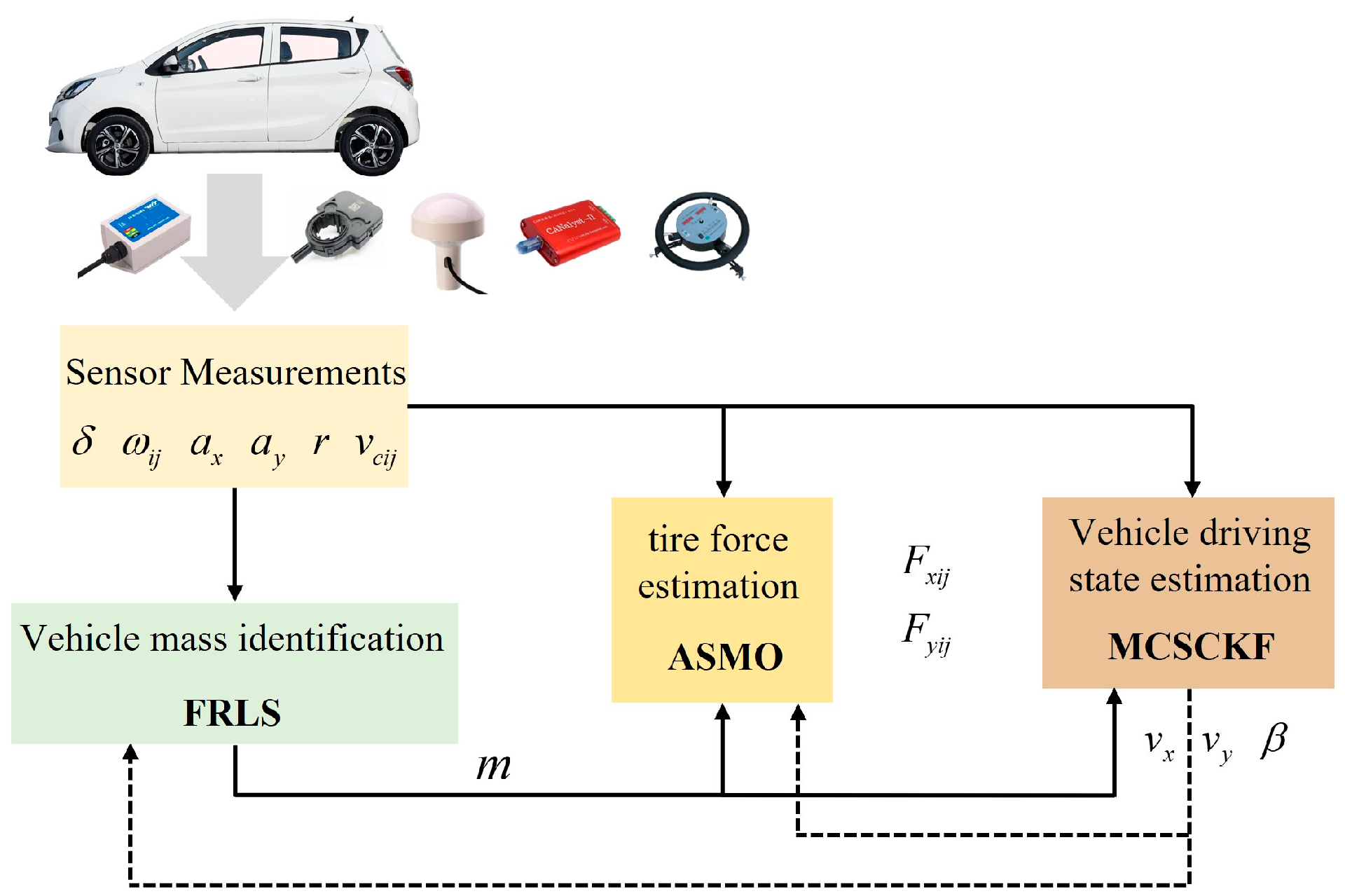
- The vehicle mass is first updated in real-time, and then the longitudinal and lateral tire forces for each wheel are estimated separately based on the ASMO methodology. Based on common on-board sensors, a robust hierarchical estimation scheme is designed for vehicle states based on MCSCKF under non-Gaussian noise using the obtained mass and tire force information.
- (2)
- To verify the effectiveness of the proposed method, two typical test scenarios are performed. The results demonstrate that the proposed robust hierarchical estimation scheme can accurately estimate the vehicle mass, tire force, and vehicle driving state. Moreover, the MCSCKF has better accuracy and robustness for vehicle state estimation in non-Gaussian situations compared to the conventional Kalman filter.
2. Vehicle Model
- The vertical motion of the vehicle along the Z-axis is constant, and the effect of the suspension is ignored.
- The vehicle dynamics model ignores the influence of the steering system, and the front-wheel angle is directly used as the model input.
- During the operation of the vehicle, the roll motion of the X-axis and the pitch motion of the Y-axis are ignored.
- Ignoring air and wind resistance, the vehicle is mainly subjected to tire-road forces.
2.1. Vehicle Mass Estimation Model
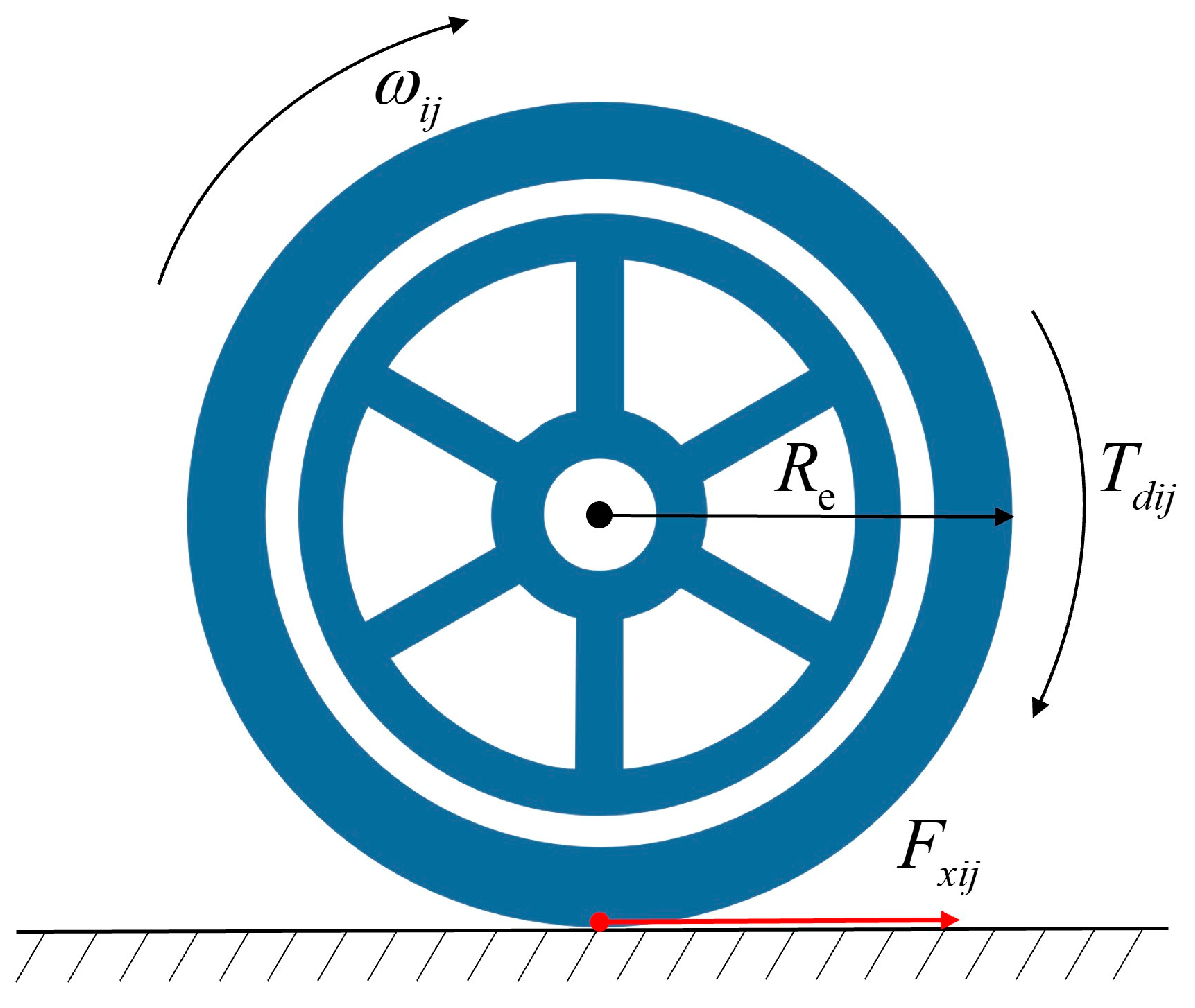
2.2. Tire Force Estimation Model
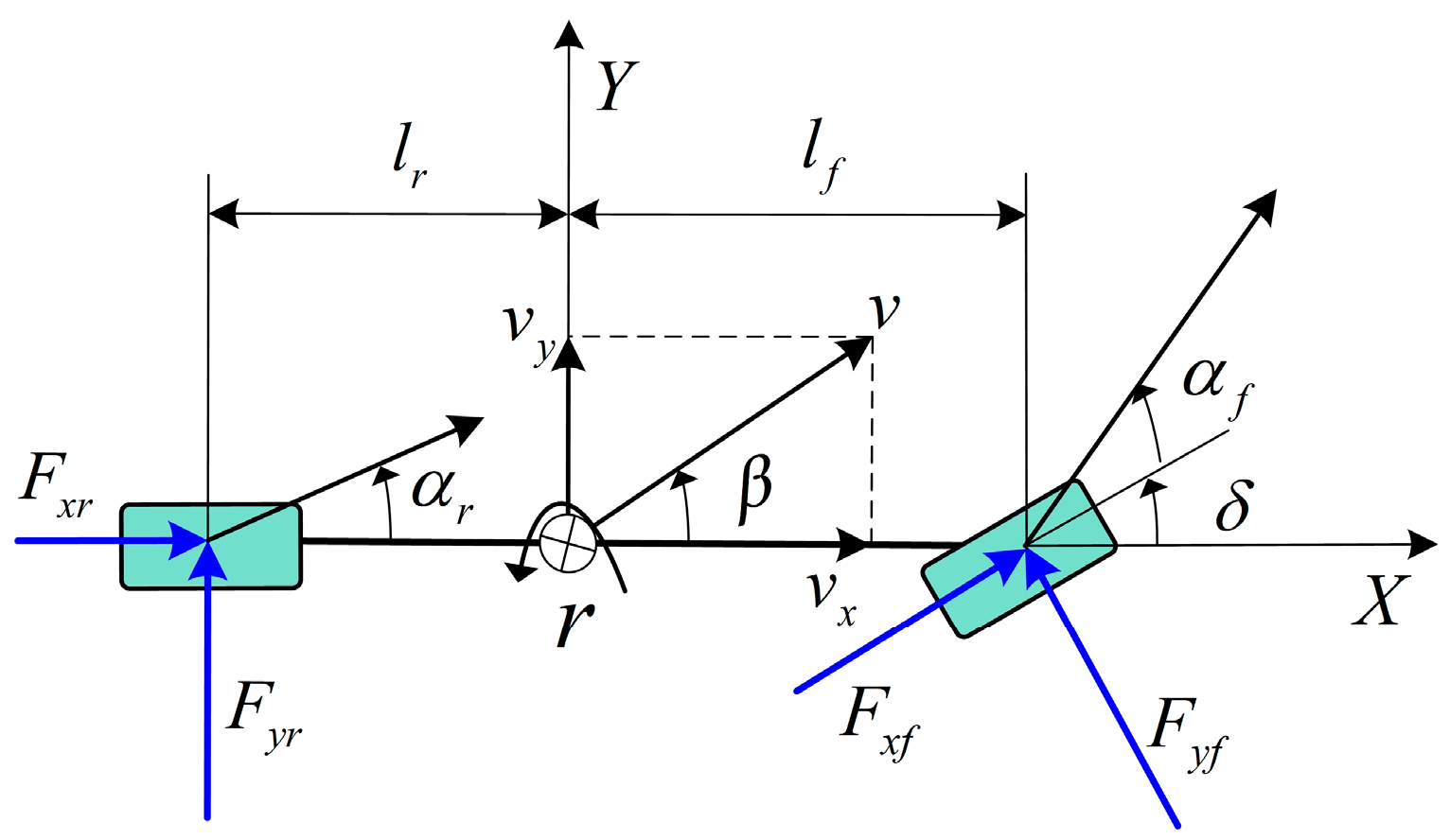
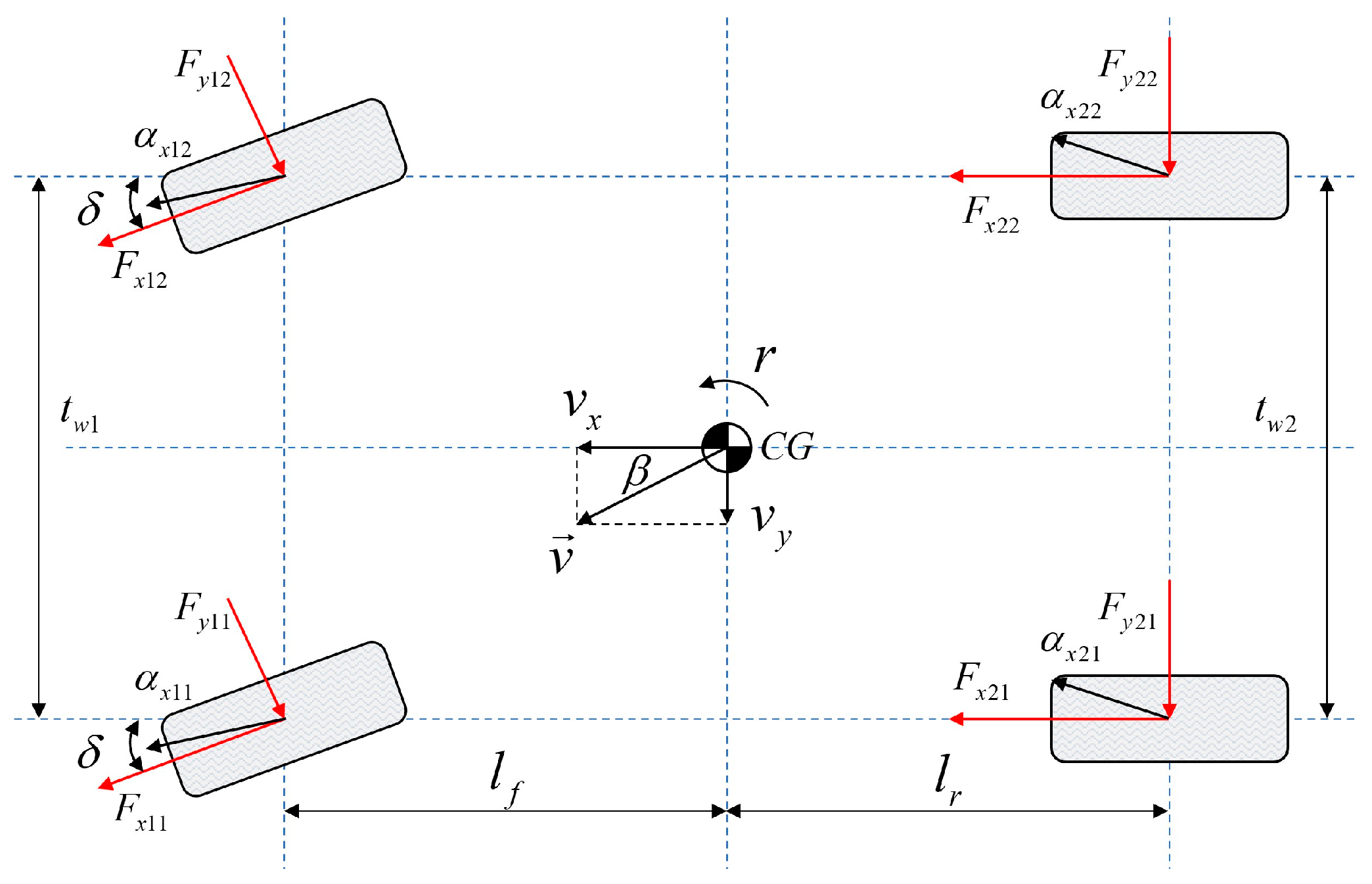
2.3. Nonlinear Three-Degree-of-Freedom Dynamics Model
2.4. Tire Vertical Force Calculation
3. Robust Hierarchical Estimation Scheme
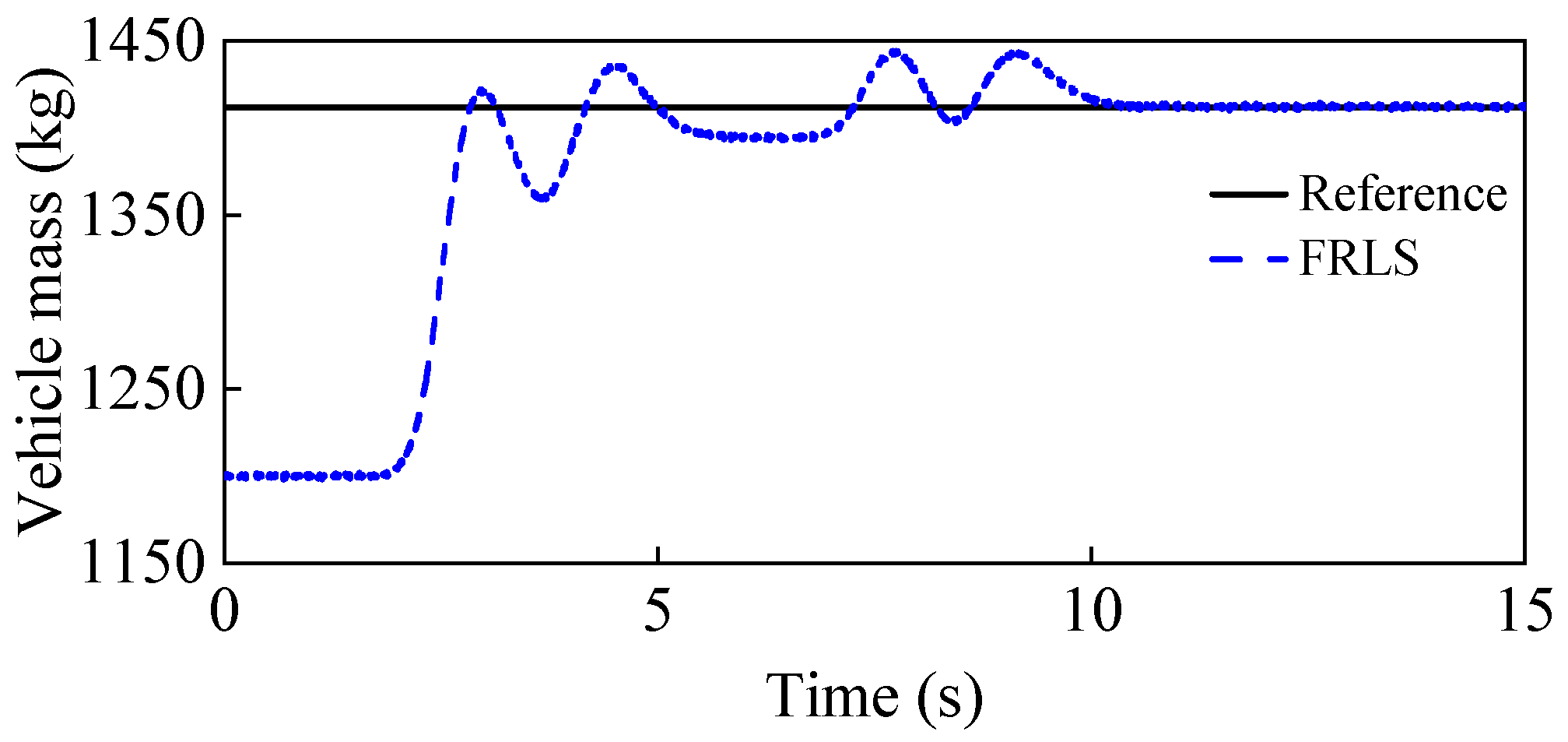
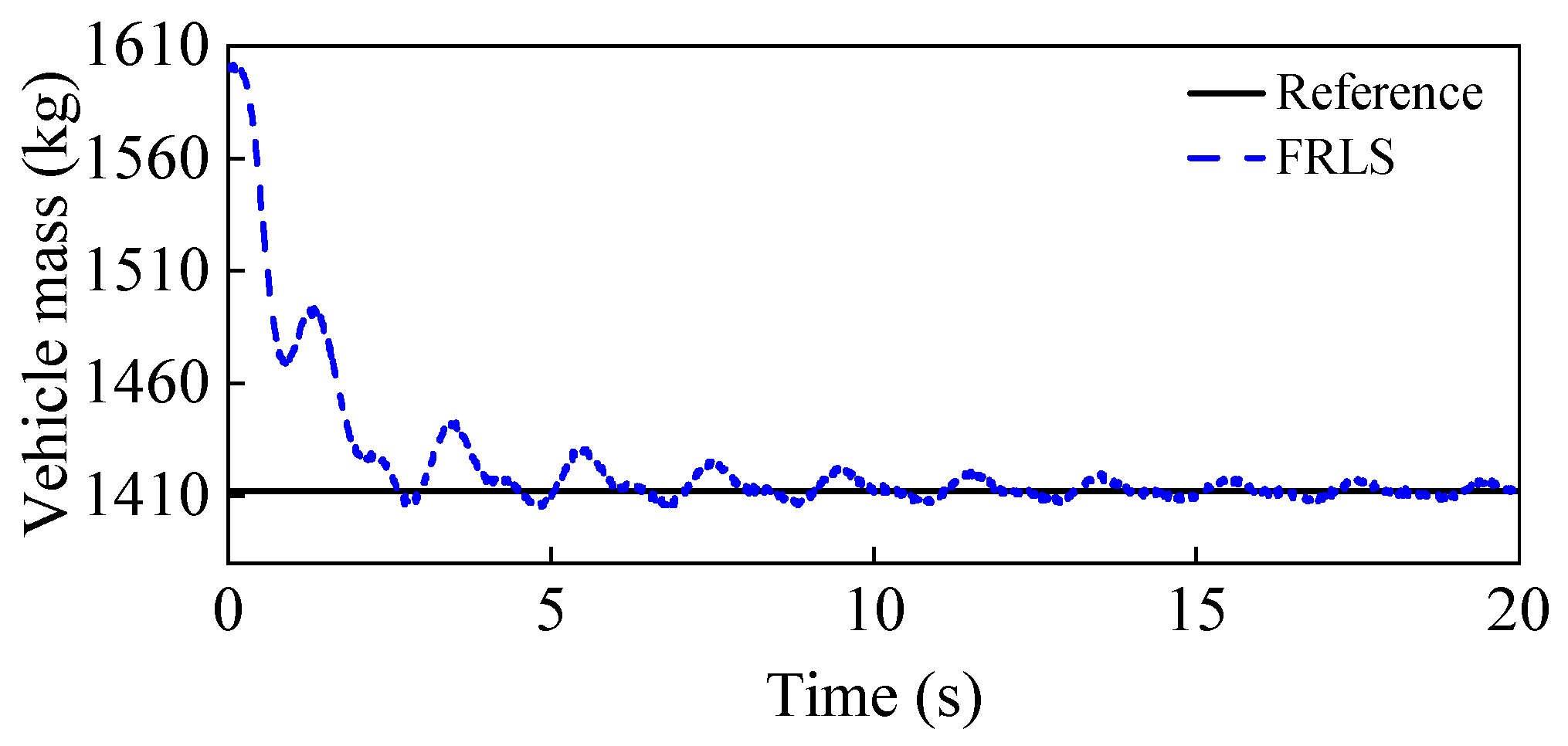
3.1. Vehicle Mass Identification
3.2. Tire Force Estimation
3.2.1. Sliding Mode Observer Design
3.2.2. Longitudinal Tire Force Estimation
3.2.3. Lateral Tire Force Estimation
3.3. Vehicle State Estimation Based on MCSCKF
3.3.1. Design of the State Estimator
3.3.2. Maximum Correntropy Square-Root Cubature Kalman Filter
- (1)
- Maximum correntropy criterion
- (2)
- Square-root cubature Kalman filter
- Predict
- 2.
- Update
- 3.
- Derivation of the MCSCKF
| Algorithm 1: MCSCKF |
| 1 Input |
| σ, a positive number |
| 2 Initialization |
| k = 1 |
| 3 Time Update |
| for i = 1, …, 2n end |
| 4 Measurement Update |
| for i = 1, …, 2n end 4.1 Initialization: t = 4.2 Iteration: then go to step 5. else t = t + 1, go to step 4.2 end 5 k = k + 1, go to step 3. |
4. Simulation Verification
4.1. Simulation Experimental Platform
4.2. Results and Discussion
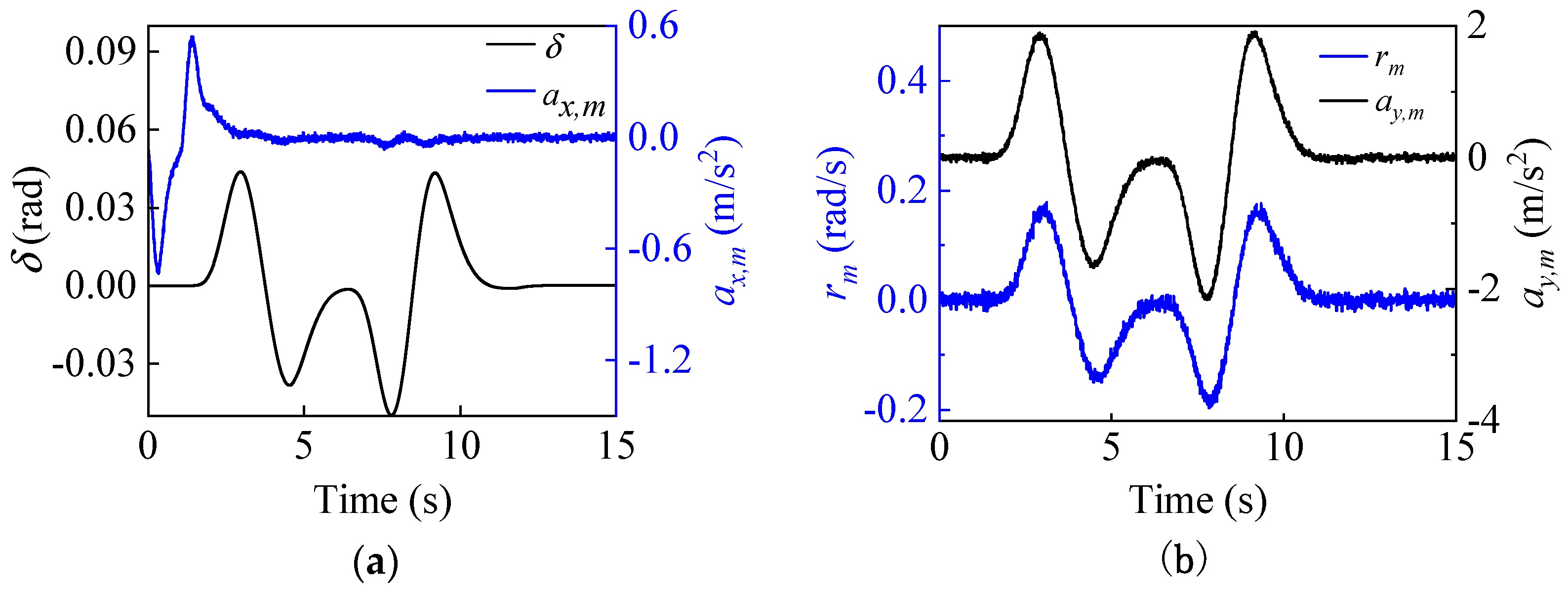
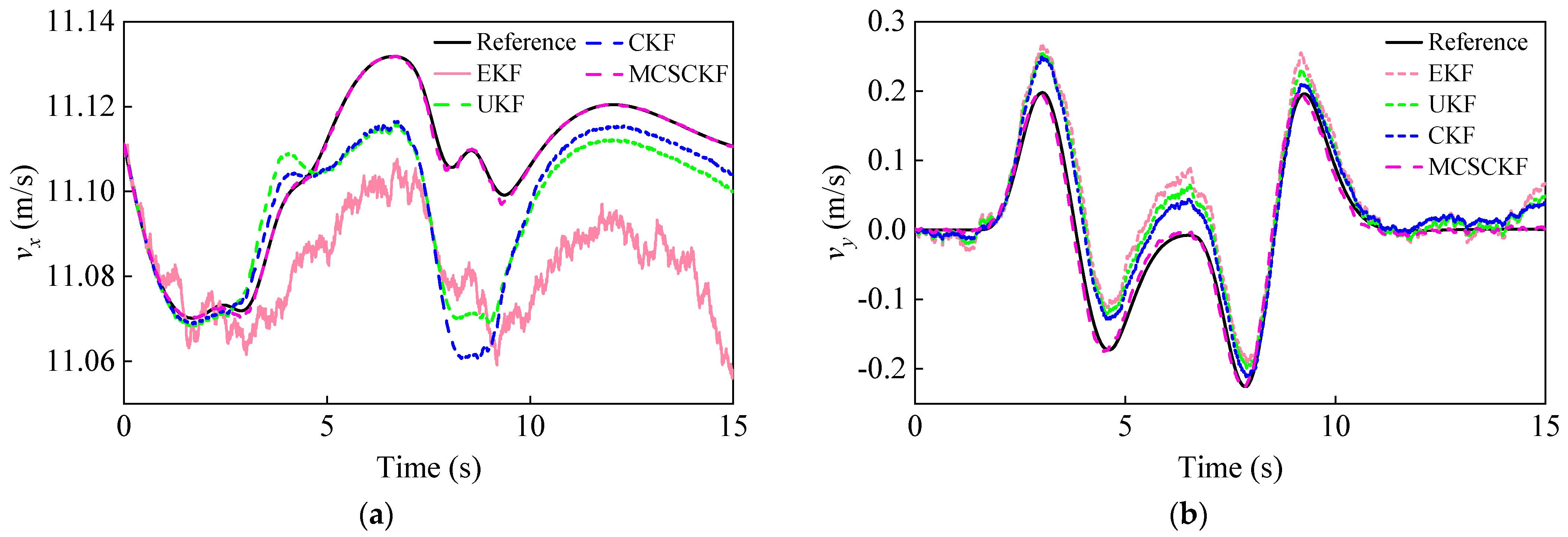
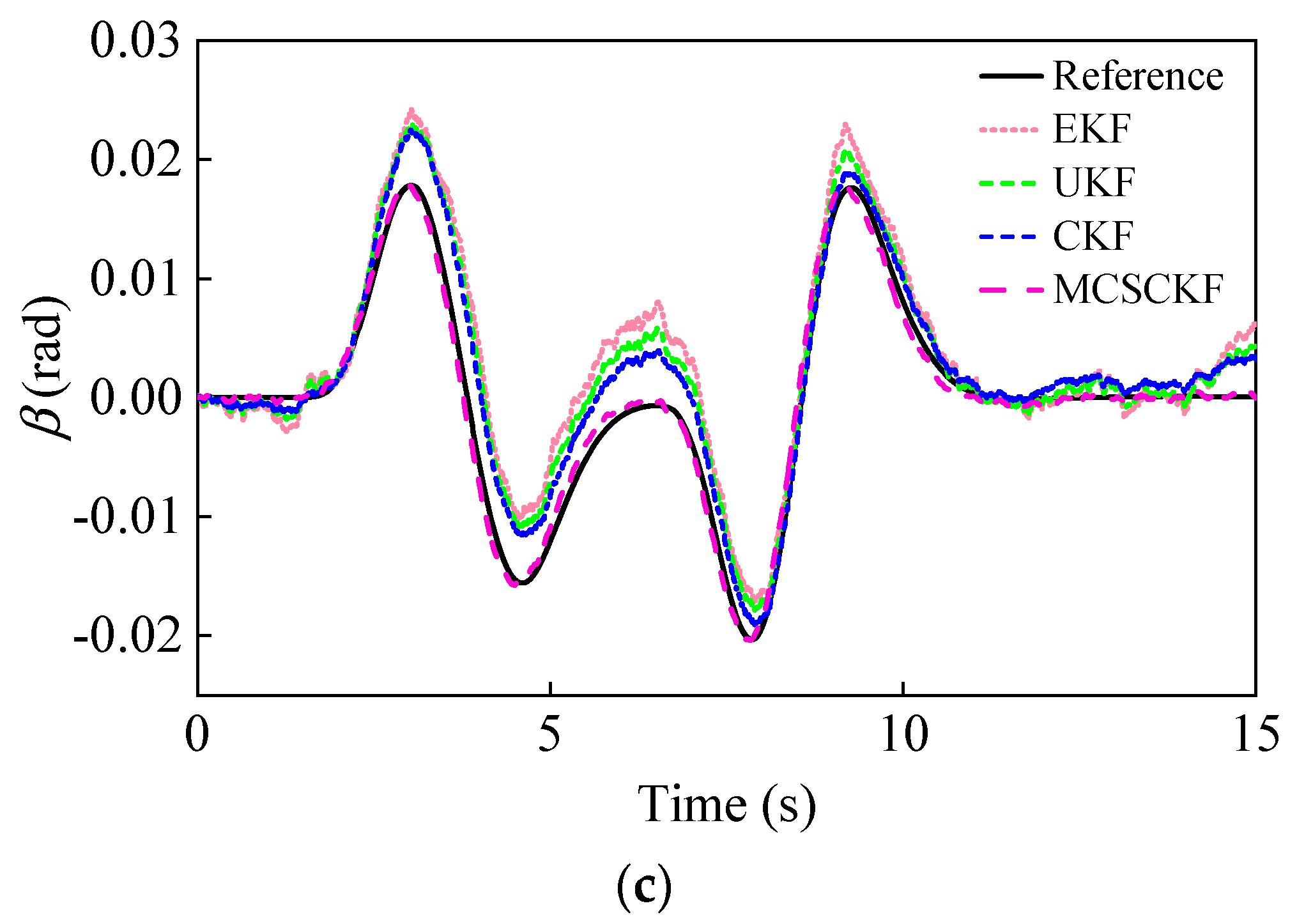
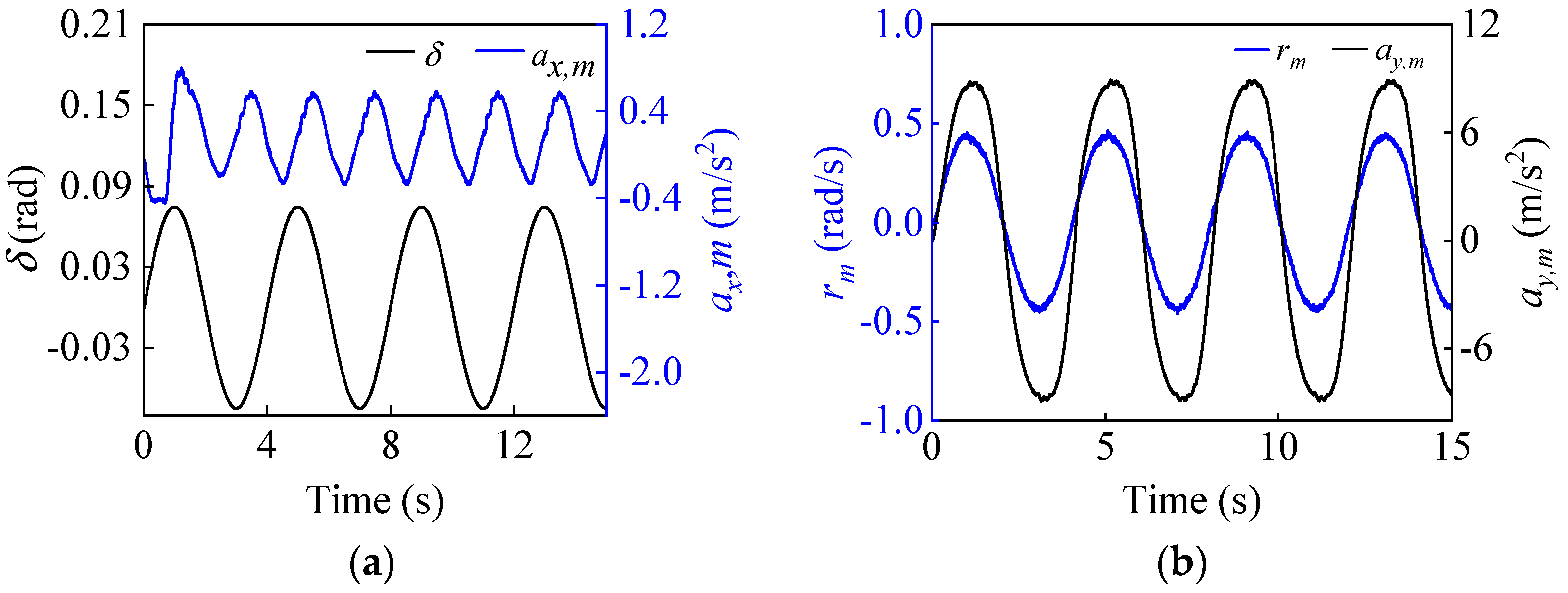
4.2.1. Double Lane Change Situation
4.2.2. Sinusoidal Steering Condition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, X.; Wang, Z.; Zhang, L.; Wang, C. Longitudinal vehicle speed estimation for four-wheel-independently-actuated electric vehicles based on multi-sensor fusion. IEEE Trans. Veh. Technol. 2020, 69, 12797–12806. [Google Scholar] [CrossRef]
- Han, K.; Choi, M.; Lee, B.; Choi, S.B. Development of a traction control system using a special type of sliding mode controller for hybrid 4WD vehicles. IEEE Trans. Veh. Technol. 2017, 67, 264–274. [Google Scholar] [CrossRef]
- Wang, Y.; Geng, K.; Xu, L.; Ren, Y.; Dong, H.; Yin, G. Estimation of sideslip angle and tire cornering stiffness using fuzzy adaptive robust cubature Kalman filter. IEEE Trans. Syst. Man Cybern. A 2020, 52, 1451–1462. [Google Scholar] [CrossRef]
- Park, G. Vehicle Sideslip Angle Estimation Based on Interacting Multiple Model Kalman Filter Using Low-Cost Sensor Fusion. IEEE Trans. Veh. Technol. 2022, 71, 6088–6099. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Yan, B.; Liu, C.; Wang, X.; Fang, J. Simultaneous estimation of tire side-slip angle and lateral tire force for vehicle lateral stability control. Mech. Syst. Signal Process. 2019, 132, 168–182. [Google Scholar] [CrossRef]
- Viehweger, M.; Vaseur, C.; van Aalst, S.; Acosta, M.; Regolin, E.; Alatorre, A.; Desmet, W.; Naets, F.; Ivanov, V.; Ferrara, A.; et al. Vehicle state and tyre force estimation: Demonstrations and guidelines. Veh. Syst. Dyn. 2021, 59, 675–702. [Google Scholar] [CrossRef]
- Singh, K.B.; Arat, M.A.; Taheri, S. Literature review and fundamental approaches for vehicle and tire state estimation. Veh. Syst. Dyn. 2019, 57, 1643–1665. [Google Scholar] [CrossRef]
- Jin, X.; Yin, G. Estimation of lateral tire–road forces and sideslip angle for electric vehicles using interacting multiple model filter approach. J. Frankl. Inst. 2015, 352, 686–707. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Chen, J. Fusion algorithm design based on adaptive SCKF and integral correction for side-slip angle observation. IEEE Trans. Industr. Electr. 2017, 65, 5754–5763. [Google Scholar] [CrossRef]
- Wan, W.; Feng, J.; Song, B.; Li, X. Vehicle state estimation using interacting multiple model based on square root cubature Kalman filter. Appi. Sci. 2021, 11, 10772. [Google Scholar]
- Wilkin, M.A.; Manning, W.J.; Crolla, D.A.; Levesley, M.C. Use of an extended Kalman filter as a robust tyre force estimator. Veh. Syst. Dyn. 2006, 44, 50–59. [Google Scholar] [CrossRef]
- Doumiati, M.; Victorino, A.C.; Charara, A.; Lechner, D. Onboard real-time estimation of vehicle lateral tire–road forces and sideslip angle. IEEE/ASME Trans. Mech. 2010, 16, 601–614. [Google Scholar] [CrossRef]
- Rezaeian, A.; Zarringhalam, R.; Fallah, S.; Melek, W.; Khajepour, A.; Chen, S.K.; Moshchuck, N.; Litkouhi, B. Novel tire force estimation strategy for real-time implementation on vehicle applications. IEEE Trans. Veh. Technol. 2014, 64, 2231–2241. [Google Scholar] [CrossRef]
- Rath, J.J.; Veluvolu, K.C.; Defoort, M.; Soh, Y.C. Higher-order sliding mode observer for estimation of tyre friction in ground vehicles. IET Control Theory Appl. 2014, 8, 399–408. [Google Scholar] [CrossRef]
- Acosta, M.; Kanarachos, S. Tire lateral force estimation and grip potential identification using Neural Networks, Extended Kalman Filter, and Recursive Least Squares. Neural Comput. Appl. 2018, 30, 3445–3465. [Google Scholar] [CrossRef]
- Guo, H.; Cao, D.; Chen, H.; Lv, C.; Wang, H.; Yang, S. Vehicle dynamic state estimation: State of the art schemes and perspectives. IEEE/CAA J. Autom. Sin. 2018, 5, 418–431. [Google Scholar] [CrossRef]
- Li, L.; Jia, G.; Ran, X.; Song, J.; Wu, K. A variable structure extended Kalman filter for vehicle sideslip angle estimation on a low friction road. Veh. Syst. Dyn. 2014, 52, 280–308. [Google Scholar] [CrossRef]
- Chen, Z.; Duan, Y.; Zhang, Y. Automated Vehicle Path Planning and Trajectory Tracking Control Based on Unscented Kalman Filter Vehicle State Observer; No. 2021-01-0337; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Vargas-Meléndez, L.; Boada, B.L.; Boada, M.J.L.; Gauchía, A.; Díaz, V. A sensor fusion method based on an integrated neural network and Kalman filter for vehicle roll angle estimation. Sensors 2016, 16, 1400. [Google Scholar] [CrossRef]
- Pryseley, A.; Tchonlafi, C.; Verbeke, G.; Molenberghs, G. Estimating negative variance components from Gaussian and non-Gaussian data: A mixed models approach. Comput. Stat. Data An. 2011, 55, 1071–1085. [Google Scholar] [CrossRef]
- Mohseni, H.R.; Kringelbach, M.L.; Woolrich, M.W.; Baker, A.; Aziz, T.Z.; Probert-Smith, P. Non-Gaussian probabilistic MEG source localisation based on kernel density estimation. NeuroImage 2014, 87, 444–464. [Google Scholar] [CrossRef]
- Xiao, Z.; Xiao, D.; Havyarimana, V.; Jiang, H.; Liu, D.; Wang, D.; Zeng, F. Toward accurate vehicle state estimation under non-Gaussian noises. IEEE Internet Things 2019, 6, 10652–10664. [Google Scholar] [CrossRef]
- Wan, W.; Feng, J.; Song, B.; Li, X. Huber-based robust unscented Kalman filter distributed drive electric vehicle state observation. Energies 2021, 14, 750. [Google Scholar] [CrossRef]
- Liu, X.; Ren, Z.; Lyu, H.; Jiang, Z.; Ren, P.; Chen, B. Linear and nonlinear regression-based maximum correntropy extended Kalman filtering. IEEE Trans. Syst. Man Cybern. A 2019, 51, 3093–3102. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Zhang, J.; Razzaqi, A.A. Maximum correntropy delay Kalman filter for SINS/USBL integrated navigation. ISA Trans. 2021, 117, 274–287. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Chen, X.; Xu, Y.; Liu, X.; Shi, C. Maximum correntropy generalized high-degree cubature Kalman filter with application to the attitude determination system of missile. Aerosp. Sci. Technol. 2019, 95, 105441. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P. Maximum correntropy square-root cubature Kalman filter with application to SINS/GPS integrated systems. ISA Trans. 2018, 80, 195–202. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Chen, L.; Jiang, H.; Cai, Y.; Li, Y. Estimation of longitudinal force, lateral vehicle speed and yaw rate for four-wheel independent driven electric vehicles. Mech. Syst. Signal Process. 2018, 101, 377–388. [Google Scholar] [CrossRef]
- Naets, F.; van Aalst, S.; Boulkroune, B.; El Ghouti, N.; Desmet, W. Design and experimental validation of a stable two-stage estimator for automotive sideslip angle and tire parameters. IEEE Trans. Veh. Technol. 2017, 66, 9727–9742. [Google Scholar] [CrossRef]
- Yan, X.; Edwards, C. Nonlinear robust fault reconstruction and estimation using a sliding mode observer. Automatica 2007, 43, 1605–1614. [Google Scholar] [CrossRef]
- Song, R.; Fang, Y. Vehicle state estimation for INS/GPS aided by sensors fusion and SCKF-based algorithm. Mech. Syst. Signal Process. 2021, 150, 107315. [Google Scholar] [CrossRef]
- Qi, D.; Feng, J.; Wan, W.; Song, B. A novel maximum correntropy adaptive extended Kalman filter for vehicle state estimation under non-Gaussian noise. Meas. Sci. Technol. 2022, 34, 025114. [Google Scholar] [CrossRef]



| Vehicle Parameter | Value | Unit |
|---|---|---|
| Sprung mass () | 1270 | kg |
| Unsprung mass () | 142 | kg |
| Vehicle mass () | 1412 | kg |
| Yaw moment of inertia () | 1536.7 | kg·m2 |
| Distance from the front and rear axles to the CG () | 1.015/1.895 | m |
| The wheelbase of the front and rear wheels () | 1.675/1.675 | m |
| The effective rolling radius of the tire () | 0.325 | m |
| Height of CG () | 0.54 | m |
| Sensor Parameter | ||
| Type of Sensor | Standard Deviation () | |
| Value | Unit | |
| INS (Inertial Navigation System) sensor (100 Hz) | ||
| Yaw rate gyroscope | deg/s | |
| Longitudinal accelerometer | m/s2 | |
| Lateral accelerometer | m/s2 | |
| CAN bus (50 Hz) | ||
| Steering wheel sensor | deg | |
| Wheel speed sensor | m/s | |
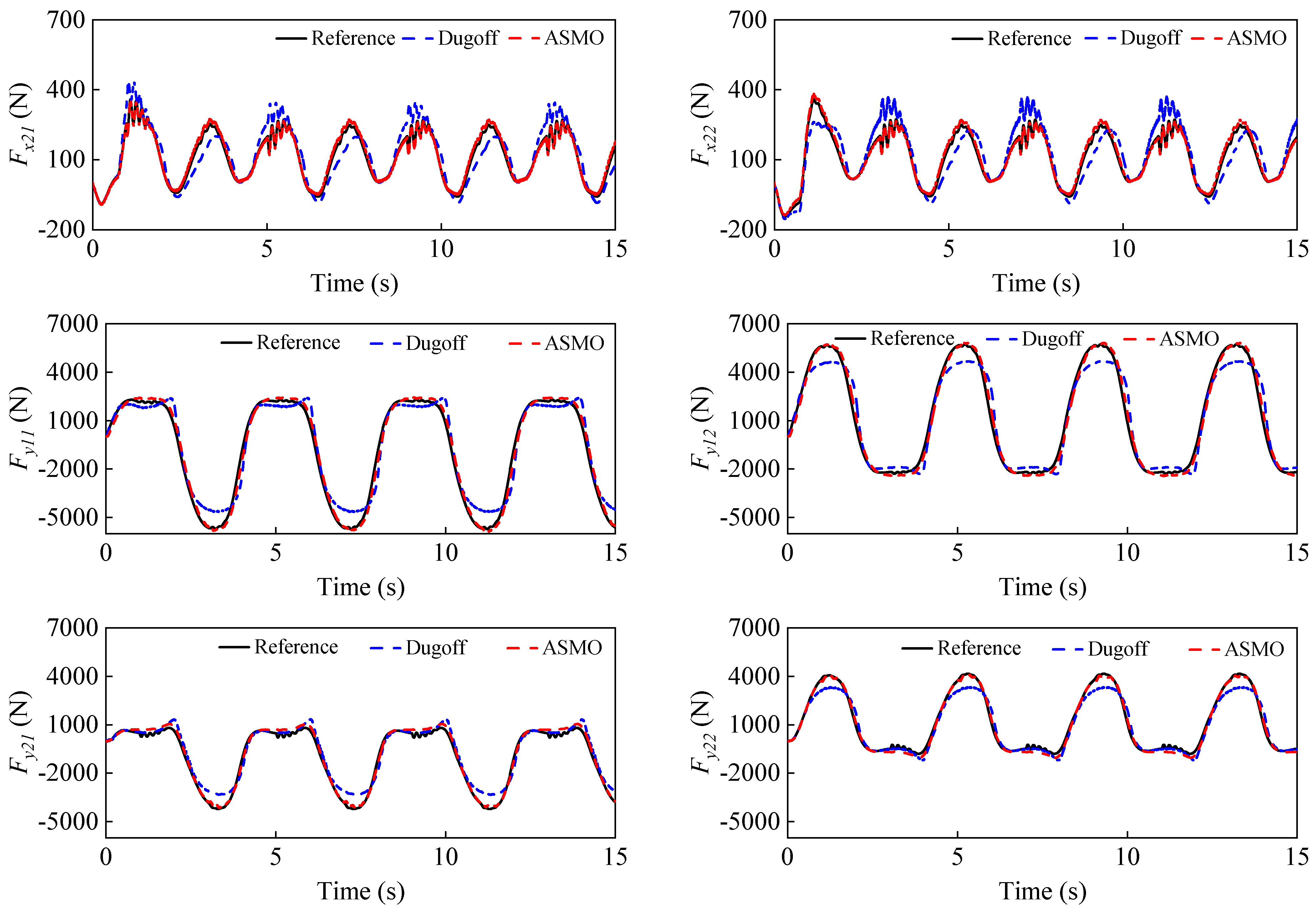
| Method | Tire Force | Fx11 | Fx12 | Fx21 | Fx22 | Fy11 | Fy12 | Fy21 | Fy22 |
|---|---|---|---|---|---|---|---|---|---|
| System Maximum Values (N) | 7.3 | 8.7 | 16.5 | 17.6 | 828.1 | 956.3 | 390.1 | 512.4 | |
| Dugoff | RMSE (N) | 3.34 | 3.10 | 1.57 | 1.77 | 17.30 | 19.17 | 11.35 | 14.61 |
| Percentage Errors (%) | 45.8 | 35.6 | 9.5 | 10.1 | 2.1 | 2.0 | 2.9 | 2.9 | |
| ASMO | RMSE | 0.98 | 0.92 | 0.86 | 0.81 | 10.75 | 11.42 | 8.90 | 9.23 |
| Percentage Errors (%) | 13.4 | 10.6 | 5.2 | 4.6 | 1.3 | 1.2 | 2.3 | 1.8 | |
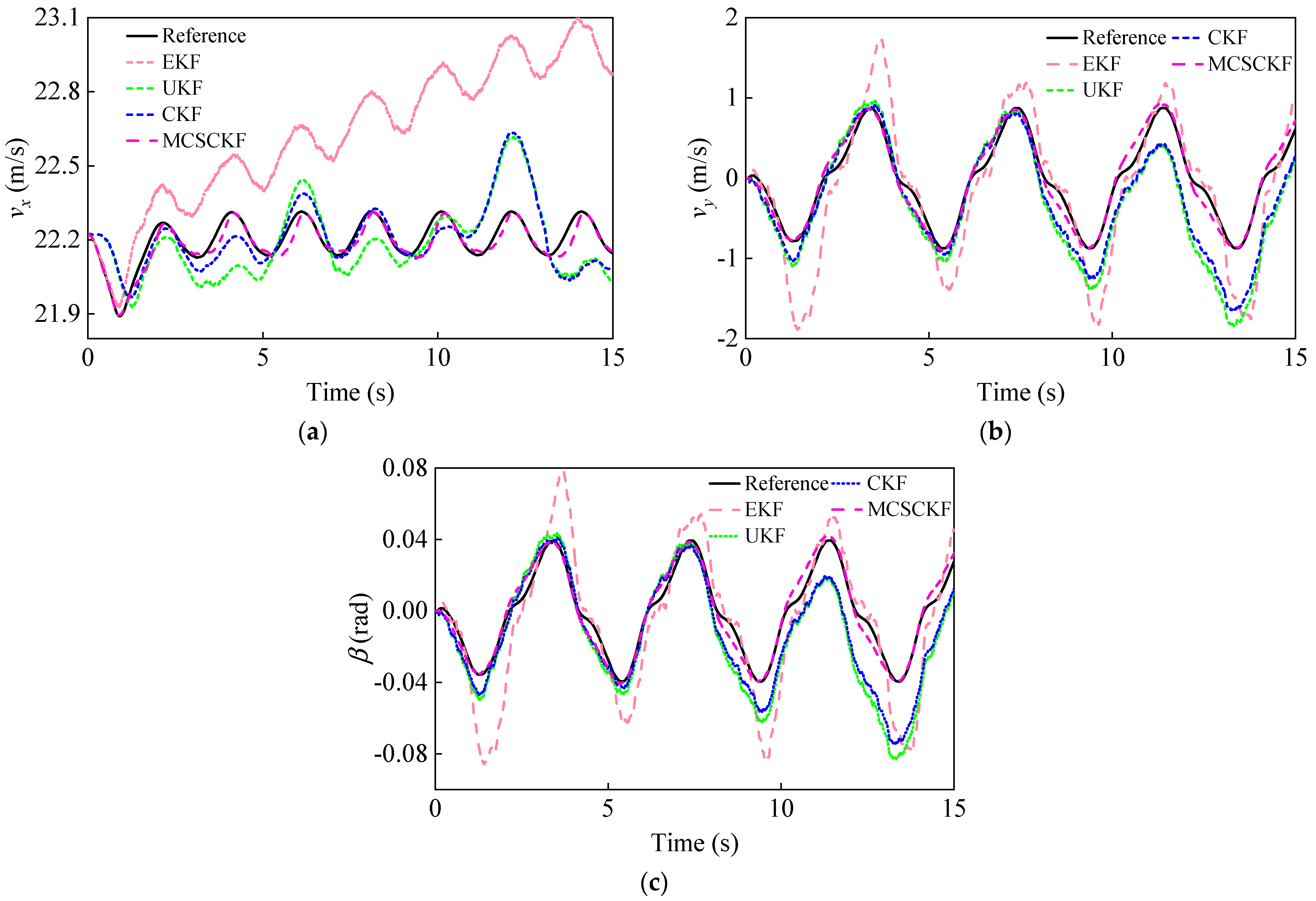
| Filter | (m/s) | (m/s) | (rad) | |
|---|---|---|---|---|
| System Maximum Values | 11.13 | 0.20 | 0.0179 | |
| EKF | RMSE | 0.0353 | 0.0447 | 0.0040 |
| Percentage Errors (%) | 0.32 | 22.4 | 22.3 | |
| UKF | RMSE | 0.0140 | 0.0345 | 0.0031 |
| Percentage Errors (%) | 0.13 | 17.2 | 17.3 | |
| CKF | RMSE | 0.0142 | 0.0277 | 0.0025 |
| Percentage Errors (%) | 0.13 | 13.9 | 14.0 | |
| MCSCKF | RMSE | 0.0015 | 0.0092 | 0.0008 |
| Percentage Errors (%) | 0.01 | 4.6 | 4.5 |
| Filter | Average Iteration Number | Maximum Iteration Number | Minimum Iteration Number |
|---|---|---|---|
| MCSCKF | 2.0218 | 3 | 1 |
| Method | Tire Force | Fx11 | Fx12 | Fx21 | Fx22 | Fy11 | Fy12 | Fy21 | Fy22 |
|---|---|---|---|---|---|---|---|---|---|
| System Maximum Values (N) | 587.6 | 511.8 | 358.4 | 358.3 | 2303.0 | 5730.5 | 801.0 | 4162.6 | |
| Dugoff | RMSE (N) | 90.41 | 79.87 | 54.11 | 58.67 | 686.73 | 728.52 | 431.74 | 420.31 |
| Percentage Errors (%) | 15.4 | 15.6 | 15.1 | 16.4 | 29.9 | 12.7 | 54.0 | 10.1 | |
| ASMO | RMSE | 13.40 | 15.04 | 12.07 | 12.83 | 312.95 | 317.89 | 194.06 | 172.42 |
| Percentage Errors (%) | 2.3 | 2.9 | 3.4 | 3.6 | 13.6 | 5.5 | 24.2 | 4.1 | |
| Filter | (m/s) | (m/s) | (rad) | |
|---|---|---|---|---|
| System Maximum Values | 23.31 | 0.87 | 0.0394 | |
| EKF | RMSE | 0.4931 | 0.4781 | 0.0216 |
| Percentage Errors (%) | 2.1 | 55.0 | 54.8 | |
| UKF | RMSE | 0.1372 | 0.4428 | 0.0199 |
| Percentage Errors (%) | 0.59 | 51.0 | 50.5 | |
| CKF | RMSE | 0.1202 | 0.3685 | 0.0166 |
| Percentage Errors (%) | 0.52 | 42.4 | 42.1 | |
| MCSCKF | RMSE | 0.0314 | 0.1047 | 0.0047 |
| Percentage Errors (%) | 0.13 | 12.0 | 11.9 |
| Filter | Average Iteration Number | Maximum Iteration Number | Minimum Iteration Number |
|---|---|---|---|
| MCSCKF | 2.2115 | 4 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, D.; Feng, J.; Li, Y.; Wang, L.; Song, B. A Robust Hierarchical Estimation Scheme for Vehicle State Based on Maximum Correntropy Square-Root Cubature Kalman Filter. Entropy 2023, 25, 453. https://doi.org/10.3390/e25030453
Qi D, Feng J, Li Y, Wang L, Song B. A Robust Hierarchical Estimation Scheme for Vehicle State Based on Maximum Correntropy Square-Root Cubature Kalman Filter. Entropy. 2023; 25(3):453. https://doi.org/10.3390/e25030453
Chicago/Turabian StyleQi, Dengliang, Jingan Feng, Yongbin Li, Lei Wang, and Bao Song. 2023. "A Robust Hierarchical Estimation Scheme for Vehicle State Based on Maximum Correntropy Square-Root Cubature Kalman Filter" Entropy 25, no. 3: 453. https://doi.org/10.3390/e25030453
APA StyleQi, D., Feng, J., Li, Y., Wang, L., & Song, B. (2023). A Robust Hierarchical Estimation Scheme for Vehicle State Based on Maximum Correntropy Square-Root Cubature Kalman Filter. Entropy, 25(3), 453. https://doi.org/10.3390/e25030453






